2020版江苏高考数学名师大讲坛一轮复习教程学案:第38课__基本不等式及其简单应用(2) 含解析
江苏省苏州市第五中学2020届高考数学 专题讲练三 基本不等式及应用(无答案)
高三数学专题讲座之三 基本不等式及应用命题趋势与复习策略:基本不等式作为高考C 级知识点,是每年高考必考的一个重要知识点,但它主要作为工具来用,而且主要用于求一些最值问题。
使用基本不等式时,务必要注意看清基本不等式成立的条件是否具备?尤其是要看清等号能否成立?在解答题中使用时,必须要交代等号成立的条件(即说明何时取等号)。
对于一些复杂的问题,使用基本不等式时往往要做以下一些工作:(1)分类讨论;(2)等价变形(目标可以使用基本不等式);(3)消元化归等。
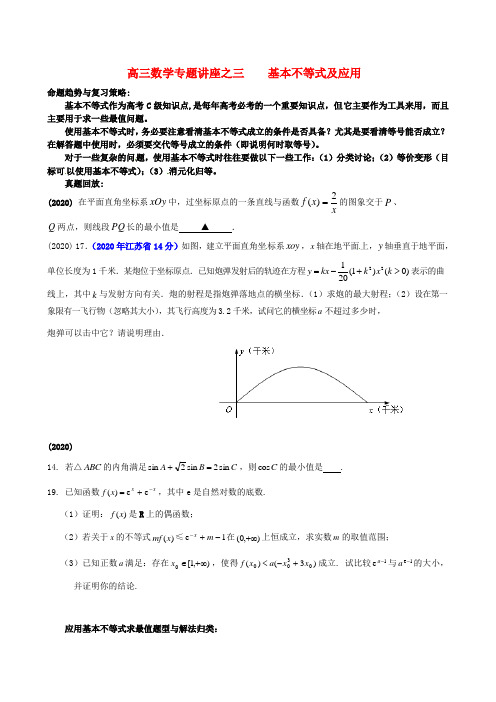
真题回放:(2020) 在平面直角坐标系xOy 中,过坐标原点的一条直线与函数x x f 2)(=的图象交于P 、 Q 两点,则线段PQ 长的最小值是 ▲ .(2020) 17.(2020年江苏省14分)如图,建立平面直角坐标系xoy ,x 轴在地平面上,y 轴垂直于地平面,单位长度为1千米.某炮位于坐标原点.已知炮弹发射后的轨迹在方程221(1)(0)20y kx k x k =-+>表示的曲线上,其中k 与发射方向有关.炮的射程是指炮弹落地点的横坐标.(1)求炮的最大射程;(2)设在第一象限有一飞行物(忽略其大小),其飞行高度为3.2千米,试问它的横坐标a 不超过多少时,炮弹可以击中它?请说明理由.(2020)14. 若△ABC 的内角满足C B A sin 2sin 2sin =+,则C cos 的最小值是 .19. 已知函数x x x f -+=e e )(,其中e 是自然对数的底数.(1)证明:)(x f 是R 上的偶函数;(2)若关于x 的不等式)(x mf ≤1e -+-m x 在),0(+∞上恒成立,求实数m 的取值范围;(3)已知正数a 满足:存在),1[0+∞∈x ,使得)3()(0300x x a x f +-<成立. 试比较1e -a 与1e -a 的大小,并证明你的结论.应用基本不等式求最值题型与解法归类:1.已知12x <,则函数242121x x y x -+=-的最大值是________ 同步练:函数()2225x y x x +=>-+的最小值等于________ 2.双曲线()222211,1x y a b a b -=≥≥的离心率为2,则213b a+的最小值为________ 3.若,,,x a b y 成等差数列,,,,x c d y 成等比数列,则的()2a b cd+取值范围是______4.已知正实数,x y 满足24xy x y ++=,则x y +的最小值是________5.若0,0a b >>,且11121a b b +=++,则2a b +的最小值为_____________6.设,x y 为实数,若2241x y xy ++=,则2x y +的最大值是_______________同步练:设实数,x y 满足2210x xy --=,则x y -的取值范围是_______________7.若三角形的三个内角的弧度数分别为,,αβγ,则41αβγ++的最小值是_____________ 8.设2,0a b b +=>,则12a a b+的最小值等于______________ 同步练:设正实数,,x y z 满足21x y z ++=,则()41x y x y y z ++++的最小值是_________ 9.若0a b >>,则()211a ab a a b ++-的最小值等于______________ 10.若,,0a b c >,且()423a a b c bc +++=-2a b c ++的最小值为______11.已知关于x 的一元二次不等式20ax bx c ++≥()a b <的解集为R ,则24a b c M b a++=-的最小值是________________同步练:已知关于x 的一元二次不等式220ax x b ++>的解集是1|x x a ⎧⎫≠-⎨⎬⎩⎭,则()227a b a b a b ++>- 的最小值等于________12.在ABC ∆中,分,,a b c 别是角,,A B C 的对边,且sin sin cos sin sin cos A B C B C A = sin sin cos C A B +,则2ab c 的最大值是______________应用基本不等式求最值的应用1.若对任意0,0x y >>,不等式()2x xy a x y +≤+恒成立,则实数a 的最小值是______.2.已知:x >y >0,且xy =1,若x 2+y 2≥a (x -y )恒成立,则实数a 的取值范围是_____.同步练:设102m <<,若1212k m m +≥-恒成立,则实数k 的最大值为______________3.若()42log 34log a b ab +=,则a b +的最小值是___________4.已知,x y 为正实数,且满足3x y xy ++=,若对任意满足条件的,x y ,都有不等式 ()()210x y a x y +-++≥恒成立,则实数a 的取值范围是__________。
2020版江苏高考数学名师大讲坛一轮复习教程学案:第35课__不等式的解法 Word版含解析

____第35课__不等式的解法____1. 理解一元二次不等式与相应的一元二次方程、二次函数之间的关系.2. 熟练掌握一元二次不等式的解法,善于运用数形结合解不等式.3. 能够利用同解变形解决分式不等式、高次不等式以及指对数不等式,逐步形成等价转化思想.4. 会解含参数的不等式,能够对参数进行分类讨论.1. 阅读:必修5第75~80页.2. 解悟:①二次函数图象、一元二次不等式的解与一元二次方程的解有怎样的内在联系?②阅读教材第80页第11题,体现了不等式怎样进行转化?3. 践习:在教材空白处,完成必修5第77页练习第4、5、6题.基础诊断1. 函数y =x 2+x -12的定义域是解析:由x 2+x -12≥0,解得x ≤-(-∞,-4]∪[3,+∞).2. 不等式2x 2+2x -4≤12的解集为__[-3,1]__. 解析:因为2x 2+2x -4≤12,所以2x 2+2x -4≤2-1,所以x 2+2x -4≤-1,x 2+2x -3≤0,解得-3≤x ≤1,所以原不等式的解集为[-3,1].3. 不等式x -12x +1≤0的解集为__⎝⎛⎦⎤-12,1__. 解析:因为x -12x +1≤0,所以⎩⎪⎨⎪⎧x -1≥0,2x +1<0或⎩⎪⎨⎪⎧x -1≤0,2x +1>0,解得-12<x ≤1,则原不等式的解集为⎝⎛⎦⎤-12,1. 4. 若二次不等式ax 2+bx +1>0的解集为⎩⎨⎧⎭⎬⎫x|-1<x<13,则a =__-3__,b =__-2__. 解析:因为一元二次不等式ax 2+bx +1>0的解集为⎩⎨⎧⎭⎬⎫x|-1<x<13,所以方程ax 2+bx +1=0的解为-1和13,所以⎩⎪⎨⎪⎧a -b +1=0,19a +13b +1=0,解得⎩⎪⎨⎪⎧a =-3,b =-2. 范例导航 考向❶ 解不等式例1 解下列关于x 的不等式:(1) 2x 2+4x +5>0;(2) x 2-2ax -3a 2<0(a<0);(3) x -2x +3≤2. 解析:(1) 因为Δ=42-4×2×5=-24<0,所以方程2x 2+4x +5=0没有实数根,所以不等式2x 2+4x +5>0恒成立,所以不等式2x 2+4x +5>0的解集为R.(2) 因为x 2-2ax -3a 2=0,所以x 1=3a ,x 2=-a .又因为a <0,所以不等式解集为{x |3a <x <-a }.(3) 原不等式化为x -2x +3-2≤0,即-x -8x +3≤0,即x +8x +3≥0,等价于(x +3)(x +8)≥0,且x ≠-3,所以原不等式解集为{x |x ≤-8或x >-3}.解关于x 的不等式:ax 2-(a +1)x +1<0.解析:当a =0时,不等式为-x +1<0,所以不等式解集为(1,+∞);当a ≠0时,原不等式化为a (x -1)·⎝⎛⎭⎫x -1a <0. ①当a <0时,1a <0<1,不等式为(x -1)(x -1a )>0,其解集为⎩⎨⎧⎭⎬⎫x |x <1a 或x >1. ②当0<a <1时,1a >1,不等式为(x -1)(x -1a )<0,其解集为{x |1<x <1a}. ③当a =1时,不等式为(x -1)(x -1)<0,其解集为∅.④当a >1时,1a <1,不等式为(x -1)(x -1a )<0,其解集为{x |1a<x <1}. 考向❷ 一元二次不等式的恒成立问题例2 设函数f(x)=mx 2-mx -1.(1) 若关于x 的不等式f(x)<0的解集为R ,求实数m 的取值范围;(2) 若对于x ∈[1,3], f (x )<-m +5恒成立,求实数m 的取值范围.解析:(1) ①当m =0时,f (x )<0,即为-1<0,其解集为R ,符合题意;②当m ≠0时,f (x )<0恒成立,即为mx 2-mx -1<0恒成立,由⎩⎪⎨⎪⎧m <0,Δ=(-m )2-4m ·(-1)<0, 解得-4<m <0, 综上,所求m 的取值范围为(-4,0].(2) f (x )<-m +5在[1,3]上恒成立,即mx 2-mx -1<-m +5,化为mx 2-mx +m -6<0在[1,3]上恒成立.方法一:若m =0,不等式为-6<0,显然成立;若m <0,由二次函数g (x )=mx 2-mx +m -6=m (x -12)2+34m -6可知, g (x )在[1,3]上为减函数,所以g (x )max =g (1)=m -6,由m -6<0得m <6,故m <0时,f (x )<-m +5在[1,3]上恒成立;若m >0,由二次函数g (x )=mx 2-mx +m -6=m (x -12)2+34m -6可知, g (x )在[1,3]上为增函数,所以g (x )max =g (3)=7m -6,由7m -6<0得m <67, 故0<m <67时,f (x )<-m +5在[1,3]上恒成立. 综上,所求m 的取值范围为m <67. 方法二:若m =0,不等式为-6<0,显然成立;若m ≠0,因为x 2-x +1>0,所以将mx 2-mx +m <6化为m <6x 2-x +1. 令函数h (x )=6x 2-x +1=6⎝⎛⎭⎫x -122+34,由x ∈[1,3],得67≤h (x )≤6, 所以所求m 的取值范围为m <67.若不等式x 2-2x +5≥a 2-3a 对任意实数x 恒成立,则实数a 的取值范围为__[-1,4]__. 解析:令f (x )=x 2-2x +5=(x -1)2+4,所以f (x )min =4.若不等式x 2-2x +5≥a 2-3a 对任意实数x 恒成立,只需a 2-3a ≤4,解得-1≤a ≤4.考向❸ 一元二次不等式的应用例3 一个服装厂生产风衣,月销售量x(件)与售价p(元/件)之间的关系为p =160-2x ,生产x 件的成本R =500+30x(元).(1) 该厂月产量多大时,月利润不少于1 300元?(2) 当月产量为多少时,可获得最大利润,最大利润是多少?解析:(1) 由题意知月利润y =px -R ,所以y =(160-2x)x -(500+30x),即y =-2x 2+130x -500.由月利润不少于1 300元,得-2x 2+130x -500≥1 300,解得20≤x ≤45.故该厂月产量在20~45件时,月利润不少于1 300元.(2) 由(1)得y =-2x 2+130x -500=-2(x -652)2+3 2252, 由题意知,x 为正整数.故当x =32或33时,y 最大为1 612.所以当月产量为32或33件时,可获最大利润,最大利润为1 612元.某商场若将进货单价为8元/件的商品按每件10元出售,每天可销售100件,现准备采用提高售价,减少进货量的办法来增加利润,已知这种商品每件销售价提高1元,销售量就要减少10件.问该商场将销售价每件定为多少元时,才能使得每天所赚的利润最多?销售价每件定为多少元时,才能保证每天所赚的利润在300元以上?解析:设每件提高x 元(0≤x ≤10),即每件获利润(2+x)元,每天可销售(100-10x)件,设每天获得总利润为y 元,由题意有y =(2+x)(100-10x)=-10x 2+80x +200=-10(x -4)2+360,所以当x =4时,y max =360元,即当定价为每件14元时,每天所赚利润最多.要使每天利润在300元以上,则有-10x 2+80x +200>300,即x 2-8x +10<0,解得4-6<x<4+ 6.故每件定价在4-6元到4+6元之间时,能确保每天赚300元以上.自测反馈1. 已知函数f(x)=⎩⎪⎨⎪⎧x +2, x ≤0,-x +2, x>0, 则不等式f(x)≥x 2的解集为__[-1,1]__. 解析:当x ≤0时,f(x)=x +2,代入不等式得x +2≥x 2,即x 2-x -2≤0,解得-1≤x ≤2,所以原不等式的解集为[-1,0];当x>0时,f(x)=-x +2,代入不等式得-x +2≥x 2,即x 2+x -2≤0,解得-2≤x ≤1,所以原不等式的解集为(0,1].综上,不等式f(x)≥x 2的解集为[-1,1].2. 1<|x +2|<5的解集为__(-7,-3)∪(-1,3)__.解析:由1<|x +2|<5可得⎩⎪⎨⎪⎧1<|x +2|,|x +2|<5,所以不等式组的解集为{x|-7<x<-3或-1<x<3}. 3. 已知函数f(x)=(ax -1)(x +b),如果不等式f(x)>0的解集是(-1,3),那么不等式f(-2x)<0的解集是__⎝⎛⎭⎫-∞,-32∪⎝⎛⎭⎫12,+∞__. 解析:因为不等式f(x)>0的解集是(-1,3),所以(ax -1)(x +b)>0,所以(-ax +1)(x +b)<0,所以a =-1,b =-3,所以f(-2x)=[-(-2x)-1][(-2x)-3]<0,解得x>12或x<-32. 4. 当x ∈(1,2)时,不等式x 2+mx +4<0恒成立,则实数m 的取值范围是__(-∞,-5]__.解析:根据题意可构造函数f(x)=x 2+mx +4,x ∈(1,2).因为当x ∈(1,2)时,不等式x 2+mx +4<0恒成立,即⎩⎪⎨⎪⎧f (1)≤0,f (2)≤0,解得⎩⎪⎨⎪⎧m ≤-5,m ≤-4,即m ≤-5.综上,m 的取值范围为(-∞,-5].1. 不等式的解法,理清其步骤,体会等价转化、数形结合、分类讨论等各种数学方法.2. 解含参数不等式时,要根据参数的取值范围进行分类讨论.3. 你还有哪些体悟,写下来:。
专题09 基本不等式的应用(解析版)-2020年高考数学二轮专项提升(江苏)

专题09 基本不等式的应用1、【2019年高考江苏】在平面直角坐标系xOy 中,P 是曲线4(0)y x x x=+>上的一个动点,则点P 到直线x +y =0的距离的最小值是_____. 【答案】4. 【解析】设01(,)P x x,则4d ==≥2、【2019年高考天津卷文数】设0,0,24x y x y >>+=,则(1)(21)x y xy++的最小值为__________.【答案】92【解析】(1)(21)2212552x y xy y x xy xy xy xy xy++++++===+. 因为0,0,24x y x y >>+=,所以24x y +=≥,2,02xy ≤<≤,当且仅当22x y ==时取等号成立. 又因为519225=22xy +≥+⨯, 所以(1)(21)x y xy ++的最小值为92.3、【2019年高考浙江卷】若0,0a b >>,则“4a b +≤”是 “4ab ≤”的( )A . 充分不必要条件B . 必要不充分条件C . 充分必要条件D . 既不充分也不必要条件【答案】A【解析】当0, 0a >b >时,a b +≥当且仅当a b =时取等号,则当4a b +≤时,有4a b ≤+≤,解得4ab ≤,充分性成立;当=1, =4a b 时,满足4ab ≤,但此时=5>4a+b ,必要性不成立,综上所述,“4a b +≤”是“4ab ≤”的充分不必要条件.4、【2018年高考天津卷文数】(2018天津文科)已知,a b ∈R ,且360a b -+=,则128ab +的最小值为 . 【答案】14【解析】由a −3b +6=0可知a −3b =−6,且2a +18b =2a +2−3b ,因为对于任意x ,2x >0恒成立,结合基本不等式的结论可得:2a +2−3b ≥2×√2a ×2−3b =2×√2−6=14.当且仅当{2a =2−3ba −3b =6,即{a =3b =−1 时等号成立. 综上可得2a +18b 的最小值为14.【名师点睛】利用基本不等式求最值时,要灵活运用以下两个公式: ①22,,2a b a b ab ∈+≥R ,当且仅当a b =时取等号;②,a b +∈R ,a b +≥,当且仅当a b =时取等号.解题时要注意公式的适用条件、等号成立的条件,同时求最值时注意“1的妙用”.5、【2018年高考江苏卷】在ABC △中,角,,A B C 所对的边分别为,,a b c ,120ABC ∠=︒,ABC ∠的平分线交AC 于点D ,且1BD =,则4a c +的最小值为___________. 【答案】9【解析】由题意可知,S △ABC =S △ABD +S △BCD ,由角平分线性质和三角形面积公式得12acsin120°=12a ×1×sin60°+12c ×1×sin60°,化简得ac =a +c,1a+1c=1,因此4a +c =(4a +c )(1a +1c )=5+ca +4a c≥5+2√c a ⋅4a c=9,当且仅当c =2a =3时取等号,则4a +c 的最小值为9.6、【2017年高考江苏卷】某公司一年购买某种货物600吨,每次购买x 吨,运费为6万元/次,一年的总存储费用为4x 万元.要使一年的总运费与总存储费用之和最小,则x 的值是___________. 【答案】30【解析】总费用为600900464()4240x x x x+⨯=+≥⨯=,当且仅当900x x =,即30x =时等号成立.一、三个不等式关系:(1)a ,b ∈R ,a 2+b 2≥2ab ,当且仅当a =b 时取等号. (2)a ,b ∈R +,a +b ≥2ab ,当且仅当a =b 时取等号. (3)a ,b ∈R ,a 2+b 22≤(a +b 2)2,当且仅当a =b 时取等号.上述三个不等关系揭示了a 2+b 2 ,ab ,a +b 三者间的不等关系.其中,基本不等式及其变形:a ,b ∈R +,a +b ≥2ab (或ab ≤(a +b 2)2),当且仅当a =b 时取等号,所以当和为定值时,可求积的最值;当积为定值是,可求和的最值. 二、.算术平均数与几何平均数 设a >0,b >0,则a ,b 的算术平均数为a +b2,几何平均数为ab ,基本不等式可叙述为两个正数的算术平均数不小于它们的几何平均数. 三、.利用基本不等式求最值问题 已知x >0,y >0,则(1)如果积xy 是定值p ,那么当且仅当x =y 时,x +y 有最小值是2p .(简记:积定和最小) (2)如果和x +y 是定值p ,那么当且仅当x =y 时,xy 有最大值是p 24.(简记:和定积最大)四、对于f (x )=x +ax ,当a ≤0时,f (x )在(-∞,0),(0,+∞)为增函数;当a >0时,f (x )在(-∞,a ),(a ,+∞)为增函数;在(-a ,0),(0,a )为减函数. 注意 在解答题中利用函数f (x )=x +ax 的单调性时,需要利用导数进行证明.五、利用基本不等式解决条件最值的关键是构造和为定值或积为定值,主要有两种思路:(1)对条件使用基本不等式,建立所求目标函数的不等式求解.常用的方法有:拆项法、变系数法、凑因子法、换元法、整体代换法等.(2)条件变形,进行“1”的代换求目标函数最值.在利用基本不等式求最值时,要特别注意“拆、拼、凑”等技巧,使其满足基本不等式中“正”(即条件要求中字母为正数)、“定”(不等式的另一边必须为定值)、“等”(等号取得的条件)的条件才能应用,否则会出现错误.六、对于多元问题的不等式的基本解题思路就是把多元问题转化为单元问题。
高考一轮复习基本不等式

考点自测
1.(2013·株洲联考)“a>0 且 b>0”是“a+2 b≥ ab”成立的(
).
A.充分不必要条件 B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
2.已知 a,b∈(0,1),且 a≠b,下列各式中最大的是( ).
A.a2+b2 B.2 ab C.2ab D.a+b
3.若 lg x+lg y=2,则1x+1y的最小值是( ).A.210 B.15 C.12 D.2
(2)等号成立的条件:当且仅当___a_=___b___时取等号.
(3)其中a+2 b称为正数 a,b 的_算__术__平__均__数__, ab称为正数 a,b 的_几 ___何__平__均__数_.
2.基本不等式的变形
(1)重要不等式:a2+b2≥___2_a_b__ (a,b∈R).当且仅当 a=b 时取等号.
高考一轮复习基本不等式
抓住3个考点
基本不等式: a b ≤
a
2
b
基本不等式的变形
利用基本不等式求最值
单击标题可完成对应小部 分的学习,每小部分独立 成块,可全讲,也可选讲
助学微博
考点自测
突破3个考向
考向一 利用基本不等式求最值 【例1】 【训练1】
考向二 利用基本不等式证明不 等式
【例2】 【训练2】
结果
AD B C 1
答案显示
考向一 利用基本不等式求最值
【审题视点 】
【例 1】►(1)已知 x,y∈R+,且满足x3+4y=1,则 xy 的最
(1) 直 接 利 用 基 本 不等式求解;
大值为________.
(2) 先 变 形 再 利 用
(2)若函数 f(x)=x+x-1 2(x>2)在 x=a 处取最小值,
2020届高三文理科数学一轮复习《基本不等式》专题汇编(学生版)

《基本不等式》专题一、相关知识点1.基本不等式:ab ≤a +b2(1)基本不等式成立的条件:a >0,b >0.(2)等号成立的条件:当且仅当a =b 时取等号. 2.几个重要的不等式(1)a 2+b 2≥2ab (a ,b ∈R); (2)a +b ≥2ab (a >0,b >0).(3)b a +ab ≥2(a ,b 同号且不为零); (4)ab ≤⎝⎛⎭⎫a +b 22(a ,b ∈R);(5)⎝⎛⎭⎫a +b 22≤a 2+b 22(a ,b ∈R).2(a 2+b 2)≥(a +b )2(a ,b ∈R).(6)a 2+b 22≥(a +b )24≥ab (a ,b ∈R).(7)a 2+b 22≥a +b 2≥ab ≥21a +1b(a >0,b >0). 以上不等式等号成立的条件均为a =b . 3.算术平均数与几何平均数设a >0,b >0,则a ,b 的算术平均数为a +b2,几何平均数为ab ,基本不等式可叙述为:两个正数的算术平均数不小于它们的几何平均数. 4.利用基本不等式求最值问题 已知x >0,y >0,则:(1)如果积xy 是定值p ,那么当且仅当x =y 时,x +y 有最小值是2p .(简记:积定和最小) (2)如果和x +y 是定值p ,那么当且仅当x =y 时,xy 有最大值是p 24.(简记:和定积最大)5.重要不等式链 若a ≥b >0,则a ≥a 2+b 22≥a +b 2≥ab ≥2aba +b≥b . 题型一 基本不等式的判断1.若a ,b ∈R ,则下列恒成立的不等式是( )A.|a +b |2≥|ab | B .b a +ab ≥2 C.a 2+b 22≥⎝⎛⎭⎫a +b 22 D .(a +b )⎝⎛⎭⎫1a +1b ≥4 2.若a ,b ∈R ,且ab >0,则下列不等式中,恒成立的是( )A .a 2+b 2>2abB .a +b ≥2abC .1a +1b >2abD .b a +ab ≥23.下列命题中正确的是( )A .函数y =x +1x 的最小值为2 B .函数y =x 2+3x 2+2的最小值为2C .函数y =2-3x -4x (x >0)的最小值为2-4 3D .函数y =2-3x -4x(x >0)的最大值为2-4 34.若a >b >1,P =lg a ·lg b ,Q =12(lg a +lg b ),R =lg ⎝⎛⎭⎫a +b 2,则( )A .R <P <QB .Q <P <RC .P <Q <RD .P <R <Q题型二 利用基本不等式求最值类型一 直接法或配凑法利用基本不等式求最值1.若实数x ,y 满足xy =1,则x 2+2y 2的最小值为________.2.已知a >0,b >0,且2a +b =4,则1ab 的最小值为3.已知0<x <1,则x (3-3x )取得最大值时x 的值为4.已知x <0,则函数y =4x +x 的最大值是5.函数f (x )=xx +1的最大值为6.若x >1,则x +4x -1的最小值为________.7.设0<x <2,则函数y =x (4-2x )的最大值为________.8.若x ,y 均为正数,则3x y +12yx +13的最小值是9.已知a ,b ∈R ,且a -3b +6=0,则2a +18b 的最小值为________.10.已知x <54,则f (x )=4x -2+14x -5的最大值为________.11.设x >0,则函数y =x +22x +1-32的最小值为12.已知x ,y 为正实数,则4x x +3y +3yx的最小值为13.函数y =x 2+2x -1(x >1)的最小值为________.14.已知a >0,b >0,a ,b 的等比中项是1,且m =b +1a ,n =a +1b ,则m +n 的最小值是15.已知x ,y 都为正实数,且x +y +1x +1y =5,则x +y 的最大值是16.已知a >b >0,则2a +4a +b +1a -b的最小值为17.已知正数a ,b 满足2a 2+b 2=3,则a b 2+1的最大值为________.类型二 常数代换法利用基本不等式求最值1.已知a >0,b >0,a +b =1,则1a +1b 的最小值为________.2.已知a >0,b >0,a +2b =3,则2a +1b 的最小值为________.3.已知正实数x ,y 满足2x +y =2,则2x +1y 的最小值为________.4.已知正项等比数列{a n }的公比为2,若a m a n =4a 22,则2m +12n 的最小值为5.已知向量a =(3,-2),b =(x ,y -1),且a ∥b ,若x ,y 均为正数,则3x +2y 的最小值是6.已知x >0,y >0,且4x +y =xy ,则x +y 的最小值为7.若直线x a +yb =1(a >0,b >0)过点(1,2),则2a +b 的最小值为________.8.已知a >0,b >0,函数f (x )=a log 2x +b 的图像经过点⎝⎛⎭⎫4,12,则1a +2b 的最小值为________.9.已知函数y =log a (x +3)-1(a >0且a ≠1)的图象恒过定点A ,若点A 在直线mx +ny +1=0上,其中mn >0,则1m +1n 的最小值为10.已知x >0,y >0,lg 2x +lg 8y =lg 2,则1x +13y 的最小值是11.已知直线l :ax +by -ab =0(a >0,b >0)经过点(2,3),则a +b 的最小值为________.12.已知x ,y 均为正实数,且1x +2+1y +2=16,则x +y 的最小值为13.若a ,b ,c 都是正数,且a +b +c =2,则4a +1+1b +c 的最小值是14.已知正数x ,y 满足x +2y =3,则y x +1y 的最小值为________.15.设a >0,b >1,若a +b =2,则3a +1b -1的最小值为________.16.已知x >0,y >0,且2x +8y -xy =0,求:(1)xy 的最小值;(2)x +y 的最小值.类型三 通过消元法利用基本(均值)不等式求最值1.若正实数m ,n 满足2m +n +6=mn ,则mn 的最小值是________.2.已知正实数x ,y 满足xy +2x +y =4,则x +y 的最小值为________.3.设x ,y 均为正数,且xy +x -y -10=0,则x +y 的最小值是________.4.已知x >0,y >0,且2x +4y +xy =1,则x +2y 的最小值是________.类型四:利用基本不等式求参数值或取值范围1.若对于任意的x >0,不等式xx 2+3x +1≤a 恒成立,则实数a 的取值范围为2.已知函数y =x +mx -2(x >2)的最小值为6,则正数m 的值为________.3.若对x >0,y >0,x +2y =1,有2x +1y ≥m 恒成立,则m 的最大值是________.4.已知a >0,b >0,若不等式3a +1b ≥ma +3b恒成立,则m 的最大值为5.正数a ,b 满足1a +9b =1,若不等式a +b ≥-x 2+4x +18-m 对任意实数x 恒成立,则实数m 的取值范围是________.6.已知不等式(x +y )⎝⎛⎭⎫1x +a y ≥9对任意的正实数x ,y 恒成立,则正实数a 的最小值为7.已知函数f (x )=3x 2+ax +26x +1,若存在x ∈N +使得f (x )≤2成立,则实数a 的取值范围为___题型三 基本不等式的综合问题类型一 基本不等式的实际应用问题1.要制作一个容积为4 m 3,高为1 m 的无盖长方体容器.已知该容器的底面造价是每平方米20元,侧面造价是每平方米10元,则该容器的最低总造价是( )A .80元B .120元C .160元D .240元2.某公司一年购买某种货物400吨,每次都购买x 吨,运费为4万元/次,一年的总存储费用为4x 万元,要使一年的总运费与总存储费用之和最小,则x =__________吨.3.某学校为了支持生物课程基地研究植物生长,计划利用学校空地建造一间室内面积为900 m 2的矩形温室,在温室内划出三块全等的矩形区域,分别种植三种植物,相邻矩形区域之间间隔1 m ,三块矩形区域的前、后与内墙各保留1 m 宽的通道,左、右两块矩形区域分别与相邻的左右内墙保留3 m 宽的通道,如图.设矩形温室的室内长为x (单位:m),三块种植植物的矩形区域的总面积为S (单位:m 2). (1)求S 关于x 的函数关系式;(2)求S 的最大值.类型二 基本不等式与函数的交汇问题1.已知A ,B 是函数y =2x 的图象上不同的两点,若点A ,B 到直线y =12的距离相等,则点A ,B 的横坐标之和的取值范围是( )A .(-∞,-1)B .(-∞,-2)C .(-∞,-3)D .(-∞,-4)类型三 基本不等式与数列的交汇问题1.已知a >0,b >0,并且1a ,12,1b 成等差数列,则a +9b 的最小值为2.已知正项等比数列{a n }的前n 项和为S n ,且S 8-2S 4=5,则a 9+a 10+a 11+a 12的最小值为3.设等差数列{a n }的公差是d ,其前n 项和是S n (n ∈N +),若a 1=d =1,则S n +8a n 的最小值是______.类型四 基本不等式与解析几何的交汇问题1. 已知直线ax +by +c -1=0(b ,c >0)经过圆x 2+y 2-2y -5=0的圆心,则4b +1c的最小值是2.当双曲线M :x 2m -y 2m 2+4=1的离心率最小时,M 的渐近线方程为3.两圆x 2+y 2-2my +m 2-1=0和x 2+y 2-4nx +4n 2-9=0恰有一条公切线,若m ∈R ,n4m2+1n2的最小值为∈R,且mn≠0,则。
(人教版)(江苏专用)2020版高考数学大一轮复习 第七章 不等式 第42讲 基本不等式及其应用学案

第42讲 基本不等式及其应用考试要求 1.基本不等式的证明过程(A 级要求);2.利用基本不等式解决简单的最大(小)值问题(C 级要求).应关注利用基本不等式把等式转化为不等式,然后研究最值问题.诊 断 自 测1.思考辨析(在括号内打“√”或“×”) (1)当a ≥0,b ≥0时,a +b2≥ab .( )(2)两个不等式a 2+b 2≥2ab 与a +b2≥ab 成立的条件是相同的.( )(3)函数y =x +1x的最小值是2.( )(4)函数f (x )=sin x +4sin x 的最小值为2.( )(5)x >0且y >0是x y +y x≥2的充要条件.( ) 解析 (2)不等式a 2+b 2≥2ab 成立的条件是a ,b ∈R ; 不等式a +b2≥ab 成立的条件是a ≥0,b ≥0.(3)函数y =x +1x值域是(-∞,-2]∪[2,+∞),没有最小值.(4)函数f (x )=sin x +4sin x 的最小值为-5.(5)x >0且y >0是x y +y x≥2的充分条件. 答案 (1)√ (2)× (3)× (4)× (5)×2.(教材改编)设x >0,y >0,且x +y =18,则xy 的最大值为________. 解析 ∵x >0,y >0,∴x +y2≥xy ,即xy ≤⎝ ⎛⎭⎪⎫x +y 22=81,当且仅当x =y =9时,(xy )max =81. 答案 813.(教材改编)若0<x <1,则x (3-2x )的取值范围是________. 解析 由0<x <1知3-2x >0,故x (3-2x )=12·2x (3-2x ) ≤12·2x +(3-2x )2=324,当且仅当x =34时,上式等号成立.∴0<x (3-2x )≤324. 答案 ⎝⎛⎦⎥⎤0,3244.(必修5P106习题16改编)已知正数x ,y 满足x +2y =1,那么1x +1y的最小值为____________.解析 因为x >0,y >0,x +2y =1,所以1x +1y =⎝ ⎛⎭⎪⎫1x +1y (x +2y )=1+2+2y x +xy≥3+22y x ·x y=3+22,当且仅当x 2=2y 2时取得最小值3+2 2. 答案 3+2 25.(教材改编)①若x ∈(0,π),则sin x +1sin x≥2;②若a ,b ∈(0,+∞),则lg a +lg b ≥2lg a ·lg b ;③若x ∈R ,则⎪⎪⎪⎪⎪⎪x +4x ≥4.其中正确结论的序号是________.解析 ①因为x ∈(0,π),所以sin x ∈(0,1], 所以①成立;②只有在lg a >0,lg b >0, 即a >1,b >1时才成立;③⎪⎪⎪⎪⎪⎪x +4x =|x |+⎪⎪⎪⎪⎪⎪4x ≥2|x |·⎪⎪⎪⎪⎪⎪4x=4,当且仅当x =±2时“=”成立.答案 ①③知 识 梳 理1.基本不等式ab ≤a +b2(1)基本不等式成立的条件:a >0,b >0. (2)等号成立的条件:当且仅当a =b 时取等号. (3)适用于求含两个代数式的最值. 2.几个重要的不等式(1)a 2+b 2≥2ab (a ,b ∈R ). (2)b a +a b≥2(a ,b 同号).(3)ab ≤⎝ ⎛⎭⎪⎫a +b 22,(a ,b ∈R ).(4)a 2+b 22≥⎝⎛⎭⎪⎫a +b 22(a ,b ∈R ). (以上不等式要根据条件合理选择其中之一) 以上不等式等号成立的条件均为a =b . 3.算术平均数与几何平均数设a >0,b >0,则a ,b 的算术平均数为a +b2,几何平均数为ab ,基本不等式可叙述为两个正数的几何平均数不大于它们的算术平均数,当两个正数相等时两者相等. 4.利用基本不等式求最值问题 已知x >0,y >0,则(1)如果积xy 是定值p ,那么当且仅当x =y 时,x +y 有最小值2p (简记:积定和最小). (2)如果和x +y 是定值p ,那么当且仅当x =y 时,xy 有最大值p 24(简记:和定积最大).考点一 利用基本不等式求最值(多维探究) 命题角度1 配凑法求最值【例1-1】 (1)已知0<x <1,则x (4-3x )取得最大值时x 的值为________. (2)已知x <54,则f (x )=4x -2+14x -5的最大值为________.(3)函数y =x 2+2x -1(x >1)的最小值为________.解析 (1)x (4-3x )=13·(3x )(4-3x )≤13·⎣⎢⎡⎦⎥⎤3x +(4-3x )22=43, 当且仅当3x =4-3x ,即x =23时,取等号.(2)因为x <54,所以5-4x >0,则f (x )=4x -2+14x -5=-(5-4x +15-4x )+3≤-2+3=1.当且仅当5-4x =15-4x,即x =1时,等号成立.故f (x )=4x -2+14x -5的最大值为1.(3)由于x >1,故y =x 2+2x -1=(x 2-2x +1)+(2x -2)+3x -1=(x -1)2+2(x -1)+3x -1=(x -1)+3x -1+2≥23+2. 当且仅当x -1=3x -1,即x =3+1时,等号成立. 答案 (1)23 (2)1 (3)23+2命题角度2 常数代换或消元法求最值【例1-2】 (1)(2018·盐城模拟)已知正数x ,y 满足x +2y -xy =0,则x +2y 的最小值为________.(2)(一题多解)(2018·南京模拟)已知x >0,y >0,x +3y +xy =9,则x +3y 的最小值为________.(3)(2017·苏州期末)已知ab =14,a ,b ∈(0,1),那么11-a +21-b 的最小值为________.解析 (1)由x +2y -xy =0,得2x +1y =1,且x >0,y >0.∴x +2y =(x +2y )×⎝ ⎛⎭⎪⎫2x +1y =4y x+xy+4≥4+4=8.当且仅当4y x =yx,即x =4,y =2时等号成立.(2)法一 (消元法) 由已知得x =9-3y1+y.因为x >0,y >0,所以0<y <3, 所以x +3y =9-3y1+y +3y=121+y+3(y +1)-6≥2121+y·3(y +1)-6=6, 当且仅当121+y =3(y +1),即y =1,x =3时,(x +3y )min =6. 法二 ∵x >0,y >0,9-(x +3y )=xy =13x ·(3y )≤13·⎝ ⎛⎭⎪⎫x +3y 22,当且仅当x =3y 时等号成立.设x +3y =t >0,则t 2+12t -108≥0, ∴(t -6)(t +18)≥0,又∵t >0,∴t ≥6.故当x =3,y =1时,(x +3y )min =6. (3)因为b =14a,a ∈(0,1),所以11-a +21-b =11-a +21-14a =11-a +24a -1+2=2a +1-4a 2+5a -1+2. 令2a +1=t ,则a =t -12,原式=t -t 2+9t 2-92+2=192-⎝ ⎛⎭⎪⎫t +92t +2≥192-2t ·92t+2=4+423,当且仅当t =322,即a =32-24∈(0,1)时取等号,故原式的最小值为4+423.答案 (1)8 (2)6 (3)4+423规律方法 (1)应用基本不等式解题一定要注意应用的前提:“一正”“二定”“三相等”.所谓“一正”是指正数,“二定”是指应用基本不等式求最值时,和或积为定值,“三相等”是指满足等号成立的条件.(2)在利用基本不等式求最值时,要根据式子的特征灵活变形,配凑出积、和为常数的形式,然后再利用基本不等式.(3)条件最值的求解通常有三种方法:一是消元法,即根据条件建立两个量之间的函数关系,然后代入代数式转化为函数的最值求解;二是将条件灵活变形,利用常数代换的方法构造和或积为常数的式子,然后利用基本不等式求解最值;三是对条件使用基本不等式,建立所求目标函数的不等式求解.易错警示 (1)利用基本不等式求最值,一定要注意应用条件;(2)尽量避免多次使用基本不等式,若必须多次使用,一定要保证等号成立的条件一致.【训练1】 (1)(一题多解)若正数x ,y 满足x +3y =5xy ,则3x +4y 的最小值是________. (2)设a +b =2,b >0,则12|a |+|a |b取最小值时,a 的值为________. 解析 (1)法一 由x +3y =5xy 及x ,y 均为正数可得15y +35x=1,∴3x +4y =(3x +4y )⎝⎛⎭⎪⎫15y +35x=95+45+3x 5y +12y 5x ≥135+125=5. (当且仅当3x 5y =12y 5x ,即x =1,y =12时,等号成立),∴3x +4y 的最小值是5.法二 由x +3y =5xy ,得x =3y5y -1,∵x >0,y >0,∴y >15,∴3x +4y =9y5y -1+4y =13⎝ ⎛⎭⎪⎫y -15+95+45-4y 5y -1+4y=135+95·15y -15+4⎝ ⎛⎭⎪⎫y -15 ≥135+23625=5, 当且仅当y =12时等号成立,∴(3x +4y )min =5.(2)∵a +b =2,b >0, ∴12|a |+|a |b =24|a |+|a |b=a +b 4|a |+|a |b=a 4|a |+b 4|a |+|a |b ≥a 4|a |+2b 4|a |×|a |b =a 4|a |+1, 当且仅当b 4|a |=|a |b时等号成立.又a +b =2,b >0, ∴当b =-2a ,a =-2时,12|a |+|a |b取得最小值. 答案 (1)5 (2)-2考点二 基本不等式的综合应用【例2】 (1)设x ,y ,z 均为大于1的实数,且z 为x 和y 的等比中项,则lg z 4lg x +lg zlg y 的最小值为________.(2)设正四面体ABCD 的棱长为6,P 是棱AB 上的任意一点(不与点A ,B 重合),且点P 到平面ACD ,平面BCD 的距离分别为x ,y ,则3x +1y的最小值是________.解析 (1)由题意得z 2=xy ,lg x >0,lg y >0, ∴lg z 4lg x +lg z lg y =12(lg x +lg y )4lg x +12(lg x +lg y )lg y =18+lg y 8lg x +12+lg x 2lg y =58+lg y 8lg x +lg x 2lg y ≥58+2116=98, 当且仅当lg y 8lg x =lg x2lg y ,即lg y =2lg x ,即y =x 2时取等号.(2)过点A 作AO ⊥平面BCD 于点O ,则O 为△BCD 的重心,所以OB =23×32×6=2,所以AO =(6)2-(2)2=2. 又V P -BCD +V P -ACD =V A -BCD ,所以13S △BCD ·y +13S △ACD ·x =13S △BCD ·2,即x +y =2.所以3x +1y =12⎝ ⎛⎭⎪⎫3x +1y (x +y )=12⎝⎛⎭⎪⎫4+x y +3y x ≥2+3,当且仅当x =3-3,y =3-1时取等号.答案 (1)98(2)2+ 3规律方法 (1)设变量时一般要把求最大值或最小值的变量定义为函数. (2)根据实际问题抽象出函数的解析式后,只需利用基本不等式求得函数的最值. (3)在求函数的最值时,一定要在定义域(使实际问题有意义的自变量的取值范围)内求解. 【训练2】 (1)(2018·泰州模拟)已知a >b >1且2log a b +3log b a =7,则a +1b 2-1的最小值为________.(2)(2018·苏、锡、常、镇四市调研)若实数x ,y 满足xy >0,则xx +y +2yx +2y的最大值为________.解析 (1)因为2log a b +3log b a =7,所以2(log a b )2-7log a b +3=0,解得log a b =12或log a b=3,因为a >b >1,所以log a b ∈(0,1),故log a b =12,从而b =a ,因此a +1b 2-1=a +1a -1=(a -1)+1a -1+1≥3,当且仅当a =2时等号成立. (2)因为xy >0,所以xx +y +2y x +2y =x (x +2y )+2y (x +y )(x +y )(x +2y )=x 2+4xy +2y 2x 2+3xy +2y 2=1+xyx 2+3xy +2y 2=1+1x y +3+2y x≤1+13+22=4-22,当且仅当x y =2y x ,即x 2=2y 2时取等号.答案 (1)3 (2)4-2 2考点三 利用基本不等式解决恒成立及实际 应用问题【例3-1】 若不等式x +2xy ≤a (x +y )对任意的实数x ,y ∈(0,+∞)恒成立,则实数a 的最小值为________.解析 由题意得a ≥x +2xyx +y =1+2yx 1+yx恒成立.令t =y x (t >0),则a ≥1+2t 1+t 2,再令1+2t =u (u >1),则t =u -12,故a ≥u1+⎝ ⎛⎭⎪⎫u -122=4u +5u-2. 因为u +5u ≥25(当且仅当u =5时等号成立),故u +5u-2≥25-2,从而0<4u +5u-2≤425-2=5+12,故a ≥5+12,即a min =5+12. 答案5+12【例3-2】 (1)已知a >0,b >0,若不等式3a +1b ≥ma +3b恒成立,则m 的最大值为________.(2)已知函数f (x )=x 2+ax +11x +1(a ∈R ),若对于任意的x ∈N *,f (x )≥3恒成立,则a 的取值范围是________.解析 (1)由3a +1b ≥ma +3b,得m ≤(a +3b )⎝ ⎛⎭⎪⎫3a +1b =9b a+ab+6.又a >0,b >0,所以9b a+a b +6≥29+6=12(当且仅当9b a =ab时等号成立),∴m ≤12,∴m 的最大值为12.(2)对任意x ∈N *,f (x )≥3恒成立,即x 2+ax +11x +1≥3恒成立,即知a ≥-⎝ ⎛⎭⎪⎫x +8x +3. 设g (x )=x +8x ,x ∈N *,则g (2)=6,g (3)=173.∵g (2)>g (3),∴g (x )min =173,∴-⎝ ⎛⎭⎪⎫x +8x +3≤-83, ∴a ≥-83,故a 的取值范围是⎣⎢⎡⎭⎪⎫-83,+∞. 答案 (1)12 (2)⎣⎢⎡⎭⎪⎫-83,+∞规律方法 (1)应用基本不等式判断不等式是否成立:对所给不等式(或式子)变形,然后利用基本不等式求解.(2)条件不等式的最值问题:通过条件转化成能利用基本不等式的形式求解.(3)求参数的值或范围:观察题目特点,利用基本不等式确定相关成立条件,从而得参数的值或范围.【训练3】 (2018·苏北四市联考)如图,墙上有一壁画,最高点A 离地面4 m ,最低点B 离地面2 m ,观察者从距离墙x (x >1)m ,离地面高a (1≤a ≤2)m 的C 处观赏该壁画,设观赏视角∠ACB =θ.(1)若a =1.5,问:观察者离墙多远时,视角θ最大? (2)若tan θ=12,当a 变化时,求x 的取值范围.解 (1) 当a =1.5时,过C 作AB 的垂线,垂足为D ,则BD =0.5,且θ=∠ACD -∠BCD , 由已知观察者离墙x m ,且x >1, 则tan ∠BCD =0.5x ,tan ∠ACD =2.5x,所以tan θ=tan(∠ACD-∠BCD)=2.5x-0.5x1+2.5×0.5x2=2x1+1.25x2=2x+1.25x≤2254=255,当且仅当x=52>1时取等号.又tan θ在⎝⎛⎭⎪⎫0,π2上单调递增,所以当观察者离墙52m时,视角θ最大.(2)由题意得tan∠BCD=2-ax,tan∠ACD=4-ax,又tan θ=12,所以tan θ=tan(∠ACD-∠BCD)=2xx2+(a-2)·(a-4)=12,所以a2-6a+8=-x2+4x.当1≤a≤2时,0≤a2-6a+8≤3,所以0≤-x2+4x≤3,即⎩⎪⎨⎪⎧x2-4x≤0,x2-4x+3≥0,解得0≤x≤1或3≤x≤4,因为x>1,所以3≤x≤4.所以x的取值范围是[3,4].一、必做题1.(教材改编)已知a,b∈R,且ab>0,则下列不等式中,恒成立的序号是________.①a2+b2>2ab;②a+b≥2ab;③1a+1b>2ab;④ba+ab≥2.解析因为a2+b2≥2ab,当且仅当a=b时,等号成立,所以①错误;对于④,因为ab>0,所以ba+ab≥2ba·ab=2.对于②,③,当a<0,b<0时,明显错误.答案④2.(教材改编)用长为16 cm的铁丝围成一个矩形,则所围成的矩形的最大面积是________ cm2.解析 设矩形长为x cm(0<x <8),则宽为(8-x )cm ,面积S =x (8-x ).由于x >0,8-x >0,可得S ≤⎝ ⎛⎭⎪⎫x +8-x 22=16,当且仅当x =8-x ,即x =4时,S max =16.所以矩形的最大面积是16 cm 2. 答案 163.当x >0时,函数f (x )=2xx 2+1有最________值,为________. 解析 由于x >0,所以f (x )=2x x 2+1=2x +1x≤22=1,当且仅当x =1时取等号. 答案 大 14.(2018·盐城模拟)函数y =x 2+2x 2+1的最小值为________.解析 y =x 2+1+1x 2+1=x 2+1+1x 2+1≥2,当且仅当x 2+1=1x 2+1,即x =0时,y 取到最小值2. 答案 25.某民营企业的一种电子产品,2015年的年产量在2014年基础上增长率为a ;2016年计划在2015年的基础上增长率为b (a ,b >0),若这两年的平均增长率为q ,则q 与a +b2的大小关系是________.解析 设2014年的年产量为1, 则2016年的年产量为(1+a )(1+b ), ∴(1+q )2=(1+a )(1+b ), ∴1+q =(1+a )(1+b )≤1+a +1+b 2=1+a +b2, ∴q ≤a +b2,当且仅当a =b 时,取“=”.答案 q ≤a +b26.(2017·天津卷)若a ,b ∈R ,ab >0,则a 4+4b 4+1ab 的最小值为________.解析 a 4+4b 4+1ab ≥4a 2b 2+1ab =4ab +1ab≥24ab ·1ab=4(前一个等号成立条件是a 2=2b 2,后一个等号成立的条件是ab =12,两个等号可以同时取得,则当且仅当a 2=22,b 2=24时取等号).7.设f (x )=x 2+x +1,g (x )=x 2+1,则f (x )g (x )的取值范围是________. 解析 f (x )g (x )=x 2+x +1x 2+1=1+x x 2+1,当x =0时,f (x )g (x )=1;当x >0时,f (x )g (x )=1+1x +1x ≤1+12=32; 当x <0时,x +1x=-⎣⎢⎡⎦⎥⎤(-x )+⎝ ⎛⎭⎪⎫-1x ≤-2,则f (x )g (x )=1+1x +1x ≥1-12=12. ∴f (x )g (x )∈⎣⎢⎡⎦⎥⎤12,32. 答案 ⎣⎢⎡⎦⎥⎤12,32 8.(2017·吉林九校第二次联考)若正数a ,b 满足1a +1b =1,则1a -1+9b -1的最小值是________.解析 ∵正数a ,b 满足1a +1b =1,∴b =a a -1>0,解得a >1.同理可得b >1,∴1a -1+9b -1=1a -1+9a a -1-1=1a -1+9(a -1)≥21a -1·9(a -1)=6,当且仅当1a -1=9(a -1),即a =43时等号成立,∴最小值为6. 答案 69.(2018·扬州一模)设正实数x ,y ,z 满足x 2-3xy +4y 2-z =0,则当xy z取得最大值时,2x+1y -2z的最大值为________.解析 由已知得z =x 2-3xy +4y 2,(*) 则xy z =xy x 2-3xy +4y 2=1x y +4yx-3≤1,当且仅当x =2y 时取等号,把x =2y 代入(*)式,得z =2y 2,所以2x +1y -2z =1y +1y -1y2=-⎝ ⎛⎭⎪⎫1y -12+1≤1.10.已知函数f (x )=x 2+3x -a(x ≠a ,a 为非零常数).(1)解不等式f (x )<x ;(2)设x >a 时,f (x )有最小值为6,求a 的值.解 (1)f (x )<x ,即x 2+3x -a<x ,整理为(ax +3)(x -a )<0.当a >0时,⎝⎛⎭⎪⎫x +3a (x -a )<0,∴解集为⎩⎨⎧x ⎪⎪⎪⎭⎬⎫-3a <x <a ; 当a <0时,⎝⎛⎭⎪⎫x +3a (x -a )>0,解集为⎩⎨⎧x ⎪⎪⎪⎭⎬⎫x >-3a,或x <a .(2)设t =x -a ,则x =t +a (t >0).∴f (t )=t 2+2at +a 2+3t=t +a 2+3t+2a≥2t ·a 2+3t+2a=2a 2+3+2a .当且仅当t =a 2+3t,即t =a 2+3时,等号成立, 即f (x )有最小值2a 2+3+2a . 依题意有2a 2+3+2a =6, 解得a =1. 二、选做题11.(一题多解)(2018·南通模拟)设实数x ,y 满足x 24-y 2=1,则3x 2-2xy 的最小值是________.解析 法一 因为x 24-y 2=1,所以3x 2-2xy =3x 2-2xy x 24-y 2=3-2yx 14-⎝ ⎛⎭⎪⎫y x 2,令k =y x ∈⎝ ⎛⎭⎪⎫-12,12,则3x 2-2xy =3-2k 14-k 2=4(3-2k )1-4k 2,再令t =3-2k ∈(2,4),则k =3-t 2,故3x 2-2xy =4t -t 2+6t -8=4-⎝ ⎛⎭⎪⎫t +8t +6≥46-28=6+42,当且仅当t =22时等号成立.法二 令t =3x 2-2xy ,则y =3x 2-t 2x ,代入方程x 24-y 2=1并化简得8x 4+(4-6t )x 2+t 2=0,令u =x 2≥4,则8u 2+(4-6t )u +t 2=0在[4,+∞)上有解,从而由⎩⎪⎨⎪⎧Δ=(4-6t )2-32t 2≥0,6t -416>0,得t 2-12t +4≥0,解得t ≥6+42,当取得最小值时,u =2+322满足题意. 法三 因为x 24-y 2=1=⎝ ⎛⎭⎪⎫x 2+y ⎝ ⎛⎭⎪⎫x2-y ,所以令x 2+y =t ,则x 2-y =1t,从而⎩⎪⎨⎪⎧x =t +1t ,y =12⎝ ⎛⎭⎪⎫t -1t ,则3x 2-2xy =6+2t 2+4t2≥6+42,当且仅当t 2=2时等号成立.答案 6+4 212.(2018·南京模拟)一位创业青年租用了如图所示的一块边长为1百米的正方形田地ABCD 来养蜂、产蜜与售蜜,他在正方形的边BC ,CD 上分别取点E ,F (不与正方形的顶点重合),连接AE ,EF ,FA ,使得∠EAF =45°.现拟将图中阴影部分规划为蜂源植物生长区,△AEF 部分规划为蜂巢区,△CEF 部分规划为蜂蜜交易区.若蜂源植物生长区的投入约为2×105元/百米2,蜂巢区与蜂蜜交易区的投入约为105元/百米2,则这三个区域的总投入最少需要多少元?解 设阴影部分面积为S ,三个区域的总投入为T .则T =2×105·S +105·(1-S )=105·(S +1),所以只要求S 的最小值即可得T 的最小值. 设∠EAB =α(0°<α<45°),在△ABE 中,因为AB =1,∠B =90°,所以BE =tan α, 则S △ABE =12AB ·BE =12tan α.又∠DAF =45°-α,所以S △ADF =12tan(45°-α).所以S =12[tan α+tan(45°-α)]=12⎝ ⎛⎭⎪⎫tan α+1-tan α1+tan α.令x =tan α∈(0,1),则S =12⎝ ⎛⎭⎪⎫x +1-x 1+x =12⎝ ⎛⎭⎪⎫x -x -1x +1=12⎝ ⎛⎭⎪⎫x +2x +1-1=12⎣⎢⎡⎦⎥⎤(x +1)+2x +1-2≥12(22-2)=2-1. 当且仅当x +1=2x +1,即x =2-1时取等号. 此时T =2×105,所以三个区域的总投入T 的最小值约为2×105元.。
2020版江苏高考数学名师大讲坛一轮复习教程学案:第34课__不等关系 含解析
第五章 不 等 式____第34课__不__等__关__系____1. 了解日常生活中的不等关系及不等式(组)的实际背景,能通过具体情境建立不等式模型.2. 掌握不等式的简单性质,深刻理解其成立的条件,并能灵活运用.3. 熟悉两个实数比较大小的方法,掌握分类讨论的标准和技巧.1. 阅读:必修5第73~74页.2. 解悟:①现实生活中大量存在不等关系,我们常常用不等式表示这样的关系;②解决相关问题时,未知量与参数的范围要时刻表明,并运用不等式有关知识解决问题;③教材第74页练习第5题,体现了不等式怎样的性质,能够写出;吗?④初中你学过哪些不等式的性质,能列举出;吗?3. 践习:在教材空白处,完成第74页练习第2、3、4题.基础诊断1. 若a 1<a 2,b 1<b 2,则a 1b 1+a 2b 2与a 1b 2+a 2b 1的大小关系是__a 1b 1+a 2b 2>a 1b 2+a 2b 1__. 解析:作差可得(a 1b 1+a 2b 2)-(a 1b 2+a 2b 1)=(a 1-a 2)(b 1-b 2).因为a 1<a 2,b 1<b 2,所以(a 1-a 2)(b 1-b 2)>0,即a 1b 1+a 2b 2>a 1b 2+a 2b 1.2. 某品牌酸奶的质量检查规定,酸奶中脂肪的含量应不少于2.5%,蛋白质的含量y 应不少于2.3%,可用不等式表示为__⎩⎨⎧x ≥2.5%,y ≥2.3%__. 3. 已知a<b<0,给出下列不等式:①|a|>|b|; ②1a -b >1a; ③1a >1b ; ④a 2>b 2.其中正确不等式的序号是__①③④__.解析:因为a<b<0,所以|a|>|b|,a 2>b 2,则①④成立;因为a<b<0,所以-b>0,所以0>a -b>a ,所以1a -b <1a ,则②不成立;因为a<b<0,所以1ab>0,所以在不等式a<b<0两边同时乘以1ab ,得1b <1a,则③成立.故选①③④. 4. 已知2<m<4,3<n<5,则m n 的取值范围是__⎝ ⎛⎭⎪⎫25,43__. 解析:因为3<n<5,所以15<1n <13.又因为2<m<4,所以25<m n <43. 范例导航考向❶ 实际问题中的不等关系例1 已知b 克糖水中有a 克糖(b>a>0),若再添加m 克糖(m>0),则糖水变甜了.试根据这个事实,写出a ,b ,m 所满足的不等式,并证明.解析:a b <a +m b +m.证明如下: 方法一:因为0<a<b ,m>0,所以a -b<0,b +m>0.因为a b -a +m b +m =a (b +m )-b (a +m )b (b +m )=m (a -b )b (b +m )<0, 所以a b <a +m b +m. 方法二:因为0<a<b ,m>0,所以b +m>0,所以要证a b <a +m b +m,即证a(b +m)<b(a +m),即am<bm. 又m>0,a<b 为已知条件,所以am<bm 成立,所以a b <a +m b +m成立. 方法三:因为a<b ,m>0,所以am<bm ,所以ab +am<ab +bm ,即a(b +m)<b(a +m).因为0<a<b ,m>0,所以b +m>0, 所以a (b +m )b (b +m )<b (a +m )b (b +m ),所以a b <a +m b +m.某野外训练活动队需要用浓度为35%~45%(35%、45%也能使用)的酒精为队员进行物理退热,现只有浓度是75%的消毒酒精,若取a 克浓度是75%的消毒酒精,加入克纯净水稀释后使用,则的取值范围为__⎣⎢⎡⎦⎥⎤2a 3,8a 7__. 解析:由题意得35%≤75%a x +a ≤45%,解得2a 3≤≤8a 7. 考向❷ 比较大小或证明不等式例2 已知<y<0,试比较(2+y 2)(-y)与(2-y 2)(+y)的大小.解析:方法一:(2+y 2)(-y)-(2-y 2)(+y)=(-y)[(2+y 2)-(+y)2]=-2y(-y).因为<y<0,所以y>0,-y<0,所以-2y(-y)>0,所以(2+y 2)(-y)>(2-y 2)(+y).方法二:因为<y<0,所以-y<0,2>y 2,所以(2+y 2)(-y)<0,(2-y 2)(+y)<0,所以0<(x 2+y 2)(x -y )(x 2-y 2)(x +y )=x 2+y 2x 2+y 2+2xy<1, 所以(2+y 2)(-y)>(2-y 2)(+y).设a>0,b>0,且a ≠b ,试比较a a b b 与a b b a 的大小. 解析:因为a>0,b>0,所以a a b b a b b a =⎝ ⎛⎭⎪⎫a b a -b. ①若a>b>0,则a b>1,a -b>0, 所以⎝ ⎛⎭⎪⎫a b a -b>1,所以a a b b >a b b a; ②若b>a>0,则a b<1,a -b<0, 所以⎝ ⎛⎭⎪⎫a b a -b>1,所以a a b b >a b b a . 综上,得a a b b >a b b a .【选讲题】 已知a ,b ,c ∈R +,且a 2+b 2=c 2,当n ∈N ,n >2时,比较a n +b n 与c n 的大小. 解析:因为a ,b ,c ∈R +,所以a n ,b n ,c n >0,a n +b nc n =⎝ ⎛⎭⎪⎫a c n +⎝ ⎛⎭⎪⎫b c n. 因为a 2+b 2=c 2,所以⎝ ⎛⎭⎪⎫a c 2+⎝ ⎛⎭⎪⎫b c 2=1,所以0<a c <1,0<b c <1.因为n ∈N ,n >2,所以⎝ ⎛⎭⎪⎫a c n <⎝ ⎛⎭⎪⎫a c 2,⎝ ⎛⎭⎪⎫b c n<⎝ ⎛⎭⎪⎫b c 2,所以a n +b n c n =⎝ ⎛⎭⎪⎫a c n+⎝ ⎛⎭⎪⎫b c n<⎝ ⎛⎭⎪⎫a c 2+⎝ ⎛⎭⎪⎫b c 2=1,即a n +b nc n <1,所以a n +b n <c n .考向❸ 不等关系的简单综合运用例3 设f()=a 2+b ,1≤f(-1)≤2,2≤f(1)≤4,求f(-2)的取值范围.解析:设f(-2)=mf(-1)+nf(1),(m ,n 为待定系数),则4a -2b =m(a -b)+n(a +b)=(m +n)a -(m -n)b,于是⎩⎨⎧m +n =4,n -m =-2,解得⎩⎨⎧m =3,n =1,所以f(-2)=3f(-1)+f(1).又1≤f(-1)≤2,2≤f(1)≤4,所以5≤3f(-1)+f(1)≤10,所以5≤f(-2)≤10.设f()=2-+1,实数a 满足|-a|<1.求证:|f()-f(a)|<2(|a|+1).解析:因为|-a|<1,所以|f()-f(a)|=|2-+1-a 2+a -1|=|2-a 2-+a|=|(+a)(-a)-(-a)|=|(-a)(+a -1)|=|-a||+a -1|<|+a -1|=|-a +2a -1|≤|-a|+|2a|+|-1|<1+2|a|+1=2(|a|+1),所以|f()-f(a)|<2(|a|+1).自测反馈1. 若a ,b 是任意实数,且a>b ,则下列结论正确的有__④__.(填序号)①a 2>b 2;②b a<1; ③lg (a -b)>0;④⎝ ⎛⎭⎪⎫12a <⎝ ⎛⎭⎪⎫12b. 解析:当0>a>b 时,有a 2<b 2成立,故①不对;当a =0时,b a<1无意义,故②不对;当0<a -b<1时,lg (a -b)<0,故③不对;因为y =⎝ ⎛⎭⎪⎫12x 是定义域为R 的减函数的,所以当a >b 时,⎝ ⎛⎭⎪⎫12a <⎝ ⎛⎭⎪⎫12b成立,故④正确. 2. 设a>0,且a ≠1,P =log a (a 3-1),Q =log a (a 2-1),则P 与Q 的大小关系是__P>Q__. 解析:因为P =log a (a 3-1),Q =log a (a 2-1),a>0,所以a 3-1>0,a 2-1>0,所以a>1.又因为(a 3-1)-(a 2-1)=a 2(a -1)>0,所以a 3-1>a 2-1,所以log a (a 3-1)>log a (a 2-1),即P>Q.3. 设0<a<b ,a +b =1,则12,b ,2ab ,a 2+b 2中最大的是__b__. 解析:因为0<a<b ,a +b =1,所以0<a<12,12<b<1,所以2a<1,2ab<b.因为a 2+b 2-b =a 2+b(b -1)=a 2-b(1-b)=a 2-ab =a(a -b).又因为a<b ,a -b<0,所以a 2+b 2-b<0,即a 2+b 2<b.综上,最大为b.4. 一家三口外出旅游,甲旅行社提出,如果户主买全票一张,其余人可享受半价优惠;乙旅行社提出,家庭旅游算集体票,按七五折优惠,如果这两家旅行社的原价相同,__甲__(填“甲”或“乙”)家旅行社的价格更优惠.解析:设这两家旅行社一张全票的价格为a ,则在甲旅行社需要花a +2×12a =2a ,在乙旅行社需要花3×0.75a =2.25a>2a ,所以甲旅行社的价格更优惠.1. 两个实数比较大小方法主要有:作差法,作商法.2. 证明不等式主要有:作差法,综合法,分析法.3. 你还有哪些体悟,写下;:。
2024年高考数学一轮总复习讲义 第一章 集合、常用逻辑用语、不等式
第一章集合、常用逻辑用语、不等式考情探究本章内容分为两部分.第一部分为集合与简易逻辑、第二部分为不等式.第一部分内容是高考必考内容,难度小,分值为5分,重点考查集合的基本运算,充分、必要条件的判断和含有一个量词命题的否定,集合的基本运算常与不等式结合,考查集合的交、并、补集运算,充分、必要条件的判断常与向量、数列、立体几何、不等式、函数等结合,考查基本概念、定理等,复习时以基础知识为主.第二部分不等式内容在高考题中多作为载体考查其他知识,例如,结合不等式的解法考查集合间的关系与运算、函数的定义域与值域的求解、函数零点的应用等;或考查用基本不等式解决最值问题或恒成立问题.此部分考题以中低档题为主,主要以选择题或填空题的形式出现,分值为5分.对于不等式及其性质内容的复习,需要结合函数的图象与性质、三角函数、数列等知识综合掌握.第一讲集合知识梳理·双基自测知识梳理知识点一集合的基本概念一组对象的总体构成一个集合.1.集合元素的三个特征:确定性、无序性、互异性.2.集合的三种表示方法:列举法、描述法、图示法.3.元素与集合的两种关系:属于,记为∈;不属于,记为∉.4.五个特定的集合及其关系图:N*或N+表示正整数集,N表示非负整数集(或自然数集),Z表示整数集,Q表示有理数集,R表示实数集.知识点二集合之间的基本关系关系定义表示相等集合A与集合B中的所有元素都相同A=B子集A中的任意一个元素都是B中的元素A⊆B真子集A是B的子集,且B中至少有一个元素不属于A A B 注意:(1)空集用∅表示.(2)若集合A中含有n个元素,则其子集的个数为2n,真子集的个数为2n -1,非空真子集的个数为2n-2.(3)空集是任何集合的子集,是任何非空集合的真子集.(4)若A⊆B,B⊆C,则A⊆C.知识点三集合的基本运算1.A∩A=A,A∩∅=∅.2.A∪A=A,A∪∅=A.3.A∩(∁U A)=∅,A∪(∁U A)=U,∁U(∁U A)=A.4.A⊆B⇔A∩B=A⇔A∪B=B⇔∁U A⊇∁U B⇔A∩(∁U B)=∅.5.∁U(A∩B)=(∁U A)∪(∁U B),∁U(A∪B)=(∁U A)∩(∁U B).双基自测题组一走出误区1.判断下列结论是否正确(请在括号中打“√”或“×”)(1)任何一个集合都至少有两个子集.(×)(2)集合{x∈N|x3=x}用列举法表示为{1,-1,0}.(×)(3){x|y=x2}={y|y=x2}={(x,y)|y=x2}.(×)(4)若5∈{1,m+2,m2+4},则m的取值集合为{1,-1,3}.(×)(5)若A∩B=A∩C,则B=C.(×)(6)设U=R,A={x|lg x<1},则∁U A={x|lg x≥1}={x|x≥10}.(×)[解析](4)当m=-1时,m+2=1,与集合中元素的互异性矛盾,故(4)错.(6)中A={x|0<x<10},∁U A={x|x≤0或x≥10},故(6)错.题组二走进教材2.(多选题)(必修1P9T1改编)已知集合A={x|x2-2x=0},则有(ACD)A.∅⊆A B.-2∈AC.{0,2}⊆A D.A⊆{y|y<3}[解析]易知A={0,2},A,C,D均正确.3.(必修1P35T9改编)已知集合U={x|-4<x<3},A={x|-2≤x<1},则∁U A =(A)A.(-4,-2)∪[1,3)B.[-2,1)C.(-4,-2]∪(1,3)D.(-2,1][解析]根据集合补集的运算解答即可.由题知,集合U={x|-4<x<3},A ={x|-2≤x<1},所以∁U A={x|-4<x<-2,或1≤x<3},即∁U A=(-4,-2)∪[1,3),故选A.4.(必修1P13T1改编)已知全集U=R,集合A={x|-1≤x<3},B={x|2x-4≥x-2},则A∪B={x|x≥-1},∁U(A∩B)={x|x<2或x≥3}.题组三走向高考5.(2023·全国甲文,1,5分)设全集U={1,2,3,4,5},集合M={1,4},N={2,5},则N∪∁U M=(A)A.{2,3,5}B.{1,3,4}C.{1,2,4,5}D.{2,3,4,5}[解析]因为U={1,2,3,4,5},M={1,4},所以∁U M={2,3,5},所以N∪∁U M={2,3,5}.故选A.6.(2023·新课标Ⅰ,1,5分)已知集合M={-2,-1,0,1,2},N={x|x2-x-6≥0},则M∩N=(C)A.{-2,-1,0,1}B.{0,1,2}C.{-2}D.{2}[解析]由x2-x-6≥0得x≥3或x≤-2,∴N={x|x≥3或x≤-2},因此M∩N={-2},故选C.7.(2023·新课标Ⅱ,2,5分)设集合A={0,-a},B={1,a-2,2a-2},若A⊆B,则a=(B)A.2B.1D.-1C.23[解析]若a-2=0,则a=2,此时A={0,-2},B={1,0,2},不满足A ⊆B;若2a-2=0,则a=1,此时A={0,-1},B={1,-1,0},满足A⊆B.故选B.考点突破·互动探究集合的基本概念——自主练透1.已知集合A={x|x2≤4},集合B={x|x∈N*,且x-1∈A},则B等于(C)A.{0,1}B.{0,1,2}C.{1,2,3}D.{1,2,3,4}[解析]因为A={x|x2≤4}=[-2,2],B={x|x∈N*,且x-1∈A},所以B={1,2,3}.2.已知集合A={(x,y)|x+y=8,x,y∈N*},B={(x,y)|y>x+1},则A∩B 中元素的个数为(B)A.2B.3C.4D.5[解析]求得集合A的元素,由此求得A∩B的元素,从而确定正确选项.依题意A={(1,7),(2,6),(3,5),(4,4),(5,3),(6,2),(7,1)},其中满足y>x+1的有(1,7),(2,6),(3,5),所以A∩B={(1,7),(2,6),(3,5)},有3个元素.故选B.3.设集合A={x|3x-1<m},若1∈A且2∉A,则实数m的取值范围是(C) A.2<m<5B.2≤m<5C.2<m≤5D.2≤m≤5[解析]∵1∈A,∴m>2,又∵2∉A,∴m≤5,因此2<m≤5.故选C.4.设a,b∈R,集合{1,a+b,a}0,ba,b a2025+b2024=0.[解析]由题意知a≠0,所以a+b=0,则ba=-1,所以a=-1,b=1,故a2025+b2024=-1+1=0.名师点拨:1.用描述法表示集合,首先要搞清楚集合中代表元素的含义,再看元素的限制条件,明白集合的类型,是数集、点集还是其他类型的集合.2.集合中元素的互异性常常容易忽略,特别是含有字母的集合,在求出字母的值后,要注意检验集合中元素是否满足互异性.分类讨论的思想方法常用于解决集合问题.集合之间的基本关系——师生共研[解析]方法一(列举法):A …,-12,12,32,52,72,…B …,-12,0,12,1,32,2,52,3,72,…显然AB .方法二(描述法):集合A x |x =k +12,k ∈Zx|x =2k +12,k ∈Z B x|x =k2,k ∈Z 2k +1可以表示任意奇数,k 可以表示任意整数,故A B .2.(多选题)已知集合A ={-3,2},B ={x |ax +1=0},且B ⊆A ,则实数a 的可能取值为(BD )A .-13B .0C .12D .13[解析]由题知B ⊆A ,B ={x |ax +1=0},所以B ={-3},{2},∅.当B ={-3}时,-3a +1=0,解得a =13;当B ={2}时,2a +1=0,解得a =-12;当B =∅时,a =0.综上可得实数a 的可能取值为13,0,-12,故选BD.名师点拨:判断集合间关系的3种方法列举法根据题中限定条件把集合元素表示出来,然后比较集合元素的异同,从而找出集合之间的关系.描述法从元素的结构特点入手,结合通分、化简、变形等技巧,从元素结构上找差异进行判断.数轴法在同一个数轴上表示出两个集合,比较端点之间的大小关系,从而确定集合与集合之间的关系.【变式训练】1.设集合M |x =k 2+14,k ∈ZN |x =k4+12,k ∈(A )A .M NB .M =NC .N MD .M ∩N =∅[解析]分别将集合M ,N 中的x 通分,分母相同,只需比较分子即可.对于集合M :x =k 2+14=2k +14,k ∈Z ,当k ∈Z 时,2k +1为奇数,对于集合N :x=k 4+12=k +24,k ∈Z ,当k ∈Z 时,k +2为整数,故M N ,故选A.2.已知集合A ={x |-1≤x ≤3},集合B ={x |1-m ≤x ≤1+m }.若B ⊆A ,则m 的取值范围是(A )A .(-∞,2]B .[-1,3]C .[-3,1]D .[0,2][解析]当B ≠∅时,要满足B⊆A ,-m ≥-1,+m ≤3,-m ≤1+m ,解得0≤m ≤2;当B =∅时,1-m >1+m ,此时m <0.综上,m 的取值范围为m ≤2.集合的基本运算——多维探究角度1集合的运算1.(2024·江苏盐城模拟)已知集合U ={x |1<x <6,x ∈N },A ={2,3},B ={2,4,5},则(∁U A )∩B 等于(A )A .{4,5}B .{2,3,4,5}C .{2}D .{2,4,5}[解析]由题意得,U ={2,3,4,5},又A ={2,3},则∁U A ={4,5},因为B ={2,4,5},所以(∁U A)∩B={4,5}.故选A.[解析]集合M中的元素是被3除余1的数,集合N中的元素是被3除余2的数,所以集合∁U(M∪N)中的元素是被3整除的数,即∁U(M∪N)={x|x=3k,k∈Z},故选A.3.(多选题)(2022·潍坊质检)已知集合A={x|-1<x≤3},集合B={x||x|≤2},则下列关系式正确的是(BD)A.A∩B=∅B.A∪B={x|-2≤x≤3}C.A∪∁R B={x|x≤-1或x>2}D.A∩∁R B={x|2<x≤3}[解析]∵A={x|-1<x≤3},B={x||x|≤2}={x|-2≤x≤2},∴A∩B={x|-1<x≤3}∩{x|-2≤x≤2}={x|-1<x≤2},A不正确;A∪B={x|-1<x≤3}∪{x|-2≤x≤2}={x|-2≤x≤3},B正确;∵∁R B={x|x<-2或x>2},∴A∪∁R B={x|-1<x≤3}∪{x|x<-2或x>2}={x|x<-2或x>-1},C不正确;A∩∁R B={x|-1<x≤3}∩{x|x<-2或x>2}={x|2<x≤3},D正确.角度2利用集合的运算求参数1.已知集合A={x|x2-3x<0},B={1,a},且A∩B有4个子集,则实数a的取值范围是(B)A.(0,3)B.(0,1)∪(1,3)C.(0,1)D.(-∞,1)∪(3,+∞)[解析]因为A∩B有4个子集,所以A∩B中有2个不同的元素,所以a∈A ,所以a 2-3a <0,解得0<a <3.又a ≠1,所以实数a 的取值范围是(0,1)∪(1,3),故选B.2.已知集合A ={x |-2≤x ≤5},B ={x |m +1≤x ≤2m -1}≠∅,若A ∩B =B ,则实数m 的取值范围为_[2,3]__.[解析]由A ∩B =B 知,B ⊆A.又B ≠∅m -1≥m +1,+1≥-2,m -1≤5,解得2≤m ≤3,则实数m 的取值范围为[2,3].[引申1]本例2中若B ={x |m +1≤x ≤2m -1}情况又如何?[解析]应对B =∅和B ≠∅进行分类.①若B =∅,则2m -1<m +1,此时m <2.②若B ≠∅,由例得2≤m ≤3.由①②可得,符合题意的实数m 的取值范围为(-∞,3].[引申2]本例2中是否存在实数m ,使A ∪B =B ?若存在,求实数m 的取值范围;若不存在,请说明理由.[解析]由A ∪B =B ,即A ⊆B+1≤-2,m -1≥5,≤-3,≥3,不等式组无解,故不存在实数m ,使A ∪B =B .[引申3]本例2中,若B ={x |m +1≤x ≤1-2m },A B ,则m 的取值范围为(-∞,-3].[解析]+1≤-2,-2m ≥5,解得m ≤-3.名师点拨:集合的基本运算的关注点1.集合是由元素组成的,从研究集合中元素的构成入手是解决集合运算问题的前提.2.有些集合是可以化简的,先化简再研究其关系并进行运算,可使问题简单明了,易于解决.3.注意数形结合思想的应用,常用的数形结合形式有数轴、坐标系和Venn 图.4.根据集合运算结果求参数,先把符号语言译成文字语言,然后应用数形结合求解.【变式训练】1.(角度1)(2023·全国乙文,2,5分)设全集U={0,1,2,4,6,8},集合M={0,4,6},N={0,1,6},则M∪∁U N=(A)A.{0,2,4,6,8}B.{0,1,4,6,8}C.{1,2,4,6,8}D.U[解析]易得∁U N={2,4,8},又M={0,4,6},∴M∪∁U N={0,2,4,6,8}.故选A.2.(角度1)(2024·上海控江中学月考)设集合A={x∈Z|x2<4},B={x|y=x-1},则A∩(∁R B)=(C)A.{x|-2<x<1}B.{x|-2<x≤1}C.{-1,0}D.{-1}[解析]A={x∈Z|x2<4}={-1,0,1},B={x|y=x-1}=[1,+∞),则∁R B =(-∞,1),所以A∩(∁R B)={-1,0},故选C.3.(多选题)(角度2)若集合A={x|x<a},B={x|lg x≥0},且满足A∪B=R,则实数a的值可以为(AC)A.2B.-1C.1D.-2[解析]集合A={x|x<a},B={x|lg x≥0},由题意得B={x|x≥1},因为A∪B=R,所以a≥1.所以实数a的取值范围是[1,+∞).故选AC.4.(角度2)已知集合A={x|-3≤x≤4},B={x|2m-1≤x≤m+1},且B⊆A,则实数m的取值范围是[-1,+∞).[解析]∵B⊆A,①当B=∅时,2m-1>m+1,解得m>2,②当B ≠∅m -1≤m +1,m -1≥-3,+1≤4,解得-1≤m ≤2.综上,实数m 的取值范围是[-1,+∞).名师讲坛·素养提升集合中的新定义问题非空数集A 如果满足:①0∉A ;②若∀x ∈A ,有1x∈A ,则称A 是“互倒集”.给出以下数集:①{x ∈R |x 2+ax +1=0};②{x |x 2-6x +1≤0}|y =2x ,x ∈[1,4]其中是“互倒集”的序号是②③.[解析]①中,{x ∈R |x 2+ax +1=0},二次方程判别式Δ=a 2-4,故-2<a <2时,方程无根,该数集是空集,不符合题意;②中,{x |x 2-6x +1≤0},即{x |3-22≤x ≤3+22},显然0∉A ,又13+22≤1x ≤13-22,即3-22≤1x ≤3+22,故1x也在集合中,符合题意;|y =2x ,x ∈[1,,|12≤y≤,0∉A ,又12≤1y ≤2,故1y也在集合A 中,符合题意.名师点拨:集合新定义问题的“3定\”1.定元素:确定已知集合中所含的元素,利用列举法写出所有元素.2.定运算:根据要求及新定义运算,将所求解集合的运算问题转化为集合的交集、并集与补集的基本运算问题,或转化为数的有关运算问题.3.定结果:根据定义的运算进行求解,利用列举法或描述法写出所求集合中的所有元素.【变式训练】(多选题)(2024·重庆市长寿中学月考)若一个集合是另一个集合的子集,则这两个集合构成“鲸吞”;若两个集合有公共元素,且互不为对方子集,则称两个集合为“蚕食”,对于集合A={-1,0,2},B={x|ax2=2,x∈R},若这两个集合构成“鲸吞”或“蚕食”,则a的值可以为(ACD)A.0B.1C.12D.-1[解析]若B⊆A,则B=∅,解得a≤0,故选AD;若两个集合有公共元素,则-1∈B,解得a=2,若2∈B,解得a=12,经检验符合题意,故选C.因此选ACD.提能训练练案[1]A组基础巩固一、单选题1.已知集合A={-1,0,1},B={m|m2-1∈A,m-1∉A},则集合B中所有元素之和为(C)A.0B.1C.-1D.2[解析]根据题意列式求得m的值,即可得出答案.根据条件分别令m2-1=-1,0,1,解得m=0,±1,±2,又m-1∉A,所以m=-1,±2,B={-1,2,-2},所以集合B中所有元素之和是-1,故选C.2.(2023·山西河津中学模拟)下列四个选项中正确的是(D)A.{1}∈{0,1}B.1⊆{0,1}C.∅∈{0,1}D.1∈{0,1}[解析]对于A:{1}⊆{0,1},故A错误;对于B:1∈{0,1},故B错误;对于C:∅⊆{0,1},故C错误;对于D:1∈{0,1},故D正确.故选D.3.下列各组集合中表示同一集合的是(B)A.M={(3,2)},N={(2,3)}B.M={2,3},N={3,2}C.M={(x,y)|x+y=1},N={y|x+y=1}D.M={2,3},N={(2,3)}[解析]由集合元素的无序性,易知{2,3}={3,2}.故选B.4.(2023·天津,1,5分)设全集U={1,2,3,4,5},集合A={1,3},B={1,2,4},则A∪(∁U B)=(A)A.{1,3,5}B.{1,3}C.{1,2,4}D.{1,2,4,5}[解析]由题意知∁U B={3,5},∴A∪(∁U B)={1,3,5},故选A.5.(2022·新高考Ⅱ卷)已知集合A={-1,1,2,4},B={x||x-1|≤1},则A∩B =(B)A.{-1,2}B.{1,2}C.{1,4}D.{-1,4}[解析]B={x|0≤x≤2},故A∩B={1,2}.故选B.6.设集合A,3,a2-3a,a+2a+B={|a-2|,0}.已知4∈A且4∉B,则实数a的取值集合为(D)A.{-1,-2}B.{-1,2}C.{-2,4}D.{4}[解析]由题意可得,①当a2-3a=4且|a-2|≠4时,解得a=-1或4.当a =-1时,集合A={2,3,4,4},不满足集合中元素的互异性,故a≠-1;当a=4时,集合A,3,4B={2,0},符合题意.②当a+2a+7=4且|a-2|≠4时,解得a=-1,由①可得不符合题意.综上,实数a的取值集合为{4}.故选D.7.设集合M |x=k3+16,k∈ZN|x=k6+13,k∈结论正确的是(B)A.M=N B.M NC.N M D.M∩N=∅[解析]解法一:由题意知M,-12,-16,16,12,56,76,N,-16,0,16,13,12,23,56,M N .故选B.解法二:M|x =2k +16,k ∈Z N|x =k +26,k ∈2k +1表示所有奇数,而k +2表示所有整数(k ∈Z ),∴M N .故选B.8.(2023·全国乙理,2,5分)设全集U =R ,集合M ={x |x <1},N ={x |-1<x <2},则{x |x ≥2}=(A )A .∁U (M ∪N )B .N ∪∁U MC .∁U (M ∩N )D .M ∪∁U N[解析]集合M ,N在数轴上的表示如图.由图可知∁U (M ∪N )={x |x ≥2}.二、多选题9.(2022·全国模拟预测)设集合A ={2,a 2-a +2,1-a },若4∈A ,则a 的值为(BC )A .-1,2B .-3C .2D .3[解析]由集合中元素的确定性知a 2-a +2=4或1-a =4.当a 2-a +2=4时,a =-1或a =2;当1-a =4时,a =-3.当a =-1时,A ={2,4,2}不满足集合中元素的互异性,故a =-1舍去;当a =2时,A ={2,4,-1}满足集合中元素的互异性,故a =2满足要求;当a =-3时,A ={2,14,4}满足集合中元素的互异性,故a =-3满足要求.综上,a =2或a =-3.故选BC.10.已知集合A ={x |1<x <2},B ={x |2a -3<x <a -2},下列说法正确的是(AD )A .不存在实数a 使得A =BB .当a =4时,A ⊆BC .当0≤a ≤4时,B ⊆AD .存在实数a 使得A ⊆(∁R B )[解析]由集合相等列方程组验算;选项B 由a =4得B =∅,故不满足A⊆B;选项C通过假设B⊆A求出实数a的取值范围可判定,通过举例判断D.若集合A=B,a-3=1,-2=2,因为此方程组无解,所以不存在实数a使得集合A=B,故选项A正确;当a=4时,B={x|5<x<2}=∅,不满足A⊆B,故选项B 错误,若B⊆A,则①当B=∅时,有2a-3≥a-2,a≥1;②当B≠∅时,有<1,a-3≥1,-2≤2,此方程组无实数解;所以若B⊆A,则有a≥1,故选项C错误;当a=1时,B=∅,∁R B=R,A⊆∁R B,故D正确,故选AD.11.已知全集U的两个非空真子集A,B满足(∁U A)∪B=B,则下列关系一定正确的是(CD)A.A∩B=∅B.A∩B=BC.A∪B=U D.(∁U B)∪A=A[解析]令U={1,2,3,4},A={2,3,4},B={1,2},满足(∁U A)∪B=B,但A∩B≠∅,A∩B≠B,故A,B均不正确;由(∁U A)∪B=B,知∁U A⊆B,∴U=A∪(∁U A)⊆(A∪B),∴A∪B=U,由∁U A⊆B,知∁U B⊆A,∴(∁U B)∪A=A,故C,D均正确.12.已知集合A={x|x2-3x+2≤0},B={x|2<2x≤8},则下列判断正确的是(CD)A.A∪B=BB.(∁R B)∪A=RC.A∩B={x|1<x≤2}D.(∁R B)∪(∁R A)={x|x≤1或x>2}[解析]因为x2-3x+2≤0,所以1≤x≤2,所以A={x|1≤x≤2};因为2<2x≤8,所以1<x≤3,所以B={x|1<x≤3}.所以A∪B={x|1≤x≤3},A∩B={x|1<x≤2}.(∁R B )∪A ={x |x ≤2或x >3},(∁R B )∪(∁R A )={x |x ≤1或x >2}.三、填空题136a -1∈N |a ∈_{1,2,3,6}__.[解析]根据已知条件,先求出a 的值,即可求解.∵6a -1∈N 且a ∈N ,∴a -1=1或a -1=2或a -1=3或a -1=6,解得a =2或a =3或a =4或a =7,∴6a -1对应的值为6,3,2,16a -1∈N |a ∈{1,2,3,6}.14.(2024·九省联考试题)已知集合A ={-2,0,2,4},B ={x ||x -3|≤m },若A ∩B =A ,则m 的最小值为_5__.[解析]∵A ∩B =A ,∴m >0,∴B =[3-m,3+m ],-m ≤-2,+m ≥4,∴m ≥5,故填5.15.(2022·天津模拟)已知集合A ={x |x 2=x },集合B ={x |1<2x <4},则集合A 的子集个数为_4__;A ∩B =_{1}__.[解析]A ={x |x 2=x }={0,1},B ={x |1<2x <4}={x |0<x <2},故集合A 的子集个数为N =22=4,A ∩B ={1}.16.已知集合A ={x |(x -1)(x -3)<0},B ={x |2<x <4},则A ∩B =_(2,3)__,A ∪B =_(1,4)__,(∁R A )∪B =_(-∞,1]∪(2,+∞)__.[解析]由已知得A ={x |1<x <3},B ={x |2<x <4},所以A ∩B ={x |2<x <3},A ∪B ={x |1<x <4},(∁R A )∪B ={x |x ≤1或x >2}.17.(2024·衡水模拟)已知集合A ={x |0<x <1},集合B ={x |-1<x <1},集合C ={x |x +m >0},若(A ∪B )⊆C ,则实数m 的取值范围是_[1,+∞)__.[解析]∵集合A ={x |0<x <1},集合B ={x |-1<x <1},∴A ∪B ={x |-1<x <1},集合C ={x |x +m >0}={x |x >-m },又(A ∪B )⊆C ,∴-m ≤-1,解得m ≥1.∴实数m 的取值范围是[1,+∞).B 组能力提升1.已知集合A ={x |-3≤x ≤0},B ={x |x 2≤4},C ={x |x ∈B ,且x ∉A },则集合C =(B )A.∅B.(0,2]C.[-3,2]D.[-3,4][解析]先根据一元二次不等式的性质求出集合B={x|-2≤x≤2},然后再根据集合C中元素的特征即可求解.由题意可知:B={x|x2≤4}={x|-2≤x≤2},因为集合A={x|-3≤x≤0},集合C={x|x∈B,且x∉A},所以C=(0,2],故选B.2.已知集合A={1,2,3,4},B={y|y=2x-3,x∈A},则集合A∩B的子集个数为(C)A.1B.2C.4D.8[解析]B={-1,1,3,5},A∩B={1,3},所以集合A∩B的子集个数为22=4.3.(多选题)(2023·重庆北碚区模拟)已知全集U={x∈N|log2x<3},A={1,2,3},∁U(A∩B)={1,2,4,5,6,7},则集合B可能为(BD)A.{2,3,4}B.{3,4,5}C.{4,5,6}D.{3,5,6}[解析]由log2x<3得0<x<23,即0<x<8,于是得全集U={1,2,3,4,5,6,7},因为∁U(A∩B)={1,2,4,5,6,7},则有A∩B={3},3∈B,C不正确;若B={2,3,4},则A∩B={2,3},∁U(A∩B)={1,4,5,6,7},矛盾,A不正确;若B={3,4,5},则A∩B={3},∁U(A∩B)={1,2,4,5,6,7},B正确;若B={3,5,6},则A∩B={3},∁U(A∩B)={1,2,4,5,6,7},D正确.4.已知全集U=R,集合A={x|x2-2x-3≤0},集合B={x|log2x≤1},则A∩(∁U B)=(D)A.(2,3]B.∅C .[-1,0)∪(2,3]D .[-1,0]∪(2,3][解析]集合U =R ,A ={x |x 2-2x -3≤0}={x |-1≤x ≤3},集合B ={x |log 2x ≤1}={x |0<x ≤2},所以∁U B ={x |x ≤0或x >2},所以A ∩(∁U B )={x |-1≤x ≤0或2<x ≤3}=[-1,0]∪(2,3],故选D.5.(2023·湖北孝感模拟)已知集合A ={x |y =ln(1-2x )},B ={x |x 2≤x },则∁A ∪B (A ∩B )=(C )A .(-∞,0)B -12,1C .(-∞,0)∪12,1D -12,0[解析]根据题意可知A ∞B =[0,1],所以A ∪B =(-∞,1],A ∩B=0∁A ∪B (A ∩B )=(-∞,0)∪12,1,故选C.6.(多选题)设集合A ={x |x =m +3n ,m ,n ∈N *),若对于任意x 1∈A ,x 2∈A ,均有x 1⊕x 2∈A ,则运算⊕可能是(AC )A .加法B .减法C .乘法D .除法[解析]由题意可设x 1=m 1+3n 1,x 2=m 2+3n 2,其中m 1,m 2,n 1,n 2∈N *,则x 1+x 2=(m 1+m 2)+3(n 1+n 2),x 1+x 2∈A ,所以加法满足条件,A 正确;x 1-x 2=(m 1-m 2)+3(n 1-n 2),当n 1=n 2时,x 1-x 2∉A ,所以减法不满足条件,B 错误;x 1x 2=m 1m 2+3n 1n 2+3(m 1n 2+m 2n 1),x 1x 2∈A ,所以乘法满足条件,C正确;x 1x 2=m 1+3n 1m 2+3n 2,当m 1m 2=n 1n 2=λ(λ>0)时,x 1x 2∉A ,所以除法不满足条件,D 错误.7.已知集合A ={x ∈R ||x +2|<3},集合B ={x ∈R |(x -m )(x -2)<0},且A ∩B =(-1,n ),则m =_-1__,n =_1__.[解析]A ={x ∈R ||x +2|<3}={x ∈R |-5<x <1},由A ∩B =(-1,n ),可知m <1,则B ={x |m <x <2},画出数轴,可得m =-1,n =1.8.已知集合A x|y =log x -12B ={x |x <2m -1},且A ⊆∁R B ,则m 的最大值是34.[解析]依题意,A x |y =log x -12x |x >12∁R B ={x |x ≥2m -1},又A ⊆∁R B ,所以2m -1≤12,解得m ≤34.故m 的最大值为34.。
2020版新设计一轮复习数学(文)江苏专版课时跟踪检测(三十八) 直线、平面平行的判定及其性质 含解析
课时跟踪检测(三十八) 直线、平面平行的判定及其性质一抓基础,多练小题做到眼疾手快1.(2019·汇龙中学测试)已知直线a 与直线b 平行,直线a 与平面α平行,则直线b 与α的位置关系为________. 解析:依题意,直线a 必与平面α内的某直线平行,又a ∥b ,因此直线b 与平面α的位置关系是平行或直线b 在平面α内.答案:平行或直线b 在平面α内2.(2018·南京模拟)在空间四边形ABCD 中,E ,F 分别是AB 和BC 上的点,若AE ∶EB =CF ∶FB =1∶2,则对角线AC 和平面DEF 的位置关系是________.解析:如图,由AE EB =CFFB 得AC ∥EF . 又因为EF ⊂平面DEF ,AC ⊄平面DEF , 所以AC ∥平面DEF . 答案:AC ∥平面DEF3.(2018·天星湖中学测试)在正方体ABCD -A 1B 1C 1D 1中,下列四对截面中彼此平行的是________(填序号). ①平面A 1BC 1和平面ACD 1; ②平面BDC 1和平面B 1D 1A ; ③平面B 1D 1D 和平面BDA 1; ④平面ADC 1和平面A 1D 1C .解析:如图,结合正方体的性质及面面平行的判定可知平面A 1BC 1∥平面ACD 1,平面BDC 1∥平面B 1D 1A .答案:①②4.如图,α∥β,△PAB 所在的平面与α,β分别交于CD ,AB ,若PC =2,CA =3,CD =1,则AB =________.解析:因为α∥β,所以CD ∥AB , 则PC PA =CDAB ,所以AB =PA ×CD PC =5×12=52.答案:525.如图,在下列四个正方体中,A,B为正方体的两个顶点,M,N,Q为所在棱的中点,则在这四个正方体中,直线AB与平面MN Q平行的是________.(填序号)解析:因为点M,N,Q分别为所在棱的中点,所以在①中AB与平面MN Q相交,在②③中均有AB∥M Q,在④中,有AB∥N Q,所以在②③④中均有AB与平面MN Q平行.答案:②③④二保高考,全练题型做到高考达标1.(2018·滨海期末)已知m,n是不重合的直线,α,β,γ是不重合的平面,已知α∩β=m,n⊂γ,若增加一个条件就能得出m∥n,则下列条件中能成为增加条件的序号是________.①m∥γ,n∥β;②α∥γ,n⊂β;③n∥β,m⊂γ.解析:对于①,若β∥γ,由m⊂β,满足m∥γ,由n⊂γ,满足n∥β,但m,n可为异面直线,则不成立;对于②,由α∥γ,且α∩β=m,β∩γ=n,由面面平行的性质定理可得m∥n,则成立;对于③,n∥β,m⊂γ,则γ∩β=m,由线面平行的性质定理可得n∥m,则成立.答案:②或③2.(2019·连云港调研)一条直线与两个平行平面中的一个成30°角,且被两平面所截得的线段长为2,那么这两个平行平面间的距离是________.解析:由题意知,两个平行平面间的距离d=2sin 30°=1.答案:13.(2018·前黄高级中学检测)已知正方体ABCD-A1B1C1D1,下列结论中,正确的是________(填序号).①AD1∥BC1;②平面AB1D1∥平面BDC1;③AD1∥DC1;④AD1∥平面BDC1.解析:如图,因为AB∥C1D1,AB=C1D1,所以四边形AD1C1B为平行四边形,故AD1∥BC1,从而①正确;易证AB1∥DC1,BD∥B1D1,又AB1∩B1D1=B1,BD∩DC1=D,故平面AB1D1∥平面BDC1,从而②正确;由图易知AD1与DC1异面,故③错误;因为AD1∥BC1,AD1⊄平面BDC1,BC1⊂平面BDC1,所以AD1∥平面BDC1,故④正确.答案:①②④4.如图,透明塑料制成的长方体容器ABCD-A1B1C1D1内灌进一些水,固定容器底面一边BC于地面上,再将容器倾斜,随着倾斜度的不同,有下面四个命题:①没有水的部分始终呈棱柱形;②水面EFGH 所在四边形的面积为定值; ③棱A 1D 1始终与水面所在平面平行; ④当容器倾斜如图所示时,BE ·BF 是定值. 其中正确命题的个数是________.解析:由题图,显然①是正确的,②是错误的; 对于③,因为A 1D 1∥BC ,BC ∥FG , 所以A 1D 1∥FG 且A 1D 1⊄平面EFGH , 所以A 1D 1∥平面EFGH (水面). 所以③是正确的;对于④,因为水是定量的(定体积V ), 所以S △BEF ·BC =V ,即12BE ·BF ·BC =V .所以BE ·BF =2VBC (定值),即④是正确的. 答案:35.在三棱锥P -ABC 中,PB =6,AC =3,G 为△PAC 的重心,过点G 作三棱锥的一个截面,使截面平行于PB 和AC ,则截面的周长为________.解析:如图,过点G 作EF ∥AC ,分别交PA ,PC 于点E ,F ,过点E 作EN ∥PB 交AB 于点N ,过点F 作FM ∥PB 交BC 于点M ,连接MN ,则四边形EFMN 是平行四边形(平面EFMN 为所求截面),且EF =MN =23AC =2,FM =EN =13PB =2,所以截面的周长为2×4=8.答案:86.设α,β,γ是三个平面,a ,b 是两条不同直线,有下列三个条件: ①a ∥γ,b ⊂β;②a ∥γ,b ∥β;③b ∥β,a ⊂γ.如果命题“α∩β=a ,b ⊂γ,且________,则a ∥b ”为真命题,则可以在横线处填入的条件是________(把所有正确的序号填上).解析:由面面平行的性质定理可知,①正确;当b ∥β,a ⊂γ时,a 和b 在同一平面内,且没有公共点,所以平行,③正确.故应填入的条件为①或③.答案:①或③7.(2018·盐城期末)已知棱长为2的正方体ABCD -A 1B 1C 1D 1,E 为棱AD 的中点,现有一只蚂蚁从点B 1出发,在正方体ABCD -A 1B 1C 1D 1表面上行走一周后再回到点B 1,这只蚂蚁在行走过程中与平面A 1EB 的距离保持不变,则这只蚂蚁行走的轨迹所围成的图形的面积为________.解析:要满足题意,则需在正方体ABCD -A 1B 1C 1D 1上过B 1作与平面A 1EB 平行的平面.取A 1D 1和BC 的中点分别为F ,G ,连结B 1F ,FD ,DG ,GB 1,则A 1F 綊ED ,所以四边形A 1FDE 是平行四边形,所以A 1E ∥FD .因为FD ⊄平面A 1EB ,A 1E ⊂平面A 1EB ,所以FD ∥平面A 1EB .同理:DG ∥平面A 1EB .又FD ∩DG =D ,所以平面DFB 1G ∥平面A 1EB ,则四边形DFB 1G所围成图形的面积即为所求.易知四边形DFB 1G 为菱形,由正方体的棱长为2,得菱形DFB 1G 的边长为5,cos∠A 1EB =15,∴sin ∠A 1EB =265,∵∠A 1EB =∠FDG ,∴S 菱形DFB 1G =5×5×sin ∠FDG =2 6. 答案:2 68.(2019·海安中学检测)如图,在棱长为1的正方体ABCD -A 1B 1C 1D 1中,点E ,F 分别是棱BC ,CC 1的中点,P 是侧面BCC 1B 1内一点,若A 1P ∥平面AEF ,则线段A 1P 长度的取值范围是________.解析:取B 1C 1的中点M ,BB 1的中点N ,连结A 1M ,A 1N ,MN ,可以证明平面A 1MN ∥平面AEF ,所以点P 位于线段MN 上,因为A1M =A 1N =1+⎝⎛⎭⎫122=52,MN=⎝⎛⎭⎫122+⎝⎛⎭⎫122=22,所以当点P 位于M ,N 处时,A 1P 的长度最长,取MN 的中点O ,连结⎝⎛⎭⎫522-⎝⎛⎭⎫242=324,A 1O ,当P 位于MN 的中点O 时,A 1P 的长度最短,此时A 1O =所以A 1O ≤A 1P ≤A 1M ,即324≤A 1P ≤52,所以线段A 1P 长度的取值范围是⎣⎡⎦⎤324,52.答案:⎣⎡⎦⎤324,529.如图,在四棱锥P -ABCD 中,AD ∥BC ,AB =BC =12AD ,E ,F ,H 分别为线段AD ,PC ,CD 的中点,AC 与BE 交于O 点,G 是线段OF 上一点.求证:(1)AP ∥平面BEF ; (2)GH ∥平面PAD . 证明:(1)连结EC ,因为AD ∥BC ,BC =12AD ,所以BC 綊AE ,所以四边形ABCE 是平行四边形, 所以O 为AC 的中点.又因为F 是PC 的中点,所以FO ∥AP , 因为FO ⊂平面BEF ,AP ⊄平面BEF , 所以AP ∥平面BEF .(2)连结FH ,OH ,因为F ,H 分别是PC ,CD 的中点, 所以FH ∥PD ,因为PD ⊂平面PAD ,FH ⊄平面PAD , 所以FH ∥平面PAD .又因为O 是AC 的中点,H 是CD 的中点, 所以OH ∥AD ,因为AD ⊂平面PAD ,OH ⊄平面PAD , 所以OH ∥平面PAD .又FH ∩OH =H ,所以平面OHF ∥平面PAD . 因为GH ⊂平面OHF ,所以GH ∥平面PAD .10.如图所示,在正方体ABCD -A 1B 1C 1D 1中,E ,F ,G ,H 分别是BC ,CC 1,C 1D 1,A 1A的中点.求证:(1)BF ∥HD 1; (2)EG ∥平面BB 1D 1D ; (3)平面BDF ∥平面B 1D 1H .证明:(1)如图所示,取BB 1的中点M ,连结MH ,MC 1,易证四边形HMC 1D 1是平行四边形, 所以HD 1∥MC 1.又因为MC 1∥BF ,所以BF ∥HD 1. (2)取BD 的中点O ,连结EO ,D 1O ,则OE 綊12DC ,又D 1G 綊12DC ,所以OE 綊D 1G ,所以四边形OEGD 1是平行四边形, 所以GE ∥D 1O .又GE ⊄平面BB 1D 1D ,D 1O ⊂平面BB 1D 1D , 所以EG ∥平面BB 1D 1D . (3)由(1)知BF ∥HD 1,又BD ∥B 1D 1,B 1D 1,HD 1⊂平面B 1D 1H ,BF ,BD ⊂平面BDF ,且B 1D 1∩HD 1=D 1,DB ∩BF =B , 所以平面BDF ∥平面B 1D 1H . 三上台阶,自主选做志在冲刺名校1.(2018·扬州期中)若半径为5的球被两个相互平行的平面截得的圆的半径分别为3和4,则这两个平面之间的距离为________.解析:∵半径为5的球被两个相互平行的平面截得的圆的半径分别为3和4,∴圆心到两个平面的距离分别为: 52-32=4,52-42=3,∴当两个平面位于球心同侧时,两平面间的距离为4-3=1,当两个平面位于球心异侧时,两平面间的距离为4+3=7.答案:1或72.如图所示,设正方体ABCD -A 1B 1C 1D 1的棱长为a ,点P 是棱AD 上一点,且AP =a3,过B 1,D 1,P 的平面交平面ABCD 于P Q ,Q 在直线CD 上,则P Q =________.解析:因为平面A 1B 1C 1D 1∥平面ABCD ,而平面B 1D 1P ∩平面ABCD =P Q ,平面B 1D 1P ∩平面A 1B 1C 1D 1=B 1D 1,所以B 1D 1∥P Q . 又因为B 1D 1∥BD , 所以BD ∥P Q , 设P Q ∩AB =M , 因为AB ∥CD , 所以△APM ∽△DP Q . 所以P Q PM =PDAP =2, 即P Q =2PM .又知△APM ∽△ADB , 所以PM BD =AP AD =13, 所以PM =13BD ,又BD =2a ,所以P Q =223a .答案:223a3.(2019·南通调研)如图,已知三棱柱ABC -A 1B 1C 1,E ,F 分别为CC 1,BB 1上的点,且EC =B 1F ,过点B 做截面BMN ,使得截面交线段AC 于点M ,交线段CC 1于点N . (1)若EC =3BF ,试确定M ,N 的位置,使平面BMN ∥平面AEF ,并说明理由;(2)若K ,R 分别为AA 1,C 1B 1的中点,求证:KR ∥平面AEF . 解:(1)当AM AC =EN EC =13时,平面BMN ∥平面AEF . 理由如下:∵EN =13EC ,BF =13EC ,∴EN 綊BF ,∴四边形BFEN 是平行四边形,∴BN ∥EF .∵AM AC =ENEC ,∴MN ∥AE ,∵MN ⊂平面BMN ,BN ⊂平面BMN ,且MN ∩BN =N ,AE ⊂平面AEF ,EF ⊂平面AEF ,且AE ∩EF =E , ∴当AM AC =EN EC =13时,平面BMN ∥平面AEF . (2)证明:连结BC 1,交FE 于点Q ,连结Q R .∵△B Q F ≌△C 1Q E ,∴B Q =C 1Q , ∴Q R ∥BB 1,且Q R =12BB 1,∴Q R 綊AK .∴四边形AKR Q 为平行四边形.连结A Q,则A Q∥KR,∵A Q⊂平面AEF,KR⊄平面AEF,∴KR∥平面AEF.。
(江苏专用)2020版高考数学总复习第二节不等式的证明和几个重要不等式的应用课件苏教版选修4_5
证:a2+2b2+c2≥10.
证明
由柯西不等式得[a2+( 2
b)2+c2]·12
2 2
2
12
≥(a+b+c)2.
因为a+b+c=5,所以(a2+2b2+c2)· 5 ≥25.
2
所以a2+2b2+c2≥10,当且仅当a=2b=c=2时取等号.
方法技巧 基本不等式、均值不等式是证明不等式的重要工具,注意基本不等式的 正向应用、逆向应用和变形应用以及不等式应用的条件.
3-1 (2018江苏四校高三调研)已知x,y均为正数,且x>y,求证:2x+
x2
1 2xy
y
2
≥2y+3.
证明 因为x>0,y>0,x-y>0,
所以2x+ x2
2.不等式证明的其他方法和技巧
(1)反证法 从否定结论出发,经过逻辑推理,导出矛盾,证实结论的否定是错误的,从 而肯定结论是正确的证明方法. (2)放缩法 欲证A≥B,可通过适当放大或缩小,借助一个或多个中间量,使得A≥C1 ≥C2≥…≥Cn≥B,利用传递性达到证明的目的.
3.柯西不等式
若a、b、c、d均为实数,则③ (a2+b2)(c2+d2)≥(ac+bd)2 ,当且仅当ad= bc时取等号. 柯西不等式的一般形式:设a1、a2、…、an、b1、b2、…、bn为实数,则( a12 + a22 +…+ an2 )( b12+ b22+…+ bn2)≥(a1b1+a2b2+…+anbn)2,当且仅当bi=0(i=1,2, …,n)或存在一个数k,使得ai=kbi(i=1,2,…,n)时,等号成立.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
____第38课__基本不等式及其简单应用(2)____
1. 运用基本不等式求最值、取值范围及不等式恒成立问题.
2. 运用基本不等式解决实际应用问题中的最值问题.
1. 阅读:必修5第99~101页.
2. 解悟:①应用基本不等式解决实际问题,首先要正确理解题意,然后通过分析、思考,将实际问题转化为数学模型,再应用基本不等式求解;②解应用题时,一定要注意变量的实际意义及其取值范围;③解应用问题时,若等号取得的条件不足,应如何处理?
3. 践习:在教材上的空白处,完成必修5第102页习题第3、4题.
基础诊断
1. 在平面直角坐标系Oy 中,曲线4x 2+9
y 2=1上的点到原点O 的最短距离为__5__.
解析:设曲线
4x 2+9y 2
=1上的点P(,y).设P(,y)到原点的距离为d =x 2+y 2=
(x 2+y 2)⎝ ⎛⎭
⎪⎫
4x 2+9y 2=
13+4y 2x 2+9x 2
y
2≥
13+2
4y 2x 2·9x 2y 2=5,当且仅当4y 2x 2=9x 2
y
2时,d 取最小值,所以曲线4x 2+9
y
2=1上的点到原点O 的最短距离为5.
2. 已知,y ,∈R +
,-2y +3=0,则y 2
xz
的最小值是__3__.
解析:因为,y ,>0,-2y +3=0,所以2y =+3,所以4y 2=2+6+92≥2x 2·9z 2+6=12,
当且仅当2
=92
,即=3时取等号,所以4y 2
≥12,y 2
xz
≥3.
3. 已知函数y =log a (+3)-1(a>0且a ≠1)的图象恒过定点A ,若点A 在直线m +ny +1=0上(其中mn>0),则1m +2
n
的最小值是__8__.
解析:由题意可得定点A(-2,-1),又因为点A 在直线m +ny +1=0上,所以2m +n =1,且mn>0,所以m>0,n>0.则1m +2n =2m +n m +4m +2n n =4+n m +4m n ≥4+4=8,当且仅当n m =4m
n 时
取等号,故1m +2
n
的最小值是8.
4. 从等腰直角三角形纸片ABC 上剪下如图所示的两个正方形,其中,BC =2,∠A =90°,
则这两个正方形面积之和的最小值为__1
2
__.
解析:设两个正方形的边长分别为a ,b ,则由题意可得a +b =BC 2=1,且13≤a ,b ≤2
3,所以
两个正方形面积之和为S =a 2
+b 2
≥2×⎝ ⎛⎭⎪
⎫a +b 22=1
2
,当且仅当a =b =12时取等号,故两个正方形面积之和最小为1
2
.
范例导航
考向❶ 基本不等式与函数综合问题
例1 设,y 是正实数,且+y =1,求x 2x +2+y 2
y +1的最小值.
解析:设+2=m ,y +1=n.
因为+y =1,所以m +n =+y +3=4,
所以x 2x +2+y 2y +1=(m -2)2m +(n -1)2n =m +n +4m +1n -6=4m +1n -2.
因为m +n =4,所以1=1
4
(m +n),
所以4m +1n -2=14(m +n)⎝ ⎛⎭⎪⎫
4m +1n -2=14⎝ ⎛⎭⎪⎫5+4n m +m n -2≥14.
当且仅当m =2n 时,取等号, 由+2=2(y +1)得=2y ,
即当=23,y =13时,x 2x +2+y 2y +1取得最小值14
.
已知实数,y 满足>y>0,且log 2+log 2y =1,求x 2+y 2
x -y
的最小值.
解析:因为log 2+log 2y =1,所以log 2y =1,所以y =2,所以x 2+y 2x -y =(x -y )2+2xy x -y =-y +
4
x -y ≥2×2=4,当且仅当=1+3,y =3-1时取等号,故x 2+y 2
x -y 的最小值为4.
考向❷ 基本不等式在实际应用问题中的运用
例2 某工厂利用辐射对食品进行灭菌消毒,现准备在该厂附近建一职工宿舍,并对宿舍进行防辐射处理,建宿舍的费用与宿舍到工厂的距离有关. 若建造宿舍的所有费用p(万元)和宿舍与工厂的距离(m )的关系式为p =k
3x +5(0≤≤8),若距离为1m 时,测算宿舍建造费用为100万元.为
了交通方便,工厂与宿舍之间还要修一条道路,已知购置修路设备需5万元,铺设路面每千米成本为6万元.设 f()为建造宿舍与修路费用之和.
(1) 求f()的表达式;
(2) 宿舍应建在离工厂多远处,可使总费用f()最小?并求最小值.
解析:(1) 根据题意得100=k 3×1+5,所以=800.故f()=800
3x +5+5+6,∈[0,8].
(2) f()=800
3x +5+2(3+5)-5≥
2
800
3x +5
·2(3x +5)-5=80-5=75, 当且仅当800
3x +5=2(3+5),即=5时,取等号,此时f()的最小值是75,
所以宿舍应建在离工厂5m 处,可使总费用f()最小,最小值为75万元.
在某次水下考古活动中,需要潜水员潜入水深为30米的水底进行作业,其用氧量包含3个方面:①下潜时,平均速度为v(米/单位时间),单位时间内用氧量为cv 2(c 为正常数);②在水底作业需5个单位时间,每个单位时间用氧量为0.4;③返回水面时,平均速度为v
2(米/单位时间),单位
时间用氧量为0.2,记该潜水员在此次考古活动中,总用氧量为y.
(1) 将y 表示为v 的函数.
(2) 设0<v ≤5,试确定下潜速度v ,使总的用氧量最少. 解析:(1) 潜入水底用时30v ,用氧量30
v ·cv 2=30cv ,
水底作业时用氧量为5×0.4=2, 返回水面用时60v ,用氧量60v ×0.2=12
v ,
所以y =30cv +2+12
v (v>0).
(2) y =30cv +2+12
v
≥2+2
30cv ·12
v
=2+1210c ,
当且仅当30cv =12
v ,即v =
2
5c
时取等号. 当
25c ≤5,即c ≥2
125
时,v =2
5c
时,y 取得最小 值为2+1210c. 当
25c >5,即0<c<2125时,y ′=30c -12v 2=30cv 2-12v 2
<0, 因此函数y =30cv +2+12
v 在(0,5]上为减函数,
所以当v =5时,y 的最小值为150c +22
5.
综上,当c ≥2
125
时,下潜速度为
2
5c
时,用氧量最小为2+1210c ; 当0<c<2125时,下潜速度为5时,用氧量最小为150c +22
5
.
自测反馈
1. 已知点(,y)在直线+3y -2=0上运动,则函数=3+27y +3的最小值是__9__.
解析:因为+3y -2=0,所以+3y =2.又因为3>0,27y >0,所以=3+27y +3=3+33y +3≥23x ·33y +3=232+3=9,当且仅当3=33y ,即=3y =1时取等号.
2. 过点(1,2)的直线l 与轴的正半轴、y 轴的正半轴分别交于A ,B 两点,O 为坐标原点,当△AOB 的面积最小时,直线l 的方程为__2+y -4=0__.
解析:由题意可设直线l 的方程为x a +y b =1,a>0,b>0.因为直线l 过点(1,2),所以1a +2
b =1,
所以1=1a +2
b
≥2
2ab ,所以ab ≥8,当且仅当1a =2b =1
2
,即a =2,b =4时取等号,此时△AOB 的面积取得最小值12ab =4,所以直线l 的方程为x 2+y
4
=1,即2+y -4=0.
3. 已知a>0,b>0,若不等式m 3a +b -3a -1
b ≤0恒成立,则实数m 的最大值为__16__.
解析:根据已知不等式,分离变量得m ≤(3a +b)⎝ ⎛⎭⎪⎫3a +1b ,a>0,b>0.由(3a +b)⎝ ⎛⎭⎪⎫
3a +1b =10+3b a +3a
b
≥10+23b a ·3a b =16,当且仅当3a b =3b
a
,即a =b 时取等号,故m 最大值为16. 4. 对于任意∈R ,不等式22-a x 2+1+3>0恒成立,则实数a 的取值范围为__(-∞,3)__.
解析:由题意得22-a x 2+1+3>0对于∈R 恒成立,即a <
2x 2+3
x 2
+1
对于∈R 恒成立.令x 2+1
=t (t ≥1),则2
=t 2
-1,所以y =2t 2+1t =2t +1t .因为y =2t +1
t
在[1,+∞)上单调递增,所以当t =1
时,y 有最小值3,所以a <3.
1. 最值问题的处理方法:①直接利用基本不等式放缩(几种配凑的技巧);②消元转化为函数求最值.
2. 在运用基本不等式求函数最值时,若等号取不到,可利用函数的单调性求解.
3. 你还有哪些体悟,写下;:。
