第五章积分
高等数学 第5章 第一节 定积分的概念
定积分存在的两个充分条件:
定理1 设 f ( x) 在区间 [a, b]上连续, 则 f ( x)在区间 [a, b] 上可积. 定理2 设 f ( x)在区间 [a, b] 上有界, 且只有有限个间断点,则
f ( x)在区间 [a, b]上可积.
6
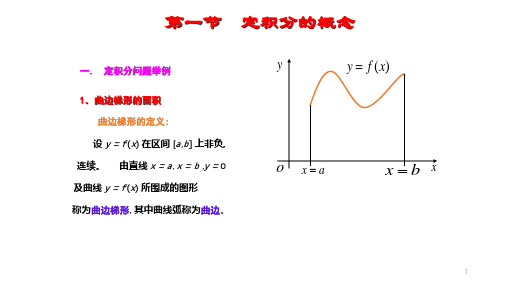
定积分的几何意义
y y f (x)
A
o xa xb x
lim
n
6n 2
3
10
1 i n
i
},
0,
n
A lim 0 i1
f ( i )xi
An
x xn1 nxn b
3
2. 变速直线运动的路程
设物体作直线运动,
已知速度 v v(t )是时间间隔 [T1 ,T2 ]上 的
连续函数, 且 v(t ) 0, 计算在这段时间内物体所经过的路程。
匀速直线运动:
路程=速度×时间.
(1) 分割
T1 t0 t1 ti1 ti tn T2 ,
v( i )
ti ti ti1
(i 1,2,, n)
(2) 近似代替
si v( i )t i
T1
i
T2
t t0 t1 t2 ti1 ti tn1 tn
(3) 求和 (4) 取极限
s
n i 1
s
i
n v(
i 1
i )t i
每 个小区间的长度 xi xi xi1 (i 1,2,n).
2
(2)近似代替
y Ai f (i )xi
(i 1,2,, n)
(3)求和
y f (x)
A1 A2
Ai
A
n i 1
Ai
n
高等数学(同济大学第五版)第五章 定积分

π
3 6 3
, M = f ( 3 ) = 3 arctan 3 =
π
3
.
因此
π
6 3
( 3−
1 3
) ≤ ∫ 1 x arctan xdx ≤
3
3
π
3
( 3−
1 3
),
即
π
9
≤ ∫ 1 x arctan xdx ≤
3
2
3
2π . 3
(4)先求函数 f ( x) = e x
f ′( x ) = e x
成 n 个长度相等的小区间, 各个小区间的长度为: Δx i =
第二步: 在第i个小区间[xi−1, xi] (i=1, 2, ⋅ ⋅ ⋅, n)上取右端点 ξ i = x i = a +
S n = ∑ f (ξ i )Δx i = ∑ [(a +
i =1 i =1 n n
b−a 2 b−a i ) +1]⋅ n n
2 2 2 2 1 1
b
b
b
b
(4) ∫0 xdx 还是 ∫0 ln(1+ x)dx ? (5) ∫0 e x dx 还是 ∫0 (1+ x)dx ? 解 (1)因为当 0≤x≤1 时, x2≥x3, 所以 ∫0 x 2 dx ≥ ∫0 x 3 dx . 又当 0<x<1 时, x2>x3, 所以 ∫0 x 2 dx > ∫0 x 3 dx . (2)因为当 1≤x≤2 时, x2≤x3, 所以 ∫1 x 2 dx ≤ ∫1 x 3 dx . 又因为当 1<x≤2 时, x2<x3, 所以 ∫1 x 2 dx < ∫1 x 3 dx . (3)因为当 1≤x≤2 时, 0≤ln x<1, ln x≥(ln x)2, 所以 ∫1 ln xdx ≥ ∫1 (ln x) 2 dx . 又因为当 1<x≤2 时, 0<ln x<1, ln x>(ln x)2, 所以 ∫1 ln xdx > ∫1 (ln x) 2 dx . (4)因为当 0≤x≤1 时, x≥ln(1+x), 所以 ∫0 xdx ≥ ∫0 ln(1+ x)dx . 又因为当 0<x≤1 时, x>ln(1+x), 所以 ∫0 xdx > ∫0 ln(1+ x)dx . (5)设f(x)=ex−1−x, 则当 0≤x≤1 时f ′(x) =ex−1>0, f(x)=ex−1−x是单调增加的. 因此当 0≤x≤1 时, f(x)≥f(0)=0, 即ex≥1+x, 所以 ∫0 e x dx ≥ ∫0 (1+ x)dx . 又因为当 0<x≤1 时, ex>1+x, 所以 ∫0 e x dx > ∫0 (1+ x)dx .
第五章 定积分的计算

z eix
第五章 定积分的计算 16
[例]计算 I
ix 令 z e 0 , 解:设 ,则
2
0
dx (1 cosx)2
(1 1)
z z 1 2 dz 4z I (1 ) dz 2 2 z 1 z 1 i(z 2 z ) 2 iz
第五章 定积分的计算 9
(2)已知 f ( z ) ( z ) 有单极点 z n (n 0,1,2, ) Γ( z n 1) Re sz (n 1) ,有 据 Γ( z )
( z n)Γ( z n 1) Re sΓ(n) lim z n z ( z 1) ( z n 1)(z n)
k 1
m
证毕.
2015/11/18
第五章 定积分的计算
6
1.3 解析函数沿闭曲线的积分,取决于曲线内包围的 孤立奇点的 性质, 这与点电荷的静电场是由点电荷所在点的性质确定的 相一致,点电荷 所在点是场的 奇异点.
解析点,无留数 有限远点奇点留数可以存在 2 或 0 [ 如 f z , Res f ( 0 ) 0 ] 说明 1 解析点不一定无留数 : f e z , Resf () 1 z 奇点不一定有留数 : f e , Resf () 0
Γ(n n 1) Γ(1) (1) n n (n)( n 1) (1) (1) n! n! (3) f ( z ) 41 1 k z 1 i ( 2 k ) i
z ( z 1)(z 2) ( z n)
( z 4 1) 0 z e 4
不是奇点未必无留数.
高等数学第05章 定积分及其应用习题详解

0
x 1 sin tdt 0dt 1 , 2
b a
f ( x)dx 在 几 何 上 表 示 由 曲 线 y f ( x) , 直 线
x a, x b 及 x 轴所围成平面图形的面积. 若 x a, b时,f ( x) 0, 则 b f ( x)dx 在几何 a
上表示由曲线 y f ( x) ,直线 x a, x b 及 x 轴所围平面图形面积的负值. (1)由下图(1)所示, 1 xdx ( A1 ) A1 0 .
n
2
i
i 1
n
2
1 1 1 1 1 n(n 1)(2n 1) = (1 )(2 ) 3 n 6 6 n n 1 1 2 当 0时 (即 n 时 ) ,由定积分的定义得: x d x = . 0 3
= 5. 利用定积分的估值公式,估计定积分
4 3
1 1
(4 x 4 2 x 3 5) dx 的值.
上任取一点 i 作乘积 f ( i ) xi 的和式:
n
f ( i ) xi c ( xi xi1 ) c(b a) ,
i 1 i 1
n
n
记 max{xi } , 则
1i n
b a
cdx lim f ( i ) xi lim c(b a) c(b a) .
x
0
(t 1)dt ,求 y 的极小值
解: 当 y x 1 0 ,得驻点 x 1 , y '' 1 0. x 1 为极小值点, 极小值 y (1)
( x 1)dx - 2
第五章二重积分

第五章 二 重 积 分1.定义:∑⎰⎰=→∆=nk k k k Df y x f 10d ),(lim d ),(σηξσ2.几何意义:3.性质:1) 比较定理: 若),(),(y x g y x f ≤,则⎰⎰⎰⎰≤DDy x g y x f .d ),(d ),(σσ2) 估值定理: 若),(y x f 在D 上连续,则.d ),(MS y x f mS D⎰⎰≤≤σ3) 中值定理: 若),(y x f 在D 上连续,则S f y x f D),(d ),(ηξσ⎰⎰=.4.计算1) 直角坐标: 2) 极坐标:i) 适合用极坐标计算的被积函数:);(),(),(22yxf x y f y x f +ii)适合用极坐标的积分域:3) 利用奇偶性.①若积分域D 关于y 轴对称,则:⎰⎰⎰⎰⎪⎩⎪⎨⎧=≥DD x x y x f y x f y x f d y x f x .),(0.),(d ),(2),(0为奇函数关于为偶函数关于σσ②若积分域关于x 轴对称,则⎰⎰⎰⎰⎪⎩⎪⎨⎧=≥DD y y y x f y x f y x f d y x f y .),(0.),(d ),(2),(0为奇函数关于为偶函数关于σσ4) 利用对称性:若D 关于x y =对称,则`.d ),(d ),(⎰⎰⎰⎰=DDx y f y x f σσ特别的: ⎰⎰⎰⎰=DDd y f d x f σσ)()(题型一 计算二重积分例5.1计算⎰⎰+Dx ye x σd )|(|2,其中D 由曲线1||||=+y x 所围成.解 由奇偶性知原式=⎰⎰⎰⎰=14D Dxd d x σσ (其中1D 为D 在第一象限的部分).3241010==⎰⎰-x xdy dx例5.2设区域D 为222R y x ≤+,则⎰⎰+D b y a x σd )(2222=.解法1)11(4)sin cos ()(224320022222222b a R d b a d d b y a x R D+=+=+⎰⎰⎰⎰πρρθθθσπ. 解法2 由于积分域222:R y x D ≤+关于直线x y =对称,则σσd b x ay d b y a x D D ⎰⎰⎰⎰+=+)()(22222222. 从而有 21)(2222=+⎰⎰σd b y ax D [左端 + 右端] σd y x b a D ⎰⎰++=)()11(212222)11(4)11(21222004322ba R d db a R +=+=⎰⎰ππρρθ 例 5.3设区域{}0,0,4|),(22≥≥≤+y x y x y x D ,)(x f 为D 上正值连续函数,b a ,为常数,则⎰⎰=++Dy f x f y f b x f a σd )()()()(.A)πab , B)π2ab , C)π)(b a +, D)π2b a +. 解法1直接法 由于积分域D 关于直线x y =对称,则⎰⎰⎰⎰++=++DDd x f y f x f b y f a d y f x f y f b x f a σσ)()()()()()()()(.原式])()()()()()()()([21⎰⎰⎰⎰+++++=D D d x f y f x f b y f a d y f y f y f b x f a σσπσ2)(21ba db a D+=+=⎰⎰.故应选(D ). 解法2 排除法取,1)(≡x f 显然符合题设条件,而⎰⎰++Dy f x f y f b x f a σd )()()()(πσ2)(21ba db a D+=+=⎰⎰. 显然(A ),(B ),(C )均不正确,故应选(D )。
第五章 积分 5-1 定积分的概念与基本性质

b
b
|
a
f (x)d
x|
|
a
f (x)|d
x.
证明 由于 | f (x) | f (x) | f (x) |, 应用性质 3
b
b
b
a | f (x)|d x | a f (x) d x a | f (x)|d x,
43
4
1
1
1
2
7 1 sin 2
1 sin 2 x 1 sin 2
, 3
3
4
所以
21
3
4
4 7
d
x
3
4
dx 1 sin 2
x
3
4
2 3
d
x
.
18
《高等数学》课件 (第五章第一节)
推论 2 设 f R [a, b], 且在 [a, b] 上 f (x) 0, 则
b
a f ( x) d x 0.
性质 2 (积分对区间的可加性) 设 a c b, f R [a, b], 则 f R [a, c], f R [c, b],
且
b
c
b
f (x) d x f (x) d x f (x) d x.
a
a
c
一般, 当上式中三个积分都存在时, 无论 a, b, c 之间具有怎样 的大小关系, 等式都成立.
当 f (x) R [a, b] 时, 可在积分的定义中, 对 [a, b] 作特殊的分
划, 并取特殊的 i [x i 1, x i] , 计算和式. 如等分区间 [a, b], 并取 点 i 为 [x i 1, x i] 的右端点 x i 或左端点 x i 1 或中点.
第五章 不定积分
例题) 第一节 不定积分的概念(例题) 例.
5 求过点 (1, 2 ) ,且在其上任意一点 (x
, y) 处的切线
的曲线方程. 斜率为 x 的曲线方程. 解:设所求曲线方程为 y=F(x),则 F ′( x ) = x . ,
1 2 y = F ( x ) = ∫ xdx = x + C 2
5 将 x = 1,y = 代入上式: 代入上式: 2 5 1 2 = ×1 + C ⇒ C = 2 2 2 1 2 故 y = x + 2为所求曲线方程 . 2
y o
F ( x)
F ( x) + C2
F(x) 是 f(x) 的一条 积分曲线. 积分曲线.
x
x
个单位, 将 F(x) 沿 y 轴平移 C 个单位,即得关于 f(x) 的 积分曲线族. 积分曲线族. 积分曲线族中的所有曲线在横坐标相同的点处的 积分曲线族中的所有曲线在横坐标相同的点处的 所有曲线 切线互相平行. 切线互相平行.
y=∫
x
已知固定成本为1000元 已知固定成本为1000元, 即当 x=0时, y=1000. 1000 = = 000. 因此有C=1000, 因此有 =1000,于是可得
y = 7 x + 50 x + 1000 ,
25 y′dx = ∫ (7 + )dx = 7 x + 50 x + C . x
x u= a
x =u a
1 1 1 du = arctan u + C = ∫ 2 a a 1+ u
1 x = arctan + C . a a
dx d( ) = a a
1 dx x ∫ a2 + x2 = a arctan a + C.
高等数学第五章定积分的概念与性质
(2)当a b 时, f ( x )dx f ( x )dx .
a b
b
a
说明 在下面的性质中,假定定积分都存 在,且不考虑积分上下限的大小.
性质1 证
a [ f ( x ) g( x )]dx a f ( x )dx a g( x )dx .
b
b
b
a [ f ( x ) g( x )]dx
0 n
2
0 x
1
2
dx lim i xi
0 i 1
n
1 1 1 1 lim 1 2 . n 6 n n 3
例2. 用定积分表示下列极限:
1 i (1) lim 1 n n i 1 n
n
1p 2 p n p (2) lim n n p 1
1 1 i sin i lim sin lim n n n n n n i 1 i 1
n n
1 sin xdx . 0
i x i
三、定积分的性质
对定积分的补充规定:
(1)当a b 时, f ( x )dx 0 ;
Ai f ( i )xi
曲边梯形面积的近似值为 A f ( i )xi
i 1
n
怎样用数学的语言描述划分不断加细?
当分割无限加细, 即小区间的最大长度
max{ x1 , x2 , xn }趋近于零 ( 0) 时,
曲边梯形面积为 A lim f ( i )xi
0 i 1
n
实例2 (求变速直线运动的路程)
设某物体作直线运动,已知速度v v (t ) 是 时 间 间 隔 [T1 , T2 ] 上 t 的 一 个 连 续 函 数 , 且 v ( t ) 0 ,求物体在这段时间内所经过的路程.
高等数学 第五章 第2节 换元积分法(中央财经大学)
f (u ) ∈ C ( I ), 又 u = ϕ ( x) 在区间 J 上可微 , 且 ϕ ( J ) ⊂ I , 则在区间 J 上有
∫ f (ϕ (x))ϕ ′( x) d x = ∫ f (u) d u
= F (u ) + C = F (ϕ ( x)) + C. 该定理称为不定积分的第一换元法,也叫“凑微分”法。
∫
f ( x) d x = F (ϕ −1 ( x)) + C ,
其中, −1 ( x) 是 ϕ (t ) 的反函数; 是积分常数。 ϕ C 该定理描述的是不定积分第二换元法。
例 解
计算
∫
dx x2 + a2
(a > 0).
此题可以用 第一换元法 计算。
现在采用第二换元法计算。
2
π π 令 x = a tan t,则 d x = a sec t d t, - < t < ,故 2 2
(u = cos x) ;
(8)
(u = sin x) ;
(9) (10)
(u = tan x) ; (u = tan x) ;
∫
例 解
计算
∫
sin 10 x cos 3 x d x.
令 u = sin x, 则 d u = cos x d x, 于是 sin 10 x cos3 x d x = ∫ u 10 (1 − u 2 ) d u = ∫ (u10 − u 12 ) d u 1 11 1 13 = u − u +C 11 13 1 11 1 = sin x − sin 13 x + C . 11 13
(u = sin x) ; (u = cos x) ; (u = tan x) ; (u = sin x) ; (u = cos x) ; (u = tan x) ;
第5章不定积分
比求导困难得多。
有些初等函数如e-x2 ,
等,原
函数必然存在,但由于其原函数不是初等函
数,我们并不能求其积分。
通过上节的学习,我们可以求一些简单 的积分,为了解决复合函数、函数的乘积等 这些复杂一些的积分问题,本节我们将学习 换元积分法和分部积分法。
5.2.1 第一换元积分法
我们先分析如何计算积分∫sin2xdx。 该积分不能直接用积分公式∫sintdt=cost+C,若想把2x 看成t 的话,被积表达式 中必须有d2x。
一些含有根式的积分如 虽然表达式很简单,但基本积
分公式和凑微分法都不能解决这类问题。 我们常用的办法是通过合适的换元把
根式去掉,从而简化计算,这就是我们要学习 的第二换元积分法。
第二换元积分法也可称作直接换元法, 通过直接代换x =φ(t),把表达式中不利于计 算的因素去掉(根式、分母复杂)。
换元时注意x=φ(t)的单调性(保证 t=φ-1(x)的存在),要把积分表达式中每一个 x 代换,积分结果要求变量回代。
其中“∫”为积分符号,x 为积分变量, f(x)为被积函数,f(x)dx 为被积表达式,C 为积 分常数。
由定义可知,求被积函数的不定积分只 须找到它的一个原函数,然后再加上任意常 数C。
5.1.3 不定积分的性质
根据不定积分的定义,我们不难得到不 定积分的以下几条性质。
(1)不定积分与导数和微分互逆性
(2)G(x)也是f(x)的一个原函数,则必 存在一个常数C0,使得G(x)=F(x)+C0这 是
因为(G(x)-F(x))'=G'(x)-F'(x)=f(x)-f(x)=0 由微分学知识可知,G(x)-F(x)必为某一常 数C0,即G(x)-F(x)= C0 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第五章积分学习目的和要求学习本章,要求读者掌握不定积分和定积分的概念及其相互关系,熟悉基本积分表并学会运用换元法和分部积分法求解积分,熟悉积分中值定理,了解广义积分的数学含义,学会计算一些简单的广义积分,并学会运用定积分计算平面图形的面积和旋转体的体积.第一节不定积分1.定义已知定义在某一区间上的一个函数,如果有这样的函数,称为函数的原函数.函数的所有原函具有这样性质的函数数的全体叫做函数叫做被积函数,x称为积分变量.2.不定积分的性质3.常用不定积分表4.基本积分方法(1)第一换元法,使若有中间变量关于变量具有原函数,则而(2)第二换元法直接引入自变量代换则(3)分部积分法具有连续导数,则设函数第二节定积分1.由曲边梯形的面积引入定积分的基本概念.在区间上连续,用分点2.定义设函数把区间分为个小区间在每个小区间上任取一点如果对任何小区间的划分方法和在小区间内的任何取法,当最大的小区间长度趋于零时均有极限S存在:则称该极限值的定积分,记为这里,|△x|表示最大的小区间长度,即.3.定积分的基本性质性质1 设上可积,并且性质2 设上可积,并且性质3 设上都可积.反之,设上也可积,且有性质4 设上可积,并且对每个则性质5 如果上也可积,且有上可积,那么它们的乘积也在上可积.性质64.积分第一中值定理设函数上至少存在一点ξ使得下式成立:5.微积分基本定理定理1 设上可积,定义如果.定理2(牛顿—莱布尼兹公式) 设上的一个原函数,则牛顿—莱布尼兹公式建立了定积分与不定积分之间的关系,它表明:定积分的值等于被积函数的任一原函数在积分区间上的增量.6.定积分的换元法和分部积分法上的连续函数,自变量是,值域含有[],且(1)换元法设的值域上的连续函数,则(2)分部积分法设上有连续导数的函数,则第三节广义积分广义积分可分为积分限为无限或被积函数无界两种情形. 1.积分区间为无限的广义积分设,若极限存在,则定义同样地可定义并定义其条件是后二者广义积分均存在.2.无界函数的广义积分设,若极限存在,则定义此时我们说广义积分存在或收敛;若极限不存在,我们说广义积分没有意义或发散.3.计算举例(1)(2)证明:积分l时发散.证设则令而当q>1时不存在,以及q=1时不存在,故积分发散.第四节积分的某些应用1.平面图形的面积设函数所围成的平面图形的面积为[例] 求椭圆的面积.解由对称性,只需计算椭圆在第一象限那部分的面积,再四倍即可,故2.旋转体的体积设立体Ω由平面图形轴旋转一周得到,为半径的圆,于是得旋转体的体积公式为由于立体Ω在x处的截面是以[例] 求椭圆轴旋转一周所得立体的体积.解所得立体,可看作平面区域绕轴旋转一周所得,利用旋转体体积公式得第五章积分例1:若h(x)是g(x)的一个原函数,则下列表达式中正确的一个是()。
解:因为各备选答案中的右端均含有积分常数C,故只须验证各备选答案中右端的导数是否等于其左端积分的被积函数。
事实上,由于g(x)未必可导,故可知(A)、(D)不正确;由题意h(x)是g(x)的一个原函数,即h'(x)=g(x),故(B)正确而(C)不正确,因此,应选(B)。
例2:例3:例4:例5:例6:例7:例8:例9:例10:例11:(图8-1)例12:例13:例14:例15:例16:例17:例18:例19:例20:例21:例22:试判断下列广义积分的敛散性。
例23:试判断下列广义积分的敛散性。
例24:例25:例26:例27:例28:第五章积分单元测试一、选择题1、幂函数的原函数一定是( )A、幂函数B、指数函数C、对数函数D、幂函数或对数函数2、函数的一个原函数是( )3、下列函数中,哪一个是函数的原函数( )4、,则f(x)=( )5、若,则f(x)=()6、过点(1,3)且切线斜率为2x 的曲线方程y=y(x)应满足的关系式是( )7、设,则()A、 B、 C、lnx D、lnx+c8、( )A、arctanxB、arctanx+cC、D、9、设,则()10、设,则f(x)=( )A、sinxB、sinx+cC、cosxD、cosx+c11、若,则.( )且f(0)=0,则()12、设13、不定积分( )14、()A、tanx+x+cB、tanx-x+cC、D、15、()A、 cotx-x+cscx+cB、-cotx-x+cscx+cC、cotx-x-cscx+cD、-cotx-x-cscx+c16、若()17、( )18、()19、()20、设是f(x)的一个原函数,则()21、设sin2x是f(x)的一个原函数,则()22、设是f(x)的一个原函数,则( )A、xcsc2-cotx+cB、xcsc2x+cotx+cC、-xcotx-cotx+cD、-xcotx+cotx+c23、设f(x)的一个原函数是cotx,则( )A、xcotx+lncosx+cB、xcot-lncosx+cC、xcotx+lnsinx+cD、xcot-lnsinx+c24、( )25、( )26、若,则a=()A、1B、-1C、0D、1/227、已知()A、F(x)- F(a)B、F(t)- F(a)C、F(x+a)- F(2a)D、F(t+a)- F(2a)28、若,则k=()A、0B、-1C、1D、1/229、设,则()A、1/2B、1C、3/2D、230、()A、eB、0C、1D、e+131、下列定积分中,值等于零的是( )32、( )A、2B、1C、1/2D、∞33、广义积分()A、不存在B、-1/2C、1/2D、234、( )A、∞B、-1/2C、2D、1/235、下列广义积分中收敛的是.() 36、下列广义积分中收敛的是()37、若收敛,则()A、P≥1B、p>1C、P≤1D、P<138、()A、发散B、-2C、2D、039、已知且,则K=( )A、2/3B、3/2C、2D、1/240、由定积分的几何意义,( )41、根据定积分的几何意义,下列各式中正确的是()42、函数的极小值是()A、1/2B、0C、1/4D、-1/443、设函数,则y有 ()A、极小值1/2B、极小值-1/2C、极大值1/2D、极大值-1/2第五章积分单元测试二、计算题(一)1、求不定积分解:2、计算不定积分解:==3、求不定积分解:4、求不定积分解:原式5、求解:6、讨论广义积分的敛散性。
若收敛,求其值。
解:=因为此极限不存在,所以广义积分发散。
三、计算题(二)1、计算解:原式=2、求不定积分。
解:令原式=3、求解:4、计算定积分解:令,则当从0变到8时, t从0变到25、计算定积分解:令当x 从-1 变到 1 时,t 从 3 变到1。
6、解:设,当x 从-5 变到 1 时,t 从 5 变到1。
7、求函数在区间[0,1]上的最大值和最小值解:最小值最大值第五章积分单元测试四、应用题1、求的极小值解:x=-1,x=0∵∴故f(x)在x=0处取极小值,极小值为f(0)=02、某商品的边际成本函数为,且固定成本为150,求总成本函数解:当Q=0时 K=150T又150=250+cc=-100总成本函数3、某商品的边际成本函数为,且固定成本为80,求总成本函数解:而80=50+CC=30∴4、生产某商品x个单位的边际收入函数(元/单位)(1)求生产X个单位时的总收入函数;(2)求该商品相应的需求函数(即平均价格是产量的函数)。
解:(1)总收入函数(K为积分常数)而R(0)=0,故k=a而此(2)需求函数且当收入为零时总消费支出5、若边际消费倾向是收入Y的函数(2)求收入由100增加到196时消费支出的增量。
解:(1)由题意∴(2)C(196)-C(100)=6、(1)某商品日产量是x个单位时,总费用F(x)的变化率为f(x)=0.2x+5(元/单位)且已知F(0)=0,求总费用F(x).(2)若销售单价是25元,求总利润G(x)(3)日产量为多少时,才能获得最大的利润?解:(1)(2)(3)得x=100为唯一驻点∵故当X=100(单位)时获利最大。
最大利润为:G(100)=1000(元)7、求曲线与直线y-x=1所围成的平面图形的面积.解:平面图形如右图中之阴影部分曲线和y=x+1的交点分别是(-1,0)和(0,1)故图形面积8、求由曲线所围成图形的面积解:先求交点∴ x=-2,x=1,交点为 (1,1) 与 (-2,-2) .9、求曲线y=lnx在区间(2,6)内的一点,使该点的切线与直线x=2,x=6以及y=lnx所围成的平面图形面积最小.解:设所求点的坐标为的切线方程为过点即平面图形的面积故所求点为(4,ln4)10、求曲线与直线x=1,x=4以及X轴所围成的平面图形分别绕X轴和Y 轴旋转而得的旋转体的体积.解:平面图形如右所示注:V也可从下式求得五、证明题证明证:作代换t=arccosx x=cost dx=-sintdt.x 从0变到1时,t 从变到0,于是左=证毕。
