勾股定理拔高
勾股定理拔高训练
1。
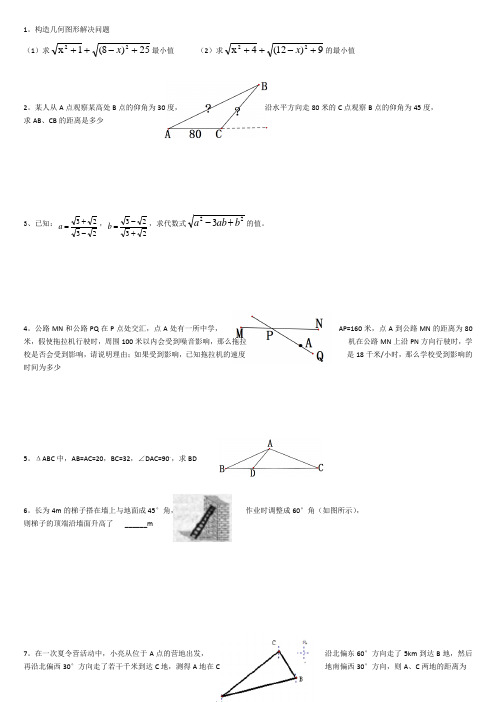
构造几何图形解决问题 (1)求25)8(1x 22+-++x 最小值 (2)求9)12(4x 22+-++x 的最小值2。
某人从A 点观察某高处B 点的仰角为30度, 沿水平方向走80米的C 点观察B 点的仰角为45度, 求AB 、CB 的距离是多少3、已知:2323-+=a ,2323+-=b ,求代数式223b ab a +-的值。
4。
公路MN 和公路PQ 在P 点处交汇,点A 处有一所中学, AP=160米,点A 到公路MN 的距离为80米,假使拖拉机行驶时,周围100米以内会受到噪音影响,那么拖拉 机在公路MN 上沿PN 方向行驶时,学校是否会受到影响,请说明理由;如果受到影响,已知拖拉机的速度 是18千米/小时,那么学校受到影响的时间为多少5。
ΔABC 中,AB=AC=20,BC=32,∠DAC=90。
,求BD6。
长为4m 的梯子搭在墙上与地面成45°角, 作业时调整成60°角(如图所示), 则梯子的顶端沿墙面升高了 ______m7。
在一次夏令营活动中,小亮从位于A点的营地出发,沿北偏东60°方向走了5km到达B地,然后再沿北偏西30°方向走了若干千米到达C地,测得A地在C 地南偏西30°方向,则A、C两地的距离为8。
如图,已知△ABC中,AB=5cm,BC=12cm,AC=13cm,那么AC边上的中线BD的长为9。
如图,A,B是公路l(l为东西走向)两旁的两个村庄,A村到公路l的距离AC=1km,B村到公路l的距离BD=2km,B村在A村的南偏东45°方向上.(1)求出A,B两村之间的距离;(2)为方便村民出行,计划在公路边新建一个公共汽车站P,要求该站到两村的距离相等,请用尺规在图中作出点P的位置(保留清晰的作图痕迹,并简要写明作法)10。
小明要测量河内小岛B到河边公路l的距离,在A点测得仰角30°,在C点测得仰角60°,又测得AC =米,则小岛B到公路l的距离为()米11。
八年级数学勾股定理拓展提高(勾股定理)拔高练习

八年级数学勾股定理拓展提高(勾股定理)拔高练习一、填空题(共5道,每道4分)1.教材1题:△ABC中,AB=15,AC=13,高AD=12,则△ABC的周长是_______.2.教材3题:在直线l上依次摆放着七个正方形(如图所示).已知斜放置的三个正方形的面积分别是1、2、3,正放置的四个正方形的面积依次是S1、S2、S3、S4,则S1+S2+S3+S4=_______.3题图3.教材4题:△ABC周长是24,M是AB4.教材5题:将一根长24cm露在杯子外面的长为hcm5.教材10题:矩形ABCD中,BC=4,DC=3F处,求EF二、解答题(共51.教材9BC沿直线BD折叠,使它落在斜边AB上的点2题图2.EBC与∠DCB互余,求+的值.3.教材12MN折叠,使点B落在CDB´C=3,求CN和AM的长.3题图4题图5题图4.教材14题:如图,某隧道的截面是一个半径为3.6米的半圆形,一辆高2.4米,宽3米的卡车能通过该隧道吗?5.教材16题:如图,某沿海城市A接到台风警报,在该市正南方向150km的B处有一台风中心正以20km/h的速度向BC方向移动,已知城市A到BC的距离AD=90km(1)台风中心经过多长时间从B点移到D点?(2)如果在距台风中心30km的圆形区域内都有受到台风破坏的危险,为让D点的游人脱离危险,游人必顺在接到台风警报后的几小时内撤离(撤离速度为6km/h)?三、证明题(共3道,每道10分)1.教材2题:如图,在正方形ABCD中,E是DC的中点,F为BC上的一点且BC=4CF,试说明△AEF是直角三角形.1题图2题图3题图2.作业1题:如图,已知P是矩形ABCD内任一点,求证:PA2+PC2=PB2+PD23.教材6题:如图所示.已知:在正方形ABCD中,∠BAC的平分线交BC于E,作EF⊥AC于F,作FG⊥AB于G。
勾股定理拓展与拔高

勾股定理拓展与拔高勾股定理拓展与拔尖二.知识点回顾1、勾股定理的应用:勾股定理反映了直角三角形三边之间的关系,是直角三角形的重要性质之一,其主要应用有:(1)已知直角三角形的两边求第三边(2)已知直角三角形的一边与另两边的关系。
求直角三角形的另两边(3)利用勾股定理可以证明线段平方关系的问题2、如何判定一个三角形是直角三角形(1)先确定最大边(如c)(2)验证c2与a2b2是否具有相等关系(3)若c2= a2b2,则△ ABC是以/ C为直角的直角三角形;若c2工a2b2 则厶ABC不是直角三角形。
3.勾股数:满足a2b2= c2的三个正整数,称为勾股数如(1)3, 4, 5; (2)5, 12,13; (3)6, 8, 10; (4)8, 15, 17 (5)7, 24, 25 (6)9, 40, 41三.典型题剖析:针对训练、延伸训练考点一证明三角形是直角三角形1、在正方形ABCD中,F为DC的中点,E为BC上一点,1且EC= 4 BC,求证:EFA=90 .FE针对训练:1、已知:在厶ABC中,/ A、/ B、/ C的对边分别是a、b、c,满足a2+b2+c2+338=10a+24b+26c试判断△ ABC的形状.考点二运用勾股定理的逆定理进行计算例、如图,等腰△ ABC中,底边BC= 20, 为AB 上A 一点,CD = 16, BD = 12, 求厶ABC的周长。
针对训练:1、.已知:如图,四边形ABCD , AD II BC, AB=4, BC=6, CD=5, AD=3.求:四边形ABCD的面积. yA考点三勾股定理的折叠问题例、如图,在矩形ABC冲,AB=3 BC=5在CD上任取一点E,连接BE将厶BCE沿BE折叠,使点E恰好落在AD边上的点F处,则CE的长为针对训练:1、如图,在矩形ABCD中,BC=6 , CD=3,将ABCD沿对角线BD翻折,点C落在点C1考点四勾股定理的卡车通过大门问例、某工厂的大门如图所示,其中四边形ABCD为长方形,上部是以的半圆,其中AD = 2.3 m,AB = 2 m,现有一辆装满货物的大卡车,宽1.6m,试猜想这辆大卡车能否通过厂门?请说明理由.题AB为直径高 2.5C考点五勾股定理的探究和应用问题例、如图所示,有一块塑料模板ABCD,长为10 cm,宽为4 cm,将你手中足够大的直角三角板PHF的直角顶点P落在AD边上(不与A、D重合)并在AD上平行移动:①能否使你的三角板两直角边分别通过点B与点C?若能,请你求出这时AP的长;若不能,请说明理由.②再次移动三角板位置,使三角板顶点P在AD上移动,直角边PH始终通过点B,另一直角边PF 与DC的延长线交于点Q,与BC交于点E,能否使CE=2 cm?若能,请你求出这时AP的长;若不能,请说明理由.针对训练:1观察下列图形,回答问题:问题(1 ):若图①中的△ DEF为直角三角形,正方形P的面积为9,正方形Q的面积为15,则正方形M的面积为。
勾股定理拔高-讲义

勾股定理 拔高训练1.如图,P 是等边三角形ABC ∆内的一点,连结PA 、P B、PC,以B P为边作60=∠PBQ ,且BQ=BP,连结CQ 、PQ ,若P A:PB:PC =3:4:5,试判断PQC ∆的形状。
2.如图,ADC ∆和BCE ∆都是等边三角形,30=∠ABC ,试说明:222BC AB BD +=3.在等腰直角三角形中,A B=A C,点D 是斜边B C的中点,点E 、F 分别为AB、AC 边上的点,且DE ⊥DF 。
(1)说明:222EF CF BE =+(2)若BE=12,CF=5,试求DEF ∆的面积。
4.为了美化环境,计划在某小区用草地铺设一个等腰三角形,使它的面积为30平方米且有一边长为10米,求另外两条边。
勾股定理提高训练(一)1、在R t△A BC 中,若直角边的长分别为1cm,2cm ,则斜边长为_____________.2、已知直角三角形的两边长为3、2,则另一条边长是________________.3.在一个直角三角形中,若斜边长为5cm ,直角边的长为3cm,则另一条直角边的长为( ). A .4cm B.4cm 或cm 34 C.cm 34 D.不存在 4、在直角三角形ABC 中,斜边AB=1,则AB 222AC BC ++的值是( ) A.2 B.4 C .6 D.85、直角三角形两直角边长分别为5和12,则它斜边上的高为_______.6、如图,学校有一块长方形花铺,有极少数人为了避开拐角走“捷径”,在花铺内走出了一条“路”.他CDB第7题FEDCBA第9题BA6cm3cm 1cm第10题图CBA24252020242572520242415们仅仅少走了 步路(假设2步为1米),却踩伤了花草.7、如图,在△ABC 中,AB=A C=13,BC=10,D 是AB 的中点,过点D 作DE ⊥AC 于点E ,则DE 的长是__.8、把一根长为10㎝的铁丝弯成一个直角三角形的两条直角边,如果要使三角形的面积是9㎝2,那么还要准备一根长为____的铁丝才能把三角形做好.9.如图,将一个边长分别为4、8的长方形纸片ABCD 折叠,使C 点与 A 点重合,则EB的长是( ). A.3ﻩﻩB .4 C D .510、如图,长方体的底面边长分别为1cm 和3cm,高为6cm.①如果用一根细线从点A 开始经过4个侧面缠绕一圈到达点B,那么所用细线最短需要__c m; ②如果从点A 开始经过4个侧面缠绕3圈到达点B,那么所用细线最短需要______cm.勾股定理提高训练(二)1、如图,每个小正方形的边长为1,A、B 、C 是小正方形的顶点,则∠AB C的度数为( ) A.90° B.60° C.45° D.30° 2、下列各组数据中,不能作为直角三角形三边长的是( ) A.9,12,15 B.43,1,45 C.0.2,0.3,0.4 D.40,41,9 3、满足下列条件的三角形中,不是直角三角形的是( ) A.三个内角比为1∶2∶1 B.三边之比为1∶2∶5 C.三边之比为3∶2∶5 D. 三个内角比为1∶2∶34、已知三角形两边长为2和6,要使这个三角形为直角三角形,则第三边的长为( ) A.2 B.102 C .10224或 D.以上都不对5、 五根小木棒,其长度分别为7,15,20,24,25,现将他们摆成两个直角三角形,其中正确的是( )A B C6、△A BC 的三边分别是7、24、25,则三角形的最大内角的度数是7、已知△ABC 的三边长满足18,10==+ab b a ,8=c ,则为 三角形.8、将直角三角形的三边扩大相同的倍数后,得到的三角形是 ( ). A.直角三角形 B.锐角三角形 C.钝角三角形 D.不是直角三角形9、在三角形ABC 中,AB=12cm ,AC =5cm ,B C=13cm ,则B C边上的高为AD= cm . 10、下列命题中是假命题的是( ).A .△ABC中,若∠B=∠C-∠A,则△ABC 是直角三角形.B .△ABC 中,若a 2=(b+c)(b-c),则△ABC 是直角三角形. C .△ABC 中,若∠A∶∠B∶∠C=3∶4∶5则△ABC是直角三角形. D.△ABC 中,若a∶b∶c=5∶4∶3则△ABC 是直角三角形.11.如图,已知四边形ABCD 中,∠B =90°,AB=3,B C=4,CD=12,AD=13,求四边形AB CD 的面积.12、如图,AB 为一棵大树,在树上距地面10m 的D 处有两只猴子,它们同时发现地面上的C 处有一筐水果,一只猴子从D 处上爬到树顶A 处,利用拉在A 处的滑绳AC ,滑到C 处,另一只猴子从D 处滑到地面B ,再由B 跑到C ,已知两猴子所经路程都是15m,求树高AB.13、如图,在梯形AB CD 中,AD∥BC,A B⊥AC,∠B=45°, AD=1,B C=4,求D C的长.15、如图,某学校(A点)与公路(直线L)的距离为300米,又与公路车站(D点)的距离为500米,第11题图BA CD .第12题图B CA DADEBC现要在公路上建一个小商店(C 点),使之与该校 A 及车站D 的距离相等,求商店与车站之间的距离.16.如图,铁路上A ,B 两点相距25k m,C ,D 为两村庄,DA⊥AB 于A ,C B⊥AB 于B,已知DA =15km ,CB =10km,现在要在铁路AB 上建一个土特产品收购站E ,使得C,D 两村到E 站的距离相等,则E 站应建在离A 站多少k m处?17、如图所示,在四边形ABCD 中,∠A=60°,∠B=∠D =90°,B C=2,C D=3,求A B的长.中考试题精选(2012广州市)在Rt △ABC 中,∠C=90°,AC=9,BC=12,则点C 到AB 的距离是( ) A.365 B. 1225 C. 94 D. 334(2012巴中市)已知a 、b、c 是△ABC 的三边长,且满足关系错误!+|a-b|=0,则△ABC 的形状为______(2013巴中)若直角三角形的两直角边长为a、b ,且满足,则该直角三角形的斜边长为 .(2013黔西南州)一直角三角形的两边长分别为3和4.则第三边的长为( )A 、5 B、7 C、5 D 、5或7 (2013柳州)在△ABC 中,∠BAC=90°,AB =3,A C=4.AD A.B.平分∠BAC 交BC 于D,则BD 的长为( ) C .D.第17题图(2012南充市) 如图,四边形ABCD中,∠BAD=∠BCD=90°,AB=AD,若四边形ABCD的面积是24c m2,则AC长是_____________cm.(2013•湘西州)如图,Rt△ABC中,∠C=90°,AD平分∠CAB,DE⊥AB于E,若AC=6,BC=8,CD=3.(1)求DE的长;(2)求△ADB的面积.(2013•达州)如图,折叠矩形纸片ABCD,使B点落在AD上一点E处,折痕的两端点分别在AB、BC上(含端点),且AB=6,BC=10。
初中数学拔高辅导(勾股定理拓展提高之动态几何)

初中数学拔高辅导(勾股定理拓展提高之动态几何)板块一:通过位置变换找勾股关系(对称变换) 教材1题:如图,在△ABC 中,AB =AC ,(1)若P 为边BC 上的中点,连结AP ,求证:BP ×CP =AB 2-AP 2;(2)若P 是BC 边上任意一点,上面的结论还成立吗?若成立请证明,若不成立请说明理由;(3)若P 是BC 边延长线上一点,线段AB 、AP 、BP 、CP 之间有什么样的关系?请证明你的结论.教材2题:如图,一个牧童在小河的南4km 的A 处牧马,而他正位于他的小屋B 的西8km 北7km 处,他想把他的马牵到小河边去饮水,然后回家.他要完成这件事情所走的最短路程是多少?教材3题:如图,E 为正方形ABCD 的边AB 上一点,AE =3 ,BE =1,P 为AC 上的动点,则PB +PE 的最小值是?教材4题:(2010宁德市)如图,四边形ABCD 是正方形,△ABE 是等边三角形,M 为对角线BD (不含B 点)上任意一点,将BM 绕点B 逆时针旋转60°得到BN ,连接EN 、AM 、CM.(1)求证:△AMB ≌△ENB ;(2)①当M 点在何处时,AM +CM 的值最小;②当M 点在何处时,AM +BM +CM的值最小,并说明理由;(3)当AM +BM +CM 的最小值为13 时,求正方形的边长.解:⑴∵△ABE 是等边三角形, ∴BA =BE ,∠ABE =60°. ∵∠MBN =60°,∴∠MBN -∠ABN =∠ABE -∠ABN. 即∠BMA =∠NBE. 又∵MB =NB ,∴△AMB ≌△ENB (SAS )⑵①当M 点落在BD 的中点时,AM +CM 的值最小ABPCB小河D CCBA②连接CE,当M点位于BD与CE的交点处时,AM+BM+CM的值最小理由如下:连接MN.由⑴知,△AMB≌△ENB,∴AM=EN.∵∠MBN=60°,MB=NB,∴△BMN是等边三角形.∴BM=MN.∴AM+BM+CM=EN+MN+CM根据“两点之间线段最短”,得EN +MN+CM=EC最短∴当M点位于BD与CE的交点处时,AM+BM+CM的值最小,即等于EC的长⑶过E点作EF⊥BC交CB的延长线于F,∴∠EBF=90°-60°=30°.设正方形的边长为x,则BF=√3/2x,EF=x/2在Rt△EFC中,∵EF²+FC²=EC²,(x/2)²+(√3/2x+x)²=(√3+1)²解得x=√2板块二:通过位置变换找勾股关系(旋转变换)教材5题:如图:正方形ABCD中有一点P,且PA=1,PB=2,PC=3,求∠APB的度数.(2012•盐城二模)阅读下列材料:问题:如图1,P为正方形ABCD内一点,且PA:PB:PC=1:2:3,求∠APB的度数.小娜同学的想法是:不妨设PA=1,PB=2,PC=3,设法把PA、PB、PC相对集中,于是他将△BCP绕点B顺时针旋转90°得到△BAE(如图2),然后连接PE,问题得以解决.请你回答:图2中∠APB的度数为135°.请你参考小娜同学的思路,解决下列问题:如图3,P是等边三角形ABC内一点,已知∠APB=115°,∠BPC=125°.(1)在图3中画出并指明以PA、PB、PC的长度为三边长的一个三角形(保留画图痕迹);(2)求出以PA、PB、PC的长度为三边长的三角形的各内角的度数分别等于60°、65°、55°.考点:旋转的性质;等边三角形的性质;勾股定理的逆定理;正方形的性质;作图—复杂作图.分析:图2中,根据旋转的性质知△BCP≌△BAE.由全等三角形的对应边相等、等腰三角形的判定推知△BPE是等腰三角形,则∠BPE=∠BEP=45°;然后由全等三角形的对应边相等、勾股定理证得∠APE=90°;最后根据图中角与角间的数量关系求得∠APB=135°;(1)设法把PA、PB、PC相对集中,将△BCP绕点B顺时针旋转60°得到△ACM,然后连接PM,问题得以解决.(2)根据旋转的性质知∠PCM=60°,△BCP≌△ACM.然后根据全等三角形的对应边、对应角相等,周角的定义以及三角形内角和定理来求以PA、PB、PC的长度为三边长的三角形的各内角的度数.解答:解:如图2.∵根据旋转的性质知∠PBE=90°,△BCP≌△BAE.∴BP=BE,PC=AE,∴∠BPE=∠BEP=45°.又PA:PB:PC=1:2:3,∴AE2=AP2+PE2,∴∠APE=90°,∴∠APB=∠APE+∠BPE=90°+45°=135°,即图2中∠APB的度数为135°.故答案是:135°;(1)如图3,将△BCP绕点C顺时针旋转60°得到△ACM,然后连接PM,△APM即为所求,即以PA、PB、PC的长度为三边长的一个三角形是△APM.以PA、PB、PC的长度为三边长的一个三角形是△APM.(2)如图3.∵根据旋转的性质知∠PCM=60°,△BCP≌△ACM.∴PC=CM,∠AMC=∠BPC=125°,∴△PCM是等边三角形,∴∠MPC=∠PMC=60°,∠AMP=∠AMC-∠PMC=65°.∵∠APB=115°,∠BPC=125°,∠APB+∠BPC+∠MPC+∠APM=360°,∴∠APM=60°,∴∠PAM=180°-∠APM-∠AMP=55°.∴以PA、PB、PC的长度为三边长的三角形的各内角的度数分别等于60°、65°、55°.故答案是:60°、65°、55°.在正方形ABCD中 PA=1 PB=2 PC=3 P在正方形内部试求角APB的度数三角形旋转问题:在正方形ABCD中,PA=1,PB=2,PC=3,P在正方形内部试求∠APB的度数.解:将△ABP旋转至△CBP',△BPP'是等腰直角三角形,∠BPP'=45.△PP'C中,PP'=2√2,P'C=AP=1,PC=3,所以△PP'C是直角三角形,∠APB=∠BP'C=∠BP'P+∠PP'C=45+90=135教材6题:如图,四边形ABCD是直角梯形,且AB=BC,PA=1,PB=2,PC=3,求梯形ABCD的面积.DCABEFMN 图①教材7题:如图,在Rt △ABC 中,∠BAC =90°,AB =AC ,E 、F 分别是BC 上两点,若∠EAF =45°,试推断BE 、CF 、EF 之间的数量关系,并说明理由.教材8题:如图,P 是等边三角形ABC 内一点,AP =3,BP =4,CP =5,求∠APB 的度数.教材9题:如图,在Rt △ABC 中,∠A =90°,D 为斜边BC 中点,DE ⊥DF ,求证:EF 2=BE 2+CF 2.教材10题:(2008天津)已知Rt △ABC 中,∠ACB =90°,CA =CB ,有一个圆心角为︒45,半径的长等于CA 的扇形CEF 绕点C 旋转,且直线CE ,CF 分别与直线AB 交于点M ,N .(Ⅰ)当扇形CEF 绕点C 在∠ACE 的内部旋转时,如图①,求证:222BN AM MN +=;(Ⅱ)当扇形CEF 绕点C 旋转至图②的位置时,关系式222BN AM MN +=是否仍然成立?若成立,请证明;若不成立,请说明理由.CABE MN 图②CBBCA。
八年级数学勾股定理拓展提高(勾股定理)拔高练习

八年级数学勾股定理拓展提高(勾股定理)拔高练习一、填空题(共5道,每道4分)1.教材1题:△ABC中,AB=15,AC=13,高AD=12,则△ABC的周长是_______.2.教材3题:在直线l上依次摆放着七个正方形(如图所示).已知斜放置的三个正方形的面积分别是1、2、3,正放置的四个正方形的面积依次是S1、S2、S3、S4,则S1+S2+S3+S4=_______.3题图5题图3.教材4题:△ABC周长是24,M是AB的中点,MC=MA=5,则△ABC的面积是_____.4.教材5题:将一根长24 cm的筷子,置于底面直径为5cm、高为12cm的圆柱形水杯中,设筷子露在杯子外面的长为hcm,则h的取值范围是_____.5.教材10题:矩形ABCD中,BC=4,DC=3,将该矩形沿对角线BD折叠,使点C落在点F处,求EF的长_____.二、解答题(共5道,每道10分)1.教材9题:如图,有一个直角三角形纸片,两直角边AC=8cm,BC=6cm,现将直角边BC沿直线BD折叠,使它落在斜边AB上的点C′处,求CD的长以及折痕BD的平方1题图2题图2.教材8题:如图,已知DE=m,BC=n,∠EBC与∠DCB互余,求+的值.3.教材12题:如图,四边形ABCD是边长为9的正方形纸片,将其沿MN折叠,使点B落在CD边上的B´处,点A对应点为A´,且B´C=3,求CN和AM的长.3题图4题图5题图4.教材14题:如图,某隧道的截面是一个半径为米的半圆形,一辆高米,宽3米的卡车能通过该隧道吗?5.教材16题:如图,某沿海城市A接到台风警报,在该市正南方向150km的B处有一台风中心正以20km/h的速度向BC方向移动,已知城市A到BC的距离AD=90km(1)台风中心经过多长时间从B点移到D点(2)如果在距台风中心30km的圆形区域内都有受到台风破坏的危险,为让D点的游人脱离危险,游人必顺在接到台风警报后的几小时内撤离(撤离速度为6km/h)三、证明题(共3道,每道10分)1.教材2题:如图,在正方形ABCD中,E是DC的中点,F为BC上的一点且BC=4CF,试说明△AEF是直角三角形.1题图2题图3题图2.作业1题:如图,已知P是矩形ABCD内任一点,求证:PA2+PC2=PB2+PD23.教材6题:如图所示.已知:在正方形ABCD中,∠BAC的平分线交BC于E,作EF⊥AC于F,作FG⊥AB于G.求证:AB2=2FG2.。
北师大版八年级上册数学第一章勾股定理拔高练习(有超纲)
一、填空题1.如图(1),在高2米,坡角为30°的楼梯表面铺地毯,地毯的长至少需________米. 图(1)2.种盛饮料的圆柱形杯(如图),测得内部底面半径为2.5㎝,高为12㎝,吸管放进杯里,杯口外面至少要露4.6㎝, 问吸管要做 ㎝。
3.已知:如图,△ABC 中,∠C = 90°,点O 为△ABC 的三条角平分线的交点,OD ⊥BC ,OE ⊥AC ,OF ⊥AB ,点D 、E 、F分别是垂足,且BC = 8cm ,CA = 6cm ,则点O 到三边AB ,AC 和BC 的距离分别等于 cm4.在一棵树的10米高处有两只猴子,一只猴子爬下树走到离树20米处的池塘的A 处。
另一只爬到树顶D 后直接跃到A 处,距离以直线计算,如果两只猴子所经过的距离相等,则这棵树高_____________________米。
5.如图是一个三级台阶,它的每一级的长宽和高分别为20dm 、3dm 、 2dm ,A 和B 是这个台阶两个相对的端点,A 点有一只蚂蚁,想到B 点去吃可口的食物,则蚂蚁沿着台阶面爬到B 点最短路程是_____________.二、选择题1.已知一个Rt △的两边长分别为3和4,则第三边长的平方是( )A 、25B 、14C 、7D 、7或25 2.Rt △一直角边的长为11,另两边为自然数,则Rt △的周长为( ) A 、121 B 、120 C 、132 D 、不能确定3.如果Rt △两直角边的比为5∶12,则斜边上的高与斜边的比为( ) A 、60∶13 B 、5∶12 C 、12∶13 D 、60∶1694.已知Rt △ABC 中,∠C=90°,若a+b=14cm ,c=10cm ,则Rt △ABC 的面积是( )A 、24cm 2B 、36cm 2C 、48cm 2D 、60cm 2 5.等腰三角形底边上的高为8,周长为32,则三角形的面积为( )A 、56B 、48C 、40D 、326.某市在旧城改造中,计划在市内一块如图所示的三角形空地上种植草皮以美化环境,已知这种草皮每平方米售价a元,则购买这种草皮至少需要( )A 、450a 元B 、225a 元C 、150a 元D 、300a 元 7.已知,如图长方形ABCD 中,AB=3cm ,AD=9cm ,将此长方形折叠,使点B 与点D 重合,折痕为EF ,则△ABE 的面积为( )A 、6cm 2B 、8cm 2C 、10cm 2D 、12cm 28.在△ABC 中,AB =15,AC =13,高AD =12,则△ABC 的周长为A .42B .32C .42或32D .37或339. 如图,正方形网格中的△ABC ,若小方格边长为1,则△ABC 是 ( )(A )直角三角形 (B)锐角三角形 (C)钝角三角形 (D)以上答案都不对三、计算1、如图,A 、B 是笔直公路l 同侧的两个村庄,且两个村庄到直路的距离分别是300m 和500m ,两村庄之间的距离为d(已知d 2=400000m 2),现要在公路上建一汽车停靠站,使两村到停靠站的距离之和最小。
勾股定理拔高题
勾股定理培优题(3、28)分类讨论思想1、已知在△ABC 中,AB=17,AC=10,BC 边上的高等于8,则△ABC 的周长为 .2、在Rt △ABC 中,已知两边长为5、12,则第三边的长为3、等腰三角形的两边长为10和12,则周长为________,底边上的高是________,面积是_________。
4.一个直角三角形,有两边长分别为6和8,下列说法正确的是( )A. 第三边一定为10B. 三角形的周长为25C. 三角形的面积为48D. 第三边可能为10方程思想5.如图,一块直角三角形的纸片,两直角边AC=6㎝,BC=8㎝。
现将直角边AC 沿直线AD 折叠,使它落在斜边AB 上,且与AE 重合,则CD 等于6.已知,如图长方形ABCD 中,AB=3cm ,AD=9cm ,将此长方形折叠,使点B 与D重合,折痕为EF ,则△ABE 的面积为( )cm 27.已知:将正长方形纸片ABCD 折叠两次,第一次折痕为AC ,第二次折痕为AE ,且点D 落在F 处.若长方形长为4,宽为3,求DE .8.已知:如图,△ABC 中,∠C =90º,AD 是角平分线,CD =15,BD =25.求AC 的长.A C DB E 1题 A BCDE FAB E F DC 第2题9、(2007•江苏)如图是一个外轮廓为矩形的机器零件平面示意图,根据图中的尺寸(单位:mm ),计算两圆孔中心A 和B 的距离为________。
6、7、如图,把矩形ABCD 纸片折叠,使点B 落在点D 处,点C 落在C ’处,折痕EF 与BD 交于点O ,已知AB=16,AD=12,求折痕EF 的长。
3.如图,ADC ∆和BCE ∆都是等边 30=∠ABC ,试说明:222BC AB BD +=9、如图,在△ABC 中,∠B=90°,AB=6cm ,BC=8cm ,点P 从点A 出发沿AB 边向点B 以1cm/秒的速度移动,点Q 从点B 出发沿BC 边向点C 以2cm/秒的速度移动.(1)如果P 、Q 分别从A 、B 同时出发,经过多长时间,使△PBQ 的面积为8cm2?(2)如果P 、Q 分别从A 、B 同时出发,当P 、Q 两点运动几秒时,PQ 有最小值,并求这个最小值.C 'FE OD CB AE D C BA。
人教版八年级数学下《勾股定理的逆定理》拔高练习
《勾股定理的逆定理》拔高练习一、选择题(本大题共5小题,共25.0分)1.(5分)下列各数中不是勾股数的是()A.3,4,5B.6,8,10C.4,5,6D.5,12,13 2.(5分)下列说法中,正确的有()①如果∠A+∠B﹣∠C=0,那么△ABC是直角三角形;②如果∠A:∠B:∠C=5:12:13,则△ABC是直角三角形;③如果三角形三边之比为,则△ABC为直角三角形;④如果三角形三边长分别是n2﹣4、4n、n2+4(n>2),则△ABC是直角三角形;A.1个B.2个C.3个D.4个3.(5分)在下列长度的各组线段中,能组成直角三角形的是()A.,,B.5、12、13C.32、42、52D.4、6、8 4.(5分)下列条件能判定△ABC为直角三角形的是()A.∠A+∠B=∠C B.∠A:∠B:∠C=1:2:4C.a2=32,b2=42,c2=52D.a=,b=,c=5.(5分)下列每一组数据中的三个数值分别为三角形的三边长,不能构成直角三角形的是()A.3、4、5B.6、8、10C.5、12、13D.5、5、7二、填空题(本大题共5小题,共25.0分)6.(5分)甲、乙两人同时从同一地点出发,甲往北偏东45°方向走了48米,乙往南偏东45°方向走了36米,这时两人相距米.7.(5分)在一款名为超级玛丽的游戏中,玛丽到达一个高为10米的高台A,利用旗杆顶部的索,划过90°到达与高台A水平距离为17米,高为3米的矮台B,玛丽在荡绳索过程中离地面的最低点的高度MN=.8.(5分)如图,已知∠A=90°,AC=AB=4,CD=2,BD=6.则∠ACD=度.9.(5分)若三角边三边长分别为15,12,9,则这个三角形最长边上的高是.10.(5分)小明用一根长30cm的铁丝围成一个斜边长为13cm的直角三角形,则直角三角形的面积是cm2.三、解答题(本大题共5小题,共50.0分)11.(10分)如图所示的一块地,∠ADC=90°,AD=12m,CD=9m,AB=25m,BC=20m,求这块地的面积.12.(10分)阅读下面材料:勾股定理的逆定理:如果是直角三角形的三条边长a,b,c,满足a2+b2=c2,那么这个三角形是直角三角形.能够成为直角三角形三条边长的正整数,称为勾股数.例如:32+42=52,3、4、5是一组勾股数.古希腊的哲学家柏拉图曾指出,如果m表示大于1的整数,a=2m,b=m2﹣1,c=m2+1,那么a,b,c为勾股数,你认为正确吗?如果正确,请说明理由,并利用这个结论得出一组勾股数.13.(10分)A,B两个居民楼在公路同侧,它们离公路的距离分别为AE=200米,BF=70米,它们的水平距离EF=390米.现欲在公路旁建一个超市P,使超市到两居民楼的距离相等,则超市应建何处?为什么?14.(10分)如图,台风中心位于点A,并沿东北方向AC移动,已知台风移动的速度为50千米/时,受影响区域的半径为130千米,B市位于点A的北偏东75°方向上,距离A点240千米处.(1)说明本次台风会影响B市;(2)求这次台风影响B市的时间.15.(10分)学完勾股定理之后,同学们想利用升旗的绳子、卷尺,测算出学校旗杆的高度.爱动脑筋的小明这样设计了一个方案:如图,小亮将升旗的绳子拉直到末端刚好接触地面,测得此时绳子末端距旗杆底端1米,然后将绳子末端拉直到距离旗杆5m处,测得此时绳子末端距离地面高度为1m,如果设旗杆的高度为x米(滑轮上方的部分忽略不计),求x的值.《勾股定理的逆定理》拔高练习参考答案与试题解析一、选择题(本大题共5小题,共25.0分)1.(5分)下列各数中不是勾股数的是()A.3,4,5B.6,8,10C.4,5,6D.5,12,13【分析】欲判断是否为勾股数,必须根据勾股数是正整数,同时还需验证两小边的平方和是否等于最长边的平方.【解答】解:A.32+42=52,能构成直角三角形,是整数,故是勾股数,此选项不符合题意;B.62+82=102,三边是整数,同时能构成直角三角形,故是勾股数,此选项不符合题意;C.42+52≠62,不是勾股数,此选项符合题意;D.52+122=132,是正整数,故是勾股数,此选项不符合题意;故选:C.【点评】此题主要考查了勾股数,解答此题要用到勾股数的定义,及勾股定理的逆定理:已知△ABC的三边满足a2+b2=c2,则△ABC是直角三角形.2.(5分)下列说法中,正确的有()①如果∠A+∠B﹣∠C=0,那么△ABC是直角三角形;②如果∠A:∠B:∠C=5:12:13,则△ABC是直角三角形;③如果三角形三边之比为,则△ABC为直角三角形;④如果三角形三边长分别是n2﹣4、4n、n2+4(n>2),则△ABC是直角三角形;A.1个B.2个C.3个D.4个【分析】根据直角三角形的判定进行分析,从而得到答案.【解答】解:①正确,由三角形内角和定理可求出∠C为90度;②不正确,因为根据三角形的内角和得不到90°的角;③正确,设三边分别为x,x,x,则有7x2+10=172;④正确,因为(n2﹣4)+(4n)2=(n+4)2.所以正确的有三个.故选:C.【点评】本题考查了直角三角形的判定:可用勾股定理的逆定理和有一角为90°来判定.3.(5分)在下列长度的各组线段中,能组成直角三角形的是()A.,,B.5、12、13C.32、42、52D.4、6、8【分析】欲判断是否为勾股数,必须根据勾股数是正整数,同时还需验证两小边的平方和是否等于最长边的平方.【解答】解:A、()2+()2≠()2,不是能够成三角形,故此选项错误;B、52+122=132,能构成直角三角形,是正整数,故此选项正确;C、92+162≠252,不能构成直角三角形,故此选项错误;D、42+62≠82,能构成直角三角形,故此选项错误.故选:B.【点评】此题主要考查了勾股定理的逆定理,解答此题要用到勾股定理的逆定理:已知△ABC的三边满足a2+b2=c2,则△ABC是直角三角形.4.(5分)下列条件能判定△ABC为直角三角形的是()A.∠A+∠B=∠C B.∠A:∠B:∠C=1:2:4C.a2=32,b2=42,c2=52D.a=,b=,c=【分析】由勾股定理的逆定理,只要验证两小边的平方和等于最长边的平方或最大角是否是90°即可.【解答】解:A、∵∠A+∠B=∠C,∴∠C=90°,故是直角三角形,正确;B、∵∠A:∠B:∠C=1:2:4,∴∠C=180°≠90°,故不是直角三角形,错误;C、a=9,b=16,c=25,∵92+162≠252,故不能判定是直角三角形;D、∵()2+()2≠()2,故不能判定是直角三角形.故选:A.【点评】本题考查勾股定理的逆定理的应用.判断三角形是否为直角三角形,已知三角形三边的长,只要利用勾股定理的逆定理加以判断即可.5.(5分)下列每一组数据中的三个数值分别为三角形的三边长,不能构成直角三角形的是()A.3、4、5B.6、8、10C.5、12、13D.5、5、7【分析】欲判断是否为勾股数,必须根据勾股数是正整数,同时还需验证两小边的平方和是否等于最长边的平方.【解答】解:A、42+32=52,能够成直角三角形,故此选项错误;B、62+82=102,能构成直角三角形,故此选项错误;C、122+52=132,能构成直角三角形,故此选项错误;D、52+52≠72,不能构成直角三角形,故此选项正确.故选:D.【点评】此题主要考查了勾股定理的逆定理:已知△ABC的三边满足a2+b2=c2,则△ABC是直角三角形.二、填空题(本大题共5小题,共25.0分)6.(5分)甲、乙两人同时从同一地点出发,甲往北偏东45°方向走了48米,乙往南偏东45°方向走了36米,这时两人相距60米.【分析】直接利用方向角画出图形,进而利用勾股定理得出答案.【解答】解:如图所示:由题意可得,∠AOB=90°,AO=48m,BO=36m,则AB==60(m).故答案为:60.【点评】此题主要考查了勾股定理的应用,正确画出图形是解题关键.7.(5分)在一款名为超级玛丽的游戏中,玛丽到达一个高为10米的高台A,利用旗杆顶部的索,划过90°到达与高台A水平距离为17米,高为3米的矮台B,玛丽在荡绳索过程中离地面的最低点的高度MN=2m.【分析】首先得出△AOE≌△OBF(AAS),进而得出CD的长,进而求出OM,MN的长即可.【解答】解:作AE⊥OM,BF⊥OM,∵∠AOE+∠BOF=∠BOF+∠OBF=90°∴∠AOE=∠OBF在△AOE和△OBF中,,∴△AOE≌△OBF(AAS),∴OE=BF,AE=OF即OE+OF=AE+BF=CD=17(m)∵EF=EM﹣FM=AC﹣BD=10﹣3=7(m),∴2EO+EF=17,则2×EO=10,所以OE=5m,OF=12m,所以OM=OF+FM=15m又因为由勾股定理得ON=OA=13,所以MN=15﹣13=2(m).答:玛丽在荡绳索过程中离地面的最低点的高度MN为2米.故答案为:2m.【点评】此题主要考查了勾股定理的应用以及全等三角形的应用,正确得出△AOE≌△OBF是解题关键.8.(5分)如图,已知∠A=90°,AC=AB=4,CD=2,BD=6.则∠ACD=45度.【分析】根据勾股定理求出BC,根据勾股定理的逆定理得到∠BCD=90°,结合图形计算,得到答案.【解答】解:∵∠A=90°,AC=AB=4,∴∠ACB=∠ABC=45°,在Rt△ABC中,BC==4,CD2+BC2=22+(4)2=36,BD2=62=36,∴CD2+BC2=BD2,∴∠BCD=90°,∴∠ACD=45°,故答案为:45.【点评】本题考查的是勾股定理和勾股定理的逆定理,如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形就是直角三角形.9.(5分)若三角边三边长分别为15,12,9,则这个三角形最长边上的高是.【分析】首先根据三角形的三边长证明三角形是直角三角形,再根据直角三角形的面积公式计算出斜边上的高即可.【解答】解:∵92+122=152,∴此三角形是直角三角形,设最长边上的高为hcm,×9×12=×15×h,解得:h=.故答案为:.【点评】此题主要考查了勾股定理逆定理,以及直角三角形的面积计算,关键是熟练掌握勾股定理的逆定理:如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形就是直角三角形.10.(5分)小明用一根长30cm的铁丝围成一个斜边长为13cm的直角三角形,则直角三角形的面积是30cm2.【分析】首先表示出两直角边长,再利用勾股定理和三角形的面积公式得出答案.【解答】解:设一条直角边长为a,则另一边长为:30﹣13﹣a=17﹣a,故a2+(17﹣a)2=132,解得:a1=5,a2=12,故两直角边的长分别为:5cm,12cm.∴直角三角形的面积=cm2.故答案为:30【点评】此题主要考查了勾股定理,正确应用勾股定理是解题关键.三、解答题(本大题共5小题,共50.0分)11.(10分)如图所示的一块地,∠ADC=90°,AD=12m,CD=9m,AB=25m,BC=20m,求这块地的面积.【分析】连接AC,运用勾股定理逆定理可证△ACD,△ABC为直角三角形,可求出两直角三角形的面积,此块地的面积为两个直角三角形的面积差.【解答】解:连接AC,则在Rt△ADC中,AC2=CD2+AD2=122+92=225,∴AC=15,在△ABC中,AB2=625,AC2+BC2=152+202=625,∴AB2=AC2+BC2,∴∠ACB=90°,∴S△ABC ﹣S△ACD=AC•BC﹣AD•CD=×15×20﹣×12×9=96.答:这块地的面积是96平方米.【点评】此题考查了勾股定理和逆定理的应用,解答此题的关键是通过作辅助线使图形转化成特殊的三角形,可使复杂的求解过程变得简单.12.(10分)阅读下面材料:勾股定理的逆定理:如果是直角三角形的三条边长a,b,c,满足a2+b2=c2,那么这个三角形是直角三角形.能够成为直角三角形三条边长的正整数,称为勾股数.例如:32+42=52,3、4、5是一组勾股数.古希腊的哲学家柏拉图曾指出,如果m表示大于1的整数,a=2m,b=m2﹣1,c=m2+1,那么a,b,c为勾股数,你认为正确吗?如果正确,请说明理由,并利用这个结论得出一组勾股数.【分析】欲判断是否为勾股数,必须根据勾股数是正整数,同时还需验证两小边的平方和是否等于最长边的平方.【解答】解:正确.理由:∵m表示大于1的整数,∴a,b,c都是正整数,且c是最大边,∵(2m)2+(m2﹣1)2=(m2+1)2,∴a2+b2=c2,即a、b、c为勾股数.当m=2时,可得一组勾股数3,4,5.【点评】本题考查了勾股数.解答此题要用到勾股数的定义,及勾股定理的逆定理:已知△ABC的三边满足a2+b2=c2,则△ABC是直角三角形.13.(10分)A,B两个居民楼在公路同侧,它们离公路的距离分别为AE=200米,BF=70米,它们的水平距离EF=390米.现欲在公路旁建一个超市P,使超市到两居民楼的距离相等,则超市应建何处?为什么?【分析】首先设EP=x米,则PF=(390﹣x)米,根据AP=PB利用勾股定理可得2002+x2=702+(390﹣x)2,再解方程即可.【解答】解:设EP=x米,则PF=(390﹣x)米,由题意得:2002+x2=702+(390﹣x)2,解得:x=150.答:超市应建在距离E处150米的位置.【点评】此题主要考查了勾股定理的应用,关键是正确理解题意,从题中抽象出勾股定理这一数学模型.领会数形结合的思想的应用.14.(10分)如图,台风中心位于点A,并沿东北方向AC移动,已知台风移动的速度为50千米/时,受影响区域的半径为130千米,B市位于点A的北偏东75°方向上,距离A点240千米处.(1)说明本次台风会影响B市;(2)求这次台风影响B市的时间.【分析】(1)作BD⊥AC于点D,在Rt△ABD中,利用特殊角的三角函数值求出BD的长与130千米相比较即可.(2)以B为圆心,以130为半径作圆交AC于E,F两点,根据垂径定理即可求出BE=BF=130,然后由勾股定理求得EF的长度,进而求出台风影响B 市的时间.【解答】解:(1)如图,作BD⊥AC于点D.在Rt△ABD中,由条件知,AB=240,∠BAC=75°﹣45°=30°,∴BD=240×=120<130,∴本次台风会影响B市.(2)如图,以点B为圆心,以130为半径作圆交AC于E,F,若台风中心移动到E时,台风开始影响B市,台风中心移动到F时,台风影响结束.由(1)得BD=240,由条件得BE=BF=130,∴EF=2=100,∴台风影响的时间t==2(小时).故B市受台风影响的时间为2小时.【点评】本题考查的是直角三角形的性质及垂径定理在实际生活中的运用,解答此题的关键是构造出直角三角形及圆.15.(10分)学完勾股定理之后,同学们想利用升旗的绳子、卷尺,测算出学校旗杆的高度.爱动脑筋的小明这样设计了一个方案:如图,小亮将升旗的绳子拉直到末端刚好接触地面,测得此时绳子末端距旗杆底端1米,然后将绳子末端拉直到距离旗杆5m处,测得此时绳子末端距离地面高度为1m,如果设旗杆的高度为x米(滑轮上方的部分忽略不计),求x的值.【分析】根据题意画出示意图,设旗杆高度为x,可得AC=AD=x,AB=(x﹣1)m,BC=5m,在Rt△ABC中利用勾股定理可求出x.【解答】解:设旗杆高度为x,可得AC=AD=x,AB=(x﹣1)m,BC=5m根据勾股定理得,绳长的平方=x2+12,右图,根据勾股定理得,绳长的平方=(x﹣1)2+52,∴x2+12=(x﹣1)2+52,解得x=12.5.答x值为12.5【点评】本题考查了勾股定理的应用,解答本题的关键是构造直角三角形,构造直角三角形的一般方法就是作垂线.。
勾股定理拓展提高之动态几何(勾股定理)拔高练习(八年级课堂实录第二讲)—--学案教案
勾股定理拓展提高之动态几何(勾股定理)拔高练习(八年级课堂实录第二讲)试卷简介:本试卷共5道选择题,每道题20分,满分100分,测试时间50分钟。
本套试卷考察了勾股定理在对称、旋转变换中的应用。
学习建议:学习建议:本讲内容主要是勾股定理的综合应用,综合利用了对称、旋转的知识,希望同学们先熟练掌握勾股定理和对称旋转的一些性质,在根据题目中的条件,把分散的条件集中起来,构造直角三角形,利用勾股定理。
建议同学们认认真真看视频,体会其中的套路。
一、单选题(共5道,每道20分)1.如图,某人在B处通过平面镜看见在B正上方3米处的A物体,已知物体A到平面镜的距离为2米,问B点到物体A的像A′的距离是()A.5米B.4米C.3米D.2米2.如图,在△ABC中,AB=AC,P是BC边上任意一点,其中AP=4,BP=2,CP=3,则等于()A.17B.19C.20D.223.如图所示,在直角三角形ABC 中,∠BAC=90°,AC=AB ,∠DAE=45°,且BD=4,CE=3 ,则DE 的长等于().A.3B.4C.5D.64.如图,P是等边三角形ABC内一点,AP=3,BP=4,CP=5,求∠APB的度数.A.90B.120C.135D.1505.如图所示,Rt△ABC中,∠BAC=90°,AB=AC,D为BC上任意一点.那么AD,BD,CD满足()A.B.C.D.无法确定推荐课程:众享在线课程/ 东区总校:郑州市文化路与黄河路交叉口中孚大厦7楼B室电话:65335902 西区总校:郑州市陇海路与桐柏路交叉口凯旋门大厦B座405室电话:68856662。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1. 直角三角形的三边为a-b ,a ,a+b 且a 、b 都为正整数,则三角形其中一边长可能为( ) A 、61 B 、71 C 、81 D 、91
2、如图,EF 为正方形ABCD 的对角线,将∠A 沿DK 折叠,使它的顶点A 落在EF 上的G 点,则∠DKG=__
3、如图,直线l 上有三个正方形a ,b ,c ,若a ,c 的面积分别为5和11,则b 的面积为___________.
4、如图所示,在边长为2的正三角形ABC 中,已知点P 是三角形内任意一点,则点P 到三角形的三边距离之和PD+PE+PF 等于________
5、如图Rt △ABC 中,AB=BC=4,D 为BC 的中点,在AC 边上存在一点E ,连接ED ,EB ,则△BDE 周长的最小值为( )
A 、25
B 、23
C 、25+2
D 、23+2
6、在△ABC 中,AB 边上的中线CD=3,AB=6,BC+AC=8,则△ABC 的面积为________
7、如图,将正方形ABCD 折叠,使顶点A 与CD 边上的点M 重合,折痕交AD 于E ,交BC 于F ,边AB 折叠后与BC 边交于点G 。
如果M 为CD 边的中点,
求证:DE :DM :EM=3:4:5。
8、△ABC 中,BC=a ,AC=b ,AB=c ,若∠C=90°,如图(1),根据勾股定理,则a b c 2
2
2
+=。
若△ABC 不是直角三角形,如图(2)和(3),请你类比勾股定理,试猜想a b 2
2
+与c 2
的关系,并证明你的结论。
方法1:若m 为奇数(m ≥3),则a=m ,b =-=+1211
2
122()()m c m 和是勾股数。
方法2:若任取两个正整数,m 和n (m>n ),则a m n b mn =-=2
2
2,,c m =2
+n 2是勾股数。
(1)在以上两种方法中任选一种,证明以a 、b 、c 为边长的△ABC 是直角三角形。
(2)请根据方法1和方法2按规律填定下列表格:
勾m
3 5 11 … 股1212()m -
4 12 60 … 弦1212()m + 5
13
61
…
m 2 3 3 4 4 4 5 5 6 … n
1 2 1 3 2 1 4 3 5 … a=m 2-n 2 3 5 8 7 12 15 9 16 11 … b=2mn 4 12 6 24 16 8 40 30 60 … c=m 2+n 2
5
13
10
25
20
17
41
34
61
…
(3)某园林管理处要在一块绿地上植树,使之构成如图8所示的图案景观,该图案由四个全等的直角三角形组成。
要求每个三角形顶点处都植一棵树,各边上相邻两棵树之间的距离均为1米,如果每个三角形最短边上都植6棵树,那么这四个直角三角形的边上共需植树___________棵。
图8。
