人教版数学八年级上册14.2.2添括号法则教案
人教版数学八年级上册14.完全平方公式-添括号法则课件

4. 给下列多项式添括号,使它们的最高次 项系数为正数. 如: – x²+ x = –(x²– x); x²– x = + (x²– x) (1) 3x²y²– 2 x³+ y³ = +( 3x²y²– 2 x³+ y³)
(2) – a³+ 2a²– a +1 = –(a³– 2a²+ a – 1 )
观察
符号均没有变化
添上“+( )”, 括号 里的各项都不变符号;
a + b – c = a + ( b – c)
符号均发生了变化
添上“–( )”, 括号
里的各项都改变符 号.
பைடு நூலகம்
a + b – c = a – ( – b +c )
添括号时,
如果括号前面是正号,括到括号里 的各项都不变符号;
如果括号前面是负号,括到括号里 的各项都改变符号.
解:(1)a (b c) a b c
(2)a (b c) a b c
(3)a (b c) a b c
(4)a (b c) a b c
上面是根据去括号法则,由左边式 子得右边式子,现在我们把上面四个式 子反过来
(1) a+b-c=a+(b-c) (2) a-b-c=a+(-b-c) (3) a+b-c=a-(-b+c) (4) a-b+c=a-(b-c)
添括号法则
1.去括号的法则是什么?
• 括号前面是“+”号,把括号和它前面的“+” 号去掉,括号里各项都不改变正负号。
• 括号前面是“-”号,把括号和它前面的“-” 号去掉,括号里各项都改变正负号。
八年级数学上册《14.2.2 (2)添括号》 精品导学案 新人教版

一、【学习目标】1.利用去括号法则得到添括号法则。
2.理解乘法公式的结构特征并能灵活应用公式进行计算。
【学习重点】掌握添括号法则的规律。
【学习难点】能利用添括号的法则灵活利用乘法公式进行计算。
【知识准备】1.去括号法则:2.平方差公式:3.完全平方公式:4.把下列各式去括号。
(1)(a+b)-c= (2)-(a-b)+c=(3)a+(b-c)= (4)a-(b+c)=【自习自疑文】一、阅读教材P155-P156内容,思考并回答下列问题:1.在等号右边的括号内填上适当的项。
(1)a+b+c=( )+c; (2)a-b+c=( )+c;(3)-a+b-c=-( )-c; (4)-a-b+c=-( )+c;(5)a+b-c=a+ ( ) (6)a-b+c=a-( );添括号法则:。
我想问:请你将预习中遇见的问题和疑问写下来,等待课堂上与同学、老师共同探究解决。
等级组长(或家长)签字【自主探究文】【探究一】判断下列运算是否正确。
(1)22()22c ca b a b --=-- (2)32(32)m n a b m n a b -+-=++-(3)232(232)x y x y -+=-+- (4)245(2)(45)a b c a b c --+=--+【探究二】运用乖法公式计算(1)()()a b c a b c +++- (2)()()a b c a b c -++-(3)(21)(12)x y y x -+-+ 2(4)()x y z -+【探究三】先化简,再求值:22()(),a a b a b a +-+==其中【探究四】22111.5,x x x-=+已知求x 的值22222.16,()4,x y xy x =-=已知(x+y )求和+y 的值【探究五】2220,b c ab bc ac ++---=已知△ABC 的三边长a,b,c 满足a 试判断△ABC 的形状【自测自结文】1.填空题:(1)a-b-c=a-( ); (2)a+b+c=a-( ).22(3)3,1,x y xy x y +==+=若则22(4)4(),,.x x a x b a b ++=-=−−=−−若则2.计算下列各题(1)(32)(32)a b c a b c -++- 2(2)(2)x y z +- (3)9910110001⨯⨯3.先化简,再求值:(x-2y+1)(x+2y-1),x=1,y=2.222.n 4.+设m+n=10,mn=24,求m 和(m-n)的值【自我小结】通过本节课的学习,你有哪些收获?还有哪些困惑呢?教师个人研修总结在新课改的形式下,如何激发教师的教研热情,提升教师的教研能力和学校整体的教研实效,是摆在每一个学校面前的一项重要的“校本工程”。
八年级数学上册高效课堂(人教版)14.2.3添括号(第二课时)优秀教学案例

三、教学策略
(一)情景创设
1.生活情境:结合学生的生活实际,创设一些与添括号相关的问题情境,如购物时如何计算总价、制作美食时如何计算食材用量等,让学生在解决问题的过程中自然地接触到添括号的方法。
3.学生跟随教师的讲解,积极参与课堂互动,提问、解答问题,加深对添括号方法的理解。
(三)学生小组讨论
1.教师布置一些具有挑战性的练习题,让学生独立思考后,进行小组讨论,共同探讨添括号的解题方法。
2.学生通过讨论,分享自己的解题思路,互相学习、借鉴,提高解决问题的能力。
3.教师巡回指导,针对学生的不同解题方法,给予及时的引导和点拨,帮助他们找到更简洁的解题途径。
2.学生之间进行相互评价,鼓励他们发现他人的优点,学习他人的长处,提高自己的学习能力。
3.教师对学生的学习成果进行评价,关注他们的进步,给予及时的表扬和鼓励,增强他们的自信心。
四、教学内容与过程
(一)导入新课
1.利用多媒体展示一些生活场景,如购物、制作美食等,引导学生思考这些问题中是否存在添括号的需要。
(四)总结归纳
1.教师组织学生对添括号的方法进行总结,引导学生发现规律,形成自己的解题技巧。
2.学生通过总结归纳,加深对添括号方法的理解,提高自己的数学思维能力。
3.教师对添括号方法进行归纳总结,提炼出关键点,方便学生记忆和复习。
(五)作业小结
1.教师布置一些有关添括号的课后练习题,让学生巩固所学知识,提高自己的实际应用能力。
2.鼓励学生提出问题,培养他们的问题意识,如学生在学习过程中遇到的困惑、疑问,教师应及时给予引导和解答。
14.2.2添括号法则课件

添括号时,如果括号前面是正号,括到括号里的各项 都不变符号; 如果括号前面是负号,括到括号里的各 项都改变符号.
也是:遇“加”不变,遇“减”都变.
例5 运用乘法公式计算:
(1) ( x +2y-3) (x- 2y +3) ; (2) (a + b +c ) 2.
解: (1) ( x +2y-3) (x- 2y +3)
= [ x+ (2y – 3 )] [ x- (2y-3) ] = x2- (2y- 3)2 = x2- ( 4y2-12y+9) = x2-4y2+12y-9. (2)(a + b +c ) 2
新人教版 ·数学 ·八年级(上) 15.2乘法公式
第3课时 添括号法则
请同学们完成下列运算并回忆去括号法则. (1)4+(5+2) (2)4-(5+2) (3)a+(b+c) (4)a-(b-c)
解:(1)4+(5+2)=4+5+2=11 (2)4-(5+2)=4-5-2=-3 (3)a+(b+c)=a+b+c (4)a-(b-c)=a-b+c
= [ (a+b) +c ]2 = (a+b)2 +2 (a+b)c +c2 = a2+2ab +b2 +2ac +2bc +c2 = a2+b2+c2 +2ab+2bc +2ac.
最新人教版初中数学八年级上册《14.2.2 完全平方公式》精品教学课件

(3)(–3a+b)2=9a2–6ab+b2.
探究新知
素养考点 2 利用完全平方公式进行简便计算
例2 运用完全平方公式计算:
(1) 1022;
(2) 992.
解: 1022 = (100+2)2 =10000+400+4 =10404.
992 = (100 –1)2 =10000 –200+1
=9801.
(1) 说一说积的次数和项数. (2) 两个完全平方式的积有相同的项吗?与a,b有什么关系? (3) 两个完全平方式的积中不同的是哪一项?与a, b有什么 关系?它的符号与什么有关?
探究新知 公式特征: 积为二次三项式; 积中两项为两数的平方和; 另一项是两数积的2倍,且与两数中间的符号相同. 公式中的字母a,b可以表示数、单项式和多项式.
方法总结:当一个数具备与整十、整百⋯ ⋯相差一个正整数时 求它的平方,我们可以通过变形运用完全平方公式进行运算较
简便.
巩固练习
利用乘法公式计算:
(1)982–101×99;
(2)20162–2016×4030+20152.
解:(1)原式=(100–2)2–(100+1)(100–1) =1002–400+4–1002+1=–395;
人教版 数学 八年级 上册
14.2 乘法公式
14.2.2 完全平方公式
导入新知
现有如图所示的三种规格的硬纸片各若干张,请你根据 二次三项式a2+2ab+b2,选取相应种类和数量的硬纸片,
拼出一个正方形,并探究所拼出的正方形的代数意义.
素养目标
3. 体验归纳添括号法则. 2. 灵活应用完全平方公式进行计算. 1. 理解并掌握完全平方公式的推导过程、 结构特点、几何解释.
14.2.2 添括号法则
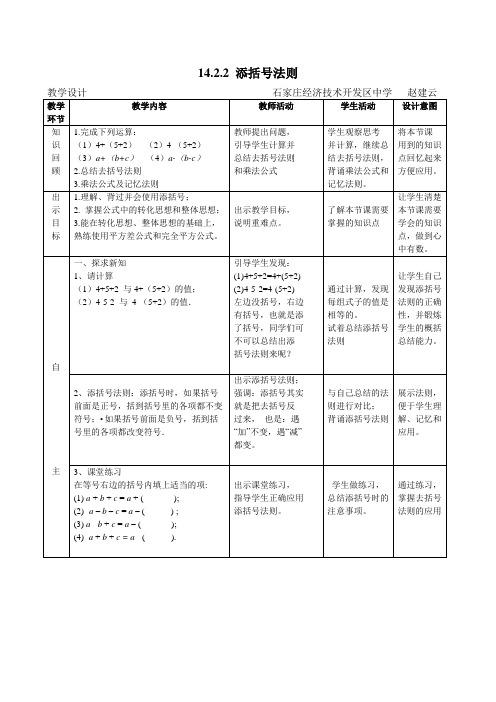
与自己总结的法
则进行对比;
背诵添括号法则
展示法则,
便于学生理
解、记忆和
应用。
3、课堂练习
在等号右边的括号内填上适当的项:
(1)a+b+c=a+ ( );
(2)a– b–c=a– ( ) ;
(3)a-b+c=a– ( );
(4)a+b+c= a- ( ).
出示课堂练习,
指导学生正确应用
添括号法则。
(1) (x+2y-3) (x- 2y+3) ;
(2) (a+b-c)2.
找学生板书;
与学生共同评价
两生板书,其他
学生做练习;
与同学交流,
与老师共同评价
通过例题训
练,使学生
进一步掌握
用添括号法
则分组的技
能。
课堂练习:
运用乘法公式计算:
(1)(a+ 2b– 1 )2;
(2)(2x+y+z) (2x–y–z)
并计算,继续总
结去括号法则,
背诵乘法公式和
记忆法则。
将本节课
用到的知识
点回忆起来
方便应用。
出
示
目
标
1.理解、背过并会使用添括号;
2.掌握公式中的转化思想和整体思想;
3.能在转化思想、整体思想的基础上,
熟练使用平方差公式和完全平方公式。
出示教学目标,
说明重难点。
了解本节课需要
掌握的知识点
让学生清楚
本节课需要
要求。
学生按要求完成
课上好课外作业
加深对所学
知识点的理
解、认识和
八年级数学上册 14.2.2添括号和公式的综合运用导学案
14.2.2添括号和公式法的综合运用 导学案学习目标:1.添括号法则.2.利用添括号法则灵活应用完全平方公式.学习重点:理解添括号法则,进一步熟悉乘法公式的合理利用.学习难点:在多项式与多项式的乘法中适当添括号达到应用公式的目的. 学习过程:一、自学指导1. 在去括号时:c b a c b a ++=++)( c b a c b a --=+-)( 也就是说,遇“加”不变,遇“减”都变.反过来,就得到了添括号法则:)(c b a c b a ++=++ )(c b a c b a +-=--也是:遇“加”不变,遇“减”都变.2. 理解法则:如果括号前面是正号,括到括号里的各项都不变符号;•如果括号前面是负号,括到括号里的各项都改变符号.二、自我尝试1、 运用法则:(1)a+b-c=a+( ) (2)a-b+c=a-( )(3)a-b-c=a-( ) (4)a+b+c=a-( )2.判断下列运算是否正确.(1)2a-b-2c =2a-(b-2c ) (2)m-3n+2a-b=m+(3n+2a-b ) (3)2x-3y+2=-(2x+3y-2) (4)a-2b-4c+5=(a-2b )-(4c+5)3. 总结:添括号法则是去括号法则反过来得到的,无论是添括号,还是去括号,运算前后代数式的值都保持不变,•所以我们可以用去括号法则验证所添括号后的代数式是否正确.三、师生互动1、在公式里运用法则例:计算:(1)(x+2y-3)(x-2y+3) (2)(a+b+c )2(3)(x+3)2 (4)(x+5)2-(x-2)(x-3)2、两公式的综合运用例:如果81362++x kx 是一个完全平方公式,则k 的值是多少?四、归纳小结 这节课你学到了什么?五、当堂训练1、 计算:2)2(c b a +- 22)()(c b a c b a ---++2、如果3642++kx x 是一个完全平方公式,则k 的值是多少?3、如果422=-y x ,那么22)()(y x y x +-的结果是多少?4、已知5=+b a 5.1=ab ,求22b a +和 2)(b a -的值5、已知31=+x x ,求221x x +和2)1(x x -的值6、已知-7=+b a 12=ab ,求ab b a -22+和 2)(b a -的值附加:证明25)12(2-+n 能被4整除。
14.2.2 完全平方公式 第2课时 课件-人教版数学八年级上册
符号改变
追问三:观察两个式了,你得出什么规律?
添上“+( )”,括号里的各项都不变符号. 添上“( )”,括号里的各项都改变符号.
【归纳】添括号法则: 两添括号时,如果括号前面是正号,括到括号里的各项都不变符号;
如果括号前面是负号,括到括号里的各项都改变符号.
a+b+c=a+(b+c)
abc=a(b+c)
课堂总结
如果括号前面是正号,
括到括号里的各项都不
添
变符号
括
号
法
则 如果括号前面是负号,
括到括号里的各项都改
变符号
a+b+c=a+(b+c) a-b-c=a- (b+c)
∴(m+n)2=64 ∴m+n=8
2. 灵活运用乘法公式计算:(xym+n)(xy+mn)
解: (xym+n)(xy+mn) =[(xy)(mn)][(xy)+(mn)] =(xy)2(mn)2 =x22xy+y2m2+2mnn2
3. 先阅读下面的内容,再解决问题. 例题:若 m2+2 mn +2 n2-6 n +9=0,求 m 和 n 的值. 解:∵ m2+2 mn +2 n2-6 n +9=0, ∴ m2+2 mn + n2+ n2-6 n +9=0. ∴( m + n )2+( n -3)2=0. ∴ m + n =0, n -3=0. ∴ m =-3, n =3.
(1)(x 2y 3)(x 2y 3) ;
(2)(a b c)2 .
把(2y3)看成一个整体.
把(a+b)看成一个整体.
解:(1) (x+2y3)(x2y+3)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《添括号法则》教学设计
教学目标:
1.类比去括号掌握添括号法则。
2.会用添括号法则,进行多项式的变形计算。
3.培养学生类比归纳的数学思想
教学重点:添括号法则及法则的应用。
教学难点:括号前面是“-”号,括到括号里的各项都要改变符号。
教学方法:探究与讲练相结合的方法
学具准备:ppt课件
课时分配:一课时
教学过程:
一、出示教学目标
学生齐读,明确本节课学习目标
二、热身运动
1.去括号的法则是什么?
课件出示:
括号前面是“+”号,把括号和它前面的“+”号去掉,括号里各项都不改变正负号;括号前面是“-”号,把括号和它前面的“-”号去掉,括号里各项都改变正负号
2我们学过哪些乘法公式?
课件出示:
平方差公式和完全平方公式
三、探究新知
学生试着把下列各式去括号:
(1)a+(b-c) (2)a-(-b+c) (3)a+(-b-c) (4)a-(-b-c)
学生探究:
我们把式子试着反写过来,观察符号归纳添括号法则
归纳添括号法则:
添括号时,如果括号前面是正号,括到括号里的各项都不变符号,如果括号前面是负号,括到括号里的各项都改变符号。
四、知识应用
知识点1:
添括号法则
1、下列各式,等号右边添的括号正确吗?若不正确,可怎样改正?
归纳检验方法:常用去括号来检验添括号的正确性。
知识点2:
利用添括号进行凑整法简便计算
2. 用简便方法计算:
(1)214a+47a+53a; (2)214a – 39a – 61a.
归纳应用方法:用添括号的方法把通过加减凑成整数的项组合在一起。
知识点3:
利用乘法公式进行计算
3.为了应用平方差公式计算(x+3y-1)(x-3y+1),下列变形正确的是( )
A.[x-(3y+1)]2 B.[x+(3y+1)]2
C.[x+(3y-1)][x-(3y-1)] D.[(x-3y)+1][(x-3y)-1] 4.下列式子中有一个不能运用乘法公式计算,这个算式是( ) A.(a+b-c)(a-b+c) B.(a-b-c)2
C.(a-b)(a+b) D.(2a+b+2)(a-2b-2)
归纳:应用方法
5.运用乘法公式计算:
(1)(a+b-c)2; (2)(3a+b-2)(3a-b+2)
归纳:
遇到() ()且括号里的项要么相同要么相反的题型,用添括号的方法想平方差公式;遇到()2的题型,用添括号的方法想完全平方公式,
知识点4:
拓展提升
6.探索x2-xy=18,xy-y2=-15时,求x2-2xy=y2的值?
五、总结达成目标。
