数学与应用数学专业-辽宁师范大学教务处
数学归纳法及其应用

原创性声明本人声明:所呈交的论文是本人在导师指导下进行的研究成果。
除了文中特别加以标注和致谢的地方外,论文中不包含其他人已发表或撰写过的研究成果。
参与同一工作的其他同志对本文研究所做的任何贡献均已在论文中作了明确的说明并表示了谢意。
签名:日期:本论文使用授权说明本人完全了解有关保留、使用学位论文的规定,即:学校有权保留论文及送交论文复印件,允许论文被查阅和借阅;学校可以公布论文的全部或部分内容。
(保密的论文在解密后应遵守此规定)学生签名:指导教师签名:日期:本科生毕业设计开题报告注:1、学院可根据专业特点,可对该表格进行适当的修改。
【内封面】南通大学毕业论文摘要数学归纳法是一种常用的证明方法,它的应用极其广泛。
本文讨论了数学归纳法的原理,以数学归纳法原理为基础,在不同条件下对数学归纳法原理进行变易,扩大数学归纳法的应用范围。
并对数学归纳法的分类、应用进行总结,给出数学归纳法在初等代数、高等代数中的应用典例。
关键字:数学归纳法、原理、变易、应用。
ABSTRACTMathematical induction is a common method of proof, and its applications is very broad. This article discusses the principle of mathematical induction, promotes the principle of mathematical induction under different conditions, and expands the range of applications induction on the basis of the principle. It summarizes the classification and application of mathematical induction. Typical examples of applications of mathematical induction are given in elementary algebra and advanced algebra.Key words: Mathematical induction,Principle,Variation,Application目录摘要 (I)ABSTRACT.................................................................................................... I I1.引言 (1)2.数学归纳法原理及变易 (1)2.1数学归纳法的本原 (3)2.2数学归纳法原理 (3)2.3数学归纳法原理变易 (4)3.数学归纳法的表现形式 (6)3.1 第一数学归纳法 (6)3.2 第二数学归纳法 (6)3.3 跳跃归纳法 (7)3.4 双向归纳法 (8)3.5 反向归纳法 (8)4.数学归纳法的应用 (10)4.1数学归纳法在初等代数中的典型应用 (10)4.1.1 证明恒等式 (10)4.1.2 证明不等式 (12)4.1.3 证明整除问题 (12)4.1.4 证明几何问题 (12)4.2 数学归纳法在高等数学中的应用 (13)4.2.1 数学归纳法证明德摩根定律推广式 (13)4.2.2 数学归纳法证明行列式 (14)5.结论 (16)参考文献 (17)致谢......................................................................... 错误!未定义书签。
自考本科各专业课程设置与教材
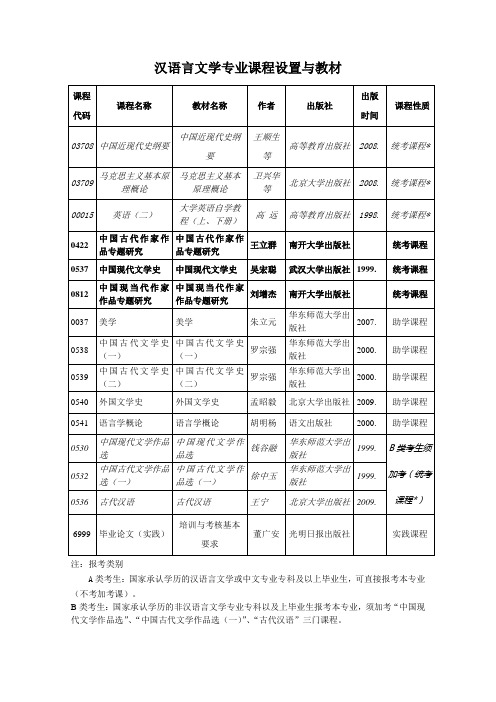
汉语言文学专业课程设置与教材
注:报考类别
A类考生:国家承认学历的汉语言文学或中文专业专科及以上毕业生,可直接报考本专业(不考加考课)。
B类考生:国家承认学历的非汉语言文学专业专科以及上毕业生报考本专业,须加考“中国现代文学作品选”、“中国古代文学作品选(一)”、“古代汉语”三门课程。
化学教育专业课程设置与教材
A类考生:化学专业专科及以上毕业生可直接报考本专业(不考加考课)。
B类考生:非化学专业专科及以上毕业生报考本专业须加考“分析化学”、“分析化学实验(实践)”两门课程。
数学教育专业课程设置与教材
A类考生:数学专业专科及以上毕业生可直接报考本专业(不考加考课)。
B类考生:非数学专业专科及以上毕业生报考本专业须加考“数学分析(二)”、“高等代数”两门课程。
小学教育课程设置与教材
A类考生:各类师范类专科及以上毕业生可以直接报考本专业,不考加考课。
B类考生:非师范类专科及以上毕业生专科报考本专业,须加考“教育原理”、“小学教育心理学”两门课程。
学前教育专业课程设置与教材
注:报考类别:
A 类考生:学前教育专业专科毕业生可以直接报考本专业(不考加考课)。
B 类考生:非本专业的专科及以上毕业生报考本专业时应加考:“学前教育学”、“学前心理学”、“学前卫生学”三门课程。
英语专业课程设置与教材
注:
A类考生:各类高等教育形式英语专业专科及以上毕业生可直接报考本专业(不考加考课)
B类考生:各类高等教育形式的其他专业专科及以上毕业生报考本专业,必须加考综合英语(二)、听力(实践)、口语(实践)三门课程。
英语教育专业课程设置与教材。
计算与科学专业相关的信息资料

计算与科学专业相关的信息资料基本信息概述信息与计算科学专业(学科代码:070102)Information and Computing Sciences (原名:计算数学)信息与计算科学专业是以信息领域为背景。
数学与信息,管理相结合的交叉学科专业。
该专业培养的学生具有良好的数学基础,能熟练地使用计算机,初步具备在信息与计算科学领域的某个方向上从事科学研究,解决实际问题,设计开发有关软件的能力.专业方向及特色:信息与计算科学专业为理科专业,包括信息科学与计算科学两个方面。
方向一是以信息科学方面为主,计算数学方面为辅;方向二是以数学方面为主,信息科学方面为辅。
[1]相近专业数学与应用数学、统计学主干学科数学、计算机科学与技术主要课程数学分析、高等代数、几何、概率统计、数学模型、离散数学、微分方程、物理学、信息处理、信息编码与信息安全、现代密码学教程、计算智能、计算机科学基础、数值计算方法、数据挖掘、最优化理论、计算机图形学、c/c++语言、java语言、汇编语言、算法与数据结构、数据库应用技术、软件系统、操作系统等。
培养目标本专业的课程体系和知识结构体现了在扎实的数学基础之上,合理架构信息科学与计算科学的专业基础理论。
通过信息论、科学计算、运筹学等方面的基础知识教育和建立数学模型、数学实践课、专业实习各环节的训练,着重培养学生解决科学计算、软件开发和设计、信息处理与编码等实际问题的能力,培养能胜任信息处理、科学与工程计算部门工作的高级专门人才。
[1]培养要求本专业学生主要学习信息科学和计算科学的基本理论、基本知识和基本方法,打好数学基础,受到较扎实的计算机训练,初步具备在信息科学与计算科学领域从事科学研究、解决实际问题及设计开发有关软件的能力。
毕业生应获得以下几方面的知识和能力:1.具有扎实的数学基础,掌握信息科学和/或计算科学的基本理论和基本知识2.能熟练使用计算机(包括常用语言、工具及一些专用软件),具有基本的算法分析、设计能力和较强的编程能力3.了解某个应用领域,能运用所学的理论、方法和技能解决某些科研或生产中的实际课题;4.对信息科学与计算科学理论、技术及应用的新发展有所了解5.掌握文献检索、资料查询的基本方法,具有一定的科学研究和软件开发能力。
1 数系与数学归纳法

1.3 错例辨析
1.证明:所有人的年龄都是一样的。
辨析:递推步对n=1不成立。从而,由n=1成立,得不到n=2成立,递推中
断。
2. 证明:任何两个正整数均相等。
下证An对于任意自然数n都成立。
因为
所以 利用归纳假设知,a-1=b-1, 从而a=b. 即Ak+1成立。
辨析:a-1与b-1不一定是正整数,它们有可能是0,从而不能够利用归纳假
1 数系与数学归纳法
1.1 内容概述
数系,是数的系统的简称。数系内容是中小学数 学的基础.从小学一年级学习自然数开始,到高 中学习复数,数系的学习始终贯穿在整个数学课 程之中. 数系由于概念比较抽象,学起来比较枯燥。中小 学由于学生理解力有限,不可避免出现不严格的 现象,只能做到“适度形式化”,“模糊”处理, “混而不错”.数系学习在中小学的主要任务是 打好基础,学会运算,提高实际运算能力。
复数的定义也可以从形式上避开对i的解释。
定义1(复数的序偶定义)将有序的实数对(a,b) 称为复数,并定义它们的运算法则如下:
定义2(复数的矩阵定义) 将二阶实数矩阵 称为复数.
7、复数不能比较大小的含义 “有序域”的概念
为什么这样就叫“有序域”? 因为根据有序域F上的正性关系可等价定义 “序关系”:对a,b∈F,定义a>b(或b<a) 当且仅当a-b>0.并且,该序对运算协调(保 序)。
第1题解法(第二数学归纳法)
第2题解法(跳跃式数学归纳法)
第3题解法(逆向数学归纳法[Cauchy])
逆向数学归纳法可形象称为“留空回填”,其中“有 无穷多个自然数使P(n)真”常取P(2k),P(2k),P(2k1).
第4题解法
第5题解法
应用数学考研录取学校排名

1 北京大学A+15东南大学A29北京航空航天大学A2 浙江大学A+16上海交通大学A30哈尔滨工业大学A3 清华大学A+17中山大学A31上海大学A4 复旦大学A+18武汉大学A19 华中科技大学32福州大学A中南大学A5 中国科学技术大学A+ A 336 南开大学A+20北京理工大学A34电子科技大学A7 四川大学A+21湖南大学35苏州大学A8 山东大学A+22西安电子科技大学A 36华中师范大学A9 新疆大学A+23华东师范大学A37华东理工大学A10 北京师范大学A+ 24西北工业大学A38首都师范大学A11 吉林大学A25西安交通大学A39厦门大学A12 南京大学A26同济大学A40陕西师范大学A13 大连理工大学 A 27重庆大学A41广州大学A14 兰州大学A28华南理工大学A42云南大学AB+等(63个):河北师范大学、西北师范大学、湘潭大学、曲阜师范大学、湖南师范大学、东北师范大学、北京交通大学、南京师范大学、暨南大学、辽宁师范大学、江苏大学、安徽师范大学、合肥工业大学、华南师范大学、南昌大学、东北大学、东华大学、广西大学、桂林电子科技大学、哈尔滨工程大学、四川师范大学、辽宁大学、河海大学、郑州大学、内蒙古大学、天津大学、长江大学、广东工业大学、北京科技大学、徐州师范大学、南京航空航天大学、上海师范大学、西南交通大学、山东科技大学、扬州大学、北京工业大学、武汉理工大学、兰州理工大学、大连海事大学、温州大学、南京信息工程大学、北方工业大学、上海理工大学、浙江工业大学、山东师范大学、宁波大学、湖南科技大学、浙江师范大学、哈尔滨理工大学、安徽大学、福建师范大学、中国矿业大学、广西师范大学、江南大学、黑龙江大学、西安建筑科技大学、河南师范大学、北京邮电大学、南京农业大学、兰州交通大学、成都理工大学、西安理工大学、长沙理工大学B等(62个):安庆师范学院、武汉科技大学、河北大学、南京财经大学、中国海洋大学、江西师范大学、重庆师范大学、杭州电子科技大学、中北大学、中国人民大学、山西大学、西南大学、青岛大学、河南大学、河北工业大学、五邑大学、太原理工大学、渤海大学、辽宁工程技术大学、湖北大学、青岛科技大学、深圳大学、西华大学、贵州大学、云南师范大学、长春工业大学、大连大学、天津工业大学、南京邮电大学、汕头大学、华北电力大学、烟台大学、聊城大学、中国农业大学、北京化工大学、中国石油大学、青岛理工大学、信阳师范学院、河北科技大学、哈尔滨师范大学、华东交通大学、西安科技大学、安徽理工大学、三峡大学、西北农林科技大学、辽宁工业大学、河南科技大学、集美大学、中国计量学院、海南大学、上海财经大学、南京理工大学、南昌航空工业学院、南华大学、南通大学、东北林业大学、宁夏大学、海南师范大学、中南民族大学、西华师范大学、安徽工业大学、中国传媒大学不跨专业:基础数学,应用数学,概率论与数理统计,计算数学,运筹学与控制论跨专业:经济学和计算机方向精算学——(华东师范大学)生物数学——(中国科学技术大学)信息安全——(山东大学)信息计算科学—(中山大学)不确定性处理的数学——(四川大学)数学物理——(中国科学技术大学)金融数学与金融工程——(山东大学)信息安全——四川大学近年来,由于受社会供求的影响,文科类的法律、工商管理、金融经济、MBA 会计,理工科类的医学、电子信息类、计算机类,社会需求量比较大,找工作普遍比较容易,待遇薪水也比较高,属于当前比较热门的专业。
考研应用数学专业排名

北京师范大学
A
40
哈尔滨工业大学
A
13
同济大学
A
27
北京航空航天大学
A
41
南京大学
A
14
北京理工大学
A
28
电子科技大学
A
B+等(63个):湖南师范大学、重庆大学、华中师范大学、东华大学、河北师范大学、桂林电子科技大学、辽宁大学、内蒙古大学、哈尔滨工程大学、南京师范大学、华南师范大学、华东理工大学、陕西师范大学、西北师范大学、广东工业大学、安徽师范大学、徐州师范大学、东北大学、北京交通大学、辽宁师范大学、上海师范大学、西南交通大学、山东科技大学、武汉理工大学、暨南大学、南京航空航天大学、郑州大学、大连海事大学、江苏大学、合肥工业大学、上海理工大学、浙江工业大学、宁波大学、四川师范大学、浙江师范大学、河海大学、北京科技大学、安徽大学、福建师范大学、中国矿业大学、广西大学、南昌大学、北方工业大学、西安建筑科技大学、河南师范大学、温州大学、成都理工大学、扬州大学、武汉科技大学、长江大学、南京信息工程大学、北京工业大学、兰州理工大学、湖南科技大学、南京财经大学、西安理工大学、青岛大学、南京农业大学、河北工业大学、五邑大学、太原理工大学、渤海大学、江南大学
B等(62个):山东师范大学、山西大学、中北大学、哈尔滨理工大学、深圳大学、广西师范大学、云南师范大学、长春工业大学、大连大学、安庆师范学院、湖北大学、汕头大学、烟台大学、黑龙江大学、河北大学、河南大学、杭州电子科技大学、西南大学、长沙理工大学、信阳师范学院、北京邮电大学、西安科技大学、兰州交通大学、南京邮电大学、西北农林科技大学、中国海洋大学、江西师范大学、集美大学、重庆师范大学、中国人民大学、上海财经大学、南京理工大学、中国计量学院、聊城大学、宁夏大学、海南师范大学、西华师范大学、辽宁工程技术大学、中国传媒大学、中国农业大学、漳州师范学院、中国地质大学、青岛科技大学、辽宁工学院、西华大学、贵州大学、安徽理工大学、哈尔滨师范大学、天津工业大学、三峡大学、华北水利水电学院、华北电力大学、重庆工学院、天津工程师范学院、山东理工大学、湖北师范学院、北京化工大学、中国石油大学、青岛理工大学、河北科技大学、华东交通大学、广西师范学院
运用非智力因素促进数学运算素养的策略探究

摘要:数学运算能力特别注重运算的几何直观化、模型归纳化、特殊到一般化、陌生到熟悉化,而非智力因素在这些能力的转化之中起着相当重要的作用.教师应将非智力因素融入课堂教学设计中,使之与智力因素深度融合,让学生获得更多的学习体验,提升数学运算素养.具体可以采取如下策略:兴趣激发,引导学生建构运算模型,发展转化思想;情感代入,以梯度问题导引,提升学生的运算能力;意志磨砺,使学生经历从特殊到一般的逻辑推理过程,深化运算素养.关键词:非智力因素;数学运算;学习力
运用非智力因素促进数薛飞|浙江省杭州市萧山区第十高级中学龚超群|浙江省武义第一中学
数学运算素养是数学学科的六大核心素养之一.数学运算,即在明晰的运算对象的基础上,依据运算法则解决数学问题,它是数学研究的主要内容,也是解决数学问题的基本手段.数学运算能力特别注重运算的几何直观化、模型归纳化、特殊到一般化、陌生到熟悉化.在这些转化的过程中,非智力因素的作用相当重要.非智力因素主要指兴趣、情感、意志等,其中,兴趣、情感能直接转化为学习动机,意志则在学生掌握知识的过程中起着积极的作用.教师可从激发学习兴趣、提升数学情感、加强意志力等角度来设计课堂教学,优化复杂的运算,增强学生的信心,培养其自觉学习的习惯,最终提升其数学运算素养.一、兴趣激发:建构运算模型,发展转化思想学习活动能否顺利开展、达成预期目标,固然要以学生的智力因素为基础和主导,但也离不开学生主体的兴趣.浓厚的学习兴趣是学习的原动力,积极的兴趣是从事学习活动并取得成就的最初条件.兴趣一般表现为人们力求认识世界、渴望获得科学文化知识和探求真理时带有情绪色彩的心理[1].从心理上看,高中生的兴趣指向事物的内部规律,不断由肤浅变得深刻;而由于学习任务和压力变大,他们对学业相关的兴趣变淡,其他方面的兴趣变浓.因此,教师可创设学生喜欢的、熟悉的真实案例情境,如以生活常识、数学文化、竞技游戏、深度的思维结论等作为课堂引入情境,以激发学生主体的好奇心或竞争意识,促使学生自主学习.需要注意的是,以非智力因素带动智力因素设计教学,选择的情境必须内容适当、难度适中.(一)以情境激发兴趣以情境激发兴趣,,建构模型化运算数学运算表现为数字的计算和估算、变量式子的组合变形与分离、几何图形中各量的确定与计算等形式,教师可以采用模型化、熟悉化、直观化和特殊化等策略来培养学生的运算能力.数学模型是参照某种事物系统的特征或数量依存关系,采用数学语言,概括地或近似地表述出的一种数学结构.建立数学模型,便于沟通实际问题与数学工具.因此,数学模型化是提高学生数学运算素养的重要途径.教师要做生活的有心人,积极利用课外时间,搜寻可促进学生学习数学的图片、视频、故事、有奖竞赛等,仔细甄别梯度并归类.然后根据教学内容以及学生的学情、兴趣点,创设能引发学生学习兴趣的情境.如此引入相关数学问题,可让学生在兴趣的推动下,将注意力从枯燥的数学概念、定理转移到具体的数学模型上来,主动去探究问题.教师再适当分析问题,教学月刊·中学版教学参考2022·3
应用数学考研录取学校排名

1 北京大学 A+ 15 东南大学 A 29 北京航空航天大学 A2 浙江大学 A+ 16 上海交通大学 A 30 哈尔滨工业大学 A3 清华大学 A+ 17 中山大学 A 31 上海大学 A4 复旦大学 A+ 18 武汉大学 A 32 福州大学 A5 中国科学技术大学 A+ 19 华中科技大学 A 33 中南大学 A6 南开大学 A+ 20 北京理工大学 A 34 电子科技大学 A7 四川大学 A+ 21 湖南大学 35 苏州大学 A8 山东大学 A+ 22 西安电子科技大学 A 36 华中师范大学 A9 新疆大学 A+ 23 华东师范大学 A 37 华东理工大学 A10 北京师范大学 A+ 24 西北工业大学 A 38 首都师范大学 A11 吉林大学 A 25 西安交通大学 A 39 厦门大学 A12 南京大学 A 26 同济大学 A 40 陕西师范大学 A13 大连理工大学 A 27 重庆大学 A 41 广州大学 A14 兰州大学 A 28 华南理工大学 A 42 云南大学 AB+等(63个):河北师范大学、西北师范大学、湘潭大学、曲阜师范大学、湖南师范大学、东北师范大学、北京交通大学、南京师范大学、暨南大学、辽宁师范大学、江苏大学、安徽师范大学、合肥工业大学、华南师范大学、南昌大学、东北大学、东华大学、广西大学、桂林电子科技大学、哈尔滨工程大学、四川师范大学、辽宁大学、河海大学、郑州大学、内蒙古大学、天津大学、长江大学、广东工业大学、北京科技大学、徐州师范大学、南京航空航天大学、上海师范大学、西南交通大学、山东科技大学、扬州大学、北京工业大学、武汉理工大学、兰州理工大学、大连海事大学、温州大学、南京信息工程大学、北方工业大学、上海理工大学、浙江工业大学、山东师范大学、宁波大学、湖南科技大学、浙江师范大学、哈尔滨理工大学、安徽大学、福建师范大学、中国矿业大学、广西师范大学、江南大学、黑龙江大学、西安建筑科技大学、河南师范大学、北京邮电大学、南京农业大学、兰州交通大学、成都理工大学、西安理工大学、长沙理工大学B等(62个):安庆师范学院、武汉科技大学、河北大学、南京财经大学、中国海洋大学、江西师范大学、重庆师范大学、杭州电子科技大学、中北大学、中国人民大学、山西大学、西南大学、青岛大学、河南大学、河北工业大学、五邑大学、太原理工大学、渤海大学、辽宁工程技术大学、湖北大学、青岛科技大学、深圳大学、西华大学、贵州大学、云南师范大学、长春工业大学、大连大学、天津工业大学、南京邮电大学、汕头大学、华北电力大学、烟台大学、聊城大学、中国农业大学、北京化工大学、中国石油大学、青岛理工大学、信阳师范学院、河北科技大学、哈尔滨师范大学、华东交通大学、西安科技大学、安徽理工大学、三峡大学、西北农林科技大学、辽宁工业大学、河南科技大学、集美大学、中国计量学院、海南大学、上海财经大学、南京理工大学、南昌航空工业学院、南华大学、南通大学、东北林业大学、宁夏大学、海南师范大学、中南民族大学、西华师范大学、安徽工业大学、中国传媒大学不跨专业:基础数学,应用数学,概率论与数理统计,计算数学,运筹学与控制论跨专业:经济学和计算机方向精算学——(华东师范大学)生物数学——(中国科学技术大学)信息安全——(山东大学) 信息计算科学—(中山大学)不确定性处理的数学——(四川大学) 数学物理——(中国科学技术大学)金融数学与金融工程—— (山东大学) 信息安全——四川大学近年来,由于受社会供求的影响,文科类的法律、工商管理、金融经济、MBA、会计,理工科类的医学、电子信息类、计算机类,社会需求量比较大,找工作普遍比较容易,待遇薪水也比较高,属于当前比较热门的专业。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
附件4
2016年高职高专应届毕业生升入本科学习
辽宁师范大学数学与应用数学专业综合课(理论)
考 试 大 纲
说明:考试时间共计150分钟,满分200分。考试分三个科目,其
中,高等代数80分、数学分析 80分、解析几何 40分。
《高等代数》考试大纲
第一章 行列式
1.行列式的定义
2.行列式的计算
3.行列式的几何意义(二阶、三阶)
第二章 矩阵
1.矩阵的运算
2.初等矩阵
3.矩阵的秩
4.求可逆矩阵的逆矩阵
第三章 线性方程组
1.向量空间
2.向量组的线性相关性
3.线性方程组求解及解的结构
第四章 欧式空间与二次型
1.矩阵的特征根与特征向量
2.矩阵的对角化问题
3.求欧氏空间的正交基及标准正交基
4.用非退化线性变换和正交变换方法化二次型为标准形
《数学分析》考试大纲
第一章 一元函数的极限与连续
1.函数的定义域及其求法
2.数列与函数的极限
3.函数的连续性
第二章 一元函数的导数与微分
1.函数导数的定义及导数求法
2.函数微分的求法
3.微分中值定理及其应用(包括:1.罗尔中值定理及其应用;2.拉格朗日中值定理及其 应用)
4.洛必达法则及其应用(用洛必达法则求函数的极限)
第三章 一元函数的积分
1.不定积分的概念
2.换元积分法与分部积分法
3.定积分及其应用
4.广义积分
第四章 多元函数微积分
1.二元函数的连续性
2.二元函数的偏导数与全微分
3.泰勒公式与极值问题
4.级数收敛性的判别
5.幂级数
6.二重积分与三重积分的计算
《解析几何》考试大纲
第一章 向量代数
1.向量的线性运算
2.向量的共线与共面
3.向量的坐标表示
4.向量的内积、外积及混合积
第二章 平面与空间直线
1.求平面方程
2.求空间直线方程
3.讨论平面与平面、直线与直线、直线与平面的位置关系及点到平面、点到直线的距离
第三章 曲面论
1.柱面
2.锥面
3.旋转曲面
