人教版七年级数学下册课件:第七章 平面直角坐标系-7.2.2 用坐标表示平移
人教版七年级数学下册第七章平面直角坐标系PPT课件全套

有序数对在生活中的应用
知 识 点 二
如图是某学校的平面示意图.如果用 (5,1)表示学校大门的位置,那么运动场表 宿舍楼 (6,8) ,(8,5)表示的场所是_____. 示为_____
有序数对在生活中的应用
知 识 点 二
如图3,甲处表示2街与5巷的十字路口,乙处表 示5街与2巷的十字路口,如果用(2,5)表示甲处的位 置,那么“(2,5)→(3,5) →(4,5) →(5,5) →(5,4) →(5,3) →(5,2)”表示从甲处到乙处的一种路线,请 你用 这种形式写出两种从甲处到乙处的最短路线.
这就是我们接下来要学习的相关概念的内容。
2、在平面内画两条互相____、原点____的数轴, 垂直 重合 横轴 组成平面直角坐标系.水平的数轴称为____或____, x轴 y轴 习惯上取向_____为正方向;竖直的数轴称为___ 右 _或____,取向____为正方向;两个坐标轴的_ 上 纵轴 ___为平面直角坐标系的原点 . 交点 y轴
D
-4 -3 -2 -1 -1 4 3 2 1
y A
O1
2 3
4
x
C
-2 -3
B
4、如图所示,在第三象限的点是(C ) A.点A B.点B C.点C D.点D
(1)
学习目标
1
会根据实际情况建立适当的坐 标系;
2
通过点的位置关系探索坐标之间 的关系及根据坐标之间的关系探 索点的位置关系.
讲授新课
认真阅读课本第67至68页的内容,
分别为:A( 0,0 ),B(6,0),C(6,6 ),D(0,6). y 2、若以线段DC所在的直线为x轴,纵轴(y 轴)位置不变,则四个顶点的坐标分别为: 6,0 ), A( 0,-6),B( 6,-6 ),C( D( 0,0 ).
用坐标表示平移-七年级数学下册课件(人教版)

7.2.2 用坐标表示平移
学习目标
1. 会用坐标表示平移. 2. 能选择合适的方法灵活解决实际生活中的问题.
回顾旧知
1. 什么叫做平移?
把一个图形整体沿某一方向 移动一定的距离,图形的这 种移动,叫做平移.
2. 平移后得到的新图形与原图形有什么关系? 平移后图形的位置改变,形状、大小不变.
课堂小结
点平移与坐标变化
简记:右加左减
A3(x,y+a)
上加下减
上移a个 单位长度
左移a个
右移a个
A2(x-a,y) 单位长度 A(x,y) 单位长度
A1(x+a,y)
下移a个 单位长度
A4(x,y-a)
布置作业
P78:习题7.2:第3题. P79:习题7.2:第4、8题.
5
A3(-4,3) 4
3 2
向下平移2个单位
A4(-4,1) 1
A2(3,3)
A4(-4,3-2) 下移2个单位长度
A4(x,y-2)
-5 -4 -3 -2 -1 0 1
-1
-2
-3
A(-2,-3)-4
2 3 4 5x
A1(3,-3)
思考对比
与横坐标x有关 右加左减
右移5个单位长度,A1(x+5,y) 上移6个单位长度,A2(x,y+6)
D. (2,1)
A1(1,2)
(名校名题)在平面直角坐标系中,将 A(n2,1)沿着 x 的正方向向右平移 3+n2 个单位后
得到 B 点.有四个点 M(﹣2n2,1)、N(3n2,1)、P(n2,n2+4)、Q(n2+1,1),一定
人教版七年级数学下册《7.2 坐标方法的简单应用 第二课时》课件ppt

4 如图,若图①中点P 的坐标为( 8 , 2) ,则它在图②中的
3
对应点P1的坐标为( D )
A.(3,2)
C.
11 (1, )
3
B. ( 8 ,1)
3
D.
(11 ,1) 3
5 如图,线段AB 经过平移得到线段A′B ′,其中点A,B 的对应 点分别为点A′,B′,这四个点都在格点上.若线段AB上有一 个点P (a,b),则点P 在A′B ′上的对应点P ′的坐标为( A ) A.(a-2,b+3)
对一个图形进行平移,这个图形上所有点的坐标都要发 生相应的变化;反过来,从图形上的点的坐标的某种变化, 我们也可以看出对这个图形进行了怎样的平移.
思考 (1)如果将这个问题中的“横坐标都减去6”“纵坐标
都减去5”相应地变为“横坐标都加3”“纵坐标都 加2”,分别能得出什么结论?画出得到的图形.
(2)如果将三角形ABC 三个顶点的横坐标都减去6,同
长度,再向上平移3个单位长度后与点B (-3,2)重合,
则点A 的坐标是( D )
A.(2,5)
B.(-8,5)
C.(-8,-1)
D.(2,-1)
2 如图为某动物园的示意图.(图中小正方形的边长代表 1个单位长度)
(1)以虎山为原点,水平向右为x 轴正方向、铅直向上 为y 轴正方向在图中建立平面直角坐标系,并写出
在平面直角坐标系中,一个点沿x 轴方向 平移a(a>0)个单位长度后的坐标是什么?
左右点的平移
y
4
如图,将点A (-2, -3)向
3
右平移5个单位长度,得到点A1,
2
平移前后的坐标 有什么关系?
1
在图上标出这个点,并写出它的 坐标. 把点A向左平移2个单位呢?
人教版七年级数学下册《用坐标表示地理位置》平面直角坐标系PPT

知识要点
知识点一:用坐标表示地理位置 利用平面直角坐标系绘制区域内一些地点分布情况平面图的 过程: (1)建立坐标系:选择一个适当的 参照点 为坐标原点,确定 x轴和y轴的 正 方向; (2)根据具体问题确定 单位长度 ;
(3)在坐标平面内画出这些点,写出各点的 坐标 和各个地 点的名称. 温馨提示:①选择坐标原点时,要以能简捷地确定平面内点的 坐标为原则;②一般将正北作为y轴正方向,将正东作为x轴正 方向;③应使尽可能多的点落在坐标轴上,使点的坐标比较简 单.
,以钟面圆心为基准,时针指向北偏东30°的时刻是1:00,那么
这个地点就用代码010045表示.按这种表示方式,南偏东45°
方向78 km的位置,可用路上经过的地方:葡萄园,杏林,桃林,梅林,山楂林,枣林,梨 园,苹果园.图略.
5.【例2】小花和爸爸、妈妈周末到动物园游玩,回到家后,她 利用平面直角坐标系画出了动物园的景区地图,如图所示.可 是她忘记了在图中标出原点和x轴、y轴,只知道马的坐标为( -3,-3),你能帮她建立平面直角坐标系并求出其他各景点的 坐标吗?
2.(北师8上P56改编)如图是象棋棋盘的一部分,若“帅”位于点 (1,-2)上,“相”位于点(3,-2)上,则“炮”位于点( C )
A.(-1,1) B.(-1,2) C.(-2,1) D.(-2,2)
知识点三:用方向和距离表示地理位置 用方向和距离表示地理位置的方法: (1)找到 参照点 ; (2)在该点建立方向标; (3)测量出方位角和两点之间的距离; (4)根据 方位角 和 距离 表示出平面内的点(x,y). 温馨提示:描述方位角时,通常写成北偏东(西)或南偏东(西)的 形式.
9.(人教7下P79、北师8上P60)如图,这是一所学校的平面示意 图,建立适当的平面直角坐标系,并写出教学楼、校门和图书 馆的坐标.
人教版七年级下册数学 第七单元 7.2.2 用坐标表示平移

7.2.2 用坐标表示平移一、教学目标1、知识与技能:掌握点的平移规律,图形平移与坐标变化的关系,能利用点的平移规律将平面图形进行平移.2、过程与方法:经历点的坐标变化与图形变化之间关系的探索过程,感受并了解图形的平移变化与点的坐标变化之间的关系 3、情感态度价值观:培养学生主动探索,敢于实践的创新精神,让学生学会主动寻求解决问题的途径,从成功中体会研究数学问题的乐趣,从而增强学生学习数学的兴趣,树立学好数学的信心。
二、学情分析1、知识掌握上,七年级学生刚刚学习直角坐标系,对直角坐标系及坐标的理解不一定很深刻,许多学生容易造成知识混乱,所以应全面系统的去讲述。
2、由于七年级学生的理解能力、思维特征和生理特征,学生好动性,注意力易分散,爱发表见解,希望得到老师的表扬等特点,所以在教学中应抓住学生这一生理心理特点,一方面要运用直观生动的形象,引发学生的兴趣,使他们的注意力始终集中在课堂上;另一方面要创造条件和机会,让学生发表见解,发挥学生学习的主动性。
3、心理上,学生对数学课的兴趣,老师应抓住这有利因素,引导学生认识到数学课的科学性,学好数学有利于其他学科的学习以及学科知识的渗透性三、教学重点、难点二、教学重点:掌握图形平移与坐标变化的关系;三、教学难点:利用图形平移与坐标变化的关系解决实际问题。
四、教学过程:(一)温故知新,复习引入复习平移概念及性质。
(1)图中小船位置的变化叫做_______.(2)什么叫平移?(3)平移之后得到的新图形与原图形有什么关系?设计说明:从学生已有的数学知识出发,回顾平移的相关知识,为新知识、新课题的学习奠定了基础,从而也很自然地过渡到新课题的学习中去。
(二)合作交流,探究新知1、探究点的平移与坐标的变化(1)如图,将点A(-2, -3)向右平移5个单位长度,得到点A1,在图上标出这个点,并写出它的坐标.问:(2)点A与点A1的纵坐标分别是多少?有什么关系?(3)点A与点A1的横坐标分别是多少?有什么关系?实践:在准备好的平面直角坐标系中找点体会平移规律问:向左平移有怎样的规律呢?如图将点B(1,-2)向左平移5个单位长度得到点B1,写出点B1的坐标,点B与点B1的纵坐标分别是多少,有什么关系?横坐标是多少,有什么关系?总结规律:在平面直角坐标系中,将点(x,y)向右或(向左)平移a个单位长度,可以得到对应点( X+a ,y )或(x-a, y )口诀:左右平移,横变纵不变,右加左减。
七年级数学下册 第七章7.2.2 用坐标表示平移备课资料教案 (新版)新人教版
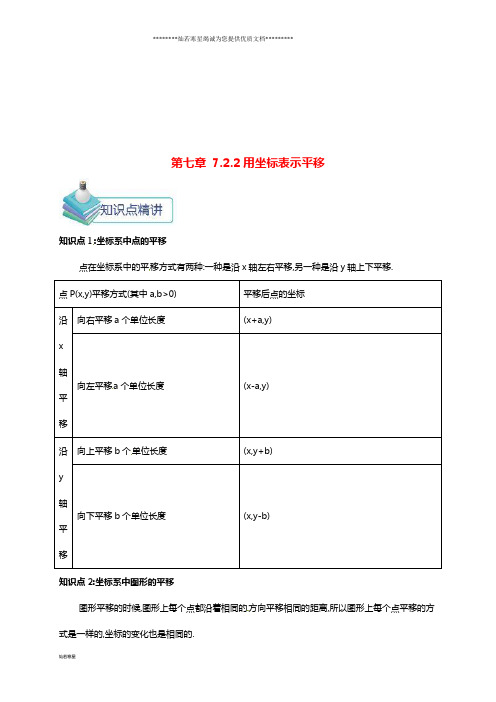
第七章7.2.2用坐标表示平移知识点1:坐标系中点的平移点在坐标系中的平移方式有两种:一种是沿x轴左右平移,另一种是沿y轴上下平移. 点P(x,y)平移方式(其中a,b>0) 平移后点的坐标沿x 轴平移向右平移a个单位长度(x+a,y) 向左平移a个单位长度(x-a,y)沿y 轴平移向上平移b个单位长度(x,y+b) 向下平移b个单位长度(x,y-b)知识点2:坐标系中图形的平移图形平移的时候,图形上每个点都沿着相同的方向平移相同的距离,所以图形上每个点平移的方式是一样的,坐标的变化也是相同的.一般地,在平面直角坐标系内,如果把一个图形各个点的横坐标都加(或减去)一个正数a,相应的新图形就是把原图形向右(或向左)平移a个单位长度;如果把图形各个点的纵坐标都加(或减去)一个正数a,相应的新图形就是把原图形向上(或向下)平移a个单位长度.考点1:点在坐标系中的平移【例】将点A(2,1)向左平移2个单位长度得到点A',则点A'的坐标是( )A.(2,3)B.(2,-1)C.(4,1)D.(0,1)答案:D点拨:将点向左平移2个单位长度,其横坐标减2,纵坐标不变,∴点A'的坐标为(2-2,1),即(0,1).故选D.考点2:图形的平移与坐标的变化【例】如图,把图①中的△ABC经过一定的变换得到图②中的△A'B'C',如果图①中△ABC上点P 的坐标为(a,b),那么这个点在图②中的对应点P'的坐标为( )A.(a-2,b-3)B.(a-3,b-2)C.(a+3,b+2)D.(a+2,b+3)答案:C点拨:由于图形向右平移了3个单位长度,向上平移了2个单位长度,因此图形上的每个点都作了相同的变化.。
人教版数学七年级下册7.4 用坐标表示平移 PPT课件
课后习题
1.在平面直角坐标系中,将点P(-2,3)沿x轴方向向右平移3 个单位得到点Q,则点Q的坐标是__(__1_,__3_)___,该点在第__一____ 象限. 2.已知点A(-4,-6),将点A先向右平移4个单位长度,再向上平 移6个单位长度,得到A′,则A′的坐标为_(__0_,__0_)_.
【小练习】 1.如图7-2-49,在平面直角坐标系中,线段A1B1是由线段 AB平移得到的,已知A,B两点的坐标分别为A(-2,3), B(-3,1),若A1的坐标为(3,4),则B1的坐标为 (2,2) .
知识梳理
图7-2-49
2.如图7-2-50所示,△ABC三个顶点A,B,C的坐标分别为A(1, 2),B(4,3),C(3,1).把△A1B1C1向右平移4个单位长 度,再向下平移3个单位长度,恰好得到△ABC,试写出 △A1B1C1三个顶点的坐标.
5.将点A(4,3)向__下____平移____4_____个单位长度后,其坐标为 (4,-1). 6.如图7-2-57所示,△A′B′C′是△ABC经过平移得到的,△ABC中 任意一点P(x1,y1)平移后的对应点为P′(x1+6,y1+4),求A′,B′, C′的坐标.
课后习题
答案:A′(2,3),B′(1,0),C′(5,1).
课后习题
12.如图7-2-60,在直角坐标系中,A(-3,4),B(-1,-2), O为坐标原点,把△AOB向右平移3个单位,得到△DEF.(1) 求D、E、F三点的坐标.(2)求△DEF的面积.
A.(1,2) B.(3,0) C.(3,4) D.(5,2)
知识梳理
【解析】将点P(3,2)向右平移2个单位后,纵坐标不变,横坐标加上2, 所得的点的坐标是(3+2,2),即(5,2).故选D. 【方法小结】本题考查了坐标与图形变化-平移,掌握平移中点的变化规 律:横坐标右移加,左移减;纵坐标上移加,下移减是解题的关键.
人教版 7.2.2用坐标表示平移
Y 4
3 2
1 -4 -3 -2 -1 0 -1 -2 -3 1 2 3 4
B’
向 上 平 移
P2(x-a, y)
向左平移 a个单位
P(x, y)
b 个 单 位 向 下 平 移
向右平移 a个单位
P1(x+a, y)
P4 (x, y-b)
按要求平移点A 并写出平移后点 的坐标。 1、B:向右平移 3个单位长度 2、C:向右平移5 个单位长度 A (-2,-3) B ( 1,-3) C ( 3,-3)
0
-1 -2 -3
1
2
3
4
x
A (-2,-3)
B (1,-3) C (3,-3)
请你观察A、B、C三点的坐标的,你能发现 什么变化吗?
y
向上平移b个单位
(x,y-b) 原图形上的点(x,y) , 向下平移b个单位
练习
线段CD是由线段AB平移得到的。点A
(–1,4)的对应点为C(4,7),则点 ( 1,2) B(–4,–1)的对应点D的坐标为 ____
把点A(-3,a)平移到点B(b,4),使得AB=5且
2,-8 。 AB//x轴,则a= ___ 4 ,b= ___
例题探索
如图, △ ABC三个顶点的坐标 A(4,3),B(3,1),C(1,2) (1)将三角形ABC三个顶点的 横坐标都减去6,纵坐标不变
(-5,2)
y 4 A1
(-2,3)
3 2
(1,2)
(4,3)
A
C
C1 B1 (-3,1) -5 -4 -3 -2 -1
1 1 -1 -2 -3 2 3
B (3,1)
4 x
人教版七年级数学下册_7.2坐标方法的简单应用
7.2 坐标方法的简单应用
学习目标
1 课时讲解 用坐标表示地理位置
用方位角及距离表示平面内点的
位置
2 课时流程 用坐标表示点的平移
用点的坐标表示图形的平移
逐点 导讲练
课堂 小结
作业 提升
感悟新知
知识点 1 用坐标表示地理位置
平面直角坐标系表示地理位置的方法:
知1-讲
感悟新知
解:如图7.2-1,选中心广 场所在位置为原点,分别 以正东、正北方向为x 轴、 y 轴的正方向建立平面直 角坐标系.
知1-练
感悟新知
1-1. 如图是某城市的部分简 图,请建立适当的平面 直角坐标系,并分别写 出各地的坐标.(每个小 正方形的边长为1)
知1-练
感悟新知
解:建立如图的平面直角坐标系. 火车站(0,0),宾馆(2,2),市场(4, 3),文化宫(-3,1),体育场(-4, 3),医院(-2,-2),超市(2,- 3).(建立平面直角坐标系不唯一)
感悟新知
知2-练
2-1. 如图,下列关于小明家相对于学校的位置描述最准确 的是( C ) A. 距离学校1 200 米处 B. 在学校的北偏东65°方向上的 1 200 米处 C. 在学校的南偏西65°方向上的1 200 米处 D. 在学校的南偏西25°方向上的1 200 米处
感悟新知
知识点 3 用坐标表示点的平移
的名称.
感悟新知
知1-讲
特别解读: (1)坐标轴的方向通常以正北为纵轴的正方向,正东为 横轴的正方向,这样可以使东西南北方向与地理位置一致. (2)平面直角坐标系变化时,坐标平面内的各点坐标发 生变化,但各点之间的相对位置并不会发生变化.
2022年人教版七年级下册数学同步培优第七章平面直角坐标系第2节第2课时用坐标表示平移
度,再向下平移2个单位长度得到点B.
(1)标出点B的位置,并写出点B的坐标;
(2)求出三角形OAB的面积.
-3-
基础巩固
7.2.2 用坐标表示平移
能力提升
解:(1)图略;点 B 的坐标为(6,2).
1
1
1
2
2
2
(2)S 三角形 OAB=6×4- × × - × × - ×6×2=10.
3.将点P(-3,y)向上平移3个单位长度,向左平移2个单位长度后
得到点Q(x,-1),则xy的值为 20 .
7.2.2 用坐标表示平移
4.
基础巩固
能力提升
将点 A(m+2,m-3)向左平移 3 个单位长度后刚好落在 y
轴上,则平移前点 A 的坐标为 (3,-2) .
5.如图,在平面直角坐标系中,将点A(2,4)向右平移4个单位长
.
12.已知三角形ABC与三角形A'B'C'在平面直角坐标系中的位
置如图所示.
(1)分别写出点B,B'的坐标:B (3,-4)
,B' (-2,0)
;
(2)若P(a,b)是三角形ABC内部一点,则平移后三角形A'B'C'内
的对应点P'的坐标为 (a-5,b+4) ;
基础巩固
7.2.2 用坐标表示平移
7.2.2 用坐标表示平移
基础巩固
能力提升
知识点1 坐标系中点的平移
1.在平面直角坐标系中,点A(1,1)经过平移后的对应点为
B(3,4),下列平移正确的是( B )
A.先向右平移2个单位长度,再向下平移3个单位长度
B.先向右平移2个单位长度,再向上平移3个单位长度
