【课标通用】中考数学总复习单元检测卷--图形与变换(含答案)
中考数学第七章图形的变化单元检测卷及答案.docx

【若缺失公式、图片现象属于系统读取不成功,文档内容齐全完整,请放心下载。
】第七章图形的变化单元检测卷(时间:120分钟总分:120分)一、选择题(每小题3分,共30分)1.下面四大国产手机品牌图标中,是轴对称图形的是( A )2.在平面直角坐标系内,线段CD是由线段AB平移得到的,点A(-2,3)的对应点为C(1,4),则点B(-4,-1)的对应点D的坐标为( D )A.(-7,-2)B.(4,2)C.(0,1)D.(-1,0)3.若a∶b=3∶4,且a+b=14,则2a-b的值是( A )A.4B.2C.20D.144.菱形不具备的性质是( D )A.是轴对称图形B.是中心对称图形C.对角线互相垂直D.对角线一定相等5.如图,有一斜坡AB,坡顶B离地面的高度BC为30 m ,斜坡的倾斜角是∶BAC ,若tan ∶BAC =25,则此斜坡的水平距离AC 为( A )A .75 mB .50 mC .30 mD .12 m6.在平面直角坐标系中,点P(-3,m 2+1)关于原点对称点在( D )A .第一象限B .第二象限C .第三象限D .第四象限7.如图,在矩形ABCD 中,AB =6,AD =3,动点P 满足S △PAB =13S 矩形ABCD ,则点P 到A ,B 两点距离之和PA +PB 的最小值为( A )A .213B .210C .3 5D .418.如图,四边形ABCD 为菱形,AB =2,∶DAB=60°,点E ,F 分别在边DC ,BC 上,且CE =13CD ,CF =13CB ,则S △CEF =( D )A.32B.33C.34D.399.如图,∶ABC中,AB=AC=10,tan A=2,BE∶AC于点E,D是线段BE上的一个动点,则CD+55BD的最小值是( B )A.2 5B.4 5C.5 3D.10解析:如图,作DH⊥AB于H,CM⊥AB于M.可求出AE=25,⊥BE=45,⊥AB=AC,BE⊥AC,CM⊥AB,⊥CM=BE=45(等腰三角形两腰上的高相等),⊥⊥DBH=⊥ABE,⊥BHD=⊥BEA,⊥sin⊥DBH=DHBD=AEAB=55,⊥DH=55BD,⊥CD +55BD =CD +DH ,⊥CD +DH ≥CM , ⊥CD +55BD ≥45,⊥CD +55BD 的最小值为4 5.10.如图,正方形ABCD 的边长为2,点E 是BC 的中点,AE 与BD 交于点P ,F 是CD 上一点,连接AF 分别交BD ,DE 于点M ,N ,且AF∶DE ,连接PN ,则以下结论中:∶S △ABM =4S △FDM ;∶PN =26515;∶tan ∶EAF =34;∶∶PMN∶∶DPE ,正确的是( A )A .∶∶∶B .∶∶∶C .∶∶∶D .∶∶∶解析:证⊥ADF⊥⊥DCE ASA ),⊥DF =CE =1,⊥AB⊥DF ,⊥⊥ABM⊥⊥FDM ,⊥S △ABM S △FDM = AB DF()2=4,⊥S △ABM =4S △FDM ;故⊥正确;可求出EN =355, AN =AD 2-DN 2=455,⊥tan ⊥EAF =EN AN =34,故⊥正确,作PH⊥AN于H.可求出AH=23×455=8515,HN=4515,⊥PN=PH2+NH2=26515,故⊥正确,⊥PN≠DN,⊥⊥DPN≠⊥PDE,⊥⊥PMN与⊥DPE不相似,故⊥错误.二、填空题(每小题4分,共24分)11.下面摆放的图案,从第2个起,每一个都是前一个按顺时针方向旋转90°得到,第2019个图案与第1个至第4个中的第3个箭头方向相同(填序号).12.在平面直角坐标系中,点M(a,b)与点N(3,-1)关于x轴对称,则a+b的值是4.13.如图,在∶ABC中,sin B=13,tan C=22,AB=3,则AC的长为3.14.已知正方形ABCD的面积是2,E为正方形一边BC在从B到C方向的延长线上的一点,若CE=2,连接AE,与正方形另外一边CD交于点F,连接BF并延长,与线段DE交于点G,则BG的长为2103.15.如果三角形有一边上的中线长等于这边的长,那么称这个三角形为“好玩三角形”.若Rt ∶ABC 是“好玩三角形”,且∶A =90°,则tan ∶ABC = 32或233. 16.如图,已知∶O 的半径为1,AB ,AC 是∶O 的两条弦,且AB =AC ,延长BO 交AC 于点D ,连接OA ,OC ,若AD 2=AB·DC ,则OD = 5-12. 解析:可证⊥ADO⊥⊥BDA ,⊥AD BD =OD AD =AO AB,设OD =x ,则BD =1+x ,⊥AD 1+x =x AD =1AB , ⊥AD =x x +1),AB =x x +1)x, ⊥DC =AC -AD =AB -AD ,AD 2=AB×DC , x x +1)()2=x x +1)x ( x x +1)x -x x +1)),整理得:x 2+x -1=0,解得:x =-1+52或x =-1-52 舍去),因此OD =5-12. 三、解答题(共66分)17.(6分)如图,将∶ABC 绕点C 顺时针旋转90°得到∶EDC.若点A ,D ,E 在同一条直线上,且∶ACB =20°,求∶CAE 及∶B 的度数.解:根据旋转的性质可知CA =CE ,且⊥ACE =90°,所以⊥ACE 是等腰直角三角形.所以⊥CAE =45°;根据旋转的性质可得⊥BCD =90°,⊥⊥ACB =20°.⊥⊥ACD =70°.⊥⊥EDC =45°+70°=115°.所以⊥B =⊥EDC =115°.18.(8分)如图,在网格中,每个小正方形的边长均为1个单位长度.我们将小正方形的顶点叫做格点,∶ABC 的三个顶点均在格点上.(1)将∶ABC 先向右平移6个单位长度,再向上平移3个单位长度,得到∶A 1B 1C 1,画出平移后的∶A1B1C1;(2)建立适当的平面直角坐标系,使得点A的坐标为(-4,3);(3)在(2)的条件下,直接写出点A1的坐标.解: 1)如图,⊥A1B1C1为所作; 2)如图; 3)点A1的坐标为 2,6).19.(8分)如图,AB,CD为两个建筑物,建筑物AB的高度为15 m,从建筑物AB的顶部A点测得建筑物CD的顶部C点的俯角∶EAC为30°,测得建筑物CD的底部D点的俯角∶EAD为45°.(1)求两建筑物底部之间的水平距离BD的长度;(2)求建筑物CD的高度(结果保留根号).解: 1)根据题意得⊥ADB=⊥EAD=45°,在Rt⊥ABD中,⊥⊥BAD=⊥ADB=45°,⊥BD=AB=15 米);2)延长DC交AE于点F,根据题意可知四边形ABDF是正方形,⊥AF=BD=DF=15,在Rt⊥AFC中,⊥⊥FAC=30°,⊥CF=AF tan⊥CAF=15tan30°=53,⊥DF=15,⊥CD=15-5 3.20.(10分)如图,在矩形ABCD中,AB=6,BC=10,将矩形沿直线EF折叠,使得点A恰好落在边BC 上,记此点为G,点E和点F分别在边AB和边AD 上.(1)当BG=32时,求AE的长;(2)在矩形翻折中,是否存在FG=CG?若存在,请求出FG的长,若不存在,请说明理由.解: 1)由折叠易知:AE=EG,设AE=EG=x,则有BE=6-x,⊥由勾股定理易得:x2= 6-x)2+32)2,解得:x=92,即:AE=92;2)如图,过F作FH⊥CG于H,连接FC,当FG =GC时,则有:AF=FG=GC=x,CH=DF=10-x;⊥GH=x- 10-x)=2x-10,在Rt⊥FGH中,由勾股定理易得:x2=62+ 2x-10)2,化简得:3x2-40x+136=0,⊥Δ=-40)2-4×3×136=-32<0,⊥此方程没有实数根.故不存在FG=GC.21.(10分)如图,一副直角三角板∶ABC和∶DEF,∶F=30°.将∶ABC和∶DEF放置如图2的位置,点B,D,C,F在同一直线上.(1)如图3,∶ABC固定不动,∶DEF绕点D逆时针旋转30°时,判断BC与EF的位置关系,并说明理由.(2)在图2的位置上,∶DEF绕点D逆时针旋转α(0<α<180°),在旋转过程中,两个三角形的边是否存在垂直关系?若存在直接写出旋转的角度,并写出哪两边垂直;若不存在,请说明理由.解: 1)BC⊥EF,理由如下:⊥⊥DEF绕点D逆时针旋转30°,⊥⊥FDC=30°,⊥⊥FDC=⊥F=30°,⊥BC⊥EF;2)当α=45°时,⊥⊥C+⊥FDC=90°,⊥B+⊥EDB=90°,⊥DF⊥AC,DE⊥AB;当α=75°时,EF⊥AC;当α=90°时,DF⊥BC;当α=120°时,EF⊥BC;当α=135°时,DE⊥AC,DF⊥AB.22.(12分)如图,已知AC,AD是∶O的两条割线,AC与∶O交于B,C两点,AD过圆心O且与∶O交于E,D两点,OB平分∶AOC.(1)求证:∶ACD∶∶ABO;(2)过点E的切线交AC于F,若EF∶OC,OC=3,求EF的值.证明: 1)⊥OB平分⊥AOC,⊥⊥BOE=12⊥AOC,又⊥⊥D=12(⊥AOC,⊥⊥D=⊥BOE,且⊥A=⊥A,⊥⊥ACD⊥⊥ABO;2)⊥EF切⊥O于E,⊥⊥OEF=90°,⊥EF⊥OC,⊥⊥DOC=⊥OEF=90°,⊥OC=OD=3,⊥CD=OC2+OD2=32,⊥⊥ACD⊥⊥ABO,⊥AD AO=CDBO,⊥AE+6AE+3=323,⊥AE=32,⊥EF⊥OC,⊥AEAO=EFOC,⊥3232+3=EF3,⊥EF=6-3 2.23.(12分)如图,在∶ABC中,∶A=90°,AB=3,AC=4,点M,Q分别是边AB,BC上的动点(点M 不与A,B重合),且MQ∶BC,过点M作BC的平行线MN,交AC于点N,连接NQ,设BQ为x.(1)试说明不论x为何值时,总有∶QBM∶∶ABC;(2)是否存在一点Q,使得四边形BMNQ为平行四边形,试说明理由;(3)当x为何值时,四边形BMNQ的面积最大,并求出最大值.解: 1)⊥MQ⊥BC,⊥⊥MQB=90°,⊥⊥MQB=⊥CAB,又⊥QBM=⊥ABC,⊥⊥QBM⊥⊥ABC;2)当BQ=MN时,四边形BMNQ为平行四边形,⊥MN⊥BQ,BQ=MN,⊥四边形BMNQ为平行四边形;3)⊥⊥A=90°,AB=3,AC=4,⊥BC=AB2+AC2=5,⊥⊥QBM⊥⊥ABC,⊥QBAB=QMAC=BMBC,即x3=QM4=BM5,解得,QM=43x,BM=53x,⊥MN⊥BC,⊥MNBC=AMAB,即MN5=3-53x3,解得,MN=5-259x,则四边形BMNQ的面积=12× 5-259x+x)×43x=-3227x-4532)2+7532,⊥当x=4532时,四边形BMNQ的面积最大,最大值为75 32.中考数学知识点代数式一、重要概念分类:1.代数式与有理式用运算符号把数或表示数的字母连结而成的式子,叫做代数式。
中考数学复习第七单元图形变换单元测试七图形变换试题
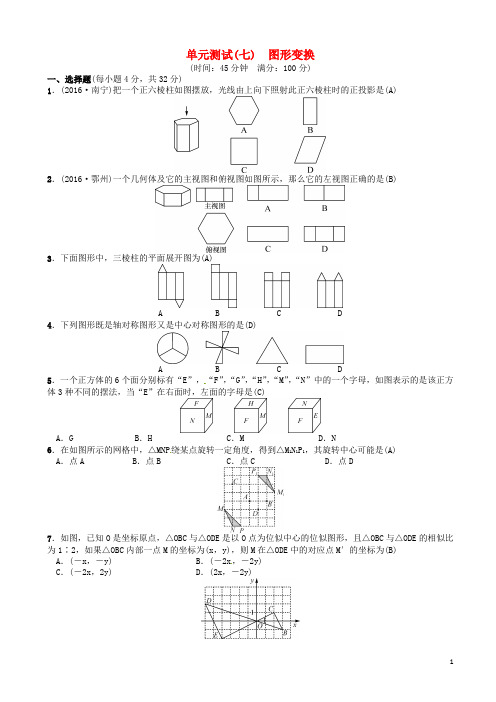
单元测试(七) 图形变换(时间:45分钟满分:100分)一、选择题(每小题4分,共32分)1.(2016·南宁)把一个正六棱柱如图摆放,光线由上向下照射此正六棱柱时的正投影是(A)2.(2016·鄂州)一个几何体及它的主视图和俯视图如图所示,那么它的左视图正确的是(B)3.下面图形中,三棱柱的平面展开图为(A)A B C D4.下列图形既是轴对称图形又是中心对称图形的是(D)A B C D5.一个正方体的6个面分别标有“E”,“F”,“G”,“H”,“M”,“N”中的一个字母,如图表示的是该正方体3种不同的摆法,当“E”在右面时,左面的字母是(C)A.G B.H C.M D.N6.在如图所示的网格中,△MNP绕某点旋转一定角度,得到△M1N1P1,其旋转中心可能是(A)A.点A B.点B C.点C D.点D7.如图,已知O是坐标原点,△OBC与△ODE是以O点为位似中心的位似图形,且△OBC与△ODE的相似比为1∶2,如果△OBC内部一点M的坐标为(x,y),则M在△ODE中的对应点M′的坐标为(B)A.(-x,-y) B.(-2x,-2y)C.(-2x,2y) D.(2x,-2y)8.已知Rt △ABC 中,∠ABC =90°,点D 是BC 中点,分别以B ,C 为圆心,大于线段12BC 长为半径作弧,两弧交于点P ,作直线PD 交AC 于点E ,连接BE ,则下列结论中不正确的是(B) A .ED ⊥BCB .BE 平分∠AEDC .E 为△ABC 的外接圆圆心D .ED =12AB提示:由作图可知,DP 是BC 的垂直平分线,因此选项A 正确;由平行线分线段成比例可知E 是AC 的中点,所以有EB =EC =EA ,选项C 正确;由中位线定理可得选项D 正确.故选B. 二、填空题(每小题5分,共20分)9.已知△ABC 的边在直线l 上,BC =5,现把△ABC 沿着直线l 向右平移到△DE F 的位置(如图所示),若EC =3,则△ABC 平移的距离为2.10.如图,如果直线m 是多边形ABCDE 的对称轴,其中∠A=130°,∠B =110°.那么∠BCD 的度数等于60度.11.如图,在平面直角坐标系中,以O 为圆心,适当长为半径画弧,交x 轴于点M ,交y 轴于点N ,再分别以点M ,N 为圆心,大于12MN 的长为半径画弧,两弧在第二象限交于点P ,若点P 的坐标为(2a ,b +1),则a与b 的数量关系为2a +b =-1.提示:由作图可知,作的是∠MON 的平分线,由角平分线的性质定理可得,-2a = b +1,即2a +b =-1.12.(2016·北京)如图,小军、小珠之间的距离为2.7 m ,他们在同一盏路灯下的影长分别为1.8 m ,1.5 m ,已知小军、小珠的身高分别为1.8 m ,1.5 m ,则路灯的高为3m.提示:因为小军、小珠都身高与影长相等,所以,∠E =∠F=45°,所以AB =BE =BF ,设路灯的高AB 为x m ,则BD =x -1.5,BC =x -1.8,又CD =2.7,所以,x -1.5+x -1.8=2.7,解得x =3. 三、解答题(共48分)13.(10分)如图,在平面直角坐标系中,四边形OABC 的顶点分别是O(0,0),A(6,0),B(3,6),C(-3,3).(1)以原点O 为位似中心,在点O 的异侧画出四边形OABC 的位似图形四边形OA 1B 1C 1,使它与四边形OABC 的相似比是1∶3;(2)直接写出点A1,B1,C1的坐标.解:(1)如图所示.(2)由图形可得:A1(-2,0),B1(-1,-2),C1(1,-1).14.(10分)如图,将△ABC绕顶点B按顺时针方向旋转60°,得到△DBE,连接AD,DC,已知∠DCB=30°.求证:DC2+BC2=AC2.证明:连接EC.由旋转知△ABC≌△DBE,∴AC=DE,BC=BE.∵∠CBE=60°,∴∠BCE=60°,EC=BC.又∵∠DCB=30°,∴∠DCE=90°.∴DC 2+EC 2=DE 2.∴DC 2+BC 2=AC 2 .15.(14分)如图1,将△ABD平移,使D沿BD的延长线移至点C得到△A′B′D′,A′B′交AC于E,AD 平分∠BAC.(1)猜想∠B′EC与∠A′之间的关系,并写出理由;(2)如图将△ABD平移至如图2所示,得到△A′B′D′,请问:A′D′平分∠B′A′C吗?为什么?图1 图2解:(1)∠B′EC=2∠A′.理由如下:∵由平移知△ABD ≌△A′B′D′,AB∥A′B′,∴∠B′EC=∠BAC,∠A′=∠BAD.又∵AD平分∠BAC, ∴∠BAC=2∠BAD.∴∠B′EC=2∠A′.(2) A′D′平分∠B′A′C.理由如下:∵AD平分∠BAC,∴∠BAD=∠CAD.∵AD∥A′D′,∴∠CAD=∠CA′D′.又由(1)可知∠B′A′D′=∠BAD,∴∠B′A′D′=∠CA′D′,即A′D′平分∠B′A′C.16.(14分)如图,在▱ABCD中,点E是边BC的中点,将△ABE沿AE折叠,使点B落在▱ABCD内部的点F处,延长AF交CD于点G,连接FC.(1)求证:∠GCF=∠GFC;(2)若AB=5,BC=6,则△ADG的周长为16.证明:∵四边形ABCD是平行四边形,∴AB∥CD. ∴∠B+∠ECG=180°.又∵△AFE是由△ABE翻折得到,∴∠AFE=∠B,EF=BE.又∵∠AFE+∠EFG=180°,∴∠ECG=∠EFG.又∵点E是边BC的中点,∴EC=BE.∴EC=EF.∴∠ECF=∠EFC.∴∠ECG-∠ECF=∠EFG-∠EFC,即∠GCF=∠GFC.。
湖南省中考数学总复习 第七单元 图形与变换单元测试07 图形与变换练习-人教版初中九年级全册数学试题
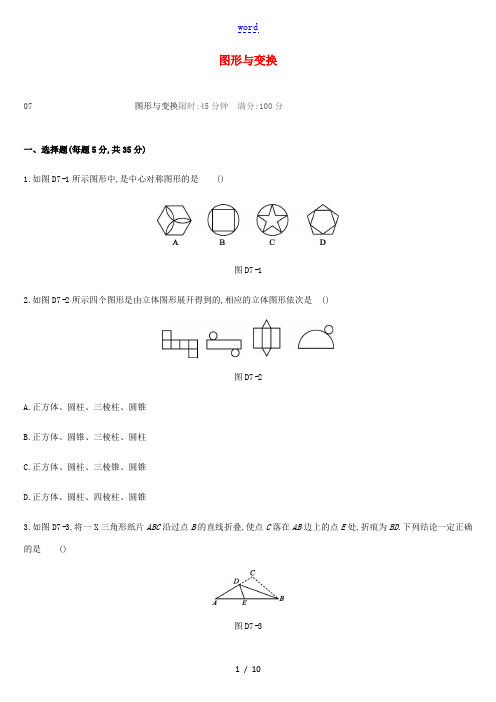
图形与变换07图形与变换限时:45分钟满分:100分一、选择题(每题5分,共35分)1.如图D7-1所示图形中,是中心对称图形的是()图D7-12.如图D7-2所示四个图形是由立体图形展开得到的,相应的立体图形依次是()图D7-2A.正方体、圆柱、三棱柱、圆锥B.正方体、圆锥、三棱柱、圆柱C.正方体、圆柱、三棱锥、圆锥D.正方体、圆柱、四棱柱、圆锥3.如图D7-3,将一X三角形纸片ABC沿过点B的直线折叠,使点C落在AB边上的点E处,折痕为BD.下列结论一定正确的是()图D7-3A.AD=BDB.AE=ACC.ED+EB=DBD.AE+CB=AB4.如图D7-4,在△ABC中,∠CAB=70°,将△ABC绕点A逆时针旋转到△AB'C'的位置,使得CC'∥AB,则∠BAB'的度数是()图D7-4A.70°B.50°C.40°D.35°5.如图D7-5,将△ABC沿水平方向向右平移到△DEF的位置.已知点A,D之间的距离为2,CE=4,则BF的长为()图D7-5A.4B.6C.8D.106.如图D7-6,在△ABC中,∠ACB=90°,∠A=30°,BC=4,以点C为圆心,CB的长为半径作弧,交AB于点D;再分别以点B和BD的长为半径作弧,两弧相交于点E,作射线CE,交AB于点F,则AF的长为()点D为圆心,大于12图D7-6A .5B .6C .7D .87.如图D7-7,在☉O 中,点C 在优弧AA ⏜上,将AA ⏜沿BC 折叠后刚好经过AB 的中点D.若☉O 的半径为√5,AB=4,则BC 的长是()图D7-7A .2√3B .3√2C .5√32D .√652二、填空题(每题5分,共20分)8.若圆柱的底面半径为2 cm,高为3 cm,则它的侧面积是 cm 2.9.一个长方体的三视图如图D7-8,若其俯视图为正方形,则这个长方体的表面积为.图D7-810.如图D7-9,在▱ABCD 中,AD=7,AB=2√3,∠B=60°.E 是边BC 上任意一点,沿AE 剪开,将△ABE 沿BC 方向平移到△DCF 的位置,得到四边形AEFD ,则四边形AEFD 周长的最小值为.图D7-911.如图D7-10,已知圆柱形容器高为1.2 m,底面周长为1 m,在容器内壁离容器底部0.3 m 的点B 处有一只蚊子,此时一只壁虎正好在容器外壁,离容器上沿0.3 m 与蚊子相对的点A 处,则壁虎捕捉蚊子的最短距离为m(容器厚度忽略不计).图D7-10三、解答题(共45分)12.(15分)如图D7-11,已知△ABC三个顶点的坐标分别是A(1,3),B(4,1),C(4,4).(1)请按要求画图:①画出△ABC向左平移5个单位长度后得到的△A1B1C1;②画出△ABC绕着原点O顺时针旋转90°后得到的△A2B2C2.(2)请写出直线B1C1与直线B2C2的交点坐标.图D7-1113.(15分)如图D7-12,已知四边形ABCD是正方形,E,F分别是DC和CB的延长线上的点,且DE=BF,连接AE,AF,EF.(1)求证:△ADE≌△ABF;(2)△ABF可以由△ADE绕旋转中心点,按顺时针方向旋转度得到;(3)若BC=8,DE=6,求△AEF的面积.图D7-1214.(15分)如图D7-13,已知△ABC的顶点坐标分别为A(3,0),B(0,4),C(-3,0).动点M,N同时从点A出发,点M沿A→C,点N沿折线A→B→C,均以每秒1个单位长度的速度移动,当一个动点到达终点C时,另一个动点也随之停止移动,移动的时间记为t秒.连接MN.(1)求直线BC的解析式;(2)移动过程中,将△AMN沿直线MN翻折,点A恰好落在BC边上点D处,求此时t的值及点D的坐标;(3)当点M,N移动时,记△ABC在直线MN右侧部分的面积为S,求S关于时间t的函数关系式.图D7-13参考答案1.B[解析] 在平面内,把一个图形绕着某个点旋转180°,如果旋转后的图形能与原来的图形重合,那么这个图形叫做中心对称图形,这个点叫做它的对称中心.根据中心对称图形的定义,得图形B是中心对称图形.故选B.2.A3.D[解析] 由折叠前后的不变性,可知CB=EB,∴AE+CB=AE+EB=AB.故选D.4.C5.C6.B[解析] 如图,连接CD.∵在△ABC中,∠ACB=90°,∠A=30°,BC=4,∴AB=2BC=8.由作法可知BC=CD=4,CE是线段BD的垂直平分线,∴CD是斜边AB上的中线.∴BD=AD=4.∴BF=DF=2.∴AF=AD+DF=4+2=6.故选B.7.B[解析] 连接OD,AC,DC,OB,OC,过点C作CE⊥AB于E,过点O作OF⊥CE于F,如图.∵D为AB的中点,∴OD⊥AB.AB=2.∴AD=BD=12在Rt△OBD中,OD=√(√5)2-22=1.∵将弧BC沿BC折叠后刚好经过AB的中点D.∴弧AC和弧CD所在的圆为等圆.⏜.∴AC=DC.∴AE=DE=1.∴AA⏜=AA易得四边形ODEF为正方形,∴OF=EF=1.在Rt△OCF中,CF=√(√5)2-12=2,∴CE=CF+EF=2+1=3.而BE=BD+DE=2+1=3,∴BC=3√2.故选B.8.12π9.6610.20[解析] 当AE⊥BC时,四边形AEFD的周长最小.∵AE⊥BC,AB=2√3,∠B=60°,∴AE=3,BE=√3.∵△ABE沿BC方向平移到△DCF的位置,∴EF=BC=AD=7.∴四边形AEFD周长的最小值为14+6=20.故答案为20.11.1.312.解:(1)①如图所示,△A1B1C1即为所求;②如图所示,△A2B2C2即为所求.(2)由图可知,交点坐标为(-1,-4). 13.解:(1)证明:∵四边形ABCD 是正方形, ∴AD=AB ,∠D=∠ABC=90°. 而F 是CB 延长线上的点, ∴∠ABF=90°=∠D. 又∵DE=BF , ∴△ADE ≌△ABF. (2)A 90 (3)∵BC=8, ∴AD=8. ∵DE=6, ∴AE=10.∵△ABF 可以由△ADE 绕旋转中心点A 按顺时针方向旋转90°得到, ∴AE=AF ,∠EAF=90°.∴△AEF 的面积为12AE 2=12×100=50.14.解:(1)设直线BC 的解析式为y=kx+b. ∵直线经过点B (0,4),C (-3,0),∴{A =4,-3A +A =0.解得{A =43,A =4.∴直线BC 的解析式为y=43x+4.(2)过点D 作DE ⊥AC 于点E ,如图.∵点M 和点N 均以每秒1个单位长度的速度移动, ∴AM=AN=t. ∵A (3,0),B (0,4), ∴OA=3,OB=4,AB=5. ∴BN=5-t.∵△DMN 是△AMN 沿直线MN 翻折得到的, ∴DN=DM=t.∴四边形DMAN 是菱形. ∴DN ∥AC ,∴AA AA =AAAA, 即5-A 5=A 6.解得t=3011.易知CD=DM=3011,∵B (0,4),C (-3,0), ∴OC=3,OB=4,BC=5.∴sin ∠BCO=AA AA =45,cos ∠BCO=AA AA =35. ∴DE=CD ·sin ∠BCO=3011×45=2411,CE=CD ·cos ∠BCO=3011×35=1811.∴OE=1511.∴点D 的坐标为-1511,2411. (3)当0≤t ≤5时,S=25t 2;当5<t ≤6时,S=S △ABC -12(6-t )·(10-t )·sin ∠BCO=12-25(t 2-16t+60)=-25t 2+325t-12.。
通用版2018年中考数学总复习单元检测七图形的变换试题新版新人教版
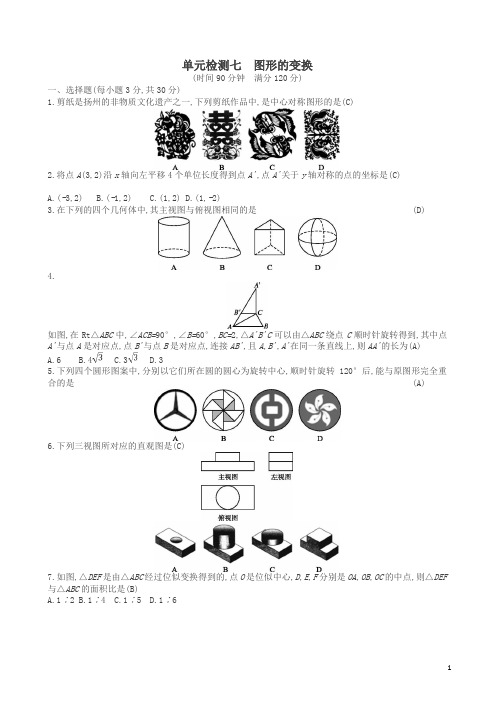
单元检测七图形的变换(时间90分钟满分120分)一、选择题(每小题3分,共30分)1.剪纸是扬州的非物质文化遗产之一,下列剪纸作品中,是中心对称图形的是(C)2.将点A(3,2)沿x轴向左平移4个单位长度得到点A',点A'关于y轴对称的点的坐标是(C)A.(-3,2)B.(-1,2)C.(1,2)D.(1,-2)3.在下列的四个几何体中,其主视图与俯视图相同的是(D)4.如图,在Rt△ABC中,∠ACB=90°,∠B=60°,BC=2,△A'B'C可以由△ABC绕点C顺时针旋转得到,其中点A'与点A是对应点,点B'与点B是对应点,连接AB',且A,B',A'在同一条直线上,则AA'的长为(A)A.6B.4C.3D.35.下列四个圆形图案中,分别以它们所在圆的圆心为旋转中心,顺时针旋转120°后,能与原图形完全重合的是(A)6.下列三视图所对应的直观图是(C)7.如图,△DEF是由△ABC经过位似变换得到的,点O是位似中心,D,E,F分别是OA,OB,OC的中点,则△DEF 与△ABC的面积比是(B)A.1∶2B.1∶4C.1∶5D.1∶6(第7题图)(第8题图)8.如图,△ABC的面积为6,AC=3,现将△ABC沿AB所在直线翻折,使点C落在直线AD上的C'处,P为直线AD上的一点,则线段BP的长不可能是(A)A.3B.4C.5.5D.109.如图,正方形OABC的两边OA,OC分别在x轴、y轴上,点D(5,3)在边AB上,以C为中心,把△CDB旋转90°,则旋转后点D的对应点D'的坐标是(C)A.(2,10)B.(-2,0)C.(2,10)或(-2,0)D.(10,2)或(-2,0)10.如图,一张三角形纸片ABC,其中∠C=90°,AC=4,BC=3.现小林将纸片做三次折叠:第一次使点A落在C处;将纸片展平做第二次折叠,使点B落在C处;再将纸片展平做第三次折叠,使点A落在B处.这三次折叠的折痕长依次记为a,b,c,则a,b,c的大小关系是(D) A.c>a>b B.b>a>cC.c>b>aD.b>c>a二、填空题(每小题5分,共20分)11.在平面直角坐标系中,点A的坐标是(2,-3),作点A关于x轴的对称点,得到点A',再作点A'关于y轴的对称点,得到点A″,则点A″的坐标是(-2,3).12.如图,这是一个长方体的主视图和俯视图,由图示数据(单元: cm)可以得出该长方体的体积是18 cm3.〚导学号92034220〛13.如图,直线y=x+1与x轴交于点A,与y轴交于点B,△BOC与△B'O'C'是以点A为位似中心的位似图形,且相似比为1∶3,则点B的对应点B'的坐标为(-8,-3)或(4,3).14.如图,在正方形ABCD中,AD=1,将△ABD绕点B顺时针旋转45°得到△A'BD',此时A'D'与CD交于点E,则DE的长度为2-.三、解答题(共70分)15.(6分)如图,在水平地面上竖立着一面墙AB,墙外有一盏路灯D.光线DC恰好通过墙的最高点B,且与地面形成37°角.墙在灯光下的影子为线段AC,并测得AC=5.5米.(1)求墙AB的高度(结果精确到0.1米);(参考数据:tan 37°≈0.75,sin 37°≈0.60,cos 37°≈0.80)如果要缩短影子AC的长度,同时不能改变墙的高度和位置,请你写出两种不同的方法.解(1)在Rt△ABC中,AC=5.5米,∠C=37°,tan∠C=,∴AB=AC·tan C=5.5×0.75≈4.1米;(2)要缩短影子AC的长度,增大∠C的度数即可.因此第一种方法是增加路灯D的高度,第二种方法是使路灯D向墙靠近.〚导学号92034221〛16.(6分)如图,△ABC和△DBC是两个具有公共边的全等三角形,AB=AC=3 cm,BC=2 cm,将△DBC沿射线BC 平移一定的距离得到△D1B1C1,连接AC1,BD1.如果四边形ABD1C1是矩形,求平移的距离.7 cm.17.(6分)一个几何体的三视图如图所示,求该几何体的表面积.解观察该几何体的三视图发现其为半个圆柱,∴其表面积为π×12+(π+2)×2=3π+4.18.(8分)如图,P是等边三角形ABC内一点,将线段AP绕点A顺时针旋转60°得到线段AQ,连接BQ.若PA=6,PB=8,PC=10,求四边形APBQ的面积.S四边形APBQ=24+9.19.(8分)如图,在一面与地面垂直的围墙的同侧有一根高10米的旗杆AB和一根高度未知的电线杆CD,它们都与地面垂直,为了测得电线杆的高度,一个小组的同学进行了如下测量:某时刻,在太阳光照射下,旗杆落在围墙上的影子EF的长度为2米,落在地面上的影子BF的长为10米,而电线杆落在围墙上的影子GH 的长度为3米,落在地面上的影子DH的长为5米.依据这些数据,该小组的同学计算出了电线杆的高度.(1)该小组的同学在这里利用的是投影的有关知识进行计算的;试计算出电线杆的高度,并写出计算的过程.解(1)平行;(2)过点E作EM⊥AB于M,过点G作GN⊥CD于N,则MB=EF=2米,ND=GH=3米,ME=BF=10米,NG=DH=5米,所以AM=10-2=8米,由平行投影可知,=,即=,解得CD=7米,即电线杆的高为7米.20.(8分)如图,折叠矩形ABCD的一边AD,使点D落在BC边的点F处,已知折痕AE=5,且tan∠EFC=,求矩的周长.解∵△AFE和△ADE关于AE对称,∴∠AFE=∠D=90°,AF=AD,EF=DE.∵tan∠EFC==,∴可设EC=3x,CF=4x,那么EF=5x,∴DE=EF=5x.∴DC=DE+CE=3x+5x=8x.∴AB=DC=8x.∵∠EFC+∠AFB=90°,∠BAF+∠AFB=90°,∴∠EFC=∠BAF.∴tan∠BAF=tan∠EFC=,∴=.∵AB=8x,∴BF=6x.∴BC=BF+CF=10x.∴AD=10x.在Rt△ADE中,由勾股定理,得AD2+DE2=AE2.∴(10x)2+(5x)2=(5)2.解得x=1.∴AB=8x=8,AD=10x=10.∴矩形ABCD的周长=8×2+10×2=36.21.(8分)下列3×3网格图都是由9个相同的小正方形组成,每个网格图中有3个小正方形已涂上阴影,请在余下的6个空白小正方形中,按下列要求涂上阴影:(1)选取1个涂上阴影,使4个阴影小正方形组成一个轴对称图形,但不是中心对称图形;(2)选取1个涂上阴影,使4个阴影小正方形组成一个中心对称图形,但不是轴对称图形;(3)选取2个涂上阴影,使5个阴影小正方形组成一个轴对称图形.1、图2、图3中,均只需画出符合条件的一种情形)如图1所示;(2)如图2所示;(3)如图3所示.22.(10分)如图,方格纸中的每个小方格都是边长为1的正方形,△ABC的顶点都在格点上,请完成下列任务:(1)将△ABC绕点C按顺时针方向旋转90°后得到△A1B1C;(2)求线段AC旋转到A1C的过程中,所扫过的图形的面积;(3)以点O为位似中心,相似比为2,在O同侧将△A1B1C放大得到△A2B2C2(在网格之内画图).如图所示:△A1B1C即为所求;(2)AC所扫过的图形的面积S==;(3)如图所示:△A2B2C2即为所求.〚导学号92034222〛23.(10分)在数学兴趣小组活动中,小明进行数学探究活动,将边长为2的正方形ABCD与边长为2的正方形AEFG按图1位置放置,AD与AE在同一直线上,AB与AG在同一直线上.(1)小明发现DG⊥BE,请你帮他说明理由;(2)如图2,小明将正方形ABCD绕点A逆时针旋转,当点B恰好落在线段DG上时,请你帮他求出此时BE的长.ABCD和四边形AEFG都为正方形,∴AD=AB,∠DAG=∠BAE=90°,AG=AE,∴△ADG≌△ABE(SAS).∴∠AGD=∠AEB.如图1,延长EB交DG于点H,在△ADG中,∵∠AGD+∠ADG=90°,∴∠AEB+∠ADG=90°.在△EDH中,∵∠AEB+∠ADG+∠DHE=180°,∴∠DHE=90°.∴DG⊥BE.(2)∵四边形ABCD和四边形AEFG都为正方形,∴AD=AB,∠DAB=∠GAE=90°,AG=AE,∴∠DAB+∠BAG=∠GAE+∠BAG,即∠DAG=∠BAE,∴△ADG≌△ABE(SAS).∴DG=BE.如图2,过点A作AM⊥DG交DG于点M,则∠AMD=∠AMG=90°,∵BD为正方形ABCD的对角线,∴∠MDA=45°.在Rt△AMD中,∵∠MDA=45°,AD=2,∴DM=AM=.在Rt△AMG中,根据勾股定理得GM==, ∴DG=DM+GM=+,∴BE=DG=+.。
2020中考数学总复习单元测试(7):平行四边形与图形变换(答案)
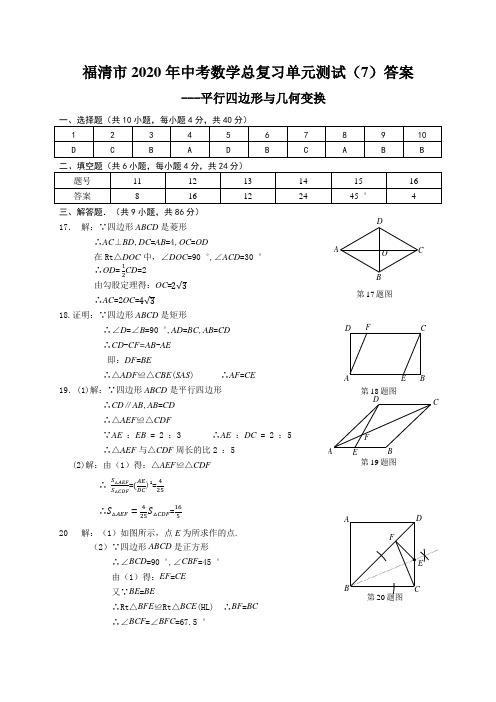
福清市2020年中考数学总复习单元测试(7)答案---平行四边形与几何变换一、选择题(共10小题,每小题4分,共40分)1 2 3 4 5 6 7 8 9 10D C B A D B C A B B二、填空题(共6小题,每小题4分,共24分)题号11 12 13 14 15 16 答案8 16 12 24 45︒ 4 三、解答题.(共9小题,共86分)17.解:∵四边形ABCD是菱形∴AC⊥BD,DC=AB=4,OC=OD在Rt△DOC中,∠DOC=90︒,∠ACD=30︒∴OD=12CD=2由勾股定理得:OC=2√3∴AC=2OC=4√318.证明:∵四边形ABCD是矩形∴∠D=∠B=90︒,AD=BC,AB=CD∴CD-CF=AB-AE即:DF=BE∴△ADF≌△CBE(SAS) ∴AF=CE19.(1)解:∵四边形ABCD是平行四边形∴CD∥AB,AB=CD∴△AEF≌△CDF∵AE:EB= 2 :3 ∴AE:DC= 2 :5∴△AEF与△CDF周长的比2 :5(2)解:由(1)得:△AEF≌△CDF∴S△AEFS△CDF=(AEDC)2=425∴S△AEF=425S△CDF=16520 解:(1)如图所示,点E为所求作的点.(2)∵四边形ABCD是正方形∴∠BCD=90︒,∠CBF=45︒由(1)得:EF=CE又∵BE=BE∴Rt△BFE≌Rt△BCE(HL) ∴BF=BC∴∠BCF=∠BFC=67.5︒第18题图BCDAFE第17题图CDABO第19题图AD CBEF第20题图CDFE21. 证明:∵四边形ABCD 是正方形∴DE =EF =GF ,∠DEF =∠GFE =90︒ ∴∠DEB =∠GFC =90︒ ∴∠B +∠BDE =90︒又∵∠A =90︒ ∴∠B +∠C =90︒ ∴∠C =∠BDE ∴△BED ∽△GFC ∴DEFC =BEGF∴DE ∙ GF = BE ∙ FC∴EF 2=BE ∙ FC22.解:连接BD∵△ABC 绕点C 逆时针旋转60° 得△EDC , ∴BC =CD ,AC =CE ,AB=DE ,∠BCD =60︒ ∴△BCD 为等边三角形∴∠DCB =60︒,BC =BD ∵AB =AC ∴CE =DE ∵BE =BE∴△BCE ≌△BDE (SSS) ∴∠CBE =∠DBE ∴∠CBE =30︒23.(1) 证明:∵△ABC 沿AC 翻折得到△AEC ∴∠ACE =∠ACB ,CE =BC ∵四边形ABCD 是平行四边形 ∴AD ∥BC ,AD =BC ∴AD ∥CE ,AD =CE∴四边形ACED 是平行四边形 又∵AC ⊥BC ∴∠ACE =90︒ ∴ACED 是矩形(2)解:过A 点作AH ⊥BD ,垂足为H 点由(1)得:DE =AC =4,BE =2BC =6,∠DEB =90︒ 由勾股定理得:BD =10在Rt △ACB 中,∠ACB =90︒ ∴AB =5 ∴S △ABD =12AD ×AC =12BD ×AH ∴AH =3×410=65在Rt △AHB 中,sin ∠ABH = AHAB =625 ∴sin ∠ABD 的值为625第21题图E DGFBA C第23题图ECBADOH第22题图ACBE24. (1)证明:∵四边形ABCD 是矩形 ∴∠C =90︒ ∵△AEF 是由△ADF 折叠得到的∴ ∠DAG =∠EAG ,∠DFA =∠EFA ,AD =AE ,DF =EF ∴△AGE ≌△AGD (SAS) ∴GE =GD 又∵EG ∥CD ∴∠EGF =∠DFG ∴∠EGF =∠DFG ∴EG =EF ∴EG =GD =DF =EF ∴四边形EFDG 是菱形(2)解:连接ED ,交GF 于O 点,由(1)得:四边形EFDG 是菱形 ∴DO ⊥GF ,OG =OF =1,DF=EG =3 ∵∠DFO =∠DFA ,∠ADF =∠DOF ∴△ADF ∽△DOF∴DFAF= OFDF∴3AF= 13∴AF = 925.(1)证明:∵CB =CE ,∴∠CBE =∠CEB ,∵∠ABC =∠CED =90°, ∴∠DEF +∠CEB =90°,∠ABF +∠CBE =90°, ∴∠DEF =∠ABF .(2)证明:作AN ⊥BF 于N ,DM ⊥BF 交BF 的延长线于M .∵∠ABN =∠DEM ,∠ANB =∠M =90°,AB =DE , ∴△ANB ≌△DME (AAS ), ∴AN =DM ,∵∠ANF =∠M =90°,∠AFN =∠DFM ,AN =DM , ∴△AFN ≌△DFM (AAS ), ∴AF =F D .(3)解:在Rt △ABC 中,∵∠ABC =90°,AC =5,BC =3,∴AB =AC 2-BC 2=4,∵EC ⊥BC ,∴∠BCE =∠ACD =90°, ∵AC =CD =5, ∴AD =5 2,∴DF =AF =12AD =522,由旋转知,∠ACB =∠DCE ,∴∠ACD =∠ACE +DCE =∠ACB +∠ACE =90°, ∴∠MED =∠CEB =45°, ∴EM =MD =2 2, 在Rt △DFM 中,FM =DF 2-DM 2=322,∴EF =EM -FM =22. 第24题图BACDGE F O另:(2)解法二:过点A作AG∥ED,交BF的延长线于点G,连接DG,AE∴∠DEG=∠AGE由(1)得:AB=ED, ∠DEG=∠ABF∴∠ABG=∠AGB∴AB=AG∴AB=ED∴四边形AEDG是平行四边形∴AF=DF(3)解法二:延长DE到G点,使得GE=DE,连接CG,AG,设AB与DG交于点O由(1)得:AF=DF,∴EF是△DAG的一条中位线∴EF=12AG依题意得:∠CEO=∠BCE=∠OBC=90︒BC=CE∴四边形OBCE是正方形∴OA=AB-OB=4-3=1OG=DE-BC=4-3=1∠AOG=90︒由勾股定理得:AG=√2∴EF=22B CAEDFGBAFDEOG。
最新2022-2021年第一轮数学中考单元测试(七)图形变换(含答案)
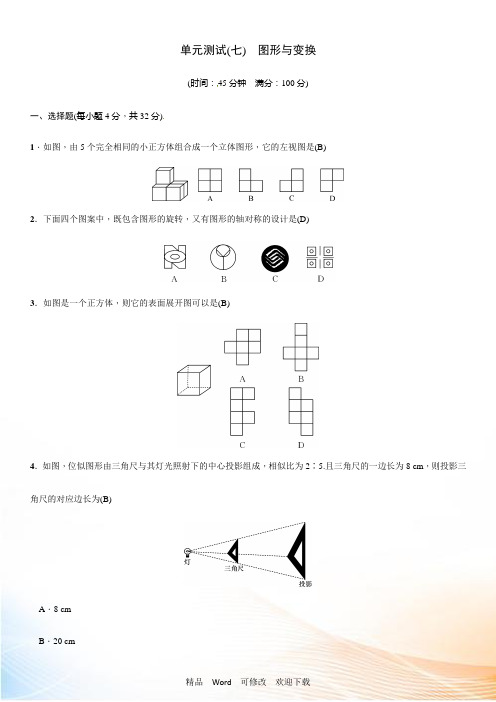
单元测试(七)图形与变换(时间:45分钟满分:100分)一、选择题(每小题4分,共32分)1.如图,由5个完全相同的小正方体组合成一个立体图形,它的左视图是(B)2.下面四个图案中,既包含图形的旋转,又有图形的轴对称的设计是(D)3.如图是一个正方体,则它的表面展开图可以是(B)4.如图,位似图形由三角尺与其灯光照射下的中心投影组成,相似比为2∶5.且三角尺的一边长为8 cm,则投影三角尺的对应边长为(B)A.8 cmB.20 cmC .3.2 cmD .10 cm5.如图,已知△OAB 是正三角形,OC ⊥OB ,OC =OB ,将△OAB 绕点O 按逆时针方向旋转,使得OA 与OC 重合,得到△OCD ,则旋转的角度是(A)A .150°B .120°C .90°D .60°6.如图,在△ABC 中,BC =5,∠A =70°,∠B =75°,把△ABC 沿直线BC 的方向平移到△DEF 的位置,若CF =3,则下列结论中错误的是(C)A .BE =3B .∠F =35°C .DF =5D .AB ∥DE7.如图,在△ABC 中,∠ACB =90°,∠ABC =30°,AB =2.将△ABC 绕直角顶点C 逆时针旋转60°得△A′B′C ,则点B 转过的路径长为(B)A.π3B.3π3C.2π3D .π8.如图,在△ABC 中,∠C =90°,∠CAB =60°,按以下步骤作图:①分别以A ,B 为圆心,以大于12AB 的长为半径作弧,两弧相交于点P 和点Q.②作直线PQ 交AB 于点D ,交BC 于点E ,连接AE ,若CE =4,则AE =(D)A.2 B.4C.4 3 D.8二、填空题(每小题4分,共16分)9.如图是由若干个大小相同的小正方体堆砌而成的几何体,那么其三种视图中面积最小的是左视图.10.(2021·广州)如图,△ABC中,AB=AC,BC=12 cm,点D在AC上,DC=4 cm.将线段DC沿着CB的方向平移7 cm得到线段EF,点E,F分别落在边AB,BC上,则△EBF的周长为13 cm.11.如图,在正方形网格中,阴影部分是涂黑7个小正方形所形成的图案,再将网格内空白的一个小正方形涂黑,使得到的新图案成为一个轴对称图形的涂法有3种.12.(2021·上海)如图,矩形ABCD中,BC=2,将矩形ABCD绕点D顺时针旋转90°,点A,C分别落在点A′,C′处,如果点A′,C′,B在同一条直线上,那么tan∠ABA′的值为5-1 2.三、解答题(共52分)13.(8分)如图,在△ABC中,先作∠BAC的平分线AD交BC于点D,再以AC边上的一点O为圆心,过A,D 两点作⊙O(用尺规作图,不写作法,保留作图痕迹)解:作出角平分线AD,再作AD的中垂线交AC于点O,最后作出⊙O.14.(10分)如图,△ABC中,∠BAC=120°,以BC为边向外作等边△BCD,把△ABD绕着点D按顺时针方向旋转60°到△ECD的位置,若AB=3,AC=2,求∠BAD的度数和AD的长.解:由∠BAC=120°知∠ABC+∠ACB=60°.又∵∠ABD=∠ABC+∠CBD=∠DCE,∠CBD=∠BCD=60°,∴∠ACB+∠BCD+∠DCE=∠ACB+∠BCD+∠ABC+∠CBD=180°,即点A,C,E在一条直线上.又∵AD=ED,∠ADE=60°,∴△ADE为等边三角形.∴∠BAD=∠E=60°,AD=AE=AC+CE=AC+AB=5.15.(10分)如图是一个立体图形的三视图.(1)请写出这个立体图形的名称;(2)计算这个立体图形的全面积.(结果保留π)解:(1)该立体图形为圆柱.(2)∵圆柱的底面半径r=5,高d=10,∴圆柱的侧面积S侧=2πrd=2π×5×10=100π.底面积为S底=πr2=25π,全面积为S全=2S底+S侧=50π+100π=150π.答:立体图形的全面积为150π.16.(12分)在边长为1的方格纸中建立直角坐标系,如图所示,O,A,B三点均为格点.(1)直接写出线段OB的长;(2)画出将△OAB向右平移2个单位,向上平移3个单位后的△O1A1B1;(3)将△OAB绕点O按逆时针方向旋转90°得到△OA′B′,请你画出△OA′B′,并求在旋转过程中,线段AB扫过的面积.解:(1)OB=3.(2)如图,△O1A1B1即为所作.(3)如图,△OA′B′即为所作,OA=22+42=25,线段AB所扫过的面积为:S扇形AOA′-S扇形BOB′=90×π×(25)2360-90×π×32360=114π.17.(12分)(2021·娄底)如图,将等腰△ABC绕顶点B按逆时针方向旋转α度到△A1BC1的位置,AB与A1C1相交于点D,AC与A1C1,BC1分别交于点E、F.(1)求证:△BCF≌△BA1D;(2)当∠C=α度时,判定四边形A1BCE的形状并说明理由.解:(1)证明:∵△ABC是等腰三角形,∴AB=BC,∠A=∠C.∵将等腰△ABC绕顶点B按逆时针方向旋转α度到△A1BC1的位置,∴A1B=AB=BC,∠A1=∠A=∠C,∠A1BD=∠CBC1.在△BCF 与△BA 1D 中,⎩⎨⎧∠C =∠A 1,CB =A 1B ,∠CBF =∠A 1BD ,∴△BC F ≌△BA 1D(ASA).(2)四边形A 1BCE 是菱形.理由如下:∵将等腰△ABC 绕顶点B 按逆时针方向旋转α度到△A 1BC 1的位置,∴∠A 1=∠A.∵∠ADE =∠A 1DB ,∴∠AED =∠A 1BD =α.∴∠DEC =180°-α.∵∠C =α,∴∠A 1=α.∴∠A 1BC =360°-∠A 1-∠C -∠A 1EC =180°-α.又∵∠A 1=∠C ,∠A 1BC =∠A 1EC.∴四边形A 1BCE 是平行四边形.∴A 1B =BC.∴四边形A 1BCE 是菱形.。
第七章《图形的变换》综合考试测试卷-2020届广东九年级数学中考总复习课件 (共31张PPT)
三、解答题(一)(本大题3小题,每小题6分,共 18分) 18. 如图S1-7-8,在边长为1个单位长度的小正方形 组成的网格中,给出了直角坐标系及格点三角形AOB (顶点是网格线的交点).
(1)画出将△AOB沿y轴翻折后得到的△AOB1,则点 B1的坐标为__(__-_3_,__0_)___; (2)画出将△AOB沿射线AB1方向平移2.5个单位后 得到的△A2O2B2,则点A2的坐标为_(__-_1_._5_,__2_)__.
解:(1)如答图S1-7-5. Rt△AB1C1与Rt△ABC关于点A对称. (2)Rt△AB2C2如答图S1-7-5.
23. 如图S1-7-13,在△ABC中,∠ABC=90°. (1)作线段AC的垂直平分线,交AC于点O;(保留 作图痕迹,请标明字母) (2)连接BO并延长至点D,使得OD=OB,连接DA,DC, 证明四边形ABCD是矩形.
(1)证明:①∵△ABE绕点B顺时针旋转90°后得 到△CBF,∴△AEB≌△CFB.∴AE=CF. ②如答图S1-7-7,延长AE交CF于点M,由①知, △AEB≌△CFB, ∴∠F=∠AEB,∠BAE=∠BCF. ∵∠AEB+∠BAE+∠ABE=180°, ∴∠F+∠BAM+∠CBF=180°. ∵四边形ABCD是正方形,∴∠ABC=90°. ∴∠AMF=360°-∠ABC-∠F-∠BAM∠CBF=90°.∴AE⊥CF.
(2)解:①如答图S1-7-8,连接EF.由旋转知, BE⊥BF且BE=BF,∴∠BFE=45°. 在Rt△BEF中,BE=BF=2,∴EF2=8. ∵∠BEF=45°,∠AEB=135°, ∴∠AEB+∠BEF=180°. ∴点A,E,F在同一条直线上.
由(1)知,AE⊥CF,在Rt△ECF中,CE=5,利用勾
中考数学函数与几何图形及变换练习题(含答案)
中考数学二轮复习拔高训练卷专题4 函数与几何图形及变换一、单选题(共12题;共24分)1. ( 2分) 把直线y=-x+3向上平移m个单位长度后,与直线y=2x+4的交点在第一象限,则m的取值范围是()A. 1<m<7B. 3<m<4C. m>1D. m <42. ( 2分) 如图,一次函数y= 34x+6的图像与x轴、y轴分别交于点A,B,过点B的直线l平分△ABO 的面积,则直线l相应的函数表达式为()A. y= 35x+6 B. y= 53x+6 C. y= 23x+6 D. y= 32x+63. ( 2分) 如图,A是反比例函数y=kx图象上一点,过点A作AB⊥x轴于点B,点P在y轴上,△ABP 的面积为1,则k的值为()A. 1B. 2C. -1D. -24. ( 2分)的图象经过点C,则k的值如图,菱形OABC的顶点B在y轴上,顶点A的坐标为(3,2).若反比例函数y=kx为()A. -6B. -3C. 3D. 65. ( 2分) 将二次函数y=5x2的图象先向右平移2个单位,再向下平移3个单位,得到的函数图象的解析式为().A. y=5(x+2)2+3B. y=5(x-2)2+3C. y=5(x+2)2-3D. y=5(x-2)2-36. ( 2分) 在平面直角坐标系中,若将抛物线y=2x2 - 4x+3先向右平移3个单位长度,再向上平移2个单位长度,则经过这两次平移后所得抛物线的顶点坐标是()A. (-2,3)B. (-1,4)C. (1,4)D. (4,3)7. ( 2分) 将抛物线y=2x2-12x+16绕它的顶点旋转180°,所得抛物线的解析式是().A. y=-2x2-12x+16B. y=-2x2+12x-16C. y=-2x2+12x-19D. y=-2x2+12x-208. ( 2分 ) 如图,等边三角形ABC 的边长为4厘米,长为1厘米的线段MN 在△ABC 的边AB 上沿AB 方向以1厘米/秒的速度向B 点运动(运动开始时,点M 与点A 重合,点N 到达点B 时运动终止),过点M 、N 分别作AB 边的垂线,与△ABC 的其它边交于P 、Q 两点.线段MN 在运动的过程中,四边形MNQP 的面积为S ,运动的时间为t .则大致反映S 与t 变化关系的图象是( )A. B.C. D.9. ( 2分 ) 如图,O 为坐标原点,边长为√2的正方形OABC 的顶点A 在x 轴的正半轴上,将正方形OABC 绕顶点O 顺时针旋转75°,使点B 落在某抛物线的图象上,则该抛物线的解析式可能为( )A. y=23x 2B. y=﹣13x 2C. y=﹣12x 2 D. y=﹣3x 210. ( 2分) 如图,在△ABC中,∠B=90°,∠C=30°,AB=6cm,动点P从点B开始沿边BA、AC向点C以3cm/s的速度移动,动点Q从点B开始沿边BC向点C以√3cm/s的速度移动,设△BPQ的面积为y(cm2).运动时间为x(s),则下列图象能反映y与x之间关系的是()A. B.C. D.11. ( 2分) 如图,点C、D是以线段AB为公共弦的两条圆弧的中点,AB=4,点E,F分别是线段CD,AB上的动点,设AF=x,AE2-FE2=y,则能表示y与x的函数关系的图象是()A. B.C. D.12. ( 2分) 如图,在△ABC中,∠C=90°,AB=10cm,BC=8cm,点P从点A沿AC向点C以1cm/s 的速度运动,同时点Q从点C沿CB向点B以2cm/s的速度运动(点Q运动到点B停止),在运动过程中,四边形PABQ的面积最小值为()A. 19cm2B. 16cm2C. 15cm2D. 12cm 2二、填空题(共5题;共12分)13. ( 4分) 将抛物线y=−2x2+1向右平移1个单位,再向下平移3个单位后所得到新抛物线的解析式是________,顶点坐标是________.图象上的一点,过点C向坐标轴引垂线,垂足为A、B,14. ( 2分) 如图,已知点C为反比例函数y= −6x那么四边形AOBC的面积为________。
2018年中考数学总复习单元检测七图形的变换试题新版新人教版2018011214
单元检测七图形的变换(时间90分钟满分120分)一、选择题(每小题3分,共30分)1.剪纸是扬州的非物质文化遗产之一,下列剪纸作品中,是中心对称图形的是(C)2.将点A(3,2)沿x轴向左平移4个单位长度得到点A',点A'关于y轴对称的点的坐标是(C)A.(-3,2)B.(-1,2)C.(1,2)D.(1,-2)3.在下列的四个几何体中,其主视图与俯视图相同的是(D)4.如图,在Rt△ABC中,∠ACB=90°,∠B=60°,BC=2,△A'B'C可以由△ABC绕点C顺时针旋转得到,其中点A'与点A是对应点,点B'与点B是对应点,连接AB',且A,B',A'在同一条直线上,则AA'的长为(A)A.6B.4C.3D.35.下列四个圆形图案中,分别以它们所在圆的圆心为旋转中心,顺时针旋转120°后,能与原图形完全重合的是(A)6.下列三视图所对应的直观图是(C)7.如图,△DEF是由△ABC经过位似变换得到的,点O是位似中心,D,E,F分别是OA,OB,OC的中点,则△DEF与△ABC的面积比是(B)A.1∶2B.1∶4C.1∶5D.1∶6(第7题图)(第8题图)8.如图,△ABC的面积为6,AC=3,现将△ABC沿AB所在直线翻折,使点C落在直线AD上的C'处,P为直线AD上的一点,则线段BP的长不可能是(A)A.3B.4C.5.5D.109.如图,正方形OABC的两边OA,OC分别在x轴、y轴上,点D(5,3)在边AB上,以C为中心,把△CDB旋转90°,则旋转后点D的对应点D'的坐标是(C)A.(2,10)B.(-2,0)C.(2,10)或(-2,0)D.(10,2)或(-2,0)10.如图,一张三角形纸片ABC,其中∠C=90°,AC=4,BC=3.现小林将纸片做三次折叠:第一次使点A落在C处;将纸片展平做第二次折叠,使点B落在C处;再将纸片展平做第三次折叠,使点A落在B处.这三次折叠的折痕长依次记为a,b,c,则a,b,c的大小关系是(D) A.c>a>b B.b>a>cC.c>b>aD.b>c>a二、填空题(每小题5分,共20分)11.在平面直角坐标系中,点A的坐标是(2,-3),作点A关于x轴的对称点,得到点A',再作点A'关于y轴的对称点,得到点A″,则点A″的坐标是(-2,3).12.如图,这是一个长方体的主视图和俯视图,由图示数据(单元: cm)可以得出该长方体的体积是18 cm3.〚导学号92034220〛13.如图,直线y=x+1与x轴交于点A,与y轴交于点B,△BOC与△B'O'C'是以点A为位似中心的位似图形,且相似比为1∶3,则点B的对应点B'的坐标为(-8,-3)或(4,3).14.如图,在正方形ABCD中,AD=1,将△ABD绕点B顺时针旋转45°得到△A'BD',此时A'D'与CD交于点E,则DE的长度为2-.三、解答题(共70分)15.(6分)如图,在水平地面上竖立着一面墙AB,墙外有一盏路灯D.光线DC恰好通过墙的最高点B,且与地面形成37°角.墙在灯光下的影子为线段AC,并测得AC=5.5米.(1)求墙AB的高度(结果精确到0.1米);(参考数据:tan 37°≈0.75,sin 37°≈0.60,cos 37°≈0.80)(2)如果要缩短影子AC的长度,同时不能改变墙的高度和位置,请你写出两种不同的方法.在Rt△ABC中,AC=5.5米,∠C=37°,tan∠C=,∴AB=AC·tan C=5.5×0.75≈4.1米;(2)要缩短影子AC的长度,增大∠C的度数即可.因此第一种方法是增加路灯D的高度,第二种方法是使路灯D向墙靠近.〚导学号92034221〛16.(6分)如图,△ABC和△DBC是两个具有公共边的全等三角形,AB=AC=3 cm,BC=2 cm,将△DBC沿射线BC平移一定的距离得到△D1B1C1,连接AC1,BD1.如果四边形ABD1C1是矩形,求平移的距离.7 cm.17.(6分)一个几何体的三视图如图所示,求该几何体的表面积.,∴其表面积为π×12+(π+2)×2=3π+4.18.(8分)如图,P是等边三角形ABC内一点,将线段AP绕点A顺时针旋转60°得到线段AQ,连接BQ.若PA=6,PB=8,PC=10,求四边形APBQ的面积.S四边形APBQ=24+9.19.(8分)如图,在一面与地面垂直的围墙的同侧有一根高10米的旗杆AB和一根高度未知的电线杆CD,它们都与地面垂直,为了测得电线杆的高度,一个小组的同学进行了如下测量:某时刻,在太阳光照射下,旗杆落在围墙上的影子EF的长度为2米,落在地面上的影子BF的长为10米,而电线杆落在围墙上的影子GH的长度为3米,落在地面上的影子DH的长为5米.依据这些数据,该小组的同学计算出了电线杆的高度.(1)该小组的同学在这里利用的是投影的有关知识进行计算的;(2)试计算出电线杆的高度,并写出计算的过程.平行;(2)过点E作EM⊥AB于M,过点G作GN⊥CD于N,则MB=EF=2米,ND=GH=3米,ME=BF=10米,NG=DH=5米,所以AM=10-2=8米,由平行投影可知,=,即=,解得CD=7米,即电线杆的高为7米.20.(8分)如图,折叠矩形ABCD的一边AD,使点D落在BC边的点F处,已知折痕AE=5,且tan∠EFC=,求矩形ABCD的周长.和△ADE关于AE对称,∴∠AFE=∠D=90°,AF=AD,EF=DE.∵tan∠EFC==,∴可设EC=3x,CF=4x,那么EF=5x,∴DE=EF=5x.∴DC=DE+CE=3x+5x=8x.∴AB=DC=8x.∵∠EFC+∠AFB=90°,∠BAF+∠AFB=90°,∴∠EFC=∠BAF.∴tan∠BAF=tan∠EFC=,∴=.∵AB=8x,∴BF=6x.∴BC=BF+CF=10x.∴AD=10x.在Rt△ADE中,由勾股定理,得AD2+DE2=AE2.∴(10x)2+(5x)2=(5)2.解得x=1.∴AB=8x=8,AD=10x=10.∴矩形ABCD的周长=8×2+10×2=36.21.(8分)下列3×3网格图都是由9个相同的小正方形组成,每个网格图中有3个小正方形已涂上阴影,请在余下的6个空白小正方形中,按下列要求涂上阴影:(1)选取1个涂上阴影,使4个阴影小正方形组成一个轴对称图形,但不是中心对称图形;(2)选取1个涂上阴影,使4个阴影小正方形组成一个中心对称图形,但不是轴对称图形;(3)选取2个涂上阴影,使5个阴影小正方形组成一个轴对称图形.(请将三个小题依次作答在图1、图2、图3中,均只需画出符合条件的一种情形)如图1所示;(2)如图2所示;(3)如图3所示.22.(10分)如图,方格纸中的每个小方格都是边长为1的正方形,△ABC的顶点都在格点上,请完成下列任务:(1)将△ABC绕点C按顺时针方向旋转90°后得到△A1B1C;(2)求线段AC旋转到A1C的过程中,所扫过的图形的面积;(3)以点O为位似中心,相似比为2,在O同侧将△A1B1C放大得到△A2B2C2(在网格之内画图).如图所示:△A1B1C即为所求;(2)AC所扫过的图形的面积S==;(3)如图所示:△A2B2C2即为所求.〚导学号92034222〛23.(10分)在数学兴趣小组活动中,小明进行数学探究活动,将边长为2的正方形ABCD与边长为2的正方形AEFG按图1位置放置,AD与AE在同一直线上,AB与AG在同一直线上.(1)小明发现DG⊥BE,请你帮他说明理由;(2)如图2,小明将正方形ABCD绕点A逆时针旋转,当点B恰好落在线段DG上时,请你帮他求出此时BE的长.ABCD和四边形AEFG都为正方形,∴AD=AB,∠DAG=∠BAE=90°,AG=AE,∴△ADG≌△ABE(SAS).∴∠AGD=∠AEB.如图1,延长EB交DG于点H,在△ADG中,∵∠AGD+∠ADG=90°,∴∠AEB+∠ADG=90°.在△EDH中,∵∠AEB+∠ADG+∠DHE=180°,∴∠DHE=90°.∴DG⊥BE.(2)∵四边形ABCD和四边形AEFG都为正方形,∴AD=AB,∠DAB=∠GAE=90°,AG=AE,∴∠DAB+∠BAG=∠GAE+∠BAG,即∠DAG=∠BAE,∴△ADG≌△ABE(SAS).∴DG=BE.如图2,过点A作AM⊥DG交DG于点M,则∠AMD=∠AMG=90°,∵BD为正方形ABCD的对角线,∴∠MDA=45°.在Rt△AMD中,∵∠MDA=45°,AD=2,∴DM=AM=.在Rt△AMG中,根据勾股定理得GM==, ∴DG=DM+GM=+,∴BE=DG=+.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
单元检测(七) 图形与变换 (时间:120分钟 满分:150分) 一、选择题(本大题共10小题,每小题5分,满分50分,在每小题给出的四个选项中,只有一项是符合题目要求的) 1.(2018·江苏苏州)下列四个图案中,不是轴对称图案的是( )
答案B 解析本题解答时要找出图形的对称轴.A,C,D都是轴对称图形,只有B是中心对称图形,故选B. 2.(2018·广西柳州)如图,这是一个机械模具,则它的主视图是( )
答案C 解析从正面观察该组合体,所得到的平面图形含有三个小正方形,左上角含有一个圆,故选C. 3.(2018·山东莱芜)已知圆锥的三视图如图所示,则这个圆锥的侧面展开图的面积为( )
A.60π cm2 B.65π cm2 C.120π cm2 D.130π cm2 答案B
解析因为圆锥的侧面展开图是扇形,先求得圆锥的母线l==13(cm),再根据扇形的面积公式S扇形=×10π×13=65π(cm2).故选B. 4.(2018·贵州安顺)已知△ABC(AC合要求的作图痕迹是( ) 答案D 解析选项A,该作图痕迹表示AB=PB,不符合题意;选项B,该作图痕迹表示作线段AC的垂直平分线交BC于点P,即PA=PC,不符合题意;选项C,该作图痕迹表示AC=PC,不符合题意;选项D,该作图痕迹表
示作线段AB的垂直平分线交BC于点P,即PA=PB,故PA+PC=BC,符合题意.故选D. 5.(2018·辽宁抚顺)已知点A的坐标为(1,3),点B的坐标为(2,1),将线段AB沿某一方向平移后,点A的对应点的坐标为(-2,1),则点B的对应点的坐标为( ) A.(5,3) B.(-1,-2) C.(-1,-1) D.(0,-1) 答案C 解析由图形在坐标平面内的平移特征可知,点A的平移过程与点B的平移过程相同,点A向左平移3个单位,再向下平移2个单位得到对应点(-2,1),故点B向左平移3个单位,再向下平移2个单位得到对应点(-1,-1).故选C. 6.
(2018·山东济宁)如图,在平面直角坐标系中,点A,C在x轴上,点C的坐标为(-1,0),AC=2.将Rt△ABC先绕点C顺时针旋转90°,再向右平移3个单位长度,则变换后点A的对应点坐标是( ) A.(2,2) B.(1,2) C.(-1,2) D.(2,-1) 答案A 解析将Rt△ABC先绕点C顺时针旋转90°,再向右平移3个单位长度,因此,点A也先绕点C顺时针旋转90°后对应点的坐标为(-1,2),再向右平移3个单位长度后对应点的坐标为(2,2),故选A. 7.
(2018·芜湖模拟)如图,线段AB两个端点的坐标分别为A(2,2)、B(3,1),以原点O为位似中心,在第一象限内将线段AB扩大为原来的2倍后得到线段CD,则端点C的坐标为( ) A.(3,1) B.(3,3) C.(4,4) D.(4,1) 答案C 解析以原点O为位似中心,在第一象限内将线段AB扩大为原来的2倍后得到线段CD,∴A点与C点是对应点,∵C点的对应点A的坐标为(2,2),位似比为1∶2,∴点C的坐标为(4,4),故选C. 8.
(2018·湖北武汉)如图,在☉O中,点C在优弧上,将弧沿BC折叠后刚好经过AB的中点D.若☉O的半径为,AB=4,则BC的长是( ) A.2 B.3
C. D. 答案B 解析
连接AC、DC、OD,过C作CE⊥AB于E,过O作OF⊥CE于F, ∵沿BC折叠,
∴∠CDB=∠H,
∵∠H+∠A=180°,∠CDA+∠CDB=180°,
∴∠A=∠CDA,∴CA=CD. ∵CE⊥AD,∴AE=ED=1. ∵OA=,AD=2,∴OD=1. ∵OD⊥AB,∴OFED为正方形. ∴OF=1,OC=. ∴CF=2,CE=3.∴CB=3. 9.
(2018·贵州贵阳)已知二次函数y=-x2+x+6及一次函数y=-x+m,将该二次函数在x轴上方的图象沿x轴翻折到x轴下方,图象的其余部分不变,得到一个新函数(如图所示),当直线y=-x+m与新图象有
4个交点时,m的取值范围是( ) A.-C.-2答案D 解析在抛物线y=-x2+x+6中,令y=0时,即-x2+x+6=0,解得x1=-2,x2=3,即抛物线y=-x2+x+6与x轴交点坐标分别为(-2,0),(3,0). ∵抛物线y=-x2+x+6沿x轴翻折到x轴下方,
∴此时新抛物线y=x2-x-6(y<0)与y轴交点坐标为(0,-6).
当直线y=-x+m过(-2,0),(0,-2)时,m=-2,此时直线y=-x+m与x轴下方图象只有三个交点,如图所示,要使直线y=-x+m与新图象有4个交点,需y=-x+m与y=x2-x-6有两个交点,则-x+m=x2-x-6有两个不同解,整理得x2=m+6,所以m>-6时,y=-x+m与y=x2-x-6有两个交点,m的取值范围是-62. 10.
(2018·山东滨州)如图,∠AOB=60°,点P是∠AOB内的定点,且OP=,若点M、N分别是射线OA、OB上异于点O的动点,则△PMN周长的最小值是( )
A. B. C.6 D.3 〚导学号16答案D 解析
分别以OA、OB为对称轴作点P的对称点P2,P1,连接点P1,P2,分别交射线OA、OB于点M、N,则此时△PMN的周长有最小值,△PMN的周长等于=PM+PN+MN=P1N+P2M+MN=P1P2,根据对称的性质可 知,OP1=OP2=OP=,∠P1OP2=120°,∠OP1M=30°,过点O作MN的垂线段,垂足为Q,在△OP1Q中,可知P1Q=,所以P1P2=2P1Q=3,故△PMN的周长的最小值为3. 二、填空题(本大题共4小题,每小题5分,满分20分) 11.
(2017·江苏南京二模)如图,∠3=40°,直线b平移后得到直线a,则∠1+∠2= °. 答案220 解析如
图,∵直线b平移后得到直线a, ∴a∥b,
∴∠1+∠4=180°,
即∠4=180°-∠1. ∵∠5=∠3=40°,
∴∠2=∠4+∠5=180°-∠1+40°,
∴∠1+∠2=220°.故答案为220.
12.(2018·明光二模)把直线y=-x-1沿x轴向右平移3个单位长度,所得直线的函数解析式为 . 答案y=-x+
解析把函数y=-x-1沿x轴向右平移3个单位长度,可得到的图象的函数解析式是:y=-(x-3)-1=-x+. 13.(2018·甘肃白银)已知某几何体的三视图如图所示,其中俯视图是正六边形,则该几何体的侧面积是 . 答案108 解析因为俯视图是正六边形,主视图和左视图是矩形,可知这个几何体是一个正六棱柱.正六棱柱的侧面展开图是一个矩形,矩形的一条边是正六边形的周长即3×6=18,矩形的另一条边长是主视图的高即6,所以展开图的矩形的面积等于18×6=108. 14.
(2017·黑龙江牡丹江改编)如图,矩形ABCD的边BC在x轴上,点A在第二象限,点D在第一象限,AB=2,OD=4,将△DOC绕点O旋转,使点D落在x轴上,则点C对应点的坐标是 . 答案(-1,)或(1,-) 解析在矩形ABCD中, ∵CD=AB=2,∠DCO=90°,∵OD=4,
∴∠DOC=60°,OC=2,
①当顺时针旋转至△OD'C'时,如图,∠D'OC'=∠DOC=60°,OC'=OC=2,
过C'作C'E⊥OD'于E,则OE=OC'=1,C'E=OC'=,∴C'(1,-), ②当逆时针旋转至△OD″C″时,如图,∠D″OC″=∠DOC=60°,OC″=OC=2,
过C″作C″F⊥OD″于F,则OF=OC″=1,C″F=OC″=,∴C″(-1,). 综上所述:点C对应点的坐标是(1,-),(-1,).
三、(本大题共2小题,每小题13分,满分26分) 15.(2018·北京)下面是小东设计的“过直线外一点作这条直线的平行线”的尺规作图过程. 已知:直线l及直线l外一点P. 求作:直线PQ,使得PQ∥l. 作法:如图: ①在直线l上取一点A,作射线PA,以点A为圆心,AP长为半径画弧,交PA的延长线于点B;
②直线l上取一点C(不与点A重合),作射线BC,以点C为圆心,CB长为半径画弧,交BC的延长线于
点Q; ③作直线PQ. 所以直线PQ就是所求作的直线. 根据小东设计的尺规作图过程, (1)使用直尺和圆规,补全图形;(保留作图痕迹) (2)完成下面的证明. 证明:∵AB= ,CB= , ∴PQ∥l( )
写出推理的依据: 解(1)如图所示:
(2)PA,CQ;①连接三角形两边中点的线段叫做三角形的中位线;②三角形的中位线平行于第三边;③两点确定一条直线. 16.(2018·铜陵模拟)把直线y=-x+3向上平移m个单位后,与直线y=2x+4的交点在第一象限,求m的取值范围. 解方法一:直线y=-x+3向上平移m个单位后可得:y=-x+3+m,
联立两直线解析式得
解得 即交点坐标为, ∵交点在第一象限,
