第四节 广 义 积 分
合集下载
第九章财务管理之股利分配
普通股（面额1元，已发行200 000股） 资本公积 未分配利润 股东权益合计
220 000 780 000 1 600 000 2 600 000
•
• 假定该公司本年盈余为440 000元，某股东 持有20 000股普通股，发放股票股利的影 响见下表
项目
发放前
发放后
ห้องสมุดไป่ตู้
每股收益EPS 440 000÷200 000=2.2 2
后的10%提取，决定公积金达到注册资本的 50%，可不再提取。
•
（三）计提法定公益金； • 法定公益金按当年净利润的5%～10%提取
，主要用于职工宿舍等集体福利设施支出 。 （四）计提任意公积金； （五）向投资者分配利润或向股东支付股利
•
二、利润分配方案的确定
主要是考虑确定以下四个方面的内容： • 第一，选择股利政策类型； • 第二，确定股利支付水平的高低； • 第三，确定股利支付形式，即确定合适
•
二、固定股利政策
1.内容：公司将每年派发的股利额固定在某一特 定水平上，不论公司的盈利情况和财务状况如 何，派发的股利额均保持不变。
2.依据：股利重要论 3.优点： （1）有利于稳定公司股票价格，增强投资者对
公司的信心。 （2）有利于投资者安排收入与支出。
•
4.缺点： （1）公司股利支付与公司盈利相脱离，造成
• 因而股利无关论又被称为完全市场理论 。
•
（三）税收效应理论
• 税收效应理论：股利政策不仅与股价相 关，由于税收影响，企业应采取低股利 政策。
• 理论假设：对股利和资本收益征收不同 税率。
•
• 股利分配政策的意义： 1.股利分配政策在一定程度上决定企业的
第四节阶跃函数和冲激函数
t
x
dx
0,
t,
t<0 t>0
t
t
t
t
x
dx
t
t
'x
dx
tdt 1
'tdt 0
• 四.冲激函数的性质：
• 1.与普通函数的乘积： f t t f 0 t
筛选特性
f
t tdt
f
0 tdt
f
0
f t ' t f 0 ' t f ' 0 t
f
t
' t dt
f
' 0
• 而一些广义函数间乘积无定义如：δ(t)ε(t);δ(t)δ(t);δ(t)δ’(t)等。
第四节 阶跃函数和冲激函数
• 一. 阶跃函数和冲激函数
rn(t)
1
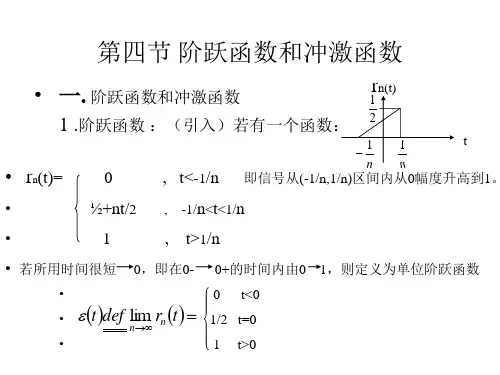
1 .阶跃函数 ：（引入）若有一个函数： 2
n 1
1
t
n
• rn(t)=
0
, t<-1/n 即信号从(-1/n,1/n)区间内从0幅度升高到1。
•
½+nt/2 , -1/n<t<1/n
•
1
, t>1/n
• 若所用时间很短 0，即在0- 0+的时间内由0 1，则定义为单位阶跃函数
波形如图:
t
t 0,t 0
• 冲激函 t
dt
t
t
x
dx
• 二.冲激函数的广义定义
• <1>δ(t)广义定义：对一个性能良好的函数φ(t)（检验函数）有以下定义
则δ(t) 为冲激函数：
(t ) (t )dt
，(0φ)(t)为一般函数，性能良好
广义特征根问题求解的神经网络方法分析
积也是一个特征 向量：Ａ ） ＝
为单位 向量 ，即我们要求
） 因此 ，通常在 正则化方面 要求特 征 向量是关于矩 阵ｊ的模 。 ５ ｝
‘ ｒ
：
１
（） ２
显然，当ｊ ，这里 ５ ｝ 是单位阵 ，广义特征根 问题就简化为普通 的特征根 问题。 基于罚函数方法 ，文献 １－ １ 出了求解普通的特征根问题 的多层神经网络模型 。但是，我们知道， ７８给 基于罚函数的方法有三个基本缺 陷： （ ）没有一个调节这个 罚参数 的准 则可 以利用 ； （ ）所得到 １ ２ 的解可能不是可行解 ； （ ）这些模型 的稳定性通常无法证 明，可参看三个典型 的罚函数模型 。 ３ 正是 由于这些 明显 的缺 陷，罚 函数方法在传统 的优化计算中几乎是不可行 的 ，实际计算中更没有用 它的。因此 ，基于罚 函数方法构造 的神经 网络基础是不可靠 的。正是基 于此种考虑，一个求解广义
一
于受到计算时间 的限制 ，对 大规模的科学计算 问题 已经很不适用 。由于神经 网络算法具有实时计算 以及易于 电路模拟实现 的两大强大功效， 自从Ｈｏ ｆ ｌ与Ｔ ｎ ｎ ｐｅ ｉ ｄ ａ ｋ 的开创性工作开始，最近２ 余年 已 ０ 有许多文献研究 了最优化 问题 的神经 网络求解，可参看文献 ［－ ］ ３ ６ 。有关最优化 问题求解的神经网络 的一些基本模型、方法表述等可 以参看文献 ［］ ７。 特征根 问题的神经网络求解也有文献涉及 ，例如文献 ［－ ］ ７８ 就提 出了相应 的网络模型，他们的网 络模型是基于罚函数方法的。但是，我们知道基于罚函数方法所寻找到的解很可能不是可行解 ，更别 说最优解 了，可参看文献 ［］ ９ 中的论述 。另外，网络的收敛性在这种 方法 中更是没法 证明。因此，这 种方法所得到的网络模型是不可靠 的，其有效性与可靠性都有极大 的缺陷。这里我们提出求解广义特 征根 问题的神经网络模型，与 已有 的网络相 比较，这里的模型一直保持轨道是可行 的，而且全局拟收 敛到广义特征 向量 。当然 ，所提 出的网络模型具有实时计算的强大功效，而且可 以电路模拟实现，从 这点来讲 ，这个方法就可以用于解决大规模的计算 问题 。因此 ，这里 的方法也优于已有的传统方法。 文章下面是这样安排 的：第一节给出所研究 的问题表述；第 二节讨论所考虑 问题求解 的神经网 络方法 的启发性分析 ：第三节讨论 了网络 的结构，最主要 的是给 出了稳定性研究 ：第 四节是全文 的 结论 以及 一 些 讨 论 。
高二数学-定积分概念-课件
若x a,取x 0,则同理可证 (a) f (a); 若x b,取x 0,则同理可证 (b) f (b).
定理2： （原函数存在定理）
如果f (x)在闭区间 [a,b]上连续，则函数
（x)
x
f (t)dt
a
就是f (x)在[a,b]上的一个原函数。
定积分
二、牛顿-莱不尼茨公式（微积分基本公式）
(i)分割：在 [a ,b ] 内n 插 1 个入 a 分 x 0 点 x n 1 x n b ， 得 n 个小 [x i 1 ,x i]i区 ,1 ,2 , ,n 间 .记 x i x i x i 1
(ii)作积：任取i [xi1,xi]i 1,2,,n
得第i个小曲边梯形面积 似的 值近y
(如图 )的面积。
y
解： 依题意，所求面积为
y=sinx
A0 sinxdx
o
x
cosx
0
(1)(1) 2
例4 设f (x)在[0,)内连续，f且 (x) 0.证明
x
tf(t)dt
F(x)
0 x
在(0,)内卫单调增加函数。
0 f (t)dt
证
x
x
x
x(fx) f(t)d tf(x) t(ft)dtf(x) (xt)f(t)dt
定理3：如果 F(x)是连续函 f (x数 )在区[间 a,b]上的一个 原函数，则
b
b
f (x)dxF(b)F(a)[F(x)]
(微积分基本公式）
a
证明：函数(x)
x
f
a (t)dt也是f (x)的一个原函数，从而
a
F(x)(x) C.令x a有F(a) C.即F(x)(x) F(a)
第5章“积零为整”的数学方法
分区间，a称为积分下限，b称为积分上限，Sn为积分和或 Riemann和。
10
2018年5月19日星期六
注 ①定积分是一个极限，它的结果为常数，只和f(x)、
[a,b]有关，和分划方法、ξi的取法无关，也与积分变量无关：
b
a
f ( x)dx f (t )dt f (u)du
a a
无限减小时，若
f ( )x
i 1 i
n
i
的极限存在，则其极限值就是所要求的面积：
S lim
x 0
f ( )x
i 1 i
n
i
很多实际问题的解决，也可归结为这类和式极限的问题。 因此，数学家们将这类和式极限进行深入的研究就抽象出一个
新概念——定积分。
8
2018年5月19日星期六
1 1
f ( x) a 2 f 2 ( x) a n f n ( x)dx
a1 f1 ( x)dx a 2 f 2 ( x)dx a n f n ( x)dx
21
2018年5月19日星期六
基本积分表
kdx kx C
1 x dx ln x C x x e dx e C
n i 1
S lim
0
f ( )x
i 1 i n
n
i
存在，且极限值与[a,b]的分划方法和点ξi的取法无关，则称f(x) 在[a,b]上可积，并称此极限值为f(x)在[a,b]上的定积分，记为
b
a
f ( x)dx lim
0
f ( )x
i 1 i
i
其中∫为积分符号，f(x)为被积函数，x为积分变量。[a,b]为积
10
2018年5月19日星期六
注 ①定积分是一个极限，它的结果为常数，只和f(x)、
[a,b]有关，和分划方法、ξi的取法无关，也与积分变量无关：
b
a
f ( x)dx f (t )dt f (u)du
a a
无限减小时，若
f ( )x
i 1 i
n
i
的极限存在，则其极限值就是所要求的面积：
S lim
x 0
f ( )x
i 1 i
n
i
很多实际问题的解决，也可归结为这类和式极限的问题。 因此，数学家们将这类和式极限进行深入的研究就抽象出一个
新概念——定积分。
8
2018年5月19日星期六
1 1
f ( x) a 2 f 2 ( x) a n f n ( x)dx
a1 f1 ( x)dx a 2 f 2 ( x)dx a n f n ( x)dx
21
2018年5月19日星期六
基本积分表
kdx kx C
1 x dx ln x C x x e dx e C
n i 1
S lim
0
f ( )x
i 1 i n
n
i
存在，且极限值与[a,b]的分划方法和点ξi的取法无关，则称f(x) 在[a,b]上可积，并称此极限值为f(x)在[a,b]上的定积分，记为
b
a
f ( x)dx lim
0
f ( )x
i 1 i
i
其中∫为积分符号，f(x)为被积函数，x为积分变量。[a,b]为积
第四节广义相对论简介
爱因斯坦广义相对 原理 191 年 任何参考系中( 的物理规律都是相同的 都是相同 在任何参考系中( 惯系 的物理规律都是相同的 广义相对性原理。 ， 广义相对性原理。
非惯性系和惯性系
a −a
光滑表面
以车厢为参考系，当列车加速运行时， 以车厢为参考系，当列车加速运行时，小球会相 对于车厢加速向后运动． 对于车厢加速向后运动．
第四节广义相对论简介
安陆市第一高级中学
内容回顾
一、狭义相对论的两点假设： 狭义相对论的两点假设： 1、狭义相对性原理 在不同的惯性参考系 一切物理规律都是相同 惯性参考系， 在不同的惯性参考系，一切物理规律都是相同 的 2、光速不变原理 真空中的光速在不同的惯性参考系中是相同的， 真空中的光速在不同的惯性参考系中是相同的 在不同的惯性参考系中是相同 光速与光源、观察者间的相对运动没有关系。 光速与光源、观察者间的相对运动没有关系。
1919年 29日 发生日全食， 1919年5月29日，发生日全食，英国考察队分赴几内亚湾 1919 和巴西进行观测，证实了爱因斯坦的预言， 和巴西进行观测，证实了爱因斯坦的预言，这是对广义相对论 的最早证实． 的最早证实．
透镜效应
星球的强引力场能使背后传来的光线汇聚， 星球的强引力场能使背后传来的光线汇聚，这 星球的强引力场能使背后传来的光线汇聚 种现象叫做引力透镜效应． 种现象叫做引力透镜效应．
二、广义相对性原理和等效原理
2、等效原理： 等效原理： 一个均匀的引力场与一个做匀加速 均匀的引力场与一个做匀加速运动的参考系 一个均匀的引力场与一个做匀加速运动的参考系 等价。 等价。
三、广义相对论的几个结论
1、物质的引力使光线发生弯曲
飞船外观察者看到这束光是直 线传播的（水平向右） 线传播的（水平向右） 如果飞船做匀速直线运动， 如果飞船做匀速直线运动， 船上观察者记录下的光的径迹是一 条直线（虚线） 条直线（虚线） 如果飞船做匀加速运动， 如果飞船做匀加速运动，在 光向右传播的同时， 光向右传播的同时，飞的速度也在 不断增大， 不断增大，因此船上观察者记录下 的光的径迹是一条抛物线。 的光的径迹是一条抛物线。
广义笛卡尔积
广义笛卡尔积假设集合A={a,b}，集合B={0,1,2}，则两个集合的笛卡尔积为{(a,0),(a,1),(a,2), (b,0),(b,1),(b,2)}。
可以扩展到多个集合的情况。
类似的例子有，如果A表示某学校学生的集合，B表示该学校所有课程的集合，则A与B的笛卡尔积表示所有可能的选课情况。
数据库求广域笛卡尔积问题R： A B C S: A B Ca 3 db 1 fb 4 t r 3 er 3 e d 3 t求R×SA B C A B CA B C b 1 fA B C r 3 eA B C d 3 ta 3 d A B Ca 3 db 1 fa 3 d r 3 ea 3 d d 3 tb 4 t A B Cb 4 t b 1 fb 4 t r 3 eb 4 t d 3 tr 3 e A B Cr 3 e b 1 fr 3 e r 3 er 3 e d 3 t(1) 选择（Selection） 在给定关系R中选择满足条件的元组。
记为： 其中F表示选择条件，是一个逻辑表达式，它的值为“真”或“假”。
逻辑表达式是由属性名、常量、简单函数和比较运算符、逻辑运算符组成的有意义的式子。
通常情况下，逻辑表达式是由逻辑运算符连接由比较运算符组成的比较关系式而成。
即通过逻辑运算符将比较关系式XqY连接起来组成逻辑表达式。
当然单独的比较关系式也是一个逻辑表达式。
（2）投影（Projection） 在给定关系R(U)中选择若干属性列组成的新关系。
记为： 其中A为R中属性组，且AíU。
在关系二维表中，选择是一种水平操作，它针对二维表中行，而投影是一种垂直操作，它针对二维表中的属性列。
（3）连接（Join） 连接也称为条件连接，它从两个关系的笛卡儿积中选择满足条件的元组。
记为： 其中A和B分别是关系R和S上度数相同且可比属性组，q为比较运算符。
在连接中有三种最常见的连接，一种是等值连接，一种是自然连接，还有半连接。
广义相对论简介课件PPT
对于高速转动的圆盘， 除了转动轴的位置外，各点都 在做加速运动，越是靠近边缘， 加速度越大，方向指向盘心．
地面上看到：越是靠近边缘，速度越大．根据狭义相对论， 靠近边缘部位的时间进程较慢．
圆盘上的人认为：盘上存在引力场，方向由盘心指向边缘， 靠近边缘的位置引力势较低，得出：引力势较低的位置，时间进 程比较慢．
狭义相对论
广义相对论
广
爱因
义
斯坦 不同的惯性 相对 参考系中一
更进一步
任何参考系 （包括非惯性
相 对
性原 切物理规律
系）中物理规 性
理 都是相同的
律都是相同的 原
理
光 真空中的光 速 速在不同惯 恒 性参考系中 定 都是相等的
一个均匀的 等 引力场与一个 效 做匀加速运动 原 的参考系等价 理
对于时空观的认识
第十五章 相对论简介
第四节 广义相对论简介
复习
一、狭义相对论的两点假设： 1、狭义相对性原理
在不同的惯性参考系，一切物理规律都是 相同的 2、光速不变原理
真空中的光速在不同的惯性参考系中是相 同的，光速与光源、观察者间的相对运动没有 关系。
二、由狭义相对论推出的几个结论 1、“同时”的相对性 2、动尺变短
文章的时间脉络清晰，无科学性错误.
公开课
点击这里输入您的课程标题
授课教师：七彩办公 时间：201X年X月
内容
1 这里输入您的标题一 2 这里输入您的标题二 3 这里输入您的标题三
4 这里输入您的标题四 5 这里输入您的标题五
章节
1 这里输入您的标题一
点击这里输入您的标题
添加 文字
添加 文字
点击此处添加文字 点击此处添加文字
地面上看到：越是靠近边缘，速度越大．根据狭义相对论， 靠近边缘部位的时间进程较慢．
圆盘上的人认为：盘上存在引力场，方向由盘心指向边缘， 靠近边缘的位置引力势较低，得出：引力势较低的位置，时间进 程比较慢．
狭义相对论
广义相对论
广
爱因
义
斯坦 不同的惯性 相对 参考系中一
更进一步
任何参考系 （包括非惯性
相 对
性原 切物理规律
系）中物理规 性
理 都是相同的
律都是相同的 原
理
光 真空中的光 速 速在不同惯 恒 性参考系中 定 都是相等的
一个均匀的 等 引力场与一个 效 做匀加速运动 原 的参考系等价 理
对于时空观的认识
第十五章 相对论简介
第四节 广义相对论简介
复习
一、狭义相对论的两点假设： 1、狭义相对性原理
在不同的惯性参考系，一切物理规律都是 相同的 2、光速不变原理
真空中的光速在不同的惯性参考系中是相 同的，光速与光源、观察者间的相对运动没有 关系。
二、由狭义相对论推出的几个结论 1、“同时”的相对性 2、动尺变短
文章的时间脉络清晰，无科学性错误.
公开课
点击这里输入您的课程标题
授课教师：七彩办公 时间：201X年X月
内容
1 这里输入您的标题一 2 这里输入您的标题二 3 这里输入您的标题三
4 这里输入您的标题四 5 这里输入您的标题五
章节
1 这里输入您的标题一
点击这里输入您的标题
添加 文字
添加 文字
点击此处添加文字 点击此处添加文字
(二十四)古代汉语的修辞..
分为藏头和歇后两种。
恰当地运用藏词，可以使文章幽默诙谐。但
有时影响了语言的完整性。
后来，藏头逐渐被淘汰了，歇后却发展成为 一种辞格。
返回本章目录
藏词－藏头 原 文
《后汉书· 左雄传》
出 处 及 所 藏 词 语 箫韶九成，凤凰来仪。
《尚书· 益稷》
故能降来仪之瑞。 痛心拔脑，有如孔怀。
陆机《与长沙顾母书》
受任、奉命于败军之际、 危难之间。
受任于败军之际， 奉命于危难之间。《出师表》
东市买骏马，西市买鞍鞯， 东市、西市、南市、北市 南市买辔头，北市买长鞭。 买骏马、鞍鞯、辔头、长
《木兰诗》
鞭。 不以外物得失、自己境遇
不以物喜，不以己悲。
《岳阳楼记》
而欢喜或悲观。
返回本章目录
第四节
错 综
返回本章目录
错综－定义
(二十四）古代汉语的修辞
第一节 倒 置 第六节 委 婉
第二节 合 叙
第三节 互 文 第四节 错 综 第五节 藏 词
第七节 代 称
第八节 用 典
第九节 古汉语修
辞著作
1
第一节
倒 置
返回本章目录
倒置－定义
【倒置】
在辞赋、骈文或散文中，为了
对仗、平仄、押韵的需要，或者为 了造成一种特殊的意境，常常故意
师之耳在鼓， 师之目在旗。
叙
师之耳目，在吾旗鼓。
《左传· 成公二年》
饮食君之酒肉。
《庄子· 徐无鬼》
饮君之酒，食君之肉。 水不积，则润不博； 火不积，则晖不博。
水火不积，则晖润不博。
《荀子· 天论》
返回本章目录
合叙－举例2 合 叙 举 例 分 叙
Lebesgue积分
（点
{ } 集） 记 T =maxΔxi 称为分割 T 的纯度或模。 1≤i≤n
的分
割
L 积分
设 E ⊂ Rn 是一个非空可测集，如果
n
E = U Ei ，其中各 Ei 为互不相交的非空 i=1
{ } 可测集，则称有限集 D = Ei 是 E 的一个
{ } 可测分割。设 D' = En' 是 E 的另一分割
积分的绝对连续性是 L-积分的重要特征，在连续函数平均逼近定理、 可测函数列控制收敛定理、L 积分中牛顿—莱布尼兹公式的推广应用等 很多重要定理的证明中都用到此性质。
⑵ L 积分的绝对可积性：
f (x) L 可积的充分必要条件为 f (x) L 可积。
134
由此，对于 L 积分可积亦绝对可积。这一特性与 R 积分有所不同。
R 积分的可积性可能依赖于被积函数的正负值相消；而 L 积分主要依靠 f
的绝对值受到一定的“控制”，当 f < g ，无论 f 如何复杂，若 g 可积，
则 f 必定可积。由此，显示了 L 积分较 R 积分的优越性；并说明 L 积分
可以看成 R 定积分的推广，但不是 R 广义积分的推广。
⑶ 变上限积分函数的绝对连续性：
130
收敛定理是 L 积分的重要结论；L 积分的绝对连续性是 L 积分的重要特 征，很多问题的证明用此性质；可测函数可以用连续函数平均逼近、零 测度集不影响函数的可积性及积分值等等是很有用的结论。对于 L 积分 性质的学习，要注意分清哪些只需积分有意义就成立，哪些必须函数可 积才成立。
3、函数列积分的极限定理理论上很重要，是全章的重点之一。注意 掌握几个定理各自的特点、条件、结论和相互联系，会用于解决问题。
[ ] a , b 积分区域， f (x) 是被积函数。
{ } 集） 记 T =maxΔxi 称为分割 T 的纯度或模。 1≤i≤n
的分
割
L 积分
设 E ⊂ Rn 是一个非空可测集，如果
n
E = U Ei ，其中各 Ei 为互不相交的非空 i=1
{ } 可测集，则称有限集 D = Ei 是 E 的一个
{ } 可测分割。设 D' = En' 是 E 的另一分割
积分的绝对连续性是 L-积分的重要特征，在连续函数平均逼近定理、 可测函数列控制收敛定理、L 积分中牛顿—莱布尼兹公式的推广应用等 很多重要定理的证明中都用到此性质。
⑵ L 积分的绝对可积性：
f (x) L 可积的充分必要条件为 f (x) L 可积。
134
由此，对于 L 积分可积亦绝对可积。这一特性与 R 积分有所不同。
R 积分的可积性可能依赖于被积函数的正负值相消；而 L 积分主要依靠 f
的绝对值受到一定的“控制”，当 f < g ，无论 f 如何复杂，若 g 可积，
则 f 必定可积。由此，显示了 L 积分较 R 积分的优越性；并说明 L 积分
可以看成 R 定积分的推广，但不是 R 广义积分的推广。
⑶ 变上限积分函数的绝对连续性：
130
收敛定理是 L 积分的重要结论；L 积分的绝对连续性是 L 积分的重要特 征，很多问题的证明用此性质；可测函数可以用连续函数平均逼近、零 测度集不影响函数的可积性及积分值等等是很有用的结论。对于 L 积分 性质的学习，要注意分清哪些只需积分有意义就成立，哪些必须函数可 积才成立。
3、函数列积分的极限定理理论上很重要，是全章的重点之一。注意 掌握几个定理各自的特点、条件、结论和相互联系，会用于解决问题。
[ ] a , b 积分区域， f (x) 是被积函数。