中档解答题专项训练(二)

合集下载

高中数学三角函数专项训练(含答案)

高中数学三角函数专项训练(含答案)一、填空题1．如图，在ABC 中，1cos 3BAC ∠=-，2AC =，D 是边BC 上的点，且2BD DC =，AD DC =，则AB 等于______.2．如图，在矩形ABCD 中，AB a ，2BC a =，点E 为AD 的中点，将△ABE 沿BE 翻折到△A BE '的位置，在翻折过程中，A '不在平面BCDE 内时，记二面角A DC B '--的平面角为α，则当α最大时，cos α的值为______．3．三棱锥P ABC -中，PA ⊥平面ABC ，直线PB 与平面ABC 所成角的大小为30，23AB =60ACB ∠=︒，则三棱锥P ABC -的外接球的表面积为________．4．已知函数23tan ,,,2332()63233,,33x x f x x ππππππ⎧⎛⎤⎛⎫∈-⋃ ⎪⎪⎥⎝⎦⎝⎭⎪=⎨⎛⎤⎪+∈ ⎥⎪⎝⎦⎩若()f x 在区间D 上的最大值存在，记该最大值为{}K D ，则满足等式{[0,)}3{[,2]}K a K a a =⋅的实数a 的取值集合是___________. 5．在长方体1111ABCD A B C D -中，13AB =，5AD =，112AA =，过点A 且与直线CD 平行的平面α将长方体分成两部分.现同时将两个球分别放入这两部分几何体内，则在平面α变化的过程中，这两个球的半径之和的最大值为___________.6．平行六面体1111ABCD A B C D -的各棱长均相等，1160BAD DAA A AB ∠=∠=∠=，直线1AC ⋂平面1A BD E =，则异面直线1D E 与AD 所成角的余弦值为_________.7．在锐角△ABC 的内角A ，B ，C 的对边分别为a ，b ，c ,若2cos b a a C -=，则ac的取值范围是______．8．在ABC 中，sin 2sin B C =，2BC =.则CA CB ⋅的取值范围为___________.（结果用区间表示）9．已知ABC 为等边三角形，点G 是ABC 的重心．过点G 的直线l 与线段AB 交于点D ，与线段AC 交于点E ．设AD AB λ=，AE AC μ=，则11λμ+=__________；ADE 与ABC 周长之比的取值范围为__________．10．在平面直角坐标系xOy 中，已知直线2y x =+与x 轴，y 轴分别交于M ，N 两点，点P 在圆22()2x a y -+=上运动.若MPN ∠恒为锐角，则实数a 的取值范围是________.二、单选题11．已知函数()()2212sin 2,2212,x a x af x x a x a x a π⎧⎡⎤⎛⎫-+<⎪ ⎪⎢⎥=⎝⎭⎨⎣⎦⎪-+++≥⎩，若函数()f x 在[)0,∞+内恰有5个零点，则a 的取值范围是（） A ．75,42⎛⎫ ⎪⎝⎭B ．7,24⎛⎫ ⎪⎝⎭C ．75,2,342⎛⎫⎛⎫⋃ ⎪ ⎪⎝⎭⎝⎭D ．75,22,42⎛⎫⎛⎫⋃ ⎪ ⎪⎝⎭⎝⎭12．函数()()sin 04f x x πωω⎛⎫=+> ⎪⎝⎭在7,44ππ⎛⎫⎪⎝⎭内恰有两个最小值点，则ω的范围是（） A ．13,47⎛⎤⎥⎝⎦B ．13,37⎛⎤ ⎥⎝⎦C ．4,33⎛⎤ ⎥⎝⎦D ．4,43⎛⎤ ⎥⎝⎦13．已知无穷项实数列{}n a 满足： 1a t =，且 14111n n n a a a +=--，则（） A ．存在1t >，使得20111a a = B ．存在0t <，使得20211a a =C ．若2211a a =，则21a a =D ．至少有2021个不同的t ，使得20211a a = 14．已知ABC 的内角分别为,,A B C，2cos 12A A =，且ABC 的内切圆面积为π，则AB AC ⋅的最小值为（） A ．6B ．8C ．10D ．1215．已知,a b Z ∈，满足)sin 50a b ︒=，则a b +的值为（）A ．1B ．2C ．3D ．416．如图所示，已知△ABC ，D 是AB 的中点，沿直线CD 将△ACD 翻折成△ACD '，所成二面角A CD B '--的平面角为α，则（）A ．A DB α'∠≤ B ．A DB α'∠≥C ．A CB α∠'≤D ．A CB α'∠≥17．已知函数()()sin f x x ωφ=+π0,02ωφ⎛⎫><< ⎪⎝⎭在π5π,88⎛⎫ ⎪⎝⎭上单调，且π3π088f f ⎛⎫⎛⎫-== ⎪ ⎪⎝⎭⎝⎭，则π2f ⎛⎫⎪⎝⎭的值为（） A 2B ．1 C ．1- D ．218．已知函数()()3log 911x f x x+=-，下列说法正确的是（）A ．()f x 既不是奇函数也不是偶函数B ．()f x 的图象与sin y x =有无数个交点C ．()f x 的图象与2y =只有一个交点D ．()()21f f -<-19．已知直线1y x =+上有两点1122(,),(,)A a b B a b ，且12a a >.已知1122,,,a b a b 满足12122||a a b b +22221122a b a b ++||23AB =，则这样的点A 个数为（）A ．1B ．2C ．3D ．420．设函数()sin cos f x a x b x ωω=+()0ω>在区间,62ππ⎡⎤⎢⎥⎣⎦上单调，且2236f f f πππ⎛⎫⎛⎫⎛⎫==- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，当12x π=时，()f x 取到最大值4，若将函数()f x 的图象上各点的横坐标伸长为原来的2倍得到函数()g x 的图象，则函数()3y g x x π=+为（） A ．4B ．5C ．6D ．7三、解答题21．如图，湖中有一个半径为1千米的圆形小岛，岸边点A 与小岛圆心C 相距3千米，为方便游人到小岛观光，从点A 向小岛建三段栈道AB ，BD ，BE ，湖面上的点B 在线段AC 上，且BD ，BE 均与圆C 相切，切点分别为D ，E ，其中栈道AB ，BD ，BE 和小岛在同一个平面上.沿圆C 的优弧（圆C 上实线部分）上再修建栈道DE .记CBD ∠为θ.()1用θ表示栈道的总长度()f θ，并确定sin θ的取值范围；()2求当θ为何值时，栈道总长度最短.22．已知函数 f （x ）＝a （|sin x |+|cos x |）﹣sin2x ﹣1，a ∈R ．（1）写出函数 f （x ）的最小正周期（不必写出过程）；（2）求函数 f （x ）的最大值；（3）当a ＝1时，若函数 f （x ）在区间（0，k π）（k ∈N*）上恰有2015个零点，求k 的值． 23．已知()3,sin a x ω=，1,2cos 3b x πω⎛⎫⎛⎫=+ ⎪ ⎪⎝⎭⎝⎭，其中0>ω，()f x a b =⋅，且函数()f x 在12x π=处取得最大值.（1）求ω的最小值，并求出此时函数()f x 的解析式和最小正周期；（2）在(1)的条件下，先将()y f x =的图像上的所有点向右平移4π个单位，再把所得图像上所有点的横坐标伸长为原来的2倍(纵坐标不变)，然后将所得图像上所有的点向下平移y g x 的图像.若在区间5,33ππ⎡⎤⎢⎥⎣⎦上，方程()210g x a +-=有两个不相等的实数根，求实数a 的取值范围；（3）在(1)的条件下，已知点P 是函数()y h x =图像上的任意一点，点Q 为函数()y f x =图像上的一点，点,6A π⎛ ⎝⎭，且满足12OP OQ OA =+，求()104h x +≥的解集.24．已知函数()()()()2cos +2cos 02f x x x x πϕϕϕϕ⎛⎫=+++<< ⎪⎝⎭.（1）求()f x 的最小正周期；（2）若13f π⎛⎫= ⎪⎝⎭，求当()2f x =时自变量x 的取值集合.25．已知函数()cos s co )f x x x x =-. （1）求()f x 的最小正周期及对称中心；（2）若将函数()y f x =的图象向左平移m 个单位所得图象关于y 轴对称，求m 的最小正值.26．已知函数22cos 3sin 2f xxx a 的最小值为0.(1)求a 的值及函数()y f x =图象的对称中心；(2)若关于x 的方程()0f x m -=在区间70,6π⎡⎤⎢⎥⎣⎦上有三个不相等的实数根1x ，2x ，3x ，求m的取值范围及()123tan 2x x x ++的值.27．对于函数()f x ，若存在定义域中的实数a ，b 满足0b a >>且()()2()02a bf a f b f +==≠，则称函数()f x 为“M 类” 函数. （1）试判断()sin f x x =，x ∈R 是否是“M 类” 函数，并说明理由；（2）若函数()2|log 1|f x x =-，()0,x n ∈，*n N ∈为“M 类” 函数，求n 的最小值. 28．将函数()4sin cos 6g x x x π⎛⎫=+ ⎪⎝⎭的图象向左平移02πϕϕ⎛⎫<≤ ⎪⎝⎭个单位长度后得到()f x 的图象.（1）若()f x 为偶函数，求ϕ；（2）若()f x 在7,6ππ⎛⎫ ⎪⎝⎭上是单调函数，求ϕ的取值范围.29．已知(1,sin )a x =，(1,cos )b x =，(0,1)e =，且(cos sin )x x -∈. （1）若()//a e b +，求sin cos x x 的值；（2）设()()f x a b me a b =⋅+⋅-，m R ∈，若()f x 的最大值为12-，求实数m 的值.30．函数()sin()f x A x ωϕ=+（其中0,0,||2A πωϕ>><）的部分图象如图所示，把函数()f x 的图像向右平移4π个单位长度，再向下平移1个单位，得到函数()g x 的图像.（1）当17,424x ππ⎡⎤∈⎢⎥⎣⎦时，求()g x 的值域（2）令()=()3F x f x -，若对任意x 都有2()(2)()20F x m F x m -+++≤恒成立，求m 的最大值【参考答案】一、填空题 1．32253．20π 4．47,912ππ⎧⎫⎨⎬⎩⎭ 5．16538 6．567．32⎝⎭8．8,83⎛⎫ ⎪⎝⎭9． 3 213,32⎡⎢⎣⎦10．71a 或4a二、单选题11．D 12．B 13．D 14．A 15．B 16．B 17．D 18．C 19．D 20．D 三、解答题21．()1()1232sin tan f θπθθθ=-+++，1sin ,13θ⎡⎫∈⎪⎢⎣⎭；()2当3πθ=时，栈道总长度最短.【解析】()1连CD ，CE ，由切线长定理知：1tan tan CD BE BD θθ===，1sin sin CD BC θθ==，130sin AB AC BC θ=-=-≥，1sin 3θ≥，即01sin 3θ=，00,2πθ⎛⎫∈ ⎪⎝⎭，则()1232sin tan f θπθθθ=-+++，0,2πθθ⎡⎫∈⎪⎢⎣⎭，进而确定sin θ的取值范围； ()2根据()12cos 23sin f θθθπθ-=-++求导得()()2cos 2cos 1sin f θθθθ--'=，利用增减性算出()min 533f πθ=+，进而求θ得取值. 【详解】解：()1连CD ，CE ，由切线长定理知：1tan tan CD BE BD θθ===，1sin sin CD BC θθ==， CBE CBD θ∠=∠=，又CD BD ⊥，CE BE ⊥，故2DCE πθ∠=-，则劣弧DE 的长为2πθ-，因此，优弧DE 的长为2πθ+，又3AC =，故130sin AB AC BC θ=-=-≥，1sin 3θ≥，即01sin 3θ=，00,2πθ⎛⎫∈ ⎪⎝⎭，所以，()1232sin tan f θπθθθ=-+++，0,2πθθ⎡⎫∈⎪⎢⎣⎭，则1sin ,13θ⎡⎫∈⎪⎢⎣⎭； ()2()12cos 23sin f θθθπθ-=-++，0,2πθθ⎡⎫∈⎪⎢⎣⎭，其中01sin 3θ=，00,2πθ⎛⎫∈ ⎪⎝⎭，()()2cos 2cos 1sin f θθθθ--'=故3θ=时，()min 33f θ=+ 所以当3πθ=时，栈道总长度最短.【点睛】本题主要考查导数在函数当中的应用，属于中档题. 22．（1）最小正周期为π．（2）见解析（3）k ＝1008．【解析】（1）由题意结合周期函数的定义直接求解即可；（2）令t ，t ∈[1，则当0,2x π⎡⎤∈⎢⎥⎣⎦时，()()2f x t at t μ==-，当,2x π⎛⎤∈π ⎥⎝⎦时，()()22f x v t t at ==+-，易知()()t v t μ≤，分类比较()1v 、v的大小即可得解；（3）转化条件得当且仅当sin2x ＝0时，f （x ）＝0，则x ∈（0，π]时，f （x ）有且仅有两个零点，结合函数的周期即可得解. 【详解】（1）函数 f （x ）的最小正周期为π．（2）∵f （x ）＝a （|sin x |+|cos x |）﹣sin2x ﹣1＝sin2x ﹣1＝（sin2x +1），令t =t ∈[1]，当0,2x π⎡⎤∈⎢⎥⎣⎦时，()()(21f x t at t t μ==-≤≤，当,2x π⎛⎤∈π ⎥⎝⎦时，()()(221f x v t t at t ==+-≤≤，∵()()()2222220t v t at t t at t μ-=--+-=-+≤即()()t v t μ≤.∴()()(){}max max max 1,f x v t v v ==，∵()11v a =-，v，∴当1a ≤-()f x 最大值为1a -；当1a >-()f x .（3）当a ＝1时，f （x ）sin 21x -，若f （x ）＝0sin 21x =+即22sin 22sin 2sin x x x =+，∴当且仅当sin2x ＝0时，f （x ）＝0，∴x ∈（0，π]时，f （x ）有且仅有两个零点分别为2π，π， ∴2015＝2×1007+1， ∴k ＝1008．【点睛】本题考查了三角函数的综合问题，考查了分类讨论思想和转化化归思想，属于难题.23．（1）ω的最小值为1，()sin 23f x x π⎛⎫=+ ⎪⎝⎭，T π=，（2）104a <≤（3）原不等式的解集为3,22428k k xx k Z ππππ⎧⎫+≤≤+∈⎨⎬⎩⎭【解析】【分析】（1）先将()f x 化成正弦型，然后利用()f x 在12x π=处取得最大值求出ω，然后即可得到()f x 的解析式和周期（2）先根据图象的变换得到()sin 6x y g x π⎛⎫-= ⎝=⎪⎭，然后画出()g x 在区间5,33ππ⎡⎤⎢⎥⎣⎦上的图象，条件转化为()g x 的图象与直线12y a =-有两个交点即可（3）利用坐标的对应关系式，求出()h x 的函数的关系式，进一步利用三角不等式的应用求出结果．【详解】（1）因为()3,sin a x ω=，1,2cos 3b x πω⎛⎫⎛⎫=+ ⎪ ⎪⎝⎭⎝⎭所以()32sin cos 3f x a b x x πωω⎛⎫=⋅=++ ⎪⎝⎭212sin cos sin cos 2x x x x x x ωωωωωω⎛⎫== ⎪ ⎪⎝⎭11cos 21sin 2sin 22222x x x x ωωωω-=+=+sin 23x πω⎛⎫=+ ⎪⎝⎭因为()f x 在12x π=处取得最大值.所以22,1232k k Z πππωπ⨯+=+∈，即121,k k Z ω=+∈当0k =时ω的最小值为1此时()sin 23f x x π⎛⎫=+ ⎪⎝⎭，T π=（2）将()y f x =的图像上的所有的点向右平移4π个单位得到的函数为33sin 2sin 243262y x x πππ⎛⎫⎛⎫⎛⎫=-++=-+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，再把所得图像上所有的点的横坐标伸长为原来的2倍(纵坐标不变)得到的函数为3sin 62y x π⎛⎫=-+ ⎪⎝⎭，然后将所得图像上所有的点向下平移32个单位，得到函数()sin 6x y g x π⎛⎫-= ⎝=⎪⎭()sin 6g x x π⎛⎫=- ⎪⎝⎭在区间5,33ππ⎡⎤⎢⎥⎣⎦上的图象为：方程()210g x a +-=有两个不相等的实数根等价于()g x 的图象与直线12y a =-有两个交点所以11212a ≤-<，解得104a <≤（3）设(),P x y ，()00,Q x y因为点3,6A π⎛ ⎝⎭，且满足12OP OQ OA =+ 所以00126132x x y y π⎧=+⎪⎪⎨⎪=⎪⎩002332x x y y π⎧=-⎪⎪⎨⎪=⎪⎩因为点()00,Q x y 为函数()y f x =图像上的一点所以332sin 2233y x ππ⎛⎫⎛⎫=-+ ⎪ ⎪⎝⎭⎝⎭即1()sin 423y h x x π⎛⎫==- ⎪⎝⎭因为()104h x +≥，所以1sin 432x π⎛⎫-≥- ⎪⎝⎭所以7242,636k x k k Z πππππ-≤-≤+∈所以3,22428k k x k Z ππππ+≤≤+∈ 所以原不等式的解集为3,22428k k xx k Z ππππ⎧⎫+≤≤+∈⎨⎬⎩⎭【点睛】本题考查的知识要点：三角函数关系式的变换，正弦型函数的性质的应用，平面向量的数量积的应用，三角不等式的解法及应用，主要考查学生的运算能力和转换能力，属于中档题．24．（1）π；（2）12x x k ππ⎧=-+⎨⎩或()4x k k Z ππ⎫=+∈⎬⎭【解析】【分析】（1）由辅助角公式可得()f x 2sin 2216x πϕ⎛⎫=+++ ⎪⎝⎭，再求周期即可；（2）由13f π⎛⎫= ⎪⎝⎭求出12πϕ=，再解方程2sin 2123x π⎛⎫++= ⎪⎝⎭即可.【详解】解：（1）()()()()2cos 2cos f x x x x ϕϕϕ=++++()()2cos21x x ϕϕ=++++2sin 2216x πϕ⎛⎫=+++ ⎪⎝⎭，则()f x 的最小正周期为2T ππω==.（2）因为13f π⎛⎫= ⎪⎝⎭，所以2sin 221136ππϕ⎛⎫⨯+++= ⎪⎝⎭，即()526k k Z πϕπ+=∈，解得()5212k k Z ππϕ=-∈. 因为02πϕ<<，所以12πϕ=.因为()2f x =，所以2sin 2123x π⎛⎫++= ⎪⎝⎭，即1sin 232x π⎛⎫+= ⎪⎝⎭，则2236x k πππ+=+或()52236x k k Z πππ+=+∈，解得12x k ππ=-+或()4x k k Z ππ=+∈.故当()2f x =时，自变量x 的取值集合为12x x k ππ⎧=-+⎨⎩或()4x k k Z ππ⎫=+∈⎬⎭.【点睛】本题考查了三角恒等变换，重点考查了解三角方程，属中档题. 25．（1）π，1,()2122k k Z ππ⎛⎫+-∈⎪⎝⎭；（2）3π 【解析】【分析】（1）直接利用三角函数关系式的变换，把函数的关系式变形成正弦型函数，进一步求出函数的周期和对称中心.（2）利用（1）的关系式，利用整体思想的应用对函数的关系式进行平移变换和对称性的应用求出最小值. 【详解】（1）因为2()cos cos )cos cos f x x x x x x x =-=-1cos 212sin 2262x x x π+⎛⎫=-=-- ⎪⎝⎭，所以最小正周期为22T ππ==，由正弦函数的对称中心知26x k ππ-=，解得212k x ππ=+，k Z ∈，所以对称中心为1,()2122k k Z ππ⎛⎫+-∈⎪⎝⎭；（2）()y f x =的图象向左平移m 个单位所得解析式是1sin 2262y x m π⎛⎫=+-- ⎪⎝⎭，因为其图象关于y 轴对称，所以262m k πππ-=+，k Z ∈，解得23k m ππ=+，k Z ∈，所以m 的最小正值是3π. 【点睛】本题考查的知识要点：三角函数关系式的恒等变换，正弦型函数的性质的应用，主要考查学生的运算能力和转换能力及思维能力，属于基础题型.26．(1)1，,2212k ππ⎛⎫- ⎪⎝⎭，k Z ∈；(2)[)3,4，【解析】（1）由题得()2sin 216f x x a π⎛⎫=+++ ⎪⎝⎭，求出a 的值即得函数()y f x =图象的对称中心；（2）作出函数()y f x =在70,6x π⎡⎤∈⎢⎥⎣⎦上的大致图象，求出123523x x x π++=即得解.【详解】(1)()cos 2212sin 216x x a x a f x π⎛⎫=++=+++ ⎪⎝⎭，由已知可得()2110a ⨯-++=，∴1a =，()2sin 226f x x π⎛⎫=++ ⎪⎝⎭，令26x k ππ+=可得()y f x =图象的对称中心为,2212k ππ⎛⎫- ⎪⎝⎭，k Z ∈. (2)()y f x =在70,6x π⎡⎤∈⎢⎥⎣⎦上的大致图象如图所示，由图可得[)3,4m ∈，所以123x x π+=，2343x x π+=，所以123523x x x π++=，所以()1235tan 2tan33x x x π++==-.【点睛】本题主要考查三角恒等变换和三角函数的图象和性质，考查三角函数图象的综合应用，意在考查学生对这些知识的理解掌握水平和分析推理能力. 27．（1）不是.见解析（2）最小值为7. 【解析】（1）不是，假设()f x 为M 类函数，得到2b a k π=+或者2b a k ππ+=+，代入验证不成立.（2）()221log ,02log 1,2x x f x x x -<≤⎧=⎨->⎩，得到函数的单调区间，根据题意得到326480b b b ---=，得到()6,7b ∈，得到答案. 【详解】（1）不是.假设()f x 为M 类函数，则存在0b a >>，使得sin sin a b =，则2b a k π=+，k Z ∈或者2b a k ππ+=+，k Z ∈，由sin 2sin2a ba +=，当2b a k π=+，k Z ∈时，有()sin 2sin a a k π=+，k Z ∈，所以sin 2sin a a =±，可得sin 0a =，不成立；当2b a k ππ+=+，k Z ∈时，有sin 2sin()2a k ππ=+，k Z ∈，所以sin 2a =±，不成立，所以()f x 不为M 类函数.（2）()221log ,02log 1,2x x f x x x -<≤⎧=⎨->⎩，则()f x 在()0,2单调递减，在()2,+∞单调递增，又因为()f x 是M 类函数，所以存在02a b <<<，满足2221log log 12|log 1|2a ba b +-=-=-，由等式可得：()2log 2ab =，则4ab =，所以()22142(4)0222a a b a a a -+-=+-=>，则2log 102a b +->，所以得22log 12log 12a b b +⎛⎫-=- ⎪⎝⎭，从而有222log 1log 2a b b +⎛⎫+= ⎪⎝⎭，则有()224a b b +=，即248b b b ⎛⎫+= ⎪⎝⎭，所以43288160b b b -++=，则()()3226480b b b b ----=，由2b >，则326480b b b ---=，令()32648g x x x x =---，当26x <<时，()()26480g x x x x =---<，且()6320g =-<，()7130g =>，且()g x 连续不断，由零点存在性定理可得存在()6,7b ∈，使得()0g b =，此时()0,2a ∈，因此n 的最小值为7. 【点睛】本题考查了函数的新定义问题，意在考查学生对于函数的理解能力和应用能力. 28．（1）6π=ϕ；（2）,62ππϕ⎡⎤∈⎢⎥⎣⎦【解析】【分析】（1）根据三角恒等变换对()4sin cos 6g x x x π⎛⎫=+ ⎪⎝⎭化简变形为()2sin 216g x x π⎛⎫=+- ⎪⎝⎭，然后可得到图象左移之后的函数()2sin 2216f x x ϕπ⎛⎫=++- ⎪⎝⎭，利用三角函数偶函数的性质即可求出ϕ；（2）先求出2222,22662x πππϕπϕπϕ⎛⎫++∈++++ ⎪⎝⎭，再根据ϕ的范围求出26πϕ+和22πϕ+的范围，从而根据单调性列出关于ϕ的不等式，解之即可求得结果. 【详解】（1）()()14sin sin 21cos 22g x x x x x x ⎫=-=--⎪⎪⎝⎭2sin 216x π⎛⎫=+- ⎪⎝⎭，∴()2sin 2216f x x ϕπ⎛⎫=++- ⎪⎝⎭.又()f x 为偶函数，则()262k k Z ππϕπ+=+∈，02πϕ<≤，∴6π=ϕ；（2）7,6x ππ⎛⎫∈ ⎪⎝⎭，∴2222,22662x πππϕπϕπϕ⎛⎫++∈++++⎪⎝⎭.02πϕ<≤，∴72,666πππϕ⎛⎫+∈ ⎪⎝⎭，32,222πππϕ⎛⎫+∈ ⎪⎝⎭()f x 在7,6ππ⎛⎫ ⎪⎝⎭是单调函数，∴26202ππϕπϕ⎧+≥⎪⎪⎨⎪<≤⎪⎩， ∴,62ππϕ⎡⎤∈⎢⎥⎣⎦.【点睛】本题考查三角恒等变换、三角函数的图象变换及性质，以及基本的运算能力和逻辑推理能能力，综合性较强，属于有一定难度的中档题. 29．(1)0 (2)32【解析】【分析】（1）通过()//a e b +可以算出()(1,sin 1)//1,cos cos sin 1x x x x +⇒=+，移项、两边平方即可算出结果.（2）通过向量的运算，解出()()f x a b me a b =⋅+⋅-，再通过最大值根的分布，求出m 的值. 【详解】（1）通过()//a e b +可以算出()(1,sin 1)//1,cos cos sin 1x x x x +⇒=+，即2cos sin 1(cos sin )112sin cos 1sin cos 0x x x x x x x x -=⇒-=⇒-=⇒= 故答案为0.（2）()1sin cos (sin cos )f x x x m x x =++-，设()cos sin x x t t ⎡-=∈⎣，22112sin cos sin cos 2t x x t x x --=⇒=，22113()()1222t g t f x mt t mt -==+-=--+，即213(),22g t t mt t ⎡=--+∈⎣的最大值为12-； ①当11m m -≤⇒≥-时，max 1313()(1)2222g x g m m ==--+=-⇒=（满足条件）；②当11m m <-≤⇒<-时，222max 1311()()22222g x g m m m m =-=-++=-⇒=-（舍）；③当m m -><max 131()2222g x g m ==-⨯-=-⇒=故答案为32m = 【点睛】当式子中同时出现sin cos ,sin cos ,sin cos x x x x x x +-时，常常可以利用换元法，把sin cos x x 用sin cos ,sin cos x x x x +-进行表示，但计算过程中也要注意自变量的取值范围；二次函数最值一定要注意对称轴是否在规定区间范围内，再讨论最后的结果.30．（1）1,0⎡⎤⎢⎥⎣⎦（2）265- 【解析】【分析】（1）根据图象的最低点求得A 的值，根据四分之一周期求得ω的值，根据点7,112π⎛⎫- ⎪⎝⎭求得ϕ的值，由此求得函数()f x 的解析式，进而根据图象平移变换求得()g x 的解析式，并由此求得17,424x ππ⎡⎤∈⎢⎥⎣⎦时()g x 的值域.（2）先求得()f x 的值域，由此求得()F x 的值域.令()[4,2]t F x =∈--对题目所给不等式换元，根据二次函数的性质列不等式组，解不等式组求得m 的取值范围，由此求得m 的最大值. 【详解】（1）根据图象可知171,4123A T ππ==- 2,2,()sin(2)T f x x Tππωϕ∴=∴===+ 代入7,112π⎛⎫-⎪⎝⎭得，7sin 1,2,63k k Z ππϕϕπ⎛⎫+=-=+∈ ⎪⎝⎭， ||,0,23k ππϕϕ<∴==()sin 23f x x π⎛⎫∴=+ ⎪⎝⎭把函数()f x 的图像向右平移4π个单位长度，再向下平移1个单位，得到函数()g x ()sin 21sin 21436g x x x πππ⎛⎫⎛⎫⎛⎫∴=-+-=-- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，设26t x π=-，则5,34t ππ⎡⎤∈⎢⎥⎣⎦，此时sin t ⎡⎤∈⎢⎥⎣⎦，所以值域为1,0⎡⎤⎢⎥⎣⎦. （2）由（1）可知()sin 2[1,1]3f x x π⎛⎫=+∈- ⎪⎝⎭()()3[4,2]F x f x =-∈--对任意x 都有2()(2)()20F x m F x m -+++≤恒成立令()[4,2]t F x =∈--，2()(2)2h t t m t m =-+++，是关于t 的二次函数，开口向上则max ()0h t ≤恒成立而()h t 的最大值，在4t =-或2t =-时取到最大值则(2)0(4)0h h -≤⎧⎨-≤⎩，4(2)(2)2016(2)(4)20m m m m -+-++≤⎧⎨-+-++≤⎩，解得103265m m ⎧≤-⎪⎪⎨⎪≤-⎪⎩所以265m ≤-，则m 的最大值为265-. 【点睛】本小题主要考查由三角函数图像求三角函数的解析式，考查三角函数图像变换，考查不等式恒成立问题，考查化归与转化的数学思想方法，属于中档题.。

高中数学解析几何压轴题专项拔高训练(二)

高中数学解析几何压轴题专项拔高训练一．选择题（共15小题）1．已知倾斜角α≠0的直线l过椭圆（a＞b＞0）的右焦点交椭圆于A、B两点，P为右准线上任意一点，则∠APB为（）A．钝角B．直角C．锐角D．都有可能考点：直线与圆锥曲线的综合问题．专题：压轴题．分析：根据题设条件推导出以AB为直径的圆与右准线相离．由此可知∠APB为锐角．解答：解：如图，设M为AB的中点，过点M作MM1垂直于准线于点M1，分别过A、B作AA1、BB1垂直于准线于A1、B1两点．则∴以AB为直径的圆与右准线相离．∴∠APB为锐角．点评：本题考查圆锥曲线的性质和应用，解题时作出图形，数形结合，往往能收到事半功倍之效果．2．已知双曲线（a＞0，b＞0）的右焦点为F，右准线为l，一直线交双曲线于P．Q两点，交l于R点．则（）A．∠PFR＞∠QFR B．∠PFR=∠QFRC．∠PFR＜∠QFR D．∠PFR与∠AFR的大小不确定考点：直线与圆锥曲线的综合问题．专题：计算题；压轴题．分析：设Q、P到l 的距离分别为d1，d2，垂足分别为M，N，则PN∥MQ，=，又由双曲线第二定义可知，由此能够推导出RF是∠PFQ的角平分线，所以∠PFR=∠QFR．解答：解：设Q、P到l 的距离分别为d1，d2，垂足分别为M，N，则PN∥MQ，∴=，又由双曲线第二定义可知，∴，，∴，∴RF是∠PFQ的角平分线，∴∠PFR=∠QFR故选B．点评：本题考查双曲线的性质和应用，解题时利用双曲线第二定义综合平面几何知识求解．3．设椭圆的一个焦点为F，点P在y轴上，直线PF交椭圆于M、N，，则实数λ1+λ2=（）A．B．C．D．考点：直线与圆锥曲线的综合问题．专题：综合题；压轴题．分析：设直线l的斜率为k，则直线l的方程是y=k（x﹣c）．将直线l的方程代入到椭圆C的方程中，消去y并整理得（b2+a2k2）x2﹣2a2ck2x+a2c2k2﹣a2b2=0．然后利用向量关系及根与系数的关系，可求得λ1+λ2的值．解答：解：设M，N，P点的坐标分别为M（x1，y1），N（x2，y2），P（0，y0），又不妨设F点的坐标为（c，0）．显然直线l存在斜率，设直线l的斜率为k，则直线l的方程是y=k（x﹣c）．将直线l的方程代入到椭圆C的方程中，消去y并整理得（b2+a2k2）x2﹣2a2ck2x+a2c2k2﹣a2b2=0．∴，．又∵，将各点坐标代入得，=．故选C．点评：本题以向量为载体，考查直线与椭圆的位置关系，是椭圆性质的综合应用题，解题时要注意公式的合理选取和灵活运用．4．中心在原点，焦点在x轴上的双曲线C1的离心率为e，直线l与双曲线C1交于A，B两点，线段AB中点M在一象限且在抛物线y2=2px（p＞0）上，且M到抛物线焦点的距离为p，则l的斜率为（）A．B．e2﹣1 C．D．e2+1考点：圆锥曲线的综合．专题：综合题；压轴题；圆锥曲线的定义、性质与方程．分析：利用抛物线的定义，确定M的坐标，利用点差法将线段AB中点M的坐标代入，即可求得结论．解答：解：∵M在抛物线y2=2px（p＞0）上，且M到抛物线焦点的距离为p，∴M的横坐标为，∴M（，p）设双曲线方程为（a＞0，b＞0），A（x1，y1），B（x2，y2），则，两式相减，并将线段AB中点M的坐标代入，可得∴∴故选A．点评：本题考查双曲线与抛物线的综合，考查点差法的运用，考查学生的计算能力，属于中档题．5．已知P为椭圆上的一点，M，N分别为圆（x+3）2+y2=1和圆（x﹣3）2+y2=4上的点，则|PM|+|PN|的最小值为（）A．5B．7C．13 D．15考点：圆与圆锥曲线的综合；椭圆的简单性质．专题：计算题；压轴题．分析：由题意可得：椭圆的焦点分别是两圆（x+3）2+y2=1和（x﹣3）2+y2=4的圆心，再结合椭圆的定义与圆的有关性质可得答案．解答：解：依题意可得，椭圆的焦点分别是两圆（x+3）2+y2=1和（x﹣3）2+y2=4的圆心，所以根据椭圆的定义可得：（|PM|+|PN|）min=2×5﹣1﹣2=7，故选B．点评：本题考查圆的性质及其应用，以及椭圆的定义，解题时要认真审题，仔细解答，注意公式的合理运用．6．过双曲线﹣=0（b＞0，a＞0）的左焦点F（﹣c，0）（c＞0），作圆x2+y2=的切线，切点为E，延长FE 交双曲线右支于点P，若=（+），则双曲线的离心率为（）A．B．C．D．考点：圆与圆锥曲线的综合．专题：综合题；压轴题．分析：由=（+），知E为PF的中点，令右焦点为F′，则O为FF′的中点，则PF′=2OE=a，能推导出在Rt△PFF′中，PF2+PF′2=FF′2，由此能求出离心率．解答：解：∵若=（+），∴E为PF的中点，令右焦点为F′，则O为FF′的中点，则PF′=2OE=a，∵E为切点，∴OE⊥PF∴PF′⊥PF∵PF﹣PF′=2a∴PF=PF′+2a=3a在Rt△PFF′中，PF2+PF′2=FF′2即9a2+a2=4c2∴离心率e==．故选：A．点评：本题考查圆与圆锥曲线的综合运用，解题时要认真审题，仔细解答，注意挖掘题设中的隐含条件．7．设椭圆的左焦点为F，在x轴上F的右侧有一点A，以FA为直径的圆与椭圆在x轴上方部分交于M、N两点，则的值为（）A．B．C．D．考点：圆与圆锥曲线的综合．专题：计算题；压轴题．分析：若以FA为直径的圆与椭圆大x轴上方的部分交于短轴端点，则M、N重合（设为M），此时A为椭圆的右焦点，由此可知=，从而能够得到结果．解答：解：若以FA为直径的圆与椭圆大x轴上方的部分交于短轴端点，则M、N重合（设为M），此时A为椭圆的右焦点，则==．故选A．点评：本题考查圆锥曲线的性质和应用，解题时要注意合理地选取特殊点．8．已知定点A（1，0）和定直线l：x=﹣1，在l上有两动点E，F且满足，另有动点P，满足（O为坐标原点），且动点P的轨迹方程为（）A．y2=4x B．y2=4x（x≠0）C．y2=﹣4x D．y2=﹣4x（x≠0）考点：圆锥曲线的轨迹问题．专题：计算题；压轴题．分析：设P（x，y），欲动点P的轨迹方程，即寻找x，y之间的关系式，利用向量间的关系求出向量、的坐标后垂直条件即得动点P的轨迹方程．解答：解：设P（x，y），E（﹣1，y1），F（﹣1，y2）（y1，y2均不为零）由∥⇒y1=y，即E（﹣1，y）．由∥⇒．由y2=4x（x≠0）．故选B．点评：本题主要考查了轨迹方程的问题．本题解题的关键是利用了向量平行和垂直的坐标运算求得轨迹方程．9．已知抛物线过点A（﹣1，0），B（1，0），且以圆x2+y2=4的切线为准线，则抛物线的焦点的轨迹方程（）A．+=1（y≠0）B．+=1（y≠0）C．﹣=1（y≠0）D．﹣=1（y≠0）考点：圆锥曲线的轨迹问题．专题：综合题；压轴题．分析：设出切线方程，表示出圆心到切线的距离求得a和b的关系，再设出焦点坐标，根据抛物线的定义求得点A，B到准线的距离等于其到焦点的距离，然后两式平方后分别相加和相减，联立后，即可求得x和y的关系式．解答：解：设切线ax+by﹣1=0，则圆心到切线距离等于半径∴=2∴，∴a2+b2=设抛物线焦点为（x，y），根据抛物线定义可得平方相加得：x2+1+y2=4（a2+1）①平方相减得：x=4a，∴②把②代入①可得：x2+1+y2=4（+1）即：∵焦点不能与A，B共线∴y≠0∴∴抛物线的焦点轨迹方程为故选B．点评：本题以圆为载体，考查抛物线的定义，考查轨迹方程，解题时利用圆的切线性质，抛物线的定义是关键．10．如图，已知半圆的直径|AB|=20，l为半圆外一直线，且与BA的延长线交于点T，|AT|=4，半圆上相异两点M、N与直线l的距离|MP|、|NQ|满足条件，则|AM|+|AN|的值为（）A．22 B．20 C．18 D．16考点：圆与圆锥曲线的综合；抛物线的定义．专题：计算题；压轴题．分析：先以AT的中点O为坐标原点，AT的中垂线为y轴，可得半圆方程为（x﹣12）2+y2=100，根据条件得出M，N在以A为焦点，PT为准线的抛物线上，联立半圆方程和抛物线方程结合根与系数的关系，利用抛物线的定义即可求得答案．解答：解：以AT的中点O为坐标原点，AT的中垂线为y轴，可得半圆方程为（x﹣12）2+y2=100又，设M（x1，y1），N（x2，y2），M，N在以A为焦点，PT为准线的抛物线上；以AT的垂直平分线为y轴，TA方向为x轴建立坐标系，则有抛物线方程为y2=8x（y≥0），联立半圆方程和抛物线方程，消去y得：x2﹣16x+44=0∴x1+x2=16，|AM|+|AN|=|MP|+|NQ|=x1+x2+4=20．故选B．点评：本小题主要考查抛物线的定义、圆的方程、圆与圆锥曲线的综合等基础知识，考查运算求解能力，考查数形结合思想、化归与转化思想．属于基础题．11．椭圆与双曲线有公共的焦点F1，F2，P是两曲线的一个交点，则cos∠F1PF2=（）A．B．C．D．考点：圆锥曲线的共同特征．专题：综合题；压轴题；圆锥曲线的定义、性质与方程．分析：利用双曲线、椭圆的定义，建立方程，求出|PF1|=，|PF2|=，再利用余弦定理，即可求得结论．解答：解：不妨令P在双曲线的右支上，由双曲线的定义|PF1|﹣|PF2|=2①由椭圆的定义|PF1|+|PF2|=2②由①②可得|PF1|=，|PF2|=∵|F1F2|=4∴cos∠F1PF2==故选A．点评：本题考查圆锥曲线的共同特征，利用双曲线、椭圆的定义，建立方程是关键．12．曲线（|x|≤2）与直线y=k（x﹣2）+4有两个交点时，实数k的取值范围是（）C．D．A．B．（，+∞）考点：直线与圆锥曲线的关系．专题：计算题；压轴题．分析：如图，求出BC的斜率，根据圆心到切线的距离等于半径，求得切线BE的斜率k′，由题意可知，k′＜k≤K BC，从而得到实数k的取值范围．解答：解：曲线即x2+（y﹣1）2=4，（y≥1），表示以A（0，1）为圆心，以2为半径的圆位于直线y=1 上方的部分（包含圆与直线y=1 的交点C和D），是一个半圆，如图：直线y=k（x﹣2）+4过定点B（2，4），设半圆的切线BE的切点为E，则BC的斜率为K BC==．设切线BE的斜率为k′，k′＞0，则切线BE的方程为y﹣4=k′（x﹣2），根据圆心A到线BE距离等于半径得2=，k′=，由题意可得k′＜k≤K BC，∴＜k≤，故选A．点评：本题考查直线和圆的位置关系，点到直线的距离公式，倾斜角和斜率的关系，体现了数形结合的数学思想，判断k′＜k≤K BC，是解题的关键．13．设抛物线y2=12x的焦点为F，经过点P（1，0）的直线l与抛物线交于A，B两点，且，则|AF|+|BF|=（）A．B．C．8D．考点：直线与圆锥曲线的关系．专题：计算题；压轴题．分析：根据向量关系，用坐标进行表示，求出点A，B的坐标，再利用抛物线的定义，可求|AF|+|BF|．解答：解：设A（x1，y1），B（x2，y2），则∵P（1，0）∴=（1﹣x2，﹣y2），=（x1﹣1，y1）∵，∴2（1﹣x2，﹣y2）=（x1﹣1，y1）∴将A（x1，y1），B（x2，y2）代入抛物线y2=12x，可得，又∵﹣2y2=y1∴4x2=x1又∵x1+2x2=3解得∵|AF|+|BF|=故选D．点评：本题重点考查抛物线的定义，考查向量知识的运用，解题的关键是确定点A，B的横坐标．14．已知双曲线上的一点到其左、右焦点的距离之差为4，若已知抛物线y=ax2上的两点A（x1，y1），B（x2，y2）关于直线y=x+m对称，且，则m的值为（）A．B．C．D．考点：直线与圆锥曲线的关系．专题：综合题；压轴题．分析：y1=2x12，y2=2x22，A点坐标是（x1，2x12），B点坐标是（x2，2x22）A，B的中点坐标是（，）因为A，B关于直线y=x+m对称，所以A，B的中点在直线上，且AB与直线垂直=+m，由此能求得m．解答：解：y1=2x12，y2=2x22，A点坐标是（x1，2x12），B点坐标是（x2，2x22），A，B的中点坐标是（，），因为A，B关于直线y=x+m对称，所以A，B的中点在直线上，且AB与直线垂直=+m，，x12+x22═+m，x2+x1=﹣，因为，所以xx12+x22=（x1+x2）2﹣2x1x2=，代入得，求得m=．故选B．点评：本题主要考查直线与圆锥曲线的综合应用能力，具体涉及到轨迹方程的求法及直线与椭圆的相关知识，解题时要注意合理地进行等价转化．15．已知双曲线上存在两点M，N关于直线y=x+m对称，且MN的中点在抛物线y2=9x上，则实数m的值为（）A．4B．﹣4 C．0或4 D．0或﹣4考点：直线与圆锥曲线的关系．专题：综合题；压轴题．分析：根据双曲线上存在两点M，N关于直线y=x+m对称，求出MN中点P（﹣，m），利用MN的中点在抛物线y2=9x上，即可求得实数m的值．解答：解：∵MN关于y=x+m对称∴MN垂直直线y=x+m，MN的斜率﹣1，MN中点P（x0，x0+m）在y=x+m上，且在MN上设直线MN：y=﹣x+b，∵P在MN上，∴x0+m=﹣x0+b，∴b=2x0+m由消元可得：2x2+2bx﹣b2﹣3=0∴M x+N x=﹣b，∴x0=﹣，∴b=∴MN中点P（﹣，m）∵MN的中点在抛物线y2=9x上，∴∴m=0或4故选D．点评：本题考查直线与双曲线的位置关系，考查对称性，考查抛物线的标准方程，解题的关键是确定MN中点P 的坐标．二．解答题（共15小题）16．已知椭圆C：，F1，F2是其左右焦点，离心率为，且经过点（3，1）（1）求椭圆C的标准方程；（2）若A1，A2分别是椭圆长轴的左右端点，Q为椭圆上动点，设直线A1Q斜率为k，且，求直线A2Q斜率的取值范围；（3）若Q为椭圆上动点，求cos∠F1QF2的最小值．考点：椭圆的简单性质；椭圆的应用．专题：压轴题；圆锥曲线的定义、性质与方程．分析：（1）根据椭圆的离心率为，且经过点（3，1），求椭圆C的标准方程；（2）设A2Q的斜率为k'，Q（x0，y0），则可得kk'==，利用，即可求直线A2Q斜率的取值范围；（3）利用椭圆的定义、余弦定理，及基本不等式，即可求cos∠F1QF2的最小值．解答：解：（1）∵椭圆的离心率为，且经过点（3，1），建立方程，求出几何量，即可∴，∴椭圆C的标准方程为…（3分）（2）设A2Q的斜率为k'，Q（x0，y0），则，…（5分）∴kk'=及…（6分）则kk'==又…（7分）∴，故A2Q斜率的取值范围为（）…（8分）（3）设椭圆的半长轴长、半短轴长、半焦距分别为a，b，c，则有，由椭圆定义，有…（9分）∴cos∠F1QF2=…（10分）=…（11分）≥…（12分）==…（13分）∴cos∠F1QF2的最小值为．（当且仅当|QF1|=|QF2|时，即Q取椭圆上下顶点时，cos∠F1QF2取得最小值）…（14分）点评：本题考查椭圆的标准方程与几何性质，考查椭圆的定义，考查余弦定理，考查基本不等式的运用，综合性强．17．已知椭圆x2+=1的左、右两个顶点分别为A，B．双曲线C的方程为x2﹣=1．设点P在第一象限且在双曲线C上，直线AP与椭圆相交于另一点T．（Ⅰ）设P，T两点的横坐标分别为x1，x2，证明x1•x2=1；（Ⅱ）设△TAB与△POB（其中O为坐标原点）的面积分别为S1与S2，且•≤15，求S﹣S的取值范围．考点：直线与圆锥曲线的关系；平面向量数量积的运算．专题：压轴题；圆锥曲线的定义、性质与方程．分析：（Ⅰ）设直线AP的方程与椭圆方程联立，确定P、T的横坐标，即可证得结论；（Ⅱ）利用•≤15，结合点P是双曲线在第一象限内的一点，可得1＜x1≤2，利用三角形的面积公式求面积，从而可得S﹣S的不等式，利用换元法，再利用导数法，即可求S﹣S的取值范围．解答：（Ⅰ）证明：设点P（x1，y1）、T（x2，y2）（x i＞0，y i＞0，i=1，2），直线AP的斜率为k（k＞0），则直线AP的方程为y=k（x+1），代入椭圆方程，消去y，整理，得（4+k2）x2+2k2x+k2﹣4=0，解得x=﹣1或x=，故x2=．同理可得x1=．所以x1•x2=1．（Ⅱ）设点P（x1，y1）、T（x2，y2）（x i＞0，y i＞0，i=1，2），则=（﹣1﹣x1，y1），=（1﹣x1，y1）．因为•≤15，所以（﹣1﹣x1）（1﹣x1）+y12≤15，即x12+y12≤16．因为点P在双曲线上，所以，所以x12+4x12﹣4≤16，即x12≤4．因为点P是双曲线在第一象限内的一点，所以1＜x1≤2．因为S1=|y2|，S2=，所以S﹣S==由（Ⅰ）知，x1•x2=1，即．设t=，则1＜t≤4，S﹣S=5﹣t﹣．设f（t）=5﹣t﹣，则f′（t）=﹣1+=，当1＜t＜2时，f'（t）＞0，当2＜t≤4时，f'（t）＜0，所以函数f（t）在（1，2）上单调递增，在（2，4]上单调递减．因为f（2）=1，f（1）=f（4）=0，所以当t=4，即x1=2时，S﹣S的最小值为f（4）=0，当t=2，即x1=时，S﹣S的最大值为f（2）=1．所以S﹣S的取值范围为[0，1]．点评：本小题主要考查椭圆与双曲线的方程、直线与圆锥曲线的位置关系、函数最值等知识，考查数形结合、化归与转化、函数与方程的数学思想方法，以及推理论证能力和运算求解能力．18．设椭圆D：=1（a＞b＞0）的左、右焦点分别为F1、F2，上顶点为A，在x轴负半轴上有一点B，满足，且AB⊥AF2．（Ⅰ）若过A、B、F2三点的圆C恰好与直线l：x﹣y﹣3=0相切，求圆C方程及椭圆D的方程；（Ⅱ）若过点T（3，0）的直线与椭圆D相交于两点M、N，设P为椭圆上一点，且满足（O为坐标原点），求实数t取值范围．考点：直线与圆锥曲线的综合问题；椭圆的应用．专题：压轴题；圆锥曲线的定义、性质与方程．分析：（Ⅰ）利用，可得F1为BF2的中点，根据AB⊥AF2，可得a，c的关系，利用过A、B、F2三点的圆C恰好与直线l：相切，求出a，即可求出椭圆的方程与圆的方程；（Ⅱ）设直线MN方程代入椭圆方程，利用韦达定理及向量知识，即可求实数t取值范围．解答：解：（Ⅰ）由题意知F1（﹣c，0），F2（c，0），A（0，b）．因为AB⊥AF2，所以在Rt△ABF2中，，又因为，所以F1为BF2的中点，所以又a2=b2+c2，所以a=2c．所以F2（，0），B（﹣，0），Rt△ABF2的外接圆圆心为F1（﹣，0），半径r=a，因为过A、B、F2三点的圆C恰好与直线l：相切，所以=a，解得a=2，所以c=1，b=．所以椭圆的标准方程为：，圆的方程为（x+1）2+y2=1；（Ⅱ）设直线MN方程为y=k（x﹣3），M（x1，y1），N（x2，y2），P（x，y），则直线方程代入椭圆方程，消去y可得（4k2+3）x2﹣24k2x+36k2﹣12=0，∴△=（24k2）﹣4（4k2+3）（36k2﹣12）＞0，∴k2＜，x1+x2=，x1x2=，∵，∴x1+x2=tx，y1+y2=ty，∴tx=，ty=，∴x=，y=，代入椭圆方程可得3×[]2+4×[]2=12，整理得=∵k2＜，∴0＜t2＜4，∴实数t取值范围是（﹣2，0）∪（0，2）．点评：本题考查椭圆方程与圆的方程，考查直线与圆的位置关系，考查直线与椭圆的位置关系，难度大19．已知F1、F2为椭圆C：的左，右焦点，M为椭圆上的动点，且•的最大值为1，最小值为﹣2．（1）求椭圆C的方程；（2）过点作不与y轴垂直的直线l交该椭圆于M，N两点，A为椭圆的左顶点．试判断∠MAN是否为直角，并说明理由．考点：直线与圆锥曲线的综合问题．专题：计算题；压轴题；圆锥曲线的定义、性质与方程．分析：（1）设M（x'，y'），化简•=x'2+2b2﹣a2（﹣a≤x≤a），从而求最值，进而求椭圆方程；（2）设直线MN的方程为x=ky﹣6并与椭圆联立，利用韦达定理求•的值，从而说明是直角．解答：解：（1）设M（x'，y'），则y'2=b2﹣x'2，•=x'2+2b2﹣a2（﹣a≤x≤a），则当x'=0时，•取得最小值2b2﹣a2=﹣2，当x'=±a时，•取得最大值b2=1，∴a2=4，故椭圆的方程为．（2）设直线MN的方程为x=ky﹣，联立方程组可得，化简得：（k2+4）y2﹣2.4ky﹣=0，设M（x1，y1），N（x2，y2），则y1+y2=，y1y2=﹣，又A（﹣2，0），•=（x1+2，y1）•（x2+2，y2）=（k2+1）y1y2+k（y1+y2）+==﹣（k2+1）+k+=0，所以∠MAN为直角．点评：本题考查了圆锥曲线方程的求法及直线与圆锥曲线的位置关系应用，同时考查了向量的应用，属于难题．20．如图，P是抛物线y2=2x上的动点，点B，C在y轴上，圆（x﹣1）2+y2=1内切于△PBC，求△PBC面积的最小值．考点：圆与圆锥曲线的综合．专题：综合题；压轴题；圆锥曲线的定义、性质与方程．分析：设P（x0，y0），B（0，b），C（0，c），设b＞c．直线PB：y﹣b=，化简，得（y0﹣b）x﹣x0y+x0b=0，由圆心（1，0）到直线PB的距离是1，知，由此导出（x0﹣2）b2+2y0b﹣x0=0，同理，（x0﹣2）c2+2y0c﹣x0=0，所以（b﹣c）2=，从而得到S△PBC=，由此能求出△PBC面积的最小值．解答：解：设P（x0，y0），B（0，b），C（0，c），设b＞c．直线PB的方程：y﹣b=，化简，得（y0﹣b）x﹣x0y+x0b=0，∵圆心（1，0）到直线PB的距离是1，∴，∴（y0﹣b）2+x02=（y0﹣b）2+2x0b（y0﹣b）+x02b2，∵x0＞2，上式化简后，得（x0﹣2）b2+2y0b﹣x0=0，同理，（x0﹣2）c2+2y0c﹣x0=0，∴b+c=，bc=，∴（b﹣c）2=，∵P（x0，y0）是抛物线上的一点，∴，∴（b﹣c）2=，b﹣c=，∴S△PBC===（x0﹣2）++4≥2+4=8．当且仅当时，取等号．此时x0=4，y0=．∴△PBC面积的最小值为8．点评：本昰考查三角形面积的最小值的求法，具体涉及到抛物线的性质、抛物线和直线的位置关系、圆的简单性质、均值定理等基本知识，综合性强，难度大，对数学思想的要求较高，解题时要注意等价转化思想的合理运用．21．已知直L1：2x﹣y=0，L2：x﹣2y=0．动圆（圆心为M）被L1L2截得的弦长分别为8，16．（Ⅰ）求圆心M的轨迹方程M；（Ⅱ）设直线y=kx+10与方程M的曲线相交于A，B两点．如果抛物y2=﹣2x上存在点N使得|NA|=|NB|成立，求k的取值范围．考点：圆与圆锥曲线的综合；直线与圆相交的性质．专题：综合题；压轴题．分析：（Ⅰ）设M（x，y），M到L1，L2的距离分别为d1，d2，则d12+42=d22+82．所以，由此能求出圆心M的轨迹方程．（Ⅱ）设A（x1，y1），B（x2，y2），由，得（1﹣k2）x2﹣20kx﹣180=0．AB的中点为，AB的中垂线为，由，得．由此能求出k的取值范围．解答：解：（Ⅰ）设M（x，y），M到L1，L2的距离分别为d1，d2，则d12+42=d22+82．…（2分）∴，∴x2﹣y2=80，即圆心M的轨迹方程M：x2﹣y2=80．…（4分）（Ⅱ）设A（x1，y1），B（x2，y2），由，得（1﹣k2）x2﹣20kx﹣180=0．①∴AB的中点为，…（6分）∴AB的中垂线为，即，…（7分）由，得②…（8分）∵存在N使得|NA|=|NB|成立的条件是：①有相异二解，并且②有解．…（9分）∵①有相异二解的条件为，∴⇒且k≠±1．③…（10分）②有解的条件是，∴，④…（11分）根据导数知识易得时，k3﹣k+40＞0，因此，由③④可得N点存在的条件是：﹣1或1＜k＜．…（12分）点评：本题主要考查双曲线标准方程，简单几何性质，直线与椭圆的位置关系，圆的简单性质等基础知识．考查运算求解能力，推理论证能力；考查函数与方程思想，化归与转化思想．22．已知直线l1：ax﹣by+k=0；l2：kx﹣y﹣1=0，其中a是常数，a≠0．（1）求直线l1和l2交点的轨迹，说明轨迹是什么曲线，若是二次曲线，试求出焦点坐标和离心率．（2）当a＞0，y≥1时，轨迹上的点P（x，y）到点A（0，b）距离的最小值是否存在？若存在，求出这个最小值．考点：圆锥曲线的轨迹问题．专题：综合题；压轴题；分类讨论；转化思想．分析：（1）联立直线l1和l2的方程，消去参数即可得到交点的轨迹方程，根据a的取值a＞0，﹣1＜a＜0，a=﹣1，a＜﹣1说明轨迹曲线，利用二次曲线判断形状，直接求出焦点坐标和离心率．（2）通过a＞0，y≥1时，说明轨迹的图形，求出轨迹上的点P（x，y）到点A（0，b）距离的表达式，通过配方讨论b与的大小，求出|PA|的最小值．解答：解：（1）由消去k，得y2﹣ax2=1①当a＞0时，轨迹是双曲线，焦点为，离心率；②当﹣1＜a＜0时，轨迹是椭圆，焦点为，离心率；③当a=﹣1时，轨迹是圆，圆心为（0，0），半径为1；④当a＜﹣1时，轨迹是椭圆，焦点为，离心率（2）当a＞0时，y≥1时，轨迹是双曲线y2﹣ax2=1的上半支．∵|PA|2=x2+（y﹣b）2==①当b＞时，|PA|的最小值为；②当b≤时，|PA|的最小值为|1﹣b|点评：本题考查知识点比较多，涉及参数方程，双曲线方程椭圆方程，圆的方程，两点的距离公式等等，涉及分类讨论思想二次函数的最值，是难度比较大，容易出错的题目，考试常靠题型，多以压轴题为主．23．如图，ABCD是边长为2的正方形纸片，沿某动直线l为折痕将正方形在其下方的部分向上翻折，使得每次翻折后点B都落在边AD上，记为B'；折痕与AB交于点E，以EB和EB’为邻边作平行四边形EB’MB．若以B为原点，BC所在直线为x轴建立直角坐标系（如下图）：（Ⅰ）．求点M的轨迹方程；（Ⅱ）．若曲线S是由点M的轨迹及其关于边AB对称的曲线组成的，等腰梯形A1B1C1D1的三边A1B1，B1C1，C1D1分别与曲线S切于点P，Q，R．求梯形A1B1C1D1面积的最小值．考点：圆锥曲线的轨迹问题；向量在几何中的应用．专题：计算题；压轴题．分析：（1）设出M的坐标，根据两点关于直线对称时两点连线与对称轴垂直，且两点的中点在对称轴上，再根据平行四边形的对角线对应的向量等于两邻边对应向量的和得到点M的轨迹方程；（2）利用函数在切点处的导数值为曲线的切线斜率，求出腰A1B1的方程，分别令y=0和y=1求出与两底的交点横坐标，利用梯形的面积公式表示出梯形A1B1C1D1面积，利用基本不等式求出其最小值．解答：解：（1）如图，设M（x，y），B′（x0，2），又E（0，b）显然直线l的斜率存在，故不妨设直线l的方程为y=kx+b，则而BB′的中点在直线l上，故，①由于⇒代入①即得，又0≤x0≤2点M的轨迹方程（0≤x≤2）﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣（6分）（2）易知曲线S的方程为（﹣2≤x≤2）设梯形A1B1C1D1的面积为s，点P的坐标为．由题意得，点Q的坐标为（0，1），直线B1C1的方程为y=1．对于有∴∴直线A1B1的方程为，即：令y=0得，，∴．令y=1得，，∴所以当且仅当，即时，取“=”且，时，s有最小值为．梯形A1B1C1D1的面积的最小值为﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣（15分）点评：本题考查两点关于一条直线对称的充要条件；向量运算的几何意义；曲线在切点处的导数值为曲线的切线斜率；利用基本不等式求函数的最值．属于一道难题．24．（1）已知一个圆锥母线长为4，母线与高成45°角，求圆锥的底面周长．（2）已知直线l与平面α成φ，平面α外的点A在直线l上，点B在平面α上，且AB与直线l成θ，①若φ=60°，θ=45°，求点B的轨迹；②若任意给定φ和θ，研究点B的轨迹，写出你的结论，并说明理由．考点：圆锥曲线的轨迹问题；旋转体（圆柱、圆锥、圆台）．专题：综合题；压轴题．分析：（1）由圆锥的母线长为4，母线与高成45°角，知高和底面半径与母线构成一个等腰直角三角形，由勾股定理可知底面半径为2，由圆周公式2πR可算出底面周长．（2）①设l∩α=C，点A在平面α上的射影为点O．建立空间直角坐标系，设|AC|=a，有A（0，0，asin60°），C（0，﹣acos60°）．设B（x，y，0），则=（0，﹣acos60°，﹣asin60°）．=（x，y，﹣asin60°）．所以．又由|•cos45°，知﹣acos60°•y+a2sin60°=a，平方整理得，由此知点B的轨迹．②设l∩α=C，点A在平面α上的射影为点O．如图建立空间直角坐标系，设|AC|=a，有A（0，0，asinφ），C（0，﹣acosφ），（0＜φ＜）．设B（x，y，0），则（6分）=（0，﹣acosφ，﹣asinφ）．=（x，y，﹣asinφ）．所以φ．由|•cosθ=a••cosθ．知cos2θ•x2+（cos2θ﹣cos2φ）y2+a2ysinφsin2φ+a2sin2φ（cos2θ﹣sin2φ）=0．故当φ=时，点B的轨迹为圆；当θ＜φ＜时，点B的轨迹为椭圆；当θ=φ＜时，点B的轨迹为抛物线；当θ＞φ时，点B的轨迹为双曲线．解答：解：（1）∵圆锥的母线长为4，母线与高成45°角，高和底面半径与母线构成一个等腰直角三角形，即高和底面半径长度一样，则由勾股定理可知底面半径为2，则由圆周公式2πR可算出底面周长4π；（2分）（2）①设l∩α=C，点A在平面α上的射影为点O．如图建立空间直角坐标系，设|AC|=a，有A（0，0，asin60°），C（0，﹣acos60°）．设B（x，y，0），则=（0，﹣acos60°，﹣asin60°）．=（x，y，﹣asin60°）．∴．又∵|•cos45°=a•．∴﹣acos60°•y+a2sin60°=a．（11分）平方整理得cos245°•x2+（cos245°﹣cos260°）y2+a2ysin60°sin120°+a2sin260°（cos245°﹣sin260°）=0．即，∴点B的轨迹椭圆；（4分）②设l∩α=C，点A在平面α上的射影为点O．如图建立空间直角坐标系，设|AC|=a，有A（0，0，asinφ），C（0，﹣acosφ），（0＜φ＜）．设B（x，y，0），则（6分）=（0，﹣acosφ，﹣asinφ）．=（x，y，﹣asinφ）．∴φ．又∵|•cosθ=a••cosθ．∴﹣acosφ•y+a2sinφ=a．（11分）平方整理得cos2θ•x2+（cos2θ﹣cos2φ）y2+a2ysinφsin2φ+a2sin2φ（cos2θ﹣sin2φ）=0．i．当cos2θ﹣cos2φ=0，即θ=φ时，上式为抛物线方程；ii．当cos2θ﹣cos2φ＞0，即θ＜φ时，上式为椭圆方程；iii．当cos2θ﹣cos2φ＜0，即θ＞φ时，上式为双曲线方程．（14分）故当φ=时，点B的轨迹为圆；当θ＜φ＜时，点B的轨迹为椭圆；当θ=φ＜时，点B的轨迹为抛物线；当θ＞φ时，点B的轨迹为双曲线．（16分）点评：第（1）题考查圆锥的性质和应用，是基础题，解题时要认真审题，仔细解答．第（2）题考查圆锥曲线的轨迹的求法和判断，对数学思维的要求比较高，要求学生理解“存在”、“恒成立”，以及运用一般与特殊的关系进行否定，本题有一定的探索性．综合性强，难度大，易出错．25．已知椭圆C的中心在原点，一个焦点，且长轴长与短轴长的比是．（1）求椭圆C的方程；（2）若椭圆C在第一象限的一点P的横坐标为1，过点P作倾斜角互补的两条不同的直线PA，PB分别交椭圆C 于另外两点A，B，求证：直线AB的斜率为定值；（3）求△PAB面积的最大值．考点：椭圆的标准方程；直线的斜率；直线与圆锥曲线的综合问题．专题：压轴题．分析：（1）待定系数法求椭圆的方程．（2）设出A、B坐标，利用一元二次方程根与系数的关系，求出A、B横坐标之差，纵坐标之差，从而求出AB斜率．（3）设出AB直线方程，与椭圆方程联立，运用根与系数的关系求AB长度，计算P到AB的距离，计算△PAB面积，使用基本不等式求最大值．解答：解：（Ⅰ）设椭圆C的方程为．由题意，解得a2=4，b2=2．所以，椭圆C的方程为．故点P（1，）（Ⅱ）由题意知，两直线PA，PB的斜率必存在，设PB的斜率为k，则PB的直线方程为．由得，．设A（x A，y A），B（x B，y B），则，同理可得．则，．所以直线AB的斜率为定值．（Ⅲ）设AB的直线方程为，由得．由，得m2＜8．此时，．由椭圆的方程可得点P（1，），根据点到直线的距离公式可得P到AB的距离为，由两点间的距离公式可得=，故===≤×=．因为m2=4使判别式大于零，所以当且仅当m=±2时取等号，所以△PAB面积的最大值为．点评：直线与圆锥曲线的综合问题，注意应用一元二次方程根与系数的关系，式子的化简变形，是解题的难点和关键．26．已知点B（0，1），A，C为椭圆上的两点，△ABC是以B为直角顶点的直角三角形．（I）当a=4时，求线段BC的中垂线l在x轴上截距的取值范围．（II）△ABC能否为等腰三角形？若能，这样的三角形有几个？考点：直线与圆锥曲线的综合问题；椭圆的简单性质．专题：综合题；压轴题；圆锥曲线中的最值与范围问题．分析：（I）依题意，可知椭圆的方程为：+y2=1，设C（4cosθ，sinθ），可求得直线l的方程为y=﹣x++，令y=0得x==cosθ（cosθ≠0），利用余弦cosθ的有界性即可求得线段BC的中垂线l在x轴上截距的取值范围；（II）当等腰直角三角形ABC的两条腰AB与BC不关于y轴对称时，设出AB的方程为y=kx+1（k＞0），BC的方程为y=﹣x+1，利用直线与方程与椭圆方程联立，利用等腰直角三角形ABC中的两腰|AB|=|BC|，借助基本不等式即可求得a的取值范围；同理可求两条腰AB与BC关于y轴对称时a的取值范围．解答：解：（I）∵a=4，∴椭圆的方程为：+y2=1，故B（0，1），设C（4cosθ，sinθ），则BC的中点M（2cosθ，），∵BC的斜率k BC=，∴线段BC的中垂线l的斜率k=﹣=﹣，∴直线l的方程为：y﹣=﹣（x﹣2cosθ），∴y=﹣x++，令y=0得：x==cosθ（cosθ≠0）∵﹣1≤cosθ≤1且cosθ≠0，∴﹣≤x=cosθ≤且x≠0，∴线段BC的中垂线l在x轴上截距的取值范围为[﹣，0）∪（0，]．（II）当等腰直角三角形ABC的两条腰AB与BC不关于y轴对称时，作图如右，设此时过B（0，1）的AB的方程为y=kx+1（k＞0），则BC的方程为y=﹣x+1，由得：（a2k2+1）x2+2a2kx=0，设该方程两根为x1，x2，则x1+x2=﹣，x1x2=0，则|AB|==|x1﹣x2|•=•。

专题8.7 高考解答题热点题型-立体几何(解析版)

高考理科数学一轮复习：题型全归纳与高效训练突破专题8.7高考解答题热点题型---立体几何目录一、题型综述 (1)二题型全归纳 (1)题型一空间点、线、面的位置关系及空． (1)题型二平面图形的折叠问题 (7)题型三立体几何中的探索性问题 (10)三、高效训练突破 (15)一、题型综述立体几何是每年高考的重要内容，基本上都是一道客观题和一道解答题，客观题主要考查考生的空间想象能力及简单的计算能力．解答题主要采用证明与计算相结合的模式，即首先利用定义、定理、公理等证明空间线线、线面、面面的平行或垂直关系，再利用空间向量进行空间角的计算求解．重在考查考生的逻辑推理及计算能力，试题难度一般不大，属中档题，且主要有以下几种常见的热点题型．二题型全归纳题型一空间点、线、面的位置关系及空．1证明点共面或线共面的常用方法(1)直接法：证明直线平行或相交，从而证明线共面．(2)纳入平面法：先确定一个平面，再证明有关点、线在此平面内．．(3)辅助平面法：先证明有关的点、线确定平面α，再证明其余元素确定平面β，最后证明平面α，β重合．2．证明空间点共线问题的方法(1)公理法：一般转化为证明这些点是某两个平面的公共点，再根据公理3证明这些点都在这两个平面的交线上(2)纳入直线法：选择其中两点确定一条直线，然后证明其余点也在该直线上．3．证明线共点问题的常用方法先证其中两条直线交于一点，再证其他直线经过该点．4.求异面直线所成角的方法(1)几何法①作：利用定义转化为平面角，对于异面直线所成的角，可固定一条，平移一条，或两条同时平移到某个特殊的位置，顶点选在特殊的位置上．①证：证明作出的角为所求角．①求：把这个平面角置于一个三角形中，通过解三角形求空间角．(2)向量法建立空间直角坐标系，利用公式|cos θ|＝|m ·n ||m ||n |求出异面直线的方向向量的夹角．若向量夹角是锐角或直角，则该角即为异面直线所成角；若向量夹角是钝角，则异面直线所成的角为该角的补角．【例1】如图，AE ①平面ABCD ，CF ①AE ，AD ①BC ，AD ①AB ，AB ＝AD ＝1，AE ＝BC ＝2.(1)求证：BF ①平面ADE ；(2)求直线CE 与平面BDE 所成角的正弦值；(3)若二面角E －BD －F 的余弦值为13，求线段CF 的长．【解题思路】由条件知AB ，AD ，AE 两两垂直，可以A 为坐标原点建立空间直角坐标系，用空间向量解决．(1)寻找平面ADE 的法向量，证明BF →与此法向量垂直，即得线面平行．(2)CE →与平面BDE 的法向量所成角的余弦值的绝对值，即为直线CE 和平面BDE 所成角的正弦值；(3)设CF ＝h ，用h 表示二面角E －BD －F 的余弦值，通过解方程得到线段长．【规范解答】 (1)证明：以A 为坐标原点，AB 所在的直线为x 轴，AD 所在的直线为y 轴，AE 所在的直线为z 轴，建立如图所示的空间直角坐标系．则A (0,0,0)，B (1,0,0)，设F (1,2，h )．依题意，AB →＝(1,0,0)是平面ADE 的一个法向量，又BF →＝(0,2，h )，可得BF →·AB →＝0，又直线BF ①平面ADE ，所以BF ①平面ADE .(2)依题意，D (0,1,0)，E (0,0,2)，C (1,2,0)，则BD →＝(－1,1,0)，BE →＝(－1,0,2)，CE →＝(－1，－2,2)．设n ＝(x ，y ，z )为平面BDE 的法向量，则⎩⎪⎨⎪⎧ n ·BD →＝0，n ·BE →＝0，即⎩⎪⎨⎪⎧－x ＋y ＝0，－x ＋2z ＝0，不妨令z ＝1，可得n ＝(2,2,1)．因此有cos 〈CE →，n 〉＝CE →·n |CE →||n |＝－49. 所以直线CE 与平面BDE 所成角的正弦值为49. (3)设m ＝(x 1，y 1，z 1)为平面BDF 的法向量，则⎩⎪⎨⎪⎧ m ·BD →＝0，m ·BF →＝0，即⎩⎪⎨⎪⎧－x 1＋y 1＝0，2y 1＋hz 1＝0，不妨令y 1＝1，可得m ＝⎝⎛⎭⎫1，1，－2h . 由题意，有|cos 〈m ，n 〉|＝|m ·n ||m ||n |＝⎪⎪⎪⎪4－2h 3 2＋4h2＝13，解得h ＝87.经检验，符合题意．所以线段CF 的长为87. 【例2】.如图，在三棱锥P ABC 中，P A ①底面ABC ，①BAC ＝90°.点D ，E ，N 分别为棱P A ，PC ，BC 的中点，M 是线段AD 的中点，P A ＝AC ＝4，AB ＝2.(1)求证：MN ①平面BDE ；(2)已知点H 在棱P A 上，且直线NH 与直线BE 所成角的余弦值为721，求线段AH 的长．【解析】：如图，以A 为原点，分别以AB →，AC →，AP →的方向为x 轴，y 轴，z 轴的正方向建立空间直角坐标系．依题意可得A (0，0，0)，B (2，0，0)，C (0，4，0)，P (0，0，4)，D (0，0，2)，E (0，2，2)，M (0，0，1)，N (1，2，0)．(1)证明：DE →＝(0，2，0)，DB →＝(2，0，－2)．设n ＝(x ，y ，z )为平面BDE 的法向量，则⎩⎪⎨⎪⎧n ·DE →＝0，n ·DB →＝0，即⎩⎪⎨⎪⎧2y ＝0，2x －2z ＝0. 不妨设z ＝1，可取n ＝(1，0，1)．又MN →＝(1，2，－1)，可得MN →·n ＝0.因为MN ①平面BDE ，所以MN ①平面BDE .(2)依题意，设AH ＝h (0≤h ≤4)，则H (0，0，h )，进而可得NH →＝(－1，－2，h )，BE →＝(－2，2，2)．由已知，得|cos 〈NH →，BE →〉|＝|NH →·BE →||NH →||BE →|＝|2h －2|h 2＋5×23＝721，整理得10h 2－21h ＋8＝0，解得h ＝85或h ＝12. 所以，线段AH 的长为85或12. 【例3】如图，在几何体ACD －A 1B 1C 1D 1中，四边形ADD 1A 1与四边形CDD 1C 1均为矩形，平面ADD 1A 1①平面CDD 1C 1，B 1A 1①平面ADD 1A 1，AD ＝CD ＝1，AA 1＝A 1B 1＝2，E 为棱AA 1的中点．(1)证明：B 1C 1①平面CC 1E ；(2)求直线B 1C 1与平面B 1CE 所成角的正弦值．【解析】(1)证明：因为B 1A 1①平面ADD 1A 1，所以B 1A 1①DD 1，又DD 1①D 1A 1，B 1A 1∩D 1A 1＝A 1，所以DD 1①平面A 1B 1C 1D 1，又DD 1①CC 1，所以CC 1①平面A 1B 1C 1D 1.因为B 1C 1①平面A 1B 1C 1D 1，所以CC 1①B 1C 1.因为平面ADD 1A 1①平面CDD 1C 1，平面ADD 1A 1∩平面CDD 1C 1＝DD 1，C 1D 1①DD 1，所以C 1D 1①平面ADD 1A 1.经计算可得B 1E ＝5，B 1C 1＝2，EC 1＝3，从而B 1E 2＝B 1C 21＋EC 21，所以在①B 1EC 1中，B 1C 1①C 1E .又CC 1，C 1E ①平面CC 1E ，CC 1∩C 1E ＝C 1，所以B 1C 1①平面CC 1E .(2)如图，以点A 为坐标原点，建立空间直角坐标系，依题意得A (0，0，0)，C (1，0，1)，B 1(0，2，2)，C 1(1，2，1)，E (0，1，0)，则CE →＝(－1，1，－1)，B 1C →＝(1，－2，－1)．设平面B 1CE 的法向量为m ＝(x ，y ，z )，则⎩⎪⎨⎪⎧m ·B 1C →＝0，m ·CE →＝0，即⎩⎪⎨⎪⎧x －2y －z ＝0，－x ＋y －z ＝0，消去x 得y ＋2z ＝0，不妨设z ＝1，可得m ＝(－3，－2，1)为平面B 1CE 的一个法向量，易得B 1C 1→＝(1，0，－1)，设直线B 1C 1与平面B 1CE 所成角为θ，则sin θ＝|cos 〈m ，B 1C 1→〉|＝⎪⎪⎪⎪⎪⎪m ·B 1C 1→|m |·|B 1C 1→|＝⎪⎪⎪⎪⎪⎪－414×2＝277，故直线B 1C 1与平面B 1CE 所成角的正弦值为277. 题型二平面图形的折叠问题【解法】解决平面图形翻折问题的关键是抓住“折痕”，准确把握平面图形翻折前后的两个“不变”．(1)与折痕垂直的线段，翻折前后垂直关系不改变；(2)与折痕平行的线段，翻折前后平行关系不改变．【例1】如图，四边形ABCD 为正方形，E ，F 分别为AD ，BC 的中点，以DF 为折痕把①DFC 折起，使点C 到达点P 的位置，且PF ①BF .(1)证明：平面PEF ①平面ABFD ；(2)求DP 与平面ABFD 所成角的正弦值．【解题思路】(1)①翻折前后的不变关系，四边形ABFE 是矩形．①证明BF ①平面PEF .①证明平面PEF ①平面ABFD .(2)解法一：①建系：借助第(1)问，过P 作平面ABFD 的垂线为z 轴，垂足为原点，EF 所在直线为y 轴，建系．①求直线DP 的方向向量和平面ABFD 的法向量．①由公式计算所求角的正弦值．解法二：①作：过P 作PH ①EF 交EF 于点H ，连接DH .①证：证明PH ①平面ABFD ，得①PDH 为直线DP 与平面ABFD 所成角．①算：在Rt①PDH 中，PD 的长度是正方形ABCD 的边长，①PHD ＝90°，易知要求sin①PDH ，关键是求PH ；由此想到判断①PEF 的形状，进一步想到证明PF ①平面PED .【规范解答】(1)证明：由已知可得，BF ①PF ，BF ①EF ，又PF ∩EF ＝F ，所以BF ①平面PEF .又BF ①平面ABFD ，所以平面PEF ①平面ABFD .(2)解法一：作PH ①EF ，垂足为H .由(1)得，PH ①平面ABFD .以H 为坐标原点，HF →的方向为y 轴正方向，建立如图所示的空间直角坐标系Hxyz ，设正方形ABCD 的边长为2.由(1)可得，DE ①PE .又DP ＝2，DE ＝1，所以PE ＝ 3.又PF ＝1，EF ＝2，故PE ①PF .所以PH ＝32，EH ＝32，则H (0,0,0)，P ⎝⎛⎭⎫0，0，32， D ⎝⎛⎭⎫－1，－32，0，DP →＝⎝⎛⎭⎫1，32，32，HP →＝⎝⎛⎭⎫0，0，32为平面ABFD 的一个法向量．设DP 与平面ABFD 所成角为θ，则sin θ＝|HP →·DP →||HP →||DP →|＝343＝34. 所以DP 与平面ABFD 所成角的正弦值为34. 解法二：因为PF ①BF ，BF ①ED ，所以PF ①ED ，又PF ①PD ，ED ∩PD ＝D ，所以PF ①平面PED ，所以PF ①PE ，设AB ＝4，则EF ＝4，PF ＝2，所以PE ＝23，过P 作PH ①EF 交EF 于点H ，因为平面PEF ①平面ABFD ，所以PH ①平面ABFD ，连接DH ，则①PDH 即为直线DP 与平面ABFD 所成的角，因为PE ·PF ＝EF ·PH ，所以PH ＝23×24＝3，因为PD ＝4，所以sin①PDH ＝PH PD ＝34，所以DP 与平面ABFD 所成角的正弦值为34. 题型三立体几何中的探索性问题【技巧要点】对命题条件的探索的三种途径途径一：先猜后证，即先观察与尝试给出条件再证明．途径二：先通过命题成立的必要条件探索出命题成立的条件，再证明充分性．途径三：将几何问题转化为代数问题【例1】(2020·湖北“四地七校”联考)在四棱锥P －ABCD 中，底面ABCD 是边长为22的正方形，平面P AC ①底面ABCD ，P A ＝PC ＝2 2.(1)求证：PB ＝PD ；(2)若点M ，N 分别是棱P A ，PC 的中点，平面DMN 与棱PB 的交点为点Q ，则在线段BC 上是否存在一点H ，使得DQ ①PH ？若存在，求BH 的长；若不存在，请说明理由．【解题思路】 (1)要证PB ＝PD ，想到在①PBD 中，证明BD 边上的中线垂直于BD ，联系题目条件想到用面面垂直的性质证明线面垂直．(2)借助第(1)问的垂直关系建立空间直角坐标系，求平面DMN 的法向量n ，分别依据P ，B ，Q 共线和B ，C ，H 共线，设PQ →＝λPB →和BH →＝tBC →，利用垂直关系列方程先求λ再求t ，确定点H 的位置．【规范解答】 (1)证明：记AC ∩BD ＝O ，连接PO ，①底面ABCD 为正方形，①OA ＝OC ＝OB ＝OD ＝2.①P A ＝PC ，①PO ①AC ，①平面P AC ①底面ABCD ，且平面P AC ∩底面ABCD ＝AC ，PO ①平面P AC ，①PO ①底面ABCD .①BD ①底面ABCD ，①PO ①BD .①PB ＝PD .(2)存在．以O 为坐标原点，射线OB ，OC ，OP 的方向分别为x 轴、y 轴、z 轴的正方向建立空间直角坐标系如图所示，由(1)可知OP ＝2.可得P (0,0,2)，A (0，－2,0)，B (2,0,0)，C (0,2,0)，D (－2，0,0)，可得M (0，－1,1)，N (0,1,1)，DM →＝(2，－1,1)，MN →＝(0，2,0)．设平面DMN 的法向量n ＝(x ，y ，z )，①DM →·n ＝0，MN →·n ＝0，①⎩⎪⎨⎪⎧2x －y ＋z ＝0，2y ＝0. 令x ＝1，可得n ＝(1,0，－2)．记PQ →＝λPB →＝(2λ，0，－2λ)，可得Q (2λ，0,2－2λ)，DQ →＝(2λ＋2,0,2－2λ)，DQ →·n ＝0，可得2λ＋2－4＋4λ＝0，解得λ＝13. 可得DQ →＝⎝⎛⎭⎫83，0，43. 记BH →＝tBC →＝(－2t,2t,0)，可得H (2－2t,2t,0)，PH →＝(2－2t,2t ，－2)，若DQ ①PH ，则DQ →·PH →＝0，83(2－2t )＋43×(－2)＝0，解得t ＝12. 故BH ＝ 2.故在线段BC 上存在一点H ，使得DQ ①PH ，此时BH＝ 2.【例2】如图，在四棱锥PABCD中，P A①平面ABCD，底面ABCD为菱形，E为CD的中点．(1)求证：BD①平面P AC；(2)若①ABC＝60°，求证：平面P AB①平面P AE；(3)棱PB上是否存在点F，使得CF①平面P AE？说明理由．【解】(1)证明：因为P A①平面ABCD，所以P A①BD.因为底面ABCD为菱形，所以BD①A C.又P A∩AC＝A，所以BD①平面P A C.(2)证明：因为P A①平面ABCD，AE①平面ABCD，所以P A①AE.因为底面ABCD为菱形，①ABC＝60°，且E为CD的中点，所以AE①CD，所以AB①AE.又AB∩P A＝A，所以AE ①平面P AB .因为AE ①平面P AE ，所以平面P AB ①平面P AE .(3)棱PB 上存在点F ，使得CF ①平面P AE .取F 为PB 的中点，取G 为P A 的中点，连接CF ，FG ，EG .则FG ①AB ，且FG ＝12AB . 因为底面ABCD 为菱形，且E 为CD 的中点，所以CE ①AB ，且CE ＝12AB . 所以FG ①CE ，且FG ＝CE .所以四边形CEGF 为平行四边形．所以CF ①EG .因为CF ①平面P AE ，EG ①平面P AE ，所以CF ①平面P AE .【例3】图1是由矩形ADEB ，Rt①ABC 和菱形BFGC 组成的一个平面图形，其中AB ＝1，BE ＝BF ＝2，①FBC ＝60°.将其沿AB ，BC 折起使得BE 与BF 重合，连接DG ，如图2.(1)证明：图2中的A ，C ，G ，D 四点共面，且平面ABC ①平面BCGE ；(2)求图2中的二面角B －CG －A 的大小．【解析】：(1)证明：由已知得AD ①BE ，CG ①BE ，所以AD ①CG ，故AD ，CG 确定一个平面，从而A ，C ，G ，D 四点共面．由已知得AB ①BE ，AB ①BC ，故AB ①平面BCGE .又因为AB ①平面ABC ，所以平面ABC ①平面BCGE .(2)作EH ①BC ，垂足为H .因为EH ①平面BCGE ，平面BCGE ①平面ABC ，所以EH ①平面ABC .由已知，菱形BCGE 的边长为2，①EBC ＝60°，可求得BH ＝1，EH ＝ 3.以H 为坐标原点，HC →的方向为x 轴的正方向，建立如图所示的空间直角坐标系H xyz ，则A (－1，1，0)，C (1，0，0)，G (2，0，3)，CG →＝(1，0，3)，AC →＝(2，－1，0)．设平面ACGD 的法向量为n ＝(x ，y ，z )，则⎩⎪⎨⎪⎧CG →·n ＝0AC →·n ＝0，即⎩⎨⎧x ＋3z ＝0，2x －y ＝0. 所以可取n ＝(3，6，－3)．又平面BCGE 的法向量可取为m ＝(0，1，0)，所以cos n ，m ＝n ·m |n ||m |＝32. 因此二面角B CG A 的大小为30°.三、高效训练突破1.(2020·深圳模拟)已知四棱锥PABCD，底面ABCD为菱形，PD＝PB，H为PC上的点，过AH的平面分别交PB，PD于点M，N，且BD①平面AMHN.(1)证明：MN①PC；(2)当H为PC的中点，P A＝PC＝3AB，P A与平面ABCD所成的角为60°，求AD与平面AMHN所成角的正弦值．【解析】(1)证明：连接AC、BD且AC∩BD＝O，连接PO.因为ABCD为菱形，所以BD①AC，因为PD＝PB，所以PO①BD，因为AC∩PO＝O且AC、PO①平面P AC，所以BD①平面P AC，因为PC①平面P AC，所以BD①PC，因为BD①平面AMHN，且平面AMHN∩平面PBD＝MN，所以BD①MN，MN①平面P AC，所以MN①P C.(2)由(1)知BD ①AC 且PO ①BD ，因为P A ＝PC ，且O 为AC 的中点，所以PO ①AC ，所以PO ①平面ABCD ，所以P A 与平面ABCD 所成的角为①P AO ，所以①P AO ＝60°，所以AO ＝12P A ，PO ＝32P A ，因为P A ＝3AB ，所以BO ＝36P A . 以OA →，OD →，OP →分别为x ，y ，z 轴，建立空间直角坐标系，如图所示．设P A ＝2，所以O (0，0，0)，A (1，0，0)，B (0，－33，0)，C (－1，0，0)，D (0，33，0)，P (0，0，3)，H (－12，0，32)，所以BD →＝(0，233，0)，AH →＝(－32，0，32)，AD →＝(－1，33，0)．设平面AMHN 的法向量为n ＝(x ，y ，z )，所以⎩⎪⎨⎪⎧n ·BD →＝0，n ·AH →＝0，即⎩⎨⎧233y ＝0，－32x ＋32z ＝0，令x ＝2，则y ＝0，z ＝23，所以n ＝(2，0，23)，设AD 与平面AMHN 所成角为θ，所以sin θ＝|cos 〈n ，AD →〉|＝|n ·AD →|n ||AD →||＝34. 所以AD 与平面AMHN 所成角的正弦值为34. 2．(2020·河南联考)如图所示，在四棱锥P －ABCD 中，底面ABCD 为平行四边形，平面P AD ①平面ABCD ，①P AD 是边长为4的等边三角形，BC ①PB ，E 是AD 的中点．(1)求证：BE ①PD ；(2)若直线AB 与平面P AD 所成角的正弦值为154，求平面P AD 与平面PBC 所成的锐二面角的余弦值．【解析】：(1)证明：因为①P AD 是等边三角形，E 是AD 的中点，所以PE ①AD .又平面P AD ①平面ABCD ，平面P AD ∩平面ABCD ＝AD ，PE ①平面P AD ，所以PE ①平面ABCD ，所以PE ①BC ，PE ①BE .又BC ①PB ，PB ∩PE ＝P ，所以BC ①平面PBE ，所以BC ①BE .又BC ①AD ，所以AD ①BE .又AD ∩PE ＝E 且AD ，PE ①平面P AD ，所以BE ①平面P AD ，所以BE ①PD .(2)由(1)得BE ①平面P AD ，所以①BAE 就是直线AB 与平面P AD 所成的角．因为直线AB 与平面P AD 所成角的正弦值为154，即sin①BAE ＝154 ，所以cos①BAE ＝14. 所以cos①BAE ＝AE AB ＝2AB ＝14，解得AB ＝8，则BE ＝AB 2－AE 2＝215.由(1)得EA ，EB ，EP 两两垂直，所以以E 为坐标原点，EA ，EB ，EP 所在直线分别为x 轴，y 轴，z 轴，建立如图所示的空间直角坐标系，则点P (0，0，23)，A (2，0，0)，D (－2，0，0)，B (0，215，0)，C (－4，215，0)，所以PB →＝(0，215，－23)，PC →＝(－4，215，－23)．设平面PBC 的法向量为m ＝(x ，y ，z )，由⎩⎪⎨⎪⎧PB →·m ＝0，PC →·m ＝0，得⎩⎨⎧215y －23z ＝0，－4x ＋215y －23z ＝0，解得⎩⎨⎧x ＝0，z ＝5y . 令y ＝1，可得平面PBC 的一个法向量为m ＝(0，1，5)．易知平面P AD 的一个法向量为n ＝(0，1，0)，设平面P AD 与平面PBC 所成的锐二面角的大小为θ，则cos θ＝⎪⎪⎪⎪m ·n |m ||n |＝⎪⎪⎪⎪⎪⎪（0，1，5）·（0，1，0）6×1＝66. 所以平面P AD 与平面PBC 所成的锐二面角的余弦值为66. 3.(2020·云南师范大学附属中学3月月考)如图，在直三棱柱ABC A 1B 1C 1中，①ABC 是边长为2的正三角形，AA 1＝26，D 是CC 1的中点，E 是A 1B 1的中点．(1)证明：DE ①平面A 1BC;(2)求点A 到平面A 1BC 的距离．【解析】 (1)证明：如图取A 1B 的中点F ，连接FC ，FE .因为E ，F 分别是A 1B 1，A 1B 的中点，所以EF ①BB 1，且EF ＝12BB 1. 又在平行四边形BB 1C 1C 中，D 是CC 1的中点，所以CD ①BB 1，且CD ＝12BB 1，所以CD ①EF ，且CD ＝EF . 所以四边形CFED 是平行四边形，所以DE ①CF .因为DE ①/平面A 1BC ，CF ①平面A 1BC ，所以DE ①平面A 1BC .(2)法一：(等体积法)因为BC ＝AC ＝AB ＝2，AA 1＝26，三棱柱ABC A 1B 1C 1为直三棱柱，所以V 三棱锥A 1－ABC ＝13S ①ABC ×AA 1＝13×34×22×26＝2 2. 又在①A 1BC 中，A 1B ＝A 1C ＝27，BC ＝2，BC 边上的高h ＝ A 1B 2－⎝⎛⎭⎫12BC 2＝33，所以S ①A 1BC ＝12BC ·h ＝3 3. 设点A 到平面A 1BC 的距离为d ，则V 三棱锥A －A 1BC ＝13S ①A 1BC ×d ＝13×33×d ＝3d . 因为V 三棱锥A 1－ABC ＝V 三棱锥A －A 1BC ，所以22＝3d ，解得d ＝263，所以点A 到平面A 1BC 的距离为263. 法二：(向量法)由题意知，三棱柱ABC A 1B 1C 1是正三棱柱．取AB 的中点O ，连接OC ，OE .因为AC ＝BC ，所以CO ①AB .又平面ABC ①平面ABB 1A 1，平面ABC ∩平面ABB 1A 1＝AB ，所以CO ①平面ABB 1A 1.因为O 为AB 的中点，E 为A 1B 1的中点，所以OE ①AB ，所以OC ，OA ，OE 两两垂直．如图，以O 为坐标原点，以OA ，OE ，OC 所在直线分别为x 轴，y 轴，z 轴建立空间直角坐标系，则C (0，0，3)，A (1，0，0)，A 1(1，26，0)，B (－1，0，0)．则BA 1→＝(2，26，0)，BC →＝(1，0，3)．设平面A 1BC 的法向量为n ＝(x ，y ，z )，则由⎩⎪⎨⎪⎧n ①BA 1→，n ①BC →，可得⎩⎪⎨⎪⎧n ·BA 1→＝2x ＋26y ＝0，n ·BC →＝x ＋3z ＝0，整理得⎩⎨⎧x ＋6y ＝0，x ＋3z ＝0，令x ＝6，则y ＝－1，z ＝－ 2. 所以n ＝(6，－1，－2)为平面A 1BC 的一个法向量．而BA →＝(2，0，0)，所以点A 到平面A 1BC 的距离d ＝|BA →·n ||n |＝6×26＋1＋2＝263. 4．(2020·湖北十堰4月调研)如图，在三棱锥P －ABC 中，M 为AC 的中点，P A ①PC ，AB ①BC ，AB ＝BC ，PB ＝2，AC ＝2，①P AC ＝30°.(1)证明：BM ①平面P AC ；(2)求二面角B －P A －C 的余弦值．【答案】：见解析(1)证明：因为P A ①PC ，AB ①BC ，所以MP ＝MB ＝12AC ＝1，又MP 2＋MB 2＝BP 2，所以MP ①MB .因为AB ＝BC ，M 为AC 的中点，所以BM ①AC ，又AC ∩MP ＝M ，所以BM ①平面P AC .(2)法一：取MC 的中点O ，连接PO ，取BC 的中点E ，连接EO ，则OE ①BM ，从而OE ①AC . 因为P A ①PC ，①P AC ＝30°，所以MP ＝MC ＝PC ＝1. 又O 为MC 的中点，所以PO ①AC .由(1)知BM ①平面P AC ，OP ①平面P AC ，所以BM ①PO . 又BM ∩AC ＝M ，所以PO ①平面ABC .以O 为坐标原点，OA ，OE ，OP 所在直线分别为x 轴，y 轴，z 轴，建立空间直角坐标系，如图所示，由题意知A ⎝⎛⎭⎫32，0，0，B ⎝⎛⎭⎫12，1，0，P ⎝⎛⎭⎫0，0，32，BP →＝⎝⎛⎭⎫－12，－1，32，BA →＝(1，－1，0)，设平面APB 的法向量为n ＝(x ，y ，z )，则⎩⎪⎨⎪⎧n ·BP→＝－12x －y ＋32z ＝0，n ·BA →＝x －y ＝0，令x ＝1，得n ＝(1，1，3)为平面APB 的一个法向量，易得平面P AC 的一个法向量为π＝(0，1，0)，cos 〈n ，π〉＝55，由图知二面角B －P A －C 为锐角，所以二面角B －P A －C 的余弦值为55. 法二：取P A 的中点H ，连接HM ，HB ，因为M 为AC 的中点，所以HM ①PC ，又P A ①PC ，所以HM ①P A .由(1)知BM ①平面P AC ，则BH ①P A ，所以①BHM 为二面角B －P A －C 的平面角．因为AC ＝2，P A ①PC ，①P AC ＝30°，所以HM ＝12PC ＝12.又BM ＝1，则BH ＝BM 2＋HM 2＝52，所以cos①BHM ＝HM BH ＝55，即二面角B －P A －C 的余弦值为55.5．(2020·合肥模拟)如图，在多面体ABCDEF 中，四边形ABCD 是正方形，BF ①平面ABCD ，DE ①平面ABCD ，BF ＝DE ，M 为棱AE 的中点．(1)求证：平面BDM ①平面EFC ；(2)若DE ＝2AB ，求直线AE 与平面BDM 所成角的正弦值．【答案】：见解析(1)证明：连接AC ，交BD 于点N ，连接MN ，则N 为AC 的中点，又M 为AE 的中点，所以MN ①EC . 因为MN ①平面EFC ，EC ①平面EFC ，所以MN ①平面EFC .因为BF ，DE 都垂直底面ABCD ，所以BF ①DE . 因为BF ＝DE ，所以四边形BDEF 为平行四边形，所以BD ①EF .因为BD ①平面EFC ，EF ①平面EFC ，所以BD ①平面EFC .又MN ∩BD ＝N ，所以平面BDM ①平面EFC . (2)因为DE ①平面ABCD ，四边形ABCD 是正方形，所以DA ，DC ，DE 两两垂直，如图，建立空间直角坐标系D xyz .设AB ＝2，则DE ＝4，从而D (0，0，0)，B (2，2，0)，M (1，0，2)，A (2，0，0)，E (0，0，4)，所以DB →＝(2，2，0)，DM →＝(1，0，2)，设平面BDM 的法向量为n ＝(x ，y ，z )，则⎩⎪⎨⎪⎧n ·DB →＝0，n ·DM →＝0，得⎩⎪⎨⎪⎧2x ＋2y ＝0，x ＋2z ＝0.令x ＝2，则y ＝－2，z ＝－1，从而n ＝(2，－2，－1)为平面BDM 的一个法向量．因为AE →＝(－2，0，4)，设直线AE 与平面BDM 所成的角为θ，则 sin θ＝|cos 〈n ·AE →〉|＝⎪⎪⎪⎪⎪⎪n ·AE →|n |·|AE →|＝4515，所以直线AE 与平面BDM 所成角的正弦值为4515.6.(2020·河南郑州三测)如图①，①ABC 中，AB ＝BC ＝2，①ABC ＝90°，E ，F 分别为边AB ，AC 的中点，以EF 为折痕把①AEF 折起，使点A 到达点P 的位置(如图①)，且PB ＝BE .(1)证明：EF ①平面PBE ；(2)设N 为线段PF 上的动点(包含端点)，求直线BN 与平面PCF 所成角的正弦值的最大值．【解析】：(1)证明：因为E ，F 分别为边AB ，AC 的中点，所以EF ①BC . 因为①ABC ＝90°，所以EF ①BE ，EF ①PE ，又BE ∩PE ＝E ，所以EF ①平面PBE . (2)取BE 的中点O ，连接PO ，因为PB ＝BE ＝PE ，所以PO ①BE .由(1)知EF ①平面PBE ，EF ①平面BCFE ，所以平面PBE ①平面BCFE . 又PO ①平面PBE ，平面PBE ∩平面BCFE ＝BE ，所以PO ①平面BCFE .过点O 作OM ①BC 交CF 于点M ，分别以OB ，OM ，OP 所在的直线为x 轴，y 轴，z 轴建立空间直角坐标系，如图所示，则B ⎝⎛⎭⎫12，0，0，P ⎝⎛⎭⎫0，0，32，C ⎝⎛⎭⎫12，2，0， F ⎝⎛⎭⎫－12，1，0，PC →＝⎝⎛⎭⎫12，2，－32， PF →＝⎝⎛⎭⎫－12，1，－32，由N 为线段PF 上一动点，得PN →＝λPF →(0≤λ≤1)，则可得N ⎝⎛⎭⎫－λ2，λ，32（1－λ），BN →＝⎝⎛⎭⎫－λ＋12，λ，32（1－λ）.设平面PCF 的法向量为m ＝(x ，y ，z )，则⎩⎪⎨⎪⎧PC →·m ＝0，PF →·m ＝0，即⎩⎨⎧12x ＋2y －32z ＝0，－12x ＋y －32z ＝0，取y ＝1，则x ＝－1，z ＝3，所以m ＝(－1，1，3)为平面PCF 的一个法向量．设直线BN 与平面PCF 所成的角为θ，则sin θ＝|cos 〈BN →，m 〉|＝|BN →·m ||BN →|·|m |＝25·2λ2－λ＋1＝25·2⎝⎛⎭⎫λ－142＋78≤25·78＝47035(当且仅当λ＝14时取等号)，所以直线BN 与平面PCF 所成角的正弦值的最大值为47035.7．(2020·山东淄博三模)如图①，已知正方形ABCD 的边长为4，E ，F 分别为AD ，BC 的中点，将正方形ABCD 沿EF 折成如图①所示的二面角，且二面角的大小为60°，点M 在线段AB 上(包含端点)，连接AD .(1)若M 为AB 的中点，直线MF 与平面ADE 的交点为O ，试确定点O 的位置，并证明直线OD ①平面EMC ； (2)是否存在点M ，使得直线DE 与平面EMC 所成的角为60°？若存在，求此时二面角M EC F 的余弦值；若不存在，说明理由．【答案】见解析【解析】：(1)因为直线MF ①平面ABFE ，故点O 在平面ABFE 内，也在平面ADE 内，所以点O 在平面ABFE 与平面ADE的交线(即直线AE )上(如图所示)．因为AO ①BF ，M 为AB 的中点，所以①OAM ①①FBM ，所以OM ＝MF ，AO ＝BF ，所以AO ＝2. 故点O 在EA 的延长线上且与点A 间的距离为2. 连接DF ，交EC 于点N ，因为四边形CDEF 为矩形，所以N 是EC 的中点．连接MN ，则MN 为①DOF 的中位线，所以MN ①OD ，又MN ①平面EMC ，OD ①/ 平面EMC ，所以直线OD ①平面EMC . (2)由已知可得EF ①AE ，EF ①DE ，又AE ∩DE ＝E ，所以EF ①平面ADE .所以平面ABFE ①平面ADE ，易知①ADE 为等边三角形，取AE 的中点H ，则易得DH ①平面ABFE ，以H 为坐标原点，建立如图所示的空间直角坐标系，则E (－1，0，0)，D (0，0，3)，C (0，4，3)，F (－1，4，0)，所以ED →＝(1，0，3)，EC →＝(1，4，3)．设M (1，t ，0)(0≤t ≤4)，则EM →＝(2，t ，0)，设平面EMC 的法向量为m ＝(x ，y ，z )，则⎩⎪⎨⎪⎧m ·EM →＝0，m ·EC →＝0①⎩⎨⎧2x ＋ty ＝0，x ＋4y ＋3z ＝0，取y ＝－2，则x ＝t ，z ＝8－t 3，所以m ＝⎝ ⎛⎭⎪⎫t ，－2，8－t 3为平面EMC 的一个法向量．要使直线DE 与平面EMC 所成的角为60°，则82t 2＋4＋（8－t ）23＝32，所以23t 2－4t ＋19＝32，整理得t 2－4t ＋3＝0，解得t＝1或t ＝3，所以存在点M ，使得直线DE 与平面EMC 所成的角为60°，取ED 的中点Q ，连接QA ，则QA →为平面CEF 的法向量，易得Q ⎝⎛⎭⎫－12，0，32，A (1，0，0)，所以QA →＝⎝⎛⎭⎫32，0，－32.设二面角M －EC －F 的大小为θ，则|cos θ|＝|QA →·m ||QA →|·|m |＝|2t －4|3t 2＋4＋（8－t ）23＝|t －2|t2－4t ＋19. 因为当t ＝2时，cos θ＝0，平面EMC ①平面CDEF ，所以当t ＝1时，cos θ＝－14，θ为钝角；当t ＝3时，cos θ＝14，θ为锐角．综上，二面角M －EC －F 的余弦值为±14.。

二次函数详解(附习题、答案)

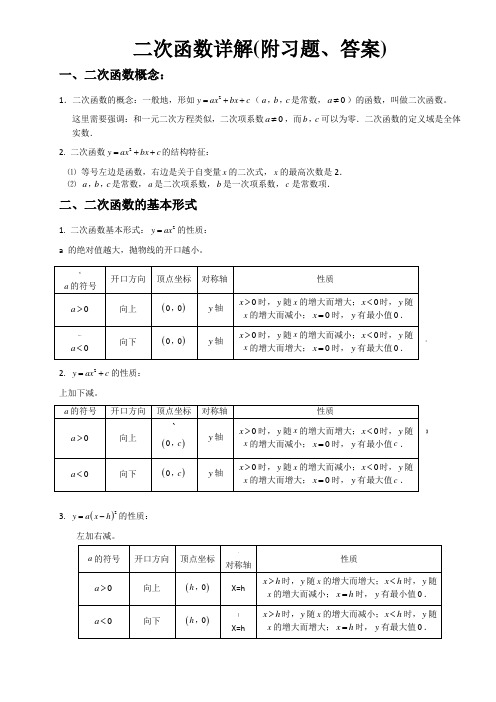
二次函数详解(附习题、答案)一、二次函数概念：1．二次函数的概念：一般地，形如2y ax bx c =++（a b c ，，是常数，0a ≠）的函数，叫做二次函数。

这里需要强调：和一元二次方程类似，二次项系数0a ≠，而b c ，可以为零．二次函数的定义域是全体实数．2. 二次函数2y ax bx c =++的结构特征：⑴ 等号左边是函数，右边是关于自变量x 的二次式，x 的最高次数是2． ⑵ a b c ，，是常数，a 是二次项系数，b 是一次项系数，c 是常数项．二、二次函数的基本形式1. 二次函数基本形式：2y ax =的性质： a 的绝对值越大，抛物线的开口越小。

:2. 2y ax c =+的性质：上加下减。

】3. ()2y a x h =-的性质：左加右减。

4. ()2y a x h k =-+的性质：?三、二次函数图象的平移1. 平移步骤：方法一：⑴ 将抛物线解析式转化成顶点式()2y a x h k =-+，确定其顶点坐标()h k ，； ⑵ 保持抛物线2y ax =的形状不变，将其顶点平移到()h k ，处，具体平移方法如下：【或左(h <0)】向右(h >0)【或左(h 平移|k|个单位2. 平移规律在原有函数的基础上“h 值正右移，负左移；k 值正上移，负下移”．概括成八个字“左加右减，上加下减”．方法二： ~⑴c bx ax y ++=2沿y 轴平移:向上（下）平移m 个单位，c bx ax y ++=2变成m c bx ax y +++=2（或m c bx ax y -++=2）⑵c bx ax y ++=2沿轴平移：向左（右）平移m 个单位，c bx ax y ++=2变成c m x b m x a y ++++=)()(2（或c m x b m x a y +-+-=)()(2）四、二次函数()2y a x h k =-+与2y ax bx c =++的比较从解析式上看，()2y a x h k =-+与2y ax bx c =++是两种不同的表达形式，后者通过配方可以得到前者，即22424b ac b y a x a a -⎛⎫=++ ⎪⎝⎭，其中2424b ac b h k a a -=-=，．五、二次函数2y ax bx c =++图象的画法五点绘图法：利用配方法将二次函数2y ax bx c =++化为顶点式2()y a x h k =-+，确定其开口方向、对称轴及顶点坐标，然后在对称轴两侧，左右对称地描点画图.一般我们选取的五点为：顶点、与y 轴的交点()0c ，、以及()0c ，关于对称轴对称的点()2h c ，、与x 轴的交点()10x ，，()20x ，（若与x 轴没有交点，则取两组关于对称轴对称的点）.画草图时应抓住以下几点：开口方向，对称轴，顶点，与x 轴的交点，与y 轴的交点.【六、二次函数2y ax bx c =++的性质1. 当0a >时，抛物线开口向上，对称轴为2bx a =-，顶点坐标为2424b ac b a a ⎛⎫-- ⎪⎝⎭，．当2b x a <-时，y 随x 的增大而减小；当2b x a >-时，y 随x 的增大而增大；当2bx a=-时，y 有最小值244ac b a-．2. 当0a <时，抛物线开口向下，对称轴为2b x a =-，顶点坐标为2424b ac b a a ⎛⎫-- ⎪⎝⎭，．当2bx a <-时，y 随x 的增大而增大；当2b x a >-时，y 随x 的增大而减小；当2bx a=-时，y 有最大值244ac b a -．七、二次函数解析式的表示方法1. 一般式：2y ax bx c =++（a ，b ，c 为常数，0a ≠）；2. 顶点式：2()y a x h k =-+（a ，h ，k 为常数，0a ≠）；3. 两根式：12()()y a x x x x =--（0a ≠，1x ，2x 是抛物线与x 轴两交点的横坐标）..注意：任何二次函数的解析式都可以化成一般式或顶点式，但并非所有的二次函数都可以写成交点式，只有抛物线与x 轴有交点，即240b ac -≥时，抛物线的解析式才可以用交点式表示．二次函数解析式的这三种形式可以互化.八、二次函数的图象与各项系数之间的关系1. 二次项系数a二次函数2y ax bx c =++中，a 作为二次项系数，显然0a ≠．⑴ 当0a >时，抛物线开口向上，a 的值越大，开口越小，反之a 的值越小，开口越大； ⑵ 当0a <时，抛物线开口向下，a 的值越小，开口越小，反之a 的值越大，开口越大．总结起来，a 决定了抛物线开口的大小和方向，a 的正负决定开口方向，a 的大小决定开口的大小． 2. 一次项系数b 】在二次项系数a 确定的前提下，b 决定了抛物线的对称轴． ⑴ 在0a >的前提下，当0b >时，02ba-<，即抛物线的对称轴在y 轴左侧；当0b =时，02ba-=，即抛物线的对称轴就是y 轴；当0b <时，02ba->，即抛物线对称轴在y 轴的右侧． ⑵ 在0a <的前提下，结论刚好与上述相反，即当0b >时，02ba->，即抛物线的对称轴在y 轴右侧；当0b =时，02ba-=，即抛物线的对称轴就是y 轴；当0b <时，02ba-<，即抛物线对称轴在y 轴的左侧．总结起来，在a 确定的前提下，b 决定了抛物线对称轴的位置．<ab 的符号的判定：对称轴abx 2-=在y 轴左边则0>ab ，在y 轴的右侧则0<ab ，概括的说就是“左同右异” 总结：3. 常数项c⑴ 当0c >时，抛物线与y 轴的交点在x 轴上方，即抛物线与y 轴交点的纵坐标为正； ⑵ 当0c =时，抛物线与y 轴的交点为坐标原点，即抛物线与y 轴交点的纵坐标为0； ⑶ 当0c <时，抛物线与y 轴的交点在x 轴下方，即抛物线与y 轴交点的纵坐标为负．总结起来，c 决定了抛物线与y 轴交点的位置．总之，只要a b c ，，都确定，那么这条抛物线就是唯一确定的．二次函数解析式的确定：@根据已知条件确定二次函数解析式，通常利用待定系数法．用待定系数法求二次函数的解析式必须根据题目的特点，选择适当的形式，才能使解题简便．一般来说，有如下几种情况：1. 已知抛物线上三点的坐标，一般选用一般式；2. 已知抛物线顶点或对称轴或最大（小）值，一般选用顶点式；3. 已知抛物线与x 轴的两个交点的横坐标，一般选用两根式；4. 已知抛物线上纵坐标相同的两点，常选用顶点式．九、二次函数图象的对称二次函数图象的对称一般有五种情况，可以用一般式或顶点式表达 1. 关于x 轴对称2y ax bx c =++关于x 轴对称后，得到的解析式是2y ax bx c =---；~()2y a x h k =-+关于x 轴对称后，得到的解析式是()2y a x h k =---；2. 关于y 轴对称2y ax bx c =++关于y 轴对称后，得到的解析式是2y ax bx c =-+；()2y a x h k =-+关于y 轴对称后，得到的解析式是()2y a x h k =++；3. 关于原点对称2y ax bx c =++关于原点对称后，得到的解析式是2y ax bx c =-+-； ()2y a x h k =-+关于原点对称后，得到的解析式是()2y a x h k =-+-； 4. 关于顶点对称（即：抛物线绕顶点旋转180°）2y ax bx c =++关于顶点对称后，得到的解析式是222b y ax bx c a=--+-；()2y a x h k =-+关于顶点对称后，得到的解析式是()2y a x h k =--+．/5. 关于点()m n ，对称 ()2y a x h k =-+关于点()m n ，对称后，得到的解析式是()222y a x h m n k =-+-+-根据对称的性质，显然无论作何种对称变换，抛物线的形状一定不会发生变化，因此a 永远不变．求抛物线的对称抛物线的表达式时，可以依据题意或方便运算的原则，选择合适的形式，习惯上是先确定原抛物线（或表达式已知的抛物线）的顶点坐标及开口方向，再确定其对称抛物线的顶点坐标及开口方向，然后再写出其对称抛物线的表达式．十、二次函数与一元二次方程：1. 二次函数与一元二次方程的关系（二次函数与x 轴交点情况）：一元二次方程20ax bx c ++=是二次函数2y ax bx c =++当函数值0y =时的特殊情况. 图象与x 轴的交点个数：① 当240b ac ∆=->时，图象与x 轴交于两点()()1200A x B x ，，，12()x x ≠，其中的12x x ，是一元二次方程()200ax bx c a ++=≠的两根．这两点间的距离21AB x x =-.，② 当0∆=时，图象与x 轴只有一个交点；③ 当0∆<时，图象与x 轴没有交点.1' 当0a >时，图象落在x 轴的上方，无论x 为任何实数，都有0y >； 2' 当0a <时，图象落在x 轴的下方，无论x 为任何实数，都有0y <．2. 抛物线2y ax bx c =++的图象与y 轴一定相交，交点坐标为(0，)c ；3. 二次函数常用解题方法总结：⑴ 求二次函数的图象与x 轴的交点坐标，需转化为一元二次方程；⑵ 求二次函数的最大（小）值需要利用配方法将二次函数由一般式转化为顶点式；⑶ 根据图象的位置判断二次函数2y ax bx c =++中a ，b ，c 的符号，或由二次函数中a ，b ，c 的符号判断图象的位置，要数形结合；⑷ 二次函数的图象关于对称轴对称，可利用这一性质，求和已知一点对称的点坐标，或已知与x 轴的一个交点坐标，可由对称性求出另一个交点坐标.`⑸ 与二次函数有关的还有二次三项式，二次三项式2(0)ax bx c a ++≠本身就是所含字母x 的二次函数；下面以0a >时为例，揭示二次函数、二次三项式和一元二次方程之间的内在联系：二次函数图像参考：，十一、函数的应用二次函数应用⎧⎪⎨⎪⎩刹车距离何时获得最大利润最大面积是多少2-32y=-2x 2y=3(x+4)22y=3x 2y=-2(x-3)2二次函数考查重点与常见题型1．考查二次函数的定义、性质，有关试题常出现在选择题中，如：…已知以x 为自变量的二次函数2)2(22--+-=m m x m y 的图像经过原点，则m 的值是2．综合考查正比例、反比例、一次函数、二次函数的图像，习题的特点是在同一直角坐标系内考查两个函数的图像，试题类型为选择题，如：如图，如果函数b kx y +=的图像在第一、二、三象限内，那么函数12-+=bx kx y 的图像大致是（）y y y y1 10 x o-1 x 0 x 0 -1 x A B C D3．考查用待定系数法求二次函数的解析式，有关习题出现的频率很高，习题类型有中档解答题和选拔性的综合题，如：已知一条抛物线经过(0,3)，(4,6)两点，对称轴为35=x ，求这条抛物线的解析式。

中考数学中档题突破专项训练一网格作图题类型三：平移、对称在网格中的作图

类型三：平移、对称在网格中的作图
1.(2022·蚌埠模拟)如图，在每个小正方形的边长为 1 个单位长度的网格中，点 A，B，C 均是格点(网格线的交点)．
(1)在图中将△ABC 平移得到△A′B′C′，使得点 B 的对应点为点 C，作出平移后的图形△A′B′C′； (2)用无刻度直尺在图中的线段 AB 上找一点 P，使∠ACP＝∠APC. 解：(1)如图，△A′B′C′即为所求．
(3)求出△A2B2C2 的面积．
解：(3)△A2B2C2 的面积为
1
1
1
3×4－2×1×4－2×1×3＝－2×2×3＝5.5.
(2)如图，点 P 即为所求．
2．(2022·福田区模拟)线段 AB 在平面直角坐标系中的位置如图所示，其中每个小正方形的边长为 1 个单位长度．
(1)将线段 AB 向左平移 6 个单位长度，作出平移后的线段 A1B1； (2)再将线段 AB 绕点(2，0)顺时针旋转 180°后得到线段 A2B2；解：(1)如图，线段 A1B1 为所求． (2)如图，线段 A2B2 为所求．
4．在如图所示的正方形网格中，每个小正方形的边长均为 1 个单位长度， △ABC 的三个顶点都在格点上．
(1)在网格中画出△ABC 向下平移 3 个单位长度得到的△A1B1C1； (2)在网格中画出△ABC 关于直线 m 对称的△A2B2C2；解：(1)如图，△A1B1C1 即为所求．
(2)如图，△A2B2C2 即为所求．
(3)观察线段 A1B1 和线段 A2B2，它们是否关于某点成中心对称？若是，请写出对称)．
3．如图，在边长为 1 个单位长度的小正方形组成的 12×12 网格中，给出了以格点(网格线的交点)为端点的线段 AB.

高考数学复数多选题专项训练之知识梳理与训练附解析(2)

高考数学复数多选题专项训练之知识梳理与训练附解析(2)一、复数多选题1．下列说法正确的是（） A ．若2z =，则4z z ⋅=B ．若复数1z ，2z 满足1212z z z z +=-，则120z z =C ．若复数z 的平方是纯虚数，则复数z 的实部和虛部相等D ．“1a ≠”是“复数()()()211z a a i a R =-+-∈是虚数”的必要不充分条件答案：AD 【分析】由求得判断A ；设出，，证明在满足时，不一定有判断B ；举例说明C 错误；由充分必要条件的判定说明D 正确. 【详解】若，则，故A 正确；设，由，可得则，而不一定为0，故B 错误；当时解析：AD 【分析】由z 求得z z ⋅判断A ；设出1z ，2z ，证明在满足1212z z z z +=-时，不一定有120z z =判断B ；举例说明C 错误；由充分必要条件的判定说明D 正确. 【详解】若2z =，则24z z z ⋅==，故A 正确；设()11111,z a bi a b R =+∈，()22222,z a b i a b R =+∈ 由1212z z z z +=-，可得()()()()222222121212121212z z a a b b z z a a b b +=+++=-=-+-则12120a a b b +=，而()()121122121212121212122z z a bi a b i a a bb a b i b a i a a a b i b a i =++=-++=++不一定为0，故B 错误；当1z i =-时22z i =-为纯虚数，其实部和虚部不相等，故C 错误；若复数()()()211z a a i a R =-+-∈是虚数，则210a -≠，即1a ≠±所以“1a ≠”是“复数()()()211z a a i a R =-+-∈是虚数”的必要不充分条件，故D 正确；【点睛】本题考查的是复数的相关知识，考查了学生对基础知识的掌握情况，属于中档题. 2．已知复数()(()()211z m m m i m R =-+-∈，则下列说法正确的是（）A ．若0m =，则共轭复数1z =- B ．若复数2z =，则m C ．若复数z 为纯虚数，则1m =±D ．若0m =，则2420z z ++=答案：BD 【分析】根据每个选项里的条件，求出相应的结果，即可判断选项的正误. 【详解】对于A ，时，，则，故A 错误；对于B ，若复数，则满足，解得，故B 正确；对于C ，若复数z 为纯虚数，则满足，解得，解析：BD 【分析】根据每个选项里的条件，求出相应的结果，即可判断选项的正误. 【详解】对于A ，0m =时，1z =-，则1z =-，故A 错误；对于B ，若复数2z =，则满足(()21210m m m ⎧-=⎪⎨-=⎪⎩，解得m ，故B 正确；对于C ，若复数z为纯虚数，则满足(()21010m m m ⎧-=⎪⎨--≠⎪⎩，解得1m =-，故C 错误；对于D ，若0m =，则1z =-+，()()221420412z z ++=+--+=+，故D 正确. 故选：BD. 【点睛】本题主要考查对复数相关概念的理解，注意不同情形下的取值要求，是一道基础题. 3．设i 为虚数单位，复数()(12)z a i i =++，则下列命题正确的是（） A ．若z 为纯虚数，则实数a 的值为2B ．若z 在复平面内对应的点在第三象限，则实数a 的取值范围是(,)122-C ．实数12a =-是z z =（z 为z 的共轭复数）的充要条件 D ．若||5()z z x i x R +=+∈，则实数a 的值为2【分析】首先应用复数的乘法得，再根据纯虚数概念、复数所在象限，以及与共轭复数或另一个复数相等，求参数的值或范围，进而可确定选项的正误【详解】∴选项A ：为纯虚数，有可得，故正确选项B解析：ACD 【分析】首先应用复数的乘法得2(12)z a a i =-++，再根据纯虚数概念、复数所在象限，以及与共轭复数或另一个复数相等，求参数的值或范围，进而可确定选项的正误【详解】()(12)2(12)z a i i a a i =++=-++∴选项A ：z 为纯虚数，有20120a a -=⎧⎨+≠⎩可得2a =，故正确选项B ：z 在复平面内对应的点在第三象限，有20120a a -<⎧⎨+<⎩解得12a <-，故错误选项C ：12a =-时，52z z ==-；z z =时，120a +=即12a =-，它们互为充要条件，故正确选项D ：||5()z z x i x R +=+∈时，有125a +=，即2a =，故正确故选：ACD 【点睛】本题考查了复数的运算及分类和概念，应用复数乘法运算求得复数，再根据复数的概念及性质、相等关系等确定参数的值或范围 4．复数21iz i+=-，i 是虚数单位，则下列结论正确的是（）A ．|z |=B ．z 的共轭复数为3122i + C ．z 的实部与虚部之和为2D ．z 在复平面内的对应点位于第一象限答案：CD 【分析】根据复数的四则运算，整理复数，再逐一分析选项，即得. 【详解】由题得，复数，可得，则A 不正确；的共轭复数为，则B 不正确；的实部与虚部之和为，则C 正确；在复平面内的对应点为，位于第一【分析】根据复数的四则运算，整理复数z ，再逐一分析选项，即得. 【详解】由题得，复数22(2)(1)13131(1)(1)122i i i i z i i i i i ++++====+--+-，可得||2z ==，则A 不正确；z 的共轭复数为1322i -，则B 不正确；z 的实部与虚部之和为13222+=，则C 正确；z 在复平面内的对应点为13(,)22，位于第一象限，则D 正确.综上，正确结论是CD. 故选：CD 【点睛】本题考查复数的定义，共轭复数以及复数的模，考查知识点全面. 5．已知复数z ，下列结论正确的是（） A ．“0z z +=”是“z 为纯虚数”的充分不必要条件 B ．“0z z +=”是“z 为纯虚数”的必要不充分条件 C ．“z z =”是“z 为实数”的充要条件 D ．“z z ⋅∈R ”是“z 为实数”的充分不必要条件答案：BC 【分析】设，可得出，利用复数的运算、复数的概念结合充分条件、必要条件的定义进行判断，从而可得出结论. 【详解】设，则，则，若，则，，若，则不为纯虚数，所以，“”是“为纯虚数”必要不充分解析：BC 【分析】设(),z a bi a b R =+∈，可得出z a bi =-，利用复数的运算、复数的概念结合充分条件、必要条件的定义进行判断，从而可得出结论. 【详解】设(),z a bi a b R =+∈，则z a bi =-，则2z z a +=，若0z z +=，则0a =，b R ∈，若0b =，则z 不为纯虚数，所以，“0z z +=”是“z 为纯虚数”必要不充分条件；若z z =，即a bi a bi +=-，可得0b =，则z 为实数，“z z =”是“z 为实数”的充要22z z a b ⋅=+∈R ，z ∴为虚数或实数，“z z ⋅∈R ”是“z 为实数”的必要不充分条件.故选：BC. 【点睛】本题考查充分条件、必要条件的判断，同时也考查了共轭复数、复数的基本概念的应用，考查推理能力，属于基础题.6．对任意1z ，2z ，z C ∈，下列结论成立的是（） A ．当m ，*n N ∈时，有m n m n z z z +=B ．当1z ，2zC ∈时，若22120z z +=，则10z =且20z = C ．互为共轭复数的两个复数的模相等，且22||||z z z z ==⋅ D ．12z z =的充要条件是12=z z答案：AC 【分析】根据复数乘法的运算律和复数的模及共轭复数的概念可判断出答案A 和C 正确；C 中可取，进行判断；D 中的必要不充分条件是. 【详解】解：由复数乘法的运算律知，A 正确；取，；，满足，但且不解析：AC 【分析】根据复数乘法的运算律和复数的模及共轭复数的概念可判断出答案A 和C 正确；C 中可取11z =，2z i =进行判断；D 中12z z =的必要不充分条件是12=z z .【详解】解：由复数乘法的运算律知，A 正确；取11z =，；2z i =，满足22120z z +=，但10z =且20z =不成立，B 错误；由复数的模及共轭复数的概念知结论成立，C 正确；由12z z =能推出12=z z ，但12||||z z =推不出12z z =，因此12z z =的必要不充分条件是12=z z ，D 错误.故选：AC 【点睛】本题主要考查复数乘法的运算律和复数的基本知识以及共轭复数的概念，属于基础题. 7．i 是虚数单位，下列说法中正确的有（） A ．若复数z 满足0z z ⋅=，则0z =B ．若复数1z ，2z 满足1212z z z z +=-，则120z z =C ．若复数()z a ai a R =+∈，则z 可能是纯虚数D ．若复数z 满足234z i =+，则z 对应的点在第一象限或第三象限答案：AD 【分析】A 选项，设出复数，根据共轭复数的相关计算，即可求出结果；B 选项，举出反例，根据复数模的计算公式，即可判断出结果；C 选项，根据纯虚数的定义，可判断出结果；D 选项，设出复数，根据题解析：AD 【分析】A 选项，设出复数，根据共轭复数的相关计算，即可求出结果；B 选项，举出反例，根据复数模的计算公式，即可判断出结果；C 选项，根据纯虚数的定义，可判断出结果；D 选项，设出复数，根据题中条件，求出复数，由几何意义，即可判断出结果. 【详解】A 选项，设(),z a bi a b R =+∈，则其共轭复数为(),z a bi a b R =-∈，则220z z a b ⋅=+=，所以0ab ，即0z =；A 正确；B 选项，若11z =，2z i =，满足1212z z z z +=-，但12z z i =不为0；B 错；C 选项，若复数()z a ai a R =+∈表示纯虚数，需要实部为0，即0a =，但此时复数0z =表示实数，故C 错；D 选项，设(),z a bi a b R =+∈，则()2222234z a bi a abi b i =+=+-=+，所以22324a b ab ⎧-=⎨=⎩，解得21a b =⎧⎨=⎩或21a b =-⎧⎨=-⎩，则2z i =+或2z i =--，所以其对应的点分别为()2,1或()2,1--，所以对应点的在第一象限或第三象限；D 正确. 故选：AD.8．以下命题正确的是（）A ．0a =是z a bi =+为纯虚数的必要不充分条件B ．满足210x +=的x 有且仅有iC ．“在区间(),a b 内()0f x '>”是“()f x 在区间(),a b 内单调递增”的充分不必要条件D ．已知()f x =()1878f x x '=答案：AC 【分析】利用纯虚数的概念以及必要不充分条件的定义可判断A 选项的正误；解方程可判断B 选项的正误；利用导数与函数单调性的关系结合充分不必要条件的定义可判断C 选项的正误；利用基本初等函数的导数公式解析：AC 【分析】利用纯虚数的概念以及必要不充分条件的定义可判断A 选项的正误；解方程210x +=可判断B 选项的正误；利用导数与函数单调性的关系结合充分不必要条件的定义可判断C 选项的正误；利用基本初等函数的导数公式可判断D 选项的正误.综合可得出结论. 【详解】对于A 选项，若复数z a bi =+为纯虚数，则0a =且0b ≠，所以，0a =是z a bi =+为纯虚数的必要不充分条件，A 选项正确；对于B 选项，解方程210x +=得x i =±，B 选项错误；对于C 选项，当(),x a b ∈时，若()0f x '>，则函数()f x 在区间(),a b 内单调递增，即“在区间(),a b 内()0f x '>”⇒“()f x 在区间(),a b 内单调递增”. 反之，取()3f x x =，()23f x x '=，当()1,1x ∈-时，()0f x '≥，此时，函数()y f x =在区间()1,1-上单调递增，即“在区间(),a b 内()0f x '>”⇐/“()f x 在区间(),a b 内单调递增”.所以，“在区间(),a b 内()0f x '>”是“()f x 在区间(),a b 内单调递增”的充分不必要条件. C 选项正确；对于D 选项，()11172488f x xx ++===，()1878f x x -'∴=，D 选项错误.故选：AC. 【点睛】本题考查命题真假的判断，涉及充分条件与必要条件的判断、实系数方程的根以及导数的计算，考查推理能力与计算能力，属于中等题.9．若复数z 满足()1z i i +=，则（）A ．1z i =-+B ．z 的实部为1C ．1z i =+D ．22z i =答案：BC 【分析】先利用复数的运算求出复数z ，然后逐个分析判断即可【详解】解：由，得，所以z 的实部为1，，，故选：BC 【点睛】此题考查复数的运算，考查复数的模，考查复数的有关概念，考查共轭解析：BC 【分析】先利用复数的运算求出复数z ，然后逐个分析判断即可【详解】解：由()1z i i +=，得2(1)2(1)11(1)(1)2i i z i i i i --====-++-，所以z 的实部为1，1z i =+，22z i =-，故选：BC 【点睛】此题考查复数的运算，考查复数的模，考查复数的有关概念，考查共轭复数，属于基础题 10．已知1z ，2z 为复数，下列命题不正确的是（） A ．若12z z =，则12=z z B ．若12=z z ，则12z z =C ．若12z z >则12z z >D ．若12z z >，则12z z >答案：BCD 【分析】根据两个复数之间不能比较大小，得到C 、D 两项是错误的，根据复数的定义和复数模的概念，可以断定A 项正确，B 项错误，从而得到答案. 【详解】因为两个复数之间只有等与不等，不能比较大小解析：BCD 【分析】根据两个复数之间不能比较大小，得到C 、D 两项是错误的，根据复数的定义和复数模的概念，可以断定A 项正确，B 项错误，从而得到答案. 【详解】因为两个复数之间只有等与不等，不能比较大小，所以C 、D 两项都不正确；当两个复数的模相等时，复数不一定相等，比如11i i -=+，但是11i i -≠+，所以B 项是错误的；因为当两个复数相等时，模一定相等，所以A 项正确；故选：BCD. 【点睛】该题考查的是有关复数的问题，涉及到的知识点有两个复数之间的关系，复数模的概念，属于基础题目.11．若复数z 满足()234z i i +=+（i 为虚数单位），则下列结论正确的有（）A ．z 的虚部为3B ．z =C ．z 的共轭复数为23i +D ．z 是第三象限的点答案：BC 【分析】利用复数的除法求出复数，利用复数的概念与几何意义可判断各选项的正误. 【详解】，，所以，复数的虚部为，，共轭复数为，复数在复平面对应的点在第四象限. 故选：BD. 【点睛】本题考解析：BC 【分析】利用复数的除法求出复数z ，利用复数的概念与几何意义可判断各选项的正误. 【详解】()234z i i +=+，34232iz i i+∴=-=-+，所以，复数z 的虚部为3-，z =共轭复数为23i +，复数z 在复平面对应的点在第四象限. 故选：BD. 【点睛】本题考查复数的四则运算、虚部、模、共轭复数以及几何意义，考查计算能力，属于基础题.12．已知复数12z =-+（其中i 为虚数单位，，则以下结论正确的是（）．A ．20zB ．2z z =C ．31z =D ．1z =答案：BCD 【分析】计算出，即可进行判断. 【详解】，，故B 正确，由于复数不能比较大小，故A 错误；，故C 正确；，故D 正确. 故选：BCD. 【点睛】本题考查复数的相关计算，属于基础题.解析：BCD 【分析】计算出23,,,z z z z ，即可进行判断. 【详解】122z =-+，221313i i=2222z z ，故B 正确，由于复数不能比较大小，故A 错误； 33131313i i i 1222222z ，故C 正确；2213122z，故D 正确.故选：BCD. 【点睛】本题考查复数的相关计算，属于基础题.13．已知复数012z i =+（i 为虚数单位）在复平面内对应的点为0P ，复数z 满足|1|||z z i -=-，下列结论正确的是（）A ．0P 点的坐标为(1,2)B ．复数0z 的共轭复数对应的点与点0P 关于虚轴对称C ．复数z 对应的点Z 在一条直线上D ．0P 与z 对应的点Z 间的距离的最小值为2答案：ACD 【分析】根据复数对应的坐标，判断A 选项的正确性.根据互为共轭复数的两个复数坐标的对称关系，判断B 选项的正确性.设出，利用，结合复数模的运算进行化简，由此判断出点的轨迹，由此判读C 选项的正确解析：ACD 【分析】根据复数对应的坐标，判断A 选项的正确性.根据互为共轭复数的两个复数坐标的对称关系，判断B 选项的正确性.设出z ，利用|1|||z z i -=-，结合复数模的运算进行化简，由此判断出Z 点的轨迹，由此判读C 选项的正确性.结合C 选项的分析，由点到直线的距离公式判断D 选项的正确性. 【详解】复数012z i =+在复平面内对应的点为0(1,2)P ，A 正确；复数0z 的共轭复数对应的点与点0P 关于实轴对称，B 错误；设(,)z x yi x y R =+∈，代入|1|||z z i -=-，得|(1)(1)i|x yi x y -+=+-，即=y x =；即Z 点在直线y x =上，C 正确；易知点0P 到直线y x =的垂线段的长度即为0P 、Z 之间距离的最小值，结合点到直线的距2=，故D 正确. 故选：ACD【点睛】本小题主要考查复数对应的坐标，考查共轭复数，考查复数模的运算，属于基础题.14．已知复数cos sin 22z i ππθθθ⎛⎫=+-<< ⎪⎝⎭（其中i 为虚数单位）下列说法正确的是（）A ．复数z 在复平面上对应的点可能落在第二象限B ．z 可能为实数C ．1z =D ．1z的虚部为sin θ 答案：BC【分析】分、、三种情况讨论，可判断AB 选项的正误；利用复数的模长公式可判断C 选项的正误；化简复数，利用复数的概念可判断D 选项的正误.【详解】对于AB 选项，当时，，，此时复数在复平面内的点解析：BC【分析】分02θπ-<<、0θ=、02πθ<<三种情况讨论，可判断AB 选项的正误；利用复数的模长公式可判断C 选项的正误；化简复数1z ，利用复数的概念可判断D 选项的正误. 【详解】对于AB 选项，当02θπ-<<时，cos 0θ>，sin 0θ<，此时复数z 在复平面内的点在第四象限；当0θ=时，1z R =-∈；当02πθ<<时，cos 0θ>，sin 0θ>，此时复数z 在复平面内的点在第一象限.A 选项错误，B 选项正确；对于C 选项，1z ==，C 选项正确；对于D 选项，()()11cos sin cos sin cos sin cos sin cos sin i i z i i i θθθθθθθθθθ-===-++⋅-，所以，复数1z 的虚部为sin θ-，D 选项错误. 故选：BC.15．若复数351i z i-=-，则（）A ．z =B ．z 的实部与虚部之差为3C ．4z i =+D ．z 在复平面内对应的点位于第四象限答案：AD【分析】根据复数的运算先求出复数z ，再根据定义、模、几何意义即可求出.【详解】解：，，z 的实部为4，虚部为，则相差5，z 对应的坐标为，故z 在复平面内对应的点位于第四象限，所以AD 正解析：AD【分析】根据复数的运算先求出复数z ，再根据定义、模、几何意义即可求出.【详解】解：()()()()351358241112i i i i z i i i i -+--====---+，z ∴==z 的实部为4，虚部为1-，则相差5，z 对应的坐标为()41-,，故z 在复平面内对应的点位于第四象限，所以AD 正确，故选：AD.16．设复数z 满足1z i z +=，则下列说法错误的是（） A ．z 为纯虚数B ．z 的虚部为12i -C ．在复平面内，z 对应的点位于第三象限D ．2z =答案：AB【分析】先由复数除法运算可得，再逐一分析选项，即可得答案.【详解】由题意得：，即，所以z 不是纯虚数，故A 错误；复数z 的虚部为，故B 错误；在复平面内，对应的点为，在第三象限，故C 正确解析：AB【分析】先由复数除法运算可得1122z i =--，再逐一分析选项，即可得答案. 【详解】由题意得：1z zi +=，即111122z i i -==---，所以z 不是纯虚数，故A 错误；复数z 的虚部为12-，故B 错误；在复平面内，z 对应的点为11(,)22--，在第三象限，故C 正确；2z ==，故D 正确. 故选：AB【点睛】本题考查复数的除法运算，纯虚数、虚部的概念，复平面内点所在象限、复数求模的运算等知识，考查计算求值的能力，属基础题.17．下面是关于复数21i z =-+（i 为虚数单位）的命题，其中真命题为（） A ．||2z = B ．22z i =C ．z 的共轭复数为1i +D ．z 的虚部为1- 答案：BD【分析】把分子分母同时乘以，整理为复数的一般形式，由复数的基本知识进行判断即可.【详解】解：，，A 错误；，B 正确；z 的共轭复数为，C 错误；z 的虚部为，D 正确.故选：BD.【点解析：BD【分析】把21iz =-+分子分母同时乘以1i --，整理为复数的一般形式，由复数的基本知识进行判断即可.【详解】解：22(1)11(1)(1)i z i i i i --===---+-+--，||z ∴=A 错误；22i z =，B 正确；z 的共轭复数为1i -+，C 错误；z 的虚部为1-，D 正确.故选：BD.【点睛】本题主要考查复数除法的基本运算、复数的基本概念，属于基础题.18．若复数z 满足(1i)3i z +=+（其中i 是虚数单位），复数z 的共轭复数为z ，则（）A ．|z |=B ．z 的实部是2C ．z 的虚部是1D ．复数z 在复平面内对应的点在第一象限答案：ABD【分析】把已知等式变形，然后利用复数代数形式的乘除运算化简，求出复数，根据共轭复数概念得到，即可判断.【详解】，，，故选项正确，的实部是，故选项正确，的虚部是，故选项错误，复解析：ABD【分析】把已知等式变形，然后利用复数代数形式的乘除运算化简，求出复数z ，根据共轭复数概念得到z ，即可判断.【详解】(1i)3i z +=+，()()()()3134221112i i i i z i i i i +-+-∴====-++-，z ∴==，故选项A 正确，z 的实部是2，故选项B 正确，z 的虚部是1-，故选项C 错误，复数2z i =+在复平面内对应的点为()2,1，在第一象限，故选项D 正确.故选：ABD .【点睛】本题主要考查的是复数代数形式的乘除运算，考查了复数的代数表示及几何意义，是基础题.19．已知复数12ω=-（i 是虚数单位），ω是ω的共轭复数，则下列的结论正确的是（）A ．2ωω=B ．31ω=-C ．210ωω++=D ．ωω> 答案：AC【分析】根据复数的运算进行化简判断即可.【详解】解：∵所以，∴，故A 正确，，故B 错误，，故C 正确，虚数不能比较大小，故D 错误，故选：AC.【点睛】本题主要考查复数的有关概念解析：AC【分析】根据复数的运算进行化简判断即可.【详解】解：∵12ω=-所以122ω=--，∴2131442ωω=--=--=，故A 正确，3211131222244ωωω⎛⎫⎛⎫⎛⎫==---+=--= ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭，故B 错误，21111022ωω++=--++=，故C 正确，虚数不能比较大小，故D 错误，故选：AC .【点睛】本题主要考查复数的有关概念和运算，结合复数的运算法则进行判断是解决本题的关键．属于中档题．20．已知i 为虚数单位，则下列选项中正确的是（）A ．复数34z i =+的模5z =B ．若复数34z i =+，则z （即复数z 的共轭复数）在复平面内对应的点在第四象限C ．若复数()()2234224m m m m +-+--i 是纯虚数，则1m =或4m =-D ．对任意的复数z ，都有20z答案：AB【分析】求解复数的模判断；由共轭复数的概念判断；由实部为0且虚部不为0求得值判断；举例说明错误．【详解】解：对于，复数的模，故正确；对于，若复数，则，在复平面内对应的点的坐标为，在第四解析：AB【分析】求解复数的模判断A ；由共轭复数的概念判断B ；由实部为0且虚部不为0求得m 值判断C ；举例说明D 错误．【详解】解：对于A ，复数34z i =+的模||5z ==，故A 正确；对于B ，若复数34z i =+，则34z i =-，在复平面内对应的点的坐标为(3,4)-，在第四象限，故B 正确；对于C ，若复数22(34)(224)m m m m i +-+--是纯虚数，则223402240m m m m ⎧+-=⎨--≠⎩，解得1m =，故C 错误；对于D ，当z i 时，210z =-<，故D 错误．故选：AB ．【点睛】本题考查复数代数形式的乘除运算，考查复数的基本概念，考查复数模的求法，属于基础题．21．已知i 为虚数单位，下列说法正确的是( )A ．若,x y R ∈，且1x yi i +=+，则1x y ==B ．任意两个虚数都不能比较大小C ．若复数1z ，2z 满足22120z z +=，则120z z == D ．i -的平方等于1答案：AB【分析】利用复数相等可选A ，利用虚数不能比较大小可选B ，利用特值法可判断C 错误，利用复数的运算性质可判断D 错误．【详解】对于选项A ，∵，且，根据复数相等的性质，则，故正确；对于选项B ，解析：AB【分析】利用复数相等可选A ，利用虚数不能比较大小可选B ，利用特值法可判断C 错误，利用复数的运算性质可判断D 错误．【详解】对于选项A ，∵,x y R ∈，且1x yi i +=+，根据复数相等的性质，则1x y ==，故正确；对于选项B ，∵虚数不能比较大小，故正确；对于选项C ，∵若复数1=z i ，2=1z 满足22120z z +=，则120z z ≠≠，故不正确；对于选项D ，∵复数()2=1i --，故不正确；故选：AB ．【点睛】本题考查复数的相关概念，涉及复数的概念、复数相等、复数计算等知识，属于基础题.22．设()()2225322z t t t t i =+-+++，t ∈R ，i 为虚数单位，则以下结论正确的是（）A ．z 对应的点在第一象限B ．z 一定不为纯虚数C ．z 一定不为实数D ．z 对应的点在实轴的下方答案：CD【分析】利用配方法得出复数的实部和虚部的取值范围，结合复数的概念和几何意义可判断出各选项的正误，由此可得出结论.【详解】，，所以，复数对应的点可能在第一象限，也可能在第二象限，故A 错误解析：CD【分析】利用配方法得出复数z 的实部和虚部的取值范围，结合复数的概念和几何意义可判断出各选项的正误，由此可得出结论.【详解】22549492532488t t t ⎛+⎫= ⎪⎝⎭+-->-，()2222110t t t ++=++>，所以，复数z 对应的点可能在第一象限，也可能在第二象限，故A 错误；当222530220t t t t ⎧+-=⎨++≠⎩，即3t =-或12t =时，z 为纯虚数，故B 错误；因为2220t t ++>恒成立，所以z 一定不为实数，故C 正确；由选项A 的分析知，z 对应的点在实轴的上方，所以z 对应的点在实轴的下方，故D 正确. 故选：CD.【点睛】本题考查复数的几何意义与复数的概念相关命题真假的判断，解题的关键就是求出复数虚部和实部的取值范围，考查计算能力与推理能力，属于中等题.。

高考数学中档题强化训练(1)——(3

高考数学中档题精选（1）1. 已知函数f(x)=cos x 2+cos 3x 2+cos 5x 2csc x 2 +cos 23x2 .(1) 求函数f(x)的最小正周期和值域； (2) 求函数f(x)的单调递增区间.解：(1) y=sin x 2(cos x 2+cos 3x 2+cos 5x 2)+1+cos3x2=12sinx+12(sin2x-sinx)+12(sin3x-sin2x)+12cos3x+12=12sin3x+12cos3x+12 =22sin(3x+π4)+12∴T=2π3 ,值域y ∈[1-22,1+22]. (2)由2k π-π2 ≤3x+π4 ≤2k π+π2 ,k ∈Z.得:2k π3-π4 ≤x ≤2k π3+π12(k ∈Z). 2. 设数列{a n }的前n 项和为S n ,已知a 1=1,S n =na n -2n(n-1)(n ∈N)(1)求证数列{a n }为等差数列，并写出其通项公式；(2)是否存在非零常数p 、q 使数列{S npn+q }是等差数列？若存在，试求出p 、q应满足的关系式，若不存在，请说明理由. 解：（1）当n ≥2时，a n =S n -S n-1=na n -(n-1)a n-1-4(n-1)，即a n -a n-1=4(n ≥2) ∴{a n }为等差数列.∵a 1=1,公差d=4,∴a n =4n-3. （2）若{S n pn+q }是等差数列，则对一切n ∈N ，都有S npn+q＝An+B, 即S n =(An+B)(pn+q),又S n =12(a 1+a n )n =2n 2-n,∴2n 2-n=Apn 2+(Aq+Bp)n+Bq要使上式恒成立，当且仅当⎪⎩⎪⎨⎧=-=+=012Bq Bp Aq Ap ，∵q ≠0,∴B ＝0，∴p q=-2,即：p+2q=0.3. 已知正三棱锥A-BCD 的边长为a ，E 、F 分别为AB 、BC 的中点，且AC ⊥DE. （Ⅰ）求此正三棱锥的体积；（Ⅱ）求二面角E-FD-B 的正弦值. 解：（Ⅰ）作AO ⊥平面BCD 于O,由正三棱锥的性质可知O 为底面中心，连CO,则CO ⊥BD,由三垂线定理知AC ⊥BD ，又AC ⊥ED,∴AC ⊥平面ABD,∴AC ⊥AD, AB ⊥AC,AB ⊥AD.在Rt △ACD 中，由AC 2+AD 2=2AC 2=a 2 可得：AC=AD=AB=22a .∴V=V B-ACD =13·12·AC ·AD ·AB=224a 3.（Ⅱ）过E 作EG ⊥平面BCD 于G ，过G 作GH ⊥FD 于H ，连EH ，由三垂线定理知EH ⊥FD,即∠EHG 为二面角E-FD-B 的平面角. ∵EG ＝12 AO 而AO ＝V B-ACD 13·S △BCD =66a ,∴EG=612a .又∵ED ＝AE 2+AD 2=(24a)2+(22a)2=104a ∵EF ∥AC ，∴EF ⊥DE.∴在Rt △FED 中，EH ＝EF ·ED DF =1512a ∴在Rt △EGH 中，sin ∠EHG ＝EG EH =105*选做题：定义在区间（－1,1）上的函数f(x)满足：①对任意x 、y ∈（－1,1）都有f(x)+f(y)=f(x+y1+xy );②当x ∈（－1,0）时，f(x)>0.（Ⅰ）求证：f(x)为奇函数；（Ⅱ）试解不等式f(x)+f(x-1)>f(12).A BCDE FOG H解：（Ⅰ）令x=y=0,则f(0)+f(0)=f(0),∴f(0)=0. 又令x ∈（－1,1），则-x ∈（－1,1），而f(x)+f(-x)=f(x-x1-x 2)=f(0)=0 ∴f(-x)=-f(x),即f(x)在（－1,1）上是奇函数. （Ⅱ）令－1<x 1<x 2<1,则x 1-x 2<0,1-x 1x 2>0,于是f(x 1)-f(x 2)=f(x 1)+f(-x 2)=f(x 1-x 21-x 1x 2)>0,即f(x 1)>f(x 2),所以f(x)在定义域上为减函数.从而f(x)+f(x-1)>f(12)等价与不等式⎪⎪⎩⎪⎪⎨⎧>-+-<-<-<<-)21()112(111112f x x x f x x.213503*********111210222-<<⇔⎩⎨⎧+-<<⇔⎩⎨⎧+-<-<<⇔⎪⎩⎪⎨⎧<-+-<<⇔x x x x x x x x x x x x 高考数学中档题精选（2）1. 已知z 是复数，且arg(z-i)=π4,|z|= 5 .求复数z. 解法1.设复数z-i 的模为r(r>0),则z-i=r(cosπ4 +isin π4), ∴i r z )122(22++=，042,5)122()22(,5||222=-+=++∴=r r r r z 即解得r= 2 ,z=1+2i.解法2.设z=x+yi,则5)1()0(15)01(145222222=++⇒⎩⎨⎧>+==+⇒⎪⎩⎪⎨⎧>--==+x x x x y y x y x y tg y x π解得x=1或－2(舍去)，所以z=1+2i.解法3.设)sin (cos 5θθi z +=则1sin 5cos 51cos 51sin 54-=⇒=-=θθθθπtg解得：,10103)4cos(,0cos ,1010)4sin(=-∴>=-πθθπθ.21)55255(5554sin )4sin(4cos )4cos(]4)4cos[(cos ,5524sin )4cos(4cos )4sin(]4)4sin[(sin i i z +=+=∴=---=+-==-+-=+-=∴ππθππθππθθππθππθππθθ 2. 已知f(x)=sin 2x-2(a-1)sinxcosx+5cos 2x+2-a,若对于任意的实数x 恒有|f(x)|≤6成立，求a 的取值范围.解：f(x)=(1-a)sin2x+2cos2x+5-a=5-2a+a 2 sin(2x+ψ)＋5-a.(ψ为一定角，大小与a 有关).∵x ∈R,∴[f(x)]max =5-a+5-2a+a 2 ,[f(x)]min =5-a-5-2a+a 2 .由|f(x)|≤6,得⎪⎩⎪⎨⎧-≤+-+≤+-⇔⎪⎩⎪⎨⎧-≥+---≤+-+-aa a aa a a a a a a a 1125125625562552222 .52915291111)11(25)1(251112222≤≤∴⎪⎪⎩⎪⎪⎨⎧≤≥≤≤-⇔⎪⎩⎪⎨⎧-≤+-+≤+-≤≤-a a a a a a a a a a a 3.斜三棱柱ABC-A 1B 1C 1的底面是边长为2的正三角形，顶点A 1在底面的射影O 是△ABC 的中心，异面直线AB 与CC 1所成的角为45°. (1)求证：AA 1⊥平面A 1BC ；(2)求二面角A 1－BC-A 的平面角的正弦值； (3)求这个斜三棱柱的体积.(1)由已知可得A 1-ABC 为正三棱锥，∠A 1AB=45° ∴∠AA 1B=∠AA 1C=90°即AA 1⊥A 1B,AA 1⊥A 1C∴AA 1⊥平面A 1BC(2)连AO 并延长交BC 于D,则AD ⊥BC ，连A 1D,则∠ADA 1为所求的角。

2023高考数学复习专项训练《面面垂直的判定》(含解析)

2023高考数学复习专项训练《面面垂直的判定》一、单选题（本大题共12小题，共60分）1.（5分）已知A={ x|3a−1<x<2a+3}，B={ x|x2−x−2⩽0}，A⊆B，则a的取值范围为()A. { a|a⩽−12} B. { a|a⩽12或a⩾0}C. { a|a⩾4}D. { a|a⩽0或a⩾4}2.（5分）定义：设函数f(x)的定义域为D，如果[m,n]⊆D，使得f(x)在[m,n]上的值域为[m,n]，则称函数f(x)在[m,n]上为“等域函数”，若定义域为[1e,e2]的函数g(x)= c x(c>0,c≠1)在其定义域的某个区间上为“等域函数”，则实数c的取值范围为()A. [2e2,1e) B. [2e2,1e]C. [e2e2,e1e] D. [e2e2,e1e)3.（5分）设x、y∈R，则“x≥2且y≥2”是“x2+y2≥4”.（）A. 充分非必要条件B. 必要非充分条件C. 充要条件D. 既非充分又非必要条件4.（5分）命题p：关于x的不等式ax2+ax−x−1<0的解集为(−∞,−1)∪(1a,+∞)的一个充分不必要条件是().A、a⩽−1B、a>0C、−2<a<0D、a<−2A. a⩽−1B. a>0C. −2<a<0D. a<−25.（5分）函数y=loga (2x−3)+√22(a>0且a≠1)的图像恒过定点P，且点P在幂函数f(x)的图像上，则f(4)=()A. 2B. 12C. 14D. 166.（5分）设ab>0，下面四个不等式：①|a+b|>|a|；②|a+b|<|b|；③|a+b|<|a−b|；④|a+b|>|a|−|b|；正确的是()A. ①和②B. ①和③C. ①和④D. ②和④7.（5分）已知ΔABC 的三个内角A ，B ，C 所对的边分别为a ，b ，c ，若b 2+c 2<a 2，且cos 2A −3sin A +1=0，则sin (C −A)+√32cos (2A −B)的取值范围为 ( )A. (−12,−√34) B. (−12,−√34] C. [0,√34] D. (−23,−12) 8.（5分）函数y =x 2+ln |x|的图象大致为( )A. B.C.D.9.（5分）已知函数f(x)=x 1−|x|(x ∈D)，有下列四个结论：①对任意x ∈D ，f(−x)+f(x)=0恒成立；②对任意m ∈(0,1)，方程|f(x)|=m 有两个不相等的实数根； ③存在函数g(x)使得g(x)的图象与f(x)的图象关于直线y =x 对称； ④对任意k ∈(1,+∞)，函数g(x)=f(x)−kx 在D 上有三个零点．则上述结论中正确的个数为()A. 1B. 2C. 3D. 410.（5分）已知函数f (x )的定义域为R ，f (x +2)为偶函数，f (2x +1)为奇函数，则( )A. f (−12)=0B. f (−1)=0C. f (2)=0D. f (4)=011.（5分）已知定义在R 上的奇函数f(x)，且当x ∈[0,+∞)时，f(x)单调递增，则不等式f(2x +1)+f(1)⩾0的解集是()A. (−∞,1)B. (−1,+∞)C. [−1,+∞)D. (−∞,1]12.（5分）已知集合A ={x|1<x <3}，集合B ={x|log 2(x +1)⩽2}，则A ∪B =()A 、{x|1<x <3}B 、{x|x ⩽3}C 、{x|−1<x <3}D 、{x|1−<x ⩽3} A. {x|1<x <3} B. {x|x ⩽3} C. {x|−1<x <3}D. {x|1−<x ⩽3}二、填空题（本大题共5小题，共25分）13.（5分）函数f(x)=x−1x中，若f（x）=0，则x=__________.14.（5分）某班有36名同学参加数学、物理、化学竞赛小组，每名同学至多参加两个小组，已知参加数学、物理、化学小组的人数分别为26，15，13，同时参加数学和物理小组的有6人，同时参加物理和化学小组的有4人，则只参加物理小组的有__________人，同时参加数学和化学小组的有__________人．15.（5分）写出一个同时具有下列性质①②③的函数f(x)： ______ .①f(x1x2)=f(x1)f(x2)；②当x∈(0,+∞)时，f′(x)>0；③f′(x)是奇函数.16.（5分）已知函数f(x)满足以下条件：①在R上单调递增；②对任意x1，x2，均有f(x1)⋅f(x2)=4f(x1+x2)，则f(x)的一个解析式为 ______.17.（5分）已知等式sin230°+sin230°+sin30°⋅sin30°=34sin220°+sin240°+sin20°⋅sin40°=34sin210°+sin250°+sin10°⋅sin50°=34请你写出一个具有一般性的等式，使你写出的等式包含了已知的等式，这个等式是______.三、解答题（本大题共6小题，共72分）18.（12分）已知集合A={x|1⩽x−1⩽4}，B={x|−2<x⩽3}，C={x|2a−1< x<2a+1}.(1)若x∈C是“x∈A”的充分条件，求实数a的取值范围；(2)若(A∩B)⊆C，求实数a的取值范围．19.（12分）已知函数f(x)=√3sinx+mcosx(m∈R).(Ⅰ)若m=1，求f(π12)的值；(Ⅰ)若m=√6，且f(x)=0，求tan2x.20.（12分）立德中学高一年级共有200名学生报名参加学校团委与学生会组织的社团组织．据统计，参加艺术社团组织的学生有103人，参加体育社团组织的学生有120人(并非每个学生必须参加某个社团).求在高一年级的报名学生中，同时参加这2个社团的最多有多少人？最少有多少人？21.（12分）已知sin(α−β)=12，sin(α+β)=13.(1)证明：tanα+5tanβ=0；(2)计算：tan(α−β)−tanα+tanβtan2α·tan(α−β)的值．22.（12分）在①两个相邻对称中心的距离为π2，②两条相邻对称轴的距离为π2，③两个相邻最高点的距离为，这三个条件中任选一个，补充在下面问题中，并对其求解．问题：函数f(x)=cos(ωx+φ)(ω>0,0<φ<π2)的图象过点(0,12)，且满足________，当α∈(0,π2)时，f(α2)=−√22，求sinα的值．23.（12分）已知函数f(x)=ax−2b x 2+1是定义在[−1,1]上的奇函数，且f(1)=1.(1)求a ，b 的值；(2)判断函数f(x)的单调性并用定义加以证明；(3)求使f(m −1)+f(2m −1)<0成立的实数m 的取值范围．四、多选题（本大题共5小题，共25分） 24.（5分）下列说法正确的是()A. “a >1”是“1a <1”的充分不必要条件B. 命题“∀x >1，x 2<1”的否定是“∃x <1，x 2⩾1”C. “x >1”是“(x −1)(x +2)>0”的必要条件D. 设a ，b ∈R ，则“a ≠0”是“ab ≠0”的必要不充分条件 25.（5分）设a >1，b >1且ab −(a +b)=1，那么( )A. a +b 有最小值2+2√2B. a +b 有最大值2+2√2C. ab 有最小值3+2√2D. ab 有最大值1+√226.（5分）已知x ，y ∈R ，x >0，y >0，且x +2y =1.则下列选项正确的是()A. 1x +1y 的最小值为4√2 B. x 2+y 2的最小值为15 C.x−2y x 2+y 2>1D. 2x+1+4y ⩾427.（5分）已知M 、N 均为实数集R 的子集，且N ∩∁R M =∅，则下列结论中正确的是( )A. M ∩∁R N =∅B. M ∪∁R N =RC. ∁R M ∪∁R N =∁R MD. ∁R M ∩∁R N =∁R M28.（5分）已知函数f(x)=2cos (ωx +ϕ)(ω>0,|ϕ|<π2)的图象上，对称中心与对称轴x =π12的最小距离为π4，则下列结论正确的是( )A. f (x )+f (5π6−x)=0 B. 当x ∈[π6,π2]时，f (x )⩾−√3C. 若g(x)=2cos2x ，则g (x −π6)=f (x )D. 若sin 4α−cos 4α=−45，α∈(0,π2)，则f (α+π4)的值为4−3√35答案和解析1.【答案】C;【解析】解：由题意知B ={ x |−1⩽x ⩽2}， (1)A =∅时，3a −1⩾2a +3，解得a ⩾4，满足题意；(2)A ≠∅时，a <4，由A ⊆B ，即有{2a +3⩽2，解得{a ⩽−12，可得a ∈∅；综上，a ⩾4. 故选：C.分别讨论A 是否为空集，结合集合的关系，可得a 的不等式组，解不等式可得所求范围．此题主要考查集合关系中的含参问题，注意对集合A 分空集和不是空集2种情况进行讨论，属于较易问题．2.【答案】D;【解析】解：由题意得，函数g(x)的图象与直线y =x 在[1e ,e 2]上有两个交点，即方程c x =x 在[1e,e 2]上有两个不等实根，即lnc =lnx x在[1e ,e 2]上有两个不等实根．设函数ℎ(x)=lnx x(1e⩽x ⩽e 2)，ℎ′(x)=1−lnx x 2，当1e⩽x <e 时，ℎ′(x)>0，函数ℎ(x)单调递增；当e <x ⩽e 2时，ℎ′(x)<0，函数ℎ(x)单调递减．所以ℎ(x)在x =e 处取得极大值，也是最大值，为ℎ(e)=1e .又ℎ(1e )=−e,ℎ(e 2)=2e 2，故2e 2⩽lnc <1e ，解得e 2e 2⩽c <e 1e.故选：D.由题意可得函数g(x)的图象与直线y =x 在[1e ,e 2]上有两个交点，即lnc =lnx x在[1e ,e 2]上有两个不等实根．构造函数，通过导数求函数的最值与区间端点值，数形结合求解即可．此题主要考查了导数的新定义问题，考查转化思想，属于中档题．3.【答案】A; 【解析】略4.【答案】null; 【解析】此题主要考查了一元二次不等式的解法，充分必要条件的应用，属于中档题. 先根据命题p 成立的充要条件，求出a 的取值范围，然后根据充分不必要条件的定义结合各选项可得答案.解：由题意命题p 即(ax −1)(x +1)<0的解集为(−∞,−1)∪(1a ,+∞)，即充要条件为{a <0−1⩽1a ，解得a ⩽−1，因为(−∞,−2)⫋(−∞,−1]所以a <−2是a ⩽−1的一个充分不必要条件，故选D.5.【答案】B; 【解析】此题主要考查了对数的恒过定点问题以及幂函数的解析式和求值，属于基础题.将定点代入幂函数解析式，可得a ，进而可求f(4).解：可知函数y =log a (2x −3)+√22(a >0且a ≠1)的图象恒过定点P(2,√22)，令幂函数为f(x)=x a ，代入P 点坐标，可得√22=2a ，则a =−12， f(x)=x −12，则f(4)=4−12=12.故选B.6.【答案】C;【解析】此题主要考查了不等式与绝对值不等式，根据ab >0，逐项判断即可得到答案.解：∵ab >0，∴a 、b 同号，∴ |a +b|>|a|，|a +b|=|a|+|b|，∴①④正确，故选C.7.【答案】A; 【解析】此题主要考查了二倍角公式，解三角形，以及三角恒等变换等内容，需要学生熟练掌握并巧妙变换．由题意，利用二倍角公式将cos2A −3sin A +1=0化成关于sin A 的一元二次方程，解出sin A 的值，利用cos A <0求出A 的取值；将A 的值和B =π−A −C 代入并化简，可以得到关于C 的三角函数，利用三角函数单调性求出值域，即所求．解：因为cos2A −3sin A +1=0，所以1−2sin2A −3sin A +1=0，所以sin A =12或−2(舍)，又因为cos A <0，所以A =5π6，所以sin (C −A)+√32cos (2A −B)=sin (C −5π6)+√32cos [2×−(π−5π6−C)]=sin (C −5π6)+√32sin C =−12cos C ，又因为C ∈(0,π6)，所以cos C ∈(√32,1)，所以−12cos C ∈(−12,−√34) .故选A.8.【答案】A;【解析】此题主要考查了函数图象的识别，关键是掌握函数的奇偶性和函数的单调性和函数值的变化趋势，属于基础题．先求出函数为偶函数，再根据函数值的变化趋势或函数的单调性即可判断．解：∵f(−x)=x 2+ln |x|=f(x)， ∴y =f(x)为偶函数，∴y =f(x)的图象关于y 轴对称，故排除B ，C ，当x >0时，y =x 2+ln x 为增函数，故排除D. 故选A .9.【答案】C;【解析】解：①函数的定义域是{x|x ≠±1},f(−x)+f(x)=−x 1−|−x|+x 1−|x|=0，故①正确；②y =|f(x)|=|x1−|x||={x x−1,x >1x 1−x ,0<x <1−x1+x,−1<x <0−x x+1,x <−1，函数的图象如图所示：y =m 与函数图象有2个交点，故②正确；③设函数g(x)上的任一点为P(x,y)关于y =x 的对称点为(y,x)在函数f(x)上，则x =y 1−|y|，当y >0时，y =xx+1，当y ⩽0时，y =x 1−x，当x =2时，y =23或y =−2，存在一个x 对着两个y 的值，所以不存在函数g(x)使得g(x)的图象与f(x)的图象关于直线v =x 对称，故③不正确； ④x1−|x|−kx =0，当x =0时，满足方程，所以方程的一个实数根是x =0，当x ≠0时，k =11−|x|,|x|=1−1k ，当k >1时，1−1k >0,x =±(1−1k )，)，所以函数有3个零所以满足方程g(x)=f(x)−kx=0的有三个实数根据0,±(1−1k点，故④正确．故正确的个数有3个．故选：C.①根据解析式计算f(−x)+f(x)=0；②画出函数y=|f(x)|的图象，由图象的交点个数判断实数根的个数；③假设存在函数g(x)满足条件，再根据函数的定义，判断选项；④根据f(x)−kx=0，求方程的实数根的个数，再判断定义域上的零点个数．此题主要考查函数的图象和性质，零点，重点考查数形结合分析问题的能力，推理能力，属于中档题型．10.【答案】B;【解析】本题是对函数奇偶性和周期性的综合考查，属于拔高题.推导出函数f(x)是以4为周期的周期函数，由已知条件得出f(1)=0，结合已知条件可得出结论.解：因为函数f(x+2)为偶函数，则f(2+x)=f(2−x)，可得f(x+3)=f(1−x)，因为函数f(2x+1)为奇函数，则f(1−2x)=−f(2x+1)，所以，f(1−x)=−f(x+1)，所以，f(x+3)=−f(x+1)=f(x−1)，即f(x)=f(x+4)，故函数f(x)是以4为周期的周期函数，因为函数F(x)=f(2x+1)为奇函数，则F(0)=f(1)=0，故f(−1)=−f(1)=0，其它三个选项未知.故选B.11.【答案】C;【解析】此题主要考查综合运用函数的单调性与奇偶性解不等式，属于中档题.解：因为函数在[0,+∞)上是增函数，且函数是奇函数，所以函数在(−∞,0)上是增函数，函数在x=0处连续，所以函数在R上是增函数，又f(−1)=−f(1)，所以不等式可化为f(2x+1)⩾−f(1)=f(−1)，所以2x+1⩾−1，解得x⩾−1，即不等式的解集为[−1,+∞).故选C.12.【答案】null;【解析】解：集合A={x|1<x<3}，集合B={x|log2(x+1)⩽2}={x|−1<x⩽3}，则A∪B={x|−1<x⩽3}.故选：D.求出集合A，集合B，利用并集定义能求出A∪B.此题主要考查集合的运算，考查并集定义、不等式性质等基础知识，考查运算求解能力，是基础题．13.【答案】1或-1;【解析】略14.【答案】5;8;【解析】此题主要考查运用集合间的关系确定元素个数问题以及venn图的运用，属于基础题．把集合间的关系利用方程表示出来，再解方程即可．解：由条件知，每名同学至多参加两个小组，故不可能出现一名同学同时参加数学、物理、化学小组，因为参加数学和物理小组的有6人，同时参加物理和化学小组的有4人，所以只参加物理的有15−6−4=5人．设同时参加数学和化学小组的人数有x人，则只参加数学的有26−6−x=20−x，只参加化学的有13−4−x=9−x.又总人数为36人，即20−x+x+6+4+5+9−x=36，所以44−x=36，解得x=8.即同时参加数学和化学小组的人数有8人，15.【答案】f(x)=x2;【解析】此题主要考查了幂函数的求导公式，奇函数的定义及判断，考查了计算能力，属于基础题．函数f(x)=x 2，f(x 1x 2)=(x 1x 2)2=x 12x 22=f(x 1)f(x 2)满足①，求出导函数，可判断满足②③．解：f(x)=x 2时，f(x 1x 2)=(x 1x 2)2=x 12x 22=f(x 1)f(x 2)；当x ∈(0,+∞)时，f′(x)=2x >0；f′(x)=2x 是奇函数．故答案为：f(x)=x 2.16.【答案】f （x ）=2x+2;【解析】解：因为函数f(x)满足对任意x 1，x 2，均有f(x 1)⋅f(x 2)=4f(x 1+x 2)，故考虑基本初等函数中的指数函数，又f(x)在R 上单调递增，则指数函数的底数大于1，所以f(x)的一个解析式为f(x)=2x+2. 故答案为：f(x)=2x+2.由条件②，考虑为基本初等函数中的指数函数，再利用单调性，即可得到答案．此题主要考查了基本初等函数性质的理解与应用，指数函数性质的理解与应用，考查了逻辑推理能力，属于基础题．17.【答案】si n 2α+si n 2（60°-α）+sinα•sin （60°-α）=34;【解析】解：等式的右边为常数34，等式左边的两个角之和为60°，故由归纳推理可知，满足条件的一个结论可以是：sin 2α+sin 2(60°−α)+sinα⋅sin(60°−α)=34.故答案为：sin 2α+sin 2(60°−α)+sinα⋅sin(60°−α)=34.根据两个等式的特点，确定角和角之间的关系，然后利用归纳推理归纳出结论．此题主要考查归纳推理的应用，根据归纳推理，先从条件中确定等式的规律是解决此类问题的基本思路，属于基础题．18.【答案】解：（1）集合A={x|1≤x -1≤4}={x|2≤x≤5}，C={x|2a-1＜x ＜2a+1}， ∵x ∈C 是“x ∈A”的充分条件，∴{2a +1≤52a −1≥2，解得32≤a ≤2， ∴实数a 的取值范围是[32，2]；（2）∵集合A={x|1≤x -1≤4}={x|2≤x≤5}，B={x|-2＜x≤3}，C={x|2a-1＜x ＜2a+1}， ∴A∩B={x|2≤x≤3}，（A∩B ）⊆C ，∴{2a −1<22a +1>3，解得1＜a ＜32， ∴实数a 的取值范围是（1，32）．;【解析】(1)求出集合A ，利用x ∈C 是“x ∈A ”的充分条件，列出不等式组，由此能求出实数a 的取值范围；(2)利用交集定义求出A ∩B ，利用(A ∩B)⊆C ，列出不等式组，由此能求出实数a 的取值范围．此题主要考查集合的运算，考查充分条件、子集、交集定义、不等式性质等基础知识，考查运算求解能力，是基础题．19.【答案】解：（Ⅰ）若m=1，则函数f （x ）=√3sinx+cosx=2sin （x+π6）， ∴f （π12）=2sin π4=√2．（Ⅱ）∵m=√6，f （x ）=√3sinx+√6cosx=0， ∴√3sinx-=-√6cosx ，∴tanx=-√2， ∴tan2x=2tanx 1−tan 2x =2√2．;【解析】(Ⅰ)由题意，利用两角和差的三角公式化简函数f(x)的解析式，从而得到f(π12)的值．(Ⅰ)先由题意求得tanx 的值，再利用二倍角的正切公式，计算tan2x 的值．此题主要考查两角和差的三角公式，二倍角的正切公式，属于基础题．20.【答案】解：由题意：当艺术社团组织的103名学生都参加体育社团组织时，同时参加这2个社团的学生最多，且有103人；当每个学生都参加某个社团时，同时参加这2个社团的学生最少，且有103+120-200=23人，所以同时参加这2个社团的最多有103名学生，最少有23名学生．; 【解析】由题可知当艺术社团组织的学生都参加体育社团组织时，同时参加这2个社团的人数最多，当每个学生都参加某个社团时，同时参加这2个社团的学生最少．此题主要考查集合的应用，考查运算求解能力，属于基础题．21.【答案】解：（1）证明：由条件sin(α−β)=12，sin(α+β)=13，即sinαcosβ−cosαsinβ=12，sinαcosβ+cosαsinβ=13，解得sinαcosβ=512，cosαsinβ=−112，可得tanαtanβ=-5，从而可得tanα=-5tanβ，tanα+5tanβ=0得证．（2）由tan(α−β)=tanα−tanβ1+tanαtanβ，可得tanα-tanβ=tan （α-β）（1+tanαtanβ），∴原式=tan(α−β)−tanα+tanβtan 2αtan(α−β)=tan(α−β)−tan(α−β)(1+tanαtanβ)tan 2αtan(α−β)=−tan(α−β)·tanαtanβtan 2αtan(α−β)=−tanβtanα=15．;【解析】(1)由题意，把所给条件利用两角和差的三角公式展开，化简可得结论． (2)由题意，把两角差的正切公式展开变形，代入要求的式子化简，可得结论．此题主要考查两角和差的三角公式的应用，同角三角函数的基本关系，属于中档题．22.【答案】解：由函数f(x)=cos(ωx +φ)的图象过点(0,12)，得f(0)=cosφ=12，又因为0<φ<π2，所以φ=π3，在①②③三个条件中任选一个，可知最小正周期T =π，根据T =2π|ω|，得ω=2，所以f(x)=cos(2x +π3)，由f(α2)=−√22，得cos(α+π3)=−√22，由α∈(0,π2)，得α+π3∈(π3,5π6)，所以sin(α+π3)=√1−cos 2(α+π3)=√22， sinα=sin[(α+π3)−π3]=sin(α+π3)cos π3−cos(α+π3)sin π3 =√22×12−(−√22)×√32=√2+√64. ;【解析】此题主要考查三角恒等变换和三角函数的图象和性质，属于中档题. 先由f(0)=12求出φ，由三个条件中任选一个，可知最小正周期T =π，得ω=2，求出f(x) ，结合条件以及同角三角函数关系求得sin(α+π3)，再利用两角差的正弦公式即可求解.23.【答案】null; 【解析】(1)由奇函数的性质可得f(0)=0，可求得b 的值，再由f(1)=1可求得a 的值，从而可得a ，b 的值；(2)f(x)在[−1,1]上是增函数，利用增函数的定义即可证明；(3)根据函数的奇偶性与单调性将不等式转化为关于m 的一次不等式，求解即可．此题主要考查函数奇偶性与单调性的综合，考查不等式的解法，考查转化思想与运算求解能力，属于中档题．24.【答案】AD;【解析】解：对于A ：当“a >1”时“1a <1”成立，反之不成立，故“a >1”是“1a <1”的充分不必要条件，故A 正确；对于B ：命题“任意x >1，都有x 2<1”的否定是“存在x >1，使得x 2⩾1”故B 不正确；对于C ：x >1，则(x −1)(x +2)>0，但由(x −1)(x +2)>0，不能推出x >1，故“x >1”是“(x −1)(x +2)>0”的充分不必要条件，故C 不正确；对于D ：设a ，b ∈R ，则“a ≠0”推不出“ab ≠0”，由“ab ≠0”能够推出“a ≠0”，故“a ≠0”是“ab ≠0”的必要不充分条件，故D 正确．故选：AD.直接利用充分条件和必要条件，命题的否定，简易逻辑中的相关知识的应用判断A 、B 、C 、D 的结论此题主要考查的知识要点：充分条件和必要条件，命题的否定，简易逻辑，主要考查学生的运算能力和数学思维能力，属于基础题．25.【答案】AC;【解析】解：∵a >1，b >1， ∴ab =1+(a +b)⩽(a+b 2)2(当且仅当a =b >1时，取等号)，即(a +b)2−4(a +b)−4⩾0且a +b >2， ∴a +b ⩾2+2√2，∴a +b 有最小值2+2√2，即选项A 正确，B 错误；由ab −(a +b)=1，得ab −1=a +b ⩾2√ab (当且仅当a =b >1时，取等号)，即ab −2√ab −1⩾0且ab>1， ∴ab ⩾3+2√2，∴ab 有最小值3+2√2，即选项C 正确，D 错误．故选：AC ．由(a +b)⩽(a+b 2)2，可推出a +b 的最小值；由a +b ⩾2√ab ，可推出ab 的最小值．该题考查基本不等式的应用，熟练掌握基本不等式的各种变形是解答该题的关键，考查学生的逻辑推理能力和运算能力，属于基础题．26.【答案】BD;【解析】解：对于A ：已知x ，y ∈R ，x >0，y >0，且x +2y =1，所以1x +1y =x+2y x+x+2y y=1+3+2y x+xy ⩾4+2√2，当且仅当x 2=2y 2等号成立，故A 错误；对于B ：x 2+y 2=(1−2y)2+y 2=5y 2−4y +1=5(y −25)2+15，当y =25时，最小值为15；故B 正确；对于C ：当x =12，y =14时，x−2yx 2+y 2>1不成立，故C 错误；对于D ：2x+1+4y =2x+1+22y ⩾2√2x+2y+1=4，当且仅当y =12时，等号成立，故D正确．故选：BD.直接利用不等式的性质和基本不等式的应用判断A、B、C、D的结论．此题主要考查的知识要点：不等式的性质，基本不等式的应用，主要考查学生的运算能力和数学思维能力，属于中档题．27.【答案】BD;【解析】解：因为N∩∁R M=∅，所以N⊆M，所以M∩∁R N≠∅，选项A错误；M∪∁R N=R，选项B正确；∁R M∪∁R N=∁R N，选项C错误；∁R M∩∁R N=∁R M，选项D正确．故选：BD.根据题意知N⊆M，利用交集、并集和补集的定义，判断正误即可．此题主要考查了集合的定义与运算问题，也考查了推理与判断能力，是基础题．28.【答案】BD;【解析】此题主要考查了余弦函数的图象及性质，同角三角函数关系及两角差的余弦公式，属于中档题.根据对称中心与对称轴的最小距离求出周期T，得到ω=2，再根据对称轴方程求出ϕ=−π6，再根据余弦函数的图象及性质对四个选项一一判断即可，选项D先利用同角三角函数关系及二倍角公式化简，再求出f(α+π4).解：由题有T=π，则ω=2，又由对称轴x=π12可得，2×π12+ϕ=kπ，k∈Z，又|ϕ|<π2，则ϕ=−π6，故f(x)=2cos(2x−π6)，对于A，因为f(x)+f(5π6−x)=2cos(2x−π6)+2cos(53π−2x−π6)=2cos(2x−π6)−2sin2x=2cos2x cosπ6+2sin2x sinπ6−2sin2x=√3cos2x−sin2x则f(x)+f(5π6−x)=0错误，故A选项不正确.对于B，x∈[π6,π2]，则2x−π6∈[π6,5π6]，则f(x)∈[−√3,√3]，故B选项正确；对于C，f(x)=2cos2(x−π12)，应将g(x)=2cos2x的图象向右平移π12个单位，故C选项错误．对于D，sin4α−cos4α=−cos2α=−45，且α∈(0,π2)，则2α∈(0,π)，故cos2α=45，sin2α=35，而f (α+π4)=2cos (2α+π3)=cos 2α−√3sin 2α=4−3√35，故D 选项正确；故选BD .。

2024小升初专项训练归一归总问题练习及答案

第二讲归一归总问题A 较易【例1】1．若2台收割机3天可以收割小麦450亩，则用7台收割机收割2100亩小麦需要4天．【分析】首先求出每台每天的工作效率，再求出7台1天的工作效率，因为工作量÷工作效率=工作时间，据此解答即可．【解答】解：2100÷（450÷3÷2×7）=2100÷（75×7）=2100÷525=4（天），答：用7台收割机收割2100亩小麦需要4天．故答案为：4．【点评】此题属于二次反归一问题，首先用连除求出单一量，再用除法求出部分量．【例2】2．修一段路，24人12天可以修完，现在24人修了4天后，再增加8人，还要6天才能修完．【分析】24人12天可修完，则需要总工数为24×12，现在24人修了4天后，还剩下24×（12﹣4）个工数，此时又增加了8人，则还需要24×（12﹣4）÷（24+8）天才能修完．【解答】解：24×（12﹣4）÷（24+8）=24×8÷32=6（天）答：还要6天才能修完．故答案为：6【点评】在求出需要总工数的基础上，根据总工数与每天的工数之间的关系进行解答比较简单．【例3】3．4名瓦工用面积为80平方厘米的地砖铺6平米的房间，用了3天时间：16名瓦工用另一种规格的地砖铺了12平方米的房间，用了12天时间．每名瓦工铺一块任何大小的地砖所需要的时间都相等．那么，第二个房间所用的地砖面积是10平方厘米．【分析】要想求出两次用的砖的大小关系，我们就要知道两次工作量的关系，如果第二次工作量是第一次的2倍，那么第一次砖的大小就是第二次的2倍．【解答】解：考虑两次铺砖的比例关系：16名砖瓦工铺12天所铺的块数，应是4名砖瓦工铺3天所铺块数1612=1643⨯⨯倍，但房间大小方面，第二个房间只是第一个房间12÷6=2倍，这说明第一房间的地砖大小是第二个房间地砖大小的16÷2=8倍，故知第二个房间的地砖大小为80÷8=10平方厘米．答：第二个房间所用的砖的面积是10平方厘米．【点评】此题特别注意16人工作12天是4人工作3天的16倍，而不是4倍．倍比法的好处就是直接找到倍数关系即可求解，不需要求出单位量．【例4】4．7头奶牛5天产牛奶630千克，照这样计算，15头奶牛8天可以产牛奶2160千克．【分析】以1头奶牛1天产的牛奶为单一量，则1头奶牛1天产奶（630÷5÷7=18）千克，那么15头奶牛8天可以产牛奶：18×8×15=2160千克；由此解答即可．【解答】解：（630÷7÷5）×8×15=18×8×15=2160（千克）；答：照这样计算，15头奶牛8天可产牛奶2160千克；故答案为：2160．【点评】解答此题的关键是先求得单一量，再由不变的单一量求得总量．【例5】5．加工一批39600件的大衣，30个人10天完成了13200件，其余的要求在15天内完成，要增加10人．【分析】先求出平均每人每天完成多少件大衣，然后求出剩下的大衣件数，再求出这些大衣15天需要多少人，用这个人数减去已有的30人就是要增加的人数．【解答】解：13200÷30÷10=44（件），39600﹣13200=26400（件），26400÷（44×15）=40（人），40﹣30=10（人）；答：要增加10人．故答案为：10．【点评】先求出单一的量，再根据这个量来求解．【例6】6．东风服装厂要做6500件同样的上衣，按照以往3人10天可做195件上衣的进度，如果要25天完成，需要40个工人同时做．【分析】先求出1人1天可做的上衣的件数，因为进度相同，所以再总件数除以需要的天数即可得需要多少个工人同时做．【解答】解：6500÷（195÷3÷10）÷25=6500÷6.5÷25=40（个）答：需要40个工人同时做．故答案为：40．【点评】本题考查了归一应用题，关键是先求出1人1天可做的上衣的件数．【例7】7．一台铺路机3小时铺路162米，照这样计算，2台铺路机9小时共铺路972米．【分析】照这样计算，说明一台铺路机的效率不变，先求出每台铺路机每小时铺多少米的路，然后再乘2求出2台铺路机每小时铺多少米的路，再乘9就是2台铺路机9小时可以铺路多少米．据此解答．【解答】解：162÷3×2×9=54×2×9=972（米）答：2台铺路机9小时共铺路972米．故答案为：972．【点评】本题关键是先求出单一的量，再根据单一的量求出总量．【例8】8．商店有三种颜色的油漆，红色的每桶1.5千克，黄色的每桶2千克，白色的每桶2.5千克．为了方便顾客，商店把这三种油漆整装成每桶0.5千克油漆的小桶．结果三种油漆分别装了200桶、225桶、208桶．未分装之前，红、黄、白色的油漆依次有66.7、56.25、41.6桶．【分析】漆整装成每桶0.5千克油漆的小桶，三种油漆分别装了200桶、225桶、208桶，根据每桶质量×桶数=总质量求出红、黄、白色的油漆的总质量，然后根据总质量÷原来每桶质量=原来桶数，即可得解．【解答】解：红色：（0.5×200）÷1.5≈66.7（桶）黄色：（0.5×225）÷2=56.25（桶）白色：（0.5×208）÷2.5=41.6（桶）答：未分装之前，红、黄、白色的油漆依次有66.7、56.25、41.6桶．故答案为：66.7，56.25，41.6．【点评】解答此题需要分情况探讨，明确题目中所给数量属于哪一种情况，由此选择正确的解题方法．【例9】9．四（4）班植树节参加植树活动，全班计划每小时种植20棵树，实际每小时比计划多种8棵，结果提前2小时种完，问四（4）班一共种植了140棵树．【分析】先求出实际每小时植树多少棵，提前2小时种完，用实际每小时种树的棵数乘上2小时，求出2小时里面实际多种了多少棵，再除以每小时实际比计划多种的棵数，即可求出计划植树的时间，然后乘计划每小时植树的棵数即可求解．【解答】解：（20+8）×2÷8=56÷8=7（小时）20×7=140（棵）答：四（4）班一共种植了140棵树．故答案为：140棵．【点评】解决本题也可以用方程的方法求解，设计划植树的时间是x小时，根据工作量=工作效率×工作时间分别表示出计划和实际的植树的棵数，再根据植树的棵数不变列出方程，求出计划的时间，进而求出植树的棵数，如下：设计划植树的时间是x小时，则：20x=（20+8）×（x﹣2）20x=28×（x﹣2）20x=28x﹣568x=56x=720×7=140（棵）答：四（4）班一共种植了140棵树．【例10】10．一种钢轨，4根共重1900千克，现在有95000千克钢，可以制造这种钢轨200根．（损耗忽略不计）【分析】根据题意，用1900÷4先求出平均每根钢轨重的千克数，进而看95000千克里面有多少个（1900÷4），即可得解．【解答】解：95000÷（1900÷4）=95000÷475=200（根）．答：可以制造这种钢轨200根．故答案为：200．【点评】此题属于归一应用题，关键是先求出平均每根钢轨的重量，进而得解．【例11】11．一个成年人平均每分钟呼吸16次，每次吸入500立方厘米空气．问：他在一昼夜里吸入11.52立方米空气．【分析】一昼夜是24小时，每小时是60分钟，先计算出一昼夜有多少分钟，即24×60=1440分钟，再乘16次计算出呼吸的次数，再乘每次吸入500立方厘米的空气，即可求出一昼夜吸入多少立方厘米的空气，再根据1立方米=1000000立方厘米进行单位换算，问题即可得解．【解答】解：24×60×16×500=23040×500=11520000（立方厘米）11520000立方厘米=11.52立方米答：他在一昼夜里吸入11.52立方米空气．故答案为：11.52．【点评】解决本题根据乘法的意义：求几个几是多少，用乘法求解；注意单位之间的换算．【例12】12．3名工人5小时加工零件90件，要在10小时完成540个零件的加工，需要工人9人．【分析】由“3名工人5小时加工零件90件”，可知每人每小时加工零件90÷5÷3=6（个）；要在10小时完成540个零件，那么每小时完成540÷10=54（个），因此需要工人54÷6=9（人）．【解答】解：540÷10÷（90÷5÷3）=54÷6=9（人）答：需要工人9人．故答案为：9．【点评】此题解答的关键是先求出每人每小时加工的零件个数，然后再求10小时完成540个零件需要的人数．【例13】13．5名工人5小时加工了5个零件，则1名工人1小时加工1个零件．×．（判断对错）【分析】5名工人5小时加工了5个零件，5名工人1小时加工的个数就是（5÷5）个，1名工人1小加工的个数就是[（5÷5）÷5]个，据此解答．【解答】解：（5÷5）÷5=1÷5=0.2（个）答：1名工人1小时加工0.2个零件．故答案为：×．【点评】本题的只要求出1名工人1小时加工零件的个数，进行比较既可．【例14】14．如果平均1个同学1天植树10棵，那么，3个同学4天共植树120棵．【分析】先用120棵除以4，求出3个同学1天植树多少棵，再除以3人，就是每人每天平均植树多少棵．【解答】解：120÷4÷3=30÷3=10（棵）；答：平均1个同学1天植树10棵．故答案为：10．【点评】本题考查了归一问题，根据除法平均分的意义，列出连除的算式求解即可．【例15】15．4台同样的织布机2.5小时织布1.3千米，照这样计算，6台同样的织布机4.5小时织布多少千米？【分析】求出1台织布机1小时织布1.3÷2.5÷4=0.13千米，即可求出6台同样的织布机4.5小时织布多少千米【解答】解：由题意，1台织布机1小时织布：1.3÷2.5÷4=0.13（千米），所以6台同样的织布机4.5小时织布：0.13×6×4.5=3.51（千米），答：6台同样的织布机4.5小时织布3.51千米．【点评】本题考查归一归问题，考查学生转化问题的能力，属于中档题．【例16】16．爸爸每天给小军同样多的零花钱，小军原来有一些钱，如果每天用10元，可以用6天；如果每天用15元，可以用3天，小军原来有30元．【分析】根据题意，求出爸爸每天给小军同样多的零花钱，再根据每天用10元，可以用6天，即可求出小军原来的钱．【解答】解：由题意，设爸爸每天给小军同样多的零花钱为x元，则因为每天用10元，可以用6天，所以小军原来有一些钱为6×10﹣6x，因为每天用15元，可以用3天，所以小军原来有一些钱为15×3﹣3x，所以6×10﹣6x=15×3﹣3x，解得x=5元，∴小军原来有6×10﹣6×5=30元，故答案为30．【点评】本题考查归一归问题，考查学生的计算能力，解题的关键是求出爸爸每天给小军的零花钱．【例17】17．一个手电筒每6小时耗费3个电池．电池以每包4个销售，那么要使用手电筒30小时至少需要购买电池4包．【分析】先求出30小时里面有多少个6小时，然后再乘3就是需要的电池的总数量，再用总数量除以每包的数量，由此即可求解．【解答】解：30÷6×3=5÷3=15（个）15÷4=3（包）…1（个）余下的一个还需要多买1包3+1=4（包）答：要使用手电筒30小时至少需要购买电池4包．故答案为：4．【点评】解决本题要注意，有余数的情况下根据“进一法”保留整数．【例18】18．9只母鸡在4天内下12只蛋，问4只母鸡在9天内下12只蛋．【分析】要求4只母鸡在9天内下蛋的只数，要先求出平均1只母鸡在1天内下蛋的只数，进而得解．【解答】解：平均1只母鸡在1天内下蛋的只数：12÷9÷4=13（只），4只母鸡在9天内下蛋的只数：13×4×9=12（只）；答：4只母鸡在9天内下12只蛋．故答案为：12．【点评】解决此题也可以根据“9只母鸡在4天内下12只蛋”，直接判断出“4只母鸡在9天内也是下12只蛋”．【例19】19．一户居民住宅楼原有3户装空调，现又增加一户，这4台空调全部打开时就会烧断保险丝，因此最多只能同时用3台空调．这样，在24小时内平均每户可以使用空调18小时．【分析】有四户装空调，全部打开时就会烧断保险丝，因此最多只能同时用3台空调，就要有一户不能打开，应轮流停开，一个循环须四次，各少用一次，把24小时平均分成4份，每份是24÷4=6（小时），即可求出问题．【解答】解：因为有四户装空调，全部打开时就会烧断保险丝，因此最多只能同时用3台空调，就要有一户不能打开，应轮流停开，一个循环须四次，各少用一次，把24 小时平均分成4份，即：24÷4=6（小时），24﹣6=18（小时），答：在24小时内平均每户可以使用空调18小时．【点评】本题也可以这样想：因为24小时中每一小时都有3户同时使用，所以共使用24×3=72小时，72小时平均分给4户，得72÷4=18小时．【例20】20．筑路队，修一段路，6个人45天完成，如果增加9人，18天完成．【分析】先求出6个人45天完成的工作总量，再求现在总人数，最后即可求出所用的天数．【解答】解：6×45÷（6+9）=18（天）；答：18天完成．故答案为：18．【点评】此题主要考查归总应用题的解题思路和方法．【例21】21．54人12天修水渠1944米，如果人数增加18人，天数缩到原来的一半，可修水渠1296米．【分析】先用1944÷54÷12求出一人一天可修水渠多少米，然后根据题意，用12÷2计算出后来用的天数，继而用“一人一天可修水渠的数量×后来的人数×需用的天数”进行解答即可．【解答】解：（1944÷54÷12）×（18+54）×（12÷2），=3×72×6，=1296（米）；答：可修水渠1296米．故答案为：1296．【点评】解答此题的关键是先求出一人一天可修水渠多少米，进而根据求几个相同加数的和是多少，用连乘解答即可．【例22】22．红光大队用拖拉机耕地，2台3小时耕75公亩，照这样算，4台5小时耕250公亩．【分析】根据题意，关键理解“照这样算”，意思是平均每台每小时的工作效率是一定的；首先求出1台1小时耕地多少公亩，再求4台5小时耕地多少公亩，由此列式解答．【解答】解：75÷3÷2×4×5=25÷2×4×5=12.5×4×5=250（公亩）．答：4台5小时耕250公亩．故答案为：250．【点评】此题属于二次归一问题，即用两步除法求出单一量，再用两步乘法求出总数量；解答关键是抓住“照这样算”去分析求单一量．【例23】23．某车间接到任务，要在15天制造12000个零件．后来任务增加28%日产量也提高15．这样16天完成．【分析】制造12000个零件，原任务加上增加的28%可以计算后来的任务；要在15天制造12000个零件可以计算日产量，日产量加上提高的15可得后来的日产量，后来的任务除以后来的日产量可得完成的天数．【解答】解：任务增加后需要生产的零件：12000+12000×28%=15360（个），任务增加后的日产量：12000÷15+12000÷15×15，=800+160，=960（个），完成任务需要的天数：15360÷960=16（天）．答：这样16天完成．故答案为：16．【点评】分析题干，根据数量关系分别求出任务增加后的生产总量与日产量，即可计算需要的天数．【例24】24．一批产品，28人25天可以收割完，生产5天后，此项任务要提前10天完成，应增加28人．【分析】根据题意，把每人每天的工作量看再1份，求此总工作量是多少份减去5天完成的，再求剩下的工作量用几天完成，减求原来的人数即是需要增加的人数．由此解答．【解答】解：（28×25﹣28×5）÷（25﹣5﹣10）﹣28，=（700﹣140）÷10﹣28，=560÷10﹣28，=56﹣28，=28（人）．答：应增加28人．故答案为：28．【点评】此题的解答首先把每人每天的工作量看再1份，然后进一步分析要求什么必须先求什么，理清解题思路，再列式解答即可．【例25】25．某食堂存有16人可吃15天的米，16人吃了5天后，走了6人，余下的可吃16天．【分析】根据食堂存有16人可吃15天的米，可以计算米的总量，减去16人吃了5天的，就是剩下的米，而剩下的米有（16﹣6）人吃，用剩下的米除以剩下的人数，可得余下的可以吃的天数．【解答】解：（15×16﹣5×16）÷（16﹣6），=160÷10，=16（天）．故答案为：16．【点评】分析题干，弄清数量关系是解决这个问题的关键．【例26】26．某工程队，16个工人9天能挖水沟1872米，27个工人14天能挖4914米．【分析】先用除法求出1个工人每天挖多少米，再乘上27人和14天即可．【解答】解：1872÷16÷9×27×14，=117÷9×27×14，=13×27×14，=4914（米）．故答案为：4914．【点评】先求出不变的单一的量，再求总量．【例27】27．5台车床3小时能生产零件600个，照这样计算，11台这样的车床8小时可以生产零件3520个．【分析】根据题意，5台车床3小时能生产零件600个可以求出1台车床1小时生产的零件是600÷5÷3=40（个），再根据题目给出的条件就能求出11台这样的车床8小时可以生产零件的个数．【解答】解：由题意可得，1台车床1小时生产的零件是：600÷5÷3=40（个），那么11台这样的车床8小时可以生产零件是：40×11×8=3520（个）．故答案为：3520．【点评】先根据已知条件，求出单位时间内一台车床生产的零件个数，然后再根据题中的条件和问题求出结果．【例28】28．某电子产品加工厂原计划5人16天生产2400打计算机芯片，后来由于订货增加，采用新工艺生产，工效是原来的1.5倍，但还需要8人20天才能完成生产任务．这样后来生产的数量是原计划生产数的3倍．【分析】先求出平均每人每天的工作效率是多少，然后求出后来的每人每天的工作效率是多少；用这个工作效率乘工作时间和工作人数求出后来的工作量；再用的工作量除以原来的工作量即可．【解答】解：2400÷16÷5，=150÷5，=30（打）；30×1.5×8×20，=45×8×20，=360×20，=7200（打）；7200÷2400=3；答：后来生产的生产数是原计划生产数的3倍．故答案为：3．【点评】解决本题先求出单一的量，再由单一的量求出总量．【例29】29．锅炉房按照每天4.5吨的用量储备了120天的供暖煤．供暖40天后，由于进行了技术改造，每天能节约0.9吨煤．问：这些煤共可以供暖多少天？【分析】供暖40天后，还剩下4.5×（120﹣40）=360吨，然后除以实际每天的用煤量4.5﹣0.9=3.6吨，求出技术改造后又用的天数，再加上原来的时间40天即可．【解答】解：4.5×（120﹣40）=4.5×80=360（吨）360÷（4.5﹣0.9）=100（天）100+40=140（天）答：这些煤共可以供暖140天．【点评】解答本题关键是求出剩下的吨数和实际每天的用煤量．【例30】30．一个修路队要修一条公路，计划每天修280米，20天完成任务，实际用6天完成，则实际每天比原计划多修多少米？【分析】已知计划每天修280米，要求实际每天比原计划多修了多少米，应求出实际每天修的米数．根据题意，实际每天修280×20÷6，然后用求得的结果减去280米即可．【解答】解：280×20÷6﹣280=93319333﹣280=16533（米）答：实际每天比原计划多修16533米．【点评】此题解答的关键是求出实际每天修的米数，再根据计划每天修的米数，解决问题．【例31】31．美猴王孙悟空采了许多桃子．按照3只猴子分9个桃子的标准，分给30只猴子后正好分完．孙悟空一共采了多少个桃子？【分析】用9除以3先求出1只猴子分几个桃子，再乘猴子的总只数30即可．【解答】解：9÷3×30=3×30=90（个）答：孙悟空一共采了90个桃子．【点评】解答此题的关键是先求得单一量，再由不变的单一量求得总量．【例32】32．一头牛一天要吃17.5千克青草，15头牛一星期一共要吃多少千克青草？【分析】根据题意，可用17.5乘15计算出15头牛每天吃青草的重量，然后再乘7进行计算即可得到答案．【解答】解：17.5×15×7=262.5×7=1837.5（千克）答：15头牛一星期一共要吃1837.5千克青草．【点评】本题考查了归总应用题，关键明确数量之间的关系．【例33】33．某鞋厂生产1800双鞋，把这些鞋分别装入12个纸箱和4个木箱．如果3个纸箱和2个木箱装的鞋同样多．每个纸箱和每个木箱各装鞋多少双？【分析】根据题意可知：3个纸箱装的鞋=2个木箱装的鞋，则4个木箱装的鞋=6个纸箱装的鞋，由此可以求出每个纸箱装的鞋的数量，进而求出木箱装鞋的数量．【解答】解：1800÷（12+3×2）=100（双）3×100÷2=150（双）答：每个纸箱装鞋100双，每个木箱装鞋150双．【点评】本题考查的是等量代换，也可以把12个纸箱装鞋的数量转化成8个木箱装鞋的数量来解答．【例34】34．花果山上桃树多，5只小猴分200棵．现有小猴60只，按刚才的分法分后还余90棵，请算出桃树有几棵？【分析】本题考察归一归总问题．【解答】解：每只小猴分200÷5=40（棵），现在一共分40×60=2400（棵），一共有桃树2400+90=2490（棵）．答：一共有2490棵桃树．【点评】本题难度较低，细心解答即可．【例35】35．一个工人要磨面粉200千克，3小时磨了60千克．照这样计算，磨完剩下的面粉还要几小时？【分析】通过3小时磨60千克，可以求出1小时磨粉数量．问题求磨完剩下的要几小时，所以剩下的量除以1小时磨的数量，得到问题所求．【解答】解：（200﹣60）÷（60÷3）=140÷20=7（天）答：照这样计算，磨完剩下的面粉还要7小时．【点评】解决正归一的问题首先要求出单位数量，解决反归一的问题同样也是要先求出单位数量．【例36】36．孙悟空组织小猴子摘桃子．开始时，16只小猴子2小时摘桃子640个，照这样计算，孙悟空要求它们在3小时内继续摘桃子1200个，那么需要增加多少只小猴子一起来摘桃子呢？【分析】先求出一小时一只猴子摘桃子多少，然后算出1200个桃子在3小时内需要多少猴子．【解答】解：640÷16÷2=20（个）1200÷20÷3=20（只）20﹣16=4（只）答：需要增加4只猴子．【点评】此题的关键是先归一求出一只猴子一小时摘桃子的个数，然后求解．【例37】37．王奶奶家养了5头奶牛，7天产牛奶630千克，照这样计算，8头奶牛12天可生产牛奶多少千克？【分析】以1头奶牛1天产的牛奶为单一量，则1头奶牛1天产奶（630÷5÷7=18）千克，那么8头奶牛15天可产牛奶18×8×12=1728千克；由此解答即可．【解答】解：（630÷7÷5）×8×12=18×8×12=1728（千克）；答：照这样计算，8头奶牛12天可产牛奶1728千克．【点评】解答此题的关键是先求得单一量，再由不变的单一量求得总量．【例38】38．5个人2小时植树20棵，6个人3小时植树多少棵？【分析】要求6个人3小时植树多少棵，必须先求出5个人1小时植的棵数，再求出1个人1小时所植的棵数．【解答】解：20÷5÷2×6×3=2×6×3=36（棵）答：6个人3小时植树36棵．【点评】本题考查了归一归总应用题分为两类．先求出单一量后，再用乘法求出总量．【例39】39．一项工程，8个人工作15小时可以完成，如果12个人工作，多少小时可以完成？【分析】工程总量相当于1个人工作15×8=120（小时），则12个人完成这项工程需要120÷12=10（小时），据此解答．【解答】解：15×8=120（小时）120÷12=10（小时）答：那么10小时可以完成．【点评】本题关键是先求出工程总量，相当于1个人工作15×8=120小时，进一步解决问题．【例40】40．84千克黄豆可榨12千克油，照这样计算，如果要榨120千克油需要黄豆多少千克？【分析】根据题意，我们先求出榨1千克油需要多少千克黄豆，用84÷12=7千克，再求要榨120千克油需要黄豆多少千克，列式为7×120，解决问题．【解答】解：84÷12×120=7×120=840（千克）答：要榨120千克油需要黄豆840千克．【点评】解答此题的关键是先求得单一量，再由不变的单一量求得总量．【例41】41．某厂要制造一批机床，计划每天生产64台，15天可以完成，实际提前3天完成了任务，实际每天比计划多生产机床多少台？【分析】先求出这批机床的总数，以及实际用的时间，再用总数除以实际用的时间求出实际的每天生产的台数；实际每天生产的台数减去计划每天生产的台数即可．【解答】解：（64×15）÷（15﹣3）=960÷12=80（台）；80﹣64=16（台）．答：实际每天比计划多生产机床16台．【点评】解答这类问题一般从问题出发，一步步找到要求的问题与所需的条件，再由条件回到问题即可列式解决．【例42】42．一个装订小组要装订2640本书，3小时装订了240本．照这样计算，剩下的书还需要多少小时能装订完？【分析】照这样计算，说明装订的效率不变，先求出1小时装订多少本和还剩下多少本，用剩下的本数除以装订的效率就是还需要的时间．【解答】解：（2640﹣240）÷（240÷3）=2400÷80=30（小时）；答：剩下的书还需要30小时能装订完．【点评】此题主要考查工作时间、工作效率、工作总量三者之间的数量关系，先求出不变的效率，再根据效率求解．【例43】43．一批树苗，原计划8个人栽，每人要栽28棵；后来增加到16个人栽，每人要栽几棵？【分析】首先根据题意，用原计划每人要栽树苗的棵数乘8，求出一共要栽多少棵树苗；然后用一共要栽树苗的棵数除以16，求出如果16人栽，每人只要栽多少棵即可．【解答】解：28×8÷16=224÷16=14（棵）答：后来增加到16个人栽，每人要栽16棵．【点评】此题主要考查了简单的归总应用题，要熟练掌握，解答此题的关键是先求出不变的总量，再根据总量求解．【例44】44．小红家原来每月用水28吨，使用节水龙头后，原来一年用的水，现在可以多用2个月．现在每个月用水多少吨？【分析】一年共有12个月，原来每月用水28吨，则原来每年用水28×12=336吨，现在可多用2个月，即现在可用12+2=14个月，根据除法的意义可知，现在每月用水：336÷14=24吨．【解答】解：28×12÷（12+2）=336÷14=24（吨）答：现在每个月用水24吨．【点评】首先根据乘法的意义求出原来一年用水多少吨是完成本题的关键．【例45】45．5朵玫瑰花和5朵月季花共15元，8朵玫瑰花和8朵月季花共多少元？【分析】用15÷5求出单价和，再乘相同的数量8即可．【解答】解：15÷5×8=3×8答：8朵玫瑰花和8朵月季花共24元．【点评】本题结合数据的特征，不用求两种花的各自的单价，只要求出单价和即可．【例46】46．制造一台机器，原来用144小时，改进技术后，比原来缩短24小时，原来制造50台所用时间，现在可以多制造多少台？【分析】首先求出制造50台机器所用的总时间，再除以现在的时间就是技术改进后生产的台数，据此解答即可．【解答】解：144×50÷（144﹣24）=60（台）60﹣50=10（台）答：现在可以多制造10台．【点评】本题考查的是归一归总问题，关键是求出改进技术后，生产的台数．【例47】47．一件工程，原计划60个人18天完成．现在要提前3天完成，需要增加多少人？【分析】先依据工作总量=工作时间×人数，求出工作总量，再求出实际需要的时间，然后根据人数=工作总量÷工作时间，求出实际需要的人数，最后减原计划需要的人数即可解答．【解答】解：（60×18）÷（18﹣3）﹣60=1080÷15﹣60=72﹣60=12（人）答：需要增加12人．【点评】本题属于归一应用题，只要依据数量间的等量关系，代入数据即可解答．【例48】48．一千克奶糖和一千克酥糖共25.8元，同样的8千克奶糖和8千克酥糖共多少元？【分析】用一千克奶糖和一千克酥糖的单价和25.8元乘8即可求出同样的8千克奶糖和8千克酥糖共多少元．【解答】解：25.8×8=206.4（元）答：同样的8千克奶糖和8千克酥糖共206.4元．【点评】本题用单一量的和乘相同的数量即可求出总价和．【例49】49．振华机器制造厂制造一台机器，原来用钢材1.44吨，经过技术革新，现在比原来节约0.24吨．原来制造50台机器用的钢材，现在可以制造多少台？【分析】要求现在可以制造多少台，需要先求出原来制造50台机器用多少钢材，以及现在一台机器用多少钢材；再用钢材的总吨数除以一台机器需要的吨数即可．【解答】解：（1.44×50）÷（1.44﹣0.24）=72÷1.2。

初中数字中考复习中档题训练(针对第9、16题)

2021中考数学复习资料（中档题专练）（针对广东中考第9题、第16题）1．已知：1＋3＝4＝22,1＋3＋5＝9＝32,1＋3＋5＋7＝16＝42,1＋3＋5＋7＋9＝25＝52，…，根据前面各式的规律推测：101＋103＋105＋…＋199＝()A ．7500B ．10000C ．12500D ．25002．如图所示的图形是由边长为1的小正方形按照某种规律排列而成的，按照这个规律，推测第⑦个图形中，小正方形的个数为________．3．对于①)31(3y x xy x -=-②32)1)(3(2-+=-+x x x x ，从左到右的变形，表述正确的是A ．都是因式分解B ．都是乘法运算C ．①是因式分解,②是乘法运算D ．①是乘法运算,②是因式分解4.用加减消元法解二元一次方程组x ＋3y ＝4,①2x-y ＝1②时，下列方法中无法消元的是()A .①×2－② B.②×(－3)－① C.①×(－2)＋② D.①－②×35．关于x 的一元二次方程x 2－(m 2－1)x ＋2m ＝0的两个根互为相反数，则m 的值是()A ．±1B ．－1C ．1D ．06．若关于x 的方程021=-+x x m 的解为正数，则m 的取值范围是()A ．m <2B ．m <2且m ≠0C ．m ＞2D ．m ＞2且m ≠47．若关于x 的一元一次不等式组⎩⎨⎧>+>-3120x m x 的解集为1>x ，则m 的取值范围是.8．如图，直线y ＝mx 和y ＝nx ＋2交于点(1，m )，则不等式mx ＜nx ＋2的解集为__________．9．若二次函数y ＝x 2－2x ＋k 的部分图象如图所示，则关于x 的一元二次方程x 2－2x ＋k ＝0的一个解为x 1＝3，另一个解x 2＝__________.10．有一个装有水的容器,如图所示，容器内的水面高度是10cm ，现向容器内注水，并同时开始计时，在注水过程中，水面高度以每秒0.2cm 的速度匀速增加，则容器注满水之前，容器内的水面高度与对应的注水时间满足的函数关系是（）A .正比例函数关系B .一次函数关系C .二次函数关系D .反比例函数关系11．一个多边形的内角和是其外角和的3倍，则这个多边形边数是_________.12．已知△OAB ∽△OCD ，OA OC ＝32，△OAB 与△OCD 的面积分别是S 1与S 2，周长分别是C 1与C 2，则下列说法正确的是()A ．C 1C 2＝32B ．S 1S 2＝32C ．OB CD ＝32D ．OA OD ＝3213．如图，∠A ＝∠D ，∠1＝∠2，要使△ABC ≌△DEF ，还应给出的条件是()A ．∠E ＝∠B B ．AB ＝EF C ．AF ＝CD D ．ED ＝BC第13题图第14题图第15题图14．如图，在△ABC 中，已知MN ∥BC ，DN ∥MC ．小红同学由此得出了以下四个结论：①AN CN ＝AM AB ；②AD DM ＝AM MB ；③AM MB ＝AN CN ；④AD AM ＝AN AC.其中正确结论的个数为()A ．1个B ．2个C ．3个D ．4个15．如题15图，菱形ABCD 的边长为2，∠A ＝45°，分别以点A ，B 为圆心，大于12AB 的长为半径作弧，两弧相交于M ，N 两点，作直线MN 交AD 于点E ，连接CE ，则CE 的长为________．16．如图，在矩形ABCD 中，AB ＝3，BC ＝4，AE ⊥BD 于点F ，则线段AF 的长是()A ．3B ．2.5C ．2.4D ．217．已知四边形ABCD 的对角线相等，顺次连接四边形的四条边中点，所得到的新四边形的形状一定是()A ．平行四边形B ．矩形C ．菱形D ．正方形18．若半径为6cm的圆中，一段弧长为3πcm，则这段弧所对的圆心角度数为_________．19.若正方形的外接圆半径为2，则其内切圆半径为()D.1A.2B.22C.2220．如图1，四边形ABCD为⊙O的内接四边形，∠AOC＝110°，则∠ADC＝() A．55°B．110°C．125°D．70°第20题图第21题图第22题图21．如图，PA，PB是⊙O的切线，A，B是切点，如果∠P＝60°，OA＝3，那么AB的长为_________. 22．如图，正六边形ABCDEF的边长为2，以点A为圆心，AB的长为半径，作扇形ABF，则图中阴影部分的面积为____________(结果保留根号和π)．23．如图，圆锥的底面半径OB为5cm，它的侧面展开图(扇形)的半径AB为15cm，则这个扇形的圆心角α的度数为________．第23题图第24题图第25题图24．如图，小巷左右两侧是竖直的墙，将一架梯子斜靠在左侧墙上与地面成60°角时，梯子顶端距离地面23米．若保持梯子底端位置不动，将梯子斜靠在右侧墙上时，与地面成45°角，则小巷的宽度为________米．(结果保留根号)25．如右上图，无人机于空中A处测得某建筑顶部B处的仰角为45°，测得该建筑底部C处的俯角为17°.若无人机的飞行高度AD为62m，则该建筑的高度BC约为__________m．（参考数据：sin17°≈0.29，cos17°≈0.96，tan17°≈0.31）26．如图，在矩形ABCD中，AB＝3，BC＝4，点M为边BC的中点，将△CDM沿DM折叠，使点C落在矩形内的点N处，则BN的长度是________．第26题图第27题图第28题图27．如图，在△ABC 中，∠ACB ＝80°，将△ABC 绕点C 顺时针旋转得到△EDC ，连接AE .当点B的对应点D 恰好落在AC 边上时，∠CAE 的度数是()A ．30°B ．40°C ．50°D ．60°28．如图，在等边三角形AOB 中，点A 的坐标为(1，3)，点B 在x 轴正半轴上，将△AOB 绕点O 顺时针旋转15°，此时点A 的对应点A ′的坐标是__________．29．如题29图，在矩形ABCD 中，∠BOC ＝120°，BD ＝12，点P 是AD 边上一动点，则OP 的最小值为()A ．3B ．4C ．5D ．6第29题图第30题图第31题图30．如图，已知在等腰三角形ABC 中，AC ＝BC ，OB ＝3，OC ＝4，点M 是线段BC 上的动点，点P 是线段CO 上的动点，则PM ＋PB 的最小值是________．31．如图，E 是▱ABCD 的边AD 上的点，且DE AE ＝12，连接BE 并延长，交CD 的延长线于点F ，若DE ＝DF ＝3，则▱ABCD 的周长为()A ．15B ．24C ．30D ．3632．在△ABC 中，AB ＞BC ＞AC.用直尺和圆规在边BC 上确定一点P ，使点P 分别到点A 、点B的距离相等，则符合要求的作图痕迹是()。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。