密码学中的可证明安全性 杨波
cca安全证明方法

cca安全证明方法CCA安全证明方法随着互联网的发展,网络安全问题越来越受到人们的关注。
在这个信息化时代,保护个人隐私和企业机密已经成为了一项重要的任务。
而在网络安全领域,CCA安全证明方法是一种非常有效的保护手段。
一、什么是CCA安全证明方法CCA安全证明方法是一种密码学中的概念,全称为“Chosen Ciphertext Attack Security”。
它是一种用于衡量加密算法安全性的标准,也是一种用于评估加密算法强度的方法。
简单来说,CCA安全证明方法是指在攻击者可以选择密文的情况下,加密算法仍然能够保证安全。
二、CCA安全证明方法的分类根据加密算法的不同,CCA安全证明方法可以分为对称加密算法和非对称加密算法两种。
1. 对称加密算法对称加密算法是指加密和解密使用同一个密钥的加密算法。
在对称加密算法中,CCA安全证明方法主要有两种:IND-CCA1和IND-CCA2。
IND-CCA1是指在攻击者可以选择密文的情况下,加密算法仍然能够保证安全,但是攻击者不能够获得解密后的明文。
IND-CCA2是指在攻击者可以选择密文的情况下,加密算法仍然能够保证安全,并且攻击者可以获得解密后的明文。
2. 非对称加密算法非对称加密算法是指加密和解密使用不同密钥的加密算法。
在非对称加密算法中,CCA安全证明方法主要有两种:CCA1和CCA2。
CCA1是指在攻击者可以选择密文的情况下,加密算法仍然能够保证安全,但是攻击者不能够获得解密后的明文。
CCA2是指在攻击者可以选择密文的情况下,加密算法仍然能够保证安全,并且攻击者可以获得解密后的明文。
三、CCA安全证明方法的应用CCA安全证明方法在实际应用中非常广泛。
在电子商务、在线支付、电子邮件等领域,都需要使用加密算法来保护数据的安全性。
而CCA 安全证明方法可以帮助我们评估加密算法的安全性,从而选择更加安全的加密算法来保护数据。
此外,CCA安全证明方法还可以用于评估数字签名算法的安全性。
两个可证安全短签名方案的密码学分析

案更具有吸引力 。针对在标准模型下可证安全 的两个短签名方案 ,该文指出这两个方案在多用户环境下是不安全的 ,不能抵抗密钥替换攻 击 ,即一个攻击者能够 生成一 个新公钥 满足合法签名 者生成 的合法 签名 。
关健词 :密钥替换 攻击 ;短签名 ; 双线性对
Cr p a a y i f wo Pr v b y S c r h r i n t e S h m e y t n l sso T o a l e u eS o t g a ur c e s S
[ src]Diil in tr h me rvbysc r es n admo e at c getneetsneapo fntern o oal mo e cn Abta t gt g aues e s o al eue nt t d r dl t at ra t s ic ro d m rce dl a as c p i h a r a i r . ih a
o l e v s h ursi r me n a o mp y t e s c rt n t mplm e t t . i a e h ws t tt e t ho t sg a u e s h me n y s r e a e i t agu nta d c n n ti l h e u i i he i c y e n ai on Th s p p r s o ha wo s r i n t r c e s h p o a l e u e i h t n r d l e a l n e u e a a n t e u s i i ta k n e e mu t u e e t g, a l n a v r a y c n g n r t r v b y s c r n t e sa da d mo e l i s c r g i s y s b tt on at c su d rt l — s rs t n n me y a d e s r a e e ae r a k ut h i i
北邮精品课程-现代密码学-现代密码学第一讲:绪论

现代密码学的分类
保密性
完整性
Hash
对
公
称
钥
加
加
函
密
密
数
认证性
不可否认
消 息 认 证 码
数
身
字
份
签
鉴名别源自单向函数随机数生成器
Hash函数
密码分析
被动攻击:窃听〔监 听〕信道传输的信 息,主要危害信息 系统的保密性
主动攻击:删除、插 入、篡改、信道信息 ,危害完整性、认证 性、不可否认性
密码分析
现代密码学的分类
密码设计〔防〕
密码学
密码分析〔攻〕
根本原语 密码协议 被动攻击
主动攻击
现代密码学的分类
根本原语
无密钥 (白盒)
Hash函数 随机序列生成器
单向函数 对称加密
单密钥 (一个锁,两把钥匙)
消息鉴别码
双密钥 (意见箱)
公钥加密 数字签名
流密码 分组密码
现代密码学的分类
密码协议
密钥管理 身份鉴别 平安多方计算 电子货币 电子选举 电子拍卖 零知识证明
例1 窃听 ?窃听风云?中安装窃听器, ?潜伏?监听 例2 钓鱼网站
密码分析
世界上最有用 的攻击和应 用最广泛的 攻击?
对人的攻击------威逼利诱 例1:抢劫银行,逼迫职员翻开保险箱 例2:〞力拓门 “,行业秘密信息泄露,导致中
国铁矿石谈判惨败。 例3:〞美人计“:美女间谍案
密码分析
密码学新动向
密码算法设计新思路
➢ DNA密码 ➢ 量子密码
?现代密码学?课程讲授内容
第二讲:密码学的信息论根底简介 第三讲:密码学的复杂度理论根底简介 第四讲:分组密码 第五讲:流密码 第六讲:hash函数和消息认证码 第七讲:公钥加密 第八讲:数字签名 第九讲:密钥管理和密钥生成协议 第十讲:密码协议 第十一讲:量子密码学
信任管理中的算法设计和模型分析

任管理思想的应用范围。 Jjm提出了8D3Il埘系统,用信任管理思想对域名系统进行安全性拓展。
信任管理中的算法设计和模型分析
4)本地信任策略:在分布式系统中,管理实体的数量是相当大的。每个实体都可 以对不同的用户和其它实体有不同的信任模型。例如,系统A可以信任系统B 直接认证它的用户,但不信任系统C。因此安全机制不应该强制实行统一绝对 的策略和信任关系。 这些理由足以说明认证码、X,509【l】,和更一般的,基于身份的公钥系统与ACL
网络中的委托和授权等问题。B1aze、Feig胁ba啪、Ioall赫dis和Kf:mmvtis针对
PolicyMaker存在的一些问题,给出了使用特定语亩的信任管理系统KevNote【6】l
使其更标准化,应用起来更简易。chu、Feig髓ba啪、Lamacchia等提出了REFEREE【7】
系统,特别针对网络浏览应用信任管理思想,在安全性能上有了进一步的提高。
works and翁】ture research dh_cction is djscussed.
Keyword:trust m粕agement access control authorization credential DFS
创新性声明
本人声明所呈交的论文是我个人在导师指导下进行的研究工作及取得的研究 成果。尽我所知,除了文中特别加以标注和致谢中所罗列的内容以外,论文中不 包含其他人已经发表或撰写过的研究成果;也不包含为获得西安电子科技大学或 其它教育机构的学位或证书而使用过的材料。与我一同工作的同志对本研究所做 的任何贡献均已在论文中做了明确的说明并表示了谢意.
现代密码学_第三讲 密码学基本知识

Pr[ p]Pr[c | p] { k : p d ( c )} Pr[ p | c] Pr[k ]Pr[ p d k (c)] Pr[c] { k :cC ( k )}
k
Pr[ p ]
Pr[ k ]
密 钥
Pr[c | p ]
解密算法
{k : p d k ( c )}
Pr( y
j 1
m
j
) 1
16
密码体制组成部分熵的基本关系
设(P,C,K,E,D)是一个密码体制,那么,
H(K|C)=H(K)+H(P)-H(C) 证明:首先,有H(K,P,C)=H(C|K,P)+H(K,P)。因为密钥和明 文唯一决定密文,所以,H(C|K,P)=0。又K和P是统计独立的,
所以,H(K,P)=H(P)+H(K)。 可得, H(K,P,C)=H(K,P)=H(P)+H(K) 。 同样,密钥和密文唯一决定明文,得H(P|K,C)=0,因此有
H(K,P,C)=H(K,C)。 所以,H(K|C)=H(K,C)-H(C) =H(K,P,C)-H(C) =H(K)+H(P)-H(C)
可得, H(K|C)= H(K)+ H(P) - H(C) ≈ 0.46
18
相关性(举例)
猜字母。假设收到便条“I lo_e you”,请问残缺的字母应 该是什么?在英语中符合lo_e结构的所有单词,其部分如下:
lobe lode loge lone lope lore lose love
17
举例说明(续)
根据题意,易得:
假设P={a,b}满足Pr[a]=1/4,Pr[b]=3/4。设 K={k1,k2,k3} 满足Pr[k1]=1/2, Pr[k2]=1/4, Pr[k3]=1/4。设C={1,2,3,4},加密函数定义 为ek1(a)=1, ek1(b)=2, ek2(a)=2, ek2(b)=3, ek3(a)=3, ek3(b)=4。
密码学笔记(5)——Rabin密码体制和语义安全性

密码学笔记(5)——Rabin密码体制和语义安全性⼀、Rabin密码体制 Rabin密码体制是RSA密码体制的⼀种,假定模数n=pq不能被分解,该类体制对于选择明⽂攻击是计算安全的。
因此,Rabin密码体制提供了⼀个可证明安全的密码体制的例⼦:假定分解整数问题是整数上不可⾏的,那么Rabin密码体制是安全的。
Thm1 (Rabin密码体制)设n=pq,其中p和q是素数,且p,q \equiv 3 (mod \, 4),设P=C=Z^{\star}_{n},且定义\kappa =\{(n,p,q)\}对K=(n,p,q),定义e_{K}(x)=x^{2} (mod \, n)和d_{K}=\sqrt{y} (mod \, n)n为公钥,p和q为私钥。
注:条件p,q \equiv 3 (mod \, 4)可以省去,条件P=C=Z^n_{\star}也可以弱化为P=C=Z^n,只是在使⽤更多的限制性描述的时候,简化了许多⽅⾯的计算和密码体制分析。
注意看到这个函数y=x^{2}对于加密来说不是⼀个单射,所以解密不能以⼀种明显的⽅式完成,特别的,对于y \equiv x^{2} (mod \, n),对于某⼀个x \in Z^{\star}_{n},存在y模n的是个解,除⾮有其他的冗余信息,否则⽆法确认是那⼀个值。
从Bob的观点来看解密问题,它有⼀个密⽂y,要想得到x使得x^2 \equiv y(mod \, n)这是⼀个关于Z_{n}中未知元x的⼆次⽅程,解密需要求出模n的平⽅根,等价于求解以下两个同余⽅程。
z^{2} \equiv y (mod \, p)z^{2} \equiv y (mod \, q)虽然我们可以利⽤Euler准则来判断y是否为⼀个模p或模q的⼆次剩余。
事实上,如果加密正确的执⾏,y是⼀个模p和模q的⼆次剩余,遗憾的是它并不能帮助我们找到y。
当p \equiv 3(mod \, 4)时,有⼀个简单公式来计算模p的⼆次剩余的平⽅根,假定y是⼀个模p的⼆次剩余,且y \equiv 3 (mod \, 4)那么有\begin{align} (\pm y^{\frac {p+1}{4}})^{2} \equiv & y^{\frac{p+1}{2}} (mod \, p) \\ \equiv & y^{\frac{p-1}{2}}y (mod \, p) \\ \equiv & y(mod \, p) \\ \end{align}这⾥⼜⼀次使⽤了Euler准则,即当y是⼀个模p的⼆次剩余时,有y^{\frac{p-1}{2}} \equiv 1 (mod \, p),因此,y模p的两个平⽅根为\pm y^{\frac{p+1}{4}} (mod \, p),同样的讨论可以知道,y模q的两个平⽅根为\pm y^{\frac{p+1}{4}} (mod \, q),再利⽤中国剩余定理可以得到y模n的四个平⽅根。
现代密码学 学习心得

混合离散对数及安全认证摘要:近二十年来,电子认证成为一个重要的研究领域。
其第一个应用就是对数字文档进行数字签名,其后Chaum希望利用银行认证和用户的匿名性这一性质产生电子货币,于是他提出盲签名的概念。
对于所有的这些问题以及其他的在线认证,零知识证明理论成为一个非常强有力的工具。
虽然其具有很高的安全性,却导致高负荷运算。
最近发现信息不可分辨性是一个可以兼顾安全和效率的性质。
本文研究混合系数的离散对数问题,也即信息不可识别性。
我们提供一种新的认证,这种认证比因式分解有更好的安全性,而且从证明者角度看来有更高的效率。
我们也降低了对Schnorr方案变形的实际安全参数的Girault的证明的花销。
最后,基于信息不可识别性,我们得到一个安全性与因式分解相同的盲签名。
1.概述在密码学中,可证明为安全的方案是一直以来都在追求的一个重要目标。
然而,效率一直就是一个难以实现的属性。
即使在现在对于认证已经进行了广泛的研究,还是很少有方案能兼顾效率和安全性。
其原因就是零知识协议的广泛应用。
身份识别:关于识别方案的第一篇理论性的论文就是关于零知识的,零知识理论使得不用泄漏关于消息的任何信息,就可以证明自己知道这个消息。
然而这样一种能够抵抗主动攻击的属性,通常需要许多次迭代来得到较高的安全性,从而使得协议或者在计算方面,或者在通信量方面或者在两个方面效率都十分低下。
最近,poupard和stern提出了一个比较高效的方案,其安全性等价于离散对数问题。
然而,其约减的代价太高,使得其不适用于现实中的问题。
几年以前,fiege和shamir就定义了比零知识更弱的属性,即“信息隐藏”和“信息不可分辨”属性,它们对于安全的识别协议来说已经够用了。
说它们比零知识更弱是指它们可能会泄漏秘密消息的某些信息,但是还不足以找到消息。
具体一点来说,对于“信息隐藏”属性,如果一个攻击者能够通过一个一次主动攻击发现秘密消息,她不是通过与证明者的交互来发现它的。
(完整word版)密码学与信息安全期末考试题与答案
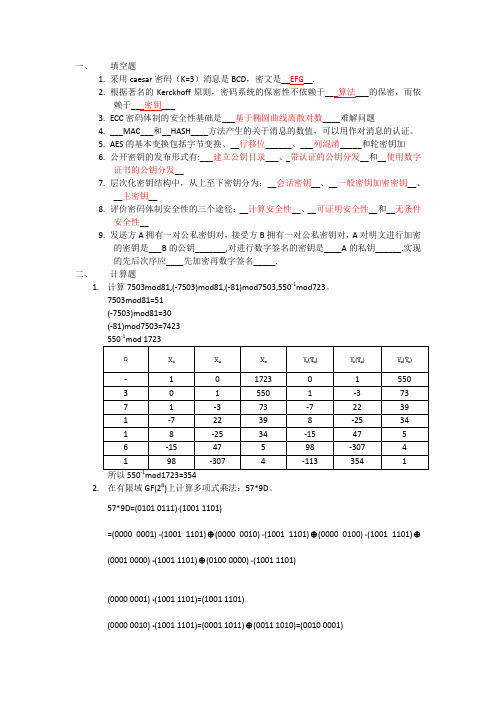
一、填空题1.采用caesar密码(K=3)消息是BCD,密文是__EFG__.2.根据著名的Kerckhoff原则,密码系统的保密性不依赖于___算法___的保密,而依赖于___密钥___3.ECC密码体制的安全性基础是___基于椭圆曲线离散对数____难解问题4.___MAC___和__HASH____方法产生的关于消息的数值,可以用作对消息的认证。
5.AES的基本变换包括字节变换、__行移位______、___列混淆_____和轮密钥加6.公开密钥的发布形式有:___建立公钥目录___、_带认证的公钥分发__和__使用数字证书的公钥分发__7.层次化密钥结构中,从上至下密钥分为:__会话密钥__、__一般密钥加密密钥__、__主密钥__8.评价密码体制安全性的三个途径:__计算安全性__、__可证明安全性__和__无条件安全性__9.发送方A拥有一对公私密钥对,接受方B拥有一对公私密钥对,A对明文进行加密的密钥是___B的公钥_______,对进行数字签名的密钥是____A的私钥______.实现的先后次序应____先加密再数字签名_____.二、计算题1.计算7503mod81,(-7503)mod81,(-81)mod7503,550-1mod723。
7503mod81=51(-7503)mod81=30(-81)mod7503=7423-1() ()()所以550mod1723=3542.在有限域GF(28)上计算多项式乘法:57*9D。
57*9D=(0101 0111)(1001 1101)=(0000 0001)(1001 1101)⊕(0000 0010)(1001 1101)⊕(0000 0100)(1001 1101)⊕(0001 0000)(1001 1101)⊕(0100 0000)(1001 1101)(0000 0001)(1001 1101)=(1001 1101)(0000 0010)(1001 1101)=(0001 1011)⊕(0011 1010)=(0010 0001)(0000 0100)(1001 1101)=(0000 0010)(0010 0001)=(0100 0010)(0001 0000)(1001 1101)=(0000 1000)[(0000 0010)(1001 1101)]=(0000 1000)(0010 0001)=(0000 0100)(0100 0010)=(0000 0010)(1000 0100)=(0001 1011)⊕(0000 1000)=(0001 0011)(0100 0000)(1001 1101)=(0010 0000)[(0000 0010)(1001 1101)]=(0010 0000)(0010 0001)=(0001 0000)(0100 0010)=(0000 1000)(1000 0100)=(0000 0100)[(0001 1011)(0000 1000)]=(0000 0100)(0001 0011)=(0000 0010)(0010 0110)=(0100 1100)所以:(0101 0111)(1001 1101)= (1001 1101)⊕(0010 0001)⊕(0100 0010)⊕(0001 0011)⊕(0100 1100)=(1010 0001)=A1三、简答题1.简述密码算法中对称、非对称算法各自的优缺点,及分析如何将两者进行结合应用。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
如果敌手已知某个密文,不能得出所对应的明文的完 整信息,该公钥加密方案称为单向加密(One way encryption,简称OWE),是一个很弱的安全概念,因为不能 防止敌手得到明文的部分信息。
杨波
Cryptology
语义安全 IBE的背景 IBE的安全性 选择明文安全的IBE方案 选择密文安IN全D的-ICBPEA方案IND-CCA IND-CCA2 EUF-CMA 规约
1 初始化:挑战者产生系统ℰ ,敌手获得系统的公开钥; 2 挑战:敌手输出两个长度相同的消息m0 和m1 。挑战者
随机选择b ∈ {0, 1} ,将mb 加密,并将密文(称为目标 密文)给敌手;
杨波
Cryptology
语义安全 IBE的背景 IBE的安全性 选择明文安全的IBE方案 选择密文安IN全D的-ICBPEA方案IND-CCA IND-CCA2 EUF-CMA 规约
杨波
Cryptology
语义安全 IBE的背景 IBE的安全性 选择明文安全的IBE方案 选择密文安IN全D的-ICBPEA方案IND-CCA IND-CCA2 EUF-CMA 规约
公钥加密方案在选择明文攻击下的不可区分性
例:ElGamal加密算法
1 密钥产生:设G是阶为大素数q的群,g为G的生成元,随 机选x ∈ Zq*,计算y = gx modq. 以x为秘密钥,(y, g, q)为 公开钥。
杨波IBE的安全性 选择明文安全的IBE方案 选择密文安IN全D的-ICBPEA方案IND-CCA IND-CCA2 EUF-CMA 规约
科学实验与思维实验
图1-1: 科学实验与思维实验
杨波
Cryptology
语义安全 IBE的背景 IBE的安全性 选择明文安全的IBE方案 选择密文安IN全D的-ICBPEA方案IND-CCA IND-CCA2 EUF-CMA 规约
杨波
Cryptology
语义安全 IBE的背景 IBE的安全性 选择明文安全的IBE方案 选择密文安IN全D的-ICBPEA方案IND-CCA IND-CCA2 EUF-CMA 规约
公钥加密方案在选择明文攻击下的不可区分性(IND-CPA)
公钥加密方案在选择明文攻击下的IND游戏(称 为IND-CPA游戏)如下:
为Diffie-Hellman3元组。 如果b = 1,则
(C1, y , C2/m1) = (gk mod p, gx mod p, gkx mod p)
为Diffie-Hellman3元组。
杨波
Cryptology
语义安全 IBE的背景 IBE的安全性 选择明文安全的IBE方案 选择密文安IN全D的-ICBPEA方案IND-CCA IND-CCA2 EUF-CMA 规约
科学实验与思维实验
图1-2: 科学实验与思维实验
杨波
Cryptology
语义安全 IBE的背景 IBE的安全性 选择明文安全的IBE方案 选择密文安IN全D的-ICBPEA方案IND-CCA IND-CCA2 EUF-CMA 规约
科学实验与思维实验
图1-3: 薛定谔的猫
系统是真空的、无光的
杨波
Cryptology
规约
2 IBE的背景 3 IBE的安全性
双线性映射 BDH假设 4 选择明文安全的IBE方案 5 选择密文安全的IBE方案
杨波
Cryptology
语义安全 IBE的背景 IBE的安全性 选择明文安全的IBE方案 选择密文安IN全D的-ICBPEA方案IND-CCA IND-CCA2 EUF-CMA 规约
公钥加密方案在选择明文攻击下的不可区分性
例:ElGamal加密算法
然而,IND CPA安全仅仅保证敌手是完全被动情况时 (即仅做监听)的安全,不能保证敌手是主动情况时(例如
向网络中注入消息)的安全。例如敌手收到密文
为C = (C1, C2) ,构造新的密文C′ = (C1, C2′ ) ,其 中C2′ = C2m′ ,解密询问后得到M = mm′ 。
2 加密:设消息m ∈ G, 随机选一与p − 1互素的整数k,计 算
c1 = gk modq, c2 = y k mmodq
密文为c = (c1, c2). 3 解密:m = c2/c1x modq.
杨波
Cryptology
语义安全 IBE的背景 IBE的安全性 选择明文安全的IBE方案 选择密文安IN全D的-ICBPEA方案IND-CCA IND-CCA2 EUF-CMA 规约
公钥加密方案在选择明文攻击下的不可区分性
例:ElGamal加密算法
安全性基于Diffie-Hellman判定性问题:设G是阶为大素 数q的群,g1, g2 为G的生成元。没有多项式时间的算法区分 以下2个分布:
随机4元组R = (g1, g2, u1, u2) ∈ G4的分布; 4元组D = (g1, g2, u1, u2) ∈ G4的分布,其 中u1 = g1r , u2 = g2r , r ∈R Zq. 变形:做代换g1 → g, g2 → gx , u1 → gy , u2 → gxy , 2个分布变 为:
公钥加密方案在选择明文攻击下的不可区分性
例:ElGamal加密算法
在ElGamal加密算法的IND-CPA游戏中,敌手输出两个 长度相同的消息m0、m1,挑战者加密mb(b ∈ {0, 1}), 得C = (C1, C2) = (gk mod p, y k mb mod p)。
如果b = 0,则
(C1, y , C2/m0) = (gk mod p, gx mod p, gkx mod p)
杨波
Cryptology
语义安全 IBE的背景 IBE的安全性 选择明文安全的IBE方案 选择密文安IN全D的-ICBPEA方案IND-CCA IND-CCA2 EUF-CMA 规约
语义安全
思维实验((thought experiment))是用来考察某种假设、 理论或原理的结果而假设的一种实验,这种实验可能在现 实中无法做到,也可能在现实中没有必要去做。思维实验和 科学实验一样,都是从现实系统出发,建立系统的模型,然 后通过模型来模拟现实系统。
−
1 2
|
其中k 是安全参数,用来确定加密方案密钥的长度。因
为任一个不作为的敌手A,都能通过对b做随机猜测,而
以
1 2
的概率赢得IND-CPA游戏。而|Pr
[b
=
b′]
−
1 2
|是敌手通过
努力得到的,故称为敌手的优势。
Definition 1.1
如果对任何多项式时间的敌手A,存在一个可忽略的函 数negl(k ) ,使得AdvℰC,PAA(k ) ≤ negl(k ) ,那么就称这个加密算 法在选择明文攻击下具有不可区分性,或者称为IND-CPA安
或者构造新的密文C′′ = (C1′′, C2′′) ,其中C1′′ = C1gk′′ , C2′′ = C2y k′′ m′ ,此时
C1′ = gk gk′′ = gk+k′′ , C2′′ = y k my k′′ m′ = y k+k′′ mm′
解密询问后仍得到M
=
mm′
。再由
M m′
mod
p
获得2012年度图灵奖。
杨波
Cryptology
语义安全 IBE的背景 IBE的安全性 选择明文安全的IBE方案 选择密文安IN全D的-ICBPEA方案IND-CCA IND-CCA2 EUF-CMA 规约
语义安全
加密方案语义安全的概念由不可区分 性(Indistinguishability) 游戏(简称IND游戏)来刻画,这种游 戏是一种思维实验,其中有2个参与者,一个称为挑战者 (challenger),另一个是敌手。挑战者建立系统,敌手对系统 发起挑战,挑战者接受敌手的挑战。
杨波
Cryptology
语义安全 IBE的背景 IBE的安全性 选择明文安全的IBE方案 选择密文安IN全D的-ICBPEA方案IND-CCA IND-CCA2 EUF-CMA 规约
公钥加密方案在选择明文攻击下的不可区分性
如果加密方案是确定的,如RSA算法、Rabin密码体制 等,每个明文对应的密文只有一个,敌手只需重新 对m0和m1 加密后,与目标密文进行比较,即赢得游戏。 因此语义安全性不适用于确定性的加密方案。 与确定性加密方案相对的是概率性的加密方案,在每次 加密时,首先选择一个随机数,再生成密文。因此同一 明文在不同的加密中得到的密文不同,如ElGamal加密 算法。
为了描述敌手的主动攻击,1990年Naor和Yung提出了 (非适应性)选择密文攻击(Chosen Ciphertext Attack,简称 为CCA)的概念,其中敌手在获得目标密文以前,可以访问 解密谕言机(Oracle)。敌手获得目标密文后,希望获得目标 密文对应的明文的部分信息。
杨波
Cryptology
,得到C
的
明文m 。可见,ElGamal加密算法不能抵抗主动攻击。
杨波
Cryptology
语义安全 IBE的背景 IBE的安全性 选择明文安全的IBE方案 选择密文安IN全D的-ICBPEA方案IND-CCA IND-CCA2 EUF-CMA 规约
公钥加密方案在选择密文攻击下的不可区分性(IND-CCA)
语义安全 IBE的背景 IBE的安全性 选择明文安全的IBE方案 选择密文安全的IBE方案
密码学中的可证明安全性
杨波
陕西师范大学计算机学院
杨波
Cryptology
语义安全 IBE的背景 IBE的安全性 选择明文安全的IBE方案 选择密文安全的IBE方案
目录
1 语义安全
IND-CPA IND-CCA IND-CCA2 EUF-CMA
