材料力学习题册答案..
材料力学第3版习题答案

材料力学第3版习题答案第一章:应力分析1. 某材料在单轴拉伸下的应力-应变曲线显示,当应力达到200 MPa 时,材料发生屈服。
若材料在该应力水平下继续加载,其应力将不再增加,但应变继续增加。
请解释这一现象,并说明材料的屈服强度是多少?答案:这种现象表明材料进入了塑性变形阶段。
在单轴拉伸试验中,当应力达到材料的屈服强度时,材料的晶格结构开始发生滑移,导致材料的变形不再需要额外的应力增加。
因此,即使继续加载,应力保持不变,但应变会因为材料内部结构的重新排列而继续增加。
在本例中,材料的屈服强度是200 MPa。
第二章:材料的弹性行为2. 弹性模量是描述材料弹性行为的重要参数。
若一块材料的弹性模量为210 GPa,当施加的应力为30 MPa时,其应变是多少?答案:弹性模量(E)与应力(σ)和应变(ε)之间的关系由胡克定律描述,即σ = Eε。
要计算应变,我们可以使用公式ε =σ/E。
将给定的数值代入,得到ε = 30 MPa / 210 GPa =1.43×10^-4。
第三章:材料的塑性行为3. 塑性变形是指材料在达到屈服点后发生的永久变形。
如果一块材料在单轴拉伸试验中,其屈服应力为150 MPa,当应力超过这个值时,材料将发生塑性变形。
请解释塑性变形与弹性变形的区别。
答案:塑性变形与弹性变形的主要区别在于材料在去除外力后是否能够恢复原状。
弹性变形是指材料在应力作用下发生的形状改变,在应力移除后能够完全恢复到原始状态,不留下永久变形。
而塑性变形是指材料在应力超过屈服点后发生的不可逆的永久变形,即使应力被移除,材料的形状也不会恢复到原始状态。
第四章:断裂力学4. 断裂韧性是衡量材料抵抗裂纹扩展的能力。
如果一块材料的断裂韧性为50 MPa√m,试样的尺寸为100 mm×100 mm×50 mm,试样中存在一个长度为10 mm的初始裂纹。
请计算在单轴拉伸下,材料达到断裂的临界应力。
材料力学习题册答案-第13章能量法

第十三章能量法一、选择题1.一圆轴在图1所示两种受扭情况下,其(A )。
A 应变能相同,自由端扭转角不同;B 应变能不同,自由端扭转角相同;C 应变能和自由端扭转角均相同;D 应变能和自由端扭转角均不同。
加F 的过程中,力偶M ( C )。
4.图3所示等截面直杆,受一对大小相等,方向相反的力F 作用。
若已知杆的拉压刚度为度。
(提示:在杆的轴向施加另一组拉力 F 。
)2•图2所示悬臂梁,当单独作用力 F 时,截面B 的转角为e ,若先加力偶M 后加F ,则在A 不做功;BC 做负功,其值为M ;做正功;1D 做负功,其值为一M2 3•图2所示悬臂梁,加载次序有下述三种方式:第一种为F 、M 同时按比例施加;第二种为 M 后加F 。
在线弹性范围内,它们的变形能应为 (D )。
A 第一种大;B 第二种大; C第三种大;D一样大。
EA 材料的泊松比为口,则由功的互等定理可知,该杆的轴向变形为Fl EA,l 为杆件长A 0 ;BcFbC;DEA7F1牛 MA B C -►-Fb .;EA先加F,后加M 第三种为先加二、计算题1图示静定桁架,各杆的拉压刚度均为EA 相等。
试求节点 C 的水平位移。
解:解法1-功能原理,因为要求的水平位移与 P 力方向一致,所以可以用这种方法。
由静力学知识可简单地求出各杆的内力,如下表所示。
2 2 —2— 21Pa Pa .2P 2aPC22EA 2EA 2EAEA解法2-卡氏定理或莫尔积分,这两种方法一致了。
在C 点施加水平单位力,则各杆的内力如下表所示。
杆N i N il i N i N i l iAB P 1 a Pa BC P1 a PaCD 0a 0BD 逅P门J 2a ^2 PaADa(^2 2)Pa EA2 2 1 Pa可得出:则C 点水平位移为:2 2 1 PaEA12•图示刚架,已知各段的拉压刚度均为EA抗弯刚度均为EI。
试求A截面的铅直位移。
解:采用图乘法,如果不计轴向拉压,在 A 点施加单位力,则刚架内力图和单位力图如图所示。
河海大学材料力学习题册答案解析
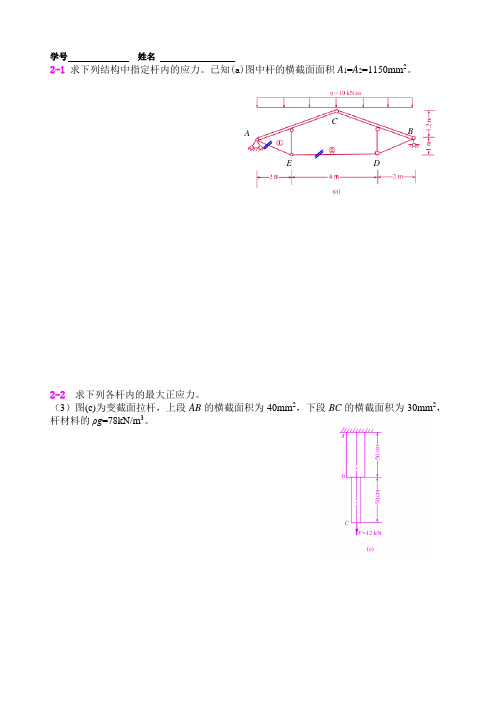
学号姓名2-1求下列结构中指定杆内的应力。
已知(a)图中杆的横截面面积A1=A2=1150mm2。
2-2求下列各杆内的最大正应力。
(3)图(c)为变截面拉杆,上段AB的横截面积为40mm2,下段BC的横截面积为30mm2,杆材料的ρg=78kN/m3。
AECDB-2-2-4 一直径为15mm ,标距为200mm 的合金钢杆,比例极限内进行拉伸试验,当轴向荷载从零缓慢地增加58.4kN 时,杆伸长了0.9mm ,直径缩小了0.022mm ,确定材料的弹性模量E 、泊松比ν。
2-6图示短柱,上段为钢制,长200mm ,截面尺寸为100×100mm 2;下段为铝制,长300mm ,截面尺寸为200×200mm 2。
当柱顶受F 力作用时,柱子总长度减少了0.4mm ,试求F 值。
已知E 钢=200GPa ,E 铝=70GPa 。
2-7 图示等直杆AC ,材料的容重为ρg ,弹性模量为E ,横截面积为A 。
求直杆B 截面的位移ΔB 。
-3-学号 姓名2-8 图示结构中,AB 可视为刚性杆,AD 为钢杆,面积A 1=500mm 2,弹性模量E 1=200GPa ;CG 为铜杆,面积A 2=1500mm 2,弹性模量E 2=100GPa ;BE 为木杆,面积A 3=3000mm 2,弹性模量E 3=10GPa 。
当G 点处作用有F =60kN 时,求该点的竖直位移ΔG 。
2-11 图示一挡水墙示意图,其中AB 杆支承着挡水墙,各部分尺寸均已示于图中。
若AB 杆为圆截面,材料为松木,其容许应力[σ]=11MPa ,试求AB 杆所需的直径。
-4-2-12 图示结构中的CD 杆为刚性杆,AB 杆为钢杆,直径d =30mm ,容许应力[σ]=160MPa ,弹性模量E =2.0×105MPa 。
试求结构的容许荷载F 。
2-14 图示AB 为刚性杆,长为3a 。
A 端铰接于墙壁上,在C 、B 两处分别用同材料、同面积的①、②两杆拉住,使AB 杆保持水平。
材料力学习题册答案-第13章 能量法

5.如下图刚架受一对平衡力F作用,各段的EI相同且等于常量,试用图乘法求两端A、B间的相对转角。
解:应用图乘法,在A、B点加一对单位力偶。它们的内力图如下图。
6.图示刚架,各段的抗弯刚度均为EI。试计算B截面的水平位移和C截面的转角。
解:应用图乘法,在B截面加一水平单位力,在C截面加一单位力偶,它们的内力图如下图。
第十三章能量法
一、选择题
1.一圆轴在图1所示两种受扭情况下,其〔A〕。
A应变能相同,自由端扭转角不同;
B应变能不同,自由端扭转角相同;
C应变能和自由端扭转角均相同;
D应变能和自由端扭转角均不同。
〔图1〕
2.图2所示悬臂梁,当单独作用力F时,截面B的转角为θ,假设先加力偶M,后加F,那么在加F的过程中,力偶M〔C〕。
A不做功;B做正功;
C做负功,其值为 ;D做负功,其值为 。
3.图2所示悬臂梁,加载次序有下述三种方式:第一种为F、M同时按比例施加;第二种为先加F,后加M;第三种为先加M,后加F。在线弹性范围内,它们的变形能应为〔D〕。
A第一种大;B第二种大;
C第三种大;D一样大。
4.图3所示等截面直杆,受一对大小相等,方向相反的力F作用。假设杆的拉压刚度为EA,材料的泊松比为μ,那么由功的互等定理可知,该杆的轴向变形为 ,l为杆件长度。〔提示:在杆的轴向施加另一组拉力F。〕
A 0;B ;
C ;D无法确定。
〔图2〕〔图3〕
二、计算题
1.图示静定桁架,各杆的拉压刚度均为EA相等。试求节点C的水平位移。
解:解法1-功能原理,因为要求的水平位移与P力方向一致,所以可以用这种方法。
由静力学知识可简单地求出各杆的内力,如下表所示。
材料力学习题册答案-第10章动载荷

第十章 动载荷、选择题1在用能量法计算冲击应力问题时,以下假设中(D )是不必要的。
A 冲击物的变形很小,可将其视为刚体;B 被冲击物的质量可以忽略,变形是线弹性的;C 冲击过程中只有应变能、势能和动能的变化,无其它能量损失;D 被冲击物只能是杆件。
2•在冲击应力和变形实用计算的能量法中,因不计被冲击物的质量,所以计算结果与实际 情况相比(D )。
A 冲击应力偏大,冲击变形偏小;B 冲击应力偏小,冲击变形偏大;C 冲击应力和冲击变形均偏大;D 冲击应力和冲击变形均偏小。
3.四种圆柱及其冲击载荷情况如图所示,柱C 上端有一橡胶垫。
其中柱( 大动应力最大。
IW、计算题1重量为P 的重物从高度H 处自由下落到钢质曲拐上, 试按第三强度准则写出危险点的相 当应力。
D )内的最解:在C 点作用静载荷P 时,BC 段产生弯曲变形, AB 段产生弯扭组合变形, C 点的静位 移:Pa 3Pl 3 Palstf C f B AB aa 3EI BC 3EI AB GI PAB ’ L 2HK d 1 JV sth 3d 4 d 4式中, I BC, I AB I PAB 12b 64 32危险点在A 截面的上下端,静应力为:.M 2 T 2 P a 2 l 2r3 W Z W Z弹簧支座,重量为 P 250 N 的重物从高度H 50 mm 自由下落到梁的中点C 处。
若铝 合金的弹性模量 E 70 GPa ,试求冲击时梁内的最大正应力。
解:在C 点作用静载荷P 时,AB 梁为静不定问题,变形协调条件为梁中点变形等于弹簧变 形,故有:式中,W Zd 3 32则动应力为:d K d r3 K d P . a 2I 2W Z2、图示横截面为b h 75mm 25mm 的铝合金简支梁,在跨中增加一刚度 K 18 kN/m 的代入数值可计算出:由结构对称,可知R A R B 50 N(资料素材和资料部分来自网络,供参考。
材料力学答案_单辉祖_习题答案第3版.pdf
解:
,
故 因为
故
圈
返回
3-12(3-23) 图示矩形截面钢杆承受一对外力偶矩
切变模量
,试求:
(1)杆内最大切应力的大小、位置和方向;
(2)横截面矩边中点处的切应力;
。已知材料的
(3)杆的单位长度扭转角。
解:
,
,
由表得
MPa
返回
第四章 弯曲应力
4-1 4-2 4-3 4-4 4-5 4-6 4-7 4-8 4-9 4-10 下页 4-1(4-1) 试求图示各梁中指定截面上的剪力和弯矩。 解:(a)
解:取消 A 端的多余约束,以 用下杆产生缩短变形。
代之,则
(伸长),在外力作
因为固定端不能移动,故变形协调条件为:
故
故 返回
6-2 图示支架承受荷载
别为
,
各杆由同一材料制成,其横截面面积分
和
。试求各杆的轴力。
解:设想在荷载 F 作用下由于各杆的变形,节点 A 移至 。此时各杆的变形
及 充方程。
如图所示。现求它们之间的几何关系表达式以便建立求内力的补
由附录Ⅳ得
返回 5-5(5-18) 试按迭加原理求图示梁中间铰 C 处的挠度 ,并描出梁挠曲线的 大致形状。已知 EI 为常量。
解:(a)由图 5-18a-1
(b)由图 5-18b-1 = 返回
5-6(5-19)
试按迭加原理求图示平面折杆自由端截面
C 的铅垂位移和水平位移。已知杆各段的横截面面积均为 A,弯曲刚度均为 EI。
及横截面上最大弯曲
得:
由几何关系得: 于是钢尺横截面上的最大正应力为:
返回
第五章 梁弯曲时的位移
5-1 5-2 5-3 5-4 5-5 5-6 5-7 5-8 5-1(5-13) 试按迭加原理并利用附录 IV 求解习题 5-4。
(完整版)材料力学课后习题答案
8-1 试求图示各杆的轴力,并指出轴力的最大值。
(2) 取1-1(3) 取2-2(4) 轴力最大值: (b)(1) 求固定端的约束反力; (2) 取1-1(3) 取2-2(4) (c)(1) 用截面法求内力,取1-1、2-2、3-3截面;(2) 取1-1(3) 取2-2 (4) 取3-3截面的右段;(5) 轴力最大值: (d)(1) 用截面法求内力,取1-1、(2) 取1-1(2) 取2-2(5) 轴力最大值: 8-2 试画出8-1解:(a) (b) (c) (d) 8-5与BC 段的直径分别为(c) (d)F RN 2F N 3 F N 1F F Fd 1=20 mm 和d 2=30 mm ,如欲使AB 与BC 段横截面上的正应力相同,试求载荷F 2之值。
解:(1) 用截面法求出(2) 求1-1、2-28-6 题8-5段的直径d 1=40 mm ,如欲使AB 与BC 段横截面上的正应力相同,试求BC 段的直径。
解:(1)用截面法求出1-1、2-2截面的轴力;(2) 求1-1、2-2截面的正应力,利用正应力相同;8-7 图示木杆,承受轴向载荷F =10 kN 作用,杆的横截面面积A =1000 mm 2,粘接面的方位角θ= 450,试计算该截面上的正应力与切应力,并画出应力的方向。
解:(1) (2) 8-14 2=20 mm ,两杆F =80 kN 作用,试校核桁架的强度。
解:(1) 对节点A(2) 列平衡方程 解得: (2) 8-15 图示桁架,杆1A 处承受铅直方向的载荷F 作用,F =50 kN ,钢的许用应力[σS ] =160 MPa ,木的许用应力[σW ] =10 MPa 。
解:(1) 对节点A (2) 84 mm 。
8-16 题8-14解:(1) 由8-14得到的关系;(2) 取[F ]=97.1 kN 。
8-18 图示阶梯形杆A 2=100 mm 2,E =200GPa ,试计算杆AC 的轴向变形 解:(1) (2) AC 8-22 图示桁架,杆1与杆2的横截面面积与材料均相同,在节点A 处承受载荷F 作用。
材力习题册参考答案1
材力习题册参考答案(1第一章绪论一、选择题1.根据均匀性假设,可认为构件的在各处相同。
A.应力B.应变 C.材料的弹性系数D.位移2.构件的强度是指,刚度是指,稳定性是指。
A.在外力作用下构件抵抗变形的能力 B.在外力作用下构件保持原有平衡状态的能力 C.在外力作用下构件抵抗强度破坏的能力3.单元体变形后的形状如下图虚线所示,则A点剪应变依次为图(a) ,图(b),图(c) 。
A.0 B.2r C.r D. 4.下列结论中( C )是正确的。
A.内力是应力的代数和; B.应力是内力的平均值;C.应力是内力的集度; D.内力必大于应力;5. 两根截面面积相等但截面形状和材料不同的拉杆受同样大小的轴向拉力,它们的应力是否相等。
A.不相等; B.相等; C.不能确定;6.为把变形固体抽象为力学模型,材料力学课程对变形固体作出一些假设,其中均匀性假设是指。
A. 认为组成固体的物质不留空隙地充满了固体的体积;B. 认为沿任何方向固体的力学性能都是相同的;C. 认为在固体内到处都有相同的力学性能;D. 认为固体内到处的应力都是相同的。
二、填空题1.材料力学对变形固体的基本假设是连续性假设,均匀性假设,各向同性假设。
2.材料力学的任务是满足强度,刚度,稳定性的要求下,为设计经济安全的构件- 1 -提供必要的理论基础和计算方法。
3.外力按其作用的方式可以分为表面力和体积力,按载荷随时间的变化情况可以分为静载荷和动载荷。
4.度量一点处变形程度的两个基本量是应变ε和切应变γ。
三、判断题1.因为构件是变形固体,在研究构件平衡时,应按变形后的尺寸进行计算。
2.外力就是构件所承受的载荷。
3.用截面法求内力时,可以保留截开后构件的任一部分进行平衡计算。
4.应力是横截面上的平均内力。
5.杆件的基本变形只是拉(压)、剪、扭和弯四种,如果还有另一种变形,必定是这四种变形的某种组合。
6.材料力学只限于研究等截面杆。
四、计算题1.图示三角形薄板因受外力作用而变形,角点B垂直向上的位移为,但AB和BC仍保持为直线。
河海大学材料力学习题册答案解析
学号 姓名2-1求下列结构中指定杆内的应力。
已知(a>图中杆的横截面面积A1=A2=1150mm2。
2-2求下列各杆内的最大正应力。
<3)图(c>为变截面拉杆,上段AB 的横截面积为40mm2,下段BC 的横截面积为30mm2,杆材料的ρg=78kN/m3。
b5E2RGbCAP 2-4一直径为15mm ,标距为200mm 的合金钢杆,比例极限内进行拉伸实验,当轴向荷载从零缓慢地增加58.4kN 时,杆伸长了0.9mm ,直径缩小了0.022mm ,确定材料的弹性模量E 、泊松比ν。
p1EanqFDPw 2-6图示短柱,上段为钢制,长200mm ,截面尺寸为100×100mm2;下段为铝制,长300mm ,截面尺寸为200×200mm2。
当柱顶受F 力作用时,柱子总长度减少了0.4mm ,试求F 值。
已知E 钢=200GPa ,E 铝=70GPa 。
DXDiTa9E3d2-7图示等直杆AC ,材料的容重为ρg ,弹性模量为E ,横截面积为A 。
求直杆B 截面的位移ΔB 。
学号 姓名2-8图示结构中,AB 可视为刚性杆,AD 为钢杆,面积A1=500mm2,弹性模量E1=200GPa ;CG 为铜杆,面积A2=1500mm2,弹性模量E2=100GPa ;BE 为木杆,面积A3=3000mm2,弹性模量E3=10GPa 。
当G 点处作用有F=60kN 时,求该点的竖直位移ΔG 。
RTCrpUDGiTA E C DB2-11图示一挡水墙示意图,其中AB杆支承着挡水墙,各部分尺寸均已示于图中。
若AB杆为圆截面,材料为松木,其容许应力[σ]=11MPa,试求AB 杆所需的直径。
5PCzVD7HxA2-12图示结构中的CD杆为刚性杆,AB杆为钢杆,直径d=30mm,容许应力[σ]=160MPa,弹性模量E=2.0×105MPa。
试求结构的容许荷载F。
jLBHrnAILg2-14图示AB为刚性杆,长为3a。
材料力学习题大全及答案
习题2-1图 习题2-2图习题2-3图 习题2-4图习题2-5图 习题2-6图材料力学习题大全及答案第1章 引 论1-1 图示矩形截面直杆,右端固定,左端在杆的对称平面内作用有集中力偶,数值为M 。
关于固定端处横截面A -A 上的内力分布,有四种答案,根据弹性体的特点,试分析哪一种答案比较合理。
正确答案是 C 。
1-2 图示带缺口的直杆在两端承受拉力F P 作用。
关于A -A 截面上的内力分布,有四种答案,根据弹性体的特点,试判断哪一种答案是合理的。
正确答案是 D 。
1-3 图示直杆ACB 在两端A 、B 处固定。
关于其两端的约束力有四种答案。
试分析哪一种答案最合理。
正确答案是 D 。
1-4 等截面直杆在两端承受沿杆轴线的拉力F P 。
关于杆中点处截面A -A 在杆变形后的位置(图中虚线所示),有四种答案,根据弹性体的特点,试判断哪一种答案是正确的。
正确答案是 D 。
1-5 图示等截面直杆在两端作用有力偶,数值为M ,力偶作用面与杆的对称面一致。
关于杆中点处截面A -A 在杆变形后的位置(对于左端,由A A '→;对于右端,由A A ''→),有四种答案,试判断哪一种答案是正确的。
正确答案是 C 。
习题2-1图习题2-2图习题2-3图习题2-4图1-6 等截面直杆,其支承和受力如图所示。
关于其轴线在变形后的位置(图中虚线所示),有四种答案,根据弹性体的特点,试分析哪一种是合理的。
正确答案是 C 。
第2章 杆件的内力分析2-1 平衡微分方程中的正负号由哪些因素所确定?简支梁受力及Ox 坐标取向如图所示。
试分析下列平衡微分方程中哪一个是正确的。
(A )d d Q x F d M(B )d d Q x F (C )d d Q x F (D )d d Q xF 2-2 对于图示承受均布载荷q 的简支梁,其弯矩图凸凹性与哪些因素相关?试判断下列四种答案中哪几种是正确的。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
21F3
练习1 绪论及基本概念 1-1 是非题
(1)材料力学是研究构件承载能力的一门学科。( 是 ) (2)可变形固体的变形必须满足几何相容条件,即变形后的固体既不可以引起“空隙”,也不产生“挤入”现象。 (是 ) (3)构件在载荷作用下发生的变形,包括构件尺寸的改变和形状的改变。( 是 ) (4)应力是内力分布集度。(是 ) (5)材料力学主要研究构件弹性范围内的小变形问题。(是 ) (6)若物体产生位移,则必定同时产生变形。 (非 ) (7)各向同性假设认为,材料沿各个方向具有相同的变形。(F) (8)均匀性假设认为,材料内部各点的力学性质是相同的。 (是) < (9)根据连续性假设,杆件截面上的内力是连续分布的,分布内力系的合力必定是一个力。(非)
(10)因为构件是变形固体,在研究构件的平衡时,应按变形后的尺寸进行计算。(非 )
1-2 填空题 (1)根据材料的主要性质对材料作如下三个基本假设:连续性假设 、均匀性假设 、 各向同性假设 。
(2)工程中的 强度 ,是指构件抵抗破坏的能力; 刚度 ,是指构件抵抗变形的能力。 (3)保证构件正常或安全工作的基本要求包括 强度 , 刚度 ,和 稳定性 三个方面。 》
(4)图示构件中,杆1发生 拉伸 变形,杆2发生 压缩 变形, 杆3发生 弯曲 变形。
(5)认为固体在其整个几何空间内无间隙地充满了物质,这样的假设称为 连续性假设 。根据这一假设构件的应力,应变和位移就可以用坐标的 连续 函数来表示。
(6)图示结构中,杆1发生 弯曲 变形,构件2 发生 剪切 变形,杆件3发生 弯曲与轴向压缩组合。 变形。
(7)解除外力后,能完全消失的变形称为 弹性变形 ,不能消失而残余的的那部分变形称为 塑性变形 。 $
12F3 (8)根据 小变形 条件,可以认为构件的变形远 小于 其原始尺寸。 1-3 选择题 (1)材料力学中对构件的受力和变形等问题可用连续函数来描述;通过试件所测得的材料的力学性能,可用于构件内部的任何部位。这是因为对可变形固体采用了( A )假设。 (A)连续均匀性; (B)各向同性; (C)小变形; (D)平面。
(2)研究构件或其一部分的平衡问题时,采用构件变形前的原始尺寸进行计算,这是因为采用了( C )假设。 (A)平面; (B)连续均匀性; (C)小变形; (D)各向同性。
(3)下列材料中,不属于各向同性材料的有( D ) (A)钢材; (B)塑料; (C)浇铸很好的混凝土; (D)松木。
— (4)关于下列结论: 1)同一截面上正应力 与切应力 必相互垂直。 2)同一截面上各点的正应力 必定大小相等,方向相同。 3)同一截面上各点的切应力 必相互平行。 现有四种答案,正确答案是( A ) (A)1对; (B)1、2对; (C)1、3对; (D)2、3对。
(5)材料力学中的内力是指(D ) (A)构件内部的力; (B)构件内部各质点间固有的相互作用力; (C)构件内部一部分与另一部分之间的相互作用力; 、 (D)因外力作用,而引起构件内部一部分对另一部分作用力的改变量
(6)以下结论中正确的是( B ) (A)杆件某截面上的内力是该截面上应力的代数和; (B)应力是内力的集度; (C)杆件某截面上的应力是该截面上内力的平均值; (D)内力必大于应力。
(7)下列结论中是正确的是( B ) (A)若物体产生位移,则必定同时产生变形; (B)若物体各点均无位移,则该物体必定无变形; (C)若物体无变形,则必定物体内各点均无位移; (D)若物体产生变形,则必定物体内各点均有位移。
(8)关于确定截面内力的截面法的适用范围,有下列说法正确的是( D ) " (A)等截面直杆; (B)直杆承受基本变形; (C)不论基本变形还是组合变形,但限于直杆的横截面; (D)不论等截面或变截面、直杆或曲杆、基本变形或组合变形、横截面或任意截面的普遍情况。
练习2 轴力与轴力图 2-1、等直杆受力如图示,求杆内最大轴力FNmax= 50kN 和最小轴力FNmin= -5kN 。
] 2-2 试求图示拉杆截面1-1,2-2,3-3上的轴力,并作出轴力图。
解:FF21N;FF2N;FF23N。
2-3、试作图示各受力杆的轴力图。 / 解:
<
3F3F1122332Fcba
2FFONF2Fx
3F2F
lllF
FllFFFF
N
F
x
xaF
aF
x
40kN60kN80kN60kNFN/kN
60
2040
x
40kN55kN
25kN20kN
2F4F
F
FN
F
NFx
x | 2-4、已知mkN 10q,试绘出图示杆件的轴力图
: 2-5、如图示受力杆,已知杆件的质量密度为33mkg 108,N 600F,考虑杆件自重,试作杆件的轴力图。(取10gm/s2)
】 2-6、图(a)所示直杆受轴向力作用,已知轴力图如图(b)所示。试绘出杆(a)所受的外力的方向和作用点,并标出力的值。
15kNq5kN5kN1m1.5mFN/kN
155
520
x
F1m100100
FN/N
200
600x
100200FN/kN1m(a)(b)1mx200kN150kN/m2m
1m
100kN45352030
(kN) , 练习3 轴向拉压杆的应力 3-1 是非题 % (1)拉杆伸长后,横向会缩短,这是因为杆有横向应力存在。(非) (2)任何轴向受拉杆件中,横截面上的最大正应力都发生在轴力最大的截面上。 (非 ) (3)构件内力的大小不但与外力大小有关,还与材料的截面形状有关。(非 ) (4)杆件的某横截面上,若各点的正应力均为零,则该截面上的轴力为零。(是 ) (5)两相同尺寸的等直杆CD和DC,如图示。杆CD受集中力F作用(不计自重),杆DC受自重作用,则杆CD中,应力的大小与杆件的横截面面积有关,杆DC中,应力的大小与杆件的横截面面积无关。 ( 是 )
【 第(5)题图 第(6)题图 (6)图示受力杆件,若AB,BC,CD三段的横截面面积分别为A,2A,3A,则各段横截面的轴力不相等,各段横截面上的正应力也不相等。 (非 )
3-2 选择题 (1)等直杆受力如图所示,其横截面面积2mm 100A,问给定横截面m-m上正应力的四个答案中正确的是( D ) (A) MPa50(压应力); (B) MPa40(压应力); (C) MPa90(压应力); (D) MPa90(拉应力)。
FN/kN
2015
30
(a)
(b)x
FABC
FF
D
FC
DDlC
5kN4kN13kNmm (2)等截面直杆受轴向拉力F作用发生拉伸变形。已知横截面面积为A,以下给出的横截面上的正应力和45斜截面上的正应力的四种结果,正确的是( A )
(A) AF,AF2; (B) AF,AF2;
《 (C) AF2,AF2; (D) A
F,AF2。
(3)如图示变截面杆AD,分别在截面A,B,C受集中力F作用。设杆件的AB段,BC段和CD段的横截面面积分别为A,2A,3A,横截面上的轴力和应力分别为CDBCABFFF,,,,,N3N21N,试
问下列结论中正确的是( D )。 (A) N3N21NFFF,CDBCAB==
(B) N3N21NFFF,CDBCAB
(C) N3N21NFFF,CDBCAB
(D) N3N21NFFF,CDBCAB==
(4)边长分别为mm 1001a和mm 502a的两正方形截面杆,其两端作用着相同的轴向载荷,两杆横截面上正应力比为( C )。 (A)1∶2; (B)2∶1; (C)1∶4; (D)4∶1 —
3-3、图示轴向拉压杆的横截面面积2mm 0001A,载荷kN 10F,纵向分布载荷的集度mkN 10q,
m 1a。试求截面1-1的正应力和杆中的最大正应力max。
解:杆的轴力如图,则截面1-1的正应力
MPa 52AN111
F
AF
最大正应力MPa 10max
A
F
3-4、图示中段开槽的杆件,两端受轴向载荷F作用,已知:kN 14F,截面尺寸mm 20b,mm 100b,
mm 4。试计算截面1-1和截面2-2上的正应力。 解:截面1-1上的正应力 $
FF45
FABC
FF
D
F11b1-12-2b022
F
FN
Fxa2a
Faa/2a/2q
1
1
