沪教版立体几何复习题

合集下载

沪教版(上海)高中数学2019-2020学年度高三数学一轮复习立体几何系列之空间直线与直线的位置关系②

沪教版（上海）高中数学2019-2020学年度高三数学一轮复习立体几何系列之空间直线与直线的位置关系②教学目标（1）从两个角度学习异面直线的概念：一、相交、平行、异面；二、共面、异面.设置问题，进行问题教学，引导学生思考——探索——得出结论.会判断、会画出空间内任意两条异面直线. （2）复习反证法，学习用反证法证明两条异面直线.（3）应用等角定理，确定异面直线所成角，利用直线平行计算异面直线所成角大小. 知识梳理（一）异面直线1、定义：把不能置于同一平面的两条直线，称为异面直线.2、与平行直线、相交直线的区别：相交直线：在同一平面内，有且只有一个交点. 平行直线：在同一平面内，没有公共点.异面直线：不同在任何一个平面内，没有公共点. 3、异面直线的画法：过渡：用两张图例说明，分别在两个平面内的直线，并不一定是异面直线.4、异面直线的判定：不平行、不相交的直线.5、空间直线的位置关系αaα aαab βb bα aβb αaβb（二）证明异面直线复习：反证法：假设否定的结论，从假设出发，引出矛盾——与条件矛盾，或者与已知的公理、定理矛盾. （三）异面直线所成角1、异面直线a 与b 所成的角：在空间内任取一点P ，过P 分别作a 和b 的平行线''a b 和,则''a b 和所成的锐角(或直角)叫做异面直线a 与b 所成的角.问题1: 理论依据—等角定理.问题2：为什么规定异面直线所成角只是锐角或直角？答：因为两条相交直线交出四个角，只要知道其中一个，就可以知道其他所有的角，因此我们只研究其中较简单的锐角或直角.2、异面直线所成角范围 0,2π⎛⎤ ⎥⎝⎦（四）问题拓展1、空间内两直线所成角范围 0,2π⎡⎤⎢⎥⎣⎦当空间两直线12l l 、所成角为直角时，12l l ⊥当空间两直线12l l 、所成角为零角时，若12l l ⋂=∅，则12l l P 若12l l ⋂≠∅，则12l l =2、异面垂直(1)定义:如果两条异面直线所成的角是直角,则这两条异面直线互相垂直[来源:学§科§网Z§X§X§K] (2)记法:异面直线a,b 互相垂直,记为a ⊥b (3)分类:⎧⎨⎩共面垂直（相交）两直线垂直异面垂直典例精讲例1.（★★★）两条异面直线指的是（ D ）（A ）空间不相交的两条直线C C 1DD 1B 1A 1AC DC 1A 1B 1D 1（B ）分别位于两个不同平面上的两条直线（C ）某平面上的一条直线和这个平面外的一条直线（D ）不能同在一个平面上的直线【说明】：异面直线概念掌握例2.（★★★）若a 、b 是两条异面直线，且分别在平面αβ、内，若l αβ⋂=，则直线l 必定（ B ）A ．分别与a 、b 相交； B. 至少与a 、b 之一相交； C. 与a 、b 都不相交； D. 至多与a 、b 之一相交. 【说明】：异面直线的概念掌握.例3.（★★★）直线l 与平面α相交于点A ，直线m 在平面α上，且不经过点A ，求证：直线l 与m 是异面直线.【说明】：学习用反证法证明异面直线.例4.（★★★）（1）正方体1111ABCD A B C D -中，哪些棱所在直线与直线1BC 成异面直线？【答案】：共有6条棱.（2）如图所示，空间四边形ABCD 中，H 、F 是AD 边上的点，G 、E 是BC 边上的点.【答案】：与AB 成异面直线的线段有：HG 、EF 、CD与CD 成异面直线的线段有：AB 、HG 、EF 与EF 成异面直线的线段有：HG 、AB 、EF 、CD 【说明】：在空间中能确定异面直线. 例5.（★★★）在长方体1111D C B A ABCD -中，3,4,51===CC BC AB .（1）11DD B C 和所成角大小. （2）11A BC C 和所成角大小；A BCD EH GF（3）11AD B C 和所成角大小. 【答案】：（1）11C C D D Q P11B CC ∴∠为异面直线11DD B C 和所成角，在11RT B C C V 中，1114,3B C BC C C ===，114tan 3B CC ∴∠=114arctan3B CC ∠=， ∴异面直线11DD B C 和所成角大小为4arctan 3.（2）11BC B C Q P ，111A C B ∴∠为异面直线11A BC C 和所成角，在11RT B C C V 中，11115,4A B AB B C BC ====，1115tan 4AC B ∴∠=, 1115arctan 4AC B ∠=， ∴异面直线11A BC C 和所成角大小为5arctan 4（3）11AD BC Q P ，设11B C BC 和相交于O ，11C OB ∴∠为异面直线11A B C D 和所成角（或其补角）在11B OC V 中，1111542B C B O C O ===，利用余弦定理，111177cos arccos 2525B OC B OC π∠=-⇒∠=-异面直线11A B C D 和所成角大小为7arccos 25例6.（★★★）在空间四边形ABCD 中，AB=CD=6，M 、N 分别是对角线AC 、BD 的中点且MN=5，求异面直线AB 、CD 所成角大小. 【答案】：取AD 中点，在ABD V 中，11,22NEAB NE AB =P在ADC V 中，11,22MECD ME CD =P NEM ∠为异面直线AB 、CD 所成角（或其补角）在NEM V 中，53MN ME ===，NE ，利用余弦定理，77cos arccos 1818NEM NEM π∠=-⇒∠=- 异面直线CD AB 和所成角大小为7arccos 18【说明】：在空间四边形中，求解异面直线所成角是一种典型问题.课堂检测1．（★★★）如果a,b 是异面直线，b,c 也是异面直线，则a,c 的位置关系是（ D ）.A ．异面； B.相交或平行； C.异面或平行； D.相交，平行，异面都有可能.[来源:学。

沪教版初中总复习专题训练中考总复习：投影与视图--巩固练习

沪教版初中数学中考总复习知识点梳理重点题型（常考知识点）巩固练习中考总复习：投影与视图—巩固练习【巩固练习】一、选择题1.下面四个几何体中，俯视图不是圆形的几何体的个数是（）.A．1个 B．2个 C．3个 D．4个2．如图，形状相同、大小相等的两个小木块放在一起，其俯视图如图所示，则其主视图是（）3．如图，夜晚，小亮从点A经过路灯C的正下方沿直线走到点B，他的影长y随他与点A之间的距离x 的变化而变化，那么表示y与x之间函数关系的图象大致为（）4．（2015春•杭州校级月考）有一个底面为正三角形的直三棱柱，三视图如图所示，则这个直棱柱的侧面积为（）A．24 B．8 C．12 D．24+85．如图，是由若干个同样大小的立方体搭成的几何体的俯视图，小正方形中的数字表示该位置立方体的个数，则这个几何体的主视图是（）6．如图是一个包装纸盒的三视图（单位：cm），则制作一个纸盒所需纸板的面积是（）A． B． C． D．二、填空题7.（2015•杭州模拟）一个直棱柱，主视图是边长为2的正方形、俯视图是边长为2的正三角形，则左视图的面积为 .8．如图，上体育课，甲、乙两名同学分别站在C，D的位置时，乙的影子恰好在甲的影子里边，已知甲、乙同学相距1米．甲身高1.8米，乙身高1.5米，则甲的影长是_________米．第8题第9题第10题9．如图，小明在A时测得某树影长为2m，B时又测得该树的影长为8m，若两次日照的光线互相垂直，则树的高度为________m．10．如图是由大小相同的小正方体组成的简单几何体的主视图和左视图，那么组成这个几何体的小正方体的个数最多为__________．11．如图是由棱长为1的正方体搭成的积木三视图，则图中棱长为1的正方体的个数是_________．12．如图，一根直立于水平地面上的木杆AB在灯光下形成影子，当木杆绕点A按逆时针方向旋转直至到达地面时，影子的长度发生变化．设垂直于地面时的影长为AC（假定AC＞AB），影长的最大值为m，最小值为n，那么下列结论：①m＞AC；②m＝AC；③n＝AB；④影子的长度先增大后减小，其中正确结论的序号是___ _____．三、解答题13．学习投影后，小明、小颖利用灯光下自己的影子长度来测量一路灯的高度，并探究影子长度的变化规律．如图，在同一时间，身高为1.6m的小明(AB)的影子BC长是3m，而小颖(EH)刚好在路灯灯泡的正下方H点，并测得HB＝6m．(1)请在图中画出形成影子的光线，并确定路灯灯泡所在的位置G；(2)求路灯灯泡的垂直高度GH；(3)如果小明沿线段BH向小颖(点H)走去，当小明走到BH中点B1处时，求其影子B1C1的长；当小明继续走剩下路程的到B2处时，求其影子B2C2的长；当小明继续走剩下路程的到B3处，……按此规律继续走下去，当小明走剩下路程的到B n处时，其影子的长为________m(直接用含n的代数式表示)．14.（2014•东海县一模）现在各地房产开发商，为了获取更大利益，缩短楼间距，以增加住宅楼栋数．合肥市某小区正在兴建的若干幢20层住宅楼，国家规定普通住宅层高宜为2.80米．如果楼间距过小，将影响其他住户的采光（如图所示，窗户高1.3米）．（1）合肥的太阳高度角（即正午太阳光线与水平面的夹角）：夏至日为81.4度，冬至日为34.88度．为了不影响各住户的采光，两栋住宅楼的楼间距至少为多少米？（2）有关规定：平行布置住宅楼，其建筑间距应不小于南侧建筑高度的1.2倍；按照此规定，是否影响北侧住宅楼住户的全年的采光？若有影响，试求哪些楼层的住户受到影响？（本题参考值：sin81.4°=0.99，cos81.4°=0.15，tan81.4°=6.61；sin34.88°=0.57，cos34.88°=0.82，tan34.88°=0.70）15．某数学兴趣小组，利用树影测量树高，如图（1），已测出树AB的影长AC为12米，并测出此时太阳光线与地面成30°角．（≈1.4，≈1.7）（1）求出树高AB；（2）因水土流失，此时树AB沿太阳光线方向倒下，在倾倒过程中，树影长度发生了变化，假设太阳光线与地面夹角保持不变．（用图（2）解答）①求树与地面成45°角时的影长；②求树的最大影长．16.如图（1）是一个三棱柱包装盒，它的底面是边长为10cm的正三角形，三个侧面都是矩形，现将宽为15cm的彩色矩形纸带AM 裁剪成一个平行四边形ABCD（如图（2）），然后用这条平行四边形纸带按如图（3）的方式把这个三棱柱包装盒的侧面进行包贴（要求包贴时没有重叠部分），纸带在侧面缠绕三圈，正好将这个三棱柱包装盒的侧面全部包贴满．（1）请在图（2）中，计算裁剪的角度∠BAD；（2）计算按图（3）方式包贴这个三棱柱包装盒所需的矩形纸带的长度．【答案与解析】一、选择题1.【答案】A；【解析】俯视图不是圆形的几何体只有正方体，所以选A.2.【答案】D；【解析】只有D答案体现了后排只有一层．3.【答案】A；【解析】根据中心投影的性质，小亮的影长y随x逐渐变小再逐渐变大，且y是x的一次函数．4.【答案】C；【解析】这个直棱柱的侧面积为：2×2×3=12．故选：C．5.【答案】D；【解析】根据俯视图可知主视图有两列，左边一列的最大高度为2，右边一列的高度是3，故选D．6.【答案】C；【解析】由三视图知此包装纸盒是一个正六棱柱，其全面积．二、填空题7．【答案】6；【解析】过A作AD⊥BC，∵俯视图是边长为2的正三角形，∴BC=2，∠B=60°，∴AD=ABsin60°=2×=3，∵主视图是边长为2的正方形，∴左视图的面积为3×=6.8．【答案】6；【解析】设甲的影长AC＝x米，则乙的影长AD＝(x-1)米．根据同一时刻物高与影长成比例，可得．解得x＝6(米)．9．【答案】4；【解析】如图，设树高CD＝h，在Rt△CEF中，由题意得ED＝2，FD＝8．由Rt△CDE∽△RFCD，可得．即．∴ CD2＝16．故CD＝4m．即树的高度为4m．10．【答案】7：【解析】由主视图知几何体左右共两排，由左视图知几何体前后三排，且左排最高两层，所以组成这个几何体的小正方体的个数最多为7个．11．【答案】6；【解析】主视图能反映每一列的最大高度，左视图能反映每一行的最大高度，俯视图能反映行列数，由三视图可发现俯视图中行列的高度如图所示，则图中棱长为1的正方体的个数是1+1+1+1+2＝6（个）．12．【答案】①③④；【解析】如图所示．当AB转至AE时影长最大值m＝AD＞AC，当AB转至AB′时影长最小值；当AB转至AB′时影长最小值n＝AB，影子的长度先增大后减小，所以正确结论的序号是①③④．三、解答题13.【答案与解析】解：(1)如图：(2)由题意得△ABC∽△GHC．∴．∴．∴GH＝4.8m．(3)∵△A1B1C1∽△GHC1，∴．设B1C1长为xm，则．解得，即B1C1=．同理，解得，．14.【答案与解析】解：（1）如图所示：AC为太阳光线，太阳高度角选择冬至日的34.88度，即∠ACE=34.88°，楼高AB为2.80×20=56米，窗台CD高为1米；过点C作CE垂直AB于点E，所以AE=AB﹣BE=AB﹣CD=55米；在直角三角形ACE中，由tan∠ACE=，得：BD=CE=即两栋住宅楼的楼间距至少为78.6米．（2）利用（1）题中的图：此时∠ACE=34.88°，楼高AB为2.80×20=56米，楼间距BD=CE=AB×1.2=67.2米；在直角三角形ACE中，由tan∠ACE=，得：AE=CE×tan∠ACE=67.2×0.70=47.04m则CD=BE=AB﹣AE=8.96m而8.96=2.8×3+0.56，故北侧住宅楼1至3楼的住户的采光受影响，4楼及4楼以上住户不受影响．15.【答案与解析】解：(1)AB＝ACtan30°＝12×≈7(米)．(结果也可以保留一位小数，下同)答：树高约7米．(2) 解析：①在Rt△ABC中，AB＝ACtan30°；②过B1作B1N⊥AC1，在Rt△AB1N和Rt△B1NC1中分别求AN和NC1．当树与地面成60°角时影长最大(如图AC2)①如图，B1N＝AN＝ABsin 45°＝≈5(米)．NC1＝NB1tan60°＝≈8(米)．AC1＝AN+NC1＝5+8≈13(米)．答：树与地面成45°角时影长为13米．②如图，当树与地面成60°角时影长最大，为AC2＝2AB2≈14(米)(或树与光线垂直时影长最大或光线与半径为AB的⊙A相切时影长最大)16.【答案与解析】解析：(1)观察图(3)的包贴方式知AB的长等于三棱柱的底面周长，则AB＝30．由AM＝15可以求出∠ABM＝30°．由AD∥BC求出∠BAD＝∠ABM＝30°．(2)可将三棱柱的侧面展开，利用平面图形计算MC的长．解：(1)由图(3)的包贴方法知：AB的长等于三棱柱的底面周长，∴AB＝30．∵纸带宽为15，sin∠DAB＝sin∠ABM＝，∴∠DAB＝30°．(2)在图(3)中，将三棱柱沿过点A的侧棱剪开，得到如图甲的侧面展开图，将图甲中的△ABE向左平移30 cm，△CDF向右平移30 cm，拼成如图乙中的平行四边形ABCD，此平行四边形即为图(2)中的平行四边形ABCD．由题意，知：BC＝BE+CE＝2CE＝2×，∴所需矩形纸带的长为MB+BC＝30·cos30°+ (cm)．。

沪教版五年级下学期数学练习卷：几何题1

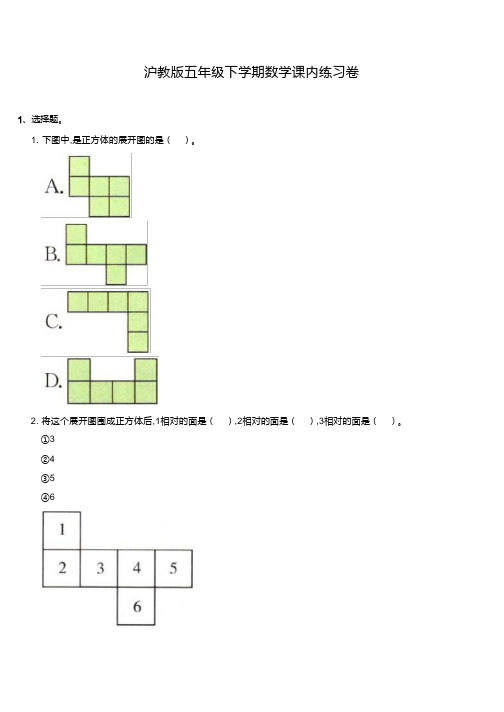
沪教版五年级下学期数学课内练习卷1. 下图中,是正方体的展开图的是（）。

2. 将这个展开图围成正方体后,1相对的面是（）,2相对的面是（）,3相对的面是（）。

①3②4③5④63. 壮壮要做一个无盖的玻璃鱼缸, 已经准备了4块长方形玻璃,其中的2块长6dm,宽4dm,另外两块长5dm,宽4dm,还需配一块（）的玻璃才能刚好合适。

①长6dm,宽5dm②长6dm,宽4dm③长5dm,宽4dm④长4dm,宽4dm4. 右图是将一个长3cm、宽与高都是2cm的长方体挖掉一个棱长1cm的小正方体,它的表面积是（）cm2。

A.35B.30C.36D.345. 下面是一个长方体纸盒的展开图,请找出相对的面:3相对的面是（）,（）相对的面是2,1相对的面是( ) 。

①2②4③5④66. 下面的图形中,（）能折成一个正方体。

7. 如图是用8个同样大小的小正方体拼成的,如果任意拿走—个小正方体,它的表面积与原来相比,（）。

①增加了②减小了③不变④无法比较8. —名油漆工粉刷—个长方体的小箱子需要用3罐油漆,现在他要粉刷—个长、宽、高都是原来4倍的大长方体箱子,需要用（）罐油漆。

①12②16③48④649. 把一个棱长3dm的正方体切成两个相等的长方体,表面积增加了（）。

①18dm2②9dm2③36dm2④无法确定10. 有一个棱长是3分米的正方体零件,从它一个面的正中间向对面挖去一个底面是边长1分米的正方形的小长方体（如图）,这个零件的表面积（）。

A.增加了10平方分米B.减少了10平方分米C.增加了12平方分米D.减少了12平方分米11. 下面图形不能折成正方体的是（）。

12. 关于下面两个图形说法正确的是（）。

①表面积和体积都一样②表面积一样,体积不一样③表面积不一样,体积一样④表面积和体积都不一样13. 一个长方体按以下三种方式分别分割成了两个长方体,表面积分别增加24cm2,32cm2,12cm2 。

原来长方体的表面积是（）cm2。

五年级下册数学总复习图形与几何沪教版 10

平行四边形的面积＝底 × 高
S＝ a h
五年级下册数学总复习图形与几何沪教版 10
五年级下册数学总复习图形与几何沪教版 10
h ┐ a
平行四边形的面积＝底×高
三角形的面积＝底×高÷2
S＝ a h÷2
五年级下册数学总复习图形与几何沪教版 10
五年级下册数学总复习图形与几何沪教版 10
S=ab
S=a 2
S=ah÷2
S=ah
S=(a+b) h÷2
a b
方格的个数 = 每排个数 × 排数长方形的面积 = 长 × 宽
S = ab
a b a
长方形的面积 = 长 × 宽正方形的面积 = 边长 × 边长
S = a2
五年级下册数学总复习图形与几何沪教版 10
h
b
a
长方形的面积＝长 × 宽
①5
② 10
③ 20 ④无法确定
10
三角形的面积＝底×高÷2
平行四边形的面积＝底×高
5
五年级下册数学总复习图形与几何沪教版 10
五年级下册数学总复习图形与几何沪教版 10
（2）小胖家的窗户是长方形的，有一块玻璃碎了，根据下面哪一条信息，玻璃店的工人
能准确的把玻璃安装上 ? （ ③ ）
（6）一块平行四边形的地，两条相邻的边长分别是 50米和30米，其中一条边上对应的高是40米，这块地的面积是（ 1200 ）平方米。
五年级下册数学总复习图形与几何沪教版 10
30 50
五年级下册数学总复习图形与几何沪教版 10
S=ab
五年级下册数学总复习图形与几何沪教版 10
S=a 2 S=ah

上海高三数学专题复习练习题：专题三空间向量与立体几何(无答案)

专题三空间向量与立体几何1.如图所示，在四棱锥S-ABCD中，底面为ABCD为正方形，SB⊥底面ABCD为正方形，SB=AB；设Q为SD中点，M为AB中点。

（1）求证：MQ//平面SBC；（2）求证：平面SDM⊥平面SCDA2.如图所示，在四棱锥P-ABCD中，底面ABCD是正方形，PA⊥底面ABCD，垂足为A，PA=AB；点M在棱PD 上，PB//平面ACM（1）试确定M的位置；（2）设点N在棱上，当N在何处时，使得MN⊥平面PAC？（3）设点E在棱PC上，当E在何处时，使得AE⊥平面PBD?BD3.如图所示，在三棱锥V-ABC 中，VC ⊥底面ABC ，AC ⊥BC ，D 是AB 的中点，且AC=BC=a ，∠VDC=θ，（20πθ<<）（1）求证：面V AB ⊥面VCD ；（2）当角θ变化时，求直线BC 与平面V AB 所成的角的取值范围。

4.平面α内有一个半圆，直径为AB ，过A 作SA ⊥平面α，在半圆上任取一点M ，连结SM 、SB ，且N 、H 分别是A 在SM 、SB 上的射影。

（1）求证：NH ⊥SB ；（2）这个图形中有多少个线面垂直关系？（3）这个图形中有多少个直角三角形？（4）这个图形中有多少对相互垂直的直线？5.已知直四棱柱ABCD-A1B1C1D1中，AA1=2，底面ABCD是直角梯形，∠A为直角，AB//CD，AB=4，AD=2，DC=1，求异面直线BC1与BD所成角的大小（结果用反三角函数值表示）6.在如图所示的几何体中，EA⊥平面ABC，DB⊥平面ABC，AC⊥BC，且AC=BC=BD=2AE，M是AB的中点。

（1）求证：CM⊥EM；（2）求CM与平面CDE所成的角。

7.如图所示，正三棱柱ABC-A 1B 1C 1的所有棱长都为2，D 为CC 1的中点，（1）求证：AB 1平面A 1BD ；（2）求二面角A-A 1D-B 的大小；（3）求点C 到平面A 1BD 的距离。

沪教版七年级数学下册第十四章全等三角形单元复习题

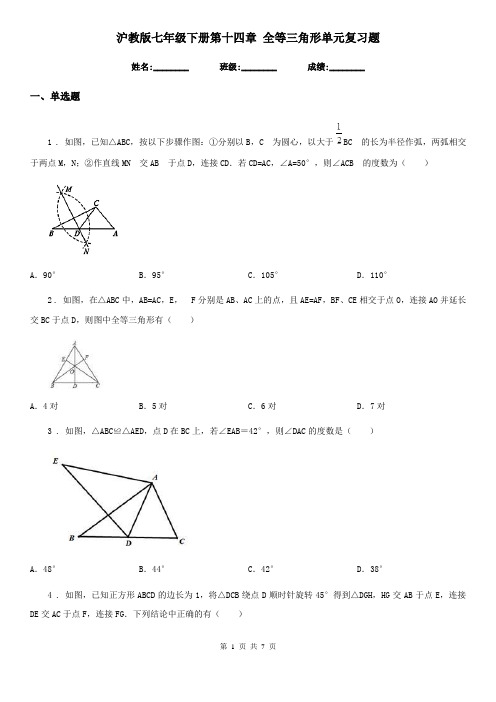
沪教版七年级下册第十四章全等三角形单元复习题姓名:________ 班级:________ 成绩:________一、单选题1 . 如图，已知△ABC，按以下步骤作图：①分别以B，C 为圆心，以大于BC 的长为半径作弧，两弧相交于两点M，N；②作直线MN 交AB 于点D，连接CD．若CD=AC，∠A=50°，则∠ACB的度数为（）A．90°B．95°C．105°D．110°2 . 如图，在△ABC中，AB=AC，E，F分别是AB、AC上的点，且AE=AF，BF、CE相交于点O，连接AO并延长交BC于点D，则图中全等三角形有（）A．4对B．5对C．6对D．7对3 . 如图，△ABC≌△AED，点D在BC上，若∠EAB＝42°，则∠DAC的度数是（）A．48°B．44°C．42°D．38°4 . 如图，已知正方形ABCD的边长为1，将△DCB绕点D顺时针旋转45°得到△DGH，HG交AB于点E，连接DE交AC于点F，连接FG．下列结论中正确的有（）①四边形AEGF是菱形；②△AED≌△GED；③∠DFG＝112.5°；④BC+FG＝1.5．A．1个B．2个C．3个D．4个5 . 如图，下列有四个说法：①∠B＞∠ACD；②∠B+∠ACB=180°-∠A；③∠A+∠B=∠ACD；④∠HEC＞∠B．正确的个数是（）A．1个B．2个C．3个D．4个6 . 如图，AC与BD相交于O，∠1=∠4，∠2=∠3，△ABC的周长为25cm，△AOD的周长为17cm，则AB=（）A．4cm ；B．8cm；C．12cm；D．无法确定；7 . 如图, A B∥CD, AC∥BD, AD与BC交于O, AE⊥BC于E, DF⊥BC于F, 那么图中全等的三角形有（）A．5对B．6对C．7对D．8对二、填空题8 . 中，厘米，厘米，点为的中点，如果点在线段上以2厘米/秒的速度由点向点运动，同时，点在线段上由点向点运动，若点的运动速度为厘米/秒，则当与全等时，的值为______厘米/秒．9 . 如图，在△ABC中，AD为△ABC的平分线，DE⊥AB于点E，DF⊥AC于点F．若△ABD的面积是20 cm2，AB＝10 cm，则DF＝______cm．10 . 如图，在△ABD中，∠C=90°，AD平分∠BAC，BC=32，AB=40，且BD：DC=5:3。

数学立体几何的复习题

数学立体几何的复习题1. 设四面体ABCD，其中AB=AC=AD=BC=BD=CD=1，做AE=BC的垂线，交BC于点E，求证：AE的垂足F、四面体的质心O、四面体外接球心O'三点共线。

2. 已知正三棱锥以底面正三角形ABC为底，高为h，点M在三棱锥内，且AM=BM=CM，求证：M点与锥心O的连线平分∠AOC。

3. 有一直角棱柱，底面为直角三角形，已知棱长为a，斜边长为c，求证：棱柱的高OA与斜边c的关系为OA=c/√3。

4. 设四棱锥ABCD，其中AB=BC=CD，且∠ABC=120°，DE是BC边的中点连线所确定的平面与AB、CD的交点，求证：DE⊥(AB,CD)。

5. 设四棱锥ABCD，其中AB=BC=CD，底面为边长为a的正三角形，求证：四棱锥的表面积S=3√3a²。

6. 已知棱长为a的正八面体OABCDEFH，点M为OH边的中点，求证：M点与平面ODC垂直。

7. 设平面上的正多边形A1A2…An，其中的一点为M，求证：M到多边形的每个顶点的距离之和是定值。

8. 设柱体ABCD-A'B'C'D'的高为h，直径为d，高柱体内一球O切于棱AB和棱BC的球面分别为点M和点N，求证：球心O与棱AA'、棱BB'、棱CC'、棱DD'的连线都经过球心O。

9. 已知棱长为a的正六面体，通过棱AB的中点连一平面，该平面与正六面体的交线为l，求证：l与BC、AC的交点均位于BD上。

10. 已知正方体ABCDE-UVWX，棱长为a，求证：平面ACW与平面DVE互相垂直。

11. 已知四棱锥的底面为边长为a的正方形，斜高为h，球O切底面的每条边所在平面的交线分别为A、B、C，求证：S(OAC)+S(OBC)+S(OCD)+S(ODA)=4h²。

12. 已知棱柱ABCDEF，底面为正方形ABCD，棱长为a，平面AEG过棱柱的棱AE，与棱柱的侧面BCEF相交于点G，求证：AG²+GE²=4a²。

上海高二立体几何练习题

上海高二立体几何练习题1. 问题描述在三维空间中，有一个直角三角形ABD，其中AB=3 cm，AD=4 cm，角BAD为直角。

又有一条直线DE与平面ABD垂直交于点D，且DE=4 cm。

点E 位于线段AB上，且AE=3 cm。

请你计算以下几个量：a) ∠ADE的度数；b) 点E到平面ABD的距离；c) 点E到线段BD的距离；d) 线段DE在平面ABD上的投影长度。

2. 解题过程a) ∠ADE的度数：根据问题描述，我们可以得知三角形ADE是等腰直角三角形。

根据勾股定理，我们可以计算∠ADE的度数。

由于AE=3 cm，DE=4 cm，我们可以计算出AD的长度为5 cm。

根据正弦定理，我们可以得到：sin(∠ADE) = AE/AD = 3/5解得：∠ADE ≈ arcsin(3/5) ≈ 36.87°b) 点E到平面ABD的距离：我们可以通过点到平面的垂直距离公式来计算点E到平面ABD的距离。

根据向量的知识，我们可以得到法向量n=(3,0,4)，点E的坐标为(3,0,0)。

点E到平面ABD的距离d = |(3,0,0)·(3,0,4)| / |(3,0,4)| = |0| / 5 = 0c) 点E到线段BD的距离：同样利用点到线段的垂直距离公式，我们可以计算点E到线段BD 的距离。

线段BD的方向向量为v = (3,0,-4)，点B的坐标为(0,0,0)，点D的坐标为(0,4,0)，点E的坐标为(3,0,0)。

点E到线段BD的距离d = |(3,0,0)·[(3,0,-4)×(3,4,-4)]| / |(3,4,-4)| = |(-16,0,-12)| / 5 ≈ 5.6569d) 线段DE在平面ABD上的投影长度：首先，根据平面法向量n=(3,0,4)和向量DE=(3,0,-4)，我们可以计算得到向量DE在平面法向量n上的投影方向向量u：u = [(3,0,-4)·(3,0,4)] / |(3,0,4)|² = -16/25 * (3,0,4) ≈ (-0.96,0,-1.28)线段DE在平面ABD上的投影长度为线段DE与投影方向向量u的点积：DE' = |DE|·|u|·cosθ = |DE|·1·cosθ = |DE|·cosθ = 4·cosθ其中，cosθ = (DE·u) / |DE|·|u| = [(3,0,-4)·(-0.96,0,-1.28)] / (4*1)= (-15.36 + 0 + 5.12) / 4 = -2.56 / 4 = -0.64因此，DE' = 4·cosθ ≈ 4·(-0.64) = -2.563. 结论总结根据计算，我们得到：a) ∠ADE的度数≈ 36.87°；b) 点E到平面ABD的距离为0；c) 点E到线段BD的距离约为5.6569；d) 线段DE在平面ABD上的投影长度约为-2.56。

沪教版(上海)高中数学2019-2020学年度高三数学一轮复习立体几何系列之空间直线与直线的位置关系

沪教版（上海）高中数学2019-2020 学年度高三数学一轮复习立体几何系列之空间直线与直线的位置关系②教学目标（1）从两个角度学习异面直线的概念：一、相交、平行、异面；二、共面、异面. 设置问题，进行问题教学，引导学生思考——探索——得出结论. 会判断、会画出空间内任意两条异面直线.（2）复习反证法，学习用反证法证明两条异面直线.（3）应用等角定理，确定异面直线所成角，利用直线平行计算异面直线所成角大小.知识梳理（一）异面直线1 、定义：把不能置于同一平面的两条直线，称为异面直线.2 、与平行直线、相交直线的区别：相交直线：在同一平面内，有且只有一个交点.平行直线：在同一平面内，没有公共点.异面直线：不同在任何一个平面内，没有公共点.3、异面直线的画法：过渡：用两张图例说明，分别在两个平面内的直线，并不一定是异面直线4、异面直线的判定：不平行、不相交的直线5、空间直线的位置关系二）证明异面直线复习：反证法：假设否定的结论，从假设出发，引出矛盾——与条件矛盾，或者与已知的公理、定理矛盾（三）异面直线所成角1、异面直线 a 与 b 所成的角：在空间内任取一点 P ，过 P 分别作 a 和 b 的平行线a '和b ',则 a '和b所成的锐角（或直角）叫做异面直线 a 与 b 所成的角 .问题 1: 理论依据—等角定理 .问题 2：为什么规定异面直线所成角只是锐角或直角？答：因为两条相交直线交出四个角，只要知道其中一个，就可以知道其他所有的角，因此我们只研究其中较简单的锐角或直角 .2 、异面直线所成角范围 0,2四）问题拓展典例精讲A ）空间不相交的两条直线1 、空间内两直线所成角范围0,2当空间两直线 l 1、l 2 所成角为直角时， l 1 l 2 当空间两直线 l 1、l 2 所成角为零角时，若 l 1 l 2，则 l 1 Pl 2若l 1 l 2，则 l 1 l 22、异面垂直（1）定义 : 如果两条异面直线所成的角是直角 , 则这两条异面直线互相垂直 [ 来源 : 学§科§网 Z § X § X § K] （2）记法 : 异面直线 a,b 互相垂直 , 记为 a ⊥ b(3) 分类 :两直线垂直共面垂直（相交）异面垂直例 1. （★★★）两条异面直线指的是（ D ）B）分别位于两个不同平面上的两条直线（C）某平面上的一条直线和这个平面外的一条直线（D）不能同在一个平面上的直线【说明】：异面直线概念掌握例 2. （★★★）若a、b 是两条异面直线，且分别在平面、内，若l，则直线l 必定（ B ）A ．分别与a、b 相交； B.至少与a、 b 之一相交；C. 与a、b 都不相交；D.至多与a、 b 之一相交.【说明】：异面直线的概念掌握例 3. （★★★）直线l 与平面相交于点A，直线m 在平面上，且不经过点A，求证：直线l 与m 是异面直线.说明】：学习用反证法证明异面直线例 4. （★★★）（1）正方体ABCD A1B1C1D1 中，哪些棱所在直线与直线BC1成异面直线？答案】：共有 6 条棱.2）如图所示，空间四边形ABCD 中，H、F 是AD边上的点，G、E 是BC边上的点【答案】：与AB 成异面直线的线段有：HG、EF、CD 与CD 成异面直线的线段有：AB、HG、EF 与EF 成异面直线的线段有：HG、AB、EF、CD 【说明】：在空间中能确定异面直线.例 5. （★★★）在长方体ABCD A1B1C1D1 中，AB 5,BC 4,CC1 3.（1）B1C和DD 1所成角大小.（2）BC和 A 1C1所成角大小；223） B 1C 和AD 1所成角大小答案】：（1）Q C 1C PD 1DB 1CC 1为异面直线 B 1C 和DD 1所成角， 4 在 RT VB 1C 1C 中， B 1C 1 BC4,C 1C 3， tan B 1CC 134B 1CC 1 arctan ，34 异面直线 B 1C 和DD 1 所成角大小为 arctan .1 1 32)Q BC PB 1C 1， A 1C 1B 1为异面直线 BC 和A 1C 1 所成角，在RTVB 1C 1C 中， A 1B 1 AB 5, B 1C 1 BC 4 ， 5tan A 1C 1B 1,45 A 1C 1B 1 arctan ， 45 异面直线 BC和A 1C 1 所成角大小为 arctan43)Q AD 1 PBC 1，设 B 1C 和 BC 1 相交于 O ，C 1OB 1为异面直线 B 1C 和AD 1 所成角（或其补角）例 6. （★★★）在空间四边形 ABCD 中，AB=CD=6，M 、N 分别是对角线 AC 、BD 的中点且 MN=5，求异面直线AB 、 CD 所成角大小 .【答案】：取 AD 中点，11在 VABD 中， NEAB,NE P AB11在 VADC 中， ME CD,ME P CD22NEM 为异面直线 AB 、 CD 所成角（或其补角）在 VNEM 中， MN5，NE ME 3，利用余弦定理，77cos NEMNEMarccos1818异面直线 AB 和CD 所成角大小为 7 arccos 18说明】：在空间四边形中，求解异面直线所成角是一种典型问题在 VB 1OC 1 中， B 1C 1 4，B 1O 5 2 725利用余弦定理， cos B 1OC 1异面直线 B 1C 和A D 1 所成角大小为C 1OB 1OC 17 arccos257 arccos25课堂检测1．（★★★）如果 a,b 是异面直线， b,c 也是异面直线，则 a,c 的位置关系是（ D） .A ．异面； B. 相交或平行； C.异面或平行； D. 相交，平行，异面都有可能 .[ 来源: 学。

沪教版初二上册《几何证明》全章复习与巩固—巩固练习(基础)

沪教版初二数学上册知识点梳理重点题型（常考知识点）巩固练习《几何证明》全章复习与巩固—巩固练习（基础）【巩固练习】一、选择题1.（2015•黄石校级模拟）命题：①对顶角相等；②垂直于同一条直线的两直线平行；③相等的角是对顶角；④同位角相等．其中假命题有（）A．1个 B．2个 C．3个 D．4个2．如图，AC=AD，BC=BD，则有（）A. AB垂直平分CDB. CD垂直平分ABC. AB与CD互相垂直平分D. CD平分∠ACB3．如果直角三角形的三条边为2，4，a，那么a的取值可以有（）A.0个B.1个C.2个D.3个4．（2016秋·泰山区期中）按下列各组数据能组成直角三角形的是（）A.11，15，13B.1，4，5C.8，15，17D.4，5，65．已知直角三角形一个锐角60°，斜边长为1，那么此直角三角形的周长是（）A．B．3 C．D．6．如图，△ABC和△DCE都是边长为4的等边三角形，点B、C、E在同一条直线上，连接 BD，则BD的长为（）A．B． C．D．第6题第7题7．如图所示，△ABC中，CD⊥AB于D，若AD=2BD，AC=5，BC=4，则BD的长为（）A． B．C．1 D．8．直角三角形有一条直角边长为13，另外两条边长都是自然数，则周长为（）A．182 B．183 C．184 D．185二、填空题9.到定点A的距离为4cm的点的轨迹是 . 10．把命题“等角的补角相等”改写成“如果……那么……”的形式是结果_________，那么__________．11．如图，在△ABC中，∠B=30°，ED垂直平分BC，ED=3．则CE长为．12．（2016秋·大祥区校级期中）如图，在△ABC中，边AB的垂直平分线交边AC于E点，△ABC与△EBC 的周长分别是24和14，则AB= ．13. 如图，已知正方形的边长为3，为边上一点，．以点为中心，把△顺时针旋转，得△，连接，则的长等于___________．14. 如图，在四边形ABCD中，AB=1，BC=2，CD=2，AD=3，且∠ABC=90°，连结AC，则△ACD的面积为 .15．一个正方体物体沿斜坡向下滑动，其截面如图所示.正方形DEFH的边长为2米，坡角∠A＝30°，∠B＝90°，BC＝6米. 当正方形DEFH运动到什么位置，即当AE等于米时，有DC＝AE＋BC.第15题第16题16．如图，四边形ABCD是边长为9的正方形纸片，为CD边上的点， =3．将纸片沿某条直线折叠，使点B落在点处，点A的对应点为，折痕分别与AD，BC边交于点M，N．则BN的长为 .三、解答题17. 如图，△ABC中，AB=AC，∠A=36°，AC的垂直平分线交AB于E，D为垂足，连接EC．（1）求∠ECD的度数；（2）若CE=5，求BC长．18.如图，已知AB=AC,AD=AE,DB与CE相交于O(1) 若DB⊥AC,CE⊥AB,D,E为垂足，试判断点O的位置及OE与OD的大小关系，并证明你的结论。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

立体几何复习题一、位置关系 1、给定空间中的直线l及平面，条件“直线l与平面内无数条直线都垂直”是“直线l与平面垂直”的（）条件 A．充要 B．充分非必要 C．必要非充分 D．既非充分又非必要 2、平面，直线b，m，且bm，则b与（）

A.b B.b与斜交 C.//b D.位置关系不确定

3、已知a、b、c是直线，是平面，给出下列命题：

①若cacbba//,,则；②若cacbba则,,//； ③若baba//,,//则；④若a与b异面，且与则ba,//相交； ⑤若a与b异面，则至多有一条直线与a，b都垂直. 其中真命题的个数是 ( ) A．1 B．2 C．3 D．4

4、“直线l平面”是“直线垂直于平面内无数条直线”________条件； 5、若nm,是两条不同的直线，、、是三个不同的平面，下列命题正确的序号是（）

①若,//,nm则nm； ②若,，则//；

③若,//,//nm则nm//； ④若//,//，m则m． A．①② B．②③ C．③④ D．①④ 6、“直线l垂直于三角形ABC的边AB、AC”是“直线l垂直于三角形ABC所在平面”的（） A．充分非必要条件 B．必要非充分条件 C．充要条件 D．既非充分也非必要条件 7、从同一点引出的4条直线可以确定n个平面，则n不可能取的值一定是（） A．6 B．4 C．3 D．1

8、已知mn，是两条不同直线，，，是三个不同平面．下列命题中正确的是（）

A．若a，，则∥ B．若mn，，则mn∥ C．若mn∥，∥，则mn∥ D．若m∥，m∥，则∥ 9、如图，正方体1111ABCDABCD，则下列四个命题：

A B C D1 A1 B1

D P ①P在直线1BC上运动时，三棱锥1ADPC的体积不变； ②P在直线1BC上运动时，直线AP与平面ACD1所成角的大小不变； ③P在直线1BC上运动时，二面角1PADC的大小不变； ④M是平面1111ABCD上到点D和1C距离相等的点，则M点的轨迹是过1D点的直线其中真命题的编号是___________.（写出所有真命题的编号） 10、四边形ABCD中, AD∥BC, AD=AB, ∠BCD=45°, ∠BAD=90°. 将△ADB沿BD折起, 使平面ABD⊥平面BCD, 构成三棱锥A-BCD. 则在三棱锥A-BCD中, 下列命题正确的是（）

A．平面ABD⊥平面ABC B．平面ADC⊥平面BDC C．平面ABC⊥平面BDC D．平面ADC⊥平面ABC

11、在正方体1111DCBAABCD的侧面11AABB内有一动点P到直线11BA与直线BC的距离相等,则动点P所在的曲线的形状为 ( )

12、已知动点P在正方体1111ABCDABCD的侧面11BBCC中,且满足11PDDBDD,则动点P的轨迹是（）的一部分 A．圆 B．椭圆 C．双曲线 D．抛物线 13、平面的斜线AB交于点B，过定点A的动直线l与AB垂直，且交于点C，则动点C的轨迹是( ) A．一条直线 B.一个圆 C.一个椭圆 D.双曲线的一支 14、已知△ABC，点P是平面ABC外一点，点O是点P在平面ABC上的射影，（1）若点P到△ABC的三边所在直线的距离相等且O点在△ABC内，则O为△ABC的心．

（2）若点P到△ABC的三个顶点的距离相等，则O为△ABC的________心；（3）若PA、PB、PC两两垂直，则O为△ ABC的________心．

A1 B1 B A P A A1 B1 B A P B A1 B1 B A P C A1 B1 B A P

A B C D

B C D 二、线线夹角（异面直线） 1、在正方体1111DCBAABCD中，则异面直线BA1与CB1所成角的大小是________. 2、如果圆锥的侧面展开图是半圆，那么这个圆锥的母线与轴线所成的角为________. 3、在长方体ABCD－A1B1C1D1中，AB＝BC＝3，AA1＝4，则异面直线AB1与 A1D所成的角为________. 4、异面直线a、b 所成的角为60°,直线l与a、b所成的角均为,则的范围是________. 5、直线a、b相交于点O且a、b成60°角，过点O与a、b都成60°角的直线有_______条 6、异面直线a、b相交于点O且a、b成80°角，过点O与a、b都成50°角的直线有_______条 7、如图所示是正方体的平面展开图．在这个正方体．．．中， ①BM与ED平行 ②CN与BE是异面直线 ③CN与BM成60°角 ④DM与BN垂直以上四个命题中，正确命题的序号是________. A.①②③ B.②④ C.③④ D.②③④

8、在棱长为2的正方体1111DCBAABCD中，O是底面ABCD的中心，E、F分别是1CC、AD的中点，那么异面直线OE和1FD所成的角为________. 9、空间四边形ABCD中，2ADBC，,EF分别是,ABCD 的中点，3EF，则异面直线,ADBC所成的角为________.

10、如图，长方体ABCD—A1B1C1D1中，AA1=AB=2，AD=1，点E、F、G分别是DD1、AB、CC1的中点，则异面直线A1E与GF所成的角是________. 11、设M、N是直角梯形ABCD两腰的中点，DE⊥AB于E(如图)．现将△ADE沿DE折起，使二面角A－DE－B为45°，此时点A在平面BCDE内的射影恰为点B，则M、N的连线与AE所成角的大小等于_________．

ABCDEMN

图1

BCD

图2

AFB

1A1

1C1

ABCDE

FG12、如图，PA平面ABC，90ACB且PAACBCa，则异面直线PB与AC所成的角为________.

三、线面角 1、如果异面直线ab、所成角为，那么的取值范围是________. 2、在长方体1111ABCDABCD中，若12,1,3ABBCAA，则1BC与平面11BBDD所成的角可用反三角函数值表示为________.

3、在长方体1111ABCDABCD中，AB=BC=2，AA1=1，则AC1与平面A1B1C1D1所成的角为________. 4、矩形ABCD中，AB＝1，2BC，PA⊥平面ABCD，PA＝1，则PC与平面ABCD所成的角是________. 5、已知长方体ABCD－A1B1C1D1中，AB＝BC＝4，CC1＝2，则直线BC1和平面DBB1D1所成的角为________. 6、PA、PB、PC是从P点引出的三条射线，每两条的夹角为60°，则直线PC与平面APB所成的角为________.

7、在正三棱柱ABC－A1B1C1中，侧棱长为,2，底面三角形的边长为1，则BC1与侧面ACC1A1

所成的角是________.

8、三棱锥P－ABC中侧面PAC与底面ABC垂直．PA＝AC＝PC＝3．AB＝BC3，则AC与平面PBC所成的角为________.

四、二面角 1、正三棱锥的侧面均为直角三角形，则它的侧面与底面所成角的余弦值________. 2、如图，在棱长为a的正方体ABCD－A1B1C1D1中，求：

（1）二面角1CBDC的大小；

（2）二面角11BBCD的大小．

3、过正方形ABCD的顶点A作PAABCD^平面，设PAABa==，（1）求二面角BPCD--的大小；（2）求二面角CPDA--的大小．

A B C D

A1 D1 C1 B1

ABC

PBCA4、如图所示，四棱锥PABCD-的底面ABCD是边长为1的菱形，60BCD?，E是CD的中点，PA⊥底面ABCD， 3PA

（1）证明：BE⊥平面PAB；（2）求二面角ABEP--的大小；（3）求PB与面PAC的角．

五、距离与几何体的体积、面积（展开图）计算 1、设圆锥的母线长为10，母线与旋转轴的夹角是30，则正圆锥的侧面积为________. 2、正四棱锥底面边长为4，侧棱长为3，则其体积为________. 3、直三棱柱ABC—A1B1C1的底面ABC为等腰直角三角形，斜边AB＝2，侧棱AA1=1,则该三棱柱的外接球的表面积为________. 4、将一个半径为2的半圆面围成一个圆锥，所得圆锥的轴截面面积等于________.

5、一个正三棱锥的底面边长为2，侧棱与底面所成角为45角，那么这个正三棱锥的体积等于________.

6、各棱长都为a的正四棱锥的体积V________. 7、已知正三棱锥的底面边长为2，高为1，则该三棱锥的侧面积为________. 8、△ABC的三边长分别是3,4,5,P为△ABC所在平面外一点,它到三边的距离都是2,则P到 的距离为________.

9、球O的半径长为103，小圆直径|AB|=30则A、B两点的球面距离为________. 10、把地球近似看成一个半径为6371km的球．已知上海的位置约为东径12127，北纬318，台北的位置约为东径12127，北纬258，则这两个城市之间的球面距离约为________.（保留到1km ） 11、正方体ABCD－A1B1C1D1的棱长为1，O是底面A1B1C1D1的中心，则O到平面ABC1D1

的距离为________.

12、三棱锥ABCD,,ABaCDb，ABDBDC,,MN分别为,ADBC的中点，P为BD上一点，则MPNP 的最小值是________.

CED