2012-2013学年海淀区高三第一学期期中练习数学(理科)
北京市海淀区高三数学第二学期期中练习参考答案与评分标准(理科)

北京市海淀区高三数学第二学期期中练习参考答案与评分标准(理科)2001.5一、选择题:(1)C ;(2)D ;(3)A ;(4)A ;(5)C ;(6)B ;(7)C ;(8)C ;(9)B ;(10)C ;(11)D ;(12)D .二、填空题:(13)12;(14)};12|{<<-x x (15)x ∈(0,2];(16)123122242、、中选一即可 三、解答题:(17)解:(Ⅰ)设z=x + yi (x ,y ∈R )依题意,xyi y x yi x z 2)(222+-=+= ∴⎪⎩⎪⎨⎧==+②① 22 222xy y x …………………………………………3分故0)(2=-y x∴22,2==x y x 得代入②∴x =±1,∴⎩⎨⎧-=-=⎩⎨⎧==1111y x y x 或 ∴z =1+i 或z = –1–i ………………………………………………5分45arg 4arg ππz z 或= ∴)45sin 45(cos 2)4sin 4(cos 2ππππi z i z +=+=或……………7分 (Ⅱ)当z =1+i 时,i z z i z -=-=1,222∴A (1,1)、B (0,2)、C (1,–1)∴|AC |=212121=⨯⨯=∆ABC S ………………………………………………10分 当z =–1–i 时,i z z i z 31,222--=-=A (–1,–1)、B (0,2)、C (–1,–3)则1=∆ABC S综上△ABC 的面积为1.…………………………………………12分(18)解:(Ⅰ)∵△ABC 是正三角形,AF 是BC 边的中线∴AF ⊥BC又D 、E 分别是AB 、AC 的中点∴BE BC 21 ∴AF ⊥DE ,AF ∩DE =G ……………………2分∴G A '⊥DE ,GF ⊥DE∴DE ⊥平面FG A '…………………………4分又DE BCED 平面⊂∴平面FG A '⊥平面BCED ……………6分(Ⅱ)∵G A '⊥DE ,GF ⊥DE∴∠GF A '是二面角A ′–DE –B 的平面角……………………7分∵平面GF A '∩平面BCED =AF作H A '⊥AG 于H∴H A '⊥平面BCED ………………………………………………9分假设E A '⊥BD ,连EH 并延长交AD 于Q∴EQ ⊥AD ……………………………………………………………10分∵AG ⊥DE∴H 是正三角形ADE 的垂心,也是中心.∵AD =DE =AE =2a ∴a AG HG a AG G A 12331,43====' 在Rt △HG A '中,31cos ='='∠G A HG GH A ∵∠GF A '=π–∠A 'GH∴31cos -='∠GF A∴)31arccos(-='∠GF A 时…………………………………………11分 即当.,)31arccos(BD E A GF A ⊥'-='∠时……………………………12分 (19)解:(Ⅰ)∵当n ≥2时,232,,431---n n n S a S 成等差数列 ∴1232432--+-=n n n S S a ∴)2(43≥-=n S a n n ………………………………………………2分∴,4)(3212-+=a a a ∵11=a ,∴212-a 类似地4)(33213-++=a a a a ∴413-=a 4)(343214-+++=a a a a a ∴ 814=a ……………………………4分 (Ⅱ)∵当≥2时,43-=n n S a ,即43+=n n a S∴⎩⎨⎧+=+=++②①434311n n n n a S a S ②–①,得n n n a a a -=++113 ∴211-=+n n a a 为常数………………………………………………6分 ∴2a ,3a ,4a ,…,n a ,…成等比数列. 其中21,212-==q a ………………………………………………7分 故1222)21()21(21,2-----=-=⋅=≥n n n n q a a n∴⎪⎩⎪⎨⎧≥==-)2( )21(--1)(n 11n a n n …………………………………………9分 (Ⅲ)∵n n a a a S +++= 21=)(132n a a a ++++∴)(lim 1lim 32n n n n a a a S ++++=∞→∞→ =34311)21(1211=+=--+………………………………12分 (20)解:(Ⅰ)由已知数据,易知函数y =f (t )的周期T =12 ……………………1分振幅A =3………………………………………………………………2分b =10……………………………………………………………………3分 ∴106sin 3+=ty π……………………………………………………4分(Ⅱ)由题意,该船进出港时,水深应不小于5+6.5=11.5(米) ∴5.11106sin 3≥+tπ…………………………………………………6分 ∴216sin ≥tπ 解得,Z)(k 652662∈+≤≤+πππππk t k …………………………8分 Z)(k 512112∈+≤≤+k t k在同一天内,取k =0或1∴1≤t ≤5或13≤t ≤17………………………………………………10分∴该船最早能在凌晨1时进港,下午17时出港,在港口内最多停留16个小时 …………………………………………………………………………12分(21)解:(Ⅰ)∵y =f (x )是以5为周期的周期函数∴f (4)=f (4–5)=f (–1)……………………………………………1分 又y =f (x ),(–1≤x ≤1)是奇函数∴f (1)= –f (–1)= –f (4)∴f (1)+f (4)=0…………………………………………………3分(Ⅱ)当x ∈[1,4]时,由题意,可设f (x )=5)2(2--x a (a ≠0)……………………………………………………5分由f (1)+f (4)=0得05)24(5)21(22=--+--a a解得a =2∴5)2(2)(2--=x x f (1≤x ≤4)…………………………………………7分 (Ⅲ)∵y =f (x ) (–1≤x ≤1)是奇函数∴f (0)= –f (–0) ∴f (0)=0………………………………………………8分 又y =f (x ) (0≤x ≤1 )是一次函数∴可设f (x )=kx (0≤x ≤1)∵35)21(2)1(2-=--=f又f (1)=k ·1=k∴ k =–3∴当0≤x ≤1时 f (x )=–3x ……………………………………………………9分 当–1≤x <0时,0<–x ≤1∴f (x )= –f (–x )= –3x∴当–1≤x ≤1时,f (x )=–3x ………………………………………………11分当4≤x ≤6时,–1≤x –5≤1∴f (x )=f (x –5)=–3(x –5)=–3x +15当6<x ≤9时 1<x –5≤45]2)5[(2)5()(2---=-=x x f x f5)7(22--x∴f (x )=⎩⎨⎧≤<--≤≤+-96 ,5)7(264 ,1532x x x x …………………………………………12分 (22)解:(Ⅰ)∵5||||||22=+=OD CO CD ,且圆D 与圆C 外切(O 为原点).∴圆D 半径r =5–2=3此时,A 、B 坐标分别为(0,0)、(0,6)P A 在x 轴上,BP 斜率k =2∴tg ∠APB =2…………………………3分 (Ⅱ)设D 点坐标为(0,a ),圆D 半径为r ,则① 16)2(22a r +=+A 、B 坐标分别为(0,a –r )、(0,a +r )设P A 、PB 斜率分别为1k ,2k ,则3,321r a k r a k +=-=② 963313322+-=-⋅++--+=∠r a r r a r a r a r a APB tg …………………………………………………6分由①解出2a 代入②,得68923346-+=-=∠r r r APB tg ,而8r –6为单调增函数,[)+∞∈,2r .∴]512,23(∈∠APB tg ∠APB 的最大值为512arctg ;……………………………………9分 (Ⅲ)假设存在Q 点,设Q (b ,0),QA 、QB 斜率分别为1k ,2k ,则br a k b r a k -+=--=21, |2||1||1|2221212r a b br br a b r a b r a b r a k k k k AQB tg -+-=--⋅-++---+=+-=∠……………………11分 将16)2(22-+=r a 代入上式,得|4122|4122|22+--=+--=∠r b b r b br AQB tg 欲使∠AQB 大小与r 无关,当且仅当122=b ,即32±=b , 此时︒=∠=∠60,3AQB AQB tg∴存在Q 点,当圆D 变动时,∠AQB 为定值︒60,Q 点坐标为(0,32±)…………………………………………………………………………………………14分 注:其他正确解法可按相应步骤给分。
2011学年海淀区理科数学高三年级第一学期期末练习及答案

2011学年海淀区理科数学高三年级第一学期期末练习第Ⅰ卷(选择题 共40分)一、选择题:本大题共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项.1.0600sin 的值为A. 23 B. 23-C . 21- D. 212. 若0.32121(),0.3,log 22a b c -===,则,,a b c 大小关系为A. a b c >>B. a c b >>C. c b a >>D. b a c >>3.一个空间几何体的三视图如图所示,则该几何体的体积为 A .12 B .6C . 4D .24. 如图,半径为2的⊙O 中,90AO B ∠=︒,D 为O B 的中点,AD 的延长线交⊙O 于点E ,则线段D E 的长为A .55B .255C .355D .325.已知各项均不为零的数列{}n a ,定义向量1(,)n n n a a +=c ,(,1)n n n =+b ,*n N ∈. 下列命题中真命题是A. 若*n N ∀∈总有//n n c b 成立,则数列{}n a 是等差数列B. 若*n N ∀∈总有//n n c b 成立,则数列{}n a 是等比数列C. 若*n N ∀∈总有n n ⊥c b 成立,则数列{}n a 是等差数列D. 若*n N ∀∈总有n n ⊥c b 成立,则数列{}n a 是等比数列ABODE正视图左视图俯视图222112216.由数字0,1,2,3,4,5组成的奇偶数字相间且无重复数字的六位数的个数是A . 72 B. 60 C. 48 D. 127. 已知椭圆E :1422=+ym x ,对于任意实数k ,下列直线被椭圆E 所截弦长与l :1+=kx y 被椭圆E 所截得的弦长不可能...相等的是 A .0kx y k ++= B .01=--y kx C .0kx y k +-= D .20kx y +-= 8. 如图所示,在正方体ABCD -A 1B 1C 1D 1中,E 是棱DD 1的中点,F 是侧面CDD 1C 1上的动点,且B 1F//面A 1BE ,则B 1F 与平面CDD 1C 1 所成角的正切值构成的集合是A. {}2B. 255⎧⎫⎨⎬⎩⎭C. D. 2{|52}5t t ≤≤第II 卷(共110分)二、填空题:本大题共6小题,每小题5分,共30分.把答案填在题中横线上.9.圆C 的极坐标方程2cos ρθ=化为直角坐标方程为,圆心的直角坐标 为 .10.某部门计划对某路段进行限速,为调查限速60 km/h 是否合理,对通过该路段的300辆汽车的车速进行检测,将所得数据按[40,50),[50,60),[60,70),[70,80]分组,绘制成如图所示频率分布直方图.则这300辆汽车中车速低于限速的汽车有 辆.11. 阅读下面的程序框图.若使输出的结果不大于37,则输入的整数i 的最大值为 .12.如图,已知10AB =,图中的一系列圆是圆心分别为A 、B 的两组同心圆,每组同心圆的半径分别是1,2,3,…,n ,….利用这两组同心圆可以画出以A 、B 为焦点的双曲线. 若其中经过点M 、N 、P 的双曲线的离心率分别是ABCDE1A 1D 1B 1C 车速O40506070800.0100.0350.030a 频率组距开始0;0S n ==n i<21nS S =++是否1n n =+S输出结束i输入,,M N P e e e .则它们的大小关系是(用“<”连接). 13. 已知函数1()sin ,[0,π]3f x x x x =-∈.01cos 3x =(0[0,π]x ∈),那么下面命题中真命题的序号是 .①()f x 的最大值为0()f x ② ()f x 的最小值为0()f x ③ ()f x 在0[0,]x 上是减函数 ④ ()f x 在0[,π]x 上是减函数14.在平面直角坐标系xOy 中,O 为坐标原点.定义()11,P x y 、()22,Q x y 两点之间的“直角距离”为1212(,)d P Q x x y y =-+-.若点()1,3A -,则(,)d A O = ; 已知点()1,0B ,点M 是直线30(0)k x y k k -++=>上的动点,(,)d B M 的最小值为 .三、解答题: 本大题共6小题,共80分.解答应写出文字说明, 演算步骤或证明过程.15.(本小题满分12分)设函数()cos(2)cos 23f x x x π=--,R x ∈.(Ⅰ)求)(x f 在(0,)2π上的值域;(Ⅱ)记ABC ∆的内角C B A ,,的对边长分别为a b c ,,,若()173f A a b ===,,,求c 的值.16.(本小题满分13分)某班将要举行篮球投篮比赛,比赛规则是:每位选手可以选择在A 区投篮2次或选择在B 区投篮3次.在A 区每进一球得2分,不进球得0分;在B 区每进一球得3分,不进球得0分,得分高的选手胜出.已知参赛选手甲在A 区和B 区每次投篮进球的概率分别为910和13(Ⅰ)如果选手甲以在A 、B 区投篮得分的期望高者为选择投篮区的标准,问选手甲应该选择哪个区投篮?(Ⅱ)求选手甲在A 区投篮得分高于在B 区投篮得分的概率.17. (本小题满分14分)如图,棱柱ABCD —1111A B C D 的所有棱长都为2, AC BD O ,侧棱1A A 与底面ABCD 的所成角为60°,1A O ⊥平面ABCD ,F 为1D C 的中点. (Ⅰ)证明:BD ⊥1A A ;(Ⅱ)证明://O F 平面11BCC B ;(Ⅲ)求二面角D -1A A -C 的余弦值.18. (本小题满分13分)已知函数1()ln(1)1a f x x ax x -=+-++ (12a ≥).(Ⅰ)当曲线()y f x =在(1,(1))f 处的切线与直线:21l y x =-+平行时,求a 的值; (Ⅱ)求函数()f x 的单调区间.A BC1B 1C 1A DF1D O19. (本小题满分14分)已知点(1,)M y 在抛物线2:2C y px =(0)p >上,M 点到抛物线C 的焦点F 的距离为2,直线:l 12y x b =-+与抛物线交于,A B 两点.(Ⅰ)求抛物线C 的方程;(Ⅱ)若以AB 为直径的圆与x 轴相切,求该圆的方程; (Ⅲ)若直线l 与y 轴负半轴相交,求A O B ∆面积的最大值.20.(本小题满分14分)已知集合{}1,2,3,,2A n = *()n N ∈.对于A 的一个子集S ,若存在不大于n 的正整数m ,使得对于S 中的任意一对元素12,s s ,都有12s s m -≠,则称S 具有性质P .(Ⅰ)当10n =时,试判断集合{}9B x A x =∈>和{}*31,C x A x k k N =∈=-∈是否具有性质P ?并说明理由. (Ⅱ)若1000n =时① 若集合S 具有性质P ,那么集合{}2001T x x S =-∈是否一定具有性质P ?并说明理由;② 若集合S 具有性质P ,求集合S 中元素个数的最大值.答案及评分参考第Ⅰ卷(选择题 共40分)一、选择题(本大题共8小题,每小题5分,共40分)题号 1 2 3 4 5 6 7 8 答案BDDCABDC第Ⅱ卷(非选择题 共110分)二、填空题(本大题共6小题,每小题5分, 共30分.有两空的题目,第一空3分,第二空2分)9. 222x y x += (1,0) 10. 180 11. 5 12. MP N e e e << 13.① ④ 14. 4 32 (1)2 3 (01)k kk k ⎧+≥⎪⎨⎪+<<⎩三、解答题(本大题共6小题,共80分) 15.(共12分)解:(I ) x x x f 2cos )32cos()(--=πx x x 2c o s 3s i n 2s i n 3c o s 2c o s -+=ππ (2)分 x x 2cos 212sin 23-=)62s i n (π-=x . .......................................4分)2,0(π∈x ,)65,6(62πππ-∈-∴x , .......................................5分 ]1,21()62s i n (-∈-∴πx ,即)(x f 在(0,2π)的值域为]1,21(- . .......................................6分(II )由(I )可知,)62sin()(π-=A A f ,1)62s i n (=-∴πA , ......................................7分π<<A 0 , 611626πππ<-<-∴A , .....................................8分3,262πππ==-∴A A . ....................................9分A bc c b acos 2222-+= , .....................................10分 把73a b ==,代入,得到2320c c -+=, ..................................11分1=∴c 或2=c . ....................................12分 16.(共13分) 解:(I )方法一设选手甲在A 区投两次篮的进球数为X ,则)109,2(~B X ,故591092)(=⨯=X E , ....................................... 2分则选手甲在A 区投篮得分的期望为6.3592=⨯. ....................................... 3分设选手甲在B 区投篮的进球数为Y ,则)31,3(~B Y ,故1313)(=⨯=Y E , ....................................... 5分则选手甲在B 区投篮得分的期望为313=⨯ . ....................................... 6分36.3> ,∴选手甲应该选择A 区投篮. .......................................7分方法二:(I )设选手甲在A 区投篮的得分为ξ,则ξ的可能取值为0,2,4,212291(0)(1)101009918(2)(1)1010100981(4)().10100P P C P ξξξ==-===⋅-====;;所以ξ的分布列为ξ0 2 4p11001810081100.......................................2分6.3=∴ξE .......................................3分 同理,设选手甲在B 区投篮的得分为η,则η的可能取值为0,3,6,9,3123223318(0)(1);327114(3)(1);339112(6)()(1);33911(9)().327P P C P C P ηηηη==-===⋅-===-====所以η的分布列为:η369p8274929127.......................................5分3E η∴=, .......................................6分 ηξE E > ,∴选手甲应该选择A 区投篮. .......................................7分(Ⅱ)设选手甲在A 区投篮得分高于在B 区投篮得分为事件C ,甲在A 区投篮得2分在B 区投篮得0分为事件1C ,甲在A 区投篮得4分在B 区投篮得0分为事件2C ,甲在A 区投篮得4分在B 区投篮得3分为事件3C ,则123C C C C = ,其中123,,C C C 为互斥事件. .......................................9分 则:12312318881881449()()= ()()()1002710027100975P C P C C C P C P C P C =++=⨯+⨯+⨯=故选手甲在A 区投篮得分高于在B 区投篮得分的概率为4975..................................13分17. (共14分)解:(I ) 棱柱ABCD —1111A B C D 的所有棱长都为2,∴四边形ABCD 为菱形,AC BD ⊥ . .......................................1分又1A O ⊥平面ABCD, BD ⊂平面ABCD ,ABC1B 1C 1A DF1D O1A O BD ∴⊥ . .......................................2分又1AC A O O = ,1,AC A O ⊂平面11ACC A ,⊥∴BD 平面11ACC A , .......................................3分⊂1AA 平面11ACC A ,∴ BD ⊥1A A . .......................................4分(Ⅱ)连结1BC四边形ABCD 为菱形,AC BD O =O ∴是BD 的中点. ....................................... 5分 又 点F 为1D C 的中点,∴在1DBC ∆中,1//BC OF , .......................................6分 ⊄OF 平面11BCC B ,⊂1BC 平面11BCC B∴//O F 平面11BCC B .......................................8分 (III )以O 为坐标系的原点,分别以1,,OA OB OA 所在直线为,,x y z 轴建立空间直角坐标系. 侧棱1A A 与底面ABCD 的所成角为60°,1A O ⊥平面ABCD .601=∠∴AO A ,在AO A Rt 1∆中,可得11,3,AO A O ==在R t A O B ∆中,22413OB AB AO =-=-=.得1(1,0,0),(0,0,3),(0,3,0),(0,3,0)A A D B - ...............................10分 设平面D AA 1的法向量为),,(1111z y x n = ⎪⎩⎪⎨⎧=⋅=⋅∴00111AD n AA n )0,3,1(),3,0,1(1--=-=AD AA11113030x z x y ⎧-+=⎪∴⎨--=⎪⎩可设)1,1,3(1-=n .......................................11分又 B D ⊥平面11ACC A所以,平面11A AC C 的法向量为2(0,3,0)n OB ==.......................................12分 55353,cos 212121-=⋅-=⋅>=<∴n n n n n n ,二面角D —1A A —C 为锐角,故二面角D —1A A —C 的余弦值是55 . ....................................14分18. (共13分) 解:2211(21)()1(1)(1)a x ax a f x a x x x --+-'=--=+++,1x >-, .......................................2分 (I )由题意可得13(1)24a f -'==-,解得3a =, ....................................3分因为(1)ln 24f =-,此时在点(1,(1))f 处的切线方程为(ln 24)2(1)y x --=--, 即2ln 22y x =-+-,与直线:21l y x =-+平行,故所求a 的值为3. ....................4分 (II ) 令()0f x '=,得到1212,0x x a=-= ,由12a ≥可知120a-≤ ,即10x ≤. ................................5分① 即12a =时,12120x x a=-==.所以,2'2()0,(1,)2(1)xf x x x =-≤∈-+∞+, ................................6分故()f x 的单调递减区间为(1,)-+∞ . ................................7分 ② 当112a <<时,1120a -<-<,即1210x x -<<=,所以,在区间1(1,2)a --和(0,)+∞上,'()0f x <; ...............................8分在区间1(2,0)a-上,'()0f x >. .................................9分故 ()f x 的单调递减区间是1(1,2)a--和(0,)+∞,单调递增区间是1(2,0)a-. .........10分③当1a ≥时,1121x a=-≤-,所以,在区间(1,0)-上()0f x '>; ................................11分在区间(0,)+∞上()0f x '< , ...............................12分故()f x 的单调递增区间是(1,0)-,单调递减区间是(0,)+∞. ............................13分 综上讨论可得: 当12a =时,函数()f x 的单调递减区间是(1,)-+∞;当112a <<时,函数()f x 的单调递减区间是1(1,2)a --和(0,)+∞,单调递增区间是1(2,0)a-;当1a ≥时,函数()f x 的单调递增区间是(1,0)-,单调递减区间是(0,)+∞. 19. (共14分)解:(Ⅰ)抛物线22y px = (0)p >的准线为2p x =-, .....................................1分 由抛物线定义和已知条件可知||1()1222p p M F =--=+=,解得2p =,故所求抛物线方程为24y x =. ......................................3分(Ⅱ)联立2124y x by x ⎧=-+⎪⎨⎪=⎩,消x 并化简整理得2880y y b +-=. 依题意应有64320b ∆=+>,解得2b >-. ..............................................4分 设1122(,),(,)A x y B x y ,则12128,8y y y y b +=-=-, .............................................5分 设圆心00(,)Q x y ,则应有121200,422x x y y x y ++===-.因为以AB 为直径的圆与x 轴相切,得到圆半径为0||4r y ==, ........................6分 又22221212121212||()()(14)()5[()4]5(6432)AB x x y y y y y y y y b =-+-=+-=+-=+ . 所以 ||25(6432)8A B r b ==+=, .........................................7分 解得85b =-. .........................................8分所以12124822224165x x b y b y b +=-+-=+=,所以圆心为24(,4)5-.故所求圆的方程为2224()(4)165x y -++=. ............................................9分方法二:联立2124y x b y x ⎧=-+⎪⎨⎪=⎩,消掉y 并化简整理得22(416)40x b x b -++=, 依题意应有2216(4)160b b ∆=+->,解得2b >-. ............................................4分 设1122(,),(,)A x y B x y ,则21212416,4x x b x x b +=+= . .............................................5分设圆心00(,)Q x y ,则应有121200,422x x y y x y ++===-,因为以AB 为直径的圆与x 轴相切,得到圆半径为0||4r y ==. .....................................6分 又2222121212121215||()()(1)()[()4]5(6432)44AB x x y y x x x x x x b =-+-=+-=+-=+ ,又||28AB r ==,所以有5(6432)8b +=, .............................................7分 解得85b =-, ..............................................8分所以12485x x +=,所以圆心为24(,4)5-.故所求圆的方程为2224()(4)165x y -++=. .............................................9分(Ⅲ)因为直线l 与y 轴负半轴相交,所以0b <,又l 与抛物线交于两点,由(Ⅱ)知2b >-,所以20b -<<,...........................................10分 直线l :12y x b =-+整理得220x y b +-=,点O 到直线l 的距离|2|255b b d --== , .................................................11分所以321||4224222AOB S AB d b b b b∆==-+=+. ..................................................12分令32()2g b b b =+,20b -<<,24()343()3g b b b b b '=+=+, b4(2,)3-- 43-4(,0)3-()g b ' + 0 - ()g b极大由上表可得()g b 最大值为432()327g -= . ...............................................13分所以当43b =-时,A O B ∆的面积取得最大值3239. ...............................................14分20.(共14分)解:(Ⅰ)当10n =时,集合{}1,2,3,,19,20A = ,{}{}910,11,12,,19,20B x A x =∈>= 不具有性质P . ...................................1分因为对任意不大于10的正整数m ,都可以找到该集合中两个元素110b =与210b m =+,使得12b b m -=成立................2分集合{}*31,C x A x k k N =∈=-∈具有性质P . ................................................3分 因为可取110m =<,对于该集合中任意一对元素112231,31c k c k =-=-,*12,k k N ∈ 都有121231c c k k -=-≠. .....................................................................4分 (Ⅱ)当1000n =时,则{}1,2,3,,1999,2000A =①若集合S 具有性质P ,那么集合{}2001T x x S =-∈一定具有性质P ....................5分 首先因为{}2001T x x S =-∈,任取02001,t x T =-∈ 其中0x S ∈, 因为S A ⊆,所以0{1,2,3,...,2000}x ∈,从而0120012000x ≤-≤,即,t A ∈所以T A ⊆. ...........................6分 由S 具有性质P ,可知存在不大于1000的正整数m , 使得对S 中的任意一对元素12,s s ,都有12s s m -≠. 对于上述正整数m ,从集合{}2001T x x S =-∈中任取一对元素11222001,2001t x t x =-=-,其中12,x x S ∈, 则有1212t t x x m -=-≠,所以集合{}2001T x x S =-∈具有性质P . .............................8分 ②设集合S 有k 个元素.由第①问知,若集合S 具有性质P ,那么集合{}2001T x x S =-∈一定具有性质P .任给x S ∈,12000x ≤≤,则x 与2001x -中必有一个不超过1000, 所以集合S 与T 中必有一个集合中至少存在一半元素不超过1000, 不妨设S 中有t 2k t ⎛⎫≥⎪⎝⎭个元素12,,,t b b b 不超过1000. 由集合S 具有性质P ,可知存在正整数1000m ≤, 使得对S 中任意两个元素12,s s ,都有12s s m -≠, 所以一定有12,,,t b m b m b m S +++∉ .又100010002000i b m +≤+=,故12,,,t b m b m b m A +++∈ , 即集合A 中至少有t 个元素不在子集S 中, 因此2k k +≤2000k t +≤,所以20002k k +≤,得1333k ≤,当{}1,2,,665,666,1334,,1999,2000S = 时, 取667m =,则易知对集合S 中任意两个元素12,y y , 都有12||667y y -≠,即集合S 具有性质P , 而此时集合S中有1333个元素.因此集合S 元素个数的最大值是1333. .....................................14分说明:其它正确解法按相应步骤给分.。
2012-2013学年第一学期浙江省湖州市高三数学(文)期末试卷(含答案)

P
C
F
D A
R
B
因为 PF ⊂ 平面 PAF ,所以 RC ⊥ PF . 因为 ∠AFP 是二面角 A − CD − P 的平面角.…………………………………………12 分 在 Rt ∆RAD 中, AF = 1 RD = 1 RA2 + AD 2 = 2 , 2 2 2 在 Rt ∆PAF 中, PF = PA2 + AF 2 =
第 5 页 共 8 页
所以 an = 3 + 3 ( n − 1) = 3n , bn = 3n −1 .………………………………………………7 分.
3n ( n − 1) 3n ( n + 1) = . …………………………………8 分 2 2 1 所以 1 = 2 = 2 1 − 1 . …………………………………………………9 分 S n 3 n ( n + 1) 3 n n + 1
(Ⅱ)由(Ⅰ)知 Sn = 3n +
(
)
所以 1 + 1 + 1 + L + 1 = 2 1 − 1 + 1 − 1 + 1 − 1 + L + 1 − 1 = 2 1 − 1 . S1 S 2 S3 Sn 3 2 2 3 3 4 n n +1 3 n +1 …………………………………………………………………………………………10 分 因为 2 1 − 1 为 n 的增函数, 3 n +1
7 C
8 A
9 D
10 B
二、填空题(本大题共 7 小题,每小题 4 分,共 28 分. ) 11. 1 16.
n 12. 4 − 1 3
2022-2023学年北京海淀区高三(上)期中数学试题及答案

2022北京海淀高三(上)期中数 学2022.11一、选择题共10小题,每小题4分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项. (1)已知全集{}0U x x =>,集合{}23A x x =≤≤,则UA =( )(A )(0,2][3,)+∞(B )(0,2)(3,)+∞(C )(,2][3,)−∞+∞(D )(,2)(3,)−∞+∞(2)在同一个坐标系中,函数log a y x =与(0x y a a =>且1)a ≠的图象可能是( )(3)已知向量,a b 在正方形网格中的位置如图所示.若网格中每个小正方形的边长均为1,则⋅=a b ( )A .4B .C .4−D .−(4)若等差数列{}n a 和等比数列{}n b 满足11a b =,222a b ==,48a =,则{}n b 的公比为( )(A )2(B )2−(C )4(D )4−(5)已知实数,a b 满足a b >,则下列不等式中正确的是( )(A )||a b >(B )||a b >(C )2a ab >(D )2ab b >(6)在平面直角坐标系xOy 中,角α与角β均以Ox 为始边,它们的终边关于直线y x =对称.若3sin 5α=,则cos β=( )(A )45−(B )45 (C )35−(D )35(7)已知函数()f x .甲同学将()f x 的图象向上平移1个单位长度,得到图象1C ;乙同学将()f x 的图象上所有点的横坐标变为原来的12(纵坐标不变),得到图象2C .若1C 与2C 恰好重合,则下列给出的()f x 中符合题意的是( )(A )12()log f x x =(B )2()log f x x =(C )()2xf x =(D )1()2xf x ⎛⎫= ⎪⎝⎭(8)已知函数()e e (0)x x f x a b ab −=+≠,则"0a b +="是"()f x 为奇函数"的( ) (A )充分而不必要条件 (B )必要而不充分条件(C )充分必要条件(D )既不充分也不必要条件(9)若P 是ABC ∆内部或边上的一个动点,且AP xAB y AC =+,则xy 的最大值是( ) (A )14(B )12(C )1 (D )2(10)我们可以用下面的方法在线段上构造出一个特殊的点集:如图,取一条长度为1的线段,第1次操作,将该线段三等分,去掉中间一段,留下两段;第2次操作,将留下的两段分别三等分,各去掉中间一段,留下四段;按照这种规律一直操作下去.若经过n 次这样的操作后,去掉的所有线段的长度总和大于99100,则n 的最小值为( ) (参考数据:1g20.301,1g30.477≈≈) (A )9(B )10(C )11(D )12第二部分(非选择题 共110分)二、填空题共5小题,每小题5分,共25分. (11)若复数12i z =−,则z =____. (12)函数1()ln 1f x x x =+−的定义域是____. (13)已知向量(1,1)=a ,(,2)x tx =+b .若存在实数x ,使得a 与b 的方向相同,则t 的一个取值为____. (14)若函数π()sin (0)6f x x ωω⎛⎫=+> ⎪⎝⎭和22()cos ()sin ()g x x x ϕϕ=+−+的图象的对称中心完全重合,则ω=____;π6g ⎛⎫= ⎪⎝⎭____.(15)已知函数21,1,(),1.x ax x f x ax x ⎧−++≤=⎨>⎩(1)当1a =时,()f x 的极值点个数为____;(2)若()f x 恰有两个极值点,则a 的取值范围是____.三、解答题共6小题,共85分.解答应写出文字说明、演算步骤或证明过程. (16)(本小题13分)已知等差数列{}n a 的前n 项和为(1,2,)n S n =,且23a =,525S =. (Ⅰ)求{}n a 的通项公式;(Ⅱ)等比数列{}n b 的首项为1,公比为q ,在下列三个条件中选择一个,使得{}n b 的每一项都是{}n a 中的项.若*(),k m b a k m =∈N ,求m .(用含k 的式子表示)条件①:1q =−; 条件②:2q =; 条件③:3q =. 注:如果选择的条件不符合要求,第(Ⅱ)问得0分.(17)(本小题14分)已知函数2()2sin cos 2cos 1f x x x x =+−. (Ⅰ)求π4f ⎛⎫− ⎪⎝⎭的值;(Ⅱ)求()f x 的最小正周期;(Ⅲ)求()f x 在区间π0,2⎡⎤⎢⎥⎣⎦上的最大值和最小值.(18)(本小题14分)已知函值321()3f x x x =−.(Ⅰ)求()f x 的单调区间;(Ⅱ)若()f x 在区间(1,]m −上的取值范围是4,03⎡⎤−⎢⎥⎣⎦,求m 的取值范围.(19)(本小题14分)某自然保护区为研究某动物种群的生活习性,设立了两个相距12km 的观测站A 和B ,观测人员分别在,A B 处观测该动物种群,如图,某一时刻,该动物种群出现在点C 处,观测人员从两个观测站分别测得30BAC ∠=︒,60ABC =︒,经过一段时间后,该动物种群出现在点D 处,观测人员从两个观测站分别测得75BAD ∠=︒45ABD ∠=︒.(注:点,,,A B C D 在同一平面内)(Ⅰ)求ABD ∆的面积; (Ⅱ)求点,C D 之问的距离.(20)(本小题15分)已知函数s (n)iexx a f x −=.(Ⅰ)当2a =时,求曲线()y f x =在点(0,(0))f 处的切线方程;(Ⅱ)当1a =时,证明:函数()2y f x =−在区间(0,π)上有且仅有一个零点; (Ⅲ)若对任意[0,π]x ∈,不等式()2cos f x x ≥−恒成立,求a 的取值范围.(21)(本小题15分)对于一个m 行n 列的数表(2,3)m n A m n ⨯≥≥,用,i j a 表示数表中第i 行第j 列的数,{},0,1i j a ∈(1,2,,;i m =1,2,,)j n =.对于给定的正整数t ,若数表m n A ⨯满足以下两个条件,则称数表 m n A ⨯具有性质()p t :①1,1j a =,,0(1,2,,)m j a j n ==;②,11,1,21,2,1,(1,2,,1)i i i i i n i n a a a a a a t i m +++−+−++−==−.(Ⅰ)以下给出数表1和数表2.(ⅰ)数表1是否具有性质(2)p ?说明理由;(ⅱ)是否存在正整数t ,使得数表2具有性质()p t ?若存在,直接写出t 的值,若不存在,说明理由; (Ⅱ)是否存在数表2023m A ⨯具有性质(6)p ?若存在,求出m 的最小值,若不存在,说明理由; (Ⅲ)给定偶数(3)n n >,对每一个{}2,3,,1t n ∈−,将集合{m n m A ⨯具有性质}()p t 中的最小元素记为()f t .求()f t 的最大值.海淀区2022—2023学年第一学期期中练习高三数学参考答案一、选择题二、填空题(11 (12)(0,1)(1,)+∞ (13)答案不唯一,小于1的实数均可(14)2;1−或1 (15)2;(0,2)三、解答题(16)(本小题13分)解:(Ⅰ)设等差数列{}n a 的公差为d ,因为253,25a S ==, 所以113,54525.2a d a d +=⎧⎪⎨⨯+=⎪⎩解得11,2.a d =⎧⎨=⎩所以21n a n =−. (Ⅱ)选择条件③.因为11,3b q ==, 所以13n n b −=. 因为m k a b =, 即1213k m −−= .得1312k m −+=.因为*k ∈N ,13k −为奇数,131k −+为偶数,所以*m ∈N .可得1312k m −+=.(17)(本小题14分)解:(Ⅰ)2()2sin()cos()2cos ()14444f ππππ−=−−+−−22(2(1222=⋅+− 1=−.(Ⅱ)()sin 2cos 2)4f x x x x π=+=+.所以()f x 的最小正周期为22T π==π. (Ⅲ)因为0,2x π≤≤所以52,444x πππ≤+≤当242x ππ+=,即8x π=时,()f x 取得最大值,所以()f x 在区间[0,]2π上的最大值为()8f π=;当5244x ππ+=,即2x π=时,()f x 取得最小值, 所以()f x 在区间[0,]2π上的最小值为()12f π=−.(18)(本小题14分)解:(Ⅰ)()f x 的定义域为R .2'()2f x x x =−,令'()0f x =,120,2x x ==.由表可得,()f x 的单调递增区间为(,0),(2,)−∞+∞;单调递减区间为(0,2). (Ⅱ)由函数解析式及(Ⅰ)可知44(1),(0)0,(2),(3)033f f f f −=−==−=.①当(1,2)m ∈−时,4(1,],()3x m f x ∀∈−≠−,不符合题意;②当[2,3]m ∈时,()f x 在区间[1,]m −上的取值范围是4[,0]3−,符合题意;③当3m >时,由()f x 在区间(2,)+∞上单调递增可知()(3)0f m f >=,不符合题意. 综合上述,[2,3]m ∈(19)(本小题14分) 解:(Ⅰ)在ABD △中,75BAD ∠=︒,45ABD ∠=︒,所以60ADB ∠=︒.由正弦定理:sin sin AD AB ABD ADB =∠∠,得sin 45sin 60AD AB=︒︒,所以,sin4512sin60AD AB︒=⋅==︒(km).1sin sin75sin(4530))2BAD∠=︒=︒+︒=+=,所以ABD△的面积为11sin123622ABDS AB AD BAD=⋅⋅∠=⨯⨯=+△(2km).(Ⅱ)由30BAC∠=︒,60ABC∠=︒, 得45CAD∠=︒,AC=在ACD△中由余弦定理,得2222cos363166260 CD AC AD AC AD CAD=+−⋅⋅∠=⨯+⨯−⨯=.所以,CD=(km).即点C, D之间的距离为km.(20)(本小题15分)解:(Ⅰ)当2a=时,()e2sinxf x x=−,则(0)1f=.'()e2cosxf x x=−,则'(0)1f=−.曲线()f x在(0,(0))f处的切线方程为1y x=−+.(Ⅱ)当1a=时,记()()2e sin2xg x f x x=−=−−,则'()e cosxg x x=−.当(0,x∈π)时,0e e1,cos1x x>=<,所以'()'(0)0g x g>=.所以()g x在(0,)π上单调递增.因为(0)10,()e20g gπ=−<π=−>,所以函数()2y f x=−在区间(0,π)上有且仅有一个零点.(Ⅲ)设()()cos2h x f x x=+−e sin cos2x a x x=−+−.则'()e cos sinxh x a x x=−−.设()e cos sinxs x a x x=−−.则'()e cos sinxs x x a x=−+.因为当[0,]x ∈π时,0e e 1,cos 1,sin 0x x x ≥=, 所以当0a ≥时,[0,]x ∈π时,'()0s x ≥, 所以'()h x 在区间[0,]π上单调递增()*.(1)当1a >时,'(0)10h a =−<,'()e 0h a ππ=+>, 且'()h x 在区间[0,]π上单调递增, 所以存在唯一0(0,)x ∈π,使得0'()0h x =. 当0(0,)x x ∈时,'()0h x <, 所以()h x 在区间0(0,)x 上单调递减. 可得0()(0)0h x h <=,所以与题意不符.(2)当1a =时,()e sin cos 2x h x x x =−+−. '()e cos sin x h x x x =−−由()*可知:'()h x 在区间[0,]π上单调递增, 所以当[0,]x ∈π时,'()'(0)0h x h ≥=. 所以()h x 在区间[0,]π上单调递增. 所以()(0)0h x h =区间[0,]π上恒成立. 符合题意. (3)当1a <时,()e sin cos 2e sin cos 2x x h x a x x x x =−+−>−+−.由(2)可知,此时()0h x >在区间[0,]π上恒成立. 综上所述,实数a 的取值范围是(,1]−∞. (21)(本小题15分) 解:(Ⅰ)(ⅰ)数表1不具有性质(2)p .理由:2,13,12,23,22,33,3||||||12a a a a a a −+−+−=≠.(ⅱ)存在. 3t =时,数表2具有性质()p t .(Ⅱ)不存在数表2023m A ⨯具有性质(6)p .假设存在m 使得数表2023m A ⨯具有性质(6)p ,则,11,1,21,2,1,||||||6(1,2,,1)i i i i i n i n a a a a a a i m +++−+−++−==−.即在这两行中,有6列的数不同,设其中有k 列是第i 行的数为1,第1i +行的数为0,则有6k −列是第i 行的数为0,第1i +行的数为1.所以,从第i 行到第1i +行,一共增加了62k −个1,1的个数的奇偶性不变. ……7分 所以,任意两行中,1的个数的奇偶性相同.与数表2023m A ⨯第一行有2023个1,最后一行有0个1矛盾. 所以,不存在具有性质(6)p 的数表2023m A ⨯.(Ⅲ)()f t 的最大值的为1n +.定义1m −行n 列的数表(1)m n B −⨯: 其第i 行第j 列为,,1,||1,2,,1(1,2,,)i j i j i j b a a i m j n +=−=−=,.则,{0,1}i j b ∈,且,0i j b =表示,1,,i j i j a a +两数相同,,1i j b =表示,1,,i j i j a a +两数不同. 因为数表m n A ⨯的第1行确定,所以给定数表(1)m n B −⨯后,数表m n A ⨯唯一确定. ①先证()1f t n ≤+.我们按照如下方式,构造数表n n B ⨯:对于第21s −行和第2s 行,1,2,,2n s =, 令21,2121,21,0s s s s b b −−−==,2,212,20,1s s s s b b −==,且在这两行其余的2n −列中,任选相同的1t −列都为1,其他列都为0. 于是可得到具有性质()p t 的数表(1)n n A +⨯如下:第1列第2列第3列第4列第n -1列第n 列第1行 第3行 第5行 … 第n +1行 即对于每个{2,3,,1}t n ∈−,当1m n =+时,都存在数表m n A ⨯具有性质()p t .所以()1f t n ≤+.②再证1t n =−时,()1f t n ≥+. 记,1,2,...(1,2,,)i i i i n S a a a i m =+++=.因为1t n =−是奇数,所以i S 与+1i S 的奇偶性不相同(1,2,,1i m =−).因为10m S n S ==,, 所以m 是奇数.我们考虑(1)m n B −⨯的第i 行和1i +行,因为1t n =−,所以这两行中都有1n −列为1,1列为0. 若这两行相同,则数表m n A ⨯的第i 行和第2i +行相同,2i i S S +=.若这两行不同,设其分别在第,p q 列为0()p q ≠,则数表m n A ⨯的第i 行和第2i +行只在第,p q 列上不同,其他列都相同,2||2i i S S +−≤. 因为1,0m S n S ==,其中n 是偶数. 所以1224311||||22m m m m m m n S S S S S S S S −−−−=−=−+−++−≤⨯. 所以1m n ≥+,即(1)1f n n −≥+. 结合①,(1)1f n n −=+.综上所述,()f t 的最大值的为1n +.。
北京市丰台区2013-2014学年度高三年级第一学期期末考试数学(理)试题(WORD精校版)

丰台区2013-2014学年度第一学期期末练习高 三 数 学(理科) 2014.1第一部分 (选择题 共40分)一、选择题共8小题,每小题5分,共40分。
在每小题列出的4个选项中,选出符合题目要求的一项。
1. 在复平面内,复数1i i-对应的点位于 (A )第一象限 (B )第二象限 (C )第三象限 (D )第四象限2. 函数11(0)=++>y x x x的最小值为 (A )1 (B )2 (C )3 (D )43. 已知命题p: ∀21x x >,22x >12x ,则p ⌝是(A )∀21x x >,22x ≤12x (B )∃21x x >,22x ≤12x (C )∀21x x >,22x <12x (D )∃21x x >,22x <12x4. 过双曲线221916x y -=的右焦点,且平行其渐近线的直线方程是(A ) 3(5)4y x =±- (B ) 4(5)3y x =±-(C ) 3(5)4y x =±+ (D ) 3(5)4y x =±+5.如图,已知曲边梯形ABCD 的曲边DC 所在的曲线方程 为1(0)y x x=>,e 是自然对数的底,则曲边梯形的 面积是(A )1 (B )e (C )1e (D )126. 已知平行四边形ABCD 中,AB=1,AD=2,∠DAB=60o,则且⋅AC AB uuu r uu u r等于(A )1 (B (C )2 (D )7.已知函数()2sin()f x x ωϕ=+(0,||)ωϕπ><的部分图象如图所示,那么()f x 的表达式为(A )5()2sin(2)6π=+f x x (B )5()2sin(2)6π=-f x x (C )()2sin(2)6f x x π=+ (D )()2sin(2)6f x x π=- 8. 如图,一个底面半径为R 的圆柱被与其底面所成角为θ(00090θ<<)的平面所截,截面是一个椭圆.当θ为30o时,这个椭圆的离心率为 (A )12 (B(C(D )23第二部分 (非选择题 共110分)二、填空题共6小题,每小题5分,共30分。
北京市2013届高三数学理试题分类汇编(含9区一模及上学期期末试题)专题:圆锥曲线(含答案)

北京2013届高三最新模拟试题分类汇编(含9区一模及上学期期末试题精选)专题:圆锥曲线一、选择题1 .(2013届北京大兴区一模理科)双曲线221x m y -=的实轴长是虚轴长的2倍,则m 等于 ( )A .14B .12C .2D .42 .(2013届北京海滨一模理科)抛物线24y x =的焦点为F ,点(,)P x y 为该抛物线上的动点,又点(1,0)A -,则||||P F P A 的最小值是( )A .12 B .2 C .2D .33 .(2013届北京市延庆县一模数学理)已知双曲线)0,0(12222>>=-b a by ax 的离心率为2,一个焦点与抛物线x y 162=的焦点相同,则双曲线的渐近线方程为( )A .x y 23±= B .x y 23±= C .x y 33±= D .x y 3±=4 .(2013届东城区一模理科)已知1(,0)F c -,2(,0)F c 分别是双曲线1C :22221x y ab-=(0,0)a b >>的两个焦点,双曲线1C 和圆2C :222x y c +=的一个交点为P ,且12212P F F P F F ∠=∠,那么双曲线1C 的离心率为 ( )A 2B C .2D 15 .(2013届门头沟区一模理科)已知P (,)x y 是中心在原点,焦距为10的双曲线上一点,且y x的取值范围为33(,)44-,则该双曲线方程是 A .221916x y -=B .221916yx-=C .221169x y -= D .221169y x -=6 .(北京市东城区2013届高三上学期期末考试数学理科试题)已知抛物线22y p x =的焦点F 与双曲线22179xy-=的右焦点重合,抛物线的准线与x 轴的交点为K ,点A 在抛物线上且|||A K A F =,则△A F K 的面积为 ( )A .4B .8C .16D .327 .(北京市海淀区北师特学校2013届高三第四次月考理科数学)方程2x xy x +=的曲线是 ( )A .一个点B .一条直线C .两条直线D .一个点和一条直线8 .(北京市海淀区北师特学校2013届高三第四次月考理科数学)已知双曲线22221(0,0)x y a b ab-=>>,过其右焦点且垂直于实轴的直线与双曲线交于,M N 两点,O 为坐标原点.若O M O N ⊥,则双曲线的离心率为 ( )A .12-+B .12+ C .12-+D .12+9 .(北京市通州区2013届高三上学期期末考试理科数学试题 )已知直线1:4360l x y -+=和直线2:1l x =-,抛物线24y x =上一动点P 到直线1l 和直线2l 的距离之和的最小值是( )A .5B .2C .115D .310.(【解析】北京市朝阳区2013届高三上学期期末考试数学理试题 )已知双曲线的中心在原点,一个焦点为)0,5(1-F ,点P 在双曲线上,且线段PF 1的中点坐标为(0,2),则此双曲线的方程是 ( )A .1422=-yxB .1422=-yx C .13222=-yxD .12322=-yx11.(【解析】北京市海淀区2013届高三上学期期末考试数学理试题 )椭圆2222:1(0)x y C a b ab+=>>的左右焦点分别为12,F F ,若椭圆C 上恰好有6个不同的点P ,使得12F F P ∆为等腰三角形,则椭圆C 的离心率的取值范围是( )A .12(,)33B .1(,1)2 C .2(,1)3D .111(,)(,1)322二、填空题12.(2013届北京西城区一模理科)在直角坐标系xO y 中,点B 与点(1,0)A -关于原点O 对称.点00(,)P x y 在抛物线24y x =上,且直线A P 与B P 的斜率之积等于2,则0x =______.13.(2013届房山区一模理科数学)已知双曲线2222:1(0,0)x y C a b ab-=>>的焦距为4,且过点(2,3),则它的渐近线方程为 .14.(北京市东城区普通高中示范校2013届高三3月联考综合练习(二)数学(理)试题 )若双曲线22221(0,0)x y a b ab-=>>与直线y =无交点,则离心率e 的取值范围是 .15.(北京市东城区普通高中示范校2013届高三3月联考综合练习(二)数学(理)试题 )已知直线:1(R )l y a x a a =+-∈,若存在实数a使得一条曲线与直线l 有两个不同的交点,且以这两个交点为端点的线段的长度恰好等于a ,则称此曲线为直线l 的“绝对曲线”.下面给出的三条曲线方程:①21y x =--;②22(1)(1)1xy -+-=;③2234x y +=.其中直线l 的“绝对曲线”有_____.(填写全部正确选项的序号)如图,16.(北京市东城区普通校2013届高三3月联考数学(理)试题 )1F 和2F 分别是双曲线22221(00)x y a b ab-=>>,的两个焦点,A和B 是以O 为圆心,以1OF 为半径的圆与 该双曲线左支的两个交点,且2F AB △是等边三角形,则双 曲线的离心率为 .17.(北京市西城区2013届高三上学期期末考试数学理科试题)已知椭圆22142xy+=的两个焦点是1F ,2F ,点P在该椭圆上.若12||||2P F P F -=,则△12P F F 的面积是______.18.(北京市顺义区2013届高三第一次统练数学理科试卷(解析))在平面直角坐标系xOy 中,设抛物线x y 42=的焦点为F ,准线为P l ,为抛物线上一点,l PA ⊥,A 为垂足.如果直线AF 的倾斜角为 120,那么=PF _______.19.(北京市昌平区2013届高三上学期期末考试数学理试题 )以双曲线221916xy-=的右焦点为圆心,并与其渐近线相切的圆的标准方程是 _____.20.(【解析】北京市海淀区2013届高三上学期期末考试数学理试题 )以y x =±为渐近线且经过点(2,0)的双曲线方程为______.21.(【解析】北京市石景山区2013届高三上学期期末考试数学理试题 )已知定点A 的坐标为(1,4),点F 是双曲线221412xy-=的左焦点,点P 是双曲线右支上的动点,则P F P A +的最小值为 .三、解答题22.(2013届北京大兴区一模理科)已知动点P 到点A (-2,0)与点B (2,0)的斜率之积为14-,点P 的轨迹为曲线C 。
2013—2014海淀区第一学期期中高三语文试题及答案

海淀区高三年级第一学期期中练习语文2013. 11一、本大题共5小题。
每小题3分,共15分。
1.下列词语,字形与加点字的注音全都正确的一项是A. 装帧出神入画应.(yīnɡ)届叱咤.(chà)风云B. 振撼美轮美奂混.(hǔn)淆卓.(zhuó)有成效C. 博弈如鲠在喉昵.(nì)称令人咋.(zé)舌D. 历炼纷至沓来偌.(nuò)大戛.(jiá)然而止2.依次填入句中横线处的词语,最恰当的一项是①“十一”长假即将结束,我们从辽阔平坦的草原驱车进入高楼林立的都市,一种随之而来,度假时的舒适惬意荡然无存。
②山南地区到处着邓芝福同志的感人事迹,他以边疆为家,为西藏的卫生事业鞠躬尽瘁,被当地百姓称为“人民的好儿子”。
③不久前,有关部门的一项研究结果表明:无论是在先天遗传方面还是在后天开发方面,母亲对儿童的影响都要超过父亲。
A. 压迫感传颂公布B. 紧迫感传颂颁布C. 紧迫感赞颂公布D. 压迫感赞颂颁布3.下列句子中加点成语使用正确的一项是A. 唐宋田园诗的创作非常兴盛,作者多为文人或仕宦,他们不吝笔墨,讴歌瓜田李下....、“把酒话桑麻”的田园生活。
B. 春节庙会上,历史悠久、陈陈相因....的民俗活动,如舞龙、扭秧歌、踩高跷、抖空竹等,让人感受到浓浓的年味儿。
C. 接到这个任务,团长董正山首先想到了胆大心细的部下高志平,于是当仁不让....地把任务交给了高志平所带的九连。
D. 根据老舍同名小说改编的话剧《我这一辈子》公演后,深受业内好评,演员方旭的表演丝丝入扣....,生动传神。
4.下列语句,没有语病的一项是A. 著名科普读物《十万个为什么》第六版是“中国一线科学家总动员”的产物,被人们称为近十年来中国科普界之未见。
B. 都市里越来越多的青年人喜欢以夜间骑行的方式来放松身心,但夜间能见度较低,所以骑行过程中要注意人身安全。
高三语文试题第1页(共8页)C. 台风“菲特”带来的降雨总量大,造成三江口洪水叠加,又由于恰逢农历天文大潮,这些是导致余姚市水灾的直接原因。
北京市海淀区2012届高三上学期期中练习(物理)WORD版
北京市海淀区2011-2012学年高三第一学期期中练习 物 理 2011.11一、本题共10小题,每小题3分,共30分。
在每小题给出的四个选项中,有的小题只有一个选项是正确的,有的小题有多个选项是正确的。
全部选对的得3分,选不全的得2分,有选错或不答的得0分。
把你认为正确答案的代表字母填写在题后的括号内。
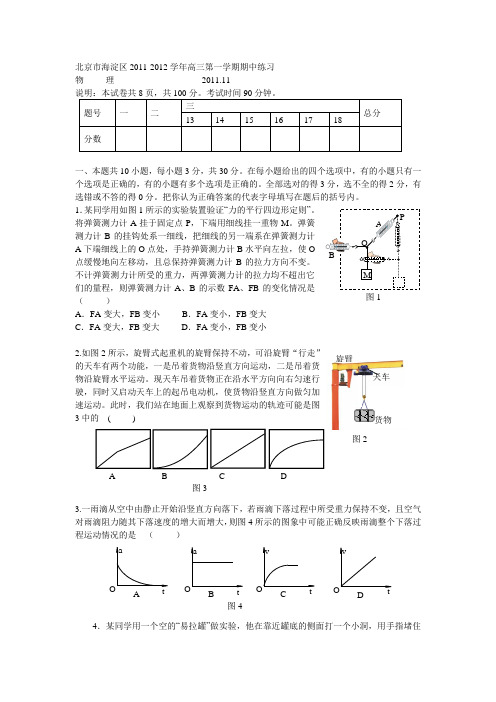
1.某同学用如图1所示的实验装置验证“力的平行四边形定则”。
将弹簧测力计A 挂于固定点P ,下端用细线挂一重物M 。
弹簧测力计B 的挂钩处系一细线,把细线的另一端系在弹簧测力计A 下端细线上的O 点处,手持弹簧测力计B 水平向左拉,使O 点缓慢地向左移动,且总保持弹簧测力计B 的拉力方向不变。
不计弹簧测力计所受的重力,两弹簧测力计的拉力均不超出它们的量程,则弹簧测力计A 、B 的示数FA 、FB 的变化情况是( )A .FA 变大,FB 变小 B .FA 变小,FB 变大 C .FA 变大,FB 变大D .FA 变小,FB 变小2.如图2所示,旋臂式起重机的旋臂保持不动,可沿旋臂“行走”的天车有两个功能,一是吊着货物沿竖直方向运动,二是吊着货物沿旋臂水平运动。
现天车吊着货物正在沿水平方向向右匀速行驶,同时又启动天车上的起吊电动机,使货物沿竖直方向做匀加速运动。
此时,我们站在地面上观察到货物运动的轨迹可能是图3中的 ( )3.一雨滴从空中由静止开始沿竖直方向落下,若雨滴下落过程中所受重力保持不变,且空气对雨滴阻力随其下落速度的增大而增大,则图4所示的图象中可能正确反映雨滴整个下落过程运动情况的是 ( )4.某同学用一个空的“易拉罐”做实验,他在靠近罐底的侧面打一个小洞,用手指堵住图4B DC A 图3 ABCDA O图1 BM 图2旋臂洞口,向“易拉罐”里面注满水,再把它悬挂在电梯的天花板上。
当电梯静止时,他移开手指,水就从洞口喷射出来,在水未流完之前,电梯启动加速上升。
关于电梯启动前、后的两个瞬间水的喷射情况,下列说法中正确的是( )A .电梯启动前后水的喷射速率不变B .电梯启动后水不再从孔中喷出C .电梯启动后水的喷射速率突然变大D .电梯启动后水的喷射速率突然变小5.如图5甲所示,一个单摆做小角度摆动,从某次摆球由左向右通过平衡位置时开始计时,相对平衡位置的位移x 随时间t 变化的图象如图5乙所示。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2012-2013海淀第一学期其中高三数学(理科)试题 第1页(共6页)海淀区高三年级第一学期期中练习数 学(理科) 2012. 11本试卷共4页,150分。
考试时长120分钟。
考生务必将答案答在答题卡上,在试卷上作答无效。
考试结束后,将本试卷和答题卡一并交回。
一、选择题:本大题共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项.1.已知全集U =R ,集合2{|1}A x x =≥,则U A =ðA .(,1)-∞B .(1,1)C .(1,)+∞D .(,1)(1,)-∞-+∞U 2.下列函数中,在定义域内是减函数的是 A .1()f x x=-B.()f x = C .1()2xf x =D .()ta n f x x =3.在平面直角坐标系xoy 中,已知(0,0)O ,(0,1)A,B ,则O A A B ⋅uur uuu r的值为A .1 B1 CD14.已知数列{}n a 的前n 项和122n n S +=-,则3a =A .1-B .2-C .4-D .8- 5.sin 15co s 15︒+︒的值为 A .12B.4C.2D.26.“0t ≥”是“函数2()f x x tx t =+-在(,)-∞+∞内存在零点”的 A .充分而不必要条件 B .必要而不充分条件 C .充分必要条件 D .既不充分也不必要条件 7.已知函数1,0,()1,0,x f x x -<⎧=⎨≥⎩则不等式(1)1x f x -≤的解集为A .[1,)-+∞B .(,1]-∞C .[1,2]D .[1,1]- 8.已知集合{(,)|()}M x y y f x ==,若对于任意11(,)x y M ∈,存在22(,)x y M ∈,使得12120x x y y +=成立,则称集合M 是“好集合”.给出下列4个集合:①1{(,)|}M x y y x==②{(,)|e 2}xM x y y ==-③{(,)|co s }M x y y x == ④{(,)|ln }M x y y x == 其中所有“好集合”的序号是A .①②④B .②③C .③④D .①③④ 二、填空题:本大题共6小题,每小题5分,共30分. 9.10e d xx =⎰ .10.设0.5a =π,3lo g 2b =,co s 2c =,则,,a b c 从大到小....的顺序为 . 11.函数211()(2)2x f x x x +=≤≤的值域为 . 12.在A B C ∆中,点M 为边A B 的中点,若O P uuu r ∥O M uuur ,且(0)O P xO A y O B x =+≠uu u r uur uu u r,则y x= .13.已知函数()y g x =的图象由()sin 2f x x =的图象向右平移(0)ϕϕ<<π个单位得到,这两个函数的部分图象 如图所示,则ϕ= .14.数列{}n a 中,如果存在k a ,使得“1k k a a ->且1k k a a +>”成立(其中2k ≥,k *∈N ),则称k a 为{}n a 的一个峰值.(Ⅰ)若2311n a n n =-+,则{}n a 的峰值为 ;(Ⅱ)若ln n a t n n =-,且{}n a 不存在峰值,则实数t 的取值范围是 .三、解答题:本大题共6小题,共80分.解答应写出文字说明,演算步骤或证明过程. 15.(本小题满分13分)已知等差数列{}n a 的前n 项和为n S ,且25a =-,520S =-. (Ⅰ)求数列{}n a 的通项公式;2012-2013海淀第一学期其中高三数学(理科)试题 第2页(共6页)(Ⅱ)求使不等式n n S a >成立的n 的最小值.16.(本小题满分13分)已知函数2()2sin c o s(2)2f x x x π=-+.(Ⅰ)求()8f π的值;(Ⅱ)求函数()f x 的最小正周期及单调递减区间.17.(本小题满分13分)在A B C ∆中,4A π∠=,tan ()7A B +=,A C =(Ⅰ)求sin C 的值; (Ⅱ)求A B C ∆的面积.18.(本小题满分13分)如图所示,已知边长为8米的正方形钢板有一个角被锈蚀,其中4A E =米,6C D =米.为了合理利用这块钢板,将在五边形A B C D E 内截取一个矩形块B N P M ,使点P 在边D E 上.(Ⅰ)设M P x =米,P N y =米,将y 表示成x 的函数,求该函数的解析式及定义域; (Ⅱ)求矩形B N P M 面积的最大值.19.(本小题满分14分)已知函数32211()(21)()32f x x a x a a x =-+++.(Ⅰ)若()f x 在1x =处取得极大值,求实数a 的值;(Ⅱ)若m ∀∈R ,直线y k x m =+都不是曲线()y f x =的切线,求k 的取值范围; (Ⅲ)若1a >-,求()f x 在区间[0,1]上的最大值.20.(本小题满分14分)已知数集12{,,A a a =…,}n a 12(1a a =<<…,2)n a n <≥具有性质P :对任意的(2)k k n ≤≤,,(1)i j i j n ∃≤≤≤,使得k i j a a a =+成立. (Ⅰ)分别判断数集{1,3,4}与{1,2,3,6}是否具有性质P ,并说明理由;(Ⅱ)求证:122n a a a ≤++…1(2)n a n -+≥; (Ⅲ)若72n a =,求数集A 中所有元素的和的最小值.NBMDF CA2012-2013海淀第一学期其中高三数学(理科)试题 第3页(共6页)参考答案及评分标准 2012.11一、选择题(本大题共8小题,每小题5分,共40分)B C B D C A D B二、填空题(本大题共6小题,每小题5分, 有两空的小题,第一空3分,第二空2分,共30分) 9.e 1- 10.a b c >> 11.5[2,]212.113.π314.10;*11{|,2}1ln 2ln ()N t t t n n n n≤=∈≥+或且三、解答题(本大题共6小题,共80分) 15.(本小题满分13分) 解:(I )设{}n a 的公差为d ,依题意,有 21515,51020a a d S a d =+=-=+=- ………………2分联立得11551020a d a d +=-⎧⎨+=-⎩解得161a d =-⎧⎨=⎩ ………………5分所以6(1)17n a n n =-+-⋅=- ………………7分 (II )因为7n a n =-,所以1(13)22nn a a n n S n +-==………………9分令(13)72n n n ->-,即215140n n -+> ………………11分解得1n <或14n >又*N n ∈,所以14n >所以n 的最小值为15 ………………13分16.(本小题满分13分)解:(Ⅰ)因为2π()2c o s c o s(2)2f x x x =-+22c o s sin 2x x =+………………2分1cos 2sin 2x x =++………………4分π(2)14x =++………………6分所以πππ()()11844f =++= ………………7分(Ⅱ)因为π()(2)14f x x =++所以2ππ2T == ………………9分又sin y x =的单调递减区间为π3π2π,2π 22k k ++(),()Z k ∈ ………………10分所以令ππ3π2π22π242k x k +<+<+………………11分解得π5πππ 88k x k +<<+………………12分所以函数()f x 的单调减区间为π5π(π+,π) 88k k +,()Z k ∈ ………………13分17.(本小题满分13分)解:(I )在ABC ∆中,因为πA B C ++= ………………1分所以ta n ta n [π()]ta n ()C A B A B =-+=-+ ………………3分 因为ta n ()7A B +=,所以tan 7C =- ………………4分2012-2013海淀第一学期其中高三数学(理科)试题 第4页(共6页)又22sin ta n 7c o s sin c o s 1C C C C C ⎧==-⎪⎨⎪+=⎩解得|s in |10C =………………5分因为(0,π),C ∈所以7s in 10C = ………………6分(II )因为π4A =,所以1ta n ta n ()71ta n B A B B++==-解得3ta n 4B =………………8分因为(0,π),C ∈ 所以3s in 5B =………………9分由正弦定理sin sin b c B C=,代入得到7c = ………………11分所以1sin 2A B C S b c A ∆=1π217sin242=⨯⨯= ………………13分18.(本小题满分13分)解:(I )作P Q A F ⊥于Q ,所以8,4P Q y E Q x =-=- ………………2分在E D F ∆中,E Q EF P QF D=所以4482x y-=- ………………4分所以1102y x =-+,定义域为|48}{x x ≤≤ ………………6分(II) 设矩形B N P M 的面积为S ,则21()(10)(10)5022x S x xy x x ==-=--+ ………………9分所以()S x 是关于x 的二次函数,且其开口向下,对称轴为10x =所以当(4,8)x ∈,()S x 单调递增 ………………11分 所以当8x =米时,矩形B N P M 面积取得最大值48平方米 ………………13分19.(本小题满分14分)解:(Ⅰ)因为22()(21)()f x x a x aa '=-+++()[(1)]x a x a =--+ ………………2分令()0f x '=,得1(1)x a =+,2x a=所以()f x ',()f x 随x 的变化情况如下表:………………4分 所以1a = ………………5分2012-2013海淀第一学期其中高三数学(理科)试题 第5页(共6页)(II )因为2211()()24a f x x +'=--………………6分因为m ∀∈R ,直线y k x m =+都不是曲线)(x f y =的切线 所以2211()()24a f x x k+'=--≠对R x ∈成立 ………………7分只要()f x '的最小值大于k所以 14k<-………………8分(III) 因为1,a >-所以10,a +>当1a ≥时,()0f x '≥对[0,1]x ∈成立 所以当1x=时,()f x 取得最大值21(1)6f a =-………………9分 当01a <<时, 在(0,)x a ∈时,()0f x '>,()f x 单调递增 在(,1)x a ∈时,()0f x '<,()f x 单调递减所以当xa=时,()f x 取得最大值3211()32f a a a=+………………10分当0a =时, 在(0,1)x ∈时,()0f x '<,()f x 单调递减所以当0x=时,()f x 取得最大值(0)0f = ………………11分当10a -<<时,在(0,1)x a ∈+时,()0f x '<,()f x 单调递减 在(1,1)x a∈+时,()0f x '>,()f x 单调递增又21(0)0,(1)6f f a ==-,当16a -<<-时,()f x 在1x=取得最大值21(1)6f a =-当06a -<时,()f x 在0x=取得最大值(0)0f =当6a=-时,()f x 在0x =,1x =处都取得最大值0. ………………14分综上所述, 当1a ≥或16a -<<-时,()f x 取得最大值21(1)6f a =-当01a <<时,()f x 取得最大值3211()32f a a a=+当6a =-时,()f x 在0x=,1x=处都取得最大值0当06a -≤时,()f x 在0x =取得最大值(0)0f =.20.(本小题满分14分)解:(Ⅰ)因为 311≠+, 所以{1,3,4} 不具有性质P .因为 2=12, 3=1+2, 6=33⨯+,所以{1,2,3,6}具有性质P ………………4分 (Ⅱ)因为集合12={,,,}n A a a a ⋅⋅⋅具有性质P :即对任意的(2),k k n ≤≤ , (1)i j i j n ∃≤≤≤,使得=+k i j a a a 成立, 又因为121<<<, 2n a a a n =⋅⋅⋅≥,所以,i k j k a a a a << 所以11,i k j k a a a a --≤≤,所以1=+2k i j k a a a a -≤即12n n a a -≤,122332212, 2,..., 2, 2n n n n a a a a a a a a ----≤≤≤≤ ………………6分 将上述不等式相加得21121+++2(+++)n n n a a a a a a --⋅⋅⋅≤⋅⋅⋅所以1212+++n n a a a a -≤⋅⋅⋅………………9分(Ⅲ)最小值为147.首先注意到1=1a ,根据性质P ,得到21=2=2a a 所以易知数集A 的元素都是整数.构造={1,2,3,6,9,18,36,72}A 或者={1,2,4,5,9,18,36,72}A ,这两个集合具有性质P , 此时元素和为147.下面,我们证明147是最小的和假设数集1212={,,,}(<<<,2)n n A a a a a a a n ⋅⋅⋅⋅⋅⋅≥,满足=1147ni i S a =≤∑最小(存在性显然,2012-2013海淀第一学期其中高三数学(理科)试题 第6页(共6页)因为满足=1147ni i a ≤∑的数集A 只有有限个).第一步:首先说明集合1212={,,,}(<<<,2)n n A a a a a a a n ⋅⋅⋅⋅⋅⋅≥中至少有8个元素:由(Ⅱ)可知21322, 2.......a a a a ≤≤又1=1a ,所以2345672, 4, 8, 16, 32, 6472a a a a a a ≤≤≤≤≤≤<, 所以8n ≥第二步:证明12336,18,9n n n a a a ---===:若36A ∈,设=36t a ,因为723636n a ==+,为了使得=1ni i S a =∑最小,在集合A中一定不含有元素k a ,使得36<72k a <,从而136n a -= ;假设36A ∉,根据性质P ,对72n a =,有,i j a a ,使得72n i j a a a ==+ 显然i j a a ≠, 所以144n i j a a a ++=而此时集合A 中至少还有5个不同于,,n i j a a a 的元素, 从而1()5149n i j S a a a a >+++=,矛盾, 所以36A ∈,进而=36t a ,且136n a -=; 同理可证:2318,9n n a a --==(同理可以证明:若18A ∈,则218n a -= 假设18A ∉.因为136,n a -=根据性质P ,有,i j a a ,使得136n i j a a a -==+ 显然i j a a ≠, 所以1144n n i j a a a a -+++=,而此时集合A 中至少还有4个不同于1,,,n n i j a a a a -的元素从而114148n n i j S a a a a a ->++++=,矛盾, 所以18A ∈,且218n a -=同理可以证明:若9A ∈,则39n a -=假设9A ∉因为218,n a -=根据性质P ,有,i j a a ,使得218n i j a a a -==+ 显然i j a a ≠, 所以12144n n n i j a a a a a --++++=而此时集合A 中至少还有3个不同于12,,,,n n n i j a a a a a --的元素从而1213147n n n i j S a a a a a a -->+++++=,矛盾, 所以9A ∈,且39n a -= )至此,我们得到了12336,18,9n n n a a a ---===. 根据性质P ,有,i j a a ,使得9i j a a =+ 我们需要考虑如下几种情形:①8,1i j a a ==, 此时集合中至少还需要一个大于等于4的元素k a ,才能得到元素8,则148S >;②7,2i j a a ==,此时集合中至少还需要一个大于4的元素k a ,才能得到元素7, 则148S >;③6,3i j a a ==,此时集合={1,2,3,6,9,18,36,72}A 的和最小,为147;④5,4i j a a ==,此时集合={1,2,4,5,9,18,36,72}A 的和最小,为147. ………14分。
