实验八 核磁共振(csy)讲解
核磁实验报告结果(3篇)

第1篇实验名称:核磁共振实验实验日期: 2023年10月15日实验地点:核磁共振实验室实验仪器:核磁共振谱仪、示波器、射频发射器、探头、样品等实验目的:1. 了解核磁共振的基本原理及其在物质结构分析中的应用。
2. 学习核磁共振谱图的解析方法。
3. 掌握核磁共振实验的基本操作流程。
实验原理:核磁共振(Nuclear Magnetic Resonance,NMR)是利用具有磁矩的原子核在外加磁场中吸收特定频率的射频能量,产生共振现象的一种技术。
通过分析共振信号,可以获得有关原子核的性质和周围环境的信息。
实验内容:1. 样品准备:选取实验样品,并将其置于核磁共振谱仪的样品管中。
2. 磁场调节:调节核磁共振谱仪的磁场强度,使其与样品中原子核的进动频率相匹配。
3. 射频发射:发射特定频率的射频脉冲,激发样品中的原子核。
4. 信号采集:利用示波器采集原子核的共振信号。
5. 数据分析:对采集到的信号进行分析,解析核磁共振谱图。
实验结果:1. 核磁共振谱图:- 通过核磁共振谱图,观察到样品中存在多种化学环境不同的氢原子核。
- 谱图中峰的位置、形状和强度反映了不同化学环境中氢原子核的性质。
2. 化学位移:- 化学位移是核磁共振谱图中峰的位置,反映了原子核周围电子云的密度。
- 通过化学位移,可以确定不同化学环境中氢原子核的种类和数量。
3. 自旋耦合:- 自旋耦合是指相邻化学环境中氢原子核之间的相互作用,表现为谱图中峰的分裂。
- 通过自旋耦合,可以确定分子中相邻原子核之间的关系。
4. 峰面积:- 峰面积反映了不同化学环境中氢原子核的数量。
- 通过峰面积,可以确定分子中不同化学环境的氢原子核的比例。
讨论与分析:1. 核磁共振谱图分析:- 根据核磁共振谱图,可以确定样品中存在的有机物结构。
- 通过比较谱图与标准谱图,可以确定有机物的种类和含量。
2. 化学位移分析:- 化学位移可以提供有关样品中氢原子核周围电子云密度和化学环境的信息。
核磁课件

常见结构单元质子的化学位移及经验计算
CH3OR CH3CO CH3N CH3C CH3OAr CH3Ar CH3C=C CH2Si (CH3Si
4
OH
3 C
N
2
H H H
1 C=CH
0 ppm
COOH
11
10
9
8
7
6
5
4
ppm
表3-5 一些常见结构单元H的化学位移范围(ppm)
1H,13C,19F,31P
原子核可看作核电荷均匀分布的球体,并象陀螺一样自旋, 有磁矩产生,是核磁共振研究的主要对象,C,H也是有机化 合物的主要组成元素。
2) 核磁共振现象
自旋量子数 I=1/2的原子核 (氢核),可当作电荷均匀分 布的球体,绕自旋轴转动时, 产生磁场,类似一个小磁铁。
当置于外加磁场H0中时, 相对于外磁场,可以有 (2I+1)种取向: 氢核(I=1/2),两种 取向(两个能级): (1)与外磁场平行,能量低, 磁量子数m=+1/2; (2)与外磁场相反,能量高, 磁量子数m=-1/2;
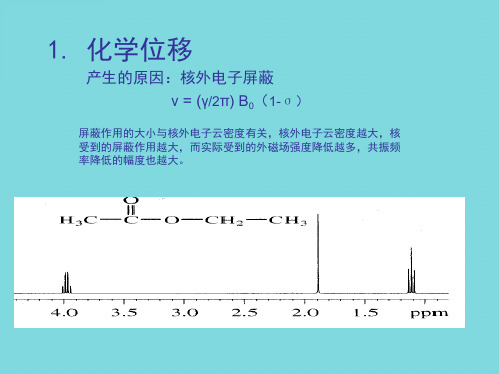
小,屏蔽强,共振需
要的磁场强度大,在高场出 现,图右侧;
大,屏蔽弱,共振需
要的磁场强度小,在低场出 现,图左侧;
= [( 样 - TMS) / TMS ] 106 (ppm)
3)影响化学位移的因素 ①诱导效应:电负性取代基的拉电子作用,使的氢质子外围电 子密度下降(σ下降,共振吸向低场位移),δ增大。 CH3F,-OH,-Cl, -Br, -I, -H, TMS 电负性:4.0 3.5 3.1 2.8 2.5 2.1 1.8 δCH3 4.06 3.40 3.10 2.68 2.16 0.23 0ppm 从中可知电负性增大,诱导作用增强, δ增大。 CHCl3 CH2Cl2 CH3Cl CH4 δCH 7.27 5.30 3.05 0.23ppm -X取代基数目增多,诱导效应增大, δ增大。 ②化学键:化学键电子云分布的不均匀性(SP3、SP2- SP2、SPSP电子云密度不同),造成感生磁场的不均匀,同时与待测质子在 空间位置也有关。 SP-SP:炔氢应比烯氢处于低场,但事实相反,这是由于其π电 子云以园柱形分布,构成筒状电子云绕 C-C键成环流,产生的感生 磁场沿键轴方向屏蔽区(+),乙炔δ2.88ppm
核磁共振光谱基本原理及实验操作

4.1拉莫尔进动
如图3-1所示,在外加磁场Ho中,自旋核绕自旋轴旋转,而自旋轴与磁场Ho又以特定夹角绕Ho旋转,类似一陀螺在重力场中运动,这样的运动称为拉莫尔进动。进动频率(又称拉莫尔频率)由下式算出
Wo=20=H0
而自旋角动量是量子化的,其在磁场方向的分量Pz和磁量子数(m)关系为Pz=mh/2,因为m共有2I+1个值,与此相应,Pz也有2I+1个值,与此相对应自旋核在z轴上的磁矩:
μ=νp
式中,ν为磁旋比,是核的特征常数。
依据量子力学原理,自旋角动量是量子化的,其状态是由核的自旋量子数Ⅰ所决定,P的绝对值为
P=h/2[Ⅰ(Ⅰ+1)]1/2
其中h为普朗克常量。
3磁场中核的自旋的能量
在一般的情况下,自选的磁矩可以任意取向,但是当把自旋的原子核放入外加磁场(Ho)中,除自旋外,原子核还将绕Ho运动,由于磁矩与磁场的相互作用,核磁矩的取向是量子化的。核磁矩的取向数可用磁量子数m来表示,m=I、I-1、I-2、…、-(I-1)、-I,共有2I+1个能级。每个能级的能量
R为照射线圈,提供一定频率的电磁波;Helmholtz线圈为扫场线圈,其通直流电所产生的附加磁场用以调节磁场的强度;D为接收线圈,与放大器和记录系统相连。这三组线圈互相垂直,互不干扰。若所提供的照射频率和磁场强度满足某种原子核的共振条件时,则该核发生能级跃迁,核磁矩方向改变,在接收线圈D中产生感应电流(不共振时无感应电流)。感应电流被放大、记录,即得核磁共振信号。
=△E/h=Ho/2
此即是产生核磁共振的条件。
二、核磁共振仪的组成
仪器的核心部分为探头,置于磁铁的两极之间。测试的样品放在此处。
磁体提供一定强度的磁场,使核磁矩发生空间量子化。永久磁铁和电磁铁的磁场强度的上限约为2.5T(即100MHz)。要想提高场强,必须使用低温超导磁体,低温是通过液氮来维持。
核磁共振ppt课件

δ 13C 96.1 192.8 77.1(3) 30.3(7), 207.3 39.5(7)
128.0(3) 67.4 116.5(4), 163.3(4) 26.3(7) 149.3(3),123.5(3), 135.5(3) 49.0(7)
精选ppt
2024/2/24
课件2021
16
7.2 1H-核磁共振波谱
(3)用一个能量恰好等于分裂后相邻能级差的电 磁波照射,该核就可以吸收此频率的波,发生能级 跃迁,从而产生 特征的NMR 吸收。
这就是核磁共振的基本原理。
精选ppt
2024/2/24
课件2021
3
1. 原子核的自旋(atomic nuclear spin )
(1)一些原子核像电子一样存在 自旋现象,因而有自旋角动量:
精选ppt
2024/2/24
课件2021
25
例题, 某质子的吸收峰与TMS峰相隔134Hz。若 用60 MHz的核磁共振仪测量,计算该质子的化学 位移值是多少?
解: δ = 134Hz / 60MHz 106 = 2.23 (ppm)
改用100 MHz的NMR仪进行测量,质子吸收峰 与TMS 峰相隔的距离,即为相对于TMS的化学 位移值Δν
在有机化合物中,各种氢核周围的化学环境不同,电 子云密度不同,屏蔽效应不同,共振频率有差异,即引起共 振吸收峰的位移,这种现象称为化学位移。
由于化学位移的大小用
与氢核所处的化学环境
密切相关,因此可用来
判断H 的化学环境,从
而推断有机化合物的分
子结构。
精选ppt
2024/2/24
课件2021
21
3. 化学位移的表示方法
核磁共振实验报告

核磁共振实验报告(总8页) -本页仅作为预览文档封面,使用时请删除本页-核磁共振实验报告一、实验目的与实验仪器1.实验目的(1)了解核磁共振的基本原理;(2)学习利用核磁共振校准磁场和测量因子g的方法:(3)掌握利用扫场法创造核磁共振条件的方法,学会利用示波器观察共振吸收信号;(4)测量19F的g N因子。
2.实验仪器NM-Ⅱ型核磁共振实验装置,水样品和聚四氟乙烯样品。
探测装置的工作原理:图一中绕在样品上的线圈是边限震荡器电路的一部分,在非磁共振状态下它处在边限震荡状态(即似振非振的状态),并把电磁能加在样品上,方向与外磁场垂直。
当磁共振发生时,样品中的粒子吸收了震荡电路提供的能量使振荡电路的Q值发生变化,振荡电路产生显著的振荡,在示波器上产生共振信号。
二、实验原理(要求与提示:限400字以内,实验原理图须用手绘后贴图的方式)原子核自旋角动量不能连续变化,只能取分立值即:P =其中I称为自旋量子数,I=0,1/2,1,3/2,2,5/2,…本实验涉及的质子和氟核 F19的自旋量子数I都等于1/2。
类似地原子核的自旋角动量在空间某一方向,例如z方向的分量不能连续变化,只能取分立的数值自旋角动量不为零的原子核具有与之相联系的核自旋磁矩, 其大小为:P 2Me g=μ 其中e 为质子的电荷,M 为质子的质量,g 是一个由原子核结构决定的因子,对不同种类的原子核g 的数值不同,g 成为原子核的g 因子。
由于核自旋角动量在任意给定的z 方向的投影只可能取(2I+1)个分立的数值,因此核磁矩在z 方向上的投影也只能取(2I+1)个分立的数值:2Me g p 2M e gmz z==μ原子核的磁矩的单位为:2Me N=μ 当不存在外磁场时,原子核的能量不会因处于不同的自旋状态而不同。
通常把B 的方向规定为z 方向,由于外磁场B 与磁矩的相互作用能为:B B P B B E z z m γγμμ-=-=-=⨯-=核磁矩在加入外场B 后,具有了一个正比于外场的频率。
核磁共振讲义核磁共振(共59张PPT)
问题:下图是氟代丙酮(CH3COCH2F)的1H谱。请画出它的质子耦合的
19F谱峰形,并标注相应的耦合常数。
4. 双共振 (double resonance)
(1)自旋去耦
H{P}
(2) NOE(nuclear Overhauser effect)
活泼氢的化学位移
化合物类型 醇 酚(分子内缔合) 其它酚 烯醇(分子内缔合) 羧酸 RC=NOH R-SH
(PPM)
化合物类型
0.5-5.5
Ar-SH
10.5-16 4-8 15-19 10-13 7.4-10.2
RSO3H RNH2, R2NH ArNH2, Ar2NH, ArNHR RCONH2, ArCONH2 RCONHR’, ArCONHR
NOE 实验
1D NOE
可以得到NOE变化
百分比
灵敏度高
2D NOESY
得到NOE交叉峰 全部信息
最常用
NOE 应用举例
5. Dynamic NMR
No Image
核磁共振仪有一定的
“时标”( time scale),即检测速度, 相当于照相机的快门。 若分子的两种形式交换 速度远远快于仪器的时 标(Δν) ,仪器测量
0.9-2.5
RCONHAr, ArCONHAr
(PPM) 3-4 11-12 0.4-3.5 2.9-4.8 5-6.5 6-8.2 7.8-9.4
化学位移图表和计算公式
• 氢谱化学位移数值已有较完善总结
• 经验公式
• 计算机预测
2. 自旋耦合与耦合常数
自旋耦合的产生
A核能级图
共振演示的实验报告

一、实验目的1. 理解共振现象的产生原理;2. 掌握共振条件的判断方法;3. 研究共振频率与固有频率的关系;4. 观察共振现象在生活中的应用。
二、实验原理共振是指在外力作用下,系统振动的频率与其固有频率相等时,系统振幅达到最大值的现象。
共振现象广泛应用于物理学、工程学、医学等领域。
实验中,我们将通过共振演示仪来观察和验证共振现象。
三、实验器材1. 共振演示仪(含弹簧、摆锤、刻度盘、固定架等);2. 秒表;3. 计算器;4. 实验记录本。
四、实验步骤1. 将共振演示仪放置在平稳的桌面上,调整固定架使弹簧垂直于桌面;2. 在摆锤上挂一个重物,调整重物质量,使其处于平衡状态;3. 使用秒表测量摆锤自由摆动的周期T,重复多次取平均值;4. 改变外力频率,通过调整摆锤的驱动力频率f,使其逐渐接近摆锤的固有频率f0;5. 观察摆锤的振幅变化,记录共振现象出现时的驱动力频率f和振幅A;6. 重复步骤3和4,改变重物质量,观察共振现象的变化。
五、实验数据1. 摆锤自由摆动的周期T(平均值):T = 2.5秒2. 共振现象出现时的驱动力频率f和振幅A:f1 = 1.6Hz,A1 = 8cmf2 = 2.0Hz,A2 = 10cmf3 = 2.4Hz,A3 = 12cm六、数据处理与分析1. 计算摆锤的固有频率f0:f0 = 1/T = 1/2.5Hz = 0.4Hz2. 分析共振现象:(1)当驱动力频率f逐渐接近摆锤的固有频率f0时,摆锤的振幅A逐渐增大;(2)当驱动力频率f等于摆锤的固有频率f0时,摆锤的振幅A达到最大值,出现共振现象;(3)当驱动力频率f大于摆锤的固有频率f0时,摆锤的振幅A逐渐减小。
3. 分析共振现象在生活中的应用:(1)在建筑工程中,通过控制结构固有频率,避免共振现象对建筑物的破坏;(2)在医学领域,共振现象可用于治疗某些疾病,如核磁共振成像(MRI);(3)在电子学领域,共振现象可用于设计滤波器、天线等电子元件。
第八章 核磁共振波谱_PPT课件
概述
核磁共振的方法与技术作为分析物质的手段 ,由 于其可深入物质内部而不破坏样品 ,并具有迅速、 准确、分辨率高等优点而得以迅速发展和广泛应用 ,已经从物理学渗透到化学、生物、地质、医疗以 及材料等学科 ,在科研和生产中发挥了巨大作用 。
核磁共振是1946年由美国斯坦福大学布洛赫 (F.Block)和哈佛大学珀赛尔(E.M.Purcell)各自独立发 现的,两人因此获得1952年诺贝尔物理学奖。50多 年来,核磁共振已形成为一门有完整理论的新学科 。
生物膜和脂质的多形性研究
化学位移各向异性的研究
脂质双分子层的脂质分子动态结构
金属离子同位素的应用
生物膜蛋白质——脂质的互相作用
动力学核磁研究
压力作用下血红蛋白质结构的变化
质子密度成像
生物体中水的研究
T1T2成像
生命组织研究中的应用
化学位移成像
生物化学中的应用
其它核的成像
在表面活性剂方面的研究
magnetic resonance spectroscopy for determining the threedimensional structure of biological macromolecules in solution".
他将获得2002年诺贝尔化学奖另一半的奖金。
If one knows all the measurements of a house one can draw a three-dimensional picture of that house. In the same way, by measuring a vast number of short distances in a protein, it is possible to create a three-dimensional picture of that protein.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验八 核磁共振(NMR )上个世纪初,人们在大量的原子光谱实验中发现了许多光谱的超精细结构,为了解释这些现象,鲍利(W.Pauli)于1924年提出了原子中存在核磁矩的假说。
以后大量的实验完全证实了他的假说,但由于很难精确测定这些超精细结构中所反映的细微能量差异,对核磁矩的进一步研究受到了极大的限制。
但人们对于核磁矩的研究并未因此而停止,在经过科学家的不懈努力下,于1939年观察到了核磁共振现象并观察了核磁矩,这一发现是Rabi 和他的同事在高真空的氢分子束实验中获得的,他也因此获得了1944年的诺贝尔物理学奖。
1945年12月,美国哈佛大学Purcel 等人报道了他们采用吸收法在石蜡样品中观察到质子的核磁共振吸收信号;1946年1月,美国斯坦福大学Bloch 等人,也报道了他们采用感应法在水样品中观察到质子的核磁共振感应信号。
两个研究小组用了稍微不同的方法,几乎同时在凝聚物质中发现了质子的核磁共振现象。
因此,1945年发现核磁共振现象的美国科学家Purcell 和Bloch 共同分享了1952年诺贝尔物理学奖。
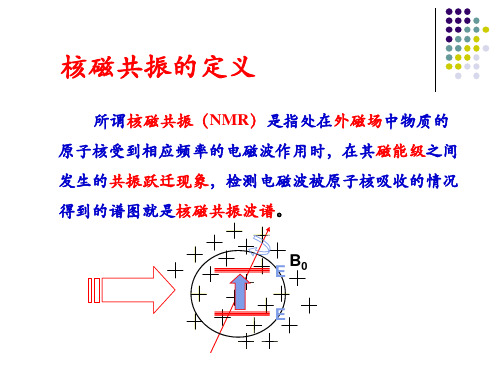
核磁共振是指处在恒定磁场中且具有原子磁矩的原子核受到某一频率电磁波辐射时引起的在能级之间的共振跃迁现象。
之后,许多物理学家进入了这个领域,取得了丰硕的成果。
1953年诞生了世界上第一台商用核磁共振波谱仪,使之在测定分子化学结构方面得到了重要应用。
1964年后,由于超导强磁场和脉冲傅立叶变换新技术的发展,使得核磁共振波谱仪的灵敏度和分辨率提高了几个数量级,从而使应用范围从有机小分子扩展到生物大分子,随着科技的进一步发展,人们又应用多重脉冲技术制造了固体核磁共振谱仪。
特别是1997年核磁共振断层扫描仪(NMR-CT )的成功研制,使得核磁共振在医学临床诊断方面得到了迅速的应用,目前,核磁共振已经广泛地应用到许多学科领域,是固体物理、化学、生物、临床诊断、计量科学和石油分析与勘探等研究中的一项重要实验技术。
它是测定原子的核磁矩和研究核结构的直接而又准确的方法,也是精确测量磁场和稳定磁场的重要方法之一。
下面,我们先来了解一下Rabi 首次观察到核磁共振的实验基本过程,从而对核磁共振有初步的体会。
Rabi 实验的基本原理如图10-1所示,把氢分子注入到A 、B 、C 磁场中,其中A 、B 为两个非匀强磁场,而C 为匀强磁场。
磁量子数m 不同的原子核经过非匀强磁场时偏转的方向不同,对于氢原子核,21±=m ,设21+=m 的核经过A 、B 、C 三个磁场后被探测器所接收;此时如果在匀强磁场C 中叠加上一射频场(辐度较小的交变磁场),当射频场的频率适合于磁场C 时,处于21+=m 状态的原子核就能吸收射频场的能量,跃迁到21-=m 的状态,因此通过磁场B 时向另一个方向偏转,不能被探测器所接收,以致于探测器接收到的粒子数减少,从而在探测器中得到了共振吸收信号。
由于它直接检测了核磁矩在磁分裂的能级上跃迁时与外界交换的射频场能量,大大提高了测量核磁矩的精度,为人们提供了观测微观世界的一个有力工具。
图10-1 Rabi 核磁共振示意图首次观察到核磁共振的实验装置和方法过于复杂,尽管如此,这一实验在物理学的发展中具有里程碑意义。
后来人们改进了核磁共振的测量方法,简化了实验装置。
目前广泛应用的测量方法是由Purcell 和Bloch 等人于1949年分别提出的。
他们利用样品对射频场的能量吸收或感应现象,直接来观察原子核在磁分裂的能级上的跃迁。
该方法不仅可以观察到共振现象,而且还可以在纯度不高的固态、气态中观察到共振现象。
由于他们大大简化了核磁共振实验方法和设备,因而使以后的几十年来核磁共振波谱学取得了惊人的发展,已成为在原子尺度上对物质结构进行实验研究的几种近代研究方法之一。
另外,它又是当前公认的精确测量磁场的标准方法之一。
在本实验中,通过对核磁共振的许多现象的观察,通过原子核旋磁比的测定,以及对磁场的测量,使实验者对核磁共振的原理以及实验技术有更深的了解。
【实验目的】1.掌握核磁共振的基本原理及其实现方法;2.掌握利用核磁共振测量顺磁物质旋磁比、g 因子的方法以及校准高斯计;3.了解核磁共振在医学、物理、化学等领域的实际应用。
【实验原理】1、几个基本参数—--原子核的自旋角动量、核磁矩、旋磁比、朗德因子N g我们知道,不仅电子有自旋运动,原子核本身也有自旋运动,因而原子核也有核自旋角动量P 。
从量子力学角度,氢原子中电子的能量是不连续的,只能取离散的数值。
类似地,核磁共振中涉及到的原子核自旋角动量也不连续,只能取离散值,其值由下式决定:)1(+=I I p(10·1) 式中π2h = ,而h 为普朗克常数,I 为核自旋量子数,只能取整数值0,1,2,3,…或半整数值1/2,3/2,5/2,…。
I 是表示某种原子核所固有的特征,对不同的核素,I 有不同的确定数值。
若核内质子数Z 与中子数N 都为偶数,那么它的质量数A=Z+N 也为偶数,这种原子核的自旋量子数I 等于零,因而自旋角动量为零,如126C 、168O 、3216S 等,这种核没有核磁共振现象。
若核内质子数Z 与中子数N 都为奇数,质量数A=Z+N 仍为偶数,则核自旋量子数I 为整数,如21H 、147N 等,1=I 。
若核的质量数A=Z+N 仍为奇数,则核自旋量子数I 为半整数, 如73Li 的23=I ,又如11H 、136C 、157N 、199F ……原子核的21=I 。
这几种核是核磁共振实验技术中最主要的研究对象。
原子核自旋角动量在空间某一方向的分量也不能连续变化,只能取离散的数值,例如z 方向角动量表示为:m p z = (10·2)其中磁量子数m 只能取I ,1-I ,…,1+-I ,I -共12+I 个数值。
自旋角动量不为零的原子核具有与之相联系的核自旋磁矩,简称核磁矩。
通常将原子核的总磁矩u 在其自旋角动量P 方向的投影μ称为核磁矩。
它们之间关系可写成:P γμ= (10·3) 对于质子而言,上式中pN M eg 2=γ称为旋磁比,定义为原子核的磁矩与自旋角动量之比,表征原子核的磁性质,可以从实验上测量得到,式中e 为质子电荷,p M 为质子质量,N g 为原子核的朗德因子,其值由原子核结构决定。
对不同种类的原子核,N g 的数值不同。
目前对各种原子核,N g 因子已能用实验方法精确测定,但在理论上尚不能精确计算,已测定的包含一个质子的11H 核的58510.5=N g 。
此外,N g 可能是正数,也可能是负数。
因此原子核自旋磁矩的方向可能与自旋角动量方向相同,也可能相反。
由于原子核角动量在任意给定的方向(如z 方向)只能取12+I 个离散的数值,核磁矩在z 方向也只能取12+I 个离散的数值,即:N pp z z gm M e gm M e g p μγμ====22 (10·4)在这个公式中,我们引入了T J M e pN /10050824.5227-⨯== μ,称为核磁子,是度量核磁矩大小的单位。
我们知道,玻尔磁子T J M e e B /102345.9224-⨯==μ,比较N μ和B μ,因为质子质量p M 是电子质量e M 的1838倍,所以核磁子是玻尔磁子的1/1838。
引入核磁子之后,旋磁比N N N p p N g g M e M eg μγ=⋅==22。
所以,N N g μγ= (10·5)2、核磁共振的量子与经典解释(1)量子解释当不存在外磁场时,每一个原子核的能量处在同一能级(某一能量状态);而当自旋量子数为I 的原子核处于沿某一方向(如Z 轴)的恒定磁场0B中时,原子核将不再只有一种能量状态。
由公式(2)和(4)可以得到核磁矩在外磁场方向(Z 轴)的投影: γγμm p z z == (10·6)核磁矩与外加恒定磁场的相互作用能量:0000B mg B m B B E N N z ⋅=⋅=-=⋅-=μγμμ (10·7)因此磁量子数m 取值不同,核磁矩的能量也就不同,从而原来简并的同一能级分裂为12+I 个子能级。
如对于质子,21=I ,则磁量子数21 , 21-=m ,即原子核原来单一的能级在磁场作用下分裂为二个能级:0121B E ⋅-= γ,0221B E ⋅= γ,这时上下能级的能量差: 00ωγ∆ =⋅=B E (10·8)其中00B γω=为经典的拉摩进动频率。
图10-2给出了质子的能级在外磁场下产生塞曼效应,分裂为两个能级的示意图。
处于恒定磁场0B中的包含大量微观磁矩的宏观体系,在热平衡状态下,上下能级的粒子数20N 、10N 应遵循玻尔兹曼分布: ⎪⎪⎭⎫ ⎝⎛-=T k E N N B ∆exp 1020 (10·9) 式中B k 为玻尔兹曼常数。
在一般情况下,T k E B <<∆,上式可近似为: Tk E N N B ∆-=11020 (10·10) 可以看出下能级的粒子数要比上能级的略多,如对于11H 核,在室温时,当恒定磁场T B 10.00=时,6107-⨯=T k EB ∆,即上下能级的粒子数相差甚微。
但正由于有这个差数,使体系宏观磁化强度M 的纵向分量不为零。
使我们观察共振现象才有可能。
从(10)式也可以看出,上下能级粒子差数由E ∆大小、系统的温度和系统的总粒子数决定。
根据爱因斯坦的辐射理论,因恒定磁场引起的核磁矩能级分裂的间隔很小,自发辐射的影响可以忽略。
若在与恒定磁场0B 垂直的方向上再施加一个高频电磁场,通常为射频场,表示为:x x x e t B B )(cos 21ω= (10·11) 其中x e为沿x 轴的单位矢量,12B 为电磁波振幅。
当射频场的频率与能级能量差满足下列关系时, E h x x ∆ωυ== ,即0B x ⋅= γω ⇒ 0B x γω= (10·12)在两个能级上的粒子将发生受激辐射与受激吸收,两个过程产生的几率P 是相等的。
几率P 与射频场辐度1B 成正比,即:1B P ∝ (10·13)在同一个射频场作用下,虽然受激辐射与受激吸收的几率P 相等同,但由于一开始处在下能级的粒子数比在上能级的略多,所以发生受激吸收的粒子数比发生受激辐射的粒子数多,即往高能级跃迁的比低能级跃迁的粒子数多,从宏观上来看,体系的总能量增加,这相当于体系从射频场中吸收能量。
这时我们观察射频场的辐度1B ,就可以看到一个被吸收的共振信号。
(2)经典解释具有角动量P 及固有磁矩μ 的粒子,在恒定磁场0B 的作用下,受到一个力矩的作用:0B L ⨯=μ (10·14)由 dtP d L =可得, 0B dtP d ⨯=μ (10·15) 方程(15)为磁矩在恒定磁场中的运动方程。
