概率论与数理统计
(完整版)概率论与数理统计知识点总结,推荐文档
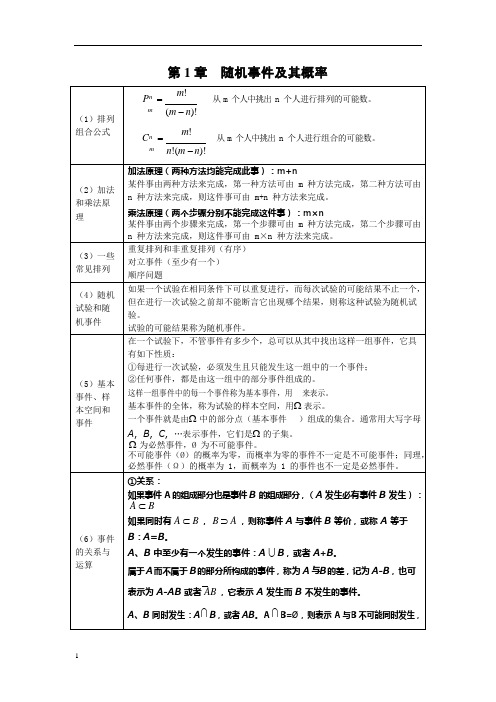
第1 章随机事件及其概率在一个试验下,不管事件有多少个,总可以从其中找出这样一组事件,它具有如下性质:①每进行一次试验,必须发生且只能发生这一组中的一个事件;②任何事件,都是由这一组中的部分事件组成的。
这样一组事件中的每一个事件称为基本事件,用来表示。
基本事件的全体,称为试验的样本空间,用Ω表示。
一个事件就是由Ω中的部分点(基本事件)组成的集合。
通常用大写字母A,B,C,…表示事件,它们是Ω的子集。
Ω为必然事件,Ø 为不可能事件。
不可能事件(Ø)的概率为零,而概率为零的事件不一定是不可能事件;同理,必然事件(Ω)的概率为 1,而概率为 1 的事件也不一定是必然事件。
1°Ω={1,2 n},12°P(1) =P(2) = P(n) =n。
设任一事件A ,它是由1,2 m组成的,则有P(A)= {(1) (2) (m)}= P(1) +P(2) + +P(m)=m=A所包含的基本事件数n 基本事件总数第二章随机变量及其分布设随机变量X 的分布律为k-P( X =k ) = e ,> 0 ,k = 0,1,2 ,k!则称随机变量X 服从参数为的泊松分布,记为X ~ () 或者P()。
泊松分布为二项分布的极限分布(np=λ,n→∞)。
e-x , x≥0,f (x) =0, x < 0 ,其中> 0 ,则称随机变量 X 服从参数为的指数分布。
X 的分布函数为1 -e-x, x≥0,F (x) =0,x<0。
记住积分公式:+∞⎰x n e -x dx =n!正态分布设随机变量 X 的密度函数为 21-( x -) 2- ∞ < x < +∞f (x ) =e 2 , , 2其中、> 0 为常数,则称随机变量 X 服从参数为、的正态分布或高斯(Gauss )分布,记为 X ~ N (,2) 。
f (x ) 具有如下性质:1° f (x ) 的图形是关于 x = 对称的;2° 当 x = 时, f ()= 1 为最大值;若 X ~ N (,2) ,则 X 2 的分布函数为1 x e- ( t - ) 2F (x ) =⎰- 2 2dt2∞参数= 0 、= 1时的正态分布称为标准正态分布,记为X ~ N (0,1) ,1 其-密x 2度函数记为 (x ) = e 22 , - ∞ < x < +∞ ,分布函数为21x - t Φ(x ) = 2⎰ e 2dt 。
概率论与数理统计基本概念

概率论与数理统计基本概念
概率论与数理统计是研究事件发生的可能性,以及由此衍生的结果
的一门学科。
它可以帮助人们提高分析和预测能力。
可以帮助我们了
解自然界及其客观原理,以及把握当代社会经济实体及其活动。
一、概率概念:
1. 随机事件:指事件发生以来,在所有结果中,用概率值去衡量其发
生的可能性,及其各个单一结果的概率分布情况;
2. 概率:是用来衡量某一随机事件发生的可能性的数值,可以给出这
个事件发生的可能性大小;
3. 概率分布:是某一随机变量及其可能取值之间发生关系的一种描述;
二、数理统计概念:
1、统计:是指对数据进行定量描述,尝试从数据中获得解释性的统计
特征;
2、变量:是指以数值形式表示的某类事物,是研究目标内容分析的一
种实际基础;
3、统计分布:是给定一组数据,通过统计手段,计算出变量的概率分
布情况,及其可能的变化规律;
4、极限定理:是一种概率论的定理,旨在探讨一个系统在重复抽样下,抽样结果的收敛情况;
5、数据描述:是指对数据的描述,可以让人简单明了地理解数据,及
其特征和趋势;
6、统计推断:是指根据统计样本信息,以概率结果作为有效依据,做
出关于总体参数情况的推断;
7、回归分析:是指建立一条回归函数模型,以描述解释变量对被解释
变量的影响;
8、判别分析:是指构建一个准确的模型,能够根据输入的观测值来准
确地判断属于哪一类人或物;
9、聚类分析:是指将一组数据进行分类,从而揭示内部数据间的关系,辅助决策;
10、卡方检验:是指判断某一种统计判断是否证实对某一总体分布结
果的检验,从而决定是否接受或拒绝假设。
概率论与数理统计知识点总结(超详细版)

概率论与数理统计知识点总结(超详细版)eik则有P(A)=k/n,其中n为样本空间中元素的个数。
在概率论中,样本空间和随机事件是基本概念。
如果事件A发生必然导致事件B发生,则称事件B包含事件A,记作A⊂B。
当A和B中至少有一个发生时,称A∪B为事件A和事件B的和事件。
当A和B同时发生时,称A∩B为事件A和事件B的积事件。
当A发生、B不发生时,称A-B为事件A和事件B的差事件。
如果A和B互不相容,即A∩B=∅,则称A和B是互不相容的,或互斥的,基本事件是两两互不相容的。
如果A∪B=S且A∩B=∅,则称事件A和事件B互为逆事件,又称事件A和事件B互为对立事件。
在概率论中,还有一些运算规则。
交换律指A∪B=B∪A,A∩B=B∩A;结合律指(A∪B)∪C=A∪(B∪C),(A∩B)∩C=A∩(B∩C);分配律指A∪(B∩C)=(A∪B)∩(A∪C),A∩(B∪C)=(A∩B)∪(A∩C);德摩根律指A∪B=A∩B,A∩B=A∪B。
频率与概率是概率论的重要概念。
在相同的条件下,进行了n次试验,在这n次试验中,事件A发生的次数n A称为事件A发生的频数,比值nAn称为事件A发生的频率。
概率指对于随机试验E的每一事件A赋予一个实数P(A),称为事件的概率。
概率P(A)满足非负性,即对于每一个事件A,0≤P(A)≤1;规范性,即对于必然事件S,P(S)=1;可列可加性,即设A1,A2,…,An是两两互不相容的事件,则有P(∪Ai)=∑P(Ai)(n可以取∞)。
概率还有一些重要性质,包括P(∅)=0,P(∪Ai)=∑P(Ai)(n可以取∞),如果A⊂B,则P(B-A)=P(B)-P(A),P(A)≤1,P(A)=1-P(A'),以及P(A∪B)=P(A)+P(B)-P(A∩B)。
等可能概型又称为古典概型,是指试验的样本空间只包含有限个元素,试验中每个事件发生的可能性相同。
如果事件A 包含k个基本事件,即A={e1}∪{e2}∪…∪{ek},则有P(A)=k/n,其中n为样本空间中元素的个数。
《概率论与数理统计》教案

《概率论与数理统计》教案第一章:概率的基本概念1.1 随机现象与样本空间1.2 事件及其运算1.3 概率的定义与性质1.4 条件概率与独立性第二章:随机变量及其分布2.1 随机变量的概念2.2 离散型随机变量及其分布2.3 连续型随机变量及其分布2.4 随机变量的数字特征(期望、方差)第三章:多维随机变量及其分布3.1 多元随机变量的概念3.2 联合分布及其性质3.3 独立性及其检验3.4 随机向量的数字特征(协方差、相关系数)第四章:大数定律与中心极限定理4.1 大数定律4.2 中心极限定理4.3 样本均值的分布4.4 样本方差的分布第五章:假设检验与置信区间5.2 常用的检验方法5.3 置信区间的估计5.4 功效分析与错误类型第六章:抽样调查与样本分布6.1 抽样调查的基本概念6.2 随机抽样方法6.3 样本分布的性质6.4 抽样误差的估计第七章:回归分析与相关分析7.1 线性回归模型7.2 回归参数的估计7.3 回归模型的检验与诊断7.4 相关分析与判定系数第八章:时间序列分析8.1 时间序列的基本概念8.2 平稳时间序列的模型8.3 时间序列的预测8.4 季节性分析与指数平滑第九章:非参数统计与生存分析9.1 非参数统计的基本概念9.2 非参数检验方法9.4 生存函数与生存分析的估计第十章:贝叶斯统计与统计软件应用10.1 贝叶斯统计的基本原理10.2 贝叶斯参数估计与预测10.3 贝叶斯统计的应用10.4 统计软件的使用与实践重点和难点解析一、随机现象与样本空间补充说明:事件的关系与包含关系,概率的基本性质(互补性、传递性等),概率的计算方法。
二、随机变量及其分布补充说明:概率质量函数与概率密度函数的区别与联系,分布函数的性质,随机变量的期望与方差的计算。
三、多维随机变量及其分布补充说明:二维随机变量的联合分布函数,条件概率的计算,独立性的数学表述与检验方法。
四、大数定律与中心极限定理补充说明:大数定律的数学表述及其含义,中心极限定理的条件与结论,样本均值与标准差的性质。
概率论与数理统计 魏宗舒版 答案完整版

则该数的最后一位数字必须是 1,设最后第二位数字为 a ,则该数的立方的最后 两位数字为 1 和 3 a 的个位数,要使 3 a 的个位数是 1,必须 a = 7 ,因此 A 所包 含的样本点只有 71 这一点,于是
。 1.12 一个人把 6 根草掌握在手中,仅露出它们的头和尾。然后请另一个人 把 6 个头两两相接,6 个尾也两两相接。求放开手以后 6 根草恰好连成一个环的 概率。并把上述结果推广到 2n 根草的情形。 解 (1)6 根草的情形。取定一个头,它可以与其它的 5 个头之一相接,再取 另一头,它又可以与其它未接过的 3 个之一相接,最后将剩下的两个头相接,故
+
P( Ac ) ] =
2 2π d
(a
+b
+
c)
=
1 πd
(a
+
b
+
c)
(用例 1.12 的结果) 1.19 己知不可能事件的概率为零,现在问概率为零的事件是否一定为不可 能事件?试举例说明之。 解 概率为零的事件不一定是不可能事件。例如向长度为 1 的线段内随机投 点。则事件 A “该点命中 AB 的中点”的概率等于零,但 A 不是不可能事件。 1.20 甲、乙两人从装有 a 个白球与 b 个黑球的口袋中轮流摸取一球,甲先取, 乙后取,每次取后都有不放回,直到两人中有一人取到白球时停止。试描述这一 随机现象的概率空间,并求甲或乙先取到白球的概率。
第一章 事件与概率
1.1 写出下列随机试验的样本空间及表示下列事件的样本点集合。 (1)10 件产品中有 1 件是不合格品,从中任取 2 件得 1 件不合格品。 (2)一个口袋中有 2 个白球、3 个黑球、4 个红球,从中任取一球,(ⅰ)得白 球,(ⅱ)得红球。
概率论与数理统计公式大全

概率论与数理统计公式大全一、概率论公式1.概率的基本性质:-非负性:对于任意事件A,有P(A)>=0;-规范性:对于必然事件S,有P(S)=1;-可列可加性:对于互不相容的事件Ai(i=1,2,...),有P(A1∪A2∪...)=P(A1)+P(A2)+...。
2.条件概率:-事件B发生的条件下,事件A发生的概率:P(A,B)=P(A∩B)/P(B);-乘法公式:P(A∩B)=P(A,B)*P(B)。
3.全概率公式:-事件A的概率:P(A)=ΣP(A,Bi)*P(Bi),其中Bi为样本空间的一个划分。
4.贝叶斯公式:-事件Bi发生的条件下,事件A发生的概率:P(Bi,A)=P(A,Bi)*P(Bi)/ΣP(A,Bj)*P(Bj),其中Bj为样本空间的一个划分。
5.独立性:-事件A与事件B相互独立的充要条件是P(A∩B)=P(A)*P(B)。
二、数理统计公式1.随机变量的概率分布:-离散型随机变量的概率分布函数:P(X=x);-连续型随机变量的概率密度函数:f(x)。
2.数理统计的基本概念:-样本均值:X̄=ΣXi/n;-样本方差:s^2=Σ(Xi-X̄)^2/(n-1);-样本标准差:s=√s^2;- 样本协方差:sxy = Σ(Xi-X̄)(Yi-Ȳ) / (n-1)。
3.大数定律:-样本均值的大数定律:当样本容量n趋向于无穷大时,样本均值X̄趋向于总体均值μ。
4.中心极限定理:-样本均值的中心极限定理:当样本容量n足够大时,样本均值X̄服从近似正态分布。
5.参数估计:-点估计:用样本统计量对总体参数进行估计;-置信区间估计:用样本统计量构造一个区间,以估计总体参数的范围。
6.假设检验:-假设检验的基本步骤:提出原假设H0和备择假设H1,选择适当的检验统计量,计算拒绝域,进行假设检验。
以上只是概率论与数理统计中的一些重要公式和定理,还有很多其他的公式和定理没有一一列举。
掌握这些公式和定理,可以帮助我们更好地理解和应用概率论与数理统计的知识。
(完整版)《概率论与数理统计》期末考试试题及解答
一、填空题(每小题3分,共15分)1.设事件仅发生一个的概率为0.3,且,则至少有一个不发B A ,5.0)()(=+B P A P B A ,生的概率为__________.答案:0.3解:3.0)(=+A B A P 即)(25.0)()()()()()(3.0AB P AB P B P AB P A P A P B A P -=-+-=+=所以1.0)(=AB P.9.0)(1)((=-==AB P AB P B A P 2.设随机变量服从泊松分布,且,则______.X )2(4)1(==≤X P X P ==)3(X P 答案:161-e 解答:λλλλλ---==+==+==≤e X P e eX P X P X P 2)2(,)1()0()1(2由 知 λλλλλ---=+e e e 22)2(4)1(==≤X P X P即 0122=--λλ 解得,故1=λ161)3(-==e X P 3.设随机变量在区间上服从均匀分布,则随机变量在区间内的概率X )2,0(2X Y =)4,0(密度为_________.=)(y fY答案:04,()()0,.Y Y X y f y F y f <<'===⎩其它 解答:设的分布函数为的分布函数为,密度为则Y (),Y F y X ()F x ()X f x2()()()((Y X X F y P Y y P X y P X F F =≤=≤=≤≤=- 因为,所以,即~(0,2)XU (0X F =()Y X F y F =故04,()()0,.Y Y Xyf y F y f<<'===⎩其它另解在上函数严格单调,反函数为(0,2)2y x=()h y=所以04,()0,.Y Xyf y f<<==⎩其它4.设随机变量相互独立,且均服从参数为的指数分布,,则YX,λ2)1(-=>eXP=λ_________,=_________.}1),{min(≤YXP答案:,2λ=-4{min(,)1}1eP X Y≤=-解答:,故2(1)1(1)P X P X e eλ-->=-≤==2λ={min(,)1}1{min(,)1}P X Y P X Y≤=->1(1)(1)P X P Y=->>.41e-=-5.设总体的概率密度为X.⎪⎩⎪⎨⎧<<+=其它,0,1,)1()(xxxfθθ1->θ是来自的样本,则未知参数的极大似然估计量为_________.nXXX,,,21Xθ答案:1111lnniixnθ==-∑解答:似然函数为111(,,;)(1)(1)(,,)nnn i niL x x x x xθθθθθ==+=+∏1ln ln(1)lnniiL n xθθ==++∑1lnln01niid L nxdθθ==++∑@解似然方程得的极大似然估计为θ.1111ln ni i x n θ==-∑二、单项选择题(每小题3分,共15分)1.设为三个事件,且相互独立,则以下结论中不正确的是,,A B C ,A B (A )若,则与也独立.()1P C =AC BC (B )若,则与也独立.()1P C =A C B (C )若,则与也独立.()0P C =A C B (D )若,则与也独立.( )C B ⊂A C 答案:(D ). 解答:因为概率为1的事件和概率为0的事件与任何事件独立,所以(A ),(B ),(C )都是正确的,只能选(D ).事实上由图可见A 与C 不独立.2.设随机变量的分布函数为,则的值为~(0,1),X N X ()x Φ(||2)P X > (A ). (B ).2[1(2)]-Φ2(2)1Φ- (C ). (D ).( )2(2)-Φ12(2)-Φ 答案:(A )解答: 所以~(0,1)X N (||2)1(||2)1(22)P X P X P X >=-≤=--<≤应选(A ).1(2)(2)1[2(2)1]2[1(2)]=-Φ+Φ-=-Φ-=-Φ3.设随机变量和不相关,则下列结论中正确的是X Y (A )与独立. (B ).X Y ()D X Y DX DY -=+ (C ).(D ).( )()D X Y DX DY -=-()D XY DXDY =解答:由不相关的等价条件知,0y x cov 0xy =⇒=),(ρ()+2cov x y D X Y DX DY -=+(,)应选(B ).4.设离散型随机变量和的联合概率分布为X Y (,)(1,1)(1,2)(1,3)(2,1)(2,2)(2,3)111169183X Y P αβ若独立,则的值为,X Y ,αβ (A ). (A ).21,99αβ==12,99αβ== (C ) (D ).( )11,66αβ==51,1818αβ==解答: 若独立则有,X Y(2,2)(2)(2)P X Y P X P Y α======1121()()()3939αβαα=+++=+, ∴29α=19β=故应选(A ).5.设总体的数学期望为为来自的样本,则下列结论中X 12,,,,n X X X μ X 正确的是(A )是的无偏估计量.(B )是的极大似然估计量.1X μ1X μ (C )是的相合(一致)估计量. (D )不是的估计量. ( )1X μ1X μ 答案:(A ) 解答:,所以是的无偏估计,应选(A ).1EX μ=1X μ三、(7分)已知一批产品中90%是合格品,检查时,一个合格品被误认为是次品的概率为0.05,一个次品被误认为是合格品的概率为0.02,求(1)一个产品经检查后被认为是合格品的概率;(2)一个经检查后被认为是合格品的产品确是合格品的概率.解:设‘任取一产品,经检验认为是合格品’A =‘任取一产品确是合格品’B =则(1) ()()(|)()(|)P A P B P A B P B P A B =+ 0.90.950.10.020.857.=⨯+⨯=(2) .()0.90.95(|)0.9977()0.857P AB P B A P A ⨯===四、(12分) 从学校乘汽车到火车站的途中有3个交通岗,假设在各个交通岗遇到红灯的事件是相互独立的,并且概率都是2/5. 设为途中遇到红灯的次数,X求的分布列、分布函数、数学期望和方差.X解:的概率分布为X3323()(()0,1,2,3.55k k kP X k C k -===即01232754368125125125125XP的分布函数为X0,0,27,01,12581(),12,125117,23,1251, 3.x x F x x x x <⎧⎪⎪≤<⎪⎪⎪=≤<⎨⎪⎪≤<⎪⎪≥⎪⎩263,55EX =⨯= .231835525DX =⨯⨯=五、(10分)设二维随机变量在区域 上服从(,)X Y {(,)|0,0,1}D x y x y x y =≥≥+≤均匀分布. 求(1)关于的边缘概率密度;(2)的分布函数与概(,)X Y X Z X Y =+率密度.(1)的概率密度为(,)X Y 2,(,)(,)0,.x y Df x y ∈⎧=⎨⎩其它22,01()(,)0,X x x f x f x y dy +∞-∞-≤≤⎧==⎨⎩⎰其它(2)利用公式()(,)Z f z f x z x dx+∞-∞=-⎰其中2,01,01(,)0,x z x x f x z x ≤≤≤-≤-⎧-=⎨⎩其它2,01, 1.0,x x z ≤≤≤≤⎧=⎨⎩其它.当 或时0z <1z >()0Z f z =时 01z ≤≤00()222zzZ f z dx x z===⎰故的概率密度为Z 2,01,()0,Z z z f z ⎧≤≤⎪=⎨⎪⎩其它.的分布函数为Z200,00,0,()()2,01,01,1, 1.1,1z z Z Z z z f z f y dy ydy z z z z z -∞<⎧<⎧⎪⎪⎪==≤≤=≤≤⎨⎨⎪⎪>⎩>⎪⎩⎰⎰ 或利用分布函数法10,0,()()()2,01,1, 1.Z D z F z P Z z P X Y z dxdy z z ⎧<⎪⎪=≤=+≤=≤≤⎨⎪⎪>⎩⎰⎰20,0,,01,1, 1.z z z z <⎧⎪=≤≤⎨⎪>⎩2,01,()()0,Z Z z z f z F z ≤≤⎧'==⎨⎩其它.六、(10分)向一目标射击,目标中心为坐标原点,已知命中点的横坐标和纵坐标相X Y 互独立,且均服从分布. 求(1)命中环形区域2(0,2)N 22{(,)|12}D x y x y =≤+≤的概率;(2)命中点到目标中心距离的数学期望.Z =1){,)}(,)DP X Y D f x y dxdy∈=⎰⎰22222880111248x y r De dxdy erdrd πθππ+--==⋅⎰⎰⎰⎰;2221122888211()8r r red ee e ------=-=-⎰ (2)22818x y EZ E edxdyπ+-+∞-∞-∞==⎰⎰22228801184r r rerdrd e r drπθπ--+∞+∞==⎰⎰⎰222888r r r reedr dr +∞---+∞+∞-∞=-+==⎰七、(11分)设某机器生产的零件长度(单位:cm ),今抽取容量为16的2~(,)X N μσ样本,测得样本均值,样本方差. (1)求的置信度为0.95的置信10x =20.16s =μ区间;(2)检验假设(显著性水平为0.05).20:0.1H σ≤ (附注)0.050.050.025(16) 1.746,(15) 1.753,(15) 2.132,t t t ===2220.050.050.025(16)26.296,(15)24.996,(15)27.488.χχχ===解:(1)的置信度为下的置信区间为μ1α- /2/2(((X t n X t n αα--+-0.02510,0.4,16,0.05,(15) 2.132X s n t α=====所以的置信度为0.95的置信区间为(9.7868,10.2132)μ (2)的拒绝域为.20:0.1H σ≤22(1)n αχχ≥- ,221515 1.6240.1S χ==⨯=20.05(15)24.996χ= 因为 ,所以接受.220.052424.996(15)χχ=<=0H 《概率论与数理统计》期末考试试题(A )专业、班级:姓名:学号:一、单项选择题(每题3分 共18分)1.D 2.A 3.B 4.A 5.A 6.B 题 号一二三四五六七八九十十一十二总成绩得 分一、单项选择题(每题3分 共18分)(1).0)(,0)(;;0)(0)();(( ).,0)(=>===A B P A P (D)B A (C)B P A P (B)B A (A)AB P B A 则同时出现是不可能事件与或互不相容互斥与则以下说法正确的是适合、若事件(2)设随机变量X 其概率分布为 X -1 0 1 2P 0.2 0.3 0.1 0.4则( )。
(完整版)概率论与数理统计知识点总结(免费超详细版)
《概率论与数理统计》第一章 概率论的基本概念§2.样本空间、随机事件1.事件间的关系 B A ⊂则称事件B 包含事件A ,指事件A 发生必然导致事件B 发生B }x x x { ∈∈=⋃或A B A 称为事件A 与事件B 的和事件,指当且仅当A ,B 中至少有一个发生时,事件B A ⋃发生B }x x x { ∈∈=⋂且A B A 称为事件A 与事件B 的积事件,指当A ,B 同时发生时,事件B A ⋂发生B }x x x { ∉∈=且—A B A 称为事件A 与事件B 的差事件,指当且仅当A 发生、B 不发生时,事件B A —发生φ=⋂B A ,则称事件A 与B 是互不相容的,或互斥的,指事件A 与事件B 不能同时发生,基本事件是两两互不相容的且S =⋃B A φ=⋂B A ,则称事件A 与事件B 互为逆事件,又称事件A 与事件B 互为对立事件2.运算规则 交换律A B B A A B B A ⋂=⋂⋃=⋃结合律)()( )()(C B A C B A C B A C B A ⋂=⋂⋃⋃=⋃⋃ 分配律 )()B (C A A C B A ⋃⋂⋃=⋂⋃)( ))(()( C A B A C B A ⋂⋂=⋃⋂ 徳摩根律B A B A A B A ⋃=⋂⋂=⋃ B —§3.频率与概率定义 在相同的条件下,进行了n 次试验,在这n 次试验中,事件A 发生的次数A n 称为事件A 发生的频数,比值n n A 称为事件A 发生的频率概率:设E 是随机试验,S 是它的样本空间,对于E 的每一事件A 赋予一个实数,记为P (A ),称为事件的概率 1.概率)(A P 满足下列条件:(1)非负性:对于每一个事件A 1)(0≤≤A P (2)规范性:对于必然事件S 1)S (=P(3)可列可加性:设n A A A ,,,21 是两两互不相容的事件,有∑===nk kn k kA P A P 11)()( (n 可以取∞)2.概率的一些重要性质: (i ) 0)(=φP(ii )若n A A A ,,,21 是两两互不相容的事件,则有∑===nk kn k kA P A P 11)()((n 可以取∞)(iii )设A ,B 是两个事件若B A ⊂,则)()()(A P B P A B P -=-,)A ()B (P P ≥ (iv )对于任意事件A ,1)(≤A P(v ))(1)(A P A P -= (逆事件的概率)(vi )对于任意事件A ,B 有)()()()(AB P B P A P B A P -+=⋃§4等可能概型(古典概型)等可能概型:试验的样本空间只包含有限个元素,试验中每个事件发生的可能性相同 若事件A包含k个基本事件,即}{}{}{2]1k i i i e e e A =,里个不同的数,则有中某,是,,k k n 2,1i i i ,21 ()中基本事件的总数包含的基本事件数S }{)(1j A n k e P A P kj i ===∑= §5.条件概率(1) 定义:设A,B 是两个事件,且0)(>A P ,称)()()|(A P AB P A B P =为事件A 发生的条件下事件B 发生的条件概率(2) 条件概率符合概率定义中的三个条件1。
概率论与数理统计公式整理(完整版)
An 1) 。
①两个事件的独立性
设事件 A 、B 满足 P(AB) P( A)P(B) ,则称事件 A 、B 是相互独立的。
若事件 A 、 B 相互独立,且 P( A) 0 ,则有
P(B | A) P( AB) P( A)P(B) P(B)
P( A)
P( A)
(14)独立 性
(15)全概 公式
布,所以(0-1)分布是二项分布的特例。
5 / 27
概率论与数理统计 公式(全)
泊松分布
设随机变量 X 的分布律为 P( X k) k e , 0 , k 0,1,2, k!
则称随机变量 X 服从参数为 的泊松分布,记为 X ~ () 或
超几何分布 几何分布
者 P( )。
泊松分布为二项分布的极限分布(np=λ,n→∞)。
当 A=Ω时,P( B )=1- P(B)
(12)条件 概率
定义 设 A、B 是两个事件,且 P(A)>0,则称 P( AB) 为事件 A 发生条件下,事 P( A)
件 B 发生的条件概率,记为 P(B / A) P( AB) 。 P( A)
条件概率是概率的一种,所有概率的性质都适合于条件概率。
2 / 27
一个事件就是由 中的部分点(基本事件 )组成的集合。通常用大写字母
A,B,C,…表示事件,它们是 的子集。 为必然事件,Ø 为不可能事件。
不可能事件(Ø )的概率为零,而概率为零的事件不一定是不可能事件;同理, 必然事件(Ω)的概率为 1,而概率为 1 的事件也不一定是必然事件。
①关系: 如果事件 A 的组成部分也是事件 B 的组成部分,(A 发生必有事件 B 发生):
设事件 B1, B2 ,…, Bn 及 A 满足
概率论与数理统计习题答案(完整版)
n1 C , 90 110 C400 C1100 所以, P1=n1/n= 200 C1500
解 (1) n= C
200 1500
90 400
C
110 1100
(2) P2=1-P{至多有一个次品} =1-P{没有次品}-P{恰有一个次品}
(2) 一个人的血型与两种抗体都发生作用的概率.
解 由已知可得: 一个人血型是AB型血的概率为0.04. (1) PA=0.34+0.04=0.38, PB=0.12+0.04=0第35页)
1. 已知随机事件A, B满足P(AB)=P(A B), 且P(A)=p,
3 1 2 n 1 2 n 1
A A ( A A ) ( A A A ) ( A A A A
A1 A2 A1 A3 A2 A1 An An1 An2 A1
)
3. 在某班学生中任选一个同学,以 A表示选到的是男同
学, B表示选到的人不喜欢唱歌, C表示选到的人是运动员.
1. 某城市共发行三种报纸A, B, C, 已知城市居民订购
A的占45%, 订购B的占35%, 订购C的占30%, 同时订购A
与B的占10%, 同时订购A与C的占8%, 同时订购B与C的占 5%, 同时订购A, B, C的占3%, 求下列事件的概率: (7) 至多订购一种报纸; P{至多订购一种报纸} =P{不订购任何报纸}+P{只订购一种报纸} =0.1+0.73=0.83 或 P{至多订购一种报纸} 或 =1-P{正好订购二种报纸}- P{订购三种报纸} =1-0.14-0.03=0.83
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第一章 矩阵与行列式 第一节 矩阵及其运算 一、矩阵的概念 人们在从事经济活动、科学研究、社会调查时, 会获得许多重要的数据资料, 将这些数据排成一个矩形的数表
111212122212nn
mmmn
aaaaaaaaaLLMMML 以便于进行储存、运算和分析, 这种矩形的数表就是矩阵. 定义1 由mn个数1,2,,;1,2,,ijaimjnLL排成m行n列的矩形
数表 111212122212nn
mmmn
aaaaaaaaaLLMMML 称为m行n列矩阵, 简称为mn矩阵, 其中ija称为矩阵的位于第i行、第j
列的元素. 通常, 我们用大写字母,,ABL表示矩阵. 例如, 记
111212122212.nn
mmmn
aaaaaaAaaaLLMMML
其中小括号“” 也可用方括号“”代替. 有时, 矩阵也简记为ijmnAa
或ijAa. 特别地, 当mn时, 称A为n阶矩阵或n阶方阵, 其中一阶方 2 线 性 代 数
阵a是一个数, 括号可略去. 元素全为实数的矩阵称为实矩阵, 元素全为复数的矩阵称为复矩阵. 本书主要在实数范围内讨论问题. 对于由n个未知量、m个方程组成的线性方程组:
11112211211222221122,,.nnnn
mmmnnm
axaxaxbaxaxaxbaxaxaxbLLLLLLLLLLLLL
(1.1.1)
称矩阵 A11121121222212nn
mmmnm
aaabaaabaaabLLMMMML
(1.1.2)
为线性方程组(1.1.1)的增广矩阵;称矩阵 A111212122212nn
mmmn
aaaaaaaaaLLMMML
(1.1.3)
为线性方程组(1.1.1)的系数矩阵;矩阵 12
m
bbBb
M (1.1.4)
称为线性方程组(1.1.1)的常数项矩阵. 显然, 线性方程组(1.1.1)由矩阵(1.1.2)完全地确定. 下面介绍一些特殊的矩阵. (1) 零矩阵 元素都是零的矩阵称为零矩阵, 记为O. (2) 列矩阵、行矩阵 在矩阵A中, 如果1n, 则 3 第 章 一 矩 式 阵 与 行 列
1121
1m
aaAa
M ,
称这种只有一列的矩阵为列矩阵;同样, 如果1m, 则 11121nAaaaL,
称这种只有一行的矩阵为行矩阵. 我们也将列矩阵和行矩阵分别称为列向量和行向量. 列向量和行向量统称为向量. 向量的元素称为分量, 有n个分量的向量称为n维向量. 矩阵与 向量有密切的联系, 矩阵ijmnAa可以看成由n个m维列向量
12,1,2,,jj
mj
aajnaLM
组成, 也可以看成由m个n维行向量12,1,2,,iiinaaaimLL组成. (3) 负矩阵 如果矩阵ijmnAa, 则ijmnAa称为矩阵A的负矩阵. (4) 行阶梯形矩阵 如果矩阵每一行的第一个非零元素所在的列中, 其下方元素全为零, 则称此矩阵为行阶梯形矩阵. 例如矩阵 10234023450056700018A, 12102032210003100000B
均为行阶梯形矩阵, 而矩阵 10232023450056700418
C
则不是行阶梯形矩阵. (5) 行最简形矩阵 如果行阶梯形矩阵中, 非零行的第一个非零元素均为1, 且其所在列的其余元素均为0, 则称此矩阵为行最简形矩阵. 例如, 矩阵 4 线 性 代 数
10603012050001100000
是行最简形矩阵. (6) 上(下)三角矩阵 n阶方阵的左上角到右下角元素的连线称为主对角线, 左下角到右上角元素的连线称为次(副)对角线. 如果方阵的主对角线下(上)方元素全为0, 则称此矩阵为上(下)三角矩阵. 矩阵
11121222000nn
nn
aaaaaaLLMMML 为上三角矩阵, 矩阵 112122
12000nnnn
aaaaaaLLMMML 为下三角矩阵. (7) 对角矩阵 如果方阵中除主对角线上的元素外, 其余元素全为0, 则称此矩阵为对角矩阵. 例如, 矩阵
12
000000nL
LMMML 为对角矩阵. (8) 单位矩阵 在对角矩阵中, 如果11,2,,iinL, 即为 100010001LLMMML
,
则称此矩阵为单位矩阵. 单位矩阵一般用E或I表示. 5 第 章 一 矩 式 阵 与 行 列
定义2 如果两个矩阵ijAa, ijBb的行数相同、列数也相同, 则称矩阵A与B为同型矩阵. 定义3 如果两个同型矩阵mnA, mnB的对应元素均相等, 即 1,2,,;1,2,,ijijabimjnLL, 则称矩阵A与B相等, 记作AB. 6 线 性 代 数
二、矩阵的运算 1. 矩阵的加法 定义4 由两个同型矩阵mnijmnAa, mnijmnBb对应元素的和, 即ijijab1,2,,;1,2,,imjnLL组成的mn矩阵称为矩阵A与B的和, 记作AB, 即 111112121121212222221122nnnn
mmmmmnmn
ababababababABabababLLMMML
.
由此定义及负矩阵的概念, 我们定义矩阵A与B的差为 ABAB.
注 只有同型矩阵才能相加(减).
2. 数与矩阵相乘(简称数乘) 定义5 数k乘矩阵A的每一个元素所得到的矩阵称为数k与矩阵A的积, 记作kA, 即
111212122212.nn
mmmn
kakakakakakakAkakakaLLMMML 矩阵的加法和数乘统称为矩阵的线性运算, 其满足如下性质: (1) ABBA; (2) ABCABC; (3) AA; (4) AAA; (5) ABAB; (6) AOA; (7) 1AA; (8) AAO. 上面的, 都是任意常数.
例1 设112034A, 403123B, 求AB和23AB. 解 7 第 章 一 矩 式 阵 与 行 列
14102(3)5110(1)3(2)43117AB
;
224120923068369AB
102133121
.
3. 矩阵与矩阵相乘(矩阵的乘法) n个变量12,,,nxxxL与m个变量12,,,myyyL之间的关系式 11111221221122221122,,.nnnn
mmmmnn
yaxaxaxyaxaxaxyaxaxaxLLLLLLLLLLLL
(1.1.5)
表示一个从变量12,,,nxxxL到变量12,,,myyyL的线性变换. 设有两个线性变换
11111221332211222233
,.zayayayzayayay
(1.1.6)
和 111112222112223311322
,,.ybxbxybxbxybxbx
(1.1.7)
若要求出从12,xx到12,zz的线性变换, 可将(1.1.7)代入(1.1.6), 得 111111221133111112122213322221112221233112112222223322
()(),()().zabababxabababxzabababxabababx
(1.1.8)
线性变换(1.1.8)可看作是先作线性变换(1.1.7)、再作线性变换(1.1.6)的结果, 我们称线性变换(1.1.8)为线性变换(1.1.6)与(1.1.7)的乘积, 相应地, 我们将线性变换(1.1.8)所对应的矩阵定义为(1.1.6)与(1.1.7)所对应的矩阵的乘积, 即
111211121321222122233132
bbaaabbaaabb
111112211331111212221332211122212331211222222332.abababababababababababab
一般地, 我们有:
