弯矩二次分配法和力矩分配法的区别
结构设计弯矩2次分配法计算

上柱
下柱 0.433
-24.59 -8.40 -0.37 -33.35
右梁 0.26 -13.35 -14.76 -4.91 -0.22 -33.24
0.215 68.95 -11.96 9.85 0.41 67.25
0.302
-16.79 0.00 0.57 -16.22
0.302
-16.79 -8.40 0.57 -24.62
0.362 18.48 -6.69 -5.03 2.89 9.65
0.362 18.48 -6.69 -5.03 4.46 11.21
0.362 18.48 -6.69 -5.03 4.15 10.90
0.425 18.48 -7.85 -5.95 3.78 8.46
0.469
-8.67 -2.95 4.84 -6.77
1.77 -1.91
-0.95
上柱
0.319
-5.89 0.00 2.55 -3.35
0.319
-5.89 -4.33 3.93 -6.30
0.319
-5.89 -2.95 3.65 -5.19
0.376
-6.95 -2.95 3.35 -6.55
D
左梁
下柱
上柱
0.531 18.48 -9.81 -7.38 5.48 6.77
-2.99 0.00 9.41 6.42
0.402 10.00 -4.02 -31.47 -2.41 -27.90 0.402 10.00 -4.02 -31.47 12.65 -12.84
0.299
-2.99 -1.75 10.38 5.64
0.402 10.00 -4.02 -31.47 13.95 -11.54
第5章 力矩分配法

BA 分配系数:
m 118
A -32 29.5 0.5 32 59 91
91
固端弯矩:
C
ql 2 24 42 M AB 32 12 12 M BC - 3Pl 3 200 4 -150 16 16
B
2
C
l
ql / 8 ql 2 /14 3ql 2 / 56 ql 2 /14 ql 2 /14 ql 2 / 28 A
SCA 4 EI l SCB 3EI l
A
l
解:仅C点有转角位移,结点转动刚度: 力矩分配系数: CA SCA 4 , CB SCB 3 传递系数:
1 3 11 384 117 384 1 12
1 12 1 24 16 384 1 48 40 384
3 16 11 128 35 128
ql
2
解:仅A点有转角位移,结点转动刚度:
1, 3, 4 分配系数: AB 8 AC AD 8 8 1 C 1, C , C AC 0 AD 传递系数: AB 2 11 2 1 1 3 2 F ql ql 固端力及约束力矩: 1P 48 3 12 16 2 分配力矩: 11ql / 48
SC S AB S AC S AD i 3i 4i 8i
• 最后根据各杆端力矩 分配结果画弯矩图。
• 注意跨中荷载的弯矩 叠加。
117 35 16 48 75 48 40 96
1 8
4 8
3 8
1 6 11 384 75 384
1 3 11 384 117 384 1 12
框架结构内力计算-竖向弯矩二次分配,水平D值法

现浇楼面
Ib=2.0I0
Ib=1.5I0
装配整体式楼面 Ib=1.5I0
Ib=1.2I0
为了简化计算,本例框架梁截面惯性矩增大系数 均采用1.2。
半边结构
(4)弯矩分配与传递
上柱
下柱 右梁
0.541 0.459
E
122.05
66.03 56.02
首先将各节点的分配系
数填在相应方框内,将 梁的固端弯矩填写在框
0.274 0.274 0.220
H
33.72
22.08 22.01 17.67
0.246
114.04 19.76
0.290 0.230 0.234
G
33.72
23.39 18.47 18.80
A
F
(4)弯矩分配与传递 上柱 第一次分配
下柱 右梁
0.541 E
66.03 20.02
43.22 34.21 36.61
左梁
0.320
122.05 28.24
上柱
下柱 右梁
0.377 0.303
J
33.81
33.27 26.74
0.232
114.04 18.63
0.274 0.274 0.220
I
33.72
22.01 22.01 17.67
0.232
114.04 18.63
0.351
C
40.03
21.61
0.298
114.04 33.98 9.32
1/2);
0.379
43.22 20.02
0.300 B
34.21
0.321
114.04 36.61 9.88
力矩分配法

第7章 力 矩 分 配 法
§7.1 基 本 概 念
五、传递系数和传递弯矩
远端弯矩与近端弯矩的
C
比值称为弯矩传递系数。
待分配力矩
Z1 MA'
D
A
Z1
Z1
C Aj
M M
jA Aj
B
MBA2iAB Z1 MCA 0 MDAiAD Z1
MBA MAB
CAB
1 2
MCA MAC
CAC
0
MDA MAC
CACMAC1
A
基本体系
MBFC9kNm ,
MCFB 0
15
R1P 15
9
A
R 1PM B F AM B FC 6kN m
20kN
2kN/m
B Z1
C
15 9
B
C
结构无结点转角位移时,交汇于结点各杆固端弯矩的代数
和,称为该结点的不平衡力矩,并规定顺时针转向为正。
MB= R 1PM B F AM B FC 6kN m
C
M BA 1 53.421 6.5 174
M BC 92.57 41.5 174
MCB 0
⑻作最终弯矩图。 SBAZB
R11
A
SBCZB
水 利 土 木 工 程 学 院 结 构 1力 学 课 程 组
4iZB = SBAZB
Z1
B
C
3iZB = SBCZB
第7章 力 矩 分 配 法
§7.2 力 矩 分 配 法 的 基 本 原 理
水 利 土 木 工 程 学 院 结 构 1力 学 课 程 组
第7章 力 矩 分 配 法
§7.2 力 矩 分 配 法 的 基 本 原 理
结构力学——力矩分配法分解

3 . 一般最终的杆端力矩与固端力矩是同量级的,要求精确 到三位有效数字,计算中取4位计算,以保证前三位的 精确度
第三节 多结点力矩分配法
计算的指导思想由两个步骤说明:
固定状态的计算(与单点固定一样)。
即刚臂→荷载→固端力矩→约束力矩;
100k0N
EI
1 EI
2 EI
0.43 0.57 0.57 0.43
-500 -1000
M3B=1000
例题:有支座移动(已知结点线位移)E=200GPa,I = 2500cm4
绘制弯矩图。
A
B
C
D
EI
EI
=1cm
10m
10m
10m
0.429 0.571
0.571 0.429
MF
3000
3000 -1500
2 . 不相邻 点可同时 释放.
例题:用力矩分配法求图示结构弯矩图(利用传递系数的概念) 。
A
EI
10m
1 EI
10m
100k0N 2 EI 3 B 3B是悬臂梁,
转动结点3 时,
10m 1m 悬臂可自由转
0.43 0.57 0.5 0.5 1 0
动,固其转动
MF
1000 刚度为零
或A
MF
100k0N
放松状态的计算(与单点放松不同)。
力矩的分配和传递是在远端约束已知的情况下进行的, 因此,分配单元的相邻结点不应同时放松。每次只能 放松一个结点,同时相邻结点保持固定,所以,整个 放松过程是轮流放松每一个结点来逐步完成的。
第三节 多结点力矩分配法
结构力学(I)力矩分配法
M1B M1FB
M1C M1FC
S1 B ( R ) M1FB 1B ( R1P ) S 1P
1
1
S1C ( R ) M 1FC 1C ( R1P ) S 1P
1
力矩分配法采用了与位移法相同的基本结 构,即固定刚结点,在固定状态下刚臂上产生 约束力矩,为恢复到原状态,将刚臂放松(加 反方向约束力矩),求出放松状态产生的杆端 力矩,将固定状态与放松状态的杆端力矩叠加 即得结构的实际杆端力矩.
一. 基本概念
远端支撑 固定 铰支 滑动 转动刚度S 4i 3i i 传递系数C 1/2 0 -1
1
1
1
可避免解联立方程 不需要求出角位移 计算程式简单机械
哈工大 土木工程学院
4i
1 / 31
2i
3i
哈工大 土木工程学院
i
2 / 31
讨论 1 点在M作用下各杆端的弯矩 1M m1 0
列表法
练习:用力矩分配法求图示结构弯矩图
B
EI
A
EI
C
40 kN
10m
10m
q 10 kN/m
M F 100
分 配 传 递
0.571 0.429 100 0 57.1 42.9 42.9 42 .9
0 0
A
4m
EI
BБайду номын сангаас
4m
EI
C
6m
28.6
M 128.6
128 .6
0
42.9
M
哈工大 土木工程学院
ql 2 /12
A
F F M BC M CB 0
第9章弯矩分配法
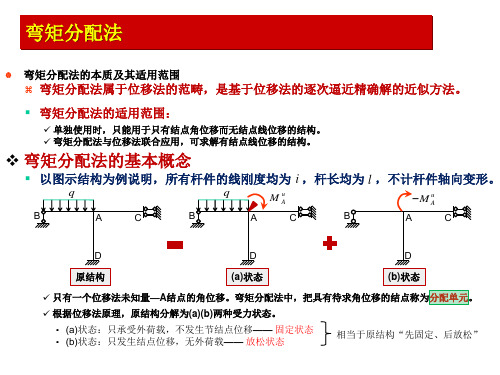
• 转动刚度不仅与杆件的弯曲线刚度 i EI l 有关,而且与杆件另一端(又称远端)的支承条件有关。 • 远端为固定支座:SAB 4i • 远端为铰支座: SAB 3i • 远端为定向滑动支座: SAB i
⑴AD杆件的处理:
(M图略)
DM端AgD的链?杆只SA产D 生 轴? 力,故
M
g AD
20kN 2m
40kNm,
SAD 0 。
⑵AC杆件的处理:
CS端AC既无?线C位C移A 又?无角位移,相当于固定端,故
S AC
4iAC
4 5EI 5
4
EI,
1 CCA 2
。
2020/5/17
弯矩分配法
弯矩分配法的分配单元数量与位移法的基本未知量数量是统一的。 理论上讲,弯矩分配法即适用于超静定结构,也适用于静定结构, 但具体应用中,如结构含有内力静定部分,应尽可能先简化结构, 以减少计算工作量。
⑵B结点的集中外力矩如何处理?
B点增加附加刚臂后,刚臂上的约束力矩,即结点不平衡力矩为
M
u B
41
M
A 1 i
A SAB 4i
M BA 2i B
A 1 i
A SAB 3i
M BA 0 B
A 1 i
A SAB i
M BA i B
2020/5/17
弯矩分配法
▪ 放松状态内力分析
✓ 传递系数:AB杆件仅A端发生转角时,B端弯矩与A端弯矩之比,称为从A到B的弯矩传递系数,记为 CAB 。
• 弯矩分配法中,结点转动在远端产生的弯矩可通过近端弯矩乘以传递系数得到。
弯矩二次分配法excel

弯矩二次分配法excel弯矩二次分配法是一种结构力学中常用的计算方法,用于计算超静定梁或桁架的内力和位移。
本文将介绍如何在Excel中使用弯矩二次分配法进行计算。
首先,我们需要确定梁或桁架的几何参数和荷载条件。
假设我们要计算一个简支梁的内力和位移,其长度为L,截面形状为矩形,弹性模量为E,惯性矩为I,荷载为集中力P施加在距离左支点a处。
在Excel中,我们可以设置以下的参数:L,a,P,E,I。
可以将这些参数放在Excel的不同单元格中,并赋予相应的数值。
接下来,我们需要进行弯矩二次分配法的计算步骤。
1. 计算反力:根据力的平衡条件,可以得到右支点的反力为RA = P * (L - a)/L,左支点的反力为RB = P * a/L。
2. 计算弯矩系数:对于简支梁,弯矩系数为1。
可以将这个系数设定为Excel中的一个单元格。
3. 计算初始剪力分布:根据几何约束和力的平衡条件,当x =0到a时,剪力为V1 = RB,当x = a到L时,剪力为V2 = -RA。
4. 计算初始弯矩分布:根据剪力的分布和弯矩的定义,可以求得初始弯矩分布为M0 = 0,M1 = V1 * x,M2 = RB * x - V2 *(x - a)。
5. 计算修正剪力分布:根据弯矩的修正条件,可以得到修正剪力分布为V'1 = V1 + (M0 - M1) / L,V'2 = V2 + (M0 - M2) / L。
6. 计算修正弯矩分布:根据修正剪力分布和弯矩的定义,可以求得修正弯矩分布为M'1 = M1 + V'1 * (x - a),M'2 = M2 + V'2 * (x - a)。
7. 计算位移:根据弯曲方程和边界条件,可以得到位移方程为y = (P * a * x * (L - x) * (L - 2a)) / (6 * E * I * L)。
通过将以上的计算公式应用到Excel中,我们可以得到弯矩分布、剪力分布和位移的数值结果。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
弯矩二次分配法和力矩分配法都是用于分配梁上荷载引起的弯矩的方法,但它们在计算过程和结果上存在一些区别。
弯矩二次分配法:
弯矩二次分配法基于假设,在梁上的弯矩分布可以近似为一个抛物线形状。
根据这个假设,它将荷载作用在梁上的弯矩分配为两个部分:一部分按照线性分布,另一部分按照二次分布。
这种方法使用解析方法,需要使用高斯消元或其他数值方法求解方程组来确定未知系数。
计算过程相对复杂,需要一定的数学计算。
弯矩二次分配法可以提供更准确的弯矩分布图,特别适用于具有不规则几何形状或变截面的梁。
力矩分配法:
力矩分配法基于简化的假设,将荷载作用在梁上的弯矩分配为一系列离散力矩。
这些力矩按照一定的比例分布在梁的不同截面上,以近似表示实际弯矩分布。
这种方法相对简单直观,不需要复杂的数学计算。
通过将荷载转化为一系列离散力矩,可以直接计算每个力矩对应的截面上的弯矩。
力矩分配法适用于简单几何形状和均匀截面的梁,但对于不规则几何形状和变截面的梁可能不够准确。
总的来说,弯矩二次分配法提供更准确的弯矩分布,适用于复杂几何形状和变截面的梁。
力矩分配法相对简单,适用于简单几何形状和均匀截面的梁。
选择使用哪种方法取决于具体的梁结构和分析要求。
