角平分线的性质定理及判定定理
角平分线的判定(用)

为了证明角平分线的判定定理, 我们可以按照以下步骤进行推导
综上所述,我们证明了角平分线 的判定定理。
03 判定定理的应用
在几何证明中的应用
证明角平分线
利用角平分线的判定定理,可以 证明某个角是另一个角的平分线。
证明等腰三角形
在三角形中,如果一个角的平分线 与对边相交,则该交点与对边的两 个端点所形成的三角形是等腰三角 形。
进行证明。
THANKS FOR WATCHING
感谢您的观看
证明线段比例
利用角平分线定理,可以证明线段 之间的比例关系。
在三角形中的运用
01
02
03
确定角的平分线
在三角形中,可以利用角 平分线的判定定理来确定 角的平分线位置。
计算线段长度
利用角平分线定理,可以 计Байду номын сангаас三角形中某些线段的 长度。
判断三角形形状
在三角形中,可以利用角 平分线的性质来判断三角 形的形状。
在日常生活中的应用
建筑设计
在建筑设计中,角平分线 的判定定理可用于确定窗 户、门等部件的位置和角 度。
道路规划
在道路规划中,可以利用 角平分线的判定定理来确 定交叉路口的角度和道路 的走向。
机械制造
在机械制造中,角平分线 的判定定理可用于确定零 件的精确位置和角度。
04 判定定理的推论与变种
推论一
角平分线的判定定理
目录
• 角平分线的定义与性质 • 角平分线的判定定理 • 判定定理的应用 • 判定定理的推论与变种
01 角平分线的定义与性质
角平分线的定义
角平分线是从一个角的顶点出发,将 该角分为两个相等的部分的一条射线。
角平分线上的任意一点到这个角的两 边的距离相等。
角平分线性质定理和判定定理
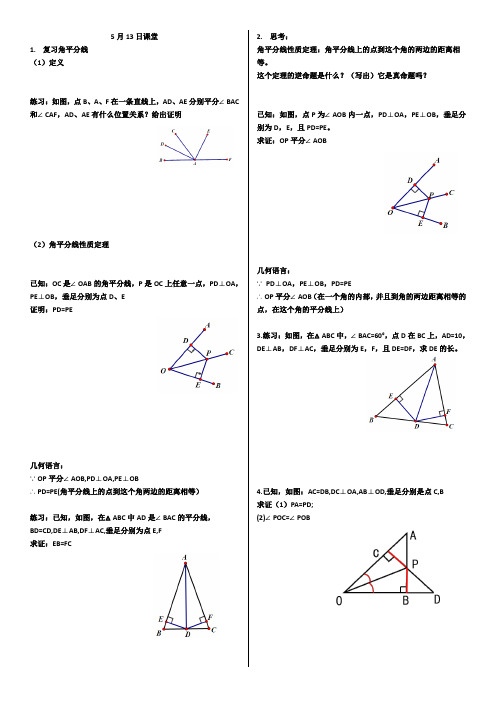
5月13日课堂
1.复习角平分线
(1)定义
练习:如图,点B、A、F在一条直线上,AD、AE分别平分∠BAC 和∠CAF,AD、AE有什么位置关系?给出证明
(2)角平分线性质定理
已知:OC是∠OAB的角平分线,P是OC上任意一点,PD⊥OA,PE⊥OB,垂足分别为点D、E
证明:PD=PE
几何语言:
∵OP平分∠AOB,PD⊥OA,PE⊥OB
∴PD=PE(角平分线上的点到这个角两边的距离相等)
练习:已知,如图,在△ABC中AD是∠BAC的平分线,
BD=CD,DE⊥AB,DF⊥AC,垂足分别为点E,F
求证:EB=FC
2.思考:
角平分线性质定理:角平分线上的点到这个角的两边的距离相等。
这个定理的逆命题是什么?(写出)它是真命题吗?
已知:如图,点P为∠AOB内一点,PD⊥OA,PE⊥OB,垂足分别为D,E,且PD=PE。
求证:OP平分∠AOB
几何语言:
∵ PD⊥OA,PE⊥OB,PD=PE
∴OP平分∠AOB(在一个角的内部,并且到角的两边距离相等的点,在这个角的平分线上)
3.练习:如图,在△ABC中,∠BAC=60°,点D在BC上,AD=10,DE⊥AB,DF⊥AC,垂足分别为E,F,且DE=DF,求DE的长。
4.已知,如图:AC=DB,DC⊥OA,AB⊥OD,垂足分别是点C,B
求证(1)PA=PD;
(2)∠POC=∠POB。
角平分线的性质

推理的理由有三个, 必须写完全,不能
少了任何一个.
判一判:(1)∵ 如下左图,AD平分∠BAC(已知),
∴ BD = CD ,
× ( 在角的平分线上的点到这个角的两边的距离相等 )
B
B
A
D A
D
C
(2)∵ 如上右图, DC⊥AC,DB⊥AB (已知)C .
∴ BD = CD ,
× ( 在角的平分线上的点到这个角的两边的距离相等 )
SPDB
1 2
·AB·PD=28.
B
(3)求∆PDB的周长.
D
CPDB PD PB DB
P
PC PB DB
BC DB AD DB
A
C
AB 14
=
知识与方法
1.应用角平分线性质: 存在角平分线 条件 涉及距离问题
2.联系角平分线性质:
面积 利用角平分线的性
又∵PE∥AB,∴∠1=∠3. B E
(
A
34 P
12 DFC
同理,∠2=∠4.
∴∠3=∠4,∴AD平分∠BAC.
4.如图,已知∠CBD和∠BCE的平分线相交于点F,
求证:点F在∠DAE的平分线上. 证明:过点F作FG⊥AE于G,
ห้องสมุดไป่ตู้E G
FH⊥AD于H,FM⊥BC于M.
C
∵点F在∠BCE的平分线上, FG⊥AE, FM⊥BC.
3.经过分析,找出由已知推出要证的结论的途径, 写出证明过程.
知识要点
性质定理:角的平分线上的点到角的两边的距离相等.
应用所具备的条件:
(1)角的平分线;
(2)点在该平分线上;
(3)垂直距离.
角平分线性质

角平分线的性质内容1.角平分线性质定理:已知:如图,点P 在AOB ∠的平分线上, , 。
求证:PD PE =证明:即:角平分线上的点到 的距离相等.总结:该定理为我们提供了证明两条垂线段 的一个新思路.[例1 ] 如图所示,AD 是BAC ∠的平分线,DE AB ⊥于E ,DF AC ⊥于F,且BD CD =.求证:BE CF =. 对应训练:1.如图,BD 是ABC ∠的平分线,DE AB ⊥于E ,236m ABCS =△,18cm AB =,12cm BC =,则DE 的长是。
2.如图,ABC △中,90C ∠=,AC BC =,AD 平分BAC ∠交BC 于D ,DE AB ⊥于E ,且10cm AB =,则DEB △的周长是。
2.判定定理(即角平分线性质定理的逆定理): 已知:点P 在AOB ∠的 ,PDOA ⊥于D ,PE OB ⊥于E ,且PD PE =求证:点P 在AOB ∠的平分线上。
证明:即:在一个角的内部, 的点,在这个角的角平分线上。
总结:该定理为我们提供了证明两个角 的一个新思路。
[例2]PB 、PC 分别是△ABC 的外角平分线且相交于P 。
求证:P 在A ∠的平分线上。
A BC DEPOAB EG C HPA B CD E PO对应训练: 如图,已知在△ABC 中,90C ∠= ,点D 是斜边AB 的中点,2AB BC =,DE AB ⊥交AC 于E . 求证:BE 平分ABC ∠.3. 如图5,已知等腰三角形ABC △中,90A ︒∠=,B ∠的平分线交AC 于点D , 过点C 作BD 的垂线交BD 的延长线于点E .求证:BD =点拨:“角平分线 + 垂线”构造全等三角形或等腰三角形课堂练习1..如图,在ABC △中,AB AC =,AD 是ABC∠的角平分线,DE AB ⊥,DF AC ⊥,垂足分别是E ,F ,则下列四个结论:①AD 上任意一点到点C ,点B 的距离相等; ②AD 上任意一点到AB ,AC 的距离相等; ③BD CD =,AD BC ⊥; ④BDE CDF ∠=∠.其中,正确的是2.如图,在△ABC 中,∠BAC ,∠BCA 的平分线相交于点O ,过点O 作DE ∥AC ,分别交AB ,BC 于点D ,E .试猜想线段AD ,CE ,DE 的数量关系, 并说明你的猜想理由。
角平分线-第1课时 角平分线的性质定理及其逆定理

∵ ⊥ , ⊥ ,∴ 是△的角平分线.
变式2 如图,在△中,,分别是,
上一点,∠ = ∘ , ⊥ 于点,若
= , = .
(1)求证:平分∠;
证明:∵
左讲
知识点1 角平分线的性质定理
例1 如图,在直角三角形中,∠ = ∘ ,平分∠,
6
⊥ 于点.若 = , = ,则的长为___.
右练
变式1 如图,在△中,∠ = ∘ ,平分∠交边于点
4
,△的面积为30, = ,则线段的长度为___.
= ,
在△和△中,ቊ
= ,
∴ △≌△(),∴ = .
∵ ⊥ , ⊥ ,∴ 平分∠.
(2)直接写出,,之间的等量关系.
解: + = .
点拨:由(1)可知 = ,∠ = ∠ = ∘ ,
知识点2 角平分线的判定定理
例2 如图,在△中,是的中点, ⊥ ,
⊥ ,垂足分别是,, = .求证:是
△的角平分线.
证明:∵ ⊥ , ⊥ ,
∴ △和△是直角三角形.
∵ 是的中点,∴ = .
又∵ = ,∴ △≌△(),∴ = .
又∵ = ,∴ △≌△(),
∴ = ,
∴ = + = + = + − = − ,
即 + = .
平分∠.若 = , = ,则△的面积
为( C )
A.15
B.20
C.25
D.50
(第4题)
5.如图,在直角三角形中,∠ = ∘ ,请用尺规作图法在边上作
一点,使得点到边,的距离相等.(保留作图痕迹,不写作法)
解:如图所示,点即为所求.
1.4.1 角平分线的性质与判定

知2-练
1
如图,在 CD 上求一点 P ,使它到边 OA , OB 的距 离相等,则点P是( A.线段CD的中点 B.CD与过点O作CD的垂线 的交点 C.CD与∠AOB的平分线的 )
交点
D.以上均不对
(来自《典中点》)
知2-练
2
如图, AD⊥OB , BC⊥OA ,垂足分别为 D , C ,
(来自《典中点》)
知2-练
4
(2015• 永州 ) 如图,在四边形 ABCD 中, AB = CD ,
BA 和 CD 的 延 长 线 交 于 点 E , 若 点 P 使 得 S△PAB = S△PCD,则满足此条件的点P( A.有且只有1个 B.有且只有2个 C.组成∠E的平分线 D.组成∠E的平分线所在的 )
等的点在这个角的平分线上. (1)书写格式:如图, ∵PD⊥OA,PE⊥OB,PD=PE, ∴点P在∠Aቤተ መጻሕፍቲ ባይዱB的平分线上
(或∠AOC=∠BOC).
(2)作用:运用角平分线的判定,可以证明两个角相等
或一条射线是角的平分线.
(来自《点拨》)
知2-讲
2.角平分线的判定定理与性质定理的关系:
(1)如图,都与距离有关:即条件PD⊥OA,PE⊥OB都
AD 与 BC 相交于点 P ,若 PA = PB ,则∠ 1 与∠ 2 的 大小关系是( A.∠1=∠2 B.∠1>∠2 C.∠1<∠2 D.无法确定
(来自《典中点》)
)
知2-练
3
如图,在△ABC中,分别与∠ABC,∠ACB相邻的 外角的平分线相交于点 F,连接AF,则下列结论正
确的是(
)
A.AF平分BC B.AF平分∠BAC C.AF⊥BC D.以上结论都正确
第1课时 角平分线的性质定理及逆定理1

OP=OP,
∠PDO=∠PEO=90°,
∴△PDO≌△PEO(AAS).
∴PD=PE(全等三角形的对应边相等).
角平分线上的点到这个角两边的距离相等.
探究2:角平分线的判定定理
已知:在∠AOB内部有一点P,且PD⊥OA,PE⊥
OB,D、E为垂足且PD=PE.求证:点P在∠AOB的角平
分线上.
BC于D,且DE⊥AB,DF⊥AC,垂足分别是E、F. 求 证:AD是EF的垂直平分线. 证明:∵AD是∠BAC 的平分线,且DE⊥AB,DF⊥AC,
证明:∵AD是∠BAC的平分线, 且DE⊥AB,DF⊥AC,
∴DE=DF,
∴Rt△ADE≌Rt△ADF, ∴AE=AF, ∴A与D都在EF的垂直平分线上, ∴AD就是EF的垂直平分线.
证明:∴PD⊥OA,PE⊥△OEP中,
OP=OP,PD=PE,
∴Rt△ODP ≌Rt△OEP(HL定理). ∴∠1=∠2(全等三角形对应角相等). ∴点P在∠AOB的角平分线上.
在一个角的内部,到角的两边距离 相等的点在这个角的角平分线上.
课堂小结
通过这节课的学习,你有哪些收获?
布置作业
1.从教材习题中选取; 2.完成练习册本课时的习题。
所有的人学习,不论向敌人或朋友都要学
习,特别是向敌人学习。 —— 斯大林
∴∠BAD=30°,
在Rt△ADE中,∠ADE=90°,AD=10 ∴DE= 1 AD= 1 ×10=5(在直角三角形中,如果一个 2 2 锐角等于30°,那么它所对的直角边等于斜边的一半)
2.如图,已知:∠C=90°,DE是AB的垂直平分
线,D为垂足,交BC于E,AB=2AC. 求证:CE=DE.
4.角平分线
第三讲角平分线的性质

D
B
例2 已知:如图,△ABC的角平分线BM、CN相交于点P. 求证:点P到三边AB、BC、CA的距离相等. 证明:过点P作PD 、PE、PF分别垂直于AB、BC、CA, 垂足为D、E、F ∵BM是△ABC的角平分线,点P在BM上 ∴PD=PE A (在角平分线上的点到角的两边的距离相等) 同理 PE=PF. D M ∴ PD=PE=PF. N P F 即点P到边AB、BC、 CA的距离相等
3.已知△ABC中, ∠C=900,AD平分∠ CAB,且 BC=8,BD=5,求点D到AB的距离是多少?
C
你会吗?
D
A
E
B
4、如图,O是三条角平分线的交点, OD⊥BC于D,OD=3, △ABC的 周长为15,求S△ABC A
N
M O B C
G D
角平分线的性质定理的逆定理:
角的内部到角的两边的距离 相等的点在角的平分线上。
G M H
练习5 1、直线表示三条相互交叉的公路,现要建 一个货物中转站,要求它到三条公路的距 离相等,则可供选择的地址有:( ) A.一处 B. 两处 C.三处 D.四处
分析:由于没有限制在 何处选址,故要求的地 址共有四处。
P2
l1
P1
P3 P4
l3
l2
角的内部到角的两边的距离相等的点 在角的平分线上。
A M
C
N
O
练习1:平分平角∠AOB。
C
B
O D
A
归纳:“过直线上一点作这条直线的垂线” 的方法。
角的平分线的性质定理:
角的平分线上的点到这个角的两边的距离相等 用数学语言表述: A D ∵ OC是∠AOB的平分线 1 P PD⊥OA于点D, O 2 C PE⊥OB于点E E ∴ PD=PE
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
流
河
路公
北
M 区
C
B A 角平分线(线段垂直平分线,等腰三角形) 角平分线的性质定理:角平分线上的点到角的两边的距离相等 用数学符号可表示:
∵点P 在∠AOB 的平分线上(或OP 平分∠AOB ) ∴ 角平分线的判定定理:
角的内部到角的两边距离相等的点在这个角的平分线上 用数学符号可表示:
∵
∴点P 在∠AOB 的平分线上(或OP 平分∠AOB )
基础闯关
1.在△ABC 中,∠C =90°,AD 是∠BAC 的角平分线,若BC =5㎝,BD =3㎝,则点D 到AB 的距离为
2.∠AOB 的平分线上一点M ,M 到OA 的距离为1.5㎝,则M 到OB 的距离为 ㎝。
3.如图,∠A =90°,BD 是△ABC 的角平分线,AC =8㎝,DC =3DA ,则点D 到BC 的距离为 。
4.如图,∠1=∠2,PD ⊥OA ,PE ⊥OB ,垂足分别为D ,E ,下列结论错误的是( ) A 、PD =PE B 、OD =OE C 、∠DPO =∠EPO D 、PD =OD
5.三角形中到三边距离相等的点是( )
A 、三条边的垂直平分线的交点
B 、三条高的交点
C 、三条中线的交点
D 、三条角平分线的交点
6.到一个角的两边距离相等的点在 .
7.如图,要在河流的南边,公路的左侧M 处建一个工厂,位置选在到河流和公路的距离相等,并且到河流
与公路交叉A 点处的距离为1cm (指图上距离),则图中工厂的位置应在 ,理由是 .
8.三角形中,到三边距离相等的点是
(A )三条高线交点.(B )三条中线交点.(C )三条角平分线交点.(D )三边垂直平分线交点.
9.如果一个三角形的一条角平分线恰好是对边上的高,那么这个三角形是 O
D
P
E
B
A 第3题图
D A
B
C
2
1D A
P
O
E B
第4题图
F
E
D
C
B
A
F E D
C
B
A
(A )直角三角形.(B )等腰三角形.(C )等边三角形.(D )等腰直角三角形 10.如图,在△ABC 中,AD 平分∠BAC ,DE ⊥AB 于E ,DF ⊥AC
于F ,M 为AD 上任意一点,则下列结论错误的是 (A )DE =DF . (B )ME =MF . (C )AE =AF . (D )BD =DC .
二.解答题:
1.如图,AD 是∠BAC 的平分线,DE ⊥AB 于E ,DF ⊥AC 于F ,且DB =DC , 求证:BE =CF 。
2.已知,如图BD 为∠ABC 的平分线,AB =BC ,点P 在BD 上,PM ⊥AD 于M ,PN ⊥CD 于D. 求证:PM =PN 。
3.如图,BD =CD ,BF ⊥AC ,CE ⊥AB .求证:D 在∠BAC 的角平分线上.
4.如图,在△ABC 中,∠B =∠C ,点D 是BC 的中点,DE ⊥AB ,DF ⊥AC ,E ,F 为垂足,求证:D 在∠BAC 的
角平分线上.
(第10题)
M
F E D
C
B
A
F
C
D
A
B
E
第6题图
C
N P
M
D
B
A
O
N
M
P
C
B
A
A
B
C
D
E
5.已知:如图,Rt △ABC 中,∠C =90o
,AC =BC,AD 为∠BAC 的平分线,AE =BC ,DE ⊥AB 垂足为E ,求证△
DBE 的周长等于AB .
6.如图,已知PA ⊥ON 于A ,PB ⊥OM 于B ,且PA =PB .∠MON =50o
,∠OPC =30o
,求∠PCA 的大小.
7、已知:如图,△ABC 是等边三角形,BD 是AC 边上的高,延长BC 到E ,使CE=CD. 求证:DB=DE
8、如图,AD 是△ABC 的角平分线,DE 、DF 分别是△ABD 和△ACD 的高. 求证:AD 垂直平分EF.
9.已知:如图,CE ⊥AB 于点E ,BD ⊥AC 于点D ,BD 、CE 交于点O ,且AO 平分∠BAC .求证:OB =OC .
10、阅读下题及其证明过程:
已知:如图,D 是△ABC 中BC 边上一点,EB=EC ,∠ABE=∠ACE ,求证:∠BAE=∠CAE. 证明:在△AEB 和△AEC 中,
⎪⎩
⎪
⎨⎧=∠=∠=AE AE ACE ABE EC EB ∴△AEB ≌△AEC(第一步) ∴∠BAE=∠CAE(第二步)
问:上面证明过程是否正确?若正确,请写出每一步推理根据;若不正确,请指出错在哪一步?并写出你认为正确的推理过程。
