圆柱的体积ppt
合集下载
圆柱的体积ppt课件

通过侧面积的一半和高计算
总结词
这种方法可以用来验证圆柱体积的计 算结果。
详细描述
侧面积是圆的周长乘以高(2πrh), 通过除以2得到侧面积的一半。然后使 用公式“侧面积的一半 x 高”计算得 出圆柱体积。
通过底面积和高的乘积计算
总结词
这种方法只适用于一些特定形状的圆柱,如球形的一部分。
详细描述
通过测量圆柱的底面积(πr²)和高,然后使用公式“底面积 x 高”计算得出圆 柱体积。这个方法只适用于底面是圆形的圆柱,对于其他形状的圆柱不适用。
THANKS
感谢观看
在物理学中,圆柱体积的概念可以用来描述一些物理现象, 例如液体或气体的流动。当液体或气体在管道中流动时,其 流速和流量可以通过圆柱体积的概念来描述。
另外,圆柱体积的概念也可以用来计算一些物理量,例如物 体的质量和重力等。
在日常生活中的应用
在日常生活中,圆柱体积的概念也有很多应用场景。例如,在购买饮料或食品时,商家会根据圆柱体 积的公式来计算价格,因为这些产品的包装通常是圆柱形的。
形状不同,圆柱是平面的圆形围 绕一个轴旋转而成,而球体是半
圆形旋转而成。
异同点二
表面积和体积计算方式不同,圆 柱的表面积和体积分别通过底面 积和高度计算,而球体的表面积 和体积则是通过4个圆形的面积
总和和高度计算。
异同点三
应用场景不同,圆柱体积常用于 计算圆柱形物体的体积,而球体 积常用于计算球形物体的体积。
圆柱体积的现实意义
圆柱体积在现实生活中的意义在于, 它表示了圆柱形物体的体积大小,对 于计算物体的存储空间、体积移动等 具有实际应用价值。
例如,在计算液体存储量、管道流量 等场合,圆柱体积公式具有重要应用 。
《圆柱的体积》课件

两人游玩期间要喝1 L水,带这壶水够喝吗?
保温杯的容积: 3.14×(8÷2)²×15
V = π(d÷2)²h
=3.14×16×15
=753.6 (cm³)
=0.7536(L) 0.7536<1 答:带这壶水不够喝。
2.一个圆柱形茶叶筒,从里面量底面半径是 6
厘米,高15厘米。这个茶叶筒能装茶叶多少
课堂练习
1.小明和妈妈出去游玩,带了一个圆柱形保温杯, 从里面量底面直径是8 cm,高是15 cm。如果 两人游玩期间要喝1 L水,带这壶水够喝吗?
比较保温杯容积和1 L的大小
保温杯容积> 1 L ,能装下,反之则不能。
教材第25页“做一做”第1题
1.小明和妈妈出去游玩,带了一个圆柱形保温杯,
从里面量底面直径是8 cm,高是15 cm。如果
高
8cm
10cm
杯子是圆柱形
牛奶体积
教材第25页例6
下图中的杯子能不能装下2袋这样的牛奶?
(数据是从杯子里面测量得到的。)
底面内直径
高
8cm
要求什么问题?
10cm
杯子是圆柱形 牛奶体积
下图中的杯子能不能装下2袋这样的牛奶?
(数据是从杯子里面测量得到的。)
底面内直径
比较杯子容积和牛奶 高
8cm
体积(2袋)的大小。
杯子是圆柱形 牛奶体积
下图中的杯子能不能装下2袋这样的牛奶?
(数据是从杯子里面测量得到的。)
牛奶的体积: 高
240×2=480(mL)
底面内直径 8cm
10cm
502.4>480
答:杯子能装下2袋这样
的牛奶。
杯子是圆柱形 牛奶体积
交流小结:计算容积时需要注意什么?
圆柱的体积ppt课件

圆柱底面积
长方体底面积
长方体的体积 =底面积 ×高 圆柱的体积 =底面积 × 高
验证猜想
底面圆周长的一半
验证猜想
圆柱的体积=底面积×高
圆柱的体积计算公式可以表示为:
圆柱的体积= 底面积 × 高
h S
V = Sh
思考: (1)已知圆的半径r和高h,怎样求圆柱的体积?
V = πr2h
(2)已知圆的直径d和高h,怎样求圆柱的体积?
杯子的底面积:3.14×(8÷2)2 =3.14×42 =3.14×16 =50.24 (cm2 )
杯子的容积: 50.24×10 =502.4 (cm3 ) =502.4 (mL)
牛奶的体积:240×2=480(mL)
502.4>480
答:杯子能装下2袋这样的牛奶。
2.挖了一口圆柱形水井,地面以下的井深10m, 底面直径为1m。挖出的土有多少立方米?
16份
32份
64份
发现:分成的扇形越多,拼成的立体图形就越接近于长方体。
合作交流
①转化为近似的长方体,什么变了? 什么没变? ②长方体的底面积、高分别与原来圆柱的哪部分 有关系? 有什么关系?
③转化得到长方体的长、宽、高分别对应圆柱的什么? ④你认为圆柱的体积可以怎样计算?
验证猜想
圆柱的高
长方体的高
大胆猜想
hS a
b a Sa a
V = Sh
h S
V = Sh
从长方体的体积计算方法类比猜想圆柱的体积计算方法。 怎样来验证圆柱的体积计算方法是不是底面积×高?
验证猜想
圆的面积计算公式是的推导
S圆=πr2
圆
长方形
利用了( 转化 )的思想方法
《圆柱的体积》课件

《圆柱的体积》
复习导入
什么是体积?
物体所占空间的大小是物体的体积。
怎样求长方体和正方体的体积?
我们会计算长长方方体体和的正体方积体=长的×体宽积×,高圆柱的 高
体积长怎样宽计算V长呢方?体 =能ab不h能将圆柱转化成我们
学过的立体图正形方,体计的算体出积它=棱的长体×积棱呢长?×棱长
棱长
V正方体 = a3
2×0.7=1.4( m³)
V =Sh
答:圆柱的体积是1.4 m³。
(2)底面半径是3.2 dm,高是5 dm。
3.14×3.2²×5=160.768(dm³) V =πr2h
答:圆柱的体积是160.768 dm³。
2.一根圆柱形木料,底面积为75 cm2 ,长为90 cm。 它的体积是多少? V =Sh
4.挖一口圆柱形水井,地面以下的井深为10 m, 底面直径为1 m。挖出的土有多少立方米?
挖出的土有 多少立方米
水井内 的体积
井深
圆柱的高
已知底面直径和高:V = π ( d÷2 ) 2h
3.14 ×(1÷2)²×10=7.85(m3)
答:挖出的土有7.85 m3。
教材第24页“做一做”第2题
计算圆柱体积的方Biblioteka 已知底面积和高:V = Sh 已知底面半径和高:V = πr2h 已知底面直径和高:V = π(d÷2)2h
圆柱体积计圆算柱公的式体是积:=底面积 × 高
V =πr²Vh = S
h
根据不同的条件可以推导出不同的公式。
已知底面积和高:V = Sh 已知底面半径和高:V = πr2h 已知底面直径和高:V = π(d÷2)2h
已知底面周长和高:V = π(C÷2π)2h
复习导入
什么是体积?
物体所占空间的大小是物体的体积。
怎样求长方体和正方体的体积?
我们会计算长长方方体体和的正体方积体=长的×体宽积×,高圆柱的 高
体积长怎样宽计算V长呢方?体 =能ab不h能将圆柱转化成我们
学过的立体图正形方,体计的算体出积它=棱的长体×积棱呢长?×棱长
棱长
V正方体 = a3
2×0.7=1.4( m³)
V =Sh
答:圆柱的体积是1.4 m³。
(2)底面半径是3.2 dm,高是5 dm。
3.14×3.2²×5=160.768(dm³) V =πr2h
答:圆柱的体积是160.768 dm³。
2.一根圆柱形木料,底面积为75 cm2 ,长为90 cm。 它的体积是多少? V =Sh
4.挖一口圆柱形水井,地面以下的井深为10 m, 底面直径为1 m。挖出的土有多少立方米?
挖出的土有 多少立方米
水井内 的体积
井深
圆柱的高
已知底面直径和高:V = π ( d÷2 ) 2h
3.14 ×(1÷2)²×10=7.85(m3)
答:挖出的土有7.85 m3。
教材第24页“做一做”第2题
计算圆柱体积的方Biblioteka 已知底面积和高:V = Sh 已知底面半径和高:V = πr2h 已知底面直径和高:V = π(d÷2)2h
圆柱体积计圆算柱公的式体是积:=底面积 × 高
V =πr²Vh = S
h
根据不同的条件可以推导出不同的公式。
已知底面积和高:V = Sh 已知底面半径和高:V = πr2h 已知底面直径和高:V = π(d÷2)2h
已知底面周长和高:V = π(C÷2π)2h
《圆柱的体积》PPT

底面积 和 高
圆柱的体积
长方体的体积 = 底面积 × 高
圆柱体的体积 = 底面积 × 高
V
=
圆柱体的体积的计算公式是:
V=Sh
×h
圆柱的体积
圆柱体的体积 = 底面积 × 高
如果知道底面的半径r和高h
圆柱体的体积的计算公式是:
V=3.14 r²h
看图说算式。
⑴ 求圆柱的体积。 (厘米)
5
16
⑵ 求圆柱的体积。 (分米)
如果可恨的挫折使你尝到苦果,朋友,奋起必将让你尝到人生的欢乐。 问渠哪得清如许,为有源头活水来。——朱熹 因果不曾亏欠过我们什么,所以请不要抱怨。 只有承担起旅途风雨,才能最终守得住彩虹满天。 遇到困难时不要放弃,要记住,坚持到底就是胜利。 永不言败,是成功者的最佳品格。 上帝从不埋怨人们的愚昧,人们却埋怨上帝的不公。 平时没有跑发卫千米,占时就难以进行一百米的冲刺。
⑵ 一个圆柱的底面半径是3 分米,高是 10 分米。它的体积是多少立方分米?
⑶ 一个圆柱的高是5 分米,底面直径是 2 分米。它的体积是多少立方分米?
先要计算出杯子的容积
(1)杯子的底面积: 3.14 ×(8÷2) 2
= 3.14 ×42 = 3.14 ×16 = 50.24 (cm2) (2)杯子的容积: 50.24 ×10 = 502.4 (cm2) = 502.4(mL) 答:502.4大于498,所以这个杯子能装下这袋奶。
8
20
(
5)×
2
3.14
×
16
2
8 × 8 × 3.14 × 20
例 根圆柱形钢材,底面积是50平 方厘米,高是2.1米,它的体积是 多少?
2.1米=210厘米
圆柱的体积
长方体的体积 = 底面积 × 高
圆柱体的体积 = 底面积 × 高
V
=
圆柱体的体积的计算公式是:
V=Sh
×h
圆柱的体积
圆柱体的体积 = 底面积 × 高
如果知道底面的半径r和高h
圆柱体的体积的计算公式是:
V=3.14 r²h
看图说算式。
⑴ 求圆柱的体积。 (厘米)
5
16
⑵ 求圆柱的体积。 (分米)
如果可恨的挫折使你尝到苦果,朋友,奋起必将让你尝到人生的欢乐。 问渠哪得清如许,为有源头活水来。——朱熹 因果不曾亏欠过我们什么,所以请不要抱怨。 只有承担起旅途风雨,才能最终守得住彩虹满天。 遇到困难时不要放弃,要记住,坚持到底就是胜利。 永不言败,是成功者的最佳品格。 上帝从不埋怨人们的愚昧,人们却埋怨上帝的不公。 平时没有跑发卫千米,占时就难以进行一百米的冲刺。
⑵ 一个圆柱的底面半径是3 分米,高是 10 分米。它的体积是多少立方分米?
⑶ 一个圆柱的高是5 分米,底面直径是 2 分米。它的体积是多少立方分米?
先要计算出杯子的容积
(1)杯子的底面积: 3.14 ×(8÷2) 2
= 3.14 ×42 = 3.14 ×16 = 50.24 (cm2) (2)杯子的容积: 50.24 ×10 = 502.4 (cm2) = 502.4(mL) 答:502.4大于498,所以这个杯子能装下这袋奶。
8
20
(
5)×
2
3.14
×
16
2
8 × 8 × 3.14 × 20
例 根圆柱形钢材,底面积是50平 方厘米,高是2.1米,它的体积是 多少?
2.1米=210厘米
圆柱的体积ppt课件
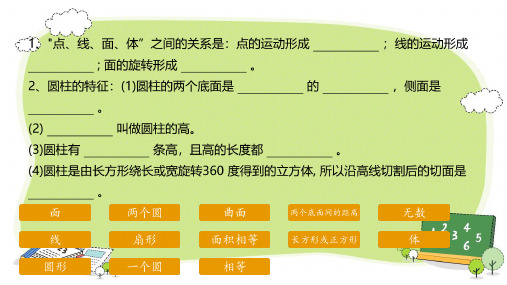
北师大版六年级数学下册第一单元《圆柱和圆锥》
圆柱的体积
第1课时
第2课时
教学目标
复习旧知
把左边的公式拖到右边相应的问题旁边
想一想,怎样计算圆柱的体积呢?
以前学习过哪些 图形的体积?
旧知识
新知识
?
这只是猜想, 还需要验证。
通过叠硬币,我们发现硬币的
( 底面)积是固定的,每增加
一(枚硬币),也(随之)增高就大增,加由一此些可,
V=πr×r× h
h
用长×宽×高能
不能推导圆柱体
积计算公式?
尝试解决下面的问题。
1.底面积 3.14×0.42=0.5024(m2) 2.体积 0.5024×5=2.5124(m3)
3.14×0.42×5 =3.14×0.8 =2.5124(m3)
答:柱子的体积是2.5124立方米。
尝试解决下面的问题。
答:这根金箍棒的体积是2512cm3。 如果这根金箍棒是铁制的,每立方厘米的铁重7.9g,这根金箍棒 重多少千克?
7.9×2512=19844.8(g)=19.8448(kg)
答:这根金箍棒重19.8448千克。
光明村李大伯家挖一口圆柱形的水井,底面周长是3.14m,深4m。挖 出了多少立方米的土?
2cm
=157(cm3)
底面半径: 3.14÷3.14÷2=0.5(m)
体积: 3.14×0.52×4
=3.14×0.25×4
=3.14×0.25×4 =3.14(m3)
答:挖出了3.14立方米的土。
一个装满稻谷的圆柱形粮囤,底面面积为2m2,高为80cm。每立方 米稻谷约重600kg,这个粮囤存放的稻谷约重多少千克?
80cm=0.8m 2×0.8×600=960(kg)
圆柱的体积
第1课时
第2课时
教学目标
复习旧知
把左边的公式拖到右边相应的问题旁边
想一想,怎样计算圆柱的体积呢?
以前学习过哪些 图形的体积?
旧知识
新知识
?
这只是猜想, 还需要验证。
通过叠硬币,我们发现硬币的
( 底面)积是固定的,每增加
一(枚硬币),也(随之)增高就大增,加由一此些可,
V=πr×r× h
h
用长×宽×高能
不能推导圆柱体
积计算公式?
尝试解决下面的问题。
1.底面积 3.14×0.42=0.5024(m2) 2.体积 0.5024×5=2.5124(m3)
3.14×0.42×5 =3.14×0.8 =2.5124(m3)
答:柱子的体积是2.5124立方米。
尝试解决下面的问题。
答:这根金箍棒的体积是2512cm3。 如果这根金箍棒是铁制的,每立方厘米的铁重7.9g,这根金箍棒 重多少千克?
7.9×2512=19844.8(g)=19.8448(kg)
答:这根金箍棒重19.8448千克。
光明村李大伯家挖一口圆柱形的水井,底面周长是3.14m,深4m。挖 出了多少立方米的土?
2cm
=157(cm3)
底面半径: 3.14÷3.14÷2=0.5(m)
体积: 3.14×0.52×4
=3.14×0.25×4
=3.14×0.25×4 =3.14(m3)
答:挖出了3.14立方米的土。
一个装满稻谷的圆柱形粮囤,底面面积为2m2,高为80cm。每立方 米稻谷约重600kg,这个粮囤存放的稻谷约重多少千克?
80cm=0.8m 2×0.8×600=960(kg)
苏教版六年级下册数学2.3 圆柱的体积课件(共15张PPT)

知识讲解 拼成的长方体与原来的圆柱有什么关系?
长方体的体积 与圆柱的体积 相等。
长方体 圆 的底面 柱 积等于 的 圆柱的 高 底面积。
底面 半径 圆柱底面ห้องสมุดไป่ตู้长的一半
长方体的高等 于圆柱的高。
知识讲解 根据上面的实验和讨论, 想一想, 可以怎样求圆柱的体积?
圆 柱 的 高
底面 半径 圆柱底面周长的一半
练习巩固 4.一个圆柱形保温茶桶,从里面量,底面半径 是3分米,高是5分米。如果每立方分米水重1 千克,这个保温茶桶能盛下150千克水吗?
3.14×32×5 =3.14×9×5 =141. 3(立方分米) 1×141. 3=141.3(千克) 141.3<150
答:这个保温茶桶不能盛下150千克水。
练习巩固 5.一个瓶子的内直径是8 cm,装入10 cm高的水后,盖好瓶
子倒过来(如下图),量得无水部分的高是2.5 cm,这个瓶 子的容积是多少?
3.14×(8÷2)2×(2.5+10) =3.14×16×12.5
=628(cm3)
=628(mL) 答:这个瓶子的容积是628毫升。
知识总结
圆柱的体积
圆柱体积=圆柱的底面积×高 V = Sh
圆柱的体积
激趣导入
什么是体积? 物体所占空间的大小是物体的体积。 怎样求长方体和正方体的体积?
高 长方体的体积=长×宽×高
长宽
正方体的体积=棱长×棱长×棱长
棱长
知识讲解
4 下面长方体、正方体和圆柱的底面积相等,高也相等。
(1)长方体和正方体的体积相等吗?为什么? (2)猜一猜,圆柱的体积与长方体、正方体的体积相等吗?
长方体的体积=底面积×高
圆柱的体积 = 底面积 × 高
