基于CMOS的Sallen-Key型二阶低通滤波器设计1
sallen-key滤波截止频率计算

sallen-key滤波截止频率计算Sallen-Key滤波器是一种常见的无源滤波器电路,常用于低通、高通和带通滤波。
它由几个放大器级联而成,通过选择合适的电阻和电容值可以实现所需的截止频率。
在这里,我们将讨论如何计算Sallen-Key滤波器的截止频率。
Sallen-Key滤波器有两个常见的类型: 低通滤波器和高通滤波器。
低通滤波器允许低频信号通过,并且削弱高频信号。
而高通滤波器则允许高频信号通过,并削弱低频信号。
首先,让我们来看看Sallen-Key低通滤波器的电路图。
```R1R2Vi----R3----┬───R4────┬──Vo││C1C2││─┴──┴─││GNDGND```在这个电路中,电阻R1和电容C1组成了一个负反馈网络,电压Vin 通过此网络输入滤波器。
通过调整电阻R2和电容C2的值,可以改变滤波器的截止频率。
为了计算Sallen-Key低通滤波器的截止频率,我们可以使用标准的频率响应公式:H(s)=Vo(s)/Vi(s)=-R4/R3*(sC2R2+1)/(sC1R1+1)其中,s是复频率,s = jw,j是虚数单位,w是角频率。
为了找到截止频率,我们需要使频率响应的幅值降低到-3dB,这相当于将传输函数H(s)的幅值部分等于1/sqrt(2)。
即:H(s), = ,-R4/R3 * (sC2R2 + 1) / (sC1R1 + 1), = 1/sqrt(2)将s替换为jw,展开频率响应式子,并将其变换为复数形式:-R4/R3 * (jwC2R2 + 1) / (jwC1R1 + 1), = 1/sqrt(2)解决这个等式可以得到一个复杂的频率响应函数。
为了简化计算,我们可以考虑只计算频率响应的幅值部分,即将s替换为jw:-R4/R3 * (jwC2R2 + 1) / (jwC1R1 + 1), = 1/sqrt(2)然后,我们可以找到滤波器的截止频率,这发生在幅值部分等于1/sqrt(2)时。
Sallen-Key二阶低通滤波器的OTRA实现

Sallen-Key二阶低通滤波器的OTRA实现
李永安
【期刊名称】《电子工程师》
【年(卷),期】2005(31)10
【摘要】基于传统Sallen-Key二阶低通滤波器,通过在二阶RC低通网络的输出端增加电阻RA,用OTRA(运算跨阻放大器)构成了新型Sallen-Key二阶低通滤波器。
与传统电路相比,该电路能减小寄生电容的影响,因而有较高的稳定性;电路参数取决于电阻之比,因而有较高的精度;极点角频率与品质因素独立可调,因而调整方便,且通带增益可调范围广,无源灵敏度较低,电路结构简单,便于电控调谐,特别适合单片集成技术。
【总页数】3页(P28-29)
【关键词】OTRA(运算跨阻放大器);Sallen-Key滤波器;极点角频率;低通滤波器【作者】李永安
【作者单位】咸阳师范学院物理学系
【正文语种】中文
【中图分类】TN713.4
【相关文献】
1.新的Q增强Sallen-Key SC低通滤波器 [J], 吴杰
2.Sallen-Key低通滤波器高频馈通现象的原因及解决 [J], 丛超;陈文奇;王闻博
3.基于OTRA电流模式二阶通用滤波器的设计 [J], 李永安
4.二阶低通滤波器仿真分析及其应用 [J], 刘增水; 陈瑜迪
5.基于OTRA的通用双二阶滤波器设计 [J], 李永安
因版权原因,仅展示原文概要,查看原文内容请购买。
二阶有源低通滤波电路的设计与分析

二阶有源低通滤波电路的设计与分析有源滤波电路是一种灵活、可靠和性能卓越的滤波器,广泛用于通信、控制和测量等领域。
本文介绍了实现二阶有源低通滤波器的基本原理,并通过计算机仿真分析了设计过程中遇到的一些问题。
一、二阶有源低通滤波器原理有源低通滤波器是一种混合型滤波器,它具有电容和电感耦合之间的耦合,从而实现了低通特性。
其基本原理是,将输入信号分别经过两个放大器,然后将放大器的输出信号反馈到电容的两个端,进而形成一个闭环系统,以构成一个连续反馈低通滤波器,达到滤波的目的。
二、有源低通滤波器的设计有源低通滤波器的设计有三个要考虑的重要参数,包括滤波器的频率特性,输入阻抗和输出阻抗。
1.滤波器频率特性:有源低通滤波器的基本频率特性可以使用Bessel函数表示。
它的特性截止频率可以用“截止频率Hz”表示。
同时,有源低通滤波器也具有频带宽和延迟特性,可以用“频带宽Hz”和“延迟时间ms”来表示。
2.输入阻抗:有源低通滤波器的输入阻抗为电子放大器的输入阻抗,由电子放大器的输入元件的参数决定,一般是50欧姆或大于50欧姆的阻抗。
3.输出阻抗:有源低通滤波器的输出阻抗取决于电子放大器的输出元件的参数,输出阻抗一般为几千欧姆以上。
三、计算机仿真分析由于有源低通滤波器的设计过程非常复杂,需要考虑很多参数,因此通常采用计算机仿真技术进行分析研究,以便验证设计方案的正确性。
在计算机仿真的分析过程中,首先要确定滤波器的输入信号的频率、幅度和相位,并计算出滤波器的输出信号特性,如频率、幅度和相位等,然后将实验结果与理论预测结果进行对比,以验证滤波器的设计方案是否正确。
四、结论有源低通滤波器是一种灵活、可靠和性能卓越的滤波器,它具有良好的性能特性,广泛应用于通信、控制和测量等领域。
其设计方案中,需要考虑多个参数,使用计算机仿真技术可以有效验证设计的正确性,也可以大大提高滤波器的性能。
二阶低频带通滤波器的设计(包括硬件电路,器件参数)
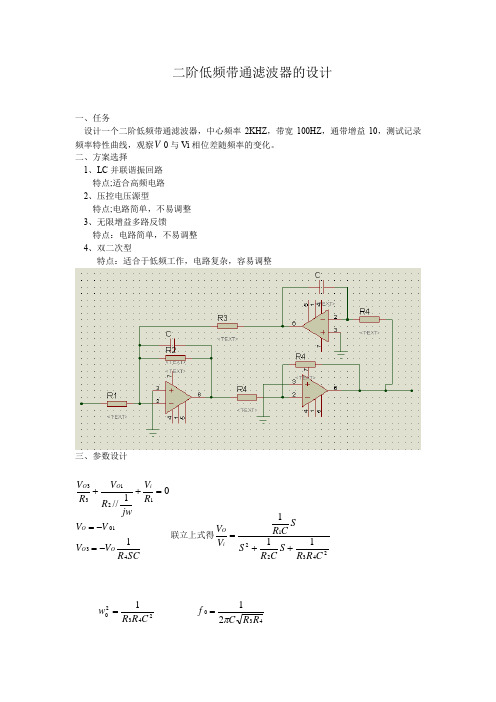
二阶低频带通滤波器的设计一、任务设计一个二阶低频带通滤波器,中心频率2KHZ ,带宽100HZ ,通带增益10,测试记录频率特性曲线,观察V 0与V i 相位差随频率的变化。
二、方案选择1、LC 并联谐振回路特点;适合高频电路 2、压控电压源型特点;电路简单,不易调整 3、无限增益多路反馈特点:电路简单,不易调整4、双二次型特点:适合于低频工作,电路复杂,容易调整三、参数设计SCR V V VV R V jwR V R V OO O i O O 430112133101//-=-==++联立上式得243221111CR R S CR SSC R V V iO ++=243201CR R w =43021R R Cfπ=又有CR Qw 201=12R R A VP =令43R R =201022101243032432========BWfQ R R A kHzR R C f R R R R R Q vp π联立上式,选择C=0.01uF ,4R =8k Ω,2R =160k Ω,1R =16k Ω四、测试结果1、中心频率为2KHZ 。
2、通带增益为103、带宽为146HZ ,未达到要求。
五、结果分析带宽未达到要求是应为R2未进行调节,应为实际所用电阻与理论是有很大的误差的。
实际调试过程中,将R3换成10K 的变位器,通过调节R3可调节中心频率,使达到要求。
将R1换成100K 变位器,通过调节R1可进行增益的调节。
六、总结与建议带通滤波器给我最大的感受是调节很麻烦,要有耐心,要仔细,不要着急。
二阶有源低通滤波器课程设计

目录一题目规定与方案论证........................................................ 错误!未定义书签。
1.1(设计题题目)二阶有源低通滤波器............................................. 错误!未定义书签。
1.1.1题目规定.................................................................................. 错误!未定义书签。
1.1.2 方案论证................................................................................. 错误!未定义书签。
1.2(实训题题目)波形发生器与计数器............................................. 错误!未定义书签。
1.2.1题目规定.................................................................................. 错误!未定义书签。
1.2.2方案论证.................................................................................. 错误!未定义书签。
二电子线路设计与实现........................................................ 错误!未定义书签。
2.1二阶有源低通滤波器........................................................................ 错误!未定义书签。
2.2十位二进制加法计数器电路设计.................................................... 错误!未定义书签。
二阶低通滤波器的设计要点

二阶低通滤波器的设计要点1.滤波器类型选择:二阶低通滤波器有许多不同的类型,包括巴特沃斯、切比雪夫、贝塞尔等。
根据实际需求选择合适的滤波器类型,以满足对于频率响应、阻带抑制等方面的要求。
2.滤波器参数选择:滤波器参数包括截止频率、阻带衰减等。
截止频率是指滤波器将信号截止的频率点,阻带衰减是指滤波器在截止频率之外的频段对信号的抑制程度。
需要根据实际应用需求选择合适的参数值,以保证所需的信号处理效果。
3.构建转移函数:根据选定的滤波器类型和参数,可以建立二阶低通滤波器的传递函数。
传递函数描述了滤波器对输入信号的响应特性,可以用于分析和设计滤波器。
4.滤波器电路实现:根据滤波器的传递函数,可以设计具体的电路实现。
常见的二阶低通滤波器电路包括RC电路、RLC电路等。
可以通过选择合适的电路拓扑和元件参数,来实现所需的滤波特性。
5.频率响应分析:设计完成后,需要进行频率响应分析,以确保滤波器的性能满足要求。
可以使用仿真工具或实验测量的方法,观察滤波器在不同频率下的响应特性。
若有需要,可以对设计参数进行调整以达到预期的性能。
6.稳定性和阻带波纹:稳定性是指滤波器的输出能否在有限时间内收敛到稳定的目标状态。
对于二阶低通滤波器,稳定性要求其传递函数的极点都位于左半平面,以保证系统的稳定性。
另外,阻带波纹是指滤波器在截止频率附近的振荡现象。
设计时需要注意减小阻带波纹的幅度,以确保输出信号的稳定性。
7.电路实现工艺:根据滤波器的实际应用场景,选择适当的电路实现工艺。
常见的工艺包括模拟电路实现、数字滤波器实现、集成电路实现等。
不同的工艺具有各自的优点和限制,需要根据实际情况选择适合的工艺。
8.优化设计:进行性能优化和设计改进。
可以通过参数调整、电路拓扑优化等方法来改进滤波器的性能。
此外,还可以使用自适应滤波、多级联结等技术来提高滤波器的性能。
总结起来,设计二阶低通滤波器需要考虑滤波器类型选择、参数选择、转移函数构建、电路实现、频率响应分析、稳定性和阻带波纹、电路实现工艺以及优化设计等要点。
二阶有源滤波器参数计算

二阶有源滤波器参数计算二阶有源滤波器设计一.滤波器类型按照在f=f0附近的频率特性,可将滤波器分为以下三种:1.巴特沃兹响应优点:巴特沃兹滤波器提供了最大的通带幅度响应平坦度,具有良好的综合性能,其脉冲响应优于切比雪夫,衰减速度优于贝塞尔。
缺点:阶跃响应存在一定的过冲和振荡。
2.切比雪夫响应优点:与巴特沃兹相比,切比雪夫滤波器具有更良好的通带外衰减。
缺点:通带内纹波令人不满,阶跃响应的振铃较严重。
3.贝塞尔响应优点:贝塞尔滤波器具有最优的阶跃响应——非常小的过冲及振铃。
缺点:与巴特沃兹相比,贝塞尔滤波器的通带外衰减较为缓慢。
(注意:巴特沃兹及贝塞尔响应的3dB衰减位于截止频率处。
而切比雪夫响应的截止频率定义为响应下降至低于纹波带的频点频率。
对于偶数阶滤波器而言,所有纹波均高于0dB的直流响应,因此截止频点位于0dB衰减处;而对于奇数阶滤波器而言,所有纹波均低于0dB的直流响应,因此截止频点定义为低于纹波带最大衰减点。
)二.最常用的有源极点对电路拓扑1.MFB拓扑也称为无限增益拓扑或Rauch拓扑;适用于高Q值高增益电路;其对元件值的改变敏感度较低。
2.Sallen-Key拓扑下列情况时,使用效果更佳:对增益精度要求较高;采用了单位增益滤波器;极点对Q值较低(如:Q<3);(特例:某些高Q值高频率滤波器若采用MFB拓扑,则C1值须很小以得到合适的电阻值。
而由于寄生电容干扰使得低容值将导致极大干扰)。
(注意:MFB拓扑不能用于电流反馈型运放,而S-K拓扑电压、电流反馈型运放均可;差分放大器只能采用MFB拓扑;S-K拓扑的运放输出阻抗随频率增加而增加,故通带外衰减能力受限,而MFB拓扑则无此问题。
)三.滤波器设计步骤1.根据应用场合确定滤波器响应类型和电路拓扑;2.确定截止频率、阶数、Q值等参数,通过滤波器设计软件得到电路及相应R、C参数;3.通过仿真实现并检验上步得到的电路能否满足设计参数要求,并进行相应优化修改;(优化方法:等比例缩放法。
电路基础课程设计实验报告--二阶低通滤波器的设计

一 题目要求与方案论证1.(设计题目)二阶有源低通滤波器 1.1题目要求设计二阶有源低通滤波器。
要求通带边界频率f C =1500Hz ,通带最大衰减3dB,阻带边界频率Hz f s 9000 ,阻带最小衰减30dB ;通带内电压放大倍数A 0=1。
分析电路工作原理,设计电路图,列出电路的传递函数,正确选择电路中的参数。
1.1.2 方案论证(1):对信号进行分析与处理时, 常常会遇到有用信号叠加上无用噪声的问题, 这些噪声有的是与信号同时产生的, 有的是传输过程中混入的。
因此, 从接收的信号中消除或减弱干扰噪声, 就成为信号传输与处理中十分重要的问题。
根据有用信号与噪声的不同特性, 消除或减弱噪声,提取有用信号的过程称为滤波, 实现滤波功能的系统称为滤波器。
滤波器分为无源滤波器与有源滤波器两种:① 无源滤波器:由电感L 、电容C 及电阻R 等无源元件组成 ② 有源滤波器:一般由集成运放与RC 网络构成,它具有体积小、性能稳定等优点,同时,由于集成运放的增益和输入阻抗都很高,输出阻抗很低,故有源滤波器还兼有放大与缓冲作用。
利用有源滤波器可以突出有用频率的信号,衰减无用频率的信号,抑制干扰和噪声,以达到提高信噪比或选频的目的,因而有源滤波器被广泛应用于通信、测量及控制技术中的小信号处理。
从功能来上有源滤波器分为: 低通滤波器(LPF )、高通滤波器(HPF )、 带通滤波器(BPF )、带阻滤波器(BEF )、 全通滤波器(APF )。
其中前四种滤波器间互有联系,LPF 与HPF 间互为对偶关系。
当LPF 的通带截止频率高于HPF 的通带截止频率时,将LPF 与HPF 相串联,就构成了BPF ,而LPF 与HPF 并联,就构成BEF 。
在实用电子电路中,还可能同时采用几种不同型式的滤波电路。
滤波电路的主要性能指标有通带电压放大倍数AVP 、通带截止频率fP 及阻尼系数Q 等。
工作原理:二阶有源滤波器是一种信号检测及传递系统中常用的基本电路, 也是高阶虑波器的基本组成单元。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
摘要低通滤波器是一个通过低频信号而衰减或抑制高频信号的部件。
在数据处理、数据传输、抑制干扰、自动化、通信以及大部分的电子系统中得到了广泛的应用。
随着现代科学技术的发展,传统的滤波器在体积、功耗、滤波等方面逐渐显现出劣势,为了满足高精度、高稳定性、高可靠性的要求,出现了有源滤波器、数字滤波器和开关电容滤波器等类型的产品。
随后新型滤波器也被广泛应用于各种集成电路系统中,提高了产品的性能,降低了生产成本,并使得产品在实际应用更加简单、便捷。
本文主要设计了一种基于CMOS的低功耗、截止频率为2KHz的二阶低通滤波器,电路为Sallen-Key结构,Sallen-Key电路具有输出阻抗低、原件差值范围小、放大能力高等优点。
本文利用Multisim软件对整个电路进行了设计及仿真,最后利用Tanner 软件完成了对整个滤波器的版图设计,设计采用0.5nm CMOS工艺。
经过实验验证,本次设计的滤波器能够满足设计要求,在一定频率范围内能很好地实现滤波功能。
关键词CMOS;低通滤波器;Multisim;TannerAbstractLow pass filter is a high frequency signal attenuation or inhibited by the low-frequency signal components. Has been widely used in data processing, data transmission, interference suppression, automation, communication and electronic system in most. With the development of modern science and technology, the traditional filter in the volume, power consumption, filter and so on gradually shows disadvantages, in order to meet the requirements of high precision, high stability, high reliability requirements, the active power filter, digital filter and a switched capacitor filter and other types of products. The new filter has been widely used in various integrated circuit system, improving the performance of the products, reduce the production cost, and makes the product more simple, convenient in practical application.In this paper, based on the design of a low power consumption, the CMOS cutoff frequency of two order 2KHz low-pass filter, circuit for the Sallen-Key structure, the Sallen-Key circuit has low output impedance, the original small, difference amplifying ability etc.. The whole circuit is designed and simulated with Multisim software, and finally completed the layout design of the filter by using the Cadence software, designed by 0.5nm CMOS process. After experimental verification, the designed filter can meet the design requirements, to achieve a good filtering function within a certain frequency range.Key wordsCMOS;Low pass filter; Multisim;Tanner目录摘要 (I)Abstract (II)第一章滤波器简介 (1)1.1 课题背景及研究意义 (1)1.2 滤波器概述 (1)1.3 滤波器国内外研究现状 (4)1.4 主要研究内容 (5)第二章滤波器总体方案设计 (6)2.1 滤波器方案选择及分析 (6)2.1.1 一阶有源滤波电路 (6)2.1.2 二阶有源滤波电路 (7)2.1.3 压控电压源(Sallen-Key)二阶有源滤波电路 (8)2.2 电路结构的选择 (10)2.3 滤波器电路的确定 (12)2.3 低功耗CMOS运算放大器的设计 (13)2.5 本章小结 (14)第三章滤波器版图设计 (15)3.1 版图设计中寄生效应的影响 (15)3.1.1 焊盘的寄生效应 (15)3.1.2 CMOS闩锁效应 (15)3.1.3 衬底耦合 (16)3.2 运算放大器的版图设计 (17)3.3 低通滤波器版图 (18)3.4 本章小结 (19)第四章二阶低通滤波电路仿真与结果分析 (20)4.1 Multisim仿真软件介绍 (20)4.2 滤波器的仿真 (20)4.3 仿真结果分析 (23)4.4 本章小结 (24)结论 (25)参考文献 (26)致谢 ......................................................................................................... 错误!未定义书签。
第一章滤波器简介1.1 课题背景及研究意义随着近些年电子技术的不断发展,集节约成本、减少通信系统调试时间等优点于一体的集成IC逐渐的成为通信系统发展的必然趋势。
而双极型晶体管工艺和GaAs 虽然在噪声处理与增益控制方面存在着诸多优势,但不方便应用于大规模集成电路系统中,相应的成本也随之增高。
随着CMOS工艺的不断发展、进步、成熟,它的噪声性能逐渐的接近了双极型晶体管工艺器件和GaAs器件,而且该工艺具有价格低、集成度高、体积较小、功耗较低等优点。
因此,IC集成电路使用了CMOS工艺己成为现实。
在本次滤波器设计中集成运算放大器是其重要组成部分,同时运算放大器也是模拟类集成电路最主要的器件类型,用途最广。
随着集成运算放大器在功耗、速度、带宽、稳定性等方面的要求越来越高。
通常在降低集成运算放大电路的功耗上采取降低工作电压的方式,可是这又为集成运算放大器的关键技术性能指标带来了问题。
用CMOS工艺实现低通滤波器的设计已成为IC设计领域的一个比较重要的研究课题。
为满足设计中滤波器的低成本、低功耗要求,选用CMOS技术设计的单芯片是滤波器芯片发展的重要里程碑之一。
利用CMOS工艺设计低频滤波器已逐渐成熟,但在理论上和实践过程中使用该工艺设计还面临着许多问题。
在当今的电信设备和各类自动控制领域,滤波器应用极为广泛。
在所有产品的电子部件结构中,其使用次数最多,技术最为复杂的即为滤波器。
滤波器设计的好坏直接决定产品的优劣,所以对与滤波器的生产和研究越来越受各国重视。
1.2 滤波器概述滤波器是一种能够通过期望频率的信号而衰减其他频率信号的部件,它可以分为有源滤波器和无源滤波器两大类。
有源滤波器的优点是:高输入阻抗和低输出阻抗,因此输入与输出之间具有良好的隔离性能,便于级联。
此外,有源滤波器体积小,重量轻,成本低而且稳定性好,方便调试和应用。
有源滤波器的缺点是:需要提供直流电源才能工作,电阻产生噪声且运算放大器等有源元件的高频特性不太好。
随着集成工艺和材料技术的发展,滤波器的发展方向是小体积,高精度和可靠性。
常见的模拟滤波器的种类如图1-1所示。
图1-1常见模拟滤波器的种类无源滤波器中使用较广泛的器件即是无源元件。
它们必须具有谐振性的特点,通过单个或组合,把一种状态的能量转换为另一种状态的能量,并重新回到初始状态。
无源滤波器大致包含以下几种:LC滤波器、机械滤波器、压电型或陶瓷滤波器、晶体滤波器、分布参数型滤波器。
晶体滤波器通常用石英材料SiO2作为主要制作材料,而陶瓷滤波器则是由错钛酸铅的陶瓷材料制作而成。
它们的工作原理大致相同,都是利用了材料本身的压电效应,产生物理形变或电场之间的能量交换,它们在本质上起到了换能器的功能,可以将电能转换成机械能,或反之。
机械滤波器由机械型的耦合元件或谐振元件组成,利用耦合元件或谐振元件构成的机械网络中产生的滤波效应。
在分布参数型滤波器中主要由親合传输线、传输线组件、谐振腔、谐振器组成。
我们知道由一条1/4波长短路的同轴线,可等效为一个并联关系的谐振电路,在超高频段中可作为滤波器的振子,各个振子之间是利用电场或磁场的耦合关系,即可实现在微波频段的滤波。
无源滤波器具有噪声低、工作频率高等优点,通常在GHz以上,并具有一定的插入损耗,若是把其集成在同一芯片内,那么仍有极大的难度。
有源滤波器可分为两类:一类为连续时间滤波器,另一类为开关电容滤波器。
连续时间滤波器可分为跨导电容型滤波器、有源RC滤波器、有源Q-增强型LC滤波器、电流传送器型滤波器。
连续时间滤波器在功能上不需要采样时钟,在对信号的连续处理时工作频率通常要比开关电容滤波器要高,同时开关电容滤波器发生的时钟馈通问题在这里将不会出现。
目前有源连续时间滤波器最多能够达到几百MHz。
相对于无源滤波器而言,易于集成在芯片内部、噪声较大、工作频率较低是有源滤波器的特点,在通带内具有一定的增益或通带内的损耗较低。
开关电容滤波器在对信号进行采样处理通常是在时间域。
它的特征量由电容比值和时钟频率所决定,根据所学过的奈奎斯特定理可知,釆样时钟频率在实际应用中必须高于其两倍的信号频率才能对输入端信号进行釆样处理,但是一般系统中所需要的时钟频率很高,不适用于高频电子线路中应用。
在研究有源高频连续时间滤波器的过程中,尽管有源RC滤波器应用较早,但从其集成于一个单块芯片的观点来看,该滤波器在性能上有所欠缺。
主要是因为在该滤波器上需要连接容量较大的电容,容值一般达到几十pF大小,这些电容要集成于芯片之上有很大的困难,大电容、大电阻同时占有非常大一部分的芯片面积。
