(完整版)指数运算(含答案)
指数函数习题(经典含答案及详细解析)

指数函数习题一、选择题1.概念运算⎩⎨⎧>≤=⊗ba b b a a b a ,那么函数x x f 21)(⊗=的图象大致为( )2.函数f (x )=x 2-bx +c 知足f (1+x )=f (1-x )且f (0)=3,那么f (b x )与f (c x )的大小关系是( )A .f (b x )≤f (c x )B .f (b x )≥f (c x )C .f (b x )>f (c x )D .大小关系随x 的不同而不同3.函数y =|2x -1|在区间(k -1,k +1)内不单调,那么k 的取值范围是( )A .(-1,+∞)B .(-∞,1)C .(-1,1)D .(0,2)4.设函数f (x )=ln[(x -1)(2-x )]的概念域是A ,函数g (x )=lg(a x -2x -1)的概念域是B ,假设A ⊆B ,那么正数a 的取值范围( )A .a >3B .a ≥3C .a > 5D .a ≥ 55.已知函数⎩⎨⎧>≤--=-77)3)(3()(6x a x x a x f x ,假设数列{a n }知足a n =f (n )(n ∈N *),且{a n }是递增数列,那么实数a 的取值范围是( )A .[94,3) B .(94,3) C .(2,3)D .(1,3) 6.已知a >0且a ≠1,f (x )=x 2-a x ,当x ∈(-1,1)时,均有f (x )<12,那么实数a 的取值范围是( ) A .(0,12]∪[2,+∞) B .[14,1)∪(1,4] C .[12,1)∪(1,2] D .(0,14)∪[4,+∞) 二、填空题7.函数y =a x (a >0,且a ≠1)在[1,2]上的最大值比最小值大a 2,那么a 的值是________. 8.假设曲线|y |=2x +1与直线y =b 没有公共点,那么b 的取值范围是________.9.(2020·滨州模拟)概念:区间[x 1,x 2](x 1<x 2)的长度为x 2-x 1.已知函数y =2|x |的概念域为[a ,b ],值域为[1,2],那么区间[a ,b ]的长度的最大值与最小值的差为________.三、解答题10.求函数y =2342x x ---+的概念域、值域和单调区间.11.(2020·银川模拟)假设函数y =a 2x +2a x -1(a >0且a ≠1)在x ∈[-1,1]上的最大值为14,求a 的值.12.已知函数f (x )=3x ,f (a +2)=18,g (x )=λ·3ax -4x 的概念域为[0,1].(1)求a 的值;(2)假设函数g (x )在区间[0,1]上是单调递减函数,求实数λ的取值范围.指数函数答案1.解析:由a ⊗b =⎩⎪⎨⎪⎧ a a ≤b b a >b 得f (x )=1⊗2x =⎩⎪⎨⎪⎧ 2x x ≤0,1 x >0.答案:A2. 解析:∵f (1+x )=f (1-x ),∴f (x )的对称轴为直线x =1,由此得b =2.又f (0)=3,∴c =3.∴f (x )在(-∞,1)上递减,在(1,+∞)上递增.若x ≥0,那么3x ≥2x ≥1,∴f (3x )≥f (2x ).若x <0,那么3x <2x <1,∴f (3x )>f (2x ).∴f (3x )≥f (2x ).答案:A3.解析:由于函数y =|2x -1|在(-∞,0)内单调递减,在(0,+∞)内单调递增,而函数在区间(k -1,k +1)内不单调,因此有k -1<0<k +1,解得-1<k <1.答案:C4. 解析:由题意得:A =(1,2),a x -2x >1且a >2,由A ⊆B 知a x -2x >1在(1,2)上恒成立,即a x -2x -1>0在(1,2)上恒成立,令u (x )=a x -2x -1,那么u ′(x )=a x ln a -2x ln2>0,因此函数u (x )在(1,2)上单调递增,那么u (x )>u (1)=a -3,即a ≥3.答案:B5. 解析:数列{a n }知足a n =f (n )(n ∈N *),那么函数f (n )为增函数,注意a 8-6>(3-a )×7-3,因此⎩⎪⎨⎪⎧ a >13-a >0a 8-6>3-a ×7-3,解得2<a <3.答案:C6. 解析:f (x )<12⇔x 2-a x <12⇔x 2-12<a x ,考查函数y =a x 与y =x 2-12的图象,当a >1时,必有a -1≥12,即1<a ≤2, 当0<a <1时,必有a ≥12,即12≤a <1, 综上,12≤a <1或1<a ≤2. 答案:C7. 解析:当a >1时,y =a x 在[1,2]上单调递增,故a 2-a =a 2,得a =32.当0<a <1时,y =a x 在[1,2]上单调递减,故a -a 2=a 2,得a =12.故a =12或32. 答案:12或328. 解析:别离作出两个函数的图象,通过图象的交点个数来判定参数的取值范围.曲线|y |=2x +1与直线y =b 的图象如下图,由图象可得:若是|y |=2x +1与直线y =b 没有公共点,那么b 应知足的条件是b ∈[-1,1]. 答案:[-1,1]9. 解析:如图知足条件的区间[a ,b ],当a =-1,b =0或a =0,b =1时区间长度最小,最小值为1,当a =-1,b =1时区间长度最大,最大值为2,故其差为1. 答案:110. 解:要使函数成心义,那么只需-x 2-3x +4≥0,即x 2+3x -4≤0,解得-4≤x ≤1.∴函数的概念域为{x |-4≤x ≤1}.令t =-x 2-3x +4,那么t =-x 2-3x +4=-(x +32)2+254, ∴当-4≤x ≤1时,t max =254,现在x =-32,t min =0,现在x =-4或x =1. ∴0≤t ≤254.∴0≤-x 2-3x +4≤52. ∴函数y =2341()2x x --+[28,1].由t =-x 2-3x +4=-(x +32)2+254(-4≤x ≤1)可知, 当-4≤x ≤-32时,t 是增函数, 当-32≤x ≤1时,t 是减函数. 依照复合函数的单调性知:y =1()2在[-4,-32]上是减函数,在[-32,1]上是增函数. ∴函数的单调增区间是[-32,1],单调减区间是[-4,-32]. 11. 解:令a x =t ,∴t >0,那么y =t 2+2t -1=(t +1)2-2,其对称轴为t =-1.该二次函数在[-1,+∞)上是增函数.①若a >1,∵x ∈[-1,1],∴t =a x ∈[1a,a ],故当t =a ,即x =1时,y max =a 2+2a -1=14,解得a =3(a =-5舍去).②假设0<a <1,∵x ∈[-1,1],∴t =a x ∈[a ,1a ],故当t =1a,即x =-1时, y max =(1a+1)2-2=14. ∴a =13或-15(舍去). 综上可得a =3或13. 12. 解:法一:(1)由已知得3a +2=18⇒3a =2⇒a =log 32.(2)现在g (x )=λ·2x -4x ,设0≤x 1<x 2≤1,因为g (x )在区间[0,1]上是单调减函数,因此g (x 1)-g (x 2)=(2x 1-2x 2)(λ-2x 2-2x 1)>0恒成立,即λ<2x 2+2x 1恒成立.由于2x 2+2x 1>20+20=2,因此实数λ的取值范围是λ≤2.法二:(1)同法一.(2)现在g (x )=λ·2x -4x ,因为g (x )在区间[0,1]上是单调减函数,因此有g ′(x )=λln2·2x -ln4·4x =ln2[-2·(2x )2+λ·2x ]≤0成立.设2x =u ∈[1,2],上式成立等价于-2u 2+λu ≤0恒成立.因为u ∈[1,2],只需λ≤2u 恒成立,因此实数λ的取值范围是λ≤2.。
高中数学必修一《指数与指数幂计算》精选例题(含答案解析)

高中数学必修一《指数与指数幂计算》精选例题(含答案解析)一、选择题1.下列说法中:①16的4次方根是2;②416的运算结果是±2;③当n 为大于1的奇数时,n a 对任意a ∈R 都有意义;④当n 为大于1的偶数时,n a 只有当a ≥0时才有意义.其中正确的是( )A .①③④B .②③④C .②③D .③④2.若2<a <3,化简(2-a )2+4(3-a )4的结果是() A .5-2a B .2a -5C .1D .-13.在(-12)-1、122-、1212-⎛⎫ ⎪⎝⎭、2-1中,最大的是() A .(-12)-1B .122-C .1212-⎛⎫⎪⎝⎭D .2-14.化简3a a 的结果是( )A .aB .12aC .a 2D .13a5.下列各式成立的是( )A.3m 2+n 2=()23m n +B .(b a )2=12a 12bC.6(-3)2=()133- D.34=1326.下列结论中,正确的个数是( )①当a <0时,()322a =a 3;②n a n =|a |(n >0);③函数y =()122x --(3x -7)0的定义域是(2,+∞); ④若100a =5,10b =2,则2a +b =1.A .0B .1C .2D .3 7.614-3338+30.125的值为________.8.若a >0,且a x =3,a y =5,则22yx a+=________. 9.若x >0,则(214x +323)(214x -323)-412x -·(x -12x )=________.三、解答题10.(1)化简:3xy 2·xy -1·xy ·(xy )-1(xy ≠0); (2)计算:122-+(-4)02+12-1-(1-5)0·238-.11.设-3<x <3,求x 2-2x +1-x 2+6x +9的值.能力提升12.化简:4133223384a a b b a -+÷(1-23b a )×3a .13.若x >0,y >0,且x -xy -2y =0,求2x -xy y +2xy的值.参考答案与解析1.D [①错,∵(±2)4=16,∴16的4次方根是±2;②错,416=2,而±416=±2.]2.C [原式=|2-a |+|3-a |,∵2<a <3,∴原式=a -2+3-a =1.]3.C [∵(-12)-1=-2,122-=22,1212-⎛⎫ ⎪⎝⎭=2,2-1=12, ∵2>22>12>-2,∴1212-⎛⎫ ⎪⎝⎭>122->2-1>(-12)-1.]4.B [12a =.]5.D [被开方数是和的形式,运算错误,A 选项错;(b a )2=b 2a 2,B 选项错;6(-3)2>0,()133-<0,C 选项错.故选D.]6.B [①中,当a <0时,()()3312222a a ⎡⎤=⎢⎥⎣⎦=(-a )3=-a 3,∴①不正确;②中,若a =-2,n =3,则3(-2)3=-2≠|-2|,∴②不正确;③中,有⎩⎨⎧ x -2≥0,3x -7≠0,即x ≥2且x ≠73, 故定义域为[2,73)∪(73,+∞),∴③不正确;④中,∵100a =5,10b =2,∴102a =5,10b =2,102a ×10b =10,即102a +b =10. ∴2a +b =1.④正确.] 7.32解析 原式=(52)2-3(32)3+3(12)3=52-32+12=32. 8.9 5 解析 22y x a +=(a x )2·()12y a =32·125=9 5. 9.-23 解析 原式=412x -33-412x +4=-23. 10.解 (1)原式=()()11132122xy xy xy -⎡⎤⎢⎥⎣⎦·(xy )-1 =13x ·2111136622y xy x y --- =13x ·13x -=⎩⎨⎧ 1, x >0-1,x <0. (2)原式=12+12+2+1-22 =22-3.11.解 原式=(x -1)2-(x +3)2 =|x -1|-|x +3|,∵-3<x <3,∴当-3<x <1时,原式=-(x -1)-(x +3)=-2x -2; 当1≤x <3时,原式=(x -1)-(x +3)=-4.∴原式=⎩⎨⎧ -2x -2 (-3<x <1)-4(1≤x <3). 12.解 原式=()111333212133338242aa b a b b a aa --÷++×13a13.解 ∵x -xy -2y =0,x >0,y >0,∴(x)2-xy-2(y)2=0,∴(x+y)(x-2y)=0,由x>0,y>0得x+y>0,∴x-2y=0,∴x=4y,∴2x-xyy+2xy =8y-2yy+4y=65.。
(完整版)指数函数与对数函数高考题及答案
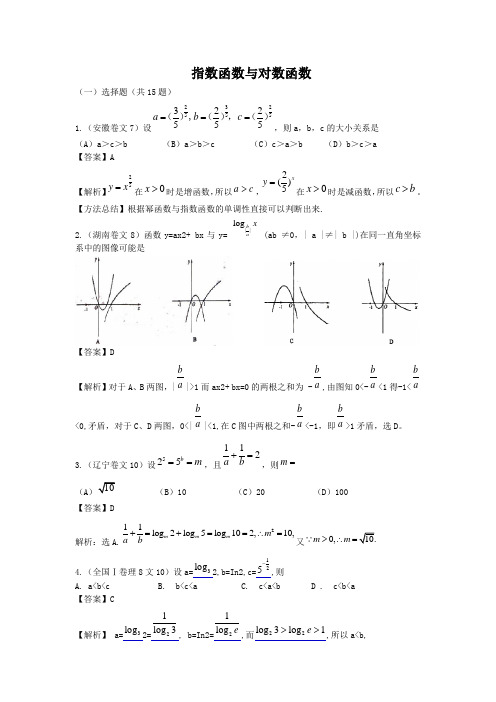
指数函数与对数函数(一)选择题(共15题)1.(安徽卷文7)设232555322555a b c ===(),(),(),则a ,b ,c 的大小关系是 (A )a >c >b (B )a >b >c (C )c >a >b (D )b >c >a【答案】A【解析】25y x =在0x >时是增函数,所以a c >,2()5xy =在0x >时是减函数,所以c b >。
【方法总结】根据幂函数与指数函数的单调性直接可以判断出来.2.(湖南卷文8)函数y=ax2+ bx 与y= ||log b ax(ab ≠0,| a |≠| b |)在同一直角坐标系中的图像可能是【答案】D【解析】对于A 、B 两图,|b a |>1而ax2+ bx=0的两根之和为 -b a ,由图知0<-b a <1得-1<ba <0,矛盾,对于C 、D 两图,0<|b a |<1,在C 图中两根之和-b a <-1,即ba >1矛盾,选D 。
3.(辽宁卷文10)设525bm ==,且112a b +=,则m =(A(B )10 (C )20 (D )100 【答案】D解析:选A.211log 2log 5log 102,10,m m m m a b +=+==∴=又0,m m >∴=4.(全国Ⅰ卷理8文10)设a=3log 2,b=In2,c=125-,则A. a<b<cB. b<c<aC. c<a<b D . c<b<a 【答案】C【解析】 a=3log 2=21log 3, b=In2=21log e ,而22log 3log 1e >>,所以a<b,c=125-=,而222log 4log 3>=>,所以c<a,综上c<a<b.【命题意图】本小题以指数、对数为载体,主要考查指数函数与对数函数的性质、实数大小的比较、换底公式、不等式中的倒数法则的应用.5.(全国Ⅰ卷理10)已知函数F(x)=|lgx|,若0<a<b,且f(a)=f(b),则a+2b 的取值范围是(A))+∞(B))+∞ (C)(3,)+∞ (D)[3,)+∞【答案】A【命题意图】本小题主要考查对数函数的性质、函数的单调性、函数的值域,考生在做本小题时极易忽视a 的取值范围,而利用均值不等式求得a+2b 2a a =+>,从而错选A,这也是命题者的用苦良心之处.【解析】因为 f(a)=f(b),所以|lga|=|lgb|,所以a=b(舍去),或1b a =,所以a+2b=2a a +又0<a<b,所以0<a<1<b ,令2()f a a a =+,由“对勾”函数的性质知函数()f a 在a ∈(0,1)上为减函数,所以f(a)>f(1)=1+21=3,即a+2b 的取值范围是(3,+∞).6.(全国Ⅰ卷文7)已知函数()|lg |f x x =.若a b ≠且,()()f a f b =,则a b +的取值范围是(A)(1,)+∞ (B)[1,)+∞ (C) (2,)+∞ (D) [2,)+∞【答案】C【命题意图】本小题主要考查对数函数的性质、函数的单调性、函数的值域,考生在做本小题时极易忽视a 的取值范围,而利用均值不等式求得a+b=12a a +≥,从而错选D,这也是命题者的用苦良心之处. 7.(山东卷文3)函数()()2log 31x f x =+的值域为A.()0,+∞ B. )0,+∞⎡⎣ C. ()1,+∞ D. )1,+∞⎡⎣ 【答案】A【解析】因为311x+>,所以()()22log 31log 10x f x =+>=,故选A 。
2021年人教版高中数学必修第一册:第4章《章末复习课》(含答案详解)

2021年人教版高中数学必修第一册:第4章《章末复习课》(含答案详解)1、指数与对数的运算【例1】计算:(1)2log32-log3+log38-5log53;(2)1.5-×0+80.25×+(×)6-.[解] (1)原式=log3-3=2-3=-1.(2)原式=+2×2+22×33-=21+4×27=110.指数、对数的运算应遵循的原则指数式的运算首先留意化简顺序,一般负指数先转化成正指数,根式化为分数指数幂运算,其次若出现分式则要留意分子、分母因式分解以到达约分的目的.对数运算首先留意公式应用过程中范围的改变,前后要等价,娴熟地运用对数的三个运算性质并结合对数恒等式,换底公式是对数计算、化简、证明常用的技巧.7n1.设3x=4y=36,则+的值为( )A.6B.3C.2D.1D [由3x=4y=36得x=log336,y=lo2、g436,∴+=2log363+log364=log369+log364=log3636=1.]指数函数、对数函数的图象及应用【例2】(1)若函数y=logax(a0,且a≠1)的图象如下图,则以下函数正确的选项是( )A B C D(2)已知函数f(x)是定义在R上的偶函数,当x≥0时,f(x)=x.①如图,画出函数f(x)的图象;②依据图象写出f(x)的单调区间,并写出函数的值域.(1)B [由已知函数图象可得,loga3=1,所以a=3.A项,函数解析式为y=3-x,在R上单调递减,与图象不符;C项中函数的解析式为y=(-x)3=-x3,当x0时,y0,这与图象不符;D项中函数解析式为y=log3(-x),在(-∞,0)上为单调3、递减函数,与图象不符;B项中对应函数解析式为y=x3,7n 与图象相符.应选B.](2)[解] ①先作出当x≥0时,f(x)=x的图象,利用偶函数的图象关于y轴对称,再作出f(x)在x∈(-∞,0)时的图象.②函数f(x)的单调递增区间为(-∞,0),单调递减区间为[0,+∞),值域为(0,1].1.识别函数的图象从以下几个方面入手:(1)单调性:函数图象的改变趋势;(2)奇偶性:函数图象的对称性;(3)特别点对应的函数值.2.指数函数与对数函数图象经过定点的实质是a0=1,loga1=0.2.函数y=1+log(x-1)的图象肯定经过点( )A.(1,1)B.(1,0)C.(2,1)D.(2,0)C [把y=logx的图象向右平移1个单位,再向上平移1个单位即可4、得到y=1+log(x-1)的图象,故其经过点(2,1).]比较大小【例3】若0xy1,则( )A.3y3xB.logx3logy3C.log4xlog4y7nD.xyC [因为0xy1,则对于A,函数y=3x在R上单调递增,故3x3y,A错误.对于B,依据底数a对对数函数y=logax的影响:当0a1时,在x∈(1,+∞)上“底小图高”.因为0xy1,所以logx3logy3,B错误.对于C,函数y=log4x在(0,+∞)上单调递增,故log4xlog4y,C正确.对于D,函数y=x在R上单调递减,故xy,5、D错误.]1.比较两数大小常用的方法有单调性法、图象法、中间值法等.2.当两个数都是指数幂或对数式时,可将其看成某个指数函数、对数函数或幂函数的函数值,然后利用该函数的单调性比较.3.比较多个数的大小时,先利用“0”“1”作为分界点,然后在各部分内再利用函数性质比较大小.4.含参数的问题,要依据参数的取值进行分类商量.3.设a=log2π,b=logπ,c=π-2,则( )A.abcB.bacC.acbD.cbaC [∵a=log2πlog22=1,b =logπlog1=0,c=π-2=,即0c1,∴acb,应选C.]指数函数、对数函数的性质【例4】(6、1)设函数f(x)=ln(1+x)-ln(1-x),则f(x)是( )A.奇函数,且在(0,1)上是增函数B.奇函数,且在(0,1)上是减函数C.偶函数,且在(0,1)上是增函数7nD.偶函数,且在(0,1)上是减函数(2)已知a0,a≠1且loga3loga2,若函数f(x)=logax在区间[a,3a]上的最大值与最小值之差为1.①求a的值;②若1≤x≤3,求函数y=(logax)2-loga+2的值域.(1)A [由题意可得,函数f(x)的定义域为(-1,1),且f(-x)=ln(1-x)-ln(1+x)=-f(x),故f(x)为奇函数.又f(x)=ln=ln,易知y=-1在(0,1)上为增函数,故f(x)在(0,1)上为增函数.](2)[7、解] ①因为loga3loga2,所以f(x)=logax在[a,3a]上为增函数.又f(x)在[a,3a]上的最大值与最小值之差为1,所以loga(3a)-logaa=1,即loga3=1,所以a=3.②函数y=(log3x)2-log3+2=(log3x)2-log3x+2=2+.令t=log3x,因为1≤x≤3,所以0≤log3x≤1,即0≤t≤1.所以y=2+∈,所以所求函数的值域为.1.把本例(1)的函数f(x)改为“f(x)=ln(x+)”,推断其奇偶性.[解] ∵f(x)=ln(x+),∴其定义域为R,又f(-x)=ln(-x +),∴f(x)+f(-x)=ln(x+)+ln(-x+)=ln1=0,∴f(-x)=-f(x),∴f(x)为奇函数.28、.把本例(2)②中的函数改为“y=a2x+ax-1”,求其最小值.[解] 由题意可知y=32x+3x-1,令3x=t,则t∈[3,27],∴f(t)=t2+t-1=2-,t∈[3,27],∴当t=3时,f(t)min=f(3)=9+3-1=11.7n1.讨论函数的性质要树立定义域优先的原则.2.换元法的作用是利用整体代换,将问题转化为常见问题.该类问题中,常设u=logax或u=ax,转化为一元二次方程、二次函数等问题.要留意换元后u的取值范围.函数的应用【例5】一种放射性元素,最初的质量为500g,按每年10%衰减.(1)求t年后,这种放射性元素的质量w的表达式;(2)由求出的函数表达式,求这种放射性元素的半衰期(结果精确到0.1).[解] (1)最初的质量为9、500g.经过1年,w=500(1-10%)=500×0.9;经过2年,w =500×0.92;由此推知,t年后,w=500×0.9t.(2)由题意得500×0.9t=250,即0.9t=0.5,两边同时取以10为底的对数,得lg0.9t=lg0.5,即tlg0.9=lg0.5,所以t=≈6.6.即这种放射性元素的半衰期约为6.6年.指数函数模型的应用在实际问题中,有关人口增长、银行利率、细胞分裂等增长率问题常可以用指数函数模型表示.通常可以表示为y=N(1+p)x(其中N为基础数,p为增长率,x 为时间)的形式.4.某化工厂生产一种溶液,按市场要求,杂质含量不能超过0.1%,若初时含杂质2%,每过滤一次可使杂质含量削减,问至少应过滤几次才能使产品到达市场要求?(已知:10、lg2≈0.3010,lg3≈0.4771)7n[解] 设过滤n次能使产品到达市场要求,依题意,得×n≤,即n≤.则n(lg2-lg3)≤-(1+lg2),故n≥≈7.4,考虑到n∈N,故n≥8,即至少要过滤8次才能到达市场要求.7。
2019大一轮高考总复习文数(北师大版)讲义第2章 第05节 指数与指数函数 Word版含答案

第五节 指数与指数函数.正整数指数函数+正整数集,叫作正整数指数函数,其中是自变量,定义域是)+∈,≠=(>,函数.分数指数幂()定义一般地,给定正实数,对于任意给定的整数、(,互素),存在唯一的正实数,使得=,它就是分数指数幂.=次幂,记作,我们把叫作的()规定:分数指数幂与根式的关系①正分数指数幂的根式形式:=(>);②负分数指数幂的根式形式:-=)(>,,∈+且>);③.的正分数指数幂等于的负分数指数幂没有意义分数指数幂:的 .的正分数指数幂等于的负分数指数幂没有意义的分数指数幂:③.指数幂的运算性质 若,>,,∈,则;+()·= ;·()()= ()()=..指数函数的图像与性质()在进行指数幂的运算时,一般用分数指数幂的形式表示,并且结果不能同时含有根号和分数指数幂,也不能既有分母又含有负指数.()指数函数=(>, ≠)的图像和性质跟的取值有关,要特别注意区分>或<<.()指数函数图像在坐标系中的位置如下图所示,即无论在轴的左侧还是右侧,底数按逆时针方向变大..判断下列结论的正误(正确的打“√”,错误的打“×”)()·=.( )()函数=·与=+都不是指数函数.( )()若<(>且≠), 则<.( )()函数=-在上为单调减函数.( )答案: ()× ()√ ()× ()√.化简 (<,<)得( )....-解析:选==-..函数()=+的值域为( ).(-,+∞).(,+∞) .().[,+∞)解析:选∵>,∴+>,即函数()=+的值域为(,+∞)..函数()=-+(>,且≠)的图像必经过点( ).() .() .().()解析:选由()=+=,知()的图像必过点(). .(教材习题改编)若+>-+,则的取值范围是.解析:因为+>-+,即-->-+⇒-->-+⇒<-⇒<-.。
指数函数习题(经典含答案及详细解析)

指数函数习题一、选择题1.定义运算⎩⎨⎧>≤=⊗ba b b a a b a ,则函数xx f 21)(⊗=的图象大致为( )2.函数f (x )=x 2-bx +c 满足f (1+x )=f (1-x )且f (0)=3,则f (b x )与f (c x)的大小关系是( ) A .f (b x)≤f (c x) B .f (b x)≥f (c x) C .f (b x)>f (c x)D .大小关系随x 的不同而不同3.函数y =|2x-1|在区间(k -1,k +1)内不单调,则k 的取值范围是( ) A .(-1,+∞) B .(-∞,1) C .(-1,1)D .(0,2)4.设函数f (x )=ln[(x -1)(2-x )]的定义域是A ,函数g (x )=lg(a x-2x-1)的定义域是B ,若A ⊆B ,则正数a 的取值范围( )A .a >3B .a ≥3C .a > 5D .a ≥55.已知函数⎩⎨⎧>≤--=-77)3)(3()(6x a x x a x f x ,若数列{a n }满足a n =f (n )(n ∈N *),且{a n }是递增数列,则实数a 的取值范围是( ) A .[94,3)B .(94,3)C .(2,3)D .(1,3)6.已知a >0且a ≠1,f (x )=x 2-a x,当x ∈(-1,1)时,均有f (x )<12,则实数a 的取值范围是( )A .(0,12]∪[2,+∞)B .[14,1)∪(1,4]C .[12,1)∪(1,2]D .(0,14)∪[4,+∞)二、填空题7.函数y =a x(a >0,且a ≠1)在[1,2]上的最大值比最小值大a2,则a 的值是________.8.若曲线|y |=2x+1与直线y =b 没有公共点,则b 的取值范围是________.9.(2011·滨州模拟)定义:区间[x 1,x 2](x 1<x 2)的长度为x 2-x 1.已知函数y =2|x |的定义域为[a ,b ],值域为[1,2],则区间[a ,b ]的长度的最大值与最小值的差为________.三、解答题 10.求函数y =2342x x ---+的定义域、值域和单调区间.11.(2011·银川模拟)若函数y =a 2x+2a x-1(a >0且a ≠1)在x ∈[-1,1]上的最大值为14,求a 的值.12.已知函数f (x )=3x,f (a +2)=18,g (x )=λ·3ax-4x的定义域为[0,1]. (1)求a 的值;(2)若函数g (x )在区间[0,1]上是单调递减函数,求实数λ的取值范围.指数函数答案1.解析:由a ⊗b =⎩⎪⎨⎪⎧a a ≤b ba >b得f (x )=1⊗2x=⎩⎪⎨⎪⎧2xx ≤0,1x >0.答案:A2. 解析:∵f (1+x )=f (1-x ),∴f (x )的对称轴为直线x =1,由此得b =2.又f (0)=3,∴c =3.∴f (x )在(-∞,1)上递减,在(1,+∞)上递增. 若x ≥0,则3x≥2x≥1,∴f (3x)≥f (2x). 若x <0,则3x<2x<1,∴f (3x)>f (2x). ∴f (3x)≥f (2x ). 答案:A3.解析:由于函数y =|2x-1|在(-∞,0)内单调递减,在(0,+∞)内单调递增,而函数在区间(k -1,k +1)内不单调,所以有k -1<0<k +1,解得-1<k <1. 答案:C4. 解析:由题意得:A =(1,2),a x-2x>1且a >2,由A ⊆B 知a x-2x>1在(1,2)上恒成立,即a x -2x -1>0在(1,2)上恒成立,令u (x )=a x -2x -1,则u ′(x )=a x ln a -2x ln2>0,所以函数u (x )在(1,2)上单调递增,则u (x )>u (1)=a -3,即a ≥3.答案:B5. 解析:数列{a n }满足a n =f (n )(n ∈N *),则函数f (n )为增函数,注意a 8-6>(3-a )×7-3,所以⎩⎪⎨⎪⎧a >13-a >0a 8-6>3-a ×7-3,解得2<a <3.答案:C6. 解析:f (x )<12⇔x 2-a x <12⇔x 2-12<a x ,考查函数y =a x 与y =x 2-12的图象,当a >1时,必有a -1≥12,即1<a ≤2,当0<a <1时,必有a ≥12,即12≤a <1,综上,12≤a <1或1<a ≤2.答案:C7. 解析:当a >1时,y =a x 在[1,2]上单调递增,故a 2-a =a 2,得a =32.当0<a <1时,y =ax在[1,2]上单调递减,故a -a 2=a 2,得a =12.故a =12或32.答案:12或328. 解析:分别作出两个函数的图象,通过图象的交点个数来判断参数的取值范围.曲线|y |=2x +1与直线y =b 的图象如图所示,由图象可得:如果|y |=2x+1与直线y =b 没有公共点,则b 应满足的条件是b ∈[-1,1]. 答案:[-1,1]9. 解析:如图满足条件的区间[a ,b ],当a =-1,b =0或a =0,b =1时区间长度最小,最小值为1,当a =-1,b =1时区间长度最大,最大值为2,故其差为1. 答案:110. 解:要使函数有意义,则只需-x 2-3x +4≥0,即x 2+3x -4≤0,解得-4≤x ≤1. ∴函数的定义域为{x |-4≤x ≤1}.令t =-x 2-3x +4,则t =-x 2-3x +4=-(x +32)2+254,∴当-4≤x ≤1时,t max =254,此时x =-32,t min =0,此时x =-4或x =1.∴0≤t ≤254.∴0≤-x 2-3x +4≤52.∴函数y =2341()2x x --+[28,1]. 由t =-x 2-3x +4=-(x +32)2+254(-4≤x ≤1)可知,当-4≤x ≤-32时,t 是增函数,当-32≤x ≤1时,t 是减函数.根据复合函数的单调性知:y =1()2[-4,-32]上是减函数,在[-32,1]上是增函数.∴函数的单调增区间是[-32,1],单调减区间是[-4,-32].11. 解:令a x=t ,∴t >0,则y =t 2+2t -1=(t +1)2-2,其对称轴为t =-1.该二次函数在[-1,+∞)上是增函数.①若a >1,∵x ∈[-1,1],∴t =a x ∈[1a,a ],故当t =a ,即x =1时,y max =a 2+2a -1=14,解得a =3(a =-5舍去). ②若0<a <1,∵x ∈[-1,1],∴t =a x∈[a ,1a ],故当t =1a,即x =-1时,y max =(1a+1)2-2=14.∴a =13或-15(舍去).综上可得a =3或13.12. 解:法一:(1)由已知得3a +2=18⇒3a=2⇒a =log 32.(2)此时g (x )=λ·2x -4x, 设0≤x 1<x 2≤1,因为g (x )在区间[0,1]上是单调减函数,所以g (x 1)-g (x 2)=(2x 1-2x 2)(λ-2x 2-2x 1)>0恒成立,即λ<2x 2+2x 1恒成立. 由于2x 2+2x 1>20+20=2, 所以实数λ的取值范围是λ≤2. 法二:(1)同法一. (2)此时g (x )=λ·2x -4x,因为g (x )在区间[0,1]上是单调减函数,所以有g ′(x )=λln2·2x -ln4·4x =ln2[-2·(2x )2+λ·2x]≤0成立. 设2x=u ∈[1,2],上式成立等价于-2u 2+λu ≤0恒成立. 因为u ∈[1,2],只需λ≤2u 恒成立, 所以实数λ的取值范围是λ≤2.。
指数对数函数图像与性质(含答案)
指数对数函数图像与性质(含答案)指数函数和对数函数是高中数学中比较重要的函数类型之一。
对数函数的定义域为正实数集,值域为实数集,图像在点(1,0)处经过y轴且单调递增。
指数函数的定义域为实数集,值域为正实数集,图像在点(0,1)处经过y轴且单调递增。
对数函数和指数函数是互为反函数的函数对,它们之间有着很多有趣的性质和运算规律。
对于指数函数,有以下基本运算规律:(1) $a^r\cdota^s=a^{r+s}$,(2) $a^r\div a^s=a^{r-s}$,(3) $(a^r)^s=a^{rs}$,(4) $(ab)^r=a^r\cdot b^r$。
对于对数函数,有以下恒等式:$\log_aN=N$,$\log_ab=\frac{1}{\log_ba}$,$\log_a\frac{M}{N}=\log_aM-\log_aN$,以及以下几个小结论:$\log_ab^n=n\log_ab$,$\log_an^M=M\log_an$,$\log_ab=\frac{\log_cb}{\log_ca}$,$\log_aa=1$,$\log_a1=0$。
在解题时,我们可以利用对数函数和指数函数的性质和运算规律,来求解函数的定义域、值域、单调性等问题。
例如,对于函数$y=-x^2+2x+1$,我们可以求出它的顶点坐标为$(1,2)$,因此它的值域为$(-\infty,2]$,并且它在区间$(0,1)$上单调递减,在区间$(1,+\infty)$上单调递增。
对于函数$y=\log_2(x^2-ax+3a)-5x+6$,我们可以先求出它的定义域为$(a-3\sqrt{a},a+3\sqrt{a})$,然后判断它在该定义域内的单调性,最后求出使其在区间$[2,+\infty)$上单调递减的$a$的取值范围。
对于函数$y=4x-\frac{12}{2-a\cdot2x+2\sqrt{a^2x^2+1}}$,我们可以先求出它的定义域为$(0,2]$,然后求出它的导数,令其为0,解出$x$的值,再求出函数在该定义域上的最大值和最小值。
第11讲 指数与对数的运算(解析版)-2021届新课改地区高三数学一轮专题复习
1第11讲:指数与对数的运算一、课程标准1、理解有理指数幂的含义,通过具体实例了解实数指数幂的意义,掌握幂的运算.2、理解对数的概念及其运算性质,知道用换底公式能将一般对数转化成自然对数或常用对数;3、了解对数的发现历史以及对简化运算的作用二、基础知识回顾1. 有关指数幂的概念(1)n次方根正数的奇次方根是一个正数,负数的奇次方根是一个负数,0的奇次方根是__0__;正数的偶次方根是两个绝对值相等、符号相反的数,0的偶次方根是__0__,负数没有偶次方根.(2)方根的性质①当n为奇数时,n a n=a;②当n为偶数时,n a n=||a=,0-a0.a aa⎧⎨⎩≥,,<(3)分数指数幂的意义①m n a(a>0,m、n都是正整数,n>1);②m na-=1mna>0,m、n都是正整数,n>1).2. 有理数指数幂的运算性质设s,t∈Q,a>0,b>0,则:(1)a s a t=as+t;(2)(a s)t=ast;(3)(ab)t=a t b t.3. 对数的相关概念(1)对数的定义:如果a b=N(a>0,a≠1),那么b叫做以a为底数N的对数,记作log a N=b.(2)常用对数和自然对数:①常用对数:以10为底N的对数,简记为:lg N;②自然对数:以e为底N 的对数,简记为:ln N.(3)指数式与对数式的相互转化:a b=N⇔log a N=b(a>0,a≠1,N>0).4. 对数的基本性质设N>0,a>0,a≠1,则:(1)log a a=1;(2)log a1=0;1(3)log a a N =N ;(4)a log aN =N .5. 对数运算的法则设M >0,N >0,a >0,a≠1,b >0,b≠1,则: (1)log a (MN)= log a M +log a N ; (2)log a MN =log a M -log a N ; (3)log a M n = n log a M . 6. 对数的换底公式设N >0,a >0,a≠1,b >0,b≠1,则log b N =log a Nlog a b .三、自主热身、归纳总结1、化简4a 23·b -13÷⎝⎛⎭⎫-23a -13b 23的结果为( ) A .-2a3b B .-8a b C .-6a b D .-6ab【答案】C【解析】原式=-6a 23-⎝⎛⎭⎫-13b -13-23=-6ab -1=-6ab . 2、(log 29)(log 32)+log a 54+log a ⎝⎛⎭⎫45a (a >0,且a ≠1)的值为( ) A .2 B .3 C .4 D .5 【答案】B【解析】 原式=(2log 23)(log 32)+log a ⎝⎛⎭⎫54×45a =2×1+log a a =3.3、 若lg 2,lg (2x +1),lg (2x +5)成等差数列,则x 的值等于( )A . 1B . 0或18C . 18 D . log 23【答案】D .【解析】由lg 2,lg (2x +1),lg (2x +5)成等差数列,知lg 2+lg (2x +5)=2lg (2x +1), ∴2(2x +5)=(2x +1)2,即(2x )2-9=0,即2x =3,∴x =log 23.故选D .4、.(多选)已知a +a -1=3,在下列各选项中,其中正确的是( )A .a 2+a -2=7B .a 3+a -3=18C .a 12+a -12=±5 D .a a +1a a =2 5【答案】ABD【解析】在选项A 中,因为a +a -1=3,所以a 2+a -2=(a +a -1)2-2=9-2=7,故A 正确;在选项B 中,因为a +a -1=3,所以a 3+a -3=(a +a -1)(a 2-1+a -2)=(a +a -1)·[(a +a -1)2-3]=3×6=18,故B 正确;在选项C 中,因为a +a -1=3,所以(a 12+a -12)2=a +a -1+2=5,且a >0,所以a 12+a -12=5,故C 错误;在选项D 中,因为a 3+a -3=18,且a >0,所以⎝⎛⎭⎫a a +1a a 2=a 3+a -3+2=20,所以a a +1a a =25,故D正确.5、log 225·log 3(22)·log 59=________. 【答案】6【解析】法一:log 225·log 3(22)·log 59=log 252·log 3232·log 532=6log 25·log 32·log 53=6. 法二:log 225·log 3(22)·log 59=lg 25lg 2·lg (22)lg 3·lg 9lg 5=lg 52lg 2·lg 232lg 3·lg 32lg 5=6. 6、 已知2lg x -y2=lg x +lg y ,则xy 的值为 .【答案】1+ 2.【解析】 利用对数的性质消去对数符号,得到关于x ,y 的方程再求解.由已知得lg ⎝⎛⎭⎫x -y 22=lg (xy),∴⎝⎛⎭⎫x -y 22=xy , 即x 2-6xy +y 2=0,∴⎝⎛⎭⎫x y 2-6⎝⎛⎭⎫x y +1=0,∴xy =3±2 2. 又∵x -y 2>0且x 、y >0,∴x >y >0,即xy >1,∴xy =3+22,xy =1+ 2.7、计算:log 5[412log 210-(33)23-7log 72]=________.【答案】0【解析】原式=log 5[2log 210-(332)23-2]=log 5(10-3-2)=log 55=1.8、化简 [(0.06415)-2.5]23-3338-π0;【答案】0【解析】[(0.06415)-2.5]23-3338-π0=⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫⎣⎢⎡⎦⎥⎤⎝⎛⎭⎫641 00015-5223-⎝⎛⎭⎫27813-1 =⎣⎡⎦⎤⎝⎛⎭⎫410315×⎝ ⎛⎭⎪⎫-52×23-⎣⎡⎦⎤⎝⎛⎭⎫32313-1=52-32-1=0.四、例题选讲 考点一 指数幂的运算例1 化简下列各式(其中各字母均为正数).(1)⎝ ⎛⎭⎪⎫-278-23+0.002-12-10(5-2)-1+π0(2)a 3b 23ab 2(a 14b 12)4a -13b 13(a >0,b >0)(3)1253[(0.064) 2.5]--3338-π0;(4)121121332a b a b ---⎛⎫ ⎪g g g 【解析】(1)原式=⎝ ⎛⎭⎪⎫-32-2+50012-10(5+2)(5-2)(5+2)+1=49+105-105-20+1=-1679.(2)原式=(a 3b 2a 13b 23)12ab 2a -13b13=a 32+16-1+13b1+13-2-13=a b .(3原式=253112536427110008-⎧⎫⎡⎤⎪⎪⎪⎪⎛⎫⎛⎫⎢⎥--⎨⎬ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎪⎪⎣⎦⎪⎪⎩⎭=152133523343102⎛⎫⨯-⨯ ⎪⎝⎭⎡⎤⎡⎤⎛⎫⎛⎫-⎢⎥⎢⎥ ⎪ ⎪⎝⎭⎝⎭⎢⎥⎢⎥⎣⎦⎣⎦-1=52-32-1=0.(4)原式=111111111533223262361566a b a ba ba b-----+-=g g =1a .变式1、.计算下列各式的值: (Ⅰ);(Ⅱ).【解析】(Ⅰ)原式=;(Ⅱ)原式=.变式2、已知1122x x-+=3,求22332223x x x x --+-+-的值.【解析】设12x =t ,则12x -=1t ,已知即t +1t =3.于是,3322x x -+=t 3+1t 3=⎝⎛⎭⎫t +1t ·⎝⎛⎭⎫t 2+1t 2-1, 而x 2+x-2=t 4+1t 4=2221()t t+-2, 将t +1t =3,平方得 t 2+1t 2+2=9,于是t 2+1t 2=7.从而,原式=⎝⎛⎭⎫t 2+1t 22-2⎝⎛⎭⎫t +1t ·⎝⎛⎭⎫t 2+1t 2-1-3=72-23×(7-1)-3=4715. 方法总结(1)指数幂的运算首先将根式、分数指数幂统一为分数指数幂,以便利用法则计算,这时要注意:①必须同底数幂相乘,指数才能相加;②运算的先后顺序. (2)当底数是负数时,先确定符号,再把底数化为正数.(3)运算结果不能同时含有根号和分数指数,也不能既有分母又含有负指数.考点二 对数的运算 例2 化简下列各式:(1)12lg 25+lg 2+lg 10+lg (0.01)-1; (2)(lg 2)2+lg 2·lg 50+lg 25;(3)计算(log 32+log 92)·(log 43+log 83); (4)2log 32-log 3329+log 38-3log 55;【解析】 (1)原式=lg ⎣⎡⎦⎤2512×2×1012×(10-2)-1 =lg ⎝⎛⎭⎫5×2×1012×102 =72lg10=72.(2) 原式=(lg 2)2+(1+lg 5)lg 2+lg 52=(lg 2+lg 5+1)lg 2+2lg 5 =(1+1)lg 2+2lg 5 =2(lg 2+lg 5) =2.(3) (log 32+log 92)·(log 43+log 83)=⎝⎛⎭⎫lg 2lg 3+lg 2lg 9·⎝⎛⎭⎫lg 3lg 4+lg 3lg 8 =⎝⎛⎭⎫lg 2lg 3+lg 22lg 3·⎝⎛⎭⎫lg 32lg 2+lg 33lg 2=3lg 22lg 3·5lg 36lg 2 =54.1(4)2log 32-log 3329+log 38-3log 55 =log 322+log 3(32×2-5)+log 323-3 =log 3(22×32×2-5×23)-3 =log 332-3 =2-3 =-1.变式1、(1)2log 32-log 3329+log 38-5log 35;(2)(log 2125+log 425+log 85)·(log 52+log 254+log 1258).【解析】(1)原式=2log 32-5log 32+2+3log 32-3=-1. (2)(方法1)原式=⎝⎛⎭⎫log 253+log 225log 24+log 25log 28 ⎝⎛⎭⎫log 52+log 54log 525+log 58log 5125=⎝⎛⎭⎫3log 25+2log 252log 22+log 253log 22⎝⎛⎭⎫log 52+2log 522log 55+3log 523log 55 =⎝⎛⎭⎫3+1+13log 25·3log 52 =13·log 55log 52·log 52 =13. (方法2)原式=⎝⎛⎭⎫lg 125lg 2+lg 25lg 4+lg 5lg 8⎝⎛⎭⎫lg 2lg 5+lg 4lg 25+lg 8lg 125=⎝⎛⎭⎫3lg 5lg 2+2lg 52lg 2+lg 53lg 2⎝⎛⎭⎫lg 2lg 5+2lg 22lg 5+3lg 23lg 5 =⎝⎛⎭⎫133·lg 5lg 2⎝⎛⎭⎫3·lg 2lg 5=13.变式2、(1)①若a =log 43,则2a +2-a = ;②化简2(lg 2)2+lg 2·lg 5+(lg 2)2-lg 2+1=__ _. 【解析】 (1)①∵a =log 43=22log 3=12log 23=log 23,∴2a +2-a=22-2-=3+log 2=3+33=433.②2(lg 2)2+lg 2·lg 5+(lg 2)2-lg 2+1 =2×⎝⎛⎭⎫12lg 22+12lg 2×lg 5+(lg 2-1)2=12lg 2(lg 2+lg 5)+1-12lg 2 =12lg 2+1-12lg 2=1.方法总结:对数的运算主要是要熟练掌握三条运算性质,不能把公式记错,当然也有一定的运算技巧,例如:(1)拆:首先利用幂的运算把底数或真数进行变形,化成分数指数幂的形式,使幂的底数最简,然后利用对数运算性质化简合并;(2)合:将对数式化为同底数的和、差、倍数运算,然后逆用对数的运算性质,转化为同底对数真数的积、商、幂的运算.考点三 指数是与对数式的综合例3 (1)已知a ,b ,c 均为正数,且3a=4b=6c,求证:2a +1b =2c ;(2)若60a =3,60b =5,求12(1)12a b b ---的值.【解析】 (1)设3a =4b =6c =k ,则k>1.由对数定义得a =log 3k ,b =log 4k ,c =log 6k , 则2a +1b =2log 3k +1log 4k =2log k 3+log k 4 =log k 9+log k 4 =log k 36.又2c =2log 6k =2log k 6=log k 36, ∴2a +1b =2c .(2)由a =log 603,b =log 605,得1-b =1-log 605=log 6012, 于是1-a -b =1-log 603-log 605=log 604,则有1-a -b 1-b =log 604log 6012=log 124, ∴121-a -b 2(1-b )=1212log 124 =12log 122=2.变式1、设2a=5b=m ,且1a +1b =2,则m 等于________.由2a =5b =m 得a =log 2m ,b =log 5m , ∴1a +1b =log m 2+log m 5=log m 10.∵1a +1b =2,∴log m 10=2,∴m 2=10,m =10.方法总结: 这是一道关于指数式与对数式的混合问题,求解这类问题,以下两点值得关注:1. 根据对数的定义,对数式与指数式能够相互转化,其解答过程体现了化归与转化的数学思想,其核心是化生为熟、化难为易、化繁为简,困难之处在于将指数由“高”降“低”,便于进一步计算,这是指、对数运算经常使用的方法.2. 不同底数的对数计算、化简与恒等证明的常用方法是利用换底公式,先将底数统一,再利用同底的对数的运算法则进行计算和化简,求得结果.五、优化提升与真题演练1、设a >0,将a 2a ·3a 2表示成分数指数幂,其结果是( )A .a 12B .a 56C .a 76D .a 32【答案】C 【解析】由题意a 2a ·3a 2=a 2-12-13=a 76.故选C.2、已知奇函数f (x )满足f (x )=f (x +4),当x ∈(0,1)时,f (x )=4x ,则f (log 4184)=( )A .B .C .D .【答案】A .【解析】∵奇函数f (x )满足f (x )=f (x +4), 当x ∈(0,1)时,f (x )=4x , ∴f (log 4184)=﹣f (log 4184﹣4) =﹣().3、(多选)已知实数a ,b 满足等式18a =19b ,下列选项有可能成立的是( ) A .0<b <a B .a <b <0 C .0<a <b D .b <a <0【答案】AB【解析】 实数a ,b 满足等式18a =19b ,即y =18x 在x =a 处的函数值和y =19x 在x =b 处的函数值相等,由下图可知A ,B 均有可能成立.4、化简:(a 23·b -1)-12·a -12·b 136a ·b 5(a >0,b >0)=________.1 【答案】1a【解析】原式=a -13·b 12·a -12·b 13a 16·b 56=a -13-12-16·b 12+13-56=1a .5、计算 3(1+2)3+ 4(1-2)4=________.【答案】2 2【解析】 3(1+2)3+ 4(1-2)4=1+2+|1-2|=2 2.6、.(1-log 63)2+log 62·log 618log 64=________.【答案】1【解析】原式=(log 66-log 63)2+log 62·log 618log 622=(log 62)2+log 62·log 6182log 62=log 62(log 62+log 618)2log 62=log 62·log 6(2×18)2log 62=log 62·log 6362log 62=2log 622log 62=1.7、若2x =3y =5z ,且x ,y ,z 都是正数,则2x ,3y ,5z 从小到大依次为. 【答案】3y<2x<5z.【解析】令2x =3y =5z =t ,则t>1,x =lg t lg 2,y =lg t lg 3,z =lg t lg 5,∴2x -3y =2lg t lg 2-3lg t lg 3=lg t·(lg 9-lg 8)lg 2·lg 3>0,∴2x>3y.同理可得:2x -5z<0,∴2x<5z.∴3y<2x<5z.8、 化简下列各式:(1)[(0.06415)-2.5]23-3338-π0;(2)56a 13·b -2·⎝ ⎛⎭⎪⎫-3a -12b -1÷⎝ ⎛⎭⎪⎫4a 23·b -312.1【解析】(1)原式=⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫⎣⎢⎡⎦⎥⎤⎝ ⎛⎭⎪⎫641 00015-5223-⎝ ⎛⎭⎪⎫27813-1 =⎣⎢⎡⎦⎥⎤⎝ ⎛⎭⎪⎫410315×⎝ ⎛⎭⎪⎪⎫-52×23-⎣⎢⎡⎦⎥⎤⎝ ⎛⎭⎪⎫32313-1 =52-32-1=0.(2)原式=-52a -16b -3÷⎝ ⎛⎭⎪⎫4a 23·b -312=-54a -16b -3÷(a 13b -32)=-54a -12·b -32 =-54·1ab 3=-5ab 4ab 2.。
2021高考数学考点精讲精练《08 指数、对数的运算》(讲解)(解析版)
考点8:指数、对数的运算【思维导图】【常见考法】考法一:指数运算1.化简2531433(2)(3)(4)a b a b a b -----⋅-÷(,0)a b >= 。
【答案】232b -【解析】依题意,原式()()25131423323342a b b -++----⋅-=⋅⋅=-.2.计算:(6+43-(0.2508) 【答案】109【解析】原式=(113223⨯)6+3443(2)⨯-1=22×33+2﹣1=108+2﹣1=109.3.计算:()(123121034310.02762563π4---⎛⎫-++-+ ⎪⎝⎭= 。
【答案】66 【解析】()(123121034310.02762563π4---⎛⎫-++-+ ⎪⎝⎭()1232312432343510.342123⨯⎛⎫⎛⎫⨯-⨯⎪⨯- ⎪⎝⎭⎝⎭⎛⎫=-++-+ ⎪⎝⎭105116413223=-++-+66= 4.已知1122x x -+=3,求33222223x xx x --++++的值为 .【答案】25【解析】解法一 ∵1122x x -+=3,∴两边平方,得(1122x x -+)2=9,即x +x -1=7.两边再平方得x 2+x -2=47,将等式1122x x -+=3两边立方,得3311222233x x x x --+++=27,即3322x x -+=18.∴原式=18224735+=+. 解法二 设12x =t ,则121xt-=,22113,7t t t t +=+=∴原式=23232424211112211323t t t t t t t t t t ⎛⎫⎛⎫++-+++ ⎪⎪⎝⎭⎝⎭=⎛⎫+++-+ ⎪⎝⎭=()3712249235⨯-+=-+.6.已知0a >,23xa =,求33x xx xa a a a--++的值为 。
. 【答案】73【解析】原式()()222211713133xx x x x x x xaa a a a a a a ----+-+==-+=-+=+.7.程4220x x --=的解为______.【答案】1x =【解析】设20x t =>,即转化为求方程220t t --=的正实数根由220t t --=得2t =或1t =-(舍)所以=22x t =,则1x =故答案为:1x =考法二:对数的运算1.= 。
(完整版)1实数指数幂及其运算--练习题
实数指数幕及其运算 日期: ___________ 姓名: 知识点1:整数指数幕
1•计算下列各式,并把结果化为只含正整数指数的形式(
指导教师: 陈婷婷
a,b均不为0) (1) 23 (2)
<24
(3) a3 (4)
2a 1 0
a3b3 2ab
a 3b2 3a2b 1
9a 2b 3
a b 0, a 知识点 1.计算: 2 :根式
(2) 3 FI 2 32
3
3 10.2 2 42
2. F列说法中正确的有: ②16的4次方根是 2 ;
3. 4. 5.
4 81
4a2 4a 1 2,则 x
化简下列各式:
2a,则实数 4x 4 3 x a的取值范围是
的值是
(3) 3 a 2 3 (4) :
a b 2
(6) n x n n ,n N ; (7)
刘
4a2 4a 1
知识点3 :分数指数幕 1.计算: 1 (1) 643 ;
1 (2) 32 5 ; 1 3 64 3 3
2. 用分数指数幕表示 3. 求下列各式的值:
(5) (6)
(3) ,( 2 83 100
0.25
2 1 2a3b2 1 1
6a%
0.5 27
9
0,y 16 81
a 5a
3
(1) 1 1002 (2) 2 83 ; (3) 3 1 4 ;
; 81
3 (4) 9 2 ;
(5) 0.008 (6) (7)
知识点 4:无理数指数幕 1.计算: 4 2 123 2 28
2.计算下列各式(式中字母均为正数)
6 (1) x 2y 3
; 2x 2 3y 3 2x 2 3y 3
知识点5:指数式的化简与计算 1.计算下列各式:
(1) 4 81
(2) 2-3 3 1.5 6 12 (3) x x3 y 1 y3 x x3
(5) 1 4、32 1 276 3
16
: 52
1 2 3.3
1乂 0 .
2.化简下列各式: _______ 3 4ab 1
4 2
3.计算: 知识点6:乘法运算在幕运算中的应用 1.已知 1 a2 1
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第1页共6页
指数运算
一、单选题(共10道,每道10分)
1.设,根据n次方根的意义,下列各式:①;②不一定等
于a;③n是奇数时,;④n是偶数时,,其中正确的有( )
A.①②③④ B.①③④
C.①②③ D.①②④
答案:A
解题思路:
试题难度:三颗星知识点:有理数指数幂的运算性质
2.计算的值是( )
A.B.
C.1 D.2
答案:C
解题思路:
故选C
第2页共6页
试题难度:三颗星知识点:根式与分数指数幂的互化及其化简运算
3.计算的值是( )
A.B.
C.6 D.
答案:C
解题思路:
故选C
试题难度:三颗星知识点:根式与分数指数幂的互化及其化简运算
4.的值为( )
A.B.
C.D.
答案:C
解题思路:
第3页共6页
故选C
试题难度:三颗星知识点:根式与分数指数幂的互化及其化简运算
5.设a>0,化简的结果是( )
A.a B.
C.D.
答案:C
解题思路:
故选C
试题难度:三颗星知识点:根式与分数指数幂的互化及其化简运算
6.可化简为( )
A.B.
C.D.
答案:D
