信号与系统作业作业1(第二章)答案
信号与系统 奥本海姆 中文答案 chapter 2

Chapter 22.1解:(a) 1[][][][0][][1][1][3][3]y n x n h n x h n x h n x h n =*=+-+-2[1]4[]2[1]2[2]2[4]n n n n n δδδδδ=+++-+---(图略)(b) 21[][2][][2]y n x n h n y n =+*=+2[3]4[2]2[1]2[]2[2]n n n n n δδδδδ=++++++--(图略)(c) 32[][][2][]y n x n h n y n =*+=(图略)2.5解:9[][][]k y n x k h n k ==-∑,由[4]5y =可知:4N ≥由[14]0y =可知:9114N ++≤,即:4N ≤ 所以:4N =2.11解:(a) 3t ≤时,()0y t =35t <≤时,3()(3)()(3)()ty t u t h t u h t d τττ=-*=--⎰3(3)3()313t tt e ed ττ-----==⎰5t >时,[]()63(5)53()31()(3)(5)()3t t e e y t t u t u h t e d ττ------=---*==⎰因此:()3(3)63(5)0,31(),3531,53t t t e y t t e e t -----⎧⎪≤⎪⎪-=<≤⎨⎪⎪-⎪>⎩(b )()(3)(5)dx t t t dtδδ=--- 3(3)3(5)()()()(3)(5)(3)(5)t t dx t g t h t h t h t e u t e u t dt----∴=*=---=---(c) ()()dy t g t dt=2.13解:(a) 将1[][]5n h n u n ⎛⎫= ⎪⎝⎭代入式子得:111[][1][]55n n u n A u n n δ-⎛⎫⎛⎫--= ⎪ ⎪⎝⎭⎝⎭即:()1[]5[1][]5nu n Au n n δ⎛⎫--= ⎪⎝⎭从而可得:51A =,即:15A = (b)由(a)可知:1[][1][]5h n h n n δ--= 则1S 的逆系统2S 的单位脉冲响应为:11[][][1]5h n n n δδ=--2.16解:(a)对。
信号与系统第2章作业解答

解:(1) f (t t0 ) (t) f (t0 ) (t)
(2) f (t t0 ) (t t0 )dt f (0)
(3) 2 et (t 3)dt e3 2 (t 3)dt e3
4
4
(4) et sin t (t 1)dt 0 0
第二章 连续时间信号的时域分析
2
n
(4) x1(n) x2 (n) 2n u(n) 3n u(n) 2k 3nk k 0
3n
n
( 2 )k
1 ( 2)n1 3n 3 [3n1 2n1]u(n)
k0 3
1 2
3
(5) x1(n) x2 (n) [(0.5)n u(n 4)][4nu(n 2)]
( 1)k u(k 4) 4nk u(n k 2) 2 k
P59 2.24 解: (2) f1 f3 r(t) r(t 1) r(t 2)
2r(t 1) 2r(t 2) 2r(t 3) r(t 2) r(t 3) r(t 4)
f1 f3
1
0
1
2
34
t
-1
r(t) 3r(t 1) 4r(t 2) 3r(t 3) r(t 4)
4
42
(2) (t 3)etdt e3
(3) (1 t)(t2 4)dt 5
(4) (t) sin 2t dt 2 (t) sin 2t dt 2
t
2t
第二章 连续时间信号的时域分析
6 / 11
P91 3.1 (5) (6) 解: 由题意知 x(n) 的波形如下图示
eatu(t) sin tu(t) a sin t cos t eat u(t) 1 a2
第二章 连续时间信号的时域分析
信号与系统课后习题与解答第二章
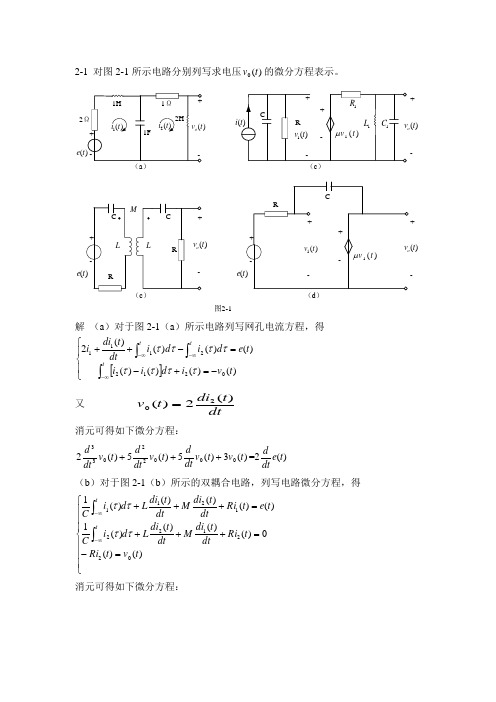
2-1 对图2-1所示电路分别列写求电压)(0t v 的微分方程表示。
2(t ei )(t +-(e )(e )(t +-图2-1解 (a )对于图2-1(a )所示电路列写网孔电流方程,得[]⎪⎩⎪⎨⎧-=+-=-++⎰⎰⎰∞-∞-∞-t t t t v i d i i t e d i d i dt t di i )()()()()()()()(202122111ττττττττ 又 dtt di t v )(2)(20= 消元可得如下微分方程:)(3)(5)(5)(200022033t v t v dt dt v dtd t v dt d +++=2)(te dt d(b )对于图2-1(b )所示的双耦合电路,列写电路微分方程,得⎪⎪⎪⎩⎪⎪⎪⎨⎧=-=+++=+++⎰⎰∞-∞-)()(0)()()()(1)()()()()(10221221211t v t Ri t Ri dt t di M dt t di L d i Ct e t Ri dtt di M dt t di L d i C ttττττ 消元可得如下微分方程:)()(1)(2)(2)(2)()(22020022203304422t e dtd MR t v C t v dt d C R t v dtd R R L t v dtd RL t v dt d M L =++⎪⎭⎫ ⎝⎛+++- (c )对于图2-1(c )所示电路列写电路方程,得⎪⎪⎩⎪⎪⎨⎧=⎥⎦⎤⎢⎣⎡+++=⎰∞-)()()(1)()()()(10101011t v t v dt d C dt t v L R t v R t v t v dt d C t i t μ 消元可得如下微分方程:)()(1)(1)()(101011022110331t i dt dR t v RL t v dt d R R L C t v dt d R C R C t v dt d CC μ=+⎪⎪⎭⎫ ⎝⎛++⎪⎪⎭⎫ ⎝⎛++ (d )对图2-1(d )所示电路列写电路方程,电流)(t i 如图2-2所示,得⎪⎪⎩⎪⎪⎨⎧==+=++⎰∞-)()()()()()()()(1)(1011t v t v t e t v t Ri t e t v d i C t Ri t μμττ 消元可得如下微分方程:(t e )(t +-图2-2)()(1)()1(00t e Rt v R t v dt d Cμμ=+-2-2 图2-3所示为理想火箭推动器模型。
信号与系统 梁风梅主编 电子工业出版社 ppt第二章答案

习题二2.1信号cos()t e wt σ可以表示为 st e 与 *s t e 之和,其中 s jw σ=+,*s jw σ=-, 粗略画出下列信号的波形,并在s 平面标出其频率位置。
(1)()cos(3)x t t =(2)3()cos(3)t x t e t -=(3)2()cos(3)t x t e t =(4)2()t x t e -=(5)3()t x t e =(6)()5x t =x (t )50t2.2粗略画出下列信号。
(1)()(3)(5)x t u t u t =---012345tx (t )1(2)()(3)(5)x t u t u t =-+-(3)2(){(3)(5)}x t t u t u t =--- x (t )902535t(4)()2(3)(5)(7)x t u t u t u t =-----2.3简化下列表达式(1)2sin ()()2t x t t t δ=+=0 (2)2()()9jw x jw ωδω+=+=2()9δω (3) ()()2sin 22()14t x t t t πδ⎧⎫-⎨⎬⎩⎭=-+=-1(1)5t δ- (4) sin()()()kw x t w wδ==k ()w δ 2.4 求下列积分(1)()()()x t x t d δτττ+∞-∞=-⎰=()()x t d δττ+∞-∞⎰=x(t) (2) ()()()x t x t d τδττ+∞-∞=-⎰=()()()x t t d x t δττ+∞-∞-=⎰ (3) 313()(23)sin()(23)sin()()222x t t t dt t dt t dt δπδπδ+∞+∞+∞-∞-∞-∞=-=-=--⎰⎰⎰=-12(4) ()()()1jwt x t t e dt t dt δδ+∞+∞-∞-∞===⎰⎰(5) ()(2)(3)(1)(3)(1)x t x t t dt x t dt x δδ+∞+∞-∞-∞=--=--=-⎰⎰(6) ()()()()t tjw x t e d d u t τδττδττ-∞-∞===⎰⎰(7) 3()(1)cos[(3)]sin[(3)]|0t x t t w t dt w w t δ+∞=-∞'=--=-=⎰(8)()(2)cos[(2)]cos[(2)](2)t tx t t w t dt w t d t δδ-∞-∞'=--=--=⎰⎰cos[(2)](2)|(2)cos[(2)]tt w t t t d w t δδ-∞-∞-----⎰1(2)sin[(2)]1tw t w t dt δ-∞=----=⎰2.5(1)求信号2()()t x t e u t -=的偶部与奇部2()()t x t e u t -=-偶部 {}{}2211()()(){()()}22t t Ev x t x t x t e u t e u t -=+-=+- 奇部{}{}2211{()}()()()()22t t Od x t x t x t e u t e u t -=--=--(2)2401|()|4t E x t dt e dt +∞+∞-∞-∞===⎰⎰ 总能量422220111|||()()|2448t t t E Ev dt e u t e u t dt e dt -+∞+∞+∞-∞-∞-∞==+-=⨯⨯=⎰⎰⎰偶部能量 422220111|||()()|2448t t t E Od dt e u t e u t dt e dt -+∞+∞+∞-∞-∞-∞==--=⨯⨯=⎰⎰⎰奇部能量 (3)由第二问可以得出信号的总能量等于其奇部与偶部能量之和。
信号与系统B第一、第二章习题d答案(2011-9-8)

信号与系统B第⼀、第⼆章习题d答案(2011-9-8)第⼀章1-1 判断下⾯的信号是否为周期信号,如果是,确定其基本周期。
)5cos(2)2cos()4()()42sin(4)2(t t t u t +-πππ解: (2)><=0100)(t t t u>-<=-0)42sin(400)()42sin(4t t t t u t ππππ不符合周期信号的定义,所以)()42sin(4t u t ππ-不是周期信号。
(4)52,12221πππ===T T ,π2521=T T 为⽆理数,所以)5cos(2)2cos(t t +π不是周期信号。
1-2 判断下⾯的序列是否为周期序列,如果是,确定其基本周期。
)6(cos )6(2k π解:N==?=Ω=Ω6322,300ππππ为有理数,所以)6(cos 2k π是周期序列,周期为620=Ω=πm N 。
1-6 判断下列信号是能量信号、还是功率信号或者都不是。
te32)3(-解:(3) ⾮周期信号[]∞==-=-====∞→-∞→--∞→--∞→--∞→-∞→?Tm i l T TT m i l T T T t m i l T T Tt m i l T TT tm i l T Tt f E 6666623232)(32)64(42)(∞=====∞→∞→∞→-∞→?36321)(21662Tm i l T T m i l T mi l T TTmi l T e T e ET dtt f TP由于能量E 和功率P 都不是有限值,所以信号2e -3t为⾮能量⾮功率信号。
⼀般来说,周期信号是功率信号,其平均功率可以在⼀个周期内计算。
属于能量信号的⾮周期信号称为脉冲信号,它在有限时间范围内有⼀定的数值,⽽当∞→t 时,数值为零;属于功率信号的⾮周期信号是当时∞→t 仍然为有限值的⼀类信号。
1-7 判断下列信号是能量信号、还是功率信号或者都不是。
信号与系统(杨晓非版)1-2-3章习题标准答案(1)

信号与系统习题解答1.12201lim|()|211lim 22lim |()|lim ()()P f t dt dt E f t dt dt f t t ττττττττττεττε→∞-→∞→∞→∞-======∞∴=⎰⎰⎰⎰总(1) f(t)=(t)解为功率信号。
()f t εε(2) f(t)=(t)-(t-1)解是矩形脉冲信号,故为能量信号。
()6()f t t t ε=(3)解:书中已作证明斜坡信号为非公非能信号。
0()2222222222()5|()|51P lim|()|1lim 2525lim|()|lim 25()j t T T T T f t e f t f t dtTdt TE f t dt dt f t ωϕττττττττ+→∞-→∞-→∞→∞--==∴======∞∴⎰⎰⎰⎰总(4)解为功率信号22222244200(24)(24)0()sin 2()lim |()|lim (sin 2)()1lim ()lim (2)(2)41()lim []4t t t j t j t t j t j tj t j t f t e t t f t dt e t dte e e dt e e e dt j e e dtττττττττττττε--→∞→∞------→∞→∞---+→∞===-==-+-=-+⎰⎰⎰⎰⎰总(5) 解:E(24)(24)01()lim[]|42424111()[1]42424124241()[1]44165lim 02()sin 2()j t j t t e e j j j j j j EP f t e t t ττττε---+→∞→∞-=----+=-+--+++-=--=+==∴=总为能量信号 221(6)()()11E lim ()lim (1)1lim()111lim 02()f t t tf t dt dt t E P f t ττττττττεττ→∞→∞--→∞→∞=+==+=-+=+==∴⎰⎰总总解:为能量信号1221()3cos(2)2cos()2()f t t t T T f t πωωπ=+==∴1.2 判断下列信号是否为周期信号,如果是周期信号,试确定其周期。
奥本海姆《信号与系统(第二版)》习题参考答案
2.23
解: x (t ) =
k = −∞
∑ δ (t − kT ) , y(t ) = x(t ) * h(t ) = x(t ) *
+∞
k = −∞
∑ δ (t − kT ) =
+∞
k = −∞
∑ x(t − kT )
+∞
(根据: x (t ) * δ (t − t 0 ) = x (t − t 0 ) ) 故: (a) T=4,则 y(t)为 x(t)以周期 4 做周期拓延;
第二章作业解答
2.1
解: (a)由多项式相乘法: x[n] = {1,2,0,−1}n =0,1, 2,3
h[n] = {2,0,2}n = −1, 0,1
1 2 0 -1 2 0 2 2 4 0 -2 2 4 0 -2 2 4 2 2 0 -2
定义域为:[0-1:3+1]=[-1,4] 即: y[n] = {2,4,2,2,0,−2}n = −1, 0,1, 2,3, 4 (b)由性质: (若 x[n] * h[n] = y[n], 则:x[n] * h[n − n0 ] = y[n − n0 ] )得:
1 τ
τ
t
(1) α ≠
β
0 t<0 ⎧ ⎪ y (t ) = x(t ) * h(t ) = ⎨ t − aτ − β ( t −τ ) e e dτ t>0 ⎪ ⎩∫0 t<0 ⎧0 = ⎨ − β t − (α − β ) t − 1] t > 0 ⎩e [e t<0 ⎧0 ⎪ −αt − βt = ⎨ e −e t>0 ⎪[ α − β ] ⎩ e −αt − e − βt =( )u (t ) β −α
信号与系统课后习题参考答案
信号与系统课后习题参考答案精心整理1-试分别指出以下波形是属于哪种信号?题图1-11-2试写出题1-1图中信号的函数表达式。
1-3已知信号)(1t x 与)(2t x 波形如题图1-3中所示,试作出下列各信号的波形图,并加以标注。
题图1-3⑴(1x ⑷2x ⑺1x 1-4 题图1-4⑴(1x ⑷2x ⑺1x 1-51-6⑴(t x 2⑶)8sin()]sin(1[)(t t t x ΩΩ+=⑷)2sin(1)(t t t x =1-7试画出下列信号的波形图:⑴)(1)(t u e t x t -+=⑵)]2()1([10cos )(---=-t u t u t e t x t π⑶)()2()(t u e t x t --=⑷)()()1(t u e t x t --= ⑸)9()(2-=t u t x ⑹)4()(2-=t t x δ1-8试求出以下复变函数的模与幅角,并画出模与幅角的波形图。
⑴)1(1)(2Ω-Ω=Ωj e j X ⑵)(1)(Ω-Ω-Ω=Ωj j e e j X ⑶Ω-Ω---=Ωj j e e j X 11)(4⑷21)(+Ω=Ωj j X1-9已知信号)]()([sin )(π--=t u t u t t x ,求出下列信号,并画出它们的波形图。
⑴)()()(221t x dtt x d t x +=⑵ττd x t x t ?∞-=)()(21-101-11⑴?∞-⑶?∞-⑸?∞-1-12⑴x 1⑶x 31-13⑴t y =)(⑶)2()(t x t y =⑷)1()1()(t x t x t y ---=⑸?∞-=2)()(t d x t y ττ⑹2()(n x n y =⑺)()(n nx n y =⑻)1()()(-=n x n x n y1-14如题图1-14中已知一线性时不变系统当输入为)(t x 时,响应为)(t y 。
试做出当输入为)(1t x 时,响应)(1t y 的波形图。
《信号与系统》课程习题与解答
《信号与系统》课程习题与解答第二章习题(教材上册第二章p81-p87)2-1,2-4~2-10,2-12~2-15,2-17~2-21,2-23,2-24第二章习题解答2-1 对下图所示电路图分别列写求电压的微分方程表示。
图(a):微分方程:11222012()2()1()()()2()()()()2()()()c cc di t i t u t e t dtdi t i t u t dtdi t u t dt du t i t i t dt ⎧+*+=⎪⎪⎪+=⎪⇒⎨⎪=⎪⎪⎪=-⎩图(b ):微分方程:⎪⎪⎪⎩⎪⎪⎪⎨⎧-==+++=+++⎰⎰2021'2'21'2'11)(01)(1Ri t v Ri Mi Li dt i Ct e Ri Mi Li dt i C)()(1)(2)()2()(2)()(33020022203304422t e dtd MR t v C t v dt d C R t v dt d C L R t v dt d RL t v dt d M L =+++++-⇒ 图(c)微分方程:dt i C i L t v ⎰==211'101)(⎪⎪⎪⎩⎪⎪⎪⎨⎧===⇒⎰dt t v L i t v L i dtdt v L i dt d)(1)(1)(10110'1122011∵ )(122111213t i dt d L C i i i i +=+=)(0(1]1[][101011022110331t e dt dR t v RL v dt d RR L C v dt d R C R C v dt d CC μ=+++++⇒图(d)微分方程:⎪⎩⎪⎨⎧+-=++=⎰)()()()()(1)()(11111t e t Ri t v t v dt t i C t Ri t e μRC v dt d 1)1(1+-⇒μ)(11t e V CR = ∵)()(10t v t v μ=)()(1)1(0'0t e R v t v R Cv v =+-⇒2-4 已知系统相应的其次方程及其对应的0+状态条件,求系统的零输入响应。
考研专业课郑君里版《信号与系统》第二章补充习题——附带答案详解
第二章 连续时间系统的时域分析1.已知连续时间信号1()e ()t f t u t -=和2()e ()t f t u t =-,求卷积积分12()()()f t f t f t =*,并画出()f t 的波形图。
解:1212()()()()()f t f t f t f t f d τττ∞-∞=*=-⎰反褶1()f τ得1()f τ-,右移t 得11[()]()f t f t ττ--=-,作出2()f τ图形及不同t 取值的1()f t τ-图形,由此可得:当0t ≤时,21()e e ee e 2ttt tt f t d d τττττ---∞-∞===⎰⎰当0t ≥时,0021()e e e e e 2t t t f t d d τττττ----∞-∞===⎰⎰综上,||111()e ()e ()e 222t t t f t u t u t --=-+=()f t 是个双边指数函数。
讨论:当1()f t 、2()f t 为普通函数(不含有()t δ、()t δ'等)时,卷积结果()f t 是一个连续函数,且()f t 非零取值区间的左边界为1()f t 、2()f t 左边界之和,右边界为1()f t 、2()f t 右边界之和,也就是说,()f t 的时宽为1()f t 、2()f t 时宽之和。
τttt2.计算题图2(a )所示函数)(1t f 和)(2t f 的卷积积分)()()(21t f t f t f *=,并画出)(t f 的图形。
解法一:图解法1212()()()()()f t f t f t f t f d τττ∞-∞=*=-⎰其中1()f t τ-的波形见题图2(b),由此可得: 当10t +≤,即1t ≤-时,()0f t = 当011t ≤+≤,即10t -≤≤时,120()2(1)t f t d t ττ+==+⎰当11t +≥但10t -≤,即01t ≤≤时,1()21f t d ττ==⎰当011t ≤-≤,即12t ≤≤时,121()21(1)t f t d t ττ-==--⎰当11t -≥,即2t ≥时,()0f t =综上,220,1,2(1),10()1,011(1),12t t t t f t t t t ≤-≥⎧⎪+-≤≤⎪=⎨≤≤⎪⎪--≤≤⎩ ()f t 波形见题图2(c)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
信号与系统作业作业1(第二章)
答案
中国传媒大学 远程教育 信号与系统 第二章作业解答
1
第二章 作业答案
2–1 已知描述某LTI连续系统的微分方程和系统的初始状态如下,试
求此系统的零输入响应。
(1))()(2)(2)(3)(tetetytyty
2)0(y,1)0(y
解:
根据微分方程,可知
特征方程为:
0)2)(1(0232
所以,其特征根为: 1,221
所以,零输入响应可设为:0)(221teCeCtyttzi
又因为 3112)0(2)0(212121CCCCyCCy
所以,03)(2teetyttzi
(2))(2)()(6)(5)(tetetytyty
1)0()0(yy
。
解:
根据微分方程,可知
特征方程为:
0)3)(2(0652
所以,其特征根为: 3,221
中国传媒大学 远程教育 信号与系统 第二章作业解答
2
所以,零输入响应可设为:0)(3221teCeCtyttzi
又因为 34132)0(1)0(212121CCCCyCCy
所以,034)(32teetyttzi
2–2 某LTI连续系统的微分方程为)(3)()(2)(3)(tetetytyty
已知1)0(y,2)0(y,试求:
(1) 系统的零输入响应)(tyzi;
(2) 输入)()(tte时,系统的零状态响应)(tyzs和全响应)(ty。
解:
(1)根据微分方程,可知
特征方程为:
0)2)(1(0232
所以,其特征根为: 1,221
所以,零输入响应可设为:0)(221teCeCtyttzi
又因为 4322)0(1)0(212121CCCCyCCy
所以,034)(2teetyttzi
(2) 可设零状态响应为:
0)(221tpeCeCty
txt
xzs
其中p 为特解,由激励信号和系统方程确定。
中国传媒大学 远程教育 信号与系统 第二章作业解答
3
因为)()(tte 所以,p 为常数,根据系统方程可知,23p 。
于是,
零状态响应可设为为:
023)(221teCeCty
txt
xzs
将上式代入原方程中,比较方程两边的系
数,可得到
22121C
C
所以,023221)(2teetyttzs
全响应为 )()()(tytytyzszi
0)23221()34()(22teeeety
tttt
zs
0)23252()(2teety
tt
zs
2–3 试求下列各LTI系统的冲激响应和阶跃响应。
(1))(2)()(3)(4)(tetetytyty
解:
根据 在激励信号为)(t的条件下,求解系统的零状态响应可得
)(21)(3teethtt
因为,单位阶跃响应tdhtg0)()(
中国传媒大学 远程教育 信号与系统 第二章作业解答
4
所以,tdeetg0321)(
0),1(61)1(2161216030teeee
tt
tt
0,6121326tee
tt
(2))(2)(2)()(2)(3)("tetetetytyty
解:
可先求系统 )()(2)(3)("tetytyty 的冲激励响应)(0th,
则,原系统的冲激响应为)(2)(2)()(0'0"0thththth。
因为)()(2)(3)("tetytyty的特征根为:1,221
所以,可设冲激响应为:)()()(2210teCeCthtt
将)(0th代入系统方程,并确定待定系数后,可得:
)()()(20teethtt
因为,)(2)(2)()(0'0"0thththth
又因为,)()2()(2'0teethtt,)()4()()(2"0teetthtt
所以,
)()(2)()2(2)()4()()(222teeteeteetthtttttt
)()2()(2teettt
因为,单位阶跃响应tdhtg0)()(
中国传媒大学 远程教育 信号与系统 第二章作业解答
5
所以,tttdteettg02)()(2)()(
)(212teett
2–4 各信号的波形如题2–4图所示,试计算下列卷积,并画出其波形。
(1))()(21tftf (2))()(31tftf
(3))()(24tftf (4))()(34tftf
题2–4 图
解:
根据 )()()(00ttftttf,可方便地得到此题的卷积结果。
(1)
(2)
中国传媒大学 远程教育 信号与系统 第二章作业解答
6
(3)
(4)
2–5 已知某LTI连续系统的冲激响应)(th和各激励信号)(te的波形如题
2–5图所示,试求此系统对激励信号的零状态响应。
题2–5图
解:
因为,)()()(thtetyzs
中国传媒大学 远程教育 信号与系统 第二章作业解答
7
所以,)2()()2()()(tttttyzs
)2()2()2()()()2()()(tttttttt
)4()4()2()2(2)(tttttt
2–6 题2–6图所示系统是由几个子系统组合而成的,各子系统的冲激响
应分别为
)()(1tth,)1()(2tth
,)1()(3tth
试求总系统的冲激响应)(th并画出其波形。
题2–6图
解: 根据系统框图,可得:
)()()()()(1321ththththth
)()1()1()(tttt
)()2()(ttt
)2()2()(tttt
此系统的单位冲激响应的波形为:
中国传媒大学 远程教育 信号与系统 第二章作业解答
8
2–7 题2–7图所示系统是由几个子系统组合而成,各子系统的冲激响应
分别为
)1()(1tth,)3()1()(2ttth
试求总系统的冲激响应)(th并画出其波形。
题2–7图
解:根据系统框图,可得:
)()()()()()(2111ththththtth
)3()1()1()1()1()(tttttt
)3()1()2()1()(ttttt
)5()3()4()2()3()1(tttttt
)5()4()2()1(tttt
此系统的单位冲激响应的波形为:
中国传媒大学 远程教育 信号与系统 第二章作业解答
9
