第四章 一次函数周周测2(4.3)
八年级数学下学期第四章一次函数章节测试(人教版)
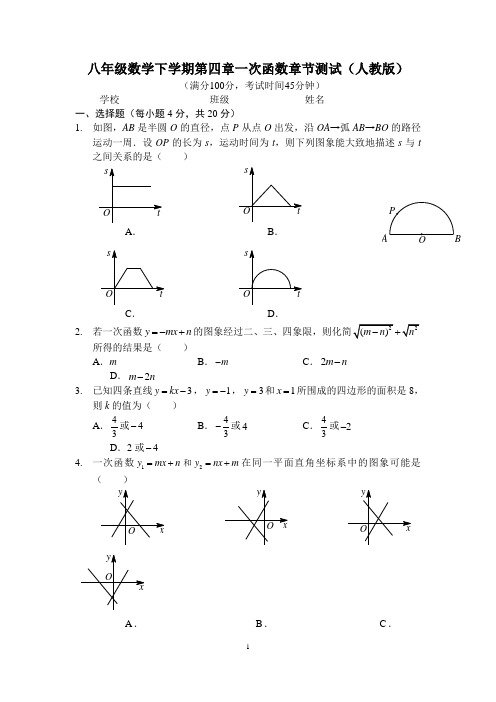
八年级数学下学期第四章一次函数章节测试(人教版)(满分100分,考试时间45分钟)学校________________ 班级_____________ 姓名________________ 一、选择题(每小题4分,共20分)1. 如图,AB 是半圆O 的直径,点P 从点O 出发,沿OA →弧AB →BO 的路径运动一周.设OP 的长为s ,运动时间为t ,则下列图象能大致地描述s 与t 之间关系的是( )A .B .C .D .2. 若一次函数y mx n =-+所得的结果是( ) A .m B .m - C .2m n - D .2m n -3. 已知四条直线3y kx =-,1y =-,3y =和1x =所围成的四边形的面积是8,则k 的值为( )A .43或4-B .43-或4C .43或2-D .2或4- 4. 一次函数1y mx n =+和2y nx m =+在同一平面直角坐标系中的图象可能是( )A .B .C .D .5. 某物流公司的快递车和货车同时从甲地出发,以各自的速度匀速向乙地行驶.快递车到达乙地后卸完物品再另装货物共用45分钟,然后立即按原路以另一速度匀速返回,直至与货车相遇.已知货车的速度为60千米/小时,两车之间的距离y (千米)与货车行驶的时间x (小时)之间的函数关系如图所示.给出以下4个结论:①快递车从甲地到乙地的速度为100千米/小时; ②甲、乙两地之间的距离为120千米;③图中点B 的坐标为(334,75);④快递车从乙地返回时的速度为90千米/小时. 其中正确的是( ) A .①②③ B .②③④ C .①③④ D .①③ 二、填空题(每小题4分,共20分)6. 若一次函数4y ax =+与2y bx =-的图象在x 轴上相交于同一点,则ba的值为_________.7. 已知直线y kx b =+平行于直线34y x =+,且过点(1,2-),则将直线y kx b =+向下平移3个单位得到的直线是______________________.8. 已知点A (0,3),B (4,1),P 为x 轴上一动点,则当AP BP +的值最小时,点P 的坐标为____________________.9. 如图,直线1y kx b =+经过点A (1-,2-)和点B (2-,0),直线22y x =经过点A ,则当12y y <时,x 的取值范围是____________________.第9题图 第10题图10. 如图,在平面直角坐标系xOy 中,长方形纸片ABCO 的顶点A ,C 分别在x______________________.三、解答题(本大题共5小题,满分60分)11. (8分)如图1,动点P 以2cm/s 的速度沿B →C →D →E →F →A 的路径匀速运动,相应的△ABP 的面积S 与时间t 之间的函数关系如图2所示,若AB =6cm ,试回答下列问题.(1)如图1,BC 的长为____________,多边形ABCDEF 的面积为____________;(2)如图2,a 的值为____________,b 的值为____________.图2图1ABCDEF12. (9分)如图,已知直线l 1:23y x =+,直线l 2:5y x =-+,直线l 1,l 2分别交x 轴于B ,C 两点,l 1,l 2相交于点A . (1)求A ,B ,C 三点的坐标;(2)求△ABC 的面积.13. (11分)星期天8:00~8:30,燃气公司给平安加气站的储气罐注入天然气,注完气之后,一位工作人员以每车20米3的加气量,依次给在加气站排队等候的若干辆车加气.储气罐中的储气量y (米3)与时间x (小时)之间的函数关系如图所示.(1)8:00~8:30,燃气公司向储气罐注入了_________米3的天然气;(2)当x ≥8.5时,求储气罐中的储气量y (米3)与时间x (小时)之间的函数关系式;(3)正在排队等候的20辆车加完气后,储气罐内还有天然气多少立方米?这20辆车在当天9:00之前能加完气吗?请说明理由.小时14. (16分)一辆客车从甲地开往乙地,一辆出租车从乙地开往甲地,两车同时出发,设客车离甲地的距离为y 1 km ,出租车离甲地的距离为y 2 km ,两车行驶的时间为x h ,y 1,y 2关于x 的函数图象如图1所示. (1)根据图象,直接写出y 1,y 2关于x 的函数关系式.(2)若两车之间的距离为s km ,求s 关于x 的函数关系式,并在图2中画出其函数图象.(3)甲、乙两地间有A ,B 两个加油站,相距200 km ,若客车进入A 加油站时,出租车恰好进入B 加油站,求A 加油站离甲地的距离.图1图215. (16分)B 岛位于自然环境优美的西沙群岛,盛产多种鱼类.A 港、B岛、C港依次在同一条直线上,一渔船从A港出发经由B岛向C港航行,航行2小时后发现鱼群,于是渔船匀速缓慢向B港方向前行打渔.在渔船出发1小时后,一艘快艇由C港出发,经由B岛匀速前往A港运送物资.当快艇到达B岛时渔船恰好打渔结束,渔船又以原速经由B岛到达C港.下面是两船离B港的距离y(海里)与渔船航行的时间x(小时)之间的函数图象,结合图象回答下列问题.(1)请直接写出m,a的值.(2)求线段MN的解析式,并写出自变量的取值范围.(3)渔船出发多长时间两船相距10海里?。
北师大版八年级数学上册第四章周周清4.1-4.4(含答案)

一次函数周周清(4.1-4.4)一、选择题(每小题4分,共28分)1.下列函数:①y =πx ;①y =2x -1;①y =1x ;①y =2-1-3x ;①y =x 2-1中,是一次函数的有( )A .4个B .3个C .2个D .1个2.已知A ,B 两地相距3千米,小黄从A 地到B 地,平均速度为4千米/小时,若用x 表示行走的时间(小时),y 表示余下的路程(千米),则y 关于x 的函数表达式是()A .y =4x(x≥0)B .y =4x -3(x≥34 ) C .y =3-4x(x≥0) D .y =3-4x(0≤x≤34 )3.已知正比例函数y =(k +5)x ,且y 随x 的增大而减小,则k 的取值范围是( ) A .k >5 B .k <5 C .k >-5 D .k <-54.已知点A(x 1,y 1)和点B(x 2,y 2)是一次函数y =(k 2+1)x +2图象上的两点,且x 1>x 2,则y 1和y 2的大小关系是( )A .y 1<y 2B .y 1=y 2C .y 1>y 2D .不确定5.一次函数y =kx -1的图象经过点P ,且y 的值随x 值的增大而增大,则点P 的坐标可以为( )A .(-5,3)B .(1,-3)C .(2,2)D .(5,-1)6.点P 位于y 轴左侧,x 轴上方,距y 轴3个单位,距x 轴4个单位,则点P 的坐标为( )A .(3,-4)B .(-3,4)C .(4,-3)D .(-4,3)7.已知一次函数y =2x +a 与y =-x +b 的图象都经过A(-2,0),且与y 轴分别交于B ,C 两点,则①ABC 的面积为( )A.4 B.5 C.6 D.7二、填空题(每小题5分,共25分)8.如果正比例函数y=(k-3)x的图象经过第一、三象限,那么k的取值范围是____.9.若一次函数y=mx+|m-1|的图象过点(0,3),且y随x的增大而增大,则m 的值为____.10.若函数y=(m+1)x2-m2是正比例函数,则其图象经过第____象限.11.一个长为100 m,宽为80 m的长方形场地要扩建成一个正方形场地,设长增加x m,宽增加y m,则y与x的函数关系式是____,自变量的取值范围是____.12.已知点(a,4)在连接点(0,8)和点(-4,0)的线段上,则a=____.三、解答题(共47分)13.(8分))已知一次函数y=ax+b.(1)当点P(a,b)在第二象限时,直线y=ax+b经过哪几个象限?(2)如果ab<0,且y随x的增大而增大,则函数的图象不经过哪些象限?14、(11分)科学研究发现,空气含氧量y(克/立方米)与海拔高度x(米)之间近似地满足一次函数关系,经测量,在海拔高度为0米的地方,空气含氧量约为299克/立方米;在海拔高度为2 000米的地方,空气含氧量约为235克/立方米.(1)求出y与x的函数关系式;(2)已知某山的海拔高度为1 200米,请你求出该山山顶处的空气含氧量约为多少?15.(13分)某通讯公司手机话费收费有A套餐(月租费15元,通话费每分钟0.1元)和B套餐(月租费0元,通话费每分钟0.15元)两种.设A套餐每月话费为y1(元),B套餐为y2(元),月通话时间为x分钟.(1)分别表示出y1与x,y2与x的函数关系式;(2)月通话时间多长时,A,B两种套餐收费一样?(3)什么情况下A套餐更省钱?16.(15分)某学校的复印任务原来由甲复印社承接,其收费y(元)与复印页数x(页)的关系如下表:(1)已知y与x满足一次函数关系,求该函数的表达式;(2)现在乙复印社表示:若学校每月先付200元的承包费,则可按每页0.15元收费,则乙复印社每月收费y(元)与复印页数x(页)之间的函数表达式为____;(不需要写出自变量的取值范围)(3)在如图所示的直角坐标系内画出(1)(2)中的函数图象,并回答每月复印页数在1 200页左右时,选择哪个复印社更合算.一次函数周周清(4.1-4.4)参考答案一、选择题(每小题4分,共28分)1.下列函数:①y =πx ;①y =2x -1;①y =1x ;①y =2-1-3x ;①y =x 2-1中,是一次函数的有( B )A .4个B .3个C .2个D .1个2.已知A ,B 两地相距3千米,小黄从A 地到B 地,平均速度为4千米/小时,若用x 表示行走的时间(小时),y 表示余下的路程(千米),则y 关于x 的函数表达式是(D )A .y =4x(x≥0)B .y =4x -3(x≥34 ) C .y =3-4x(x≥0) D .y =3-4x(0≤x≤34 )3.已知正比例函数y =(k +5)x ,且y 随x 的增大而减小,则k 的取值范围是( D ) A .k >5 B .k <5 C .k >-5 D .k <-54.已知点A(x 1,y 1)和点B(x 2,y 2)是一次函数y =(k 2+1)x +2图象上的两点,且x 1>x 2,则y 1和y 2的大小关系是( C )A .y 1<y 2B .y 1=y 2C .y 1>y 2D .不确定5.一次函数y =kx -1的图象经过点P ,且y 的值随x 值的增大而增大,则点P 的坐标可以为( C )A .(-5,3)B .(1,-3)C .(2,2)D .(5,-1)6.点P 位于y 轴左侧,x 轴上方,距y 轴3个单位,距x 轴4个单位,则点P 的坐标为( B )A.(3,-4) B.(-3,4)C.(4,-3) D.(-4,3)7.已知一次函数y=2x+a与y=-x+b的图象都经过A(-2,0),且与y轴分别交于B,C两点,则①ABC的面积为( C )A.4 B.5 C.6 D.7二、填空题(每小题5分,共25分)8.如果正比例函数y=(k-3)x的图象经过第一、三象限,那么k的取值范围是k >3.9.若一次函数y=mx+|m-1|的图象过点(0,3),且y随x的增大而增大,则m 的值为4.10.若函数y=(m+1)x2-m2是正比例函数,则其图象经过第__一、三__象限.11.一个长为100 m,宽为80 m的长方形场地要扩建成一个正方形场地,设长增加x m,宽增加y m,则y与x的函数关系式是__y=20+x__,自变量的取值范围是__x≥0__.12.已知点(a,4)在连接点(0,8)和点(-4,0)的线段上,则a=__-2__.三、解答题(共47分)13.(8分))已知一次函数y=ax+b.(1)当点P(a,b)在第二象限时,直线y=ax+b经过哪几个象限?(2)如果ab<0,且y随x的增大而增大,则函数的图象不经过哪些象限?解:(1)∵点P(a,b)在第二象限,①a<0,b>0,①直线y=ax+b经过第一、二、四象限(2)∵y随x的增大而增大,①a>0,又∵ab<0,①b<0,①一次函数y=ax+b的图象不经过第二象限14、(11分)科学研究发现,空气含氧量y(克/立方米)与海拔高度x(米)之间近似地满足一次函数关系,经测量,在海拔高度为0米的地方,空气含氧量约为299克/立方米;在海拔高度为2 000米的地方,空气含氧量约为235克/立方米.(1)求出y与x的函数关系式;解:设一次函数关系式为y=kx+b,由题意,得b=299,当x=2 000时,y=235,代入得235=2 000k+299,解得k=-4125,所以一次函数关系式为y=-4125x+299.(2)已知某山的海拔高度为1 200米,请你求出该山山顶处的空气含氧量约为多少?解:把x=1 200代入y=-4125x+299得y=-4125×1 200+299,解得y=260.6.所以该山山顶处的空气含氧量约为260.6克/立方米.15.(13分)某通讯公司手机话费收费有A套餐(月租费15元,通话费每分钟0.1元)和B套餐(月租费0元,通话费每分钟0.15元)两种.设A套餐每月话费为y1(元),B套餐为y2(元),月通话时间为x分钟.(1)分别表示出y1与x,y2与x的函数关系式;(2)月通话时间多长时,A,B两种套餐收费一样?(3)什么情况下A套餐更省钱?解:(1)y1=0.1x+15,y2=0.15x(2)由y1=y2得0.1x+15=0.15x,解得x=300,即月通话时间为300分钟时,A,B两种套餐收费一样(3)当通话时间多于300分钟时,A套餐更省钱16.(15分)某学校的复印任务原来由甲复印社承接,其收费y(元)与复印页数x(页)的关系如下表:(1)已知y与x满足一次函数关系,求该函数的表达式;(2)现在乙复印社表示:若学校每月先付200元的承包费,则可按每页0.15元收费,则乙复印社每月收费y(元)与复印页数x(页)之间的函数表达式为__y=0.15x+200__;(不需要写出自变量的取值范围)(3)在如图所示的直角坐标系内画出(1)(2)中的函数图象,并回答每月复印页数在1 200页左右时,选择哪个复印社更合算.解:(1)y=0.4x(3)画函数图象如图所示,由图象可知,当每月复印页数在1 200页左右时,应选择乙复印社更合算。
19.新人教版七年级数学上册第四章 几何图形初步周周测 2(4.3)周周练
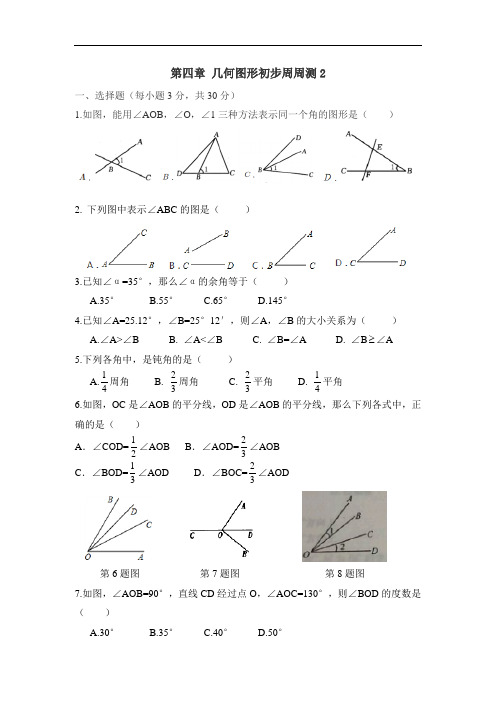
第四章几何图形初步周周测2一、选择题(每小题3分,共30分)1.如图,能用∠AOB,∠O,∠1三种方法表示同一个角的图形是()2.下列图中表示∠ABC的图是()3.已知∠α=35°,那么∠α的余角等于()A.35°B.55°C.65°D.145°4.已知∠A=25.12°,∠B=25°12′,则∠A,∠B的大小关系为()A.∠A>∠BB. ∠A<∠BC. ∠B=∠AD. ∠B ∠A5.下列各角中,是钝角的是()A.14周角 B.23周角 C.23平角 D.14平角6.如图,OC是∠AOB的平分线,OD是∠AOB的平分线,那么下列各式中,正确的是()A.∠COD=12∠AOB B.∠AOD=23∠AOBC.∠BOD=13∠AOD D.∠BOC=23∠AOD第6题图第7题图第8题图7.如图,∠AOB=90°,直线CD经过点O,∠AOC=130°,则∠BOD的度数是()A.30°B.35°C.40°D.50°8.如图,若∠1=∠2,则下列结论正确的是()A.OB平分∠AOCB.OB,OC是∠AOD的三等分线C.∠AOC=∠BODD.∠AOD=3∠BOC9.如图,在锐角内部,画1条射线,可得3个锐角;画2条不同射线,可得5个锐角;画3条不同射线,可得10个锐角;······照此规律,画10条不同射线,可得锐角()个.A.63个B.66个C.72个D.80个10.如图,已知O为直线AB上一点,OC平分∠AOD,∠BOD=3∠DOE,∠COE=α,则∠BOE的度数是()A.αB.180°—2αC.360°—4αD.2α—60°二、填空题(每小题3分,共18分)11.当时间为8时30分时,钟表的时针和分针所成的角的度数是12.一个角的补角是130°,则这个角的余角是度13.如图,已知∠AOB是直角,∠AOC是∠COB的3倍,则∠COB是度第13题图第14题图14.将长方形的纸ABCD沿AE折叠,得到如图所示的图形,已知∠CED′=50°,则∠AED的度数为15.有公共顶点的两条射线分别表示偏东15°与北偏东25°,则这两条射线组成的角度的度数是16.线段AB=20cm,AO=PO=2cm,∠POQ=60,现点P绕着点O以30°/s的速度顺时针旋转一周后停止,同时Q沿线段BA自B点向A点运动,若点P,Q 两点也能相遇,则点Q运动的速度可能是三、解答题(共8题,共72分)17.(8分)计算:(1)90°—35°41′;(2)15°36′18″ 618.(8分)如图,已知∠AOB=65°,∠AOC=15°,OD是∠BOC的平分线,求∠BOD的度数.19.(8分)如图,已知∠BOC=2∠AOB,OD平分∠AOC,∠BOD=14°,求∠AOB的度数.20.(8分)如图,∠AOB是直角,OD平分∠BOC,OE平分∠AOC,求∠EOD的度数.21.(8分)如图,OA的方向是北偏东15°,OB的方向是西偏北50°.(1)若∠AOC=∠AOB,则OC的方向是北偏东______;(2)OD是OB的反向延长线,OD的方向是南偏东______;(3)∠BOD可看作是OB绕点O逆时针方向至OD,作∠BOD的平分线OE,OE的方向是南偏西______;(4)在(1)、(2)、(3)的条件下,∠COE度数的度数是______.22.(10分)如图1,将两块直角三角尺的直角顶点C叠放在一起,(1)若∠DCE=35°,∠ACB=______;若∠ACB=140°,则∠DCE=______;(2)猜想∠ACB与∠DCE有何数量关系,并说明理由;(3)如图2,若是两个同样的直角三角尺60°锐角的顶点A重合在一起,则∠DAB与∠CAE又有何数量关系,请说明理由.23.(10分)如图1 ,∠AOC=2∠BOC,∠AOC的余角比∠BOC小30°.(1)求∠COB的度数;(2)经过点O作射线OD,使得∠AOC=4∠AOD,求∠BOD的度数(请利用图1完成);(3)如图2,在∠AOB的内部作∠EOF,OM、ON分别平分∠AOE,∠BOF,当∠EOF绕点O在∠AOB的内部转动时,请证明:∠AOB+∠EOF=2∠MON.24.(12分)如图1,已知∠AOB=70°,∠COD=40°,OM平分∠BOD,ON 平分∠AOC.(1)若∠COD可以在∠AOB内部绕O点任意旋转,则∠MON的大小是否改变?若不变请说明原因,并求出∠MON的度数;(2)如图2,当∠COD的一边射线OC与∠AOB的一边射线OA重合时,∠COD绕O点逆时针旋转x度(0°<x<40°),其他条件不变,请完成图3,并求出∠MON的度数;(3)如图4,若线段CD在线段AB上任意移动,点N,M分别平分线段AC,BD.请根据上题方法直接写出线段AB,CD,MN之间的数量关系初中数学公式大全1 过两点有且只有一条直线2 两点之间线段最短3 同角或等角的补角相等4 同角或等角的余角相等5 过一点有且只有一条直线和已知直线垂直6 直线外一点与直线上各点连接的所有线段中,垂线段最短7 平行公理经过直线外一点,有且只有一条直线与这条直线平行8 如果两条直线都和第三条直线平行,这两条直线也互相平行9 同位角相等,两直线平行10 内错角相等,两直线平行11 同旁内角互补,两直线平行12 两直线平行,同位角相等13 两直线平行,内错角相等14 两直线平行,同旁内角互补15 定理三角形两边的和大于第三边16 推论三角形两边的差小于第三边17 三角形内角和定理三角形三个内角的和等于180 °18 推论1 直角三角形的两个锐角互余19 推论2 三角形的一个外角等于和它不相邻的两个内角的和20 平行四边形判定定理 1 两组对角分别相等的四边形是平行四边形21 平行四边形判定定理 2 两组对边分别相等的四边形是平行四边形22 平行四边形判定定理 3 对角线互相平分的四边形是平行四边形23 平行四边形判定定理 4 一组对边平行相等的四边形是平行四边形24 矩形性质定理 1 矩形的四个角都是直角25 矩形性质定理 2 矩形的对角线相等26 矩形判定定理 1 有三个角是直角的四边形是矩形27 矩形判定定理 2 对角线相等的平行四边形是矩形28 菱形性质定理 1 菱形的四条边都相等29 菱形性质定理 2 菱形的对角线互相垂直,并且每一条对角线平分一组对角30 菱形面积= 对角线乘积的一半,即S= (a×b )÷231 菱形判定定理1 四边都相等的四边形是菱形32 菱形判定定理2 对角线互相垂直的平行四边形是菱形33 正方形性质定理1 正方形的四个角都是直角,四条边都相等34 正方形性质定理 2 正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角35 定理1 关于中心对称的两个图形是全等的36 定理2 关于中心对称的两个图形,对称点连线都经过对称中心,并且被对称中心平分37 逆定理如果两个图形的对应点连线都经过某一点,并且被这一点平分,那么这两个图形关于这一点对称38 等腰梯形性质定理等腰梯形在同一底上的两个角相等。
第四章 一次函数周周测5(4.4) 专题配套练习

第四章一次函数周周测5一、选择题1.函数y=x的图象与函数y=2x+1的图象的交点坐标是()A.(1,1)B.(0,0)C.(,)D.(-,-)2.若某正比例函数图象经过点(-2,3),则该正比例函数的解析式为()A.y=xB.C.D.y=6x3.当k•b<0时,一次函数y=kx-b的图象大致是()A. B. C. D.4.一次函数y=kx+b,经过(1,1),(2,-4),则k与b的值为()A. B. C. D.5.已知一次函数y=-2x+3,则与该一次函数的图象关于x轴对称的一次函数的表达式为()A.y=2x-3B.y=-2x-3C.y=2x+3D.y=-2x+36.一次函数y=x+2的图象不经过的象限是()A.一B.二C.三D.四7.一次函数y=-3x+1的图象一定经过点()A.(2,-5)B.(1,0)C.(-2,3)D.(0,-1)8.一次函数y=-2x-3的图象与y轴的交点坐标是()A.(3,0)B.(0,3)C.(-3,0)D.(0,-3)9.已知一次函数y=kx+1的图象过点(1,3),则k的值为()A.1B.2C.-1D.10.一次函数y=ax-b,若a+b=-1,则它的图象必经过点()A.(1,1)B.(-1,1)C.(1,-1)D.(-1,-1)11.已知一次函数y=mx-(m-2)过原点,则m的值为()A.m>2B.m<2C.m=2D.不能确定12.一次函数y=-4x-2的截距是()A.4B.-4C.2D.-213.若y=m+m是一次函数,则m的值等于()A.0B.-1C.0或-1D.±114.已知一次函数y=kx+b,当x增加2时,y减小5,则k的值是()A.-2.5B.-0.4C.2.5D.0.415.如图,过点A的一次函数的图象与正比例函数y=2x的图象相交于点B,能表示这个一次函数的解析式为()A.2x-y+3=0B.x-y-3=0C.2y-x+3=0D.x+y-3=0二、解答题16.已知一次函数的图象如图,求这个一次函数的解析式.17.已知一次函数y=kx+b的图象经过点(2,-5)和(6,1),求这个一次函数的解析式.18.已知一次函数图象经过(3,5)和(-4,-9)两点,(1)求此一次函数解析式;(2)若点(a,-3)在此函数图象上,求a的值.19.正比例函数y=kx和一次函数y=ax+b的图象都经过点A(1,2),且一次函数的图象交x轴于点B(4,0).求正比例函数和一次函数的表达式.20.如图,正比例函数y=2x的图象与一次函数y=kx+b的图象交于点A(m,2),一次函数图象经过点B(-2,-1)与x轴的交点为C.(1)求一次函数的解析式;(2)求△AOC的面积.第二章实数周周测11.在﹣0.101001,,0中,无理数的个数有()A.1个B.2个C.3个D.4个2.有下列说法:(1)无理数就是开方开不尽的数;(2)无理数是无限不循环小数;(3)无理数包括正无理数、零、负无理数;(4)无理数都可以用数轴上的点来表示.其中正确的说法的个数是()A.1 B.2 C.3 D.43.下列实数中,属于有理数的是()A.B.C.πD.4.立方根等于它本身的有()A.-1,0,1B.0,1C.0,-1D.15.给出下列说法:①是的平方根;②的平方根是;③;④是无理数;⑤一个无理数不是正数就是负数.其中,正确的说法有()A.①③⑤B.②④C.①③D.①6.有下列说法,其中正确说法的个数是()(1)无理数就是开方开不尽的数;(2)无理数是无限不循环小数;(3)无理数包括正无理数、零、负无理数;(4)无理数是无限不循环小数.A.0 B.1 C.2 D.37.如图,直径为1个单位长度的圆从原点沿数轴向右无滑动地滚动一周,原点滚到了点A,下列说法正确的()A.点A所表示的是πB.OA上只有一个无理数πC.数轴上无理数和有理数一样多8. 下列说法:的算术平方根是11;的立方根是;的平方根是;实数和数轴上的点一一对应,其中错误的有A. 0个B. 1个C. 2个D. 3个9.立方根等于4的数是A. 16B.C. 64D.10.下列运算中正确的是()A.B.C.D.11.的平方根是( )A.3 B.—3 C.D.12.下列说法正确的是A. 立方根是它本身的数只能是0和1B. 如果一个数有立方根,那么这个数也一定有平方根C. 16的平方根是4D. 是4的一个平方根13.若a2=16,=-2,则a+b=()A.-4B.-12C.-4或-12D.±4或±1.若一个正数的两个平方根分别是和,则下列说法中:①;②;③是的算术平方根;④是的算术平方根。
八年级数学第四章:一次函数 单元测试题

第四章:一次函数单元测试题(时间:90分钟满分:120分)一.选择题(每题3分,共30分)1.若一次函数y=kx+2的函数值y随x的增大而增大,则()A.k<0 B.k>0 C.k<﹣2 D.k>﹣22.若正比例函数y=(2k﹣1)x的图象上有一点A(x1,y1),且x1y1<0,则k的取值范围是()A.k<B.k>C.k<或k>D.无法确定3.函数y=的自变量x的取值范围是()A.x≠1 B.x≥2 C.x≠1且x≠2 D.x≤2且x≠14.若一次函数y=2x﹣3的图象平移后经过点(3,1),则下列叙述正确的是()A.沿x轴向右平移3个单位长度B.沿x轴向右平移1个单位长度C.沿x轴向左平移3个单位长度D.沿x轴向左平移1个单位长度5.在平面直角坐标系中,直线y=2x﹣3的图象不动,将坐标系向上平移2个单位后得到新的平面直角坐标系,此时该直线的解析式变为()A.y=2x﹣5 B.y=2x+5 C.y=2x+1 D.y=2x﹣16.在平面直角坐标系中,将直线y=﹣2x+2关于平行于y轴的一条直线对称后得到直线AB,若直线AB 恰好过点(6,2),则直线AB的表达式为()A.y=2x﹣10 B.y=﹣2x+14 C.y=2x+2 D.y=﹣x+57.对于正比例函数y=kx,当自变量x的值增加3时,对应的函数值y减少6,则k的值为()A.2 B.﹣2 C.﹣3 D.﹣0.58.根据如图所示的程序计算函数y的值,若输入的x值是﹣1,则输出的y值为()A.﹣3 B.﹣2 C.﹣1 D.19.如图,已知直线y=2x+4与x轴交于点A,与y轴交于点B,以点A为圆心,AB为半径画弧,交x轴正半轴于点C,则点C的坐标为()A.B.C.D.10.小刘下午5点30分放学匀速步行回家,途中路过鲜花店为过生日的妈妈选购了一束鲜花,6点20分到家,已知小刘家距学校3千米,下列图象中能大致表示小刘离学校的距离S(千米)与离校的时间t(分钟)之的关系的是()A.B.C.D.二.填空题(每题4分,共20分)11.将一次函数y=3x的图象向上平移2个单位的长度,平移后的直线与x轴的交点坐标为.12.某电影院地面的一部分为扇形,观众席的座位数按下列方式设置:排数(x) 1 2 3 4 ……座位数(y) 40 43 46 49 ……若排数x是自变量,y是因变量,则y与x之间的函数关系式为.13.若函数y=2x+3﹣m是正比例函数,则m的值为.14.已知在正比例函数y=﹣2mx中,函数y的值随x值的增大而增大,则点P(m,4)在第象限.15.若平面直角坐标系xOy中一点(x0,y0),到直线y=kx+b的距离可用公式d=来计算,例如点(1,0)到直线y=x﹣2的距离是d==.则直线y=2x到直线y=2x﹣5的距离d =.三.解答题(共50分)16.请按步骤画出函数y=﹣2x+4的图象,根据图象回答下列问题:(1)y的值随x值的增大而;(2)图象与x轴的交点坐标是,与y轴的交点坐标是;(3)当x时,y>0.17.小凡与小光从学校出发到距学校5千米的图书馆看书,途中小凡从路边超市买了一些学习用品,如图反应了他们俩人离开学校的路程s(千米)与时间t(分钟)的关系,请根据图象提供的信息回答问题:(1)先出发,先出发了分钟;(2)当t=分钟时,小凡与小光在去图书馆的路上相遇;(3)小凡与小光从学校到图书馆的平均速度各是多少千米/小时?(不包括停留的时间)18.已知直线y=2x+4,y=﹣kx+2k,与x轴所围成的面积为4,求k.19.如图1.在平面直角坐标系中,一次函数y=﹣x+2的图象与x轴,y轴分别交于点A.点C,过点1作AB⊥x轴,垂足为点A,过点C作CB⊥y轴,垂足为点C,两条垂线相交于点B.(1)线段OC,OA,AC的长分别为OC=,OA=,AC=,∠ACO=度.(2)将图1中的△ABC折叠,使点A与点C重合,再将折叠后的图形展开,折痕DE交AB于点D,交AC于点E,连接CD,如图2,求线段AD的长;(3)点M是直线AC上一个动点(不与点A、点C重合).过点M的另一条直线MN与y轴相交于点N.是否存在点M,使△AOC与△MCN全等?若存在,请求出点M的坐标;若不存在,请说明理由.20.如图1所示,在A、B两地之间有汽车站C站,客车由A地驶往C站,货车由B地驶往A地.两车同时出发,匀速行驶.图2是客车、货车离C站的路程y1,y2(千米)与行驶时间x(小时)之间的函数关系图象.(1)填空:A,B两地相距千米;货车的速度是千米/时;(2)求三小时后,货车离C站的路程y2与行驶时间x之间的函数表达式;(3)试求客车与货两车何时相距40千米?。
北师大版八年级上册第四章 一次函数周周测6(全章)

第四章 一次函数周周测6一. 选择题11. 正比例函数y=(2k-3)x 的图像过点(-3,5),则k 的值为 ( ) A. 95 B. 37 C. 35 D. 32 12. 函数y=(m-2)x n-1+n 是一次函数,m,n 应满足的条件是 ( )A. m ≠2且n=0B. m=2且n=2C. m ≠2且n=2D. m=2且n=013. 一次函数的图像交x 轴于(2,0),交y 轴于(0,3),当函数值大于0时,x 的取值范围是( )A. x>2B. x<2C. x>3D. x<314. 已知直线y=kx+b 经过(-5,1)和点(3,-3),那么k 和b 的值依次是 ( ) A. -2,-3 B. 1,-6 C. -21 D. 1,6 15. 与x 轴交点的横坐标是负数的直线是 ( )A. y=-x+2B. y=x+2C. y=xD. y=x-216. 如图2-1所示,如果k ·b<0,且k<0,那么函数y=kx+b 的图像大致是 ( )X xA B C D图2-117. 已知正比例函数y=(2m-1)x 的图像上两点A(x 1,y 1),B(x 2,y 2),当x 1<x 2时,有y 1>y 2,那么m的取值范围是 ( )A. m<21B. m>21 C. m<2 D. m>0 18. 若函数y=3x-6和y=-x+4有相等的函数值,则x 的值为 ( )A. 21B. 25C. 1D. -25 19. 某一次函数的图像经过点(-1,2),且函数y 的值随自变量x 的增大而减小,则下列函数符合上述条件的是 ( )A. y=4x+6B. y=-xC. y=-x+2D. y=-3x+520. 已知一次函数y=23x+m 和y=-21x+n 的图像都经过点A(-2,0), 且与y 轴分别交于B,C 两点,那么△ABC 的面积是 ( )A. 2B. 3C. 4D. 6二. 填空题1. 若点P(3,8)在正比例函数y=kx 的图像上,则此正比例函数是________________.2. 若一次函数y=-x+a 与一次函数y=x+b 的图像的交点坐标为(m,8),则a+b=_________.3. 若一次函数y=kx+b 交于y 轴的正半轴,且y 的值随x 的增大而减小,则k______0,b___0.(填”>””=””<”号)4. 已知一次函数y=kx+b 的图像经过点(1,3)和(-1,-1),则此一次函数关系式为________.5. 若直线y=2x+6与直线y=mx+5平行,则m=____________.6. 已知点A(-4, a),B(-2,b)都在一次函数y=21x+k(k 为常数)的图像上,则a 与b 的大小关系是a____b(填”<””=”或”>”);若k=2,则ab=___________.7. 已知点(a,4)在连结点(0,8)和点(-4,0)的线段上,则a=_________________.8. 已知一次函数y=2x-a 与y=3x-b 的图像交于x 轴上原点外的一点,则ba a =________. 9. 一次函数y=2x+b 与两坐标轴围成三角形的面积为4,则b=________________.10. 根据一次函数y=-3x-6的图像,当函数值大于零时,x 的范围是______________.三. 解答题21. 离山脚高度30m 处向上铺台阶,每上4个台阶升高1m.(1) 求离山脚高度hm 与台阶阶数n 之间的函数关系式;(2) 已知山脚至山顶高为217 m,求自变量n 的取值范围.22. 已知y-3与4x-2成正比例,且当x=1时,y=5.(1) 求y 与x 的函数关系式;(2) 求当x=-2时的函数值;(3) 如果y 的取值范围是0≤y ≤5,求x 的取值范围.23. 已知一次函数的图像经过(-3,5),(1,37)两点,求此一次函数的解析式.24. 在平面直角坐标系中作出一次函数y=3x-2与y=3x+4的图像,并回答下列问题:(1) 一次函数y=3x-2中y 的值随x 的增大怎样变化?(2) 在同一坐标系中上述两个函数图像有何位置关系?(3) 当x=8时,其对应的y 值分别是多少?25. 阅读下面的文字后,解答问题:有这样一道题目;”已知,一次函数y=kx+b 的图像经过A(0,a),B(-1,2),________,则△ABO 的面积为2,试说明理由.题目中横线部分是一段被墨水污染了的无法辨认的文字.根据现有信息,你能否求出题目中一次函数的解析式?若能,请写出适合条件的一次函数解析式?(1) 请根据你的理解,在横线上添加适当的条件,把原题补充完整.四. 应用题26. 求直线y=2x+3和y=-3x+8与x轴所围成的面积.Y=2x+327. 某厂有甲,乙两条生产线先后投产,在乙生产线投产以前,甲生产线已生产了200吨成品;从乙生产线投产开始,甲,乙两条生产线每天分别生产20吨和30吨成品.(1) 分别求出甲,乙两条生产线投产后,总产量y(吨)与从乙开始投产以来所用时间x(天)之间的函数关系式;(2) 分别指出第15天和25天结束时,哪条生产线的总产量高?28. 为了保护学生的视力,课桌椅的高度都是按一定的关系配套设计的.研究表明:假设课桌的高度为ycm,椅子的高度(不含靠背)为xcm,则y应是x的一次函数,下表列出两套符合条件的课桌椅的高度.(1)请确定y与x的函数关系式(不要求写出x的取值范围);(2)现有一把高42.0 cm的椅子和一张高78.2 cm的课桌,它们是否配套?请通过计算说明理由.29. 已知一次函数y=(3-k)x-2k2+18,(1) k为何值时,它的图像经过原点;(2) k为何值时,它的图像经过点(0,-2);(3) k为何值时,它的图像与y轴的交点在x轴的上方;(4) k为何值时,它的图像平行于直线y=-x;(5) k为何值时,y随x的增大而减小.。
第四章 一次函数单元测试卷(含解析)
第四章一次函数单元测试卷一.选择题(共10小题,满分30分,每小题3分)1.下面每个选项中给出了某个变化过程中的两个变量x和y,其中y不是x的函数的选项是()A.y:正方形的面积,x:这个正方形的周长B.y:某班学生的身高,x:这个班学生的学号C.y:圆的面积,x:这个圆的直径D.y:一个正数的平方根,x:这个正数2.鲁老师乘车从学校到省城去参加会议,学校距省城200千米,车行驶的平均速度为80千米/时.x小时后鲁老师距省城y千米,则y与x之间的函数关系式为()A.y=80x﹣200 B.y=﹣80x﹣200 C.y=80x+200 D.y=﹣80x+2003.已知一次函数y=kx+b(k≠0)经过(2,﹣1)、(﹣3,4)两点,则它的图象不经过()A.第一象限B.第二象限C.第三象限D.第四象限4.在平面直角坐标系中,过点(1,2)作直线l,若直线l与两坐标轴围成的三角形面积为4,则满足条件的直线l的条数是()A.5 B.4 C.3 D.25.下列关于一次函数y=﹣2x+3的结论中,正确的是()A.图象经过点(3,0)B.图象经过第二、三、四象限C.y随x增大而增大D.当x>时,y<06.一次函数y=kx+b的图象如图,当x<0时,y的取值范围是()A.y>0 B.y<0 C.﹣1<y<0 D.y<﹣17.已知点M(n,﹣n )在第二象限,过点M的直线y=kx+b(0<k<1)分别交x轴、y 轴于点A,B,过点M作MN⊥x轴于点N,则下列点在线段AN的是()A.((k﹣1)n,0)B.((k+)n,0)) C.(,0)D.((k+1)n,0)8.已知函数y=2x﹣3,y=﹣x+4,y=kx+9的图象交于一点,则k值为()A.2 B.﹣2 C.3 D.﹣39.如图,在平面直角坐标系中,点A的坐标为(0,5),△OAB沿x轴向右平移后得到△O′A′B′,点A的对应点A′在直线y=x上,则点B与其对应点B′之间的距离为()A.6 B.5 C.D.10.一次函数(k是自然数的常数)的图象与两坐标轴所围成的图形的面积为S k,则S1+S2+S3+…S100的值是()A.50 B.101 C.D.二.填空题(共8小题,满分24分,每小题3分)11.已知直线y=﹣2x+5,则将其向右平移1个单位后与两坐标轴围成的三角形面积为.12.函数y=的自变量x的取值范围是.13.一次函数y=(3﹣m)x+m的图象经过第一,二,四象限,则m应为.14.如图,已知直线y=3x+b与y=ax﹣2的交点的横坐标为﹣2,则关于x的方程3x+b=ax ﹣2的解为x=.15.如图,在平面直角坐标系xOy中,点B(﹣1,4),点A(﹣7,0),点P是直线y=x﹣2上一点,且∠ABP=45°,则点P的坐标为.16.如图所示,甲、乙两人相距2千米,他们同时朝同一目的地匀速直行,并同时到达目的地,已知甲速度比乙快,请根据图象判断:乙的速度是千米/小时.17.一次函数y=3x﹣6与x轴的交点坐标是,与y轴的交点坐标是.18.若直线y=2x+3与直线y=mx+5平行,则m+2的值为.三.解答题(共7小题,满分66分)19.(8分)如图,直线y=2x+3与x轴相交于点A,与y轴相交于点B.(1)求A,B两点的坐标;(2)过点B作直线BP,与x轴相交于点P,且使OP=2OA,求直线BP的函数表达式.20.(8分)A、B两辆汽车同时从相距330千米的甲、乙两地相向而行,s(千米)表示汽车与甲地的距离,t(分)表示汽车行驶的时间,如图,L1,L2分别表示两辆汽车的s 与t的关系.(1)L1表示哪辆汽车到甲地的距离与行驶时间的关系?(2)汽车B的速度是多少?(3)求L1,L2分别表示的两辆汽车的s与t的关系式.(4)2小时后,两车相距多少千米?(5)行驶多长时间后,A、B两车相遇?21.(8分)已知一次函数图象经过点(1,3)和(﹣1,7)(1)求出此函数表达式;(2)这条直线与坐标轴围成的三角形面积是多少?22.(8分)某车间的甲、乙两名工人分别同时生产500只同一型号的零件,他们生产的零件y(只)与生产时间x(分)的函数关系的图象如图所示.根据图象提供的信息解答下列问题:(1)甲每分钟生产零件只;乙在提高生产速度之前已生产了零件只;(2)若乙提高速度后,乙的生产速度是甲的2倍,请分别求出甲、乙两人生产全过程中,生产的零件y(只)与生产时间x(分)的函数关系式;(3)当两人生产零件的只数相等时,求生产的时间;并求出此时甲工人还有多少只零件没有生产.23.(10分)甲,乙两人同时各接受了600个零件的加工任务,甲比乙每分钟加工的数量多,两人同时开始加工,加工过程中其中一人因故障停止加工几分钟后又继续按原速加工,直到他们完成任务,如图表示甲比乙多加工的零件数量y(个)与加工时间x(分)之间的函数关系,观察图象解决下列问题:(1)点B的坐标是,B点表示的实际意义是;(2)求线段BC对应的函数关系式和D点坐标;(3)乙在加工的过程中,多少分钟时比甲少加工100个零件?(4)为了使乙能与甲同时完成任务,现让丙帮乙加工,直到完成.丙每分钟能加工3个零件,并把丙加工的零件数记在乙的名下,问丙应在第多少分钟时开始帮助乙?并在图中用虚线画出丙帮助后y与x之间的函数关系的图象.24.(12分)如图,直线y=﹣2x+7与x轴、y轴分别相交于点C、B,与直线y=x相交于点A.(1)求A点坐标;(2)如果在y轴上存在一点P,使△OAP是以OA为底边的等腰三角形,则P点坐标是;(3)在直线y=﹣2x+7上是否存在点Q,使△OAQ的面积等于6?若存在,请求出Q点的坐标,若不存在,请说明理由.25.(12分)我们知道,当一条直线与一个圆有两个公共点时,称这条直线与这个圆相交.类似地,我们定义:当一条直线与一个正方形有两个公共点时,称这条直线与这个正方形相交.如图,在平面直角坐标系中,正方形OABC的顶点为O(0,0)、A(1,0)、B(1,1)、C(0,1).(1)判断直线y=x+与正方形OABC是否相交,并说明理由;(2)设d是点O到直线y=﹣x+b的距离,若直线y=﹣x+b与正方形OABC相交,求d的取值范围.参考答案与试题解析1.解:A、y=(x)2=x2,y是x的函数,故A选项错误;B、每一个学生对应一个身高,y是x的函数,故B选项错误;C、y=π(x)2=πx2,y是x的函数,故C选项错误;D、y=±,每一个x的值对应两个y值,y不是x的函数,故D选项正确.故选:D.2.解:依题意有y=200﹣80x=﹣80x+200.故选:D.3.解:将(2,﹣1)、(﹣3,4)代入一次函数y=kx+b中得:,①﹣②得:5k=﹣5,解得:k=﹣1,将k=﹣1代入①得:﹣2+b=﹣1,解得:b=1,∴,∴一次函数解析式为y=﹣x+1不经过第三象限.故选:C.4.解:设过点(1,2)的直线l的函数解析式为y=kx+b,2=k+b,得b=2﹣k,∴y=kx+2﹣k,当x=0时,y=2﹣k,当y=0时,x=,令=4,解得,k1=﹣2,k2=6﹣4,k3=6+4,故满足条件的直线l的条数是3条,故选:C.5.解:A、图象经过点(,0),故原题说法错误;B、图象经过第二、一、四象限,故原题说法错误;C、y随x增大而减小,故原题说法错误;D、当x>时,y<0,故原题说法正确;故选:D.6.解:根据图象和数据可知,当x<0即图象在y轴左侧时,y的取值范围是y<﹣1.故选:D.7.解:如图所示,过M作MC⊥y轴于C,∵M(n,﹣n ),MN⊥x轴于点N,∴C(0,﹣n),N(n,0),把M(n,﹣n )代入直线y=kx+b,可得b=﹣n﹣kn,∴y=kx﹣n(1+k),令x=0,则y=﹣n(1+k),即B(0,﹣n(1+k)),∴﹣n(1+k)>﹣n,∴n(1+k)<n,令y=0,则0=kx﹣n(1+k),解得x==n(),即A(n(),0),∵0<k<1,n<0,∴n()<n(1+k)<n,∴点((k+1)n,0)在线段AN上.故选:D.8.解:联立函数y=2x﹣3、y=﹣x+4,,解得:,∴交点坐标为(3,3).∵点(3,3)在函数y=kx+9的图象上,∴3=3k+9,∴k=﹣2.故选:B.9.解:∵点A的坐标为(0,5),△OAB沿x轴向右平移后得到△O′A′B′,点A的对应点A′在直线y=x上,∴A′点纵坐标为:5,故5=x,解得:x=6,即A到A′的距离为6,则点B与其对应点B′之间的距离为6.故选:A.10.解:由题意得:函数与x轴交点为(,0),与y轴交点为(0,)∴面积为:××==S k,∴S1+S2+S3+…S100=(1﹣+﹣+…+﹣)=.故选:D.11.解:平移后解析式为:y=﹣2(x﹣1)+5=﹣2x+4,即y=﹣2x+7.当x=0时,y=7,当y=0时,x=,∴平移后得到的直线与两坐标轴围成的三角形的面积为:×7×=.故答案是:.12.解:根据题意得2x+1≥0,x﹣3≠0,解得x≥﹣且x≠3.故答案为:x≥﹣且x≠3.13.解:∵一次函数y=(3﹣m)x+m的图象经过第一,二,四象限,∴,解得m>3.故答案为:m>3.14.解:∵直线y=3x+b与y=ax﹣2的交点的横坐标为﹣2,∴当x=﹣2时,3x+b=ax﹣2,∴关于x的方程3x+b=ax﹣2的解为x=﹣2.故答案为﹣2.15.解:将线段BA绕点B逆时针旋转90°得到线段BA′,则A′(3,﹣2),取AA′的中点K(﹣2,﹣1),直线BK与直线y=x﹣2的交点即为点P.∵直线BK的解析式为y=5x+9,由,解得,∴点P坐标为(﹣,﹣),故答案为(﹣,﹣).16.解:根据题意:乙的位移匀速增加,即乙的速度是定值;前2小时从2千米运动到6千米,位移为4;故乙的速度=2千米/小时.故填2.17.解:当y=0时,3x﹣6=0,解得x=2,则一次函数与x轴的交点坐标为(2,0);当x=0时,y=3x﹣6=﹣6,则一次函数与y轴的交点坐标为(0,﹣6).故答案为(2,0),(0,﹣6).18.解:∵两直线平行∴两直线的k值相同∴m=2∴m+2=4.19.解:(1)把x=0代入y=2x+3,得y═3,∴B点坐标为(0,3);把y=0代入y=2x+3,得0=2x+3,解得x=﹣,∴A点坐标为(﹣,0);(2)∵OA=,∴OP=2OA=3,当点P在x轴正半轴上时,则P点坐标为(3,0),设直线BP的解析式为:y=kx+b,把P(3,0),B(0,3)代入得,解得,∴直线BP的解析式为:y=﹣x+3;当点P在x轴负半轴上时,则P点坐标为(﹣3,0),设直线BP的解析式为y=mx+n,把P(﹣3,0),B(0,3)代入得,解得,所以直线BP的解析式为:y=x+3;综上所述,直线BP的解析式为y=x+3或y=﹣x+3.20.解:(1)由函数图形可知汽车B是由乙地开往甲地,故L1表示汽车B到甲地的距离与行驶时间的关系;(2)(330﹣240)÷60=1.5(千米/分);(3)设L1为s1=kt+b,把点(0,330),(60,240)代入得k=﹣1.5,b=330所以s1=﹣1.5t+330;设L2为s2=k′t,把点(60,60)代入得k′=1所以s2=t;(4)当t=120时,s1=180,s2=120330﹣180﹣120=30(千米);所以2小时后,两车相距30千米;(5)当s1=s2时,﹣1.5t+330=t解得t=132即行驶132分钟,A、B两车相遇.21.解:(1)设一次函数表达式为y=kx+b,∵一次函数图象经过点(1,3)和(﹣1,7),∴,解得,∴一次函数表达式为y=﹣2x+5;(2)在y=﹣2x+5中,当x=0时,y=5;当y=0时,x=,∴直线与坐标轴交于(0,5),(,0),∴直线与坐标轴围成的三角形面积是×5×=.22.解:(1)甲每分钟生产=25只;乙的生产速度==15只/分,故乙在提高生产速度之前已生产了零件:150只;(2)结合后图象可得:甲:y=25x(0≤x≤20);甲乙提速后的速度为50只/分,故乙生产完500只零件还需7分钟,=15x(0≤x≤10),乙:y乙=kx+b,把(10,150)、(17,500),代入可得:,当10<x≤17时,设y乙解得:,=50x﹣350(10≤x≤17).故y乙=25x(0≤x≤20);综上可得:y甲y乙=(3)令y甲=y乙得25x=50x﹣350,解得:x=14,此时y甲=y乙=350只,故甲工人还有150只未生产.23.解:(1)B(15,0),B点表示的实际意义是:甲乙两人工作15分钟时,加工零件的数量相同故答案为:(15,0);甲乙两人工作15分钟时,加工零件的数量相同;(2)由图形可知:甲因故障停止加工15﹣10=5分钟后又继续按原速加工,甲105分钟时,完成任务,即甲100分钟,加工600个零件,甲加工的速度:=6,设乙每分钟加工a个零件,15a=10×6,a=4,600﹣105×4=600﹣420=180,∴C(105,180),设BC的解析式为:y=kx+b,把B(15,0)和C(105,180)代入得:,解得:,∴线段BC对应的函数关系式为:y=2x﹣30(15≤x≤105),=150,∴D(150,0);(3)当x=10时,y=6×10﹣4×10=20,∴A(10,20),易得CD:y=﹣4x+600,当y=100时,﹣2x﹣30=100,x=65,﹣4x+600=100,x=125,综上所述,乙在加工的过程中,65分钟或125分钟时比甲少加工100个零件;(4)设丙应在第x分钟时开始帮助乙,>15,由题意得:4x +(3+4)(105﹣x )=600, x=45,则丙应在第45分钟时开始帮助乙;丙帮助后y 与x 之间的函数关系的图象如右图所示.24.解:(1)解方程组:得:∴A 点坐标是(2,3); (2)设P 点坐标是(0,y ),∵△OAP 是以OA 为底边的等腰三角形, ∴OP=PA ,∴22+(3﹣y )2=y 2, 解得y=,∴P 点坐标是(0,),故答案为(0,);(3)存在;由直线y=﹣2x +7可知B (0,7),C (,0), ∵S △AOC =××3=<6,S △AOB =×7×2=7>6,∴Q 点有两个位置:Q 在线段AB 上和AC 的延长线上,设点Q 的坐标是(x ,y ), 当Q 点在线段AB 上:作QD ⊥y 轴于点D ,如图①,则QD=x , ∴S △OBQ =S △OAB ﹣S △OAQ =7﹣6=1, ∴OB•QD=1,即×7x=1,把x=代入y=﹣2x +7,得y=,∴Q 的坐标是(,),当Q 点在AC 的延长线上时,作QD ⊥x 轴于点D ,如图②则QD=﹣y , ∴S △OCQ =S △OAQ ﹣S △OAC =6﹣=,∴OC•QD=,即××(﹣y )=, ∴y=﹣,把y=﹣代入y=﹣2x +7,解得x=,∴Q 的坐标是(,﹣),综上所述:点Q 是坐标是(,)或(,﹣).25.解:(1)相交.∵直线y=x +与线段OC 交于点(0,),同时直线y=x +与线段CB 交于点(,1), ∴直线y=x +与正方形OABC 相交;(2)当直线y=﹣x +b 经过点B 时,即有1=﹣+b ,∴b=+1.即y=﹣x+1+,记直线y=﹣x+1+与x、y轴的交点分别为D、E,则D(,0),E(0,1+),解法1:在Rt△BAD中,tan∠BDA===,∴∠EDO=60°,∠OED=30度,过O作OF1⊥DE,垂足为F1,则OF1=d1,在Rt△OF1E中,∵∠OED=30°,∴d1=;法2:∴DE=(3+),过O作OF1⊥DE,垂足为F1,则OF1=d1,∴d1=×(1+)÷(3+)=,∵直线y=﹣x+b与直线y=﹣x+1+平行,法1:当直线y=﹣x+b与正方形OABC相交时,一定与线段OB相交,且交点不与点O、B重合.故直线y=﹣x+b也一定与线段OF1相交,记交点为F,则F不与点O、F1重合,且OF=d,∴当直线y=﹣x+b与正方形相交时,有0<d<;法2:当直线y=﹣x+b与直线y=x(x>0)相交时,有x=﹣x+b,即x=,当0<b<1+时,0<x<1,0<y<1,此时直线y=﹣x+b与线段OB相交,且交点不与点O、B重合;当b>1+时,x>1,此时直线y=﹣x+b与线段OB不相交.而当b≤0时,直线y=﹣x+b不经过第一象限,即与正方形OABC不相交.∴当0<b<1+时,d随b的增大而增大,则直线y=﹣x+b与正方形OABC相交,此时有0<d<.。
周测(第四章)
(1)列车在冻土地段行驶3小时的路程为______千米,行驶小时的
路程为_______千米(用含的代数式表示).
(2)在西宁到拉萨路段,列车通过非冻土地段所需时间是通过冻土地
段所需时间的2.1倍.如果通过冻土地段需要小时,那么西宁到拉萨这
_________吨
30吨
B
−
_________吨
−
_________吨
20吨
合计
35吨
15吨
/
(2)用含的代数式表示出总运费(要求:先列式,再化简).
解:总运费为
+ − + − + ( − ) = + 元.
(3)当 = 时,总运费为多少元?
分的面积为 ,则图中两块阴影部分的面积和为( B
A. + +
B. +
C. − −
D. +
)
二、填空题(每小题4分,共24分)
−
9.多项式 − + 中次数最高的项是_______.
10.写出一个只含有字母,,最高次项系数为−,且常数项为8的三
段铁路的长为多少千米?
解:西宁到拉萨这段铁路的长为 + × . = (千米).
(3)在格尔木到拉萨路段,列车通过冻土地段比通过非冻土地段多用
0.5小时,通过冻土地段需要小时.在(2)的条件下,若取 = ,
= ,则西宁到格尔木这段铁路的长为多少千米?
解:格尔木到拉萨这段铁路的长为
克按3元收费,小天寄8千克的包裹,需要支付( C
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第四章 一次函数周周测2
一、选择题
1. 若正比例函数的图象经过点(2,-3
),则这个图象必经过点( )
A. (-3,-2) B. (2,3) C. (3,-2) D. (-2,3)
2. 如果函数y=3x+m的图象一定经过第二象限,那么m
的取值范围是( )
A. m>0 B. m≥0 C. m<0 D. m≤0
3. 函数y=-x+2
的图象不经过( )
A. 第一象限 B. 第二象限 C. 第三象限 D.
第四象限
4. 设0<k<2,关于x的一次函数y=kx+2(1-x),当1≤x≤2
时的最大值是( )
A. 2k-2 B. k-1 C. k D.
k+1
5. 已知正比例函数y=kx(k≠0)的图象如图所示,则在下列选项中k
值可能是( )
A. 1 B. 2 C. 3 D. 4
6. 如图,三个正比例函数的图象对应的解析式为①y=ax,②y=bx,③y=cx,则a、b、c
的大
小关系是( )
A. a>b>c B. c>b>a C. b>a>c D. b>c>a
7. 在平面直角坐标系中,一次函数y=2x+1
的图象不经过( )
A. 第一象限 B. 第二象限 C. 第三象限 D.
第四象限
8. 已知正比例函数y=kx (k≠0),当x=-1时,y=-2
,则它的图象大致是( )
A. B. C. D.
9. 已知点P(m,n)在第四象限,则直线y=nx+m
图象大致是下列的( )
A. B. C. D.
10. 一次函数y=kx+k(k<0
)的图象大致是( )
A. B. C. D.
11. 在平面直角坐标系中,若直线y=kx+b经过第一、三、四象限,则直线y=bx+k
不经过的
象限是( )
A. 第一象限 B. 第二象限 C. 第三象限 D.
第四象限
12. 如图为一次函数y=kx+b(k≠0
)的图象,则下列正确的是( )
A. k>0,b>0 B. k>0,b<0 C. k<0,b>0 D.
k<0,b<0
13. 将直线y=-2x
向下平移两个单位,所得到的直线为( )
A. y=-2(x+2) B. y=-2(x-2) C. y=-2x-2 D. y=-2x+2
14. 将下列函数的图象沿y轴向下平移3
个单位长度后,图象经过原点的是( )
A. y=-x-3 B. y=3x C. y=x+3 D. y=2x+5
15. 将一次函数y=-2x+4的图象平移得到图象的函数关系式为y=-2x
,则移动方法为( )
A. 向左平移4个单位 B. 向右平移4
个单位
C. 向上平移4个单位 D. 向下平移4
个单位
二、填空题
16. 在一次函数y=kx+3中,y的值随着x值的增大而增大,请你写出符合条件的k的一个值:
_____________
17. 一次函数y=kx+b的图象如图所示,当y<5时,x的取值范围是______
18. 直线y=2x+1经过点(0,a),则a= _______
19. 直线y=2x-1沿y轴向上平移3个单位,则平移后直线与x轴的交点坐标为________
20. 矩形ABCD在平面直角坐标系中,且顶点O为坐标原点,已知点B(3,2
),则对角线
AC所在的直线l对应的解析式为 _____
三、解答题
21. 已知函数y=(2m-2)x+m+1的图象过一、二、四象限,求m
的取值范围.
22. 已知函数y=(2m-2)x+m+1,
(1)m
为何值时,图象过原点.
(2)已知y随x增大而增大,求m
的取值范围.
23. 已知一次函数y=kx+3的图象经过点(1,4).
(1
)求这个一次函数的解析式;
(2)求关于x的不等式kx+3≤6
的解集.
24. 一次函数y=kx+b经过点(-1,1)和点(2,7).
(1
)求这个一次函数的解析表达式.
(2)将所得函数图象平移,使它经过点(2,-1
),求平移后直线的解析式.
25. 一次函数y=1.5x-3
(1
)请在平面直角坐标系中画出此函数的图象.
(2
)求出此函数与坐标轴围成的三角形的面积.
