大学物理下册波动光学习题解答 杨体强
大学物理《普通物理学简明教程》振动、波动和光学习题精解概要

A1 φ0A2
π/4x
O
图10-17
解(1)如图10-17,两矢量间夹角为 ,所以合振动振幅
合振动初相
(2)合振动A再与第三个振动合成.根据振动叠加条件, 时合振动有极大值,即
(k=0,1,2…)
当 时合振动有极小值,即
(k=0,1,2…)
10-19当两个同方向的简谐振动合成为一个振动时,其振动表式为:
3应用同一直线上两个简谐振动的合成规律时,要特别注意它们的相位差和合成的振幅的关系;同向时,合振幅最大,反向时,合振幅最小。
10.4思考题选答
1弹簧振子的无阻尼自由振动是简谐振动,同一弹簧振子在简谐驱动力持续作用下的稳态受迫振动也是简谐振动,这两种简谐运动有什么区别?
答:弹簧振子的无阻尼自由振动是在“无阻尼”,包括没有空气等外界施加的阻力和弹簧内部的塑性因素引起的阻力的情况下发生的,是一种理想情况。由于外界不能输入能量,所以弹簧振子的机械能守恒。这时振动的频率由弹簧振子自身的因素( )决定。
解:(1)根据振动方程可知:振幅 ,角率 ,初相 ,周期 =1秒;(2)分析质点运动情况:从t=0时刻起, ;向 轴负方向运动,直到 ,即 为止;质点改变运动方向,向 轴正方向运动到位置P点。最短时间间隔为:
(3) 处的时刻。
第11章机械波基础
答:从质量的意义上来说,质量表示物体的惯性,弹簧本身的质量计入时,系统的质量增大,更不易改变运动状态。对不断地周期性改变运动状态的弹簧振
子的简谐运动来说,其进程一定要变慢。这就是说,考虑弹簧的质量时,弹簧振子的振动周期将变大。
10.5习题解答
10-1质量为10g的小球与轻弹簧组成的系统,按 的规律而振动,式中t以s为单位,试求:
式中t以s为单位。求各分振动的角频率和合振动的拍的周期。
《大学物理》(下2010.12.9)习题课

第11章光的量子效应及光子理论一、 选择题1. 金属的光电效应的红限依赖于: 【 C 】(A)入射光的频率; (B)入射光的强度;(C)金属的逸出功; (D)入射光的频率和金属的逸出功。
2. 已知某单色光照射到一金属表面产生了光电效应,若此金属的逸出电势是U 0(使电子从金属逸出需做功eU 0),则此单色光的波长λ必须满足: 【 A 】hceU )D (;hceU )C (;eU hc )B (;eU hc)A (0≥≤≥≤λλλλ 3. 关于光电效应有下列说法:(1) 任何波长的可见光照射到任何金属表面都能产生光电效应;(2) 对同一金属如有光电子产生,则入射光的频率不同,光电子的初动能不同; (3) 对同一金属由于入射光的波长不同,单位时间内产生的光电子的数目不同; (4) 对同一金属,若入射光频率不变而强度增加一倍,则饱和光电流也增加一倍。
其中正确的是: 【 D 】(A) (1),(2),(3); (B) (2),(3),(4); (C) (2),(3); (D)(2),(4)二、填空题1. 当波长为300 nm 光照射在某金属表面时,光电子的能量范围从0到.J 100.419-⨯在作上述光电效应实验时遏止电压为V 5.2U a =;此金属的红限频率Hz 104140⨯=ν。
2. 频率为100MHz 的一个光子的能量是J 1063.626-⨯,动量的大小是s N 1021.234⋅⨯-。
3. 如果入射光的波长从400nm 变到300nm ,则从表面发射的光电子的遏止电势增大(增大、减小)V 03.1U =∆。
4. 某一波长的X 光经物质散射后,其散射光中包含波长大于X 光和波长等于X 光的两种成分,其中大于X 光波长的散射成分称为康普顿散射。
三、计算题1. 已知钾的红限波长为558 nm ,求它的逸出功。
如果用波长为400 nm 的入射光照射,试求光电子的最大动能和遏止电压。
由光电方程2m mv 21A h +=ν,逸出功0h A ν=,0chA λ=,eV 23.2A =用波长为400nm 的入射光照射,光电子的最大动能:A h mv 212m -=ν A chE km -=λ,将nm 400=λ和eV 23.2A =代入得到:eV 88.0E km =遏止电压:a 2m eU mv 21=,2m a mv e21U =,V 88.0U a = 2. 从铝中移出一个电子需要4.2 eV 的能量,今有波长为200 nm 的光投射至铝表面。
波动光学答案

波动光学填空题56、杨氏双缝的间距为0.3mm ,双缝距离屏幕1500mm ,若第四到第七明纹距离为7.5mm ,则入射光波长 =___500nm____ ;若入射光的波长 =639nm ,则相邻两明纹的间距x k+1-x k =____3.195___mm 。
57、用单色光做单缝衍射实验,若缝宽变为原来的6倍,则中央明纹区宽度是原来的____1/6____倍。
58、波长为750nm 的单色平行光,垂直照射到宽度为d 的单缝上,若衍射角为3π/12时,对应的衍射图样为第一极小,则缝宽为_____1.06µm______。
59、单色平行光垂直入射于单缝上,观察夫琅和费衍射,若屏上P 点处为第3级暗纹,则单缝处波面相应地可划分为 __6___个半波带,若将单缝宽度缩小一半,P 点将是第__1__级__明__纹。
60、单色平行光垂直入射于单缝上,观察夫琅和费衍射,若屏上P 点处为第3级明纹,则单缝处波面相应地可划分为 _____个半波带,若将单缝宽度加倍,P 点将是第____级____纹。
61、一束强度为I 0的自然光垂直穿过两个叠合在一起、偏振化方向成45゜角的理想偏振片,则透射光强为____1/4____I 062、光的干涉和衍射现象反映了光的___波动_____性质.光的偏振现象说明光波是______横___波.63、单色平行光垂直入射于单缝上,观察夫琅和费衍射,若屏上P 点处为第2级明纹,则单缝处波面相应地可划分为 _____个半波带,若将单缝宽度缩小一半,P 点将是第____级____纹。
64、单色光在折射率为n=1.4的介质中传播的几何路程长度为30m ,则相当于该光在真空中传播的路程长度为____42m_____。
65、波长为λ=532nm 的单色光垂直照射到宽度为d 的单缝上,若对应第二级暗纹的衍射角θ=30°。
则缝宽d __2128______nm 。
66、光的_ 干涉____和_ 衍射____现象表明光具有波动性质,光的__偏振_____现象说明光波是横波。
医用物理学练习册---10波动光学含答案

10波动光学一、选择题1、以下叙述除哪个以外都是电磁波:(A)可见光;(B)声波;(C)X射线;(D) 射线;(E)无线电波。
[ ]2、波由一种介质进入另一介质时一定不变的物理量是:(A)频率;(B)波长;(C)波速;(D)传播方向。
[ ]3、以下哪个不是两束相干光的必备条件:(A)振动方向一致;(B)频率相同;(C)传播距离相同;(D)位相差恒定;[ ]4、光程的数值取决于:(A)光的传播距离;(B)光传播的几何距离和媒质的折射率;(C)媒质的折射率;(D)媒质对光的吸收。
[ ]5、在吹肥皂泡的过程中,以恒定的方向看到肥皂泡表面花样颜色改变,这是由下述哪个量的变化引起的:(A)折射率;(B)泡内压强;(C)泡膜的厚度;(D)表面张力系数。
[ ]6、在夫琅禾费单缝衍射实验中,仅增大缝宽而其余条件均不变时,中央明纹宽度的变化是:(A)减小;(B)增大;(C)不变; (D)先减小,后增大。
[ ]7、把双缝干涉实验装置放在折射率为n 的水中,两缝间距离为d ,双缝到屏的距离为()L d ,所用单色光在真空中波长为λ,则屏上干涉条纹中相邻的两明条纹之间的距离是:(A)/L nd λ; (B)/n L d λ;(C)/L d λ; (D)/2L nd λ。
[ ]8、波长为λ的单色光垂直投射在一单缝上,若P 点为衍射图样的二级明纹,则对P 点而言,单缝可分割成的半波带数目为:(A)2; (B)3;(C)4; (D)5。
[ ]9、用波长为600nm 和400nm 的单色光分别作单缝衍射实验,且实验装置相同,若测得600nm 光束的中央亮纹宽度为3mm ,则400nm 光束的中央亮纹宽度为:(A)3/2mm ; (B)2mm ;(C)3mm ; (D)4mm 。
[ ]10、光线通过厚度为浓度为的某种溶液,透射光是入射光的1/3,如使溶液的浓度和厚度各增加一倍,这个比值将为:(A)1/3 ; (B)1/9 ;(C)1/81 ; (D) 1/1 。
大学物理下波动光学部分总结

k = 1,2,...
rk
kR n
l0 2 f a
单缝衍 射
f x k a
k = 1,2,...
l0 2l
其他公式: 1、迈克尔逊干涉仪:
N 2 d d 2 N
' 2(n 1)t N
2 、光学仪器最小分辨角和分辨本领:
爱里斑的半角宽度:
1.22
D
光栅衍射:光栅衍射条纹是单缝衍射和多光束 干涉的综合效果。 光栅方程
(a b) sin k (k 0,1,2...)
缺级现象 最高级次满足:
ab k k' a
kmax
ab
重
类别 杨氏双 缝 劈尖干 涉 牛顿环 明纹
x
要
公
暗纹
4n 2 4n 2
例4.一束波长为 550 nm的平行光以 30º 角入射到相距为 d =1.00×10 – 3 mm 的双缝上,双缝与屏幕 E 的间距为 D=0.10m。在缝 S2上放一折射率为1.5的玻璃片,这时双缝 的中垂线上O 点处出现第8 级明条纹。求:1)此玻璃片的 厚度。2)此时零级明条纹的位置。 E S1 解:1)入射光到达双缝时已有光程差:
x
式
条纹宽度
x D nd
D k nd
D ( 2k 1) nd 2
k = 0,1,2,...
k = 0,1,2,...
2k 1 e 4n
k = 1,2,...
e
k 2n
e
k = 0,1,2,...
l
2 n
2n
(2k 1) R rk 2n
大学物理习题及解答(振动与波、波动光学)

1. 有一弹簧,当其下端挂一质量为m 的物体时,伸长量为9.8 ⨯10-2 m 。
假如使物体上下振动,且规定向下为正方向。
〔1〕t =0时,物体在平衡位置上方8.0 ⨯10-2 m处,由静止开始向下运动,求运动方程。
〔2〕t = 0时,物体在平衡位置并以0.60m/s 的速度向上运动,求运动方程。
题1分析:求运动方程,也就是要确定振动的三个特征物理量A 、ω,和ϕ。
其中振动的角频率是由弹簧振子系统的固有性质〔振子质量m 与弹簧劲度系数k 〕决定的,即m k /=ω,k 可根据物体受力平衡时弹簧的伸长来计算;振幅A 和初相ϕ需要根据初始条件确定。
解:物体受力平衡时,弹性力F 与重力P 的大小相等,即F = mg 。
而此时弹簧的伸长量m l 2108.9-⨯=∆。
如此弹簧的劲度系数l mg l F k ∆=∆=//。
系统作简谐运动的角频率为1s 10//-=∆==l g m k ω〔1〕设系统平衡时,物体所在处为坐标原点,向下为x 轴正向。
由初始条件t = 0时,m x 210100.8-⨯=,010=v 可得振幅m 100.8)/(2210102-⨯=+=ωv x A ;应用旋转矢量法可确定初相πϕ=1。
如此运动方程为])s 10cos[()m 100.8(121π+⨯=--t x〔2〕t = 0时,020=x ,120s m 6.0-⋅=v ,同理可得m 100.6)/(22202022-⨯=+=ωv x A ,2/2πϕ=;如此运动方程为]5.0)s 10cos[()m 100.6(122π+⨯=--t x2.某振动质点的x -t 曲线如下列图,试求:〔1〕运动方程;〔2〕点P 对应的相位;〔3〕到达点P 相应位置所需要的时间。
题2分析:由运动方程画振动曲线和由振动曲线求运动方程是振动中常见的两类问题。
此题就是要通过x -t 图线确定振动的三个特征量量A 、ω,和0ϕ,从而写出运动方程。
曲线最大幅值即为振幅A ;而ω、0ϕ通常可通过旋转矢量法或解析法解出,一般采用旋转矢量法比拟方便。
大学物理[下册]波动习题课
![大学物理[下册]波动习题课](https://img.taocdn.com/s3/m/ac0919ff2cc58bd63186bd9f.png)
将沿oy轴的负方向运动. 0 / 3
y
(
x,
t)
Acos[(t x ) u
0.1cos[500(t
0 ] x / 5000)
/
3]m
o
A/2 y
(2)在距原点7.5m处质点的运动方程.
y 0.1cos[500t 13 /12]m
t=0时该点的振动速度
15-5 波源作简谐运动,周期为0.02s,若该振动以100m.s-1的速度沿直 线传播,设t=0时,波源处的质点经平衡位置向正方向运动,求:(1)距波 源15.0m和5.0m处质点的运动方程和初相;(2)距波源分别为16.0m和 17.0m的两质点间的相位差.
解: (1)由题意知:T=0.02s,u=100m.s-1,可得
解: (1)已知波动方程为 y 0.20cos2.50t xm
与一般表达式 y Acos(t x / u) 0
比较,得 A 0.20m,u 2.5m s1, 0 0 / 2 1.25HZ u / 2.0m
(2)绳上的质点振动速度
15-9波动的能量与那些物理量有关?比较波动的能量与 简谐运动的能量.
从波的能量密度公式可知 w A22 sin 2 t x / u
波动的能量不但与体积有关,且与,A,,u.
波动的能量与简谐运动的能量有显著的不同,在简谐 运动系统中,动能和势能有/2的相位差,系统的机械 能是守恒的.在波动中,动能和势能的变化是同相位 的,对任何体积元来说,系统的机械能是不守恒的.
15-11波的干涉的产生条件是什么?若两波源所发出的波的 振动方向相同,频率不同,则它们在空间叠加时,加强和减弱 是否稳定?
大学物理-波动光学习题(包括振动、波动、波的干涉、光的干涉、光的衍射、光的偏振)
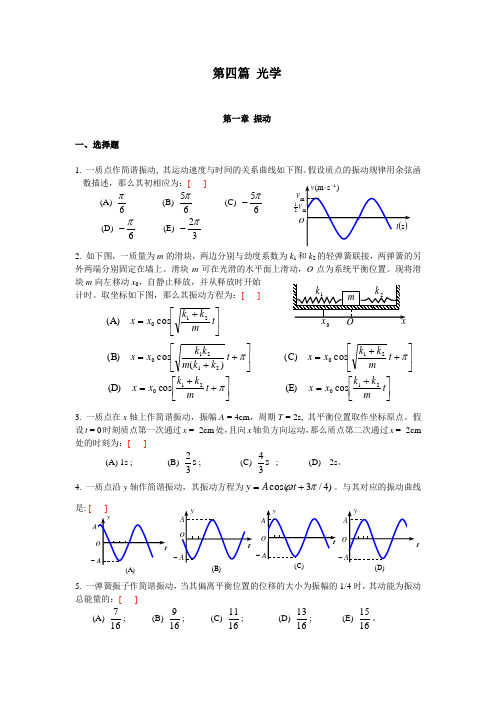
第四篇 光学第一章 振动一、选择题1. 一质点作简谐振动, 其运动速度与时间的关系曲线如下图。
假设质点的振动规律用余弦函数描述,那么其初相应为:[ ] (A)6π (B) 65π (C) 65π- (D) 6π- (E) 32π-2. 如下图,一质量为m 的滑块,两边分别与劲度系数为k 1和k 2的轻弹簧联接,两弹簧的另外两端分别固定在墙上。
滑块m 可在光滑的水平面上滑动,O 点为系统平衡位置。
现将滑块m 向左移动x0,自静止释放,并从释放时开始计时。
取坐标如下图,那么其振动方程为:[ ] ⎥⎦⎤⎢⎣⎡+=t m k k x x 210cos(A)⎥⎦⎤⎢⎣⎡++=πt k k m k k x x )(cos (B)21210⎥⎦⎤⎢⎣⎡++=πt m k k x x 210cos (C)⎥⎦⎤⎢⎣⎡++=πt m k k x x 210cos (D) ⎥⎦⎤⎢⎣⎡+=t m k k x x 210cos (E)3. 一质点在x 轴上作简谐振动,振幅A = 4cm ,周期T = 2s, 其平衡位置取作坐标原点。
假设t = 0时刻质点第一次通过x = -2cm 处,且向x 轴负方向运动,那么质点第二次通过x = -2cm 处的时刻为:[ ](A) 1s ; (B)s 32; (C) s 34; (D) 2s 。
4. 一质点沿y 轴作简谐振动,其振动方程为)4/3cos(πω+=t A y 。
与其对应的振动曲线是: [ ]5. 一弹簧振子作简谐振动,当其偏离平衡位置的位移的大小为振幅的1/4时,其动能为振动总能量的:[ ](A)167; (B) 169; (C) 1611; (D) 1613; (E) 1615。
(A)-(B)(C)(D)-06. 图中所画的是两个简谐振动的振动曲线,假设 这两个简谐振动可叠加,那么合成的余弦振动 的初相为: [ ] π21(A) π(B) π23(C) 0(D)二、填空题1. 一简谐振动的表达式为)3cos(ϕ+=t A x ,0=t 时的初位移为0.04m, s -1,那么振幅A = ,初相位 =2. 两个弹簧振子的的周期都是0.4s, 设开始时第一个振子从平衡位置向负方向运动,经过0.5s 后,第二个振子才从正方向的端点开始运动,那么这两振动的相位差为 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
波动光学习题解答1-1 在杨氏实验装置中,两孔间的距离等于通过光孔的光波长的100倍,接收屏与双孔屏相距50cm 。
求第1 级和第3级亮纹在屏上的位置以及它们之间的距离。
解: 设两孔间距为d ,小孔至屏幕的距离为D ,光波波长为λ,则有=100d λ. (1)第1级和第3级亮条纹在屏上的位置分别为 (2)两干涉条纹的间距为 1-2 在杨氏双缝干涉实验中,用06328A =λ的氦氖激光束垂直照射两小孔,两小孔的间距为1.14mm ,小孔至屏幕的垂直距离为1.5m 。
求在下列两种情况下屏幕上干涉条纹的间距。
(1)整个装置放在空气中; (2)整个装置放在n=1.33的水中。
解: 设两孔间距为d ,小孔至屏幕的距离为D ,装置所处介质的折射率为n ,则两小孔出射的光到屏幕的光程差为 所以相邻干涉条纹的间距为(1)在空气中时,n =1。
于是条纹间距为 (2)在水中时,n =1.33。
条纹间距为 1-3 如图所示,1S 、2S 是两个相干光源,它们到P 点的距离分别为1r 和2r 。
路径1S P 垂直穿过一块厚度为1t 、折射率为1n 的介质板,路径2S P 垂直穿过厚度为2t ,折射率为2n 的另一块介质板,其余部分可看做真空。
这两条路径的光程差是多少?解:光程差为 222111[r (n 1)t ][r (n 1)t ]+--+-1-4 如图所示为一种利用干涉现象测定气体折射率的原理性结构,在1S 孔后面放置一长度为l 的透明容器,当待测气体注入容器而将空气排出的过程中幕上的干涉条纹就会移动。
由移过条纹的根数即可推知气体的折射率。
(1)设待测气体的折射率大于空气折射率,干涉条纹如何移动?(2)设 2.0l cm =,条纹移过20根,光波长为589.3nm ,空气折射率为1.000276,求待测气体(氯气)的折射率。
解:(1)条纹向上移动。
(2)设氯气折射率为n,空气折射率为n 0=1.002760,则有:所以0k n =n + 1.00027600.0005893 1.0008653lλ=+=1-5 用波长为500 nm 的单色光垂直照射到由两块光学平玻璃构成的空气劈尖上。
在观察反射光的干涉现象中,距劈尖棱边1=1.56 cm 的A 处是从棱边算起的第四条暗条纹中心。
(1)求此空气劈尖的劈尖角θ;(2)改用600 nm 的单色光垂直照射到此劈尖上,仍观察反射光的干涉条纹,A 处是明条纹还是暗条纹?(3)在第(2)问的情形从棱边到A 处的范围内共有几条明纹,几条暗纹? 解:(1)棱边处是第一条暗纹中心,在膜厚度为21e 2λ=处是第二条暗纹中心,依此可知第四条暗纹中心处,即A 处膜厚度43e 2λ=, (2)由(1)知A 处膜厚为43500e 7502nm nm ⨯==,对于'600nm λ=的光,连同附加光程差,在A 处两反射光的光程差为'412e +2λ,它与波长'λ之比为4'2e 13.02λ+=,所以A 处为明纹。
(3)棱边处仍是暗纹,A 处是第三条明纹,所以共有三条明纹,三条暗纹。
1-6 在双缝干涉装置中,用一很薄的云母片(n=1.58)覆盖其中的一条狭缝,这时屏幕上的第七级明条纹恰好移动到屏幕中央零级明条纹的位置。
如果入射光的波长为5500A ,则这云母片的厚度应为多少?解:设云母片的厚度为e ,则由云母片引起的光程差为按题意得 =7δλ1-7 波长为500nm 的单色平行光射在间距为0.2mm 的双狭缝上。
通过其中一个缝的能量为另一个的2倍,在离狭缝50cm 的光屏上形成干涉图样。
求干涉条纹间距和条纹的可见度。
解:(1) 条纹间距8050100.1250.02r y cm d λ-∆==⨯= (2) 设其中一狭缝的能量为I 1, 另一狭缝能量为I 2,且满足:21=2I I而 2I=A 则有12A =2A ,因此可见度为:1-8 一平面单色光垂直照射在厚度均匀的薄油膜上,油膜覆盖在玻璃板上,油的折射率为1.20,玻璃的折射率为1.50。
若单色光的波长可由光源连续可调,可光侧到500nm 到700nm 这两个波长的单色光在反射中消失,试求油膜层的厚度。
答: 油膜上、下两表面反射光的光程差为2ne ,由反射相消条件有12(21)()22ne k k k λλ=+=+ (0,1,2,)k =⋅⋅⋅ ①当15000λ=oA 时,有111112()25002ne k k λλ=+=+ ②当27000λ=o A 时,有222212()35002ne k k λλ=+=+ ③因21λλ>,所以21k k <;又因为1λ与2λ之间不存在3λ满足3312()2ne k λ=+式即不存在 231k k k <<的情形,所以2k 、1k 应为连续整数, 即 211k k =- ④ 由②、③、④式可得: 得 13k = 2112k k =-= 可由②式求得油膜的厚度为11250067312k e nλ+==1-9 透镜表面通常镀一层MgF 2(n=1.38)一类的透明物质薄膜,目的利用干涉来降低玻璃表面的反射。
为了使透镜在可见光谱的中心波长(550nm )处产生极小的反射,则镀层必须有多厚?解:由于空气的折射率n=1,且有12n n n <<,因为干涉的互补性,波长为550nm 的光在透射中得到加强,则在反射中一定减弱。
对透射光而言,两相干光的光程差为: 由干涉加强条件: =k δλ 可得:2d=(k-1)2n λ取k=1,则膜的最小厚度为:min d 99.64nm ≈1-10 用单色光观察牛顿环,测得某一亮环的直径为3nm ,在它外边第5个亮环的直径为4.6mm ,所用平凸镜的凸面曲率半径为1.03m ,求此单色光的波长。
解:第k 级明环半径为:1-11 在迈克尔逊干涉仪的一侧光路中插入一折射率为n=1.40的透明介质膜,观察到干涉条纹移动了7条,设入射光波长为589.0nm ,求介质膜的厚度。
解: 插入厚度为d 的介质膜后,两相干光的光程差的改变量为2(n-1)d,从而引起N 条条纹的移动,根据劈尖干涉加强的条件1-12 在单缝夫琅禾费衍射中,波长为λ的单色光垂直入射在单缝上,见图。
若对应于汇聚在P 点的衍射光线在缝宽a 处的波阵面恰好分成3个半波带,图中AB=BC=CD ,则光线1和光线2在P 点的相位差为多少?P 点是明纹还是暗纹? 解:(1)相位差为2=πϕδλ∆,而3=2λδ,所以相位差为π。
(2)由夫琅和费单缝衍射条纹的明暗条件 可以判断出P 点为明纹。
1-13 波长为600nm λ=的单色光垂直入射到一光栅上,测得第二级主极大的衍射角为030,且第三级是缺级。
(1)光栅常数d 等于多少?(2)光栅上狭缝可能的最小宽度a 等于多少?(3)按照上述选定的d 和a 的值,求在屏幕上可能呈现的全部主极大的级次。
解:由衍射方程:sin d k θλ=, (2)光栅缺级级数满足:若第三级谱线缺级,透光缝可能的最小宽度为: (3)屏幕上光栅衍射谱线的最大级数:0dsin 90k λ=,k =4dλ∴=屏幕上光栅衍射谱线的缺级级数:屏幕上可能出现的全部主极大的级数为:210±±,,共5个条纹。
1-14 波长为600.0nm 的单色光垂直入射在一光栅上,第二、第三级明条纹分别出现在衍射角θ满足sin 0.20θ=与sin 0.30θ=处,第四级缺级,试问:(1)光栅上相邻两缝的间距是多大? (2)光栅狭缝的最小可能宽度a 是多大?(3)按上述选定的a 、d 值,试列出屏幕上可能呈现的全部级数 解:(1)由光栅方程波长为600nm 的第二级明条纹满足: 解得光栅相邻两缝的间距为:(2)第四级缺级,说明该方向上的干涉极大被衍射极小调制掉了,因调制掉的干涉极大级数为:当k=4时,取'=1k ,得到狭缝最小宽度为:6a=1.5104dm -=⨯ (3) 取sin 1.0θ=,得所以有可能看到的最大级数为9±.又由于48±±,级缺级,故屏幕上可能呈现的全部级数为0,1235679±±±±±±±,,,,,,。
1-15 用白光(波长从400.0nm 到700.0nm)垂直照射在每毫米中有500条刻痕的光栅上,光栅后放一焦距f=320毫米的凸透镜,试求在透镜焦平面处光屏上第一级光谱的宽度是多少?解:光栅常数 1d 0.002500mm ==, 由光栅方程 sin d k θλ=, 选取k=1,所以10400=sin 11.537k dλθ-=,0700=20.487θ 因此第一级光谱衍射角宽度:0=8.95=0.1562rad θ∆ 第一级光谱宽度:L=f 50mm θ∆=。
1-16 波长为05000A 的平行光线垂直地入射于一宽度为1mm 的狭缝,若在缝的后面有一焦距为100cm 的薄透镜,使光线焦距于一屏幕上,试问从衍射图形的中心点到下列格点的距离如何?(1)第一极小;(2)第一明文的极大处;(3)第三极小。
解:(1)由暗纹公式:a sin 22kλϕ=± 第一极小即为:k=1,故有:所以2-9-310010x 50010=0.5mm a 110f λ-⨯≈±=±⨯⨯±⨯ (2)由明纹公式:a sin (2+1)2k λϕ=±第一极大即为:k=1,故有:所以3x 0.75mm 2af λ≈±=± (3) 由暗纹公式:a sin 22k λϕ=± 第三极小即为:k=3,故有:所以3x 1.5mm af λ≈±=± 1-17 在迎面驰来的汽车上,两盏前灯相距122cm ,试问汽车离人多远的地方,眼睛恰可分辨这两盏灯?设夜间人眼瞳孔直径为5.0mm ,入射光波长05500A =λ(这里仅考虑人眼瞳孔的衍射效应)。
解:有分辨率公式: 1.22=Dλδφ 人眼可分辨的角度范围是:-9-3-31.2250010==0.134210rad 510δφ⨯⨯⨯⨯ 由关系tan =lsδφ,得到:31.2s=8.94tan 0.134210l l km δφδφ-≈==⨯ 1-18 NaCl 的晶体结构是简单的立方点阵,其分子量M=58.5,密度317.2cm g =ρ,(1)试证相邻离子间的平均距离为式中mol N A /1002.623⨯=为阿伏加德罗常数;(2)用X 射线照射晶面时,第二级光谱的最大值在掠射角炎1°的方向出现。
试计算该X 射线的波长。
解:(1)晶胞的棱边长为d,那么两离子间的平均距离0d 2d=.现计算晶胞的棱边长d,由于每个晶胞波包含四个NaCl 分子,那么密度ρ为 这里,NaCl 分子的质量由下式给出: 所以晶胞的棱边长有下面两式联立得 那么相邻两离子的平均距离0d 为(2)根据布拉格方程: 在j=2时,有0002d sin =2.819sin10.00492nm αλ== 1-29 四个理想偏振片堆叠起来,每片的通光轴相对前一个都是顺时针旋转030。
