机械传动系统的动力学模拟与分析
基于时变啮合刚度的齿轮传动系统动力学研究

基于时变啮合刚度的齿轮传动系统动力学研究摘要:本文基于时变啮合刚度的齿轮传动系统动力学研究,主要探讨了齿轮传动系统的啮合刚度随时间变化的问题,并提出了相应的动力学分析方法。
通过对齿轮传动系统的运动学和动力学分析,得出了齿轮传动系统的啮合刚度随时间变化的规律。
在此基础上,提出了一种基于时变啮合刚度的齿轮传动系统动力学分析方法,用于模拟和优化齿轮传动系统的运动和动力学性能。
通过对实际齿轮传动系统的测量和分析,验证了本文提出的动力学分析方法的有效性和实用性。
关键词:齿轮传动系统;时变啮合刚度;动力学分析;运动学分析Abstract:This paper focuses on the dynamics of gear transmission systems with time-varying mating stiffness, which is an important issue in the design and optimization of gear transmission systems. The mating stiffness of gears changes with time, and this change needs to be taken into account in the dynamics analysis of gear transmission systems. Based on the analysis of the kinematics and dynamics of gear transmission systems, the relationship between the mating stiffness and time is proposed. Based on this relationship, a dynamic analysis method for gear transmission systems is proposed, which can be used to simulate and optimize the kinematic and dynamic performance of gear transmission systems. Through the measurement and analysis of actual gear transmission systems, the effectiveness and practicality of the proposed dynamic analysis methodare verified.Keywords: Gear transmission system; Time-varying mating stiffness; Dynamic analysis; Kinematics analysis1. 引言齿轮传动系统是机械传动系统中的重要部件之一,广泛应用于各种机械设备中。
机械系统动力学的发展

然后详细介绍了机构及机械传动系统非线性动力学的研究方法,包括数学建 模、计算方法、实验设计等方面的内容,并分析了各种方法的特点和应用情况。 最后,总结了当前机构及机械传动系统非线性动力学研究的成果和不足,并指出 了需要进一步探讨的问题和研究方向。本次演示的研究综述有助于加深对机构及 机械传动系统非线性动力学领域的认识和理解,为相关研究提供参考和借鉴。
实验评估也是机械系统动力学研究的重要环节。通过实验可以验证模型的准 确性和方法的可行性,同时也可以为理论研究提供数据支持。当前,许多研究者 将实验研究和理论分析相结合,取得了很好的研究成果。
应用场景
机械系统动力学在工程实践中具有广泛的应用场景。在机械设计领域,机械 系统动力学可以帮助设计者更好地了解机械设备的动态性能,优化设计方案。例 如,通过多体动力学仿真可以模拟机器的运动和受力情况,为机器的结构设计和 优化提供依据。
研究目的与意义:本研究旨在建立完善的工程机械臂系统结构动力学模型, 分析不同工况下的动态特性,优化臂系统结构设计。通过本研究,将为工程机械 臂系统的性能提升提供重要的理论支撑和实践指导,进一步推动工程机械臂技术 的发展和应用。
研究方法:本研究采用理论分析和实验研究相结合的方法,首先通过建立完 善的工程机械臂系统结构动力学模型,对其在不同工况下的动态特性进行分析。 同时,采用有限元分析方法和优化算法对臂系统结构进行优化设计,并通过实验 验证其可行性和有效性。
未来研究方向包括:(1)研究更加准确和高效的柔性体建模方法;(2)开 发更加精确的物理特性描述模型;(3)研究实验设计与分析方法,提高实验结 果的可靠性和可重复性;(4)探索新的应用领域和实际应用案例。
摘要
机构及机械传动系统的非线性动力学是一个涉及多学科交叉的重要研究领域。 本次演示旨在综述该领域的研究现状、不足及未来研究方向。首先介绍了机构及 机械传动系统非线性动力学的背景和意义,明确了本次演示的写作目的和范围。 接着概述了当前的研究现状和争论焦点,指出了已有研究成果和不足之处。
第11章 机械系统动力学

l ——外力矩M L作用构件的角速度;
u xp、u yp、ul ——相应类速度。
3. 动力学方程
在不考虑系统势能变化的情况下(对于刚体机械系统,一般情 况下,构件重量产生的势能 构件动能,可以略去),将 E 1 J e1q12微分,得 2 E J e1q1 q
E 1 2 dJ e1 q1 q1 2 d q1
凯思方程:
是将主动力和惯性力都转化到广义坐标中,它们在广义
坐标中也同样应用达朗贝尔原理,表达式为:
( r ) M *(r ) FP Fm 0
P P 1 m 1
M个惯性力对第r个广义坐标的广义惯性力之和
P个主动力对第r个广义坐标的广义力之和
11-2 刚性机械系统动力学
系统的简化:
1. 系统的动能: 设系统有m个活动构件,则系统的总动能E:
1 m 2 2 E mi xsi ysi J sii2 2 i 1
“.”表示对时间的导数
由于xsi、ysi、i 都是广义坐标q1的函数,即 xsi xsi (q1 ) ysi ysi (q1 ) (q ) i 1 i 所以
H 13
(2)求等效转动惯量J e 根据动能等效原则,得:
1 1 2 2 2 J e12 J112 J 22 J H H m2vO2 2 2
2 2
2
vO2 2 H Je J 1 J2 J H m2 1 1 1 2 H 2 z3 2 H 由i23 1 3 2 3 H H z2 H 1 2 H 1 1 2 又 1 4
机电传动系统的动力学基础
j1
M 1
—电动机与中间传动机构的速比;
jL
M
—电动机与生产机械轴之间的速比;
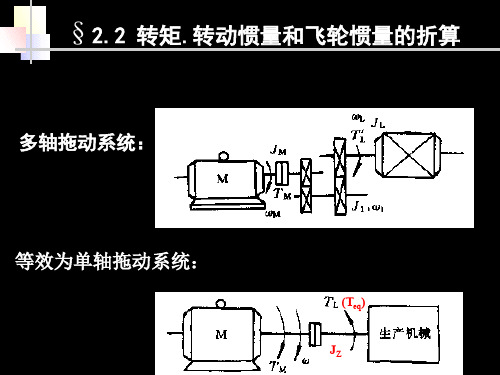
§2.2 转矩.转动惯量和飞轮惯量的折算
三、转动惯量和飞轮惯量的折算
当速比j较大时,可用适当加大电动机轴转动惯量或 飞轮惯量来考虑中间传动机构转动惯量或飞轮惯量的影响。
折算到电动机轴上的总转动惯量(工程简化式)
成正比。 TL = C n 2 C为常数
三、直线型机械特性 特点:负载转矩与转速
成正比
TL=C n C为常数
§2.3 生产机械的机械特性
四、恒功率型机械特性 特点:功率基本不变, 负载转矩与转速成反比
TL=C/n C为常数
§2.4机电传动系统的稳定运行条件
一、机电系统稳定运行的含义 1. 系统应能以一定速度匀速运行; 2. 系统受某种外部干扰(如电压波动、负载转矩
3. 在单轴拖动系统中,已知电动机输出转矩和负载转矩的作用方向 与转速的方向相同,则系统正处于
a. 加速 b. 减速 c. 匀速 d. 静止 4.在机电系统中,已知电动机输出转矩小于负载转矩,且电动机 的输出转矩作用方向与转速的方向相同,而负载转矩的方向与转速 相反,则系统正处于
a. 加速 b.减速 c.匀速 d.静止
a点: TM TL 0
当负载突然增加后 TM TL' 0 TM' TL' 0
当负载波动消除后 TM' TL 0 TM TL 0 故a点为系统的稳定平衡点。 同理b点不是稳定平衡点。
§2.3 生产机械的机械特性
机械特性:转矩与转速之间的特性关系。 生产机械的机械特性: n=f (T L) 电动机轴上的负载转矩与 转速n之间的关系特性。 电动机的机械特性:n=f (T M) 电动机轴上所产生的转矩和转速n之间关系的特性。
谐波齿轮传动系统刚体动力学模型的建立与分析

Ha m o i e r b s d Re ur n s fwa e r n c g a a e c Dy o t r m o l o u t— o y d n m i nay i de f m li b d y a c a l ss
第 3 卷第 1 8 1期 ・ 术 拳
Vof . 38 No. 11
பைடு நூலகம்
湖
南
农
机
20t1 年 11 月
NOV. 201 1
HUNAN AGR CUL I TURAL MACHI RY NE
谐波齿 轮传 动系统 刚体动力学模型 的建 立与分析
时祖 光 , 李玉光 , 王淑 芬
( 大连 大学 机械 工程 学 院 , 宁 大 连 1 6 2 ) 辽 1 6 2
摘 要 : 用 P / 件建立谐 波齿轮 的几何模 型 , 利 o r E软 将建 立好 的模型导入 R c ry 软 件 中, euD n 对其进 行仿真 , 仿 将
真 出的转速和啮合力与理论值进行 比较 , 数据能够较好的吻合 , 说明此动力学模 型的建立是合理的 , 仿真具有可信度 。 关键词 : euD n 仿真 ; R cr y ; 多刚体动力学 中途分类号 :G16 T 5 文献标识码 : A
学化 处理 , 以得 到 相 应 的数 学 表 达 式 。通 过 这 一数 学模 型 , 不
仅 可 以 准 确分 析谐 波齿 轮传 动 系统 齿 轮 之 间啮 合 力 的 变 化 规 律 ,还 可 以通 过 查 看 各 轮 的运 动 速 度 是 否 符 合 理 论 值 来 验 证
仿 真 模 型 的正 确 与 否 。 ( ) 波 齿 轮 传 动 系 统 多 刚 体 动力 学 模 型 的建 立 。 波 齿 1谐 谐 轮 传 动 系统 齿 轮 之 间 的 啮合 力 是 谐 波 齿 轮 传 动 的 主 要 动 态 特 性 之 一 , 系 统 的 动 态 响 应 、 载 能 力 、 劳 分 析 等都 具 有 重 对 承 疲 要 的 意义 。 轮 之 间啮 合 力 的计 算 一 直 是 分 析 的难 点 . 齿 由于 柔 轮 变 形 的原 因 , 致 啮 合 刚 度是 变化 的 , 加 上 轮 齿 的 啮 入 和 导 再
变速器齿轮传动的动力学特性与设计考虑

变速器齿轮传动的动力学特性与设计考虑变速器作为机械传动系统中的重要组成部分,具有调节输出转矩和转速的功能。
而其中的齿轮传动又是变速器的核心部件之一。
本文将针对变速器齿轮传动的动力学特性以及设计时需要考虑的因素进行探讨。
一、动力学特性1.1 齿轮传动的传动比传动比是变速器齿轮传动中的一个重要参数,用于描述输入轴和输出轴之间的转速比。
传动比的大小直接影响到车辆的运动性能和燃油经济性。
通常情况下,高速档的传动比较小,低速档的传动比较大。
1.2 轴向和径向负载在变速器齿轮传动过程中,齿轮承受着来自输入输出轴的轴向和径向负载。
轴向负载主要是来自于发动机的输出转矩和传动系统的摩擦力,而径向负载则包括传动器的自身重量以及运动惯性力等。
设计时需要考虑到这些负载对齿轮的影响,以保证传动可靠性和平稳性。
1.3 齿轮齿形与啮合齿轮的齿形几何结构对于传动性能具有重要影响。
齿轮的齿形主要包括齿高、齿顶高度、齿厚及啮合角等。
优良的齿形设计可以减小齿轮啮合时的摩擦和噪声,提高传动效率和寿命。
二、设计考虑2.1 齿轮材料选择齿轮传动中所使用的材料需要具备良好的机械强度和耐磨性能。
常见的齿轮材料包括低碳合金钢、淬火合金钢、渗碳钢以及高强度合金材料等。
在选择材料时需要综合考虑成本、强度、刚性、耐磨性等因素。
2.2 齿轮的润滑与冷却为了保证变速器齿轮传动的正常运行,必须对齿轮齿面进行良好的润滑。
合适的润滑方式和润滑油的选择可以减少齿轮的摩擦和磨损,并降低传动噪声。
同时,对于高功率变速器,冷却系统的设计也是至关重要的,可以有效降低齿轮传动过程中的温度。
2.3 齿轮的强度计算为了保证齿轮传动的可靠性,需要进行强度计算来确定齿轮的尺寸和齿数。
强度计算通常包括齿轮的疲劳强度和齿面强度两个方面。
其中,疲劳强度主要是考虑到齿轮长时间运转而引起的疲劳变形和断裂,而齿面强度主要是考虑到齿轮传动时所受到的最大接触应力。
2.4 齿轮的噪声与振动齿轮传动过程中会产生一定的噪声和振动。
水下ROV_扭矩工具传动系统设计及动力学分析

2023年第52卷第5期第33页石油矿场机械犗犐犔 犉犐犈犔犇 犈犙犝犐犘犕犈犖犜2023,52(5):33 42文章编号:1001 3482(2023)05 0033 10水下犚犗犞扭矩工具传动系统设计及动力学分析田鲁军1,余华强2(1.中海石油(中国)有限公司天津分公司,天津300450;2.哈尔滨工程大学机电工程学院,哈尔滨150001)摘要:ROV扭矩工具是水下油气生产系统常用的作业工具之一。
针对ROV扭矩工具的国产化问题,研制了适用于ROV扭矩工具的紧凑型变位NGW行星齿轮减速器,可以将ROV扭矩工具的动力源进行减速增扭以实现大扭矩需求。
对该减速器进行了力学分析与动力学理论分析,并用Adams软件对ROV扭矩工具进行动力学仿真分析。
理论分析和仿真分析的结果相符,证明设计的ROV扭矩工具满足使用要求。
关键词:ROV;扭矩工具;传动系统;动力学分析中图分类号:TE952 文献标识码:A 犱狅犻:10.3969/j.issn.1001 3482.2023.05.005犇犲狊犻犵狀犪狀犱犇狔狀犪犿犻犮狊犃狀犪犾狔狊犻狊狅犳犇狉犻狏犲犛狔狊狋犲犿犳狅狉犚犗犞犜狅狉狇狌犲犜狅狅犾狊TIANLujun1,YUHuaqiang2((1.犜犻犪狀犼犻狀犅狉犪狀犮犺,犆犖犗犗犆,犜犻犪狀犼犻狀300450,犆犺犻狀犪;2.犆狅犾犾犲犵犲狅犳犕犲犮犺犪狀犻犮犪犾犪狀犱犈犾犲犮狋狉犻犮犪犾犈狀犵犻狀犲犲狉犻狀犵,犎犪狉犫犻狀犈狀犵犻狀犲犲狉犻狀犵犝狀犻狏犲狉狊犻狋狔,犎犪狉犫犻狀150001,犆犺犻狀犪)犃犫狊狋狉犪犮狋:ROVtorquetoolisoneofthecommonlyusedtoolsinsubseaoilandgasproductionsys tems.AimingatthelocalizationofROVtorquetools,acompactdisplacementNGWplanetarygearreducersuitableforROVtorquetoolswasdeveloped.TheplanetaryreducerreducesthepowersourceoftheROVtorquetooltoachievehightorquerequirements.Themechanicalanaly sisanddynamictheoryanalysisofthereducerwerecarriedout,andthedynamicsimulationanal ysisoftheROVtorquetoolwascarriedoutbyAdams.Theresultsoftheoreticalanalysisandsimulationanalysisareconsistent,whichprovesthatthedesignedROVtorquetoolcanmeetoperationalrequirements.犓犲狔狑狅狉犱狊:ROV;torquetool;drivesystem;dynamicanalysis 海洋石油资源储量约占全球石油资源总储量的34%[1]。
NW型直齿行星传动的动力学建模与固有特性分析

NW型直齿行星传动的动力学建模与固有特性分析张俊;宋轶民【摘要】为揭示NW型直齿行星传动的固有特性,在系杆随动参考坐标系下建立该类传动系统的平移-扭转耦合动力学模型.通过分析各构件间的相对位移关系,推导出系统的运动微分方程,进而通过求解其特征值问题获知系统的固有频率和相应振型.固有特性分析表明,NW型行星传动有3种典型振动模式,即扭转振动模式、平移振动模式和行星轮振动模式.其中,行星轮振动模式又可细分为行星轮同振、左振、右振3种子模式,此点与NGW型行星传动颇为不同.NW型行星传动的振动模式与构件支承刚度间存在一定映射关系.其中,中心构件的支承刚度仅影响中心构件相应方向上的振动模式,而与行星轮振动模式无关;行星轮支承刚度对系统3种振动模式均有影响.%An analytical translational-rotational-coupling dynamic model was developed to evaluate the inherent characteristics of NW spur planetary gear unit. By deriving the displacement relationships between gears and carrier, the governing differential equations were obtained. The solution to associated eigenvalue problem led to natural frequencies and free vibration modes of transmission. The vibration modes are classified into three categories, I.e., rotational mode, translational mode, and planet mode based on their unique properties. And planet mode can be further classified into three sub-categories: global-planet sub-mode, left-planet sub-mode and right-planet sub-mode. The investigation into component stiffness reveals that the radial and circumferential stiffness of central component only influences rotational and translational modes, while the radial and torsional stiffness of planet affects all the three modes.【期刊名称】《天津大学学报》【年(卷),期】2011(044)008【总页数】6页(P677-682)【关键词】直齿行星传动;动力学建模;固有特性;固有频率;振动模式【作者】张俊;宋轶民【作者单位】天津大学机械工程学院,天津300072;安徽工业大学机械工程学院,马鞍山243002;天津大学机械工程学院,天津300072【正文语种】中文【中图分类】TH132.4NW型行星传动是一种较为普遍的齿轮传动类型.与同属2K-H类的NGW型行星传动相比,NW型传动具有结构紧凑、传动比大和承载能力高等优点,故常用于NGW型不适用的径向尺寸受限、传动比较大的场合[1].尽管学术界已针对NGW型行星传动动力学问题进行了广泛研究,其内容涉及自由振动分析、动态响应和振动抑制等多个方面[2-11].相比之下,针对NW型行星传动动力学的研究很少,只有文献[12]对NW型直齿行星传动的动力学问题进行了初步探讨,但该文将双联行星轮处理为单个刚性齿轮进而按照NGW型行星传动进行建模的做法尚待完善.由于双联行星轮结构的引入,NW型行星传动的动力学特性必然与NGW型传动有所不同.为明晰该类传动的动态特性,以NW型直齿行星传动为研究对象,在计入构件支承刚度、齿轮副时变啮合刚度、陀螺效应等诸多影响因素的基础上,采用集中参数法在系杆随动参考坐标系下建立系统的平移-扭转耦合动力学模型.以此为基础,通过求解系统动力学方程的特征值问题,可揭示出NW型直齿行星传动的固有特性.图1所示为NW型行星传动示意.图中,s、c、r、pn、pn′分别代表轮系中的太阳轮、系杆、内齿圈、双联行星轮1和双联行星轮2.1.1 平移-扭转耦合模型采用与文献[11]类似的方法,可在系杆随动坐标系下建立NW型直齿行星传动的平移-扭转耦合动力学模型,其模型如图2所示.各符号的含义如下:kpn为行星轮支承刚度(n=1,2,…,N);ψn为第n个行星轮中心与坐标原点的连线与x轴正向的夹角,ψn=2π(n-1)/N;kij为中心构件的支承刚度(i=c,r,s;j=x,y,u);(xi,yi,ui)为构件位移(i=c,r,s,1,2,…,N);ui、θi分别为各构件的扭转线位移与扭转角位移,ui=riθi;ri为各构件的回转半径(若i=c,则为行星轮轴心到系杆几何形心的距离;若i=r,s,1,2,…,N,则为各齿轮的基圆半径).1.2 构件相对位移分析NW型直齿行星传动中各构件间的相对位移关系如图3所示.图3中,sα、rα分别为太阳轮与行星轮以及行星轮与内齿圈间的啮合角.将各构件之间的相对位移向啮合线方向投影,并设定受压方向为正方向,可得太阳轮与行星轮pn相对位移沿啮合线方向投影内齿圈与行星轮pn′相对位移沿啮合线方向投影系杆与行星轮相对位移沿cx、cy和cu方向投影系杆与行星轮相对位移沿nx、ny方向投影式中1.3 系统运动方程设定NW型直齿行星传动的内齿圈固定,太阳轮、系杆分别连接输入端与输出端,且输入、输出扭矩分别为sT、cT.假定系杆、内齿圈、太阳轮和2个行星轮的质量分别为cm、rm、sm、nm和nm′,其转动惯量分别为cI、rI、sI、nI和nI′.分析系统中各构件的受力状况,依据牛顿第二运动定律可建立如下的运动方程.1) 系杆运动方程2) 内齿圈运动方程3) 太阳轮运动方程4) 行星轮pn运动方程5) 行星轮pn′运动方程式中分别为构件i的加速度沿x、y方向的分量,且有整理式(5)~式(9),并写成矩阵形式式中q为系统的广义坐标列阵.其余各符号含义参见文献[11].考虑到一般情况下NW型行星传动的系杆角速度较小,科氏力、离心力均可忽略,则式(10)可以简化为对式(11)求解特征值问题,可得系统的各阶固有频率和振型.不失一般性,不妨以表1所示的NW型直齿行星传动为例,采用上述动力学模型求解系统的固有频率和相应振型.由行星轮系的同心、装配和邻接条件,可知该NW型行星传动的均布行星轮个数可取3或4.对于N=3及N=4的2种情形,计算系统各阶固有频率如表2所示,其中m为固有频率的重根数.进一步分析可知系统各阶固有频率所对应的振型坐标.经归纳可知NW型直齿行星传动中存在如下3种典型振动模式,即中心构件扭转振动模式、中心构件平移振动模式和双联行星轮振动模式.各种振动模式的特点如下.(1) 中心构件扭转振动模式.当1m=时,各中心构件(太阳轮、内齿圈、系杆)仅做扭转振动,各双联行星轮做复杂平面振动,且相应行星轮的振动状态相同,而与行星轮个数无关.该振动模式的振型如图4(a)所示.(2) 中心构件平移振动模式.当2m=时,各中心构件做平移振动,各双联行星轮做复杂平面振动,且振动状态与行星轮个数相关.当4N=时,各双联行星轮振动状态呈轴向反对称;其他情况下,各双联行星轮振动状态互不相同.该振动模式的振型如图4(b)和 5(b)所示.(3) 双联行星轮振动模式.当m=N−3(N>3)时,各中心构件不振动,仅双联行星轮振动,且振动状态与行星轮个数相关.当N=4时,相应行星轮的振动状态呈轴向对称;其他情况下,各双联行星轮振动状态互不相同.该振动模式的振型如图5(c)~(e)所示.该模式下双联行星轮的振动按其特点又可细分为行星轮1、2同时做复杂平面振动、行星轮1单独做平移振动和行星轮2单独做平移振动3种方式.为区别于NGW型传动的行星轮模式,本文将之分别定义为行星轮同振模式、行星轮左振模式和行星轮右振模式.图4、图5分别示出了3N=、4N=时系统不同振动模式下的振型.图中,虚线表示各构件的初始位置,实线为构件振动后的位置,实线段为各构件振动后的横轴线.为表达清晰,图中均未绘出系杆的位置.由图5可知,NW型直齿行星传动的中心构件扭转振动模式和中心构件平移振动模式与NGW型相似[3],但其行星轮振动模式较为复杂.不难推测,正是由于双联行星轮结构的引入,造成了NW型行星传动中行星轮的振动模式趋于多样化,使得其不仅存在双联行星轮同振模式,还同时存在行星轮左振和右振模式.特别是行星轮左振和右振模式中行星轮仅做横向平移振动,这与NGW型传动中行星轮的振动状态有很大不同,在进行NW型行星传动行星轮振动抑制时应予以重视.为明晰系统中各构件支承刚度与系统振动模式间的映射关系,现分别考察内齿圈、太阳轮、系杆、行星轮支承刚度对系统固有特性的影响.不失一般性,仍以表1所示的NW型直齿行星传动为对象,分析4N=时构件支承刚度与系统振动模式间的关系.以内齿圈为例,其安装方式可分为完全浮动、周向浮动、径向浮动和完全固定4种情况.为分析上述情况下系统的固有特性,设定太阳轮、系杆和行星轮的径向支承刚度为108,N/m,太阳轮和系杆的扭转支承刚度均为0,内外齿轮副啮合刚度均取5× 108N/m,双联行星轮扭转线刚度取5× 107N/m,且相应工况下内齿圈径向和周向支承刚度设置为内齿圈完全浮动:krx=kry=kru=0;内齿圈周向浮动:krx=kry=内齿圈径向浮动内齿圈完全固定对式(11)求解特征值问题,可得不同工况下系统各阶固有频率,其计算结果如表3所示.由表3可知NW型直齿行星传动的振动模式与内齿圈支承刚度间存在如下映射关系:(1) 中心构件扭转振动模式仅受内齿圈周向支承刚度的影响,而与内齿圈径向支承刚度无关;(2) 中心构件平移振动模式仅受内齿圈径向支承刚度的影响,而与内齿圈周向支承刚度无关;(3) 行星轮振动模式既不受内齿圈径向支承刚度也不受周向支承刚度的影响.采用类似的方法可分析太阳轮、系杆、行星轮各向支承刚度的影响.限于篇幅,本文不再详列,仅给出分析结论如下.(1) 中心构件的支承刚度仅影响中心构件的振动模式,而对行星轮振动模式不产生影响.具体而言,中心构件的周向支承刚度仅影响中心构件的扭转振动模式;中心构件的径向支承刚度仅影响中心构件的平移振动模式.(2) 双联行星轮的径向支承刚度和扭转刚度对系统3种振动模式均有影响.(1) NW型直齿行星齿轮传动具有3种典型振动模式,即:中心构件扭转振动模式、中心构件平移振动模式和双联行星轮振动模式.其中,行星轮振动模式又可细分为行星轮同振模式、行星轮左振模式和行星轮右振模式,此点与NGW型行星传动颇为不同.(2) NW型直齿行星齿轮传动的振动模式与系统中构件的支承刚度间存在确定映射关系,即:中心构件的支承刚度仅影响中心构件相应方向上的振动模式,而行星轮的支承刚度则影响系统的全部3种振动模式.【相关文献】[1]饶振纲. 行星齿轮传动设计[M]. 北京:化学工业出版社,2003.Rao Zhengang. Design of Planetary Gear Transmission[M]. Beijing:Chemical Industry Press,2003(in Chinese).[2] Kahraman A. Natural modes of planetary gear trains[J]. Journal of Sound and Vibration,1994,173(1):125-130.[3] Lin J,Parker R G. Analytical characterization of the unique properties of planetary gear free vibration[J]. ASME Journal of Vibration and Acoustics,1999,121(7):316-321. [4] Kahraman A. Free torsional vibration characteristics of compound planetary gear sets[J]. Mechanism and Machine Theory,2001,36:953-971.[5]宋轶民,许伟东,张策,等. 2K-H行星传动的修正扭转模型建立与固有特性分析[J]. 机械工程学报,2006,42(5):16-21.Song Yimin,Xu Weidong,Zhang Ce,et al. Modified torsional model development and natural characteristics analysis of 2K-H epicyclic gearing[J]. Journal of Mechanical Engineering,2006,42(5):16-21(in Chinese).[6]孙涛,刘继岩. 行星齿轮传动非线性动力学方程求解与动态特性分析[J]. 机械工程学报,2002,38(3):10-15.Sun Tao,Liu Jiyan. Study on nonlinear dynamic behavior of planetary gear train solution and dynamic behavior analysis[J]. Journal of Mechanical Engineering,2002,38(3):10-15(in Chinese).[7] Lin J,Parker R G. Planetary gear parametric instability caused by mesh stiffness vibration[J]. Journal of Sound and Vibration,2002,249(1):129-145.[8]孙智民,沈允文,李素有. 封闭行星齿轮传动系统的扭转振动特性研究[J]. 航空动力学报,2001,16(2):163-166.Sun Zhimin,Shen Yunwen,Li Suyou. A study on torsional vibrations in an encased differential gear train[J]. Journal of Aerospace Power,2001,16(2):163-166(in Chinese). [9]魏大盛,王延荣. 行星轮系动态特性分析[J]. 航空动力学报,2003,18(3):450-453.Wei Dasheng,Wang Yanrong. The dynamic characteristics analysis of planet gear train[J].Journal of Aerospace Power,2003,18(3):450-453(in Chinese).[10] Ambarisha V K,Parker R G. Suppression of planet mode response in planetary gear dynamics through mesh phasing[J]. ASME Journal of Vibration and Acoustics,2006,128(4):133-142.[11]张俊,宋轶民,张策,等. NGW型直齿行星传动自由振动分析[J]. 天津大学学报,2010,43(1):90-94.Zhang Jun,Song Yimin,Zhang Ce,et al. Analysis of free vibration of NGW spur planetary gear set[J]. Journal of Tianjin University,2010,43(1):90-94(in Chinese). [12]刘欣. 基于虚拟样机技术的直齿行星传动动力学研究[D]. 天津:天津大学机械工程学院,2007.Liu Xin. Dynamics of Spur Planetary Gear Trains Based on Virtual Prototyping[D]. Tianjin:School of Mechanical Engineering,Tianjin University,2007(in Chinese).。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
机械传动系统的动力学模拟与分析
一、引言
机械传动系统是现代工业中常见的一种能量传递方式。
它由多个机械零件组成,通过齿轮、皮带等方式将驱动力传递给被驱动装置。
对机械传动系统进行动力学模拟与分析可以帮助工程师深入了解系统的性能、优化传动效率,并解决系统遇到的问题。
二、机械传动系统的基本原理
机械传动系统基于力的平衡原理,通过驱动力对被驱动装置施加力的方式实现
能量传递。
常见的机械传动系统包括齿轮传动、皮带传动以及链条传动等。
这些传动方式根据不同的需求可以实现不同速比、转矩传递等功能。
三、动力学模拟的基本方法
动力学模拟是通过数学模型和分析方法对机械传动系统进行建模和仿真,以获
得系统的运动学和动力学性能。
通常采用的方法有解析法和数值法两种。
解析法是基于数学公式的推导和解析求解,适用于简单的传动系统。
通过解析
法可以求得传动系统的运动方程、速度、加速度等参数。
然而,复杂系统的解析法模型通常非常复杂,不易求解。
数值法是通过计算机进行数值模拟和计算,适用于复杂的传动系统。
数值法模
型可以通过有限元法、欧拉法和拉格朗日法等进行建立和求解。
数值法模型可以更加真实地反映系统的实际运行情况。
四、动力学模拟与分析的应用
动力学模拟与分析在机械传动系统的设计、优化以及故障分析中起着重要作用。
在设计过程中,动力学模拟可以帮助工程师对传动系统进行仿真,评估系统的性能,并根据需要进行参数调整和优化。
通过模拟可以找出系统中的瓶颈和问题,从而提出改进的方案。
在故障分析中,动力学模拟可以帮助工程师找出传动系统中存在的问题和故障点,并进行修复和改进。
通过模拟分析可以定位故障点、寻找故障原因,并提供故障排除的方案。
五、动力学模拟与分析的挑战和展望
动力学模拟与分析的挑战主要源于模型的建立和计算的复杂性。
复杂的传动系统需要建立更为真实的模型,增加了计算的难度。
此外,涉及到非线性、随机性等问题也增加了模拟与分析的复杂性。
未来,随着计算机技术和仿真方法的不断发展,动力学模拟与分析将变得更加精确和高效。
通过机器学习和大型计算平台的应用,模拟和分析的计算速度将大大提高,可以涉及更复杂的传动系统和更真实的工况。
这将为工程师提供更好的工具和方法,以便更好地解决问题和优化传动系统。
六、结论
动力学模拟与分析是研究机械传动系统的重要手段,可以帮助工程师了解系统的性能、优化传动效率并解决问题。
本文简要介绍了机械传动系统的基本原理、动力学模拟的基本方法以及应用领域和挑战,展望了未来的发展趋势。
通过动力学模拟与分析的工作,可以更好地理解和改进机械传动系统,推动工程技术的进步与发展。
