第三章习题
中职信息技术(基础模块)第三章课后习题四

中职信息技术(基础模块)第三章课后习题四(一)选择题1.在Word 中,如果想使用一个直线箭头的形状,应选择“插入”选项卡中的“AA.形状B. 图表C. 图片D.SmartArt 图形2.在创建图形时,选择一个形状后,鼠标形状会变成_A。
A.十字形B.圆形C.手的形状D. 笔的形状3.在插入一个矩形形状后,在矩形内部输入文字,应在输入文字的位置_B_。
A.单击鼠标左键B.双击鼠标左键C.单击鼠标右键D.双击鼠标右键4.使用_-B-命令可以把若干个形状形成一个整体。
A. 对齐B.组合C. 置于顶层D.置于底层5.制作一个公司的组织结构图,可以使用_B_完成。
A. 插入图片B.插入SmartArt 图形C.插入图标D. 插入图表6.在Word 中,设计一份包含公式的数学试卷,需要使用_B--_操作。
A.插入图片B.插入符号C. 插入公式D. 插入编号7.在Word 中,鼠标指针变成_B_,可以调整公式大小。
A.十字形B.双向箭头C.单向箭头D. 圆形8.在Word 2016 中,可以使用_B_手写输入公式。
A.墨迹公式B.手写板C.表格D. 文本框(二)填空题1.Word 提供了绘制图形的功能,、星、旗帜、标注等。
2.在Word3.在Word 中,图形叠放次序包括置于顶层、4.在Word 上下型、5.在Word 中,用鼠标指针指向图形对象并单击就可选定它。
6.在Word 中,在图形中添加文字,可以右键单击该图形,然后使用命令。
7.在Word 组合键。
8.在SmartArt 提供了七类逻辑图表,_层次结构关系、9.在Word 中,公式结构包括分式、和等。
(三)简答题1.说出两种以上在Word 图形中添加文字的方法。
答:第一种方法是在图形上右键选择编辑文字,然后添加输入文字;第二种方法是选择图形后双击图形添加文字。
2.简述在Word 中绘制图形的四个阶段。
答:图形的创建步骤如下:单击“插入”选项卡“插图”组中的“形状”按钮;在弹出的下拉列表中选择所要绘制的图形,在编辑工作区中会出现一个“+”图标,按住鼠标左键拖动就会出现需要的图形。
生理学第三章 血液 习题及答案

第三章血液【测试题】一、名词解释1.凝血因子(clotting factor)2.(血浆)晶体渗透压(crystal osmotic pressure)3.血细胞比容(hematocrit value)4.红细胞凝集(agglutination)5.生理性止血(physiology hemostasis)6.血浆(plasma)7.血清(serum)8.红细胞沉降率(erythrocyte sedimentation rate)9.血液凝固(blood coagulation)10.血量(blood volume)11.血型(blood group)12.ABO 血型系统(ABO bood group system)13.红细胞渗透脆性(RBC osmotic fragility)二、填空题14.正常人血浆的pH 值为,它取决与血浆中主要缓冲对的比值。
15.根据血细胞的形态与功能特征,一般把造血过程分为、和等三个阶段。
16.正常人血小板数量是,当血小板数减少到以下时,可出现紫癜。
17.血液和组织中参与凝血的物质称为,按其发现的先后顺序,以统一命名。
18.血液凝固的三个基本步骤是、和,都需要的参与。
按始动因子的来源的不同,凝血过程包括性凝血和性凝血两条途径。
19.纤溶系统包括四种成分,即、、和。
20.ABO 血型系统将人类的血型分成、、、四种血型;Rh 血型系统将人类的血型分成和两种血型。
21.用盐析法可将血浆蛋白分为、和三大类。
其中含量最多的是,它是构成血浆渗透压的主要部分。
22.正常红细胞呈双凹圆碟形,这种形状表面积相对较大,有利于、。
23.低温储存较久的血液,血浆内钾离子浓度,红细胞内钾离子浓度,这是由于红细胞膜上活动极度降低的结果。
24.调节红细胞生成的激素是和。
25.一次急性失血超过总量的%,人体各种生命活动将会受到明显影响。
三、选择题A型题26.下述哪种因子不存在于血浆中?A.Ⅴ因子B.Ⅲ因子C.Ⅹ因子D.Ⅻ因子E.Ⅶ因子27.通常所说的血型是指:A.红细胞上受体的类型B.红细胞表面特异凝集素的类型C.红细胞表面特异凝集原的类型D.血浆中特异凝集素的类型E.血浆中特异凝集原的类型28.下列关于输血的叙述,哪一项是错误的?A.ABO 血型系统相符合便可输血,不需进行交叉配血B.O 型血的人为“万能供血者”C.AB 型血的人为“万能受血者”D.将O 型血液输给其它血型的人时,应少量而且缓慢E.Rh 阳性的人可接受Rh 阴性的血液29.冰库中储存较久的血液,血浆中哪种离子浓度较高?2+C.K+ D.Na+ E.有机负离子A.Cl- B.Ca30.生理性止血后期血凝快回缩是因为:A.纤维蛋白收缩B.红细胞叠连C.白细胞变形运动D.血小板收缩蛋白收缩E.血小板聚集31.内源性凝血与外源性凝血的主要区别是:A.前者需要血小板磷脂表面,后者不需要B.前者发生在血管内,后者发生在血管外C.前者只需体内因子,后者还需外加因子D.前者只需血浆因子,后者还需组织因子E.前者需要Ca2+,后者不需要Ca2+32.B 型血的红细胞膜上含有:A.抗原B.B 抗原C.A 和B 抗原都有D.A、B 及H 抗原均无E.H 抗原33.以下哪种情况可能发生溶血症:A.Rh(+)母亲所怀Rh(+)胎儿B.Rh(+)母亲所怀Rh(-)胎儿C.Rh(-)母亲所怀Rh(+)胎儿D.Rh(-)母亲所怀Rh(-)胎儿E.父亲是Rh(-)、母亲为Rh(+)34.某人的红细胞与B 型血的血清凝集,而其血清与B 型血的红细胞不凝,此人的血型为:A.A 型B.B 型C.AB 型D.O 型E.无法判断35.决定ABO 血型抗原的基因控制细胞合成特异的:A.抗原的肽链B.蛋白质水解酶C.磷脂酶D.转糖基酶E.转氨基酶36.血小板聚集的第二时相是由下列哪种因素引起的:A.内源性ADPB.内源性ATPC.内源性5-HTD.外源性ADPE.外源性ATP37.草酸钾之所以能抗凝是因为:A.增强血浆抗凝血酶的活性B.去除血浆中的Ca2+C.抑制凝血酶活性D.中和酸性凝血物质E.增强纤溶酶的活性38.输血时应主要考虑供血者的:A.红细胞不被受血者的红细胞所凝集B.红细胞不被受血者的血清所凝集C.红细胞不发生叠连D.血清不被受血者的血浆所凝集E.血清不被受血者的红细胞所凝集39.一般血型抗原是红细胞膜上的:A.糖原B.蛋白质C.磷脂D.脂蛋白E.糖脂或糖蛋白40.红细胞的渗透脆性是指:A.红细胞对高渗溶液的抵抗力B.红细胞对低渗溶液的抵抗力C.红细胞在生理盐溶液中破裂的特性D.红细胞耐受机械撞击的能力E.红细胞相互撞击破裂的特性41.输血原则是:A.输同型血,即交叉配血的主侧和次侧都不凝B.紧急情况下可大量输O 型血给其他血型的受血者C.只要交叉配血主侧不凝就可以输血D.只要血型相同,可不做交叉配血E.第一次配血相合输血顺利,第二次接受同一献血员血液不必做交叉配血42.父母双方一方为A 型,一方为B 型,其子女可能的血型为:A.只可能是AB 型B.只可能是A 型或B 型C.只可能是A 型、B 型、AB 型D.A 型、B 型、AB 型、O 型E.只可能是AB 型或O 型43.关于血浆渗透压的叙述,哪一项是正确的:A.血浆渗透压主要来自血浆蛋白B.血浆渗透压主要来自血浆中的电解质C.血浆蛋白减少时,血浆渗透压将明显降低D.血浆渗透压决定了血管内外水平衡E.血浆渗透压变化时,红细胞的脆性发生变化44.下列哪项不能使血沉加快:A.血浆中白蛋白增多B.血浆中纤维蛋白原增多C.红细胞发生叠连D.活动性肺结核E.风湿热45.下列关于促红细胞生成素的描述,错误的是:A.通过特异受体作用于红系集落形成单位B.它是红系集落形成单位生存和繁殖的必需条件C.它主要产生于肾髓质D.肝脏也能产生一部分E.它是一种糖蛋白46.下列凝血因子中,哪一个不是蛋白质:A.因子ⅡB.因子ⅣC.因子Ⅴ和ⅦD.因子ⅪE.因子Ⅹ和Ⅻ47.内、外源性凝血系统的根本区别在于:A.参与血液凝固的所有凝血因子都不同B.起始因子不同C.最后形成的血凝块不同D.外源性凝血不形成凝血酶原激活物E.内源性凝血不需要稳定因子48.启动外源性凝血途径的物质是:A.因子ⅢB.因子ⅫC.PF3 D.Ca2+E.凝血酶原49.关于ABO 血型系统的叙述,哪项是错误的:A.AB 型血的血清中含有抗A 和抗B 抗体B.AB 型血的红细胞膜上有A 抗原和B 抗原C.A 型血的血清中有抗B 抗体D.B 型血的血清中有抗A 抗体E.O 型血的红细胞膜上不含抗原50.Rh 血型抗体是:A.IgA B.IgDC.IgG D.IgEE.IgMB型题A.(4000~5500)×109/LB.(4.0~10)×109/LC.(3800~4600)×109/LD.(100~300)×109/LE.(4.5~5.5)×109/L51.正常成年男性红细胞计数为:52.正常人安静时的白细胞计数为:53.正常人血液中血小板计数为:A.增快B.减慢C.在正常范围内D.先不变后增快E.先不变后减慢54.将正常人的红细胞放入血沉快的人血浆中,血沉将:A.葡萄糖B.Na+C.K+D.球蛋白E.白蛋白55.血浆胶体渗透压主要来源:56.血浆晶体渗透压主要来源:A.等渗溶液B.等张溶液C.等渗和等张溶液D.既不是等渗溶液,也不是等张溶液E.高渗溶液57.0.85%NaCl58.20%葡萄糖59.1.9%尿素A.再生障碍性贫血B.缺铁性贫血C.巨幼红细胞性贫血D.地中海贫血E.溶血性贫血60.骨髓收到X 线损伤引起的贫血是:61.维生素B12和叶酸缺乏引起的贫血是:62.出现大量血红蛋白尿的贫血是:63.血红蛋白的合成减少将引起:A.8hB.3~4dC.7~14dD.一年以上E.120d64.红细胞平均寿命为:65.血小板平均寿命为:X型题66.血清与血浆的区别在于前者A.缺乏纤维蛋白原B.增加了血小板释放的物质C.缺乏某些凝血因子D.含有大量的清蛋白E.以上都不是67.如果某男是B 型血:A.他的基因型可以是AB 型B.他的父亲可以是O 型血C.他的孩子不是B 型血就是O 型血D.如果他的妻子是B 型血,孩子的血型只能是B 型或O 型E.如果他的妻子是O 型血,孩子的血型只能是B 型或O 型68.小血管损伤后,生理止血过程包括:A.受损小血管收缩B.血小板聚集形成止血栓C.受损局部血液凝固形成血凝块D.血管壁修复、伤口愈合E.以上都对69.正常人的血液在血管内不发生凝固的原因有:A.血液流动快B.血管内膜光滑完整C.纤维蛋白溶解系统的作用D.有抗凝血物质存在E.以上都不对70.血浆蛋白主要生理功能有:A.多种代谢物的运输载体B.缓冲血浆pH 变化C.参与机体的免疫功能D.参与生理性止血E.维持血浆胶体渗透压71.调节红细胞生成的物质是:A.爆式促进活性B.促红细胞生成素C.雄激素D.生长激素E.甲状腺激素72.引起血沉加快的因素有:A.白细胞增多B.血浆球蛋白增多C.血浆白蛋白减少D.血浆纤维蛋白原增多E.血浆磷脂增多73.凝血酶的直接作用是:A.激活因子XIIIB.使纤维蛋白原水解成纤维蛋白单体C.使纤维蛋白单体形成不溶性的纤维蛋白多聚体D.使可溶性的纤维蛋白多聚体形成稳固的纤维蛋白多聚体E.抑制纤溶酶活性74.下列哪种情况能使试管中的血液延缓凝血:A.血液中加入草酸钾B.将血液置于有棉花的试管中C.加入肝素D.将试管置于冰水中E.将试管壁涂上石蜡油,再放入新鲜血液75.生理性血小板致聚剂有:A.ADP B.肾上腺素C.5-HT D.细菌E.病毒76.生理性抗凝物质有:A.抗凝血酶B.蛋白质C 系统C.草酸钾D.肝素E.组织因子途径抑制物四、问答题77.简述血液凝固的基本过程。
第三章复习题

第三章 复习题一、单选1.设批产品的质量P=1.0(%),用抽样方案为(10,0)进行验收.则接收概率为在( )之间.cA.15%与35%B.50%与60%C.80%与95%D.96%与100%2.为了节省检验费用使用较小样本量,应选用 ( )抽样方案.bA.调整型B.序贯C.连续D.标准型3一个调整型抽样方案是( ).aA.依据对生产过程的质量要求AQL 和质量保证要求设计的B.依据极限质量LQ 设计的C.由主管部门或负责部门确定的D.根据交验批是否大于10批确定的提示:质量保证就是能保证质量的能力4 规定产品批的不合格品率不得超过1%。
使用某抽样检验方案,它在1%处的接收概率为98.5%,则该抽样方案的( )aA.生产方风险为1.5%B.使用方风险为98.5%C.使用方风险为1.5%D.生产方风险为98.5%5使用GB/T2828对连续批进行检验时( )。
bA. 仅使用正常抽样方案B. 按照转移规则使用不同严格度的抽样方案C. 使用不同样本量的抽样方案D. 对不同的批使用不同的检验水平6记二次抽样方案的第一、二次抽样的样本量(样本大小)分别为1n 、2n ,第一次、二次抽样的(Ac 、Re)分别为(1A 、1R )、 (2A 、2R ),第一、二次抽样的样本中不合格(品)数分别为1d 、2d 。
下述判断程序中正确的是( d )。
A. 抽两次,若1d ≤1A ,2d ≤2A ,接收,否则拒收B. 抽两次,若1d ≤1A ,1d +2d ≤2A ,接收,否则拒收C. 第一次抽1n 个,若1d ≤1A ,接收,若1d ≥1R ,拒收;若1A <1d <1R ,再抽取第二个样本,若2d ≤2A ,接收;若2d ≥2R ,拒收D. 第一次抽1n 个,若1d ≤1A ,接收,若1d ≥1R ,拒收;若1A <1d <1R ,再抽取第二个样本, 若1d +2d ≤2A ,接收;若1d +2d ≥2R ,拒收7使用计量型抽样方案,用( )判断该批是否可接收。
第三章复习题试题及答案

第三章复习题试题及答案一、单项选择题1. ()模块的主要功能是对软件的各个子系统进行统一的作管理和数据维护 [单选题] *A.总账B.系统管理(正确答案)C.系统初始化D、UFO报表2.以账套主管的身份注册系统管理,不能进行的操作是() [单选题] *A.建立账套(正确答案)B.修改账套C.年度账引入D.年度账清空3.若会计科目的编码方案为4-2-2,则正确的编码为()。
[单选题] *A.1001101B.1002002C.10010101(正确答案)D.10020214.“管理费用”科目通常设置的辅助核算是() [单选题] *A.个人往来B.部门往来(正确答案)C.项目核算D.客户行来5.()可以指定某账套的套主管。
[单选题] *A.财务主管B.软件作员C.系统管理员(正确答案)D.财务总监6.不属于建立账套时应建立的信息的是() [单选题] *A.设置账套信息B.设置单位信息C.确定核算类型D.编入期初余额(正确答案)7.以系统管理员的身份注册系统管理,不能进行的操作是() [单选题] *A.建立账套B.修改账套(正确答案)C.输出账套D.引入账套8.系统最多可以建立()套账。
[单选题] *A.996B.997C.998D.999(正确答案)9.建立套时,需要以()的身份注册系统管理 [单选题] *A admin(正确答案)B.财务主管C.账套主管D.财务总监10.一般来说,用友软件中可以为企业里每个独立核算的单位建立一个()[单选题] *A.账套(正确答案)B.报表C.账本D.账页11.对于收款凭证,通常选择()限制类型 [单选题] *A.借方必有(正确答案)B.货方必有C.凭证必有D凭证必无12.若会计科口的编码方案为4-2-2,则某会计科目的三级科目全编码为()。
[单选题] *A.100101B.10010102(正确答案)C.1001010101D.010113.对所管据的账套来说,()是级别最高的,拥有所有模块的操作权限。
新版高一数学必修第一册第三章全部配套练习题(含答案和解析)

新版高一数学必修第一册第三章全部配套练习题(含答案和解析)3.1.1 函数的概念基 础 练巩固新知 夯实基础1.下列说法正确的是( )A .函数值域中每一个数在定义域中一定只有一个数与之对应B .函数的定义域和值域可以是空集C .函数的定义域和值域一定是数集D .函数的定义域和值域确定后,函数的对应关系也就确定了2.若函数y =f (x )的定义域M ={x |-2≤x ≤2},值域为N ={y |0≤y ≤2},则函数y =f (x )的图象可能是( )3.函数f (x )=x -1x -2的定义域为( ) A .[1,2)∪(2,+∞) B .(1,+∞) C .[1,2)D .[1,+∞)4.已知函数f (x )的定义域为[-1,2),则函数f (x -1)的定义域为( )A .[-1,2)B .[0,2)C .[0,3)D .[-2,1)5.函数y =5x +4x -1的值域是( )A .(-∞,5)B .(5,+∞)C .(-∞,5)∪(5,+∞)D .(-∞,1)∪(1,+∞) 6.函数y =x +1的值域为( )A .[-1,+∞)B .[0,+∞)C .(-∞,0]D .(-∞,-1]7.已知函数f (x )=x +1x,则f (2)+f (-2)的值是( )A .-1B .0C .1D .2 8.下列函数完全相同的是( )A .f (x )=|x |,g (x )=(x )2B .f (x )=|x |,g (x )=x 2C .f (x )=|x |,g (x )=x 2x D .f (x )=x 2-9x -3,g (x )=x +39.求下列函数的定义域:(1)f (x )=1x +1; (2)y =x 2-1+1-x 2; (3)y =2x +3; (4)y =x +1x 2-1.10.求下列函数的值域:(1)y =2x +1,x ∪{1,2,3,4,5}; (2)y =x 2-4x +6,x ∪[1,5); (3)y =3-5x x -2; (4)y =x -x +1.能 力 练综合应用 核心素养11.已知等腰∪ABC 的周长为10,则底边长y 关于腰长x 的函数关系为y =10-2x ,此函数的定义域为( )A .RB .{x |x >0}C .{x |0<x <5}D.⎩⎨⎧x ⎪⎪⎭⎬⎫52<x <5 12.函数f (x )=1x 2+1(x ∪R )的值域是( )A .(0,1)B .(0,1]C .[0,1)D .[0,1]13.函数y =f (x )的图象与直线x =a 的交点个数有( )A .必有一个B .一个或两个C .至多一个D .可能两个以上 14.函数y =3-2x -x 2+14-x 2的定义域为____________________(用区间表示).15.函数y =1x -2的定义域是A ,函数y =x 2+2x -3的值域是B ,则A ∩B =________________(用区间表示).16.若函数f (2x -1)的定义域为[0,1),则函数f (1-3x )的定义域为________. 17.若函数y =ax 2+2ax +3的值域为[0,+∞),则a 的取值范围是________. 18.已知函数f (x )=x 21+x 2.(1)求f (2)+f ⎝⎛⎭⎫12,f (3)+f ⎝⎛⎭⎫13的值. (2)求证:f (x )+f ⎝⎛⎭⎫1x 是定值.(3)求f (2)+f ⎝⎛⎭⎫12+f (3)+f ⎝⎛⎭⎫13+…+f (2019)+f ⎝⎛⎭⎫12019的值.19.已知函数y =mx 2-6mx +m +8的定义域是R ,求实数m 的取值范围.20.已知函数f (x )=3-x +1x +2的定义域为集合A ,B ={x |x <a }. (1)求集合A ;(2)若A ∪B ,求a 的取值范围;(3)若全集U ={x |x ≤4},a =-1,求∪U A 及A ∩(∪U B ).【参考答案】1. C 解析 根据从集合A 到集合B 函数的定义可知,强调A 中元素的任意性和B 中对应元素的唯一性,所以A 中的多个元素可以对应B 中的同一个元素,从而选项A 错误;同样由函数定义可知,A 、B 集合都是非空数集,故选项B 错误;选项C 正确;对于选项D ,可以举例说明,如定义域、值域均为A ={0,1}的函数,对应关系可以是x →x ,x ∪A ,可以是x →x ,x ∪A ,还可以是x →x 2,x ∪A .2. B 解析 A 中定义域是{x |-2≤x ≤0},不是M ={x |-2≤x ≤2},C 中图象不表示函数关系,D 中值域不是N ={y |0≤y ≤2}.3. A 解析 由题意知,要使函数有意义,需满足⎩⎪⎨⎪⎧x -1≥0,x -2≠0即x ≥1且x ≠2.4. C 解析 ∪f (x )的定义域为[-1,2),∪-1≤x -1<2,得0≤x <3,∪f (x -1)的定义域为[0,3).5. C 解析 ∪y =5x +4x -1=5(x -1)+9x -1=5+9x -1,且9x -1≠0,∪y ≠5,即函数的值域为(-∞,5)∪(5,+∞).6. B 解析 由于x +1≥0,所以函数y =x +1的值域为[0,+∞).7. B 解析 f (2)+f (-2)=2+12-2-12=0.8. B 解析 A 、C 、D 的定义域均不同.9. 解 (1)要使函数有意义,即分式有意义,则x +1≠0,x ≠-1.故函数的定义域为{x |x ≠-1}.(2)要使函数有意义,则⎩⎪⎨⎪⎧ x 2-1≥0,1-x 2≥0,即⎩⎪⎨⎪⎧x 2≥1,x 2≤1.所以x 2=1,从而函数的定义域为{x |x =±1}={1,-1}. (3)函数y =2x +3的定义域为{x |x ∪R }.(4)因为当x 2-1≠0,即x ≠±1时,x +1x 2-1有意义,所以原函数的定义域是{x |x ≠±1,x ∪R }.10. 解 (1)∪x ∪{1,2,3,4,5},∪(2x +1)∪{3,5,7,9,11},即所求函数的值域为{3,5,7,9,11}.(2)y =x 2-4x +6=(x -2)2+2. ∪x ∪[1,5),∪其图象如图所示, 当x =2时,y =2;当x =5时,y =11. ∪所求函数的值域为[2,11).(3)函数的定义域为{x |x ≠1},y =3-5x x -2=-5(x -2)+7x -2=-5-7x -2,所以函数的值域为{y |y ≠-5}.(4)要使函数式有意义,需x +1≥0,即x ≥-1,故函数的定义域为{x |x ≥-1}.设t =x +1,则x =t 2-1(t ≥0),于是y =t 2-1-t =⎝⎛⎭⎫t -122-54,又t ≥0,故y ≥-54,所以函数的值域为{y |y ≥-54}. 11. D 解析 ∪ABC 的底边长显然大于0,即y =10-2x >0,∪x <5,又两边之和大于第三边,∪2x >10-2x ,x >52,∪此函数的定义域为⎩⎨⎧x ⎪⎪⎭⎬⎫52<x <5.12. B 解析 由于x ∪R ,所以x 2+1≥1,0<1x 2+1≤1,即0<y ≤1.13. C 解析 当a 在f (x )定义域内时,有一个交点,否则无交点.14. [-1,2)∪(2,3] 解析 使根式3-2x -x 2有意义的实数x 的集合是{x |3-2x -x 2≥0}即{x |(3-x )(x +1)≥0}={x |-1≤x ≤3},使分式14-x 2有意义的实数x 的集合是{x |x ≠±2},所以函数y =3-2x -x 2+14-x 2的定义域是{x |-1≤x ≤3}∩{x |x ≠±2}={x |-1≤x ≤3,且x ≠2}.15. [0,2)∪(2,+∞) 解析 要使函数式y =1x -2有意义,只需x ≠2,即A ={x |x ≠2};函数y =x 2+2x -3=(x +1)2-4≥0,即B ={y |y ≥0},则A ∩B ={x |0≤x <2或x >2}.16. ⎝⎛⎦⎤0,23 解 因为f (2x -1)的定义域为[0,1),即0≤x <1,所以-1≤2x -1<1.所以f (x )的定义域为[-1,1).所以-1≤1-3x <1,解得0<x ≤23.所以f (1-3x )的定义域为⎝⎛⎦⎤0,23. 17. [3,+∞) 解析 函数y =ax 2+2ax +3的值域为[0,+∞),则函数f (x )=ax 2+2ax +3的值域要包括0,即最小值要小于等于0.则{ a >0,Δ=4a 2-12a ≥0,解得a ≥3.所以a 的取值范围是[3,+∞).18. 解 (1)因为f (x )=x 21+x 2,所以f (2)+f ⎝⎛⎭⎫12=221+22+⎝⎛⎭⎫1221+⎝⎛⎭⎫122=1,f (3)+f ⎝⎛⎭⎫13=321+32+⎝⎛⎭⎫1321+⎝⎛⎭⎫132=1. (2)证明:f (x )+f ⎝⎛⎭⎫1x =x 21+x 2+⎝⎛⎭⎫1x 21+⎝⎛⎭⎫1x 2=x 21+x 2+1x 2+1=x 2+1x 2+1=1. (3)由(2)知f (x )+f ⎝⎛⎭⎫1x =1,所以f (2)+f ⎝⎛⎭⎫12=1,f (3)+f ⎝⎛⎭⎫13=1,f (4)+f ⎝⎛⎭⎫14=1,…,f (2019)+f ⎝⎛⎭⎫12019=1. 所以f (2)+f ⎝⎛⎭⎫12+f (3)+f ⎝⎛⎭⎫13+…+f (2019)+f ⎝⎛⎭⎫12019=2018. 19. 解 ∪当m =0时,y =8,其定义域是R .∪当m ≠0时,由定义域为R 可知,mx 2-6mx +m +8≥0对一切实数x 均成立,于是有⎩⎪⎨⎪⎧m >0,Δ=(-6m )2-4m (m +8)≤0,解得0<m ≤1.由∪∪可知,m ∪[0,1]. 20. 解 (1)使3-x 有意义的实数x 的集合是{x |x ≤3},使1x +2有意义的实数x 的集合是{x |x >-2}. 所以,这个函数的定义域是{x |x ≤3}∩{x |x >-2}={x |-2<x ≤3}.即A ={x |-2<x ≤3}. (2)因为A ={x |-2<x ≤3},B ={x |x <a }且A ∪B ,所以a >3.(3)因为U ={x |x ≤4},A ={x |-2<x ≤3},所以∪U A =(-∞,-2]∪(3,4]. 因为a =-1,所以B ={x |x <-1},所以∪U B =[-1,4],所以A ∩∪U B =[-1,3].3.1.2 函数的表示法基 础 练巩固新知 夯实基础1.小明骑车上学,开始时匀速行驶,途中因交通堵塞停留了一段时间后,为了赶时间加快速行驶.与以上事件吻合得最好的图象是( )2.已知f (x )是一次函数,2f (2)-3f (1)=5,2f (0)-f (-1)=1,则f (x )=( )A .3x +2B .3x -2C .2x +3D .2x -33.已知函数f (x )=⎩⎪⎨⎪⎧x +1,x ∪[-1,0],x 2+1,x ∪0,1],则函数f (x )的图象是( )4.已知函数y =f (x )的对应关系如下表,函数y =g (x )的图象是如图的曲线ABC ,其中A (1,3),B (2,1),C (3,2),则f [g (2)]的值为( )A .3B .2C .1D .0 5.函数f (x )=⎩⎪⎨⎪⎧2x 2,0≤x ≤1,2,1<x <2,3,x ≥2的值域是( )A.RB.[0,+∞)C.[0,3]D.{x |0≤x ≤2或x =3} 6.设f (x )=⎩⎪⎨⎪⎧x +1,x >0,1,x =0,-1,x <0,则f (f (0))等于( )A.1B.0C.2D.-17.已知f (2x +1)=3x -2且f (a )=4,则a 的值为________.8.已知f (x )是一次函数,且满足3f (x +1)-2f (x -1)=2x +17,求f (x )的解析式.9.已知二次函数f (x )满足f (0)=0,且对任意x ∪R 总有f (x +1)=f (x )+x +1,求f (x ).10 (1)已知f (x +1x )=x 2+1x2,求f (x )的解析式.(2)已知f (x )满足2f (x )+f (1x )=3x ,求f (x )的解析式.(3)已知f (x )+2f (-x )=x 2+2x ,求f (x )的解析式.能 力 练综合应用 核心素养11.如果f ⎝⎛⎭⎫1x =x1-x ,则当x ≠0,1时,f (x )等于( )A.1xB.1x -1C.11-xD.1x-1 12.已知x ≠0时,函数f (x )满足f (x -1x )=x 2+1x 2,则f (x )的表达式为( )A .f (x )=x +1x (x ≠0) B .f (x )=x 2+2(x ≠0)C .f (x )=x 2(x ≠0)D .f (x )=(x -1x)2(x ≠0)13.已知函数y =⎩⎪⎨⎪⎧x 2+1,x ≤0,-2x ,x >0,则使函数值为5的x 的值是( )A.-2或2B.2或-52C.-2D.2或-2或-5214.若f (x )是一次函数,2f (2)-3f (1)=5,2f (0)-f (-1)=1,则f (x )=( )A .3x +2B .3x -2C .2x +3D .2x -3 15.已知f (x -1)=x 2,则f (x )的解析式为( )A .f (x )=x 2+2x +1B .f (x )=x 2-2x +1C .f (x )=x 2+2x -1D .f (x )=x 2-2x -116.已知f (n )=⎩⎪⎨⎪⎧n -3,n ≥10,f f n +5,n <10,则f (8)=________.17.已知函数y =f (x )满足f (x )=2f (1x )+x ,则f (x )的解析式为____________.18. 已知函数f (x )=1+|x |-x2(-2<x ≤2).(1)用分段函数的形式表示该函数; (2)画出该函数的图象; (3)写出该函数的值域.19.设f (x )是R 上的函数,且满足f (0)=1,并且对任意实数x ,y ,有f (x -y )=f (x )-y (2x -y +1),求f (x )的解析式.【参考答案】1. C 解析 先分析小明的运动规律,再结合图象作出判断.距学校的距离应逐渐减小,由于小明先是匀速运动,故前段是直线段,途中停留时距离不变,后段加速,直线段比前段下降的快,故应选C.2. B 解析 设f (x )=kx +b (k ≠0),∪2f (2)-3f (1)=5,2f (0)-f (-1)=1,∪⎩⎪⎨⎪⎧ k -b =5k +b =1,∪⎩⎪⎨⎪⎧k =3b =-2,∪f (x )=3x -2. 3. A 解析 当x =-1时,y =0,排除D ;当x =0时,y =1,排除C ;当x =1时,y =2,排除B. 4. B 解析 由函数g (x )的图象知,g (2)=1,则f [g (2)]=f (1)=2.5. D 解析 当0≤x ≤1时,f (x )∪[0,2],当1<x <2时,f (x )=2,当x ≥2时,f (x )=3, ∪值域是{x |0≤x ≤2或x =3}.6. C7. 5 解析 ∪f (2x +1)=3x -2=32(2x +1)-72,∪f (x )=32x -72,∪f (a )=4,即32a -72=4,∪a =5.8. 解 设f (x )=ax +b (a ≠0),则3f (x +1)-2f (x -1)=3ax +3a +3b -2ax +2a -2b =ax +5a +b ,即ax +5a +b =2x +17不论x 为何值都成立,∪⎩⎪⎨⎪⎧ a =2,b +5a =17,解得⎩⎪⎨⎪⎧a =2,b =7,∪f (x )=2x +7. 9. 解 设f (x )=ax 2+bx +c (a ≠0),∪f (0)=c =0,∪f (x +1)=a (x +1)2+b (x +1)+c =ax 2+(2a +b )x +a +b , f (x )+x +1=ax 2+bx +x +1=ax 2+(b +1)x +1.∪⎩⎪⎨⎪⎧2a +b =b +1,a +b =1. ∪⎩⎨⎧a =12,b =12.∪f (x )=12x 2+12x .10. 解 (1)∪f (x +1x )=x 2+1x 2=(x +1x )2-2,且x +1x ≥2或x +1x ≤-2,∪f (x )=x 2-2(x ≥2或x ≤-2).(2)∪2f (x )+f (1x )=3x ,∪把∪中的x 换成1x ,得2f (1x )+f (x )=3x .∪, ∪×2-∪得3f (x )=6x -3x ,∪f (x )=2x -1x (x ≠0).(3)以-x 代x 得:f (-x )+2f (x )=x 2-2x .与f (x )+2f (-x )=x 2+2x 联立得:f (x )=13x 2-2x .11. B 解析 令1x =t ,则x =1t ,代入f ⎝⎛⎭⎫1x =x 1-x ,则有f (t )=1t1-1t =1t -1,故选B. 12. B 解析 ∪f (x -1x )=x 2+1x 2=(x -1x)2+2,∪f (x )=x 2+2(x ≠0).13. C14. B 解析 设f (x )=ax +b ,由题设有⎩⎪⎨⎪⎧ 2(2a +b )-3(a +b )=5,2(0·a +b )-(-a +b )=1.解得⎩⎪⎨⎪⎧a =3,b =-2.所以选B.15. A 解析 令x -1=t ,则x =t +1,∪f (t )=f (x -1)=(t +1)2=t 2+2t +1,∪f (x )=x 2+2x +1.16. 7 解析 因为8<10,所以代入f (n )=f (f (n +5)),即f (8)=f (f (13));因为13>10,所以代入f (n )=n -3,得f (13)=10,故得f (8)=f (10)=10-3=7.17. f (x )=-x 2+23x (x ≠0) 解析 ∪f (x )=2f (1x )+x ,∪∪将x 换成1x ,得f (1x )=2f (x )+1x .∪由∪∪消去f (1x ),得f (x )=-23x -x3,即f (x )=-x 2+23x(x ≠0).18.解 (1)∪当0≤x ≤2时,f (x )=1+x -x 2=1;∪当-2<x <0时,f (x )=1+-x -x2=1-x .所以f (x )=⎩⎪⎨⎪⎧1,0≤x ≤2,1-x ,-2<x <0.(2)函数f (x )的图象如图所示.(3)由函数f (x )的图象知,f (x )在(-2,2]上的值域为[1,3).19 .解 因为对任意实数x ,y ,有f (x -y )=f (x )-y (2x -y +1),所以令y =x ,有f (0)=f (x )-x (2x -x +1),即f (0)=f (x )-x (x +1). 又f (0)=1,∪f (x )=x (x +1)+1=x 2+x +1.3.2.1 第1课时 函数的单调性基 础 练巩固新知 夯实基础1.函数f (x )的定义域为(a ,b ),且对其内任意实数x 1,x 2均有(x 1-x 2)(f (x 1)-f (x 2))<0,则f (x )在(a ,b )上( ) A .增函数B .减函数C .不增不减函数D .既增又减函数2.若函数f (x )在区间(a ,b )上是增函数,在区间(b ,c )上也是增函数,则函数f (x )在区间(a ,b )∪(b ,c )上( )A .必是增函数B .必是减函数C .是增函数或减函数D .无法确定单调性3.如果函数f (x )在[a ,b ]上是增函数,那么对于任意的x 1,x 2∪[a ,b ](x 1≠x 2),下列结论中不正确的是( ) A.f x 1-f x 2x 1-x 2>0B .(x 1-x 2)[f (x 1)-f (x 2)]>0C .若x 1<x 2,则f (a )<f (x 1)<f (x 2)<f (b ) D.x 1-x 2f x 1-f x 2>0 4.对于函数y =f (x ),在给定区间上有两个数x 1,x 2,且x 1<x 2,使f (x 1)<f (x 2)成立,则y =f (x )( )A .一定是增函数B .一定是减函数C .可能是常数函数D .单调性不能确定5.下列函数中,在(-∞,0]内为增函数的是( ) A .y =x 2-2 B .y =3xC .y =1+2xD .y =-(x +2)26.已知函数f (x )=x 2+bx +c 的图象的对称轴为直线x =1,则( )A .f (-1)<f (1)<f (2)B .f (1)<f (2)<f (-1)C .f (2)<f (-1)<f (1)D .f (1)<f (-1)<f (2)7.若函数f (x )=2x 2-mx +3,当x ∪[-2,+∞)时是增函数,当x ∪(-∞,-2)时是减函数,则f (1)=________.8.已知函数f (x )=⎩⎪⎨⎪⎧(a -3)x +5,x ≤1,2a x ,x >1是R 上的减函数,则实数a 的取值范围是 。
第三章 习题解答-2.0
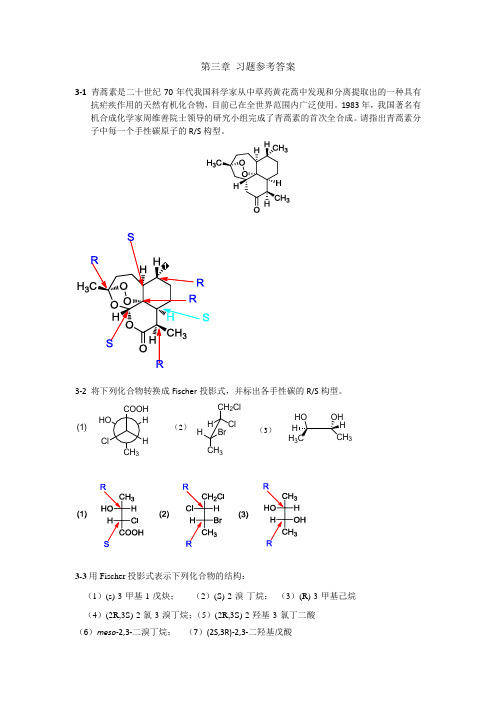
第三章 习题参考答案3-1 青蒿素是二十世纪70年代我国科学家从中草药黄花蒿中发现和分离提取出的一种具有抗疟疾作用的天然有机化合物,目前已在全世界范围内广泛使用。
1983年,我国著名有机合成化学家周维善院士领导的研究小组完成了青蒿素的首次全合成。
请指出青蒿素分子中每一个手性碳原子的R/S 构型。
3-2 将下列化合物转换成Fischer 投影式,并标出各手性碳的R/S 构型。
(2)(3)3BrHCH 3HClCH 2ClH 3H 3(1)3-3用Fischer 投影式表示下列化合物的结构:(1)(s)-3-甲基-1-戊炔; (2)(S)-2-溴-丁烷; (3)(R)-3-甲基己烷 (4)(2R,3S)-2-氯-3-溴丁烷;(5)(2R,3S)-2-羟基-3-氯丁二酸 (6)meso -2,3-二溴丁烷; (7)(2S,3R)-2,3-二羟基戊酸本题答案不唯一。
在画Fisher投影式时,习惯把含碳原子的基团放在竖键上,并把命名时编号最小的碳原子放在上端。
以下是较为符合习惯的Fisher投影式。
3-4下列化合物中哪些有手性?(1)、(3)、(5)、(7)、(9)无手性(2)、(4)、(6、)(8)、(10)有手性3-5长尾粉蚧壳虫信息素A是雌性长尾粉蚧壳虫(一种植物害虫)分泌的性激素,其外消旋体目前已被人工合成,并商业化用于农田害虫的控制和诱杀。
最近,化学家通过全合成途径确定了天然长尾粉蚧壳虫信息素的绝对构型(J. Org. Chem. 2013, 78, 6281−6284)。
通过全合成方法分别得到了A的2种立体异构体,发现其中的(S)-(+)-异构体具有吸引雄性长尾粉蚧壳虫的活性,而它的对映体(R)-( )-A则无此生物活性。
此结果表明雌性长尾粉蚧壳虫分泌的天然长尾粉蚧壳虫信息素为(S)-A。
商业化使用的外消旋体与纯的(S)-对映体生物活性相似,说明(R)-A对(S)-A的生物活性无抑制作用。
写出(R)-A和(S)-A的结构式。
模拟电子技术第三章 习题与答案

第三章习题与答案3.1 问答题:1.什么是反馈?答:在电子线路中,把输出量(电压或电流)的全部或者一部分,以某种方式反送回输入回路,与输入量(电压或电流)进行比较的过程。
2.什么是正反馈?什么是负反馈?放大电路中正、负反馈如何判断?答:正反馈:反馈回输人端的信号加强原输入端的信号,多用于振荡电路。
负反馈:反馈回输入端的信号削弱原输入端的信号,使放大倍数下降,主要用于改善放大电路的性能。
反馈极性的判断,通常采用瞬时极性法来判别。
通常假设某一瞬间信号变化为增加量时.我们定义其为正极性,用“+”表示。
假设某一瞬间信号变化为减少量时,我们定义其为负极性,用“-”表示。
首先假定输入信号某一瞬时的极性,一般都假设为正极性.再通过基本放大电路各级输入输出之间的相位变化关系,导出输出信号的瞬时极性;然后通过反馈通路确定反馈信号的瞬时极性;最后由反馈信号的瞬时极性判别净输入是增加还是减少。
凡是增强为正反馈,减弱为负反馈。
3.什么是电压负反馈?什么是电流负反馈?如何判断?答:根据反馈信号的取样方式,分为电压反馈和电流反馈。
凡反馈信号正比于输出电压,称为电压反馈;凡反馈信号正比于输出电流,称为电流反馈。
反馈信号的取样方式的判别方法,通常采用输出端短路法,方法是将放大器的输出端交流短路时,使输出电压等于零,如反馈信号消失,则为电压反馈,如反馈信号仍能存在,则为电流反馈。
这是因为电压反馈信号与输出电压成比例,如输出电压为零,则反馈信号也为零;而电流反馈信号与输出电流成比例,只有当输出电流为零时,反馈信号才为零,因此,在将负载交流短路后,反馈信号不为零。
4.什么是串联负反馈?什么是并联负反馈?如何判断?答:输入信号与反馈信号分别加在两个输入端,是串联反馈;加在同一输入端的是并联反馈。
反馈信号使净输入信号减小的,是负反馈。
判断反馈的极性,要采用瞬时极性法。
3.2 填空题:1.放大电路中,为了稳定静态工作点,可以引入直流负反馈;如果要稳定放大倍数,应引入交流负反馈;希望扩展频带,可以引入交流负反馈;如果增大输入电阻,应引入串联负反馈;如果降低输比电阻,应引入电压负反馈。
第3章习题

第3章 导数的应用3.1 微分中值定理一、填空题1. 在中的满足拉格朗日中值定理上,函数21)(]3,1[x x f -=-_______;=ξ2. 若内,则在)1,1(,1)(32--=x x f )(x f '恒不为0,即]11[)(,在-x f 不满足罗尔定理的一个条件是___________;.*3函数条件,上满足柯西中值定理的在及)0](,[)(F )(2>>==a b b a x x e x f x 即存在点_________;),,(有b a ∈ξ4.),3)(2)(1()(---=x x x x x f 则方程0)(='x f 有__________个实根,分别位于区间____________内。
二、证明)2121(,)43arccos(arccos 33≤≤-=--x x x x π。
三、说明函数]01[)(23,在区间-+=x x x f 上满足罗尔定理的三个条件,并求出ξ的值,使0)(='ξf 。
四、下列函数在给定区间上是否满足罗尔定理的条件?如果满足就求出定理中的ξ的值: 1.,32)(2--=x x x f ]3,1[- ; 2. x x x f -=3)(, ]3,0[; 3 .1)(2-=x ex f , ]1,1[- ; 4. x x f sin ln )(=, ]65,6[ππ。
五、不求导数,判断函数x x x x f 23)(23+-=的导数有几个实根,并求他们实根的所在范围。
六、下列函数在指定区间上是否满足拉格朗日中值定理的条件,如果满足,找出使定理结论成立的ξ的值:1. 12)(2++=x x x f , ]3,1[- ; 2*. ,arctan )(x x f = ]1,0[;3. ,ln )(x x f = [1,2]。
3.2 函数的单调性与极值一、填空题1. 函数xe y x=的单调增区间是___________,单调减区间是_____________;2. 32)1(x x y ⋅-=在21__________________x x 值,在处有极==_________处有极__________值;3. 方程015=-+x x 在实数范围内有___________个实根;4. 若函数b a x bx ax x f ________,21)(2==+=,则处取极大值在点=________;.*5;_________)3(2,3sin 31sin )(值为极时,πf a x x a x f =+=6. 函数)12(2431)(3≤≤-+-=x x x x f 的最大值为___________,最小值为___________; 7. 函数11)(+-=x x x f 在区间[]4,0上的最大值为___________,最小值为___________; 8.==≤-=x x x x x x f 处有最大值,在在_________)2(2sin )(π___________处有最小值;.*9设b ax ax x f +-=226)(在区间]2,1[-上的最大值为3,最小值为29-,又知。
