混凝土本构数据
混凝土随机损伤本构模型与试验研究

混凝土随机损伤本构模型与试验研究混凝土材料在工程中广泛应用,其力学性能的研究一直是工程学领域的热点。
混凝土的随机损伤本构模型是近年来混凝土力学研究的一个重要方向。
本文将介绍混凝土随机损伤本构模型及其试验研究。
一、混凝土随机损伤本构模型混凝土材料的力学性能受到多种因素的影响,如材料的组成、结构、加载方式等。
在实际工程中,混凝土材料常常会受到多种力的作用,如轴向拉拉力、剪力、弯矩等。
因此,混凝土的本构模型需要考虑多种因素的影响。
混凝土随机损伤本构模型是一种能够考虑混凝土随机损伤的力学模型。
该模型将混凝土材料视为一个由多个单元组成的体系,每个单元都有可能发生损伤。
损伤会导致单元的刚度和强度降低,最终影响整个混凝土体系的力学性能。
混凝土随机损伤本构模型的基本思想是将混凝土体系分解为多个单元,每个单元都有可能发生损伤。
单元的损伤程度可以用一个参数来表示,该参数称为损伤变量。
损伤变量的值越大,表示单元的损伤程度越严重。
混凝土随机损伤本构模型的本质是一个随机过程,其基本形式可以表示为:$$sigma_{ij}=frac{1}{V}sum_{k=1}^{N}sigma_{ij}^k(1-d_k)$$ 其中,$sigma_{ij}$表示混凝土体系的应力张量,$V$为混凝土体系的体积,$N$为单元的数量,$sigma_{ij}^k$表示第$k$个单元的应力张量,$d_k$表示第$k$个单元的损伤变量。
混凝土随机损伤本构模型的主要优点是能够考虑混凝土材料的随机性和多种因素的影响。
然而,该模型也存在一些问题,如计算复杂度较高、参数难以确定等。
二、混凝土随机损伤本构模型的试验研究混凝土随机损伤本构模型的试验研究是验证模型有效性的重要手段。
目前,国内外研究者已经开展了大量的混凝土随机损伤本构模型的试验研究,取得了一些重要的成果。
首先,研究者通过轴向拉伸试验、三轴压缩试验、剪切试验等方法,获得了混凝土材料的力学性能参数。
这些参数包括弹性模量、泊松比、极限强度、损伤变量等,为混凝土随机损伤本构模型的建立提供了基础数据。
混凝土的本构关系曲线怎么画

混凝土的本构关系曲线怎么画
混凝土的本构关系曲线是研究混凝土在不同应力下的应变变化关系的曲线。
通常,绘制混凝土的本构关系曲线需要进行以下步骤:
1. 收集实验数据:进行混凝土材料的实验,测量不同应力下的应变。
2. 绘制应力和应变的图表:选取实验数据中的应力值和对应的应变值,通过坐标轴绘制图表。
3. 拟合曲线:采用适当的数学模型,将实验数据拟合成连续的曲线。
通常,常用的拟合模型有线性弹性模型和非线性弹性模型等。
4. 添加强度削减:考虑到混凝土在受到较高应力时的强度削减,可以在曲线上进行相应的强度削减处理。
需要注意的是,混凝土的本构关系曲线受到多种因素的影响,包括混凝土配合比、配筋率、龄期等,因此在实际应用中可能会存在一定的差异。
绘制曲线时需根据具体情况进行选择和调整。
混凝土本构模型

高等混凝土结构学课程报告学生:汤鹏学号:2010202100018班级:硕士一班老师:何英明教授日期:2011.8混凝土非线性弹性本构模型有三种不同形式的基于弹性的本构模型用在一般公式中,它们是: (1)Cauchy 型;(2)Green(超弹性)型;(3)增量(亚弹性)型。
1) Cauchy 型的全应力—应变公式在Cauchy 弹性材料模型中,将当前的应力状态σij 惟一地表示成当前应变状态εkl 的函数,即σij =F ij (εkl )上式描述的弹性性质是可逆的和路径无关的,从这种意义上讲,应力由应变的当前状态惟一确定,反之亦然,材料性质与达到当前应力或应变状态的应力或应变历史没有相关性。
然而,一般地,应力由应变惟一确定或相反,而逆命题不一定正确。
而且,应变能W (εij )和余能密度函数Ω(σij )的可逆性和与路径无关的情况通常不能保证,0()()ijijij ij ij ij ij ijW d d εσεσεσεσ=Ω=⎰⎰已经证明,Cauchy 型弹性模型在加载-卸载循环中要产生能量。
这就是说,这类模型违背了热力学原理(实际上是不能接受的),这自然就让人想到第二类公式,Green 超弹性型。
一般说来,Cauchy 型各向异性线弹性模型有36个材料弹性模量。
对于最简单的各向同性线弹性材料,这个数目将减少到两个(E 和μ,或K 和G),相应的应力—应变关系简化为熟悉的广义虎克定律。
2) Green(超弹性)型的全应力—应变公式严格地说,弹性材料必须满足热力学平衡方程。
由此附加要求表征的弹性模型就叫做Green 超弹性型,此类模型的基础是假定有如下的应变能W (εij )和余能密度函数Ω(σij )ij ij ijijW σεεσ∂∂Ω==∂∂式中,W 和Ω分别是当前应变张量和应力张量分量的函数,这就保证了在加载循环过程中没有能量产生,热力学准则总能满足。
对初始各向同性弹性材料,w 或Ω分别用任意三个独立的应变或应力张量εij 或σij 的不变量表示。
ABAQUS混凝土本构关系C60
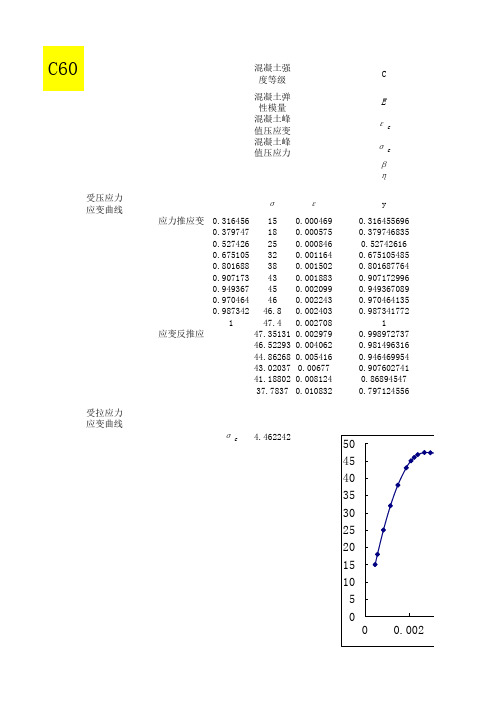
0 1.4E-05 7.02E-05 0.000173 0.000327 0.000554 0.000708 0.000821 0.000958 0.001244 0.001516 0.002625 0.00403 0.00544 0.00685 0.009663
系…
0.002
0.004
0.006
0.008
C60
混凝土强度等级 混凝土弹性模量 混凝土峰值压应变 混凝土峰值压应力
C
E
ε σ β η
c c
受压应力应变曲线 应力推应变 0.316456 0.379747 0.527426 0.675105 0.801688 0.907173 0.949367 0.970464 0.987342 1 应变反推应力
y 0.316455696 0.379746835 0.52742616 0.675105485 0.801687764 0.907172996 0.949367089 0.970464135 0.987341772 1 0.998972737 0.981496316 0.946469954 0.907602741 0.86894547 0.797124556
混凝土强度等级c混凝土弹性模量e混凝土峰值压应变c混凝土峰值压应力c受压应力应变曲线y应力推应变031645615000046903164556960379747180000575037974683505274262500008460527426160675105320001164067510548508016883800015020801687764090717343000188309071729960949367450002099094936708909704644600022430970464135098734246800024030987341772147400027081应变反推应力473513100029790998972737465229300040620981496316448626800054160946469954430203700067709076027414118802000812408689454737783700108320797124556受拉应力应变曲线c4462242混凝土强度等级cc60c400510152025303540455000002混凝土弹性模量e混凝土峰值压应变c混凝土峰值压应力c受压应力应变曲线y应力推应变0210976666667000028021097046403797471200005330379746835052742616666670000785052742616067510521333330001079067510548508016882533333000139208016877640907173286666700017460907172996094936730000194609493670890970464306666700020790970464135098734231200022280987341772131600027081应变反推应力3157349000297909991610853101528000406209814963162990845000541609464699542868025000677090760274127458680008124086894547251891400108320797124556受拉应力应变曲线c340532860混凝土圆柱体抗压强度fc079fcu混凝土结构第10页325649421900018925o00
钢筋混凝土破坏准则及本构关系
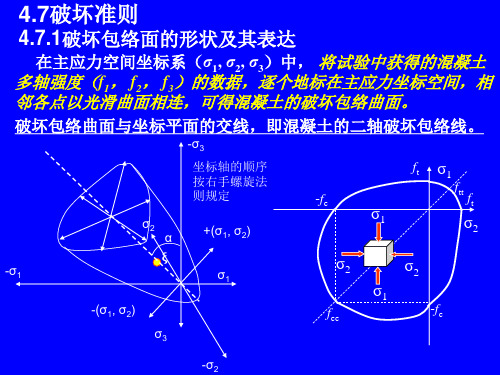
一些常用的、有代表性的混凝土破坏准则列于下表 , 同时给出了原始表达式和统一表达式,可看到两者中 参数的互换关系。
过镇海、王传志、张秀琴等搜集了国内外大量的混 凝士多轴强度试验数据,与按上述准则计算的理论值 进行全面比较,根据三项标准: ①计算值与试验强度的相符程度; ②适用的应力范围宽窄; ③理论破坏包络面几何特征的合理性等加以评定。 所得结论为: 较好的准则:过—王、Ottosen和Podgorski准则; 一般的准则:Hsieh-Ting-Chen,Kotsovos, WillamWarnke准则; 较差准则:Bresler-Pister准则。 在结构的有限元分析中,可根据结构的应力范围和 准确度要求选用合理的混凝土破坏准则。
σ3
转换过 程归纳
ξ
o
3 oct
θ
ξ
静水应力
3 oct
r σ1 =σ2 = σ3 N σ2
σ1
圆柱坐标系及主应 力空间应力分解 σ 1 -σ3 偏斜应力 平面中矢 量的方向 σ2 偏平面 P r θ N σ3 -σ1
-σ3 σ1 -σ2
ξ,r,θ的几何表示 偏平面
压子午线 θ=60o rc rt
3、以混凝土多轴强度试验资料为基础的经验回归式
随试验数据的积累,许多研究人员提出了若干基于试验结果、 较为准确、但数学形式复杂的混凝土破坏准则。准则中一般需 要包含4~5个参数。
这些破坏准则的原始表达式中采用了不同的应力量作 为变量,分5种: ①主应力—fl , f2, f3 ; ②应力不变量—Il ,J2,J3 ; ③静水压力和偏应力—ξ , r,θ; ④八面体应力— σoct ,τoct ; ⑤平均应力—σm ,τm θ。 采用上述应力量致使准则的数学形式差别很大,不 便作深入对比分析。但这些应力量借助下列基本公式 可以很方便地互相变换:
混凝土工程施工常用数据

Ф12、l=180
对拉螺栓
M12、M14、M16
扣件
3形扣件
26型、12型
碟形扣件
26型、18型
3、支承件规格
钢楞
圆钢管型
Ф48×3.5
矩形钢管型
□80×40×2.0,
□100×50×3.0
轻型槽钢型
80×40×3.0, 100×50×3.0
内卷边槽钢型
80×40×15×3.0, 100×50×20×3.0
弯曲
小于(2/1000)L
直径
-0.5
丝扣接头中心
0.25
5、滑升模板组装允许偏差
项目
允许偏差mm
备注
模板中心线与相应位置结构中心线的偏移
3
尺检
提升架横梁水平度
平面内
2
尺检
平面外
1
提升架立柱垂直度
平面内
3
2m靠尺检查
平面外
2
模板位置
上口
-1
尺检
下口
+2
千斤顶安装位置
5
尺检
相邻模板板面平整
2
尺检
操作平台水平度
长度
1500、1200、900、750、600、450
肋高
55
圆棱模板
倒棱模板
宽度
R20、R35
长度
1500、1200、900、750、600、450
肋高
55
梁腋模板
宽度
50×150、50×100
长度
1500、1200、900、750、600、450
肋高
55
柔性模板
宽度
100
长度
1500、1200、900、750、600、450
HJC本构模型(翻译)
精心整理基于大应变、高应变率、高压力的混凝土计算基本模型美国明尼苏达州霍普金斯阿连特科技股份有限公司美国佛罗里达州埃格林空军基地武器理事会怀特实验室c 特定表达式为:]ln 1][)1([*'**εσC BP D A N ++-=(1)其中,D 指损伤度(0≤D ≤1.0),c f P P '*/=指无量纲静水压力(其中P 指实际压力),.0.*/εεε=,指无量纲应变率(其中.ε为实际应变率,1.00.1-=s ε为参考应变率)。
无量纲最大静水拉力为c f T T '*/=,其中,T 指混凝土能承受的最大静水拉力。
混凝土常量参数包括A 、B 、N 、C 以及SMAX 。
其中,A 指标准凝聚强度,B 指标准强度增大系数,N 指压力增大指数,C 指应变率敏感系数,SMAX 指标准最大发展强度。
混凝土断裂损伤如图1中左下角图所示,其损伤发展累积过程与Johnson-Cook 断裂模型[2]相似。
Johnson-Cook 断裂模型描述的是等效塑性应变过程中的损伤累积,而本文模型从等效塑性应变和塑性体积应变两方面讨论损伤图错误!未指定顺序。
模型描述累积,公式表示为:(2) 其中,p ε∆和p μ∆表示一个计算循环内的等效塑性应变和塑性体积应变;)(P f f p f p =+με表示在常压作用下断裂的塑性应变。
特定表达式为:2**)(1D f p f p T P D +=+με(3)式中,D1和D2为损伤常量,P *和T *同前文定义。
由式3可以明显看出,当P *=-T *时混凝土材料不*即EFMIN 变,T 按内插后,混凝土材其中,1/0-ρρg ,g ρ对于拉力,在弹性阶段为μ⋅=e K P ,在完全密实阶段为μ⋅=1K P ,在过渡阶段为μ⋅⋅+⋅-=]1)1[(K F K F P e 。
内插因子为)/()(max c pl c F μμμμ--=,m ax μ为卸载的最大体积应变,pl μ为压力l P 时的体积应变。
混凝土参数
混凝土参数常规C10、C15、C20、C25、C30混凝土配合比该帖被浏览了137166次| 回复了32次混凝土按强度分成若干强度等级,混凝土的强度等级是按立方体抗压强度标准值fcu,k划分的。
立方体抗压强度标准值是立方抗压强度总体分布中的一个值,强度低于该值得百分率不超过5%,即有95%的保证率。
混凝土的强度分为C7.5、C10、C15、C20、C25、C30、C35、C40、C45、C50、C55、C60等十二个等级。
混凝土配合比是指混凝土中各组成材料(水泥、水、砂、石)之间的比例关系。
有两种表示方法:一种是以1立方米混凝土中各种材料用量,如水泥300千克,水180千克,砂690千克,石子1260千克;另一种是用单位质量的水泥与各种材料用量的比值及混凝土的水灰比来表示,例如前例可写成:C:S:G=1:2.3:4.2,W/C=0.6。
常用等级C20水:175kg水泥:343kg 砂:621kg 石子:1261kg配合比为:0.51:1:1.81:3.68C25水:175kg水泥:398kg 砂:566kg 石子:1261kg配合比为:0.44:1:1.42:3.17C30水:175kg水泥:461kg 砂:512kg 石子:1252kg配合比为:0.38:1:1.11:2.72. .普通混凝土配合比参考:水泥品种混凝土等级配比(单位)Kng 塌落度mm 抗压强度N/mm2水泥砂石水7天28天P.C32.5 C20 300 734 1236 195 35 21.0 29.0 1 2.45 4.12 0.65C25 320 768 1153 208 45 19.6 32.1 1 2.40 3.60 0.65C30 370 721 1127 207 45 29.5 35.2 1 1.95 3.05 0.56C35 430 642 1094 17244 32.8 44.1 1 1.49 2.54 0.40C40 480 572 1111 202 50 34.6 50.7 1 1.19 2.31 0.42P.O 32.5 C20 295 707 1203 195 30 20.2 29.1 1 2.40 4.08 0.66C25 316 719 1173 192 50 22.1 32.4 1 2.28 3.71 0.61C30 366 665 1182 187 50 27.9 37.6 1 1.82 3.23 0.51C35 429 637 1184 200 60 30.***6.2 1 1.48 2.76 0.47C40 478 *** 1128 210 60 29.4 51.0 1 1.33 2.36 0.44P.O 32.5R C25 321 749 1173 193 50 26.6 39.1 1 2.33 3.65 0.60C30 360 725 1134 198 60 29.4 44.3 1 2.01 3.15 0.55C35 431 643 1096 190 50 39.0 51.3 1 1.49 2.54 0.44C40 480 572 1111 202 40 39.3 51.0 1 1.19 2.31 0.42P.O 42.5(R) C30 352 676 1202 19055 29.***5.2 1 1.92 3.41 0.54C35 386 643 1194 197 50 34.5 49.5 1 1.67 3.09 0.51C40 398 649 1155 199 55 39.5 55.3 1 1.63 2.90 0.50C50 496 606 1297 223 45 38.4 55.9 1 1.22 2.61 0.45PII 42.5R C30 348 652 1212 188 50 31.***6.0 1 1.87 3.48 0.54C35 380 639 1187 194 50 35.0 50.5 1 1.68 3.12 0.51C40 398 649 1155 199 55 39.5 55.3 1 1.63 2.90 0.50C45 462 618 1147 203 4***2.7 59.1 1 1.34 2.48 0.44C50 480 633 1115 192 25 45.7 62.8 1 1.32 2.32 0.40 P.O 52.5R C40 392 645 1197 196 53 40.2 55.8 1 1.64 3.05 0.50C45 456 622 1156 19***2 43.5 59.5 1 1.36 2.53 0.43C50 468 626 1162192 30 45.2 61.6 1 1.33 2.47 0.41 此试验数据为标准实验室获得,砂采用中砂,细度模数为2.94,碎石为5~31.5mm连续粒级。
混凝土的强度和变形.试验基础和本构关系
混凝土的强度和变形.试验基础和本构关系混凝土的强度和变形是混凝土介质性质的两个重要方面,对于混凝土结构的设计与施工具有重要意义。
本文将从试验基础和本构关系两方面来阐述混凝土的强度和变形性质。
试验基础混凝土的力学性质可以通过单轴压缩试验、双轴剪切试验、拉伸试验等方式来进行测试。
其中,单轴压缩试验是最为基础也是最常用的一种试验方法。
单轴压缩试验的原理是将混凝土样品放置于压力机中,专门用于进行单轴压缩,通过记录每个阶段的载荷和位移,建立混凝土的应力-应变曲线,此曲线是混凝土力学性质的重要量化表达形式。
另一种常用的试验方法是拉伸试验,其与单轴压缩试验的原理类似,不过是反向加载,通常会使用圆柱试样,主要测量拉伸应变。
在双轴剪切试验中,混凝土试样被切成菱形或矩形,并放置于装有应力传感器的剪切盘上,然后施加水平和垂直挤压力, 进而研究混凝土在双轴剪切下的应力应变关系。
本构关系混凝土的本构关系是表征混凝土力学性质的数学模型。
常用的混凝土本构关系有弹性本构关系、线性本构关系和非线性本构关系等几种。
弹性本构关系是最简单的一种本构关系,它假设混凝土在荷载增加或卸载过程中都保持弹性形态。
即混凝土在弹性阶段逐渐反映应力应变的线性关系,弹性模量E为混凝土在单轴压缩状态下的峰值应力f0除以相应的应变ε0,弹性模量的值一般在10-30 GPa之间。
线性本构关系是一种更加复杂的本构模型,它包括弹性和塑性两个部分,即混凝土在加载到一定应力之后开始发生塑性变形。
这种本构关系的基本特征是,剪切强度和体积强度在整个应变区间内保持不变,并且在一定的应力下,应变达到一定程度后应力就将陡然下降。
线性本构关系是常用的本构关系之一,可用于简单的混凝土结构设计中。
非线性本构关系则是一种更加完整复杂的模型,据此可以实现更准确地计算混凝土的强度和变形性能。
这种模型包括多个塑性分支,在每个塑性分支中都有一个极限应变和一个极限应力,表示了混凝土在塑性阶段内随着应变增加而发生的不同形式的塑性变形。
(完整版)ABAQUS中的三种混凝土本构模型
(完整版)ABAQUS中的三种混凝土本构模型ABQUS中的三种混凝土本构模型ABAQUS 用连续介质的方法建立描述混凝土模型不采用宏观离散裂纹的方法描述裂纹的水平的在每一个积分点上单独计算其中。
低压力混凝土的本构关系包括:Concrete Smeared cracking model (ABAQUS/Standard)Concrete Brittle cracking model (ABAQUS/Explicit)Concrete Damage plasticity model高压力混凝土的本构关系:Cap model1、ABAQUS/Standard中的弥散裂缝模型Concrete Smeared cracking model (ABAQUS/Standard):——只能用于ABAQUS/Standard中裂纹是影响材料行为的最关键因素,它将导致开裂以及开裂后的材料的各向异性用于描述:单调应变、在材料中表现出拉伸裂纹或者压缩时破碎的行为在进行参数定义式的Keywords:*CONCRETE*TENSION STIFFENING*SHEAR RETENTION*FAILURE RATIOS2、ABAQUS/Explicit中脆性破裂模型Concrete Brittle cracking model (ABAQUS/Explicit) :适用于拉伸裂纹控制材料行为的应用或压缩失效不重要,此模型考虑了由于裂纹引起的材料各向异性性质,材料压缩的行为假定为线弹性,脆性断裂准则可以使得材料在拉伸应力过大时失效。
在进行参数定义式的Keywords*BRITTLE CRACKING,*BRITTLE FAILURE,*BRITTLE SHEAR3、塑性损伤模型Concrete Damage plasticity model:适用于混凝土的各种荷载分析,单调应变,循环荷载,动力载荷,包含拉伸开裂(cracking)和压缩破碎(crushing),此模型可以模拟硬度退化机制以及反向加载刚度恢复的混凝土力学特性在进行参数定义式的Keywords:*CONCRETE DAMAGED PLASTICITY*CONCRETE TENSION STIFFENING*CONCRETE COMPRESSION HARDENING*CONCRETE TENSION DAMAGE*CONCRETE COMPRESSION DAMAGE。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
混凝土、钢筋和砌块的本构关系 C20受压 名义应力 名义应变 真实应力 真实应变 塑性应变 9380000 0.000506 9384744 0.000506 0 11390000 0.000704 11398019 0.000704 0.000257 13400000 0.00133 13417822 0.001329 0.000804 11400000 0.00281 11432034 0.002806 0.002359 9400000 0.00413 9438822 0.004121 0.003753 7400000 0.00597 7444178 0.005952 0.005662 5400000 0.00906 5448924 0.009019 0.008807 3400000 0.0156 3453040 0.01548 0.015346 14000000 0.0408 14571200 0.03999 0.039441
E=25500MPa p=2.4e-9T/mm3 u=0.2
C20受拉 名义应力 名义应变 真实应力 真实应变 塑性应变 1540000 0.0000821 1540126 8.20966E-05 0 1340000 0.0001228 1340165 0.000122792 7.02434E-05 1140000 0.0001608 1140183 0.000160787 0.000116081 940000 0.0002148 940201.9 0.000214777 0.000177914 740000 0.0003038 740224.8 0.000303754 0.000274734 540000 0.0004805 540259.5 0.000480385 0.000459208 440000 0.0006496 440285.8 0.000649389 0.000632134 340000 0.000953 340324 0.000952546 0.000939213 240000 0.0016 240384 0.001598721 0.00158931 140000 0.003586 140502 0.003579586 0.003574095 80000 0.0082 80656 0.008166563 0.008163425 50000 0.01633 50816.5 0.0161981 0.016196139
E=25500MPa p=2.4e-9T/mm3 u=0.2 C30受压 名义应力 名义应变 真实应力 真实应变 塑性应变 14070000 0.000566 14077964 0.000566 0 17090000 0.000784 17103390 0.000783 0.000213527 20100000 0.00147 20129547 0.001469 0.000798921 17090000 0.002383 17130725 0.00238 0.001810498 14070000 0.003093 14113519 0.003088 0.002619227 10050000 0.00444 10094622 0.00443 0.004095172 7000000 0.006315 7044205 0.006295 0.006061811 5000000 0.00869 5043450 0.008652 0.008485793 3200000 0.01327 3242464 0.013183 0.013076058 2100000 0.01986 2141706 0.019665 0.019595363
E=30000MPa p=2.4e-9T/mm3 u=0.2
C30受拉 名义应力 名义应变 真实应力 真实应变 塑性应变 2010000 0.000095 2010191 9.49955E-05 0 2000000 0.000111 2000221 0.000110594 4.39272E-05 1870000 0.000123 1870231 0.000123292 6.09591E-05 1430000 0.00017 1430243 0.000170086 0.000122419 980000 0.000257 980251.6 0.000256667 0.000224 720000 0.000364 720262.4 0.000364334 0.000340334 660000 0.000404 660266.5 0.000403718 0.000381718 440000 0.000668 440294 0.000667877 0.00065321 210000 0.001816 210381.4 0.001814353 0.001807353 120000 0.004016 120481.9 0.004007957 0.004003957
E=30000MPa p=2.4e-9T/mm3 u=0.2 C35受压 名义应力 名义应变 真实应力 真实应变 塑性应变 16380000 0.000613 16390041 0.000613 0 19890000 0.000843 19906767 0.000843 0.000211216 23400000 0.001532 23435849 0.001531 0.000787971 21400000 0.00209 21444726 0.002088 0.001408454 19400000 0.00243 19447142 0.002427 0.001811179 17400000 0.00277 17448198 0.002766 0.00221379 15400000 0.00315 15448510 0.003145 0.00265616 13400000 0.00361 13448374 0.003603 0.003178103 11400000 0.00419 11447766 0.004181 0.003819342 9400000 0.00497 9446718 0.004958 0.004659278 7400000 0.00614 7445436 0.006121 0.005886306 5400000 0.0081 5443740 0.008067 0.007895943 3400000 0.01227 3441718 0.012195 0.012087397 1400000 0.0281 1439340 0.027712 0.027667994 1000000 0.0387 1038700 0.03797 0.037938185
E=31500MPa p=2.4e-9T/mm3 u=0.2
C35受拉 名义应力 名义应变 真实应力 真实应变 塑性应变 2200000 0.000095 2200209 9.49955E-05 0 2000000 0.000122 2000244 0.000121793 5.83005E-05 1850000 0.000134 1850248 0.000134191 7.54608E-05 1500000 0.000167 1500250 0.000166886 0.000119267 1100000 0.000226 1100248 0.000225475 0.000190554 700000 0.000359 700251.2 0.000358836 0.000336613 400000 0.000689 400275.4 0.000688363 0.000675665 300000 0.000993 300297.9 0.000992507 0.000982983 200000 0.001707 200341.4 0.001705545 0.001699196 100000 0.004497 100449.7 0.004486919 0.004483744 50000 0.0121 50605 0.01202738 0.012025793
E=31500MPa p=2.4e-9T/mm3 u=0.2 C40受压 名义应力 名义应变 真实应力 真实应变 塑性应变 18760000 0.000665 18772475 0.000665 0 22750000 0.000899 22770452 0.000899 0.000198596 26800000 0.00159 26842612 0.001589 0.000764122 24800000 0.00207 24851336 0.002068 0.001304784 22800000 0.00234 22853352 0.002337 0.001635728 20000000 0.00271 20054200 0.002706 0.00209095 17400000 0.0031 17453940 0.003095 0.00255982 15000000 0.00354 15053100 0.003534 0.00307221 12400000 0.00415 12451460 0.004141 0.003759874 10000000 0.00496 10049600 0.004948 0.004640047 7400000 0.00635 7446990 0.00633 0.006102231 5000000 0.00882 5044100 0.008781 0.008627485 2400000 0.0169 2440560 0.016759 0.016684938 1400000 0.0278 1438920 0.027421 0.027377519 1000000 0.0382 1038200 0.037488 0.037457675 E=32500MPa p=2.4e-9T/mm3 u=0.2
C40受拉 名义应力 名义应变 真实应力 真实应变 塑性应变 2390000 0.000104 2390249 0.000104 0 2000000 0.000137 2000275 0.000137 7.57521E-05 1850000 0.000148 1850274 0.000148 9.13659E-05 1500000 0.000179 1500269 0.000179 0.00013283 1300000 0.000203 1300264 0.000203 0.000163079 1100000 0.000236 1100259 0.000236 0.000201826 700000 0.000364 700254.8 0.000364 0.000342395 400000 0.000677 400270.8 0.000677 0.000664363 300000 0.000964 300289.1 0.000963 0.000954105 200000 0.001635 200327 0.001634 0.001627511 100000 0.004246 100424.6 0.004237 0.004233934 50000 0.01135 50567.5 0.011286 0.011284534
