2014朝阳一模答案
【解析版】【2014朝阳一模】北京市朝阳区2014届高三第一次综合练习 英语试题

(考试时间l20分钟满分l50分)本试卷共12页,共150分。
考试时长120分钟。
考生务必将答案答在答题卡上,在试卷上作答无效。
考试结束后,将本试卷和答题卡一并交回。
第一部分:听力理解(共三节,30分)第一节(共5小题;每小题l.5分,共7.5分)听下面5段对话。
每段对话后有一道小题,从每题所给的A、B、C三个选项中选出最佳选项。
听完每段对话后,你将有l0秒钟的时间来回答有关小题和阅读下一小题。
每段对话你将听一遍。
例:What is the man going to read?A.A newspaper.B.A magazine.C.A book.答案是A。
1.What are the two speakers talking about?A.A skirt.B.A clothes store.C.A blouse.2.What will the two speakers do?A.Finish a report.B.Go for a walk C.Borrow some books.3.What does the man ask the woman to do?A.Park the carB.Order the food quickly.C.Have a meal an hour later4.Where are the two speakers?A.In a store.B.In a hotel.C.At the airport.5.What is tlle woman worried about?A.Missing her flight.B.Having a traffic accident.C.Being late for the football game.第二节(共10小题;每小题l.5分,共15分)听下面4段对话或独白。
每段对话或独自后有几道小题,从每题所给的A、B、C三个选项中选出最佳选项。
2014届北京市朝阳区高三3月第一次综合测试理科数学试题(一模)含答案解析
2 . 5
(I)求 a , b 的值; (II)从参加测试的 20 位学生中任意抽取 2 位,求其中至少有一位运动协调能力或逻辑思 维能力优秀的学生的概率; (III)从参加测试的 20 位学生中任意抽取 2 位,设运动协调能力或逻辑思维能力优秀的学 生人数为 ξ ,求随机变量 ξ 的分布列及其数学期望 Eξ .
第 2 页 共 11 页
(14)如图,在四棱锥 S − ABCD 中, SB ⊥ 底面 ABCD .底 面 ABCD 为梯形, AB ⊥ AD , AB ∥ CD , AB = 1, AD = 3 ,
S
CD = 2 .若点 E 是线段 AD 上的动点,则满足 ∠SEC = 90° 的 点 E 的个数是 .
(6)执行如图所示的程序框图,输出的 S 值为 (B) −2 (D) −4
i<4?
是
否
输出 S 结束 (第 6 题图)
第 1 页 共 11 页
(7)已知函数 f ( x) =
sin x .下列命题: x2 + 1
①函数 f ( x) 的图象关于原点对称; ②函数 f ( x) 是周期函数; ③当 x =
AB 长度的最小值是 .
(11)某三棱锥的三视图如图所示,则这个三棱锥的体积 为 ;表面积为 .
1 正视图 1 1 1 侧视图
俯视图
y2 (12)双曲线 x − 2 = 1(b > 0) 的一个焦点到其渐近线的距离是 2 ,则 b = b
2
;
此双曲线的离心率为 . (13)有标号分别为 1,2,3 的红色卡片 3 张,标号分别为 1,2,3 的 蓝色卡片 3 张,现将全部的 6 张卡片放在 2 行 3 列的格内 (如图) .若颜色相同的卡片在同一行,则不同的放法种数 为 . (用数字作答)
【2014朝阳一模】北京市朝阳区2014届高三第一次综合练习 英语试题和答案

【2014朝阳一模】北京市朝阳区2014届高三第一次综合练习英语试题和答案(考试时间l20分钟满分l50分)本试卷共12页,共150分。
考试时长120分钟。
考生务必将答案答在答题卡上,在试卷上作答无效。
考试结束后,将本试卷和答题卡一并交回。
第一部分:听力理解(共三节,30分)第一节(共5小题;每小题l.5分,共7.5分)听下面5段对话。
每段对话后有一道小题,从每题所给的A、B、C三个选项中选出最佳选项。
听完每段对话后,你将有l0秒钟的时间来回答有关小题和阅读下一小题。
每段对话你将听一遍。
例:What is the man going to read?A.A newspaper.B.A magazine.C.A book.答案是A。
1.What are the two speakers talking about?A.A skirt.B.A clothes store.C.A blouse.2.What will the two speakers do?A.Finish a report.B.Go for a walk C.Borrow some books.3.What does the man ask the woman to do?A.Park the carB.Order the food quickly.C.Have a meal an hour later4.Where are the two speakers?A.In a store.B.In a hotel.C.At the airport.5.What is tlle woman worried about?A.Missing her flight.B.Having a traffic accident.C.Being late for the football game.第二节(共10小题;每小题l.5分,共15分)听下面4段对话或独白。
2014朝阳一模高三语文试卷及讲评.ppt

2014朝阳一模高三语文试卷及讲评.ppt一、选择题(本大题共12小题,每小题3分,共36分)1. 下列词语中,加点字的读音全部正确的一项是()A. 蹊跷(qī qiāo)绯红(fēi hóng)蹒跚(pán shān)恣意(zì yì)B. 蹊跷(qī qiāo)绯红(fēi hóng)蹒跚(pán shān)恣意(zì yì)C. 蹊跷(qī qiāo)绯红(fēi hóng)蹒跚(pán shān)恣意(zì yì)D. 蹊跷(qī qiāo)绯红(fēi hóng)蹒跚(pán shān)恣意(zì yì)2. 下列句子中,没有语病的一项是()A. 通过这次活动,使我们认识到了团结的重要性。
B. 他虽然年轻,但是经验丰富。
C. 这个问题,我昨天已经思考过了。
D. 他因为生病,所以没有来上课。
3-12. (略)二、填空题(本大题共4小题,每小题4分,共16分)1. 请填写下列句子中的空缺部分。
“明月几时有,把酒问青天。
”这句诗出自宋代文学家苏轼的《》。
2. 请根据上下文,填写合适的词语。
他虽然取得了优异的成绩,但是仍然保持着谦逊的态度,从不()。
3-4. (略)三、阅读理解(本大题共2小题,每小题10分,共20分)1. 阅读下面的文章,回答问题。
(文章内容略)(1)文章的中心思想是什么?(2)作者通过哪些细节来表现中心思想?2. 阅读下面的文章,回答问题。
(文章内容略)(1)文章中的主要人物是谁?(2)主要人物的性格特点是什么?四、作文(本大题共1小题,共28分)1. 请以“我眼中的传统文化”为题,写一篇不少于800字的议论文。
注意事项:1. 请在规定时间内完成试卷。
2. 请保持答题卡整洁,不要折叠、涂改。
3. 请按照题目要求,认真审题,仔细作答。
2014北京市朝阳区高三(一模)物 理

2014北京市朝阳区高三(一模)物理一、本部分共8小题,每小题6分,共120分.在每小题列出的四个选项中,选出最符合题目要求的一项.1.(6分)关于α、β、γ三种射线,下列说法正确的是()A.α射线是一种波长很短的电磁波B.γ射线是一种波长很短的电磁波C.β射线的电离能力最强D.γ射线的电离能力最强2.(6分)一束单色光由玻璃斜射向空气,下列说法正确的是()A.波长一定变长 B.频率一定变小C.传播速度一定变小 D.一定发生全反射现象3.(6分)一正弦交变电流的电压随时间变化的规律如图所示.由图可知该交变电流()A.周期为0.125sB.电压的有效值为10VC.电压的最大值为20VD.电压瞬时值的表达式为u=10sin8πt(V)4.(6分)如图所示,A、B两物块的质量分别为m和M,把它们靠在一起从光滑斜面的顶端由静止开始下滑.已知斜面的倾角为θ,斜面始终保持静止.则在此过程中物块B对物块A的压力为()A.Mgsinθ B.MgcosθC.0 D.(M+m)gsinθ5.(6分)图1为一列简谐横波在t=0时的波形图,P是平衡位置在x=1cm处的质元,Q是平衡位置在x=4cm处的质元.图2为质元Q的振动图象.则()A.t=0.3s时,质元Q的加速度达到正向最大B.波的传播速度为20m/sC.波的传播方向沿x轴负方向D.t=0.7s时,质元P的运动方向沿y轴负方向6.(6分)如图所示,真空中有A、B两个等量异种点电荷,O、M、N是AB连线的垂线上的三个点,且AO>OB.一个带负电的检验电荷仅在电场力的作用下,从M点运动到N点,其轨迹如图中实线所示.若M、N两点的电势分别为φM和φN,检验电荷通过M、N两点的动能分别为E kM和E kN,则()A.φM=φN,E kM=E kN B.φM<φN,E kM<E kNC.φM<φN,E kM>E kN D.φM>φN,E kM>E kN7.(6分)某同学利用如图所示的电路描绘小灯泡的伏安特性曲线.在实验中,他将滑动变阻器的滑片从左端匀速滑向右端,发现电流表的指针始终在小角度偏转,而电压表的示数开始时变化很小,但当滑片接近右端时电压表的示数迅速变大.为了便于操作并减小误差,你认为应采取的措施是()A.换用最大阻值更大的滑动变阻器,将导线a的M端移到电流表“3”接线柱上B.换用最大阻值更大的滑动变阻器,将导线b的N端移到电流表“0.6”接线柱上C.换用最大阻值更小的滑动变阻器,将导线a的M端移到电流表“3”接线柱上D.换用最大阻值更小的滑动变阻器,将导线b的N端移到电流表“0.6”接线柱上8.(6分)给一定质量、温度为0℃的水加热,在水的温度由0℃上升到4℃的过程中,水的体积随着温度升高反而减小,我们称之为“反常膨胀”.某研究小组通过查阅资料知道:水分子之间存在一种结合力,这种结合力可以形成多分子结构,在这种结构中,水分子之间也存在相互作用的势能.在水反常膨胀的过程中,体积减小是由于水分子之间的结构发生了变化,但所有水分子间的总势能是增大的.关于这个问题的下列说法中正确的是()A.水分子的平均动能减小,吸收的热量一部分用于分子间的结合力做正功B.水分子的平均动能减小,吸收的热量一部分用于克服分子间的结合力做功C.水分子的平均动能增大,吸收的热量一部分用于分子间的结合力做正功D.水分子的平均动能增大,吸收的热量一部分用于克服分子间的结合力做功二、解答题(共5小题,满分72分)9.(8分)如图1所示为多用电表的示意图,其中S、T为可调节的部件,现用此电表测量一阻值约为1000Ω的定值电阻,部分操作步骤如下:(1)选择开关应调到电阻档的(填“×1”、“×10”、“×100”或“×1k”)位置.(2)将红、黑表笔分别插入“+”、“﹣”插孔,把两笔尖相互接触,调节(填“S”或“T”),使电表指针指向(填“左侧”或“右侧”)的“0”位置.(3)将红、黑表笔的笔尖分别与电阻两端接触,电表示数如图2所示,该电阻的阻值为Ω.10.(10分)某实验小组采用如图1所示的装置探究“合力做功与动能变化的关系”.打点计时器工作频率为50Hz.实验的部分步骤如下:a.将木板的左端垫起,以平衡小车的摩擦力;b.在小车中放入砝码,纸带穿过打点计时器,连在小车后端,用细线连接小车和钩码;c.将小车停在打点计时器附近,接通电源,释放小车,小车拖动纸带,打点计时器在纸带上打下一系列的点,断开电源;d.改变钩码或小车中砝码的质量,更换纸带,重复b、c的操作.(1)在小车的运动过程中,对于钩码、砝码和小车组成的系统,钩码的重力做功(填“正”或“负”);(2)图2是某次实验时得到的一条纸带,他们在纸带上取计数点O、A、B、C、D和E,用最小刻度是毫米的刻度尺进行测量,读出各计数点对应的刻度x,通过计算得到各计数点到O的距离s以及对应时刻小车的瞬时速度v.请将C点对应的测量和计算结果填在下表中的相应位置.计数点x/cm s/cm v/(m•s﹣1)O 1.00 0.00 0.30A 2.34 1.34 0.38B 4.04 3.04 0.46C 5.00D 8.33 7.33 0.61E 10.90 9.90 0.70(3)实验小组认为可以通过绘△v2﹣s图(图3)线来分析实验数据(其中△v2=v2﹣,v是各计数点对应时刻小车的瞬时速度,v O是O点对应时刻小车的瞬时速度).他们根据实验数据在图3中标出了O、A、B、D、E对应的坐标点,请你在该图中标出计数点C对应的坐标点,并画出△v2﹣s图线.(4)实验小组计算了他们绘制的△v2﹣s图线的斜率,发现该斜率大于理论值,其原因可能是.11.(16分)如图所示,MN、PQ是两根足够长的光滑平行金属导轨,导轨间距为d,导轨所在平面与水平面成θ角,M、P间接阻值为R的电阻.匀强磁场的方向与导轨所在平面垂直,磁感应强度大小为B.质量为m、阻值为r的金属棒放在两导轨上,在平行于导轨的拉力作用下,以速度v匀速向上运动.已知金属棒与导轨始终垂直并且保持良好接触,重力加速度为g.求:(1)金属棒产生的感应电动势E;(2)通过电阻R电流I;(3)拉力F的大小.12.(18分)在研究某些物理问题时,有很多物理量难以直接测量,我们可以根据物理量之间的定量关系和各种效应,把不容易测量的物理量转化成易于测量的物理量.13.(4分)在利用如图所示的装置探究影响电荷间相互作用力的因素时,我们可以通过绝缘细线与竖直方向的夹角来判断电荷之间相互作用力的大小.如果A、B两个带电体在同一水平面内,B的质量为m,细线与竖直方向夹角为θ,求A、B之间相互作用力的大小.13.(14分)金属导体板垂直置于匀强磁场中,当电流通过导体板时,外部磁场的洛伦兹力使运动的电子聚集在导体板的一侧,在导体板的另一侧会出现多余的正电荷,从而形成电场,该电场对运动的电子有静电力的作用,当静电力与洛伦兹力达到平衡时,在导体板这两个表面之间就会形成稳定的电势差,这种现象称为霍尔效应.利用霍尔效应可以测量磁场的磁感应强度.如图所示,若磁场方向与金属导体板的前后表面垂直,通过如图所示的电流I,可测得导体板上、下表面之间的电势差为U,且下表面电势高.已知导体板的长、宽、高分别为a、b、c,电子的电荷量为e,导体中单位体积内的自由电子数为n.求:(1)导体中电子定向运动的平均速率v;(2)磁感应强度B的大小和方向.14.(20分)如图1所示,木板A静止在光滑水平面上,一小滑块B(可视为质点)以某一水平初速度从木板的左端冲上木板.(1)若木板A的质量为M,滑块B的质量为m,初速度为v0,且滑块B没有从木板A的右端滑出,求木板A最终的速度v;(2)若滑块B以v1=3.0m/s的初速度冲上木板A,木板A最终速度的大小为v=1.5m/s;若滑块B以初速度v2=7.5m/s 冲上木板A,木板A最终速度的大小也为v=1.5m/s.已知滑块B与木板A间的动摩擦因数μ=0.3,g取10m/s2.求木板A的长度L;(3)若改变滑块B冲上木板A的初速度v0,木板A最终速度v的大小将随之变化.请你在图2中定性画出v﹣v0图线.物理试题答案一、本部分共8小题,每小题6分,共120分.在每小题列出的四个选项中,选出最符合题目要求的一项.1.【解答】A、α射线电离本领最大,贯穿本领最小,但不属于电磁波,故A错误;B、γ射线是原子核在发生α衰变和β衰变时产生的能量以γ光子的形式释放,是高频电磁波,波长很短,故B正确;C、β射线是具有放射性的元素的原子核中的一个中子转化成一个质子同时释放出一个高速电子即β粒子,但电离能力没有α射线强,故C错误;D、γ射线不带电,没有电离能力,故D错误.故选:B.2.【解答】A、B、C、光的频率是由光源决定的,与介质无关,所以光从玻璃进入空气,频率不变,而光速增大,根据波速公式v=λf可知波长一定变长,故A正确,BC错误;D、光由玻璃斜射向空气,只有当入射角大于或等于临界角时才能发生全反射,所以不一定发生全反射.故D错误.故选:A.3.【解答】A、由图象可知,交流电压的最大值为U m=20V,电流的周期为T=0.250s,故A错误,C错误;B、电压的有效值U==10V,故B正确;D、电流的周期为T=0.250s,ω==8πrad/s,所以电压瞬时值的表达式为u=20sin8πt(V),故D错误.故选:B.4.【解答】对A、B组成的整体受力分析可知,整体受重力、支持力而做匀加速直线运动;由牛顿第二定律可知,a==gsinθ;则再对B由牛顿第二定律可知:F合=Ma=Mgsinθ;合力等于B的重力沿斜面向下的分力;故说明AB间没有相互作用力,故ABD错误,C正确.故选:C.5.【解答】A、由图2读出t=0.3s时质元Q处于正向位移最大处,根据a=﹣分析可知,其加速度为负向最大,故A错误;B、由图1读出波长λ=8cm=0.08m,由图2读出周期T=0.4s,则波速v==m/s=0.2m/s,故B错误.C、由图2知,t=0时Q点沿y轴负方向运动,根据波形的平移法可知波的传播方向沿x轴负方向,故C正确;D、==1,即t=1T,图示时刻质点P正向上运动,所以t=0.7s质元P的运动方向沿y轴正方向,故D错.故选:C.6.【解答】根据带负电粒子的运动轨迹,粒子受到的电场力指向轨迹弯曲的一侧,负电荷受到的电场力指向带正电的电荷,所以A点带正电,B点带负电;因为AO>OB,根据等量异种点电荷电场线及等势面分布特点可知,E M大于E N,φM小于φN,因此负电荷在M点的电势能高于N点,那么电荷在M点的动能小于M点,故B正确,ACD错误.故选:B.7.【解答】由图示电路图可知,电流表选择3A量程,将滑动变阻器的滑片从左端匀速滑向右端,发现电流表的指针始终在小角度偏转,说明电流表所选量程太大,应选择0.6A量程,应把导线b的N端移到电流表的“0.6”接线柱上;从左向右移动滑片时,电压表的示数开始时变化很小,当滑片接近右端时电压表的示数迅速变大,说明所选择的滑动变阻器最大阻值太大,为方便实验操作,应选择最大阻值较小的滑动变阻器,故ABC错误,D正确.故选:D.8.【解答】温度是分子平均动能的标志,温度升高,分子的平均动能最大;由题意,在水反常膨胀的过程中,虽然体积减小是由于水分子之间的结构发生了变化,但所有水分子间的总势能是增大的,说明了分子之间的相互作用力对分子做负功,即吸收的热量一部分用于克服分子间的结合力做功.故,ABC错误,D正确.故选:D.二、解答题(共5小题,满分72分)9.【解答】用欧姆表测阻值约为1000Ω的定值电阻,部分操作步骤如下:(1)选择开关应调到电阻档的“×100”位置.(2)将红、黑表笔分别插入“+”、“﹣”插孔,把两笔尖相互接触,调节欧姆调零旋钮T,使电表指针指向右侧的“0”位置.(3)将红、黑表笔的笔尖分别与电阻两端接触,由图2所示可知,该电阻的阻值为11×100=1100Ω.故答案为:(1)×100;(2)T;右侧;(3)1100.10.【解答】(1)钩码重力方向与位移方向相同,钩码重力做正功.(2)由表格数据可知O点对应着1.00cm的刻度线,由于C点与O点的距离为5.00cm,所以C点对应的刻度为6.00cm;根据匀变速直线运动的推论可知,A点的瞬时速度v A===0.38m/s,则t=0.04s,C点的瞬时速度v C===≈0.54m/s;(3)v C2=0.542≈0.29,C点对应的△v2=v2﹣=0.2,把C对应的点标在坐标系中,然后作出图象如图所示:(4)由匀变速直线运动的速度位移公式可知v2﹣=2as,△v2﹣s图象的斜率k=2a,斜率大于理论值,说明加速度a偏大,可能是平衡摩擦力时木板左端垫起得太高,过平衡摩擦力造成的.故答案为:(1)正;(2)6.00;0.54;(3)0,2;图象如图所示;(4)平衡摩擦力时木板左端垫起得太高.11.【解答】解:(1)根据法拉第电磁感应定律:E=Bdv;(2)根据闭合电路欧姆定律:;(3)导体棒的受力情况如图所示,根据牛顿第二定律有:F﹣F安﹣mgsinθ=0又因为F安=BId所以:.答:(1)金属棒产生的感应电动势是Bdv;(2)通过电阻R电流是;(3)拉力F的大小.12.【解答】解:对B球受力分析,它受重力、拉力与库仑力,如图所示,根据力的平行四边形定则,将F与G进行合成,结合三角知识,则有:F=mgtanθ,根据平衡条件,可知,A、B之间相互作用力的大小为mgtanθ,答:A、B之间相互作用力的大小为mgtanθ.13.【解答】解:(1)电流:I===nevbc,则电子平均速率:v=;(2)电子通过金属板,电子受到的电场力与洛伦兹力大小相等,方向相反,则:evB=e,磁感应强度:B=,导体板下表面电势高,则下极板带正电,上极板带负电,电子聚集在上极板上,电子受到的洛伦兹力向上,由左手定则可知,磁场方向为垂直于前后表面向里;答:(1)导体中电子定向运动的平均速率v=;(2)磁感应强度B的大小B=,方向:垂直于前后表面向里.14.【解答】解:(1)设向右为正方向,根据动量守恒定律得:mv0=(M+m)v解得:(2)由题意得:滑块B以v1=3.0m/s的初速度冲上木板A,滑块未掉下就达到共同速度,由动量守恒定律得:mv1=(M+m)v即:3m=1.5(m+M)解得:M=m ①当滑块B以v1=7.5m/s的初速度冲上木板A,滑块掉下由牛顿第二定律得:对滑块:对木板:滑块在木板上运动时间为:这段时间内滑块前进的位移为:=木板前进的位移为:木板A的长度为:L=x1﹣x2=3.375﹣0.375m=3m(3)滑块的速度比较小时,滑块掉不下去,根据动量守恒得:滑块和木板的速度相同为:,即v与v0成正比,当滑块初速度比较大时,滑块掉下,相对位移不变,设滑块掉下去时,木板的速度为v;滑块在木板上运动时间为:这段时间内滑块前进的位移为:=木板前进的位移为:即:,当且仅当,即v=3m/s时,v0有最小值,即当,滑块滑下木板,其图象如图所示:答:(1)求木板A最终的速度.(2)木板A的长度L=3m.(3)见上图.。
【2014朝阳一模】北京市朝阳区2014届高三第一次综合练习 数学理试题 Word版含答案

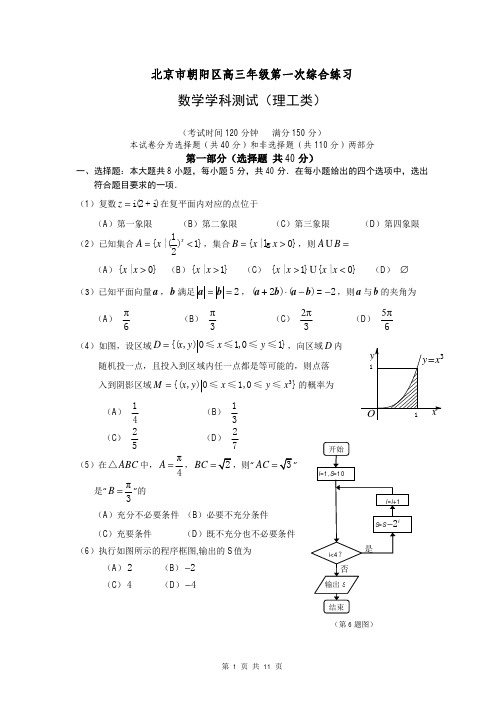
(第6题图)北京市朝阳区高三年级第一次综合练习数学学科测试(理工类)2014.3(考试时间120分钟 满分150分)本试卷分为选择题(共40分)和非选择题(共110分)两部分第一部分(选择题 共40分)一、选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,选出符合题目要求的一项. (1)复数i(2+i)z =在复平面内对应的点位于(A )第一象限 (B )第二象限 (C )第三象限 (D )第四象限 (2)已知集合1{|(1}2xA x =<,集合{|lg 0}B x x =>,则AB =(A ){|0}x x > (B ){|1}x x > (C ) {|1}{|0}x x x x >< (D ) ∅ (3)已知平面向量a ,b 满足2==a b ,(2)()=2⋅--a +b a b ,则a 与b 的夹角为(A )6π (B ) 3π(C )32π (D ) 65π(4)如图,设区域{(,)01,01}D x y x y =≤≤≤≤,向区域D 内随机投一点,且投入到区域内任一点都是等可能的,则点落 入到阴影区域3{(,)01,0}M x y x y x =≤≤≤≤的概率为(A )14(B )13(C ) 25 (D ) 27(5)在ABC △中,π4A =,BC =“AC ”是“π3B =”的(A )充分不必要条件 (B )必要不充分条件 (C )充要条件 (D )既不充分也不必要条件 (6)执行如图所示的程序框图,输出的S 值为(A )2 (B )2- (C )4 (D )4-(7)已知函数2sin ()1xf x x =+.下列命题: ①函数()f x 的图象关于原点对称; ②函数()f x 是周期函数; ③当2x π=时,函数()f x 取最大值;④函数()f x 的图象与函数1y x=的图象没有公共点,其中正确命题的序号是(A ) ①③ (B )②③ (C ) ①④ (D )②④(8)直线y x m =+与圆2216xy +=交于不同的两点M ,N ,且3MN O M O N ≥+,其中O 是坐标原点,则实数m 的取值范围是 (A )(2,22⎡-⎣ (B )(22,4⎡--⎣(C) [2,2]- (D ) [-第二部分(非选择题 共110分)二、填空题:本大题共6小题,每小题5分,共30分.把答案填在答题卡上. (9)在各项均为正数的等比数列{}n a 中,12a =,2312a a +=,则该数列的前4项和为 .(10)在极坐标系中,A 为曲线2cos ρθ=上的点,B 为曲线cos 4ρθ=上的点,则线段AB 长度的最小值是 .(11)某三棱锥的三视图如图所示,则这个三棱锥的体积为 ;表面积为 .(12)双曲线2221(0)y x b b-=>的一个焦点到其渐近线的距离是2,则b = ;此双曲线的离心率为 .(13)有标号分别为1,2,3的红色卡片3张,标号分别为1,2,3的蓝色卡片3张,现将全部的6张卡片放在2行3列的格内 (如图).若颜色相同的卡片在同一行,则不同的放法种数为 .(用数字作答)正视图俯视图(14)如图,在四棱锥S ABCD -中,SB ⊥底面ABCD .底面ABCD 为梯形,AB AD ⊥,AB ∥CD ,1,3AB AD ==,2CD =.若点E 是线段AD 上的动点,则满足90SEC ∠=︒的点E 的个数是 .三、解答题:本大题共6小题,共80分.解答应写出文字说明,演算步骤或证明过程. (15)(本小题满分13分)已知函数22()2sin()cos sin cos f x x x x x =π-⋅+-,x ∈R . (Ⅰ)求()2f π的值及函数()f x 的最小正周期; (Ⅱ)求函数()f x 在[]0,π上的单调减区间.(16)(本小题满分13分)某单位从一所学校招收某类特殊人才.对20位已经选拔入围的学生进行运动协调能力和逻辑思维能力的测试,其测试结果如下表:例如,只知道从这20位参加测试的学生中随机抽取一位,抽到运动协调能力或逻辑思维能力优秀的学生的概率为25. (I )求a ,b 的值;(II )从参加测试的20位学生中任意抽取2位,求其中至少有一位运动协调能力或逻辑思维能力优秀的学生的概率;(III )从参加测试的20位学生中任意抽取2位,设运动协调能力或逻辑思维能力优秀的学生人数为ξ,求随机变量ξ的分布列及其数学期望E ξ.BCDESA(17)(本小题满分14分)如图,四棱锥P ABCD -的底面为正方形,侧面PAD ⊥底面ABCD .PAD △为等腰直角三角形,且PA AD ⊥. E ,F 分别为底边AB 和侧棱PC 的中点.(Ⅰ)求证:EF ∥平面PAD ; (Ⅱ)求证:EF ⊥平面PCD ; (Ⅲ)求二面角E PD C --的余弦值.(18)(本小题满分13分)已知函数21()ln 2f x ax x =-,a ∈R . (Ⅰ)求函数()f x 的单调区间;(Ⅱ)若函数()f x 在区间[1,e]的最小值为1,求a 的值.(19)(本小题满分14分)已知椭圆2222:1(0)x y C a b a b +=>>经过点(Ⅰ)求椭圆C 的方程;(Ⅱ)直线(1)(0)y k x k =-≠与椭圆C 交于,A B 两点,点M 是椭圆C 的右顶点.直线AM 与直线BM 分别与y 轴交于点,P Q ,试问以线段PQ 为直径的圆是否过x 轴上的定点?若是,求出定点坐标;若不是,说明理由.(20)(本小题满分13分)从1,2,3,,n 中这n 个数中取m (,m n *∈N ,3m n ≤≤)个数组成递增等差数列,所有可能的递增等差数列的个数记为(,)f n m .(Ⅰ)当5,3n m ==时,写出所有可能的递增等差数列及(5,3)f 的值; (Ⅱ)求(100,10)f ;(Ⅲ)求证:()(1)(,)2(1)n m n f n m m -+>-.A E BCDPF北京市朝阳区高三年级第一次综合练习数学答案(理工类) 2014.3三、解答题15. (本小题满分13分) 解: ()f x =sin 2cos 2x x -)4x π=-.(Ⅰ)())12242f πππ=⋅-==.显然,函数()f x 的最小正周期为π. …………… 8分 (Ⅱ)令ππ3π2π22π242k x k +-+≤≤得 37ππππ88k x k ++≤≤,k ∈Z .又因为[]0,πx ∈,所以3π7π,88x ⎡⎤∈⎢⎥⎣⎦. 函数()f x 在[]0,π上的单调减区间为3π7π,88⎡⎤⎢⎥⎣⎦. …………… 13分 16. (本小题满分13分)解:(I )设事件A :从20位学生中随机抽取一位,抽到运动协调能力或逻辑思维能力优秀的学生.由题意可知,运动协调能力或逻辑思维能力优秀的学生共有(6)a +人. 则62()205a P A +==. 解得 2a =.所以4b =. …………… 4分(II )设事件B :从20人中任意抽取2人,至少有一位运动协调能力或逻辑思维能力优秀的学生.由题意可知,至少有一项能力测试优秀的学生共有8人.则21222062()1()195C P B P B C =-=-=. …………… 7分(III )ξ的可能取值为0,1,2.20位学生中运动协调能力或逻辑思维能力优秀的学生人数为8人.所以21222033(0)95C P C ξ===,1112822048(1)95C C P C ξ===,2822014(2)95C P C ξ===.所以ξ的分布列为所以,0E ξ=⨯33951+⨯48952+⨯1495764955==. …………… 13分17. (本小题满分14分)(Ⅰ)证明:取PD 的中点G ,连接FG ,AG .因为F ,G 分别是PC ,PD 的中点, 所以FG 是△PCD 的中位线. 所以FG ∥CD ,且12FG CD =. 又因为E 是AB 的中点,且底面ABCD 为正方形,所以1122AE AB CD ==,且AE ∥CD . 所以AE ∥FG ,且AE FG =. 所以四边形AEFG 是平行四边形. 所以EF ∥AG .又EF ⊄平面PAD ,AG ⊂平面PAD ,AE BCDPFG所以EF平面PAD . ……………4分(Ⅱ)证明: 因为平面PAD ⊥平面ABCD ,PA AD ⊥,且平面PAD 平面ABCD AD =, 所以PA ⊥平面ABCD . 所以PA AB ⊥,PA AD ⊥.又因为ABCD 为正方形,所以AB AD ⊥, 所以,,AB AD AP 两两垂直.以点A 为原点,分别以, , AB AD AP 为, , x y z 轴, 建立空间直角坐标系(如图). 由题意易知AB AD AP ==, 设2AB AD AP ===,则(0,0,0)A ,(2,0,0)B ,(2,2,0)C ,(0,2,0)D ,(0,0,2)P ,(1,0,0)E ,(1,1,1)F .因为(0,11)EF =,,(022)PD =-,,,(200)CD =-,,, 且(0,11)(0,2,2)0EF PD ⋅=⋅-=,,(0,11)(2,00)0EF CD ⋅=⋅-=,,所以EF PD ⊥,EF CD ⊥.又因为PD ,CD 相交于D ,所以EF ⊥平面PCD . …………… 9分 (Ⅲ)易得(102)EP =-,,,(0,22)PD =-,.设平面EPD 的法向量为(, , )x y z =n ,则0,0.EP PD ⎧⋅=⎪⎨⋅=⎪⎩n n 所以 20,220. x z y z -+=⎧⎨-=⎩即2,. x z y z =⎧⎨=⎩令1z =,则(2,1,1)=n .由(Ⅱ)可知平面PCD 的法向量是(0,11)EF =,, 所以cos ,2EF EF EF⋅〈〉===⋅n n n .由图可知,二面角E PD C --的大小为锐角,所以二面角E PD C --的余弦值为3. ……………14分 18. (本小题满分13分)解:函数()f x 的定义域是(0,)+∞, 1()f x ax x '=-21ax x-=.(Ⅰ)(1)当0a =时,1()0f x x'=-<,故函数()f x 在(0,)+∞上单调递减. (2)当0a <时,()0f x '<恒成立,所以函数()f x 在(0,)+∞上单调递减.(3)当0a >时,令()0f x '=,又因为0x >,解得x =①当x ∈时,()0f x '<,所以函数()f x 在单调递减.②当)x ∈+∞时,()0f x '>,所以函数()f x 在)+∞单调递增. 综上所述,当0a ≤时,函数()f x 的单调减区间是(0,)+∞,当0a >时,函数()f x 的单调减区间是,单调增区间为)+∞.…7分 (Ⅱ)(1)当0a ≤时,由(Ⅰ)可知,()f x 在[1,e]上单调递减,所以()f x 的最小值为21(e)e 112f a =-=,解得240ea =>,舍去. (2)当0a >时,由(Ⅰ)可知,①1,即1a ≥时,函数()f x 在[1,e]上单调递增, 所以函数()f x 的最小值为1(1)12f a ==,解得2a =.②当1e <<,即211e a <<时,函数()f x 在上单调递减,在上单调递增,所以函数()f x 的最小值为11ln 122f a =+=,解得e a =,舍去.③e ,即210e a <≤时,函数()f x 在[1,e]上单调递减,所以函数()f x 的最小值为21(e)e 112f a =-=,得24ea =,舍去. 综上所述,2a =. ……………13分19. (本小题满分14分)解:(Ⅰ)由题意得22=21314c a a b ⎧⎪⎪⎨⎪+=⎪⎩,解得=2a ,1b =. 所以椭圆C 的方程是2214x y +=. …………… 4分 (Ⅱ)以线段PQ 为直径的圆过x 轴上的定点.由22(1)14y k x x y =-⎧⎪⎨+=⎪⎩得2222(14)8440k x k x k +-+-=. 设1122(,),(,)A x y B x y ,则有2122814k x x k +=+,21224414k x x k -=+.又因为点M 是椭圆C 的右顶点,所以点(2,0)M .由题意可知直线AM 的方程为11(2)2y y x x =--,故点112(0,)2y P x --. 直线BM 的方程为22(2)2y y x x =--,故点222(0,)2y Q x --. 若以线段PQ 为直径的圆过x 轴上的定点0(,0)N x ,则等价于0PN QN ⋅=恒成立.又因为1012(,)2y PN x x =-,2022(,)2y QN x x =-, 所以221212001212224022(2)(2)y y y y PN QN x x x x x x ⋅=+⋅=+=----恒成立. 又因为121212(2)(2)2()4x x x x x x --=-++2222448241414k k k k -=-+++ 22414k k=+, 212121212(1)(1)[()1]y y k x k x k x x x x =--=-++22222448(1)1414k k k k k -=-+++22314k k-=+, 所以222212000212212414304(2)(2)14k y y k x x x k x x k -++=+=-=--+.解得0x =.故以线段PQ 为直径的圆过x轴上的定点(. …………… 14分 20. (本小题满分13分) 解:(Ⅰ)符合要求的递增等差数列为1,2,3;2,3,4;3,4,5;1,3,5,共4个.所以(5,3)4f =. …………… 3分 (Ⅱ)设满足条件的一个等差数列首项为1a ,公差为d ,d *∈N .1019a a d =+,10110011199a a d --==≤,d 的可能取值为1,2,,11.对于给定的d ,11091009a a d d =--≤, 当1a 分别取1,2,3,,1009d -时,可得递增等差数列1009d -个(如:1d =时,191a ≤,当1a 分别取1,2,3,,91时,可得递增等差数列91个:1,2,3,,11;2,3,4,,12;;91,92,93,,100,其它同理).所以当d 取1,2,,11时,可得符合要求的等差数列的个数为:(100,10)100119(1211)1100966506f =⋅-⋅+++=-⋅=.…………… 8分(Ⅲ)设等差数列首项为1a ,公差为d ,1(1)m a a m d =+-,1111m a a n d m m --=--≤,记11n m --的整数部分是t ,则11111n n t m m ---<--≤,即111n m n t m m --<--≤. d 的可能取值为1,2,,t ,对于给定的d ,1(1)(1)m a a m d n m d =----≤,当1a 分别取1,2,3,,(1)n m d --时,可得递增等差数列(1)n m d --个.所以当d 取1,2,,t 时,得符合要求的等差数列的个数2(1)121(,)(1)222t t m n m f n m nt m t t +--+=--⋅=-+ 22121(21)()22(1)8(1)m n m n m t m m --+-+=--+-- 易证21112(1)1n m n m n m m m --+-<---≤. 又因为211||12(1)2(1)n m n m m m m m --++-=---,2113||2(1)12(1)n m n m m m m -+---=---, 所以21211||||12(1)2(1)1n m n m n m n m m m m --+-+-->-----. 所以(1)(,)(1)2t t f n m nt m +=--⋅ (1)()(1)11(1)122(1)n m n m n m n m n m m n m m m --+--+-->⋅--⋅=--. 即()(1)(,)2(1)n m n f n m m -+>-. …………… 13分。
2014朝阳一模第24题分析
sin∠ACM= ,sin∠ADN= . AD AC ∴. ∴ .……………………… 又 ∵∠CAD=∠BAE, ∴ △BAE∽△CAD. ∴ ∴ BE=2DC· sinα. ……………
AM
AN
C
具体过程
D E
过点C作CF⊥AB于F ∵ ∠ACB=∠ADE=2α° CA=CB,DA=DB ∴ ∠BAC=∠EAD= 90 ∴ △ BAC ∽△EAD
C
A D E
B
解法2: 由特殊到一般 过点E作EF ∥AC 过点F作FG⊥EB于G
BE CD BE FE 2 EG FE 2 sin 60 3
C F D A E G B
在△ABC,CA=CB,在△AED中,DA=DE, 点D、E分别在CA、CB上. (2)若∠ACB=∠ADE=120°,将△AED绕点A 旋转至如图②所示的位置,则CD与BE的数量关 系是___________;
B
C
D A E
图①
BE EA ∴ CD DA
∵ DA=DE ∴
BE EA 2 CD DA
F
在△ABC,CA=CB,在△AED中,DA=DE, 点D、E分别在CA、CB上. (1)如图①,若∠ACB=∠ADE=90°,则CD与 BE的数量关系是___________;
C F D A E B
BE 2 (b a) 2 CD ba
在△ABC,CA=CB,在△AED中,DA=DE, 点D、E分别在CA、CB上. (1)如图①,若∠ACB=∠ADE=90°,则CD与 BE的数量关系是___________;
解法2: 过点A作DE的平行线AF ∵ ∠ACB=∠ADE=90° ∴ AF∥DE∥CB
C
2014届北京市朝阳区高三3月第一次综合练习(一模)英语试题(含答案)(2014.03)(高清版)
北京市朝阳区高三年级第一次综合练习英语试卷2014.3(考试时间l20分钟满分l50分)本试卷共12页,共150分。
考试时长120分钟。
考生务必将答案答在答题卡上,在试卷上作答无效。
考试结束后,将本试卷和答题卡一并交回。
第一部分:听力理解(共三节,30分)第一节(共5小题;每小题l.5分,共7.5分)听下面5段对话。
每段对话后有一道小题,从每题所给的A、B、C三个选项中选出最佳选项。
听完每段对话后,你将有l0秒钟的时间来回答有关小题和阅读下一小题。
每段对话你将听一遍。
例:What is the man going to read?A.A newspaper.B.A magazine.C.A book.答案是A。
1.What are the two speakers talking about?A.A skirt.B.A clothes store.C.A blouse.2.What will the two speakers do?A.Finish a report.B.Go for a walk C.Borrow some books.3.What does the man ask the woman to do?A.Park the carB.Order the food quickly.C.Have a meal an hour later4.Where are the two speakers?A.In a store.B.In a hotel.C.At the airport.5.What is tlle woman worried about?A.Missing her flight.B.Having a traffic accident.C.Being late for the football game.第二节(共10小题;每小题l.5分,共15分)听下面4段对话或独白。
每段对话或独自后有几道小题,从每题所给的A、B、C三个选项中选出最佳选项。
2014年吉林省长春市朝阳区中考数学一模试卷含答案解析(word版)
2014年吉林省长春市朝阳区中考数学一模试卷参考答案与试题解析一、选择题(每小题3分,共24分)1.(3分)在0.1,﹣3,和这四个实数中,无理数是()A.0.1 B.﹣3 C. D.分析:无理数就是无限不循环小数.理解无理数的概念,一定要同时理解有理数的概念,有理数是整数与分数的统称.即有限小数和无限循环小数是有理数,而无限不循环小数是无理数.由此即可判定选择项.解答:解:在0.1,﹣3,和这四个实数中,无理数有:.故选C.点评:此题主要考查了无理数的定义,其中初中范围内学习的无理数有:π,2π等;开方开不尽的数;以及像0.1010010001…,等有这样规律的数.2.(3分)2014年3月21日上午,我国新型导弹驱逐舰昆明舰举行入列仪式,正式加入人民海军战斗序列.昆明舰采用柴燃交替动力,配备2台QC208燃气轮机,单台功率37500马力.数据37500用科学记数表示为()A. 3.75×104B.37.5×103C.0.375×105D.3.75×103考点:科学记数法—表示较大的数.分析:科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n是负数.解答:解:37500=3.75×104,故选:A.点评:此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.3.(3分)有一组数据:2,4,3,4,5,3,4,则这组数据的众数是()A. 5 B. 4 C. 3 D. 2考点:众数.分析:根据众数的定义找出出现次数最多的数即可.解答:解:∵2,4,3,4,5,3,4中4出现了3次,出现的次数最多,∴这组数据的众数是4,故选:B.点评:本题考查了众数,一组数据中出现次数做多的数叫做众数,它反映了一组数据的多数水平,一组数据的众数可能不是唯一的.4.(3分)将“中国梦我的梦”六个字分别写在一个正方体的六个面上,这个正方体的展开图如图,那么在这个正方体中,和“我”字相对的字是()A.中B.国C.的D.梦考点:专题:正方体相对两个面上的文字.分析:正方体的表面展开图,相对的面之间一定相隔一个正方形,根据这一特点作答.解答:解:正方体的表面展开图,相对的面之间一定相隔一个正方形,“中”与“梦”是相对面,“国”与“我”是相对面,“梦”与“的”是相对面.故选B.点评:本题主要考查了正方体相对两个面上的文字,注意正方体的空间图形,从相对面入手,分析及解答问题.5.(3分)不等式组的解集是()A.﹣1<x≤1 B.﹣1<x<1 C.x>﹣1 D. x≤1考点:解一元一次不等式组.分析:分别求出不等式的解集,再找到其公共部分即可.解答:解:,由①得,x>﹣1,由②得,x≤1,故不等式组的解集为﹣1<x≤1,故选A.点评:本题考查了解一元一次不等式组,求不等式的公共解,要遵循以下原则:同大取较大,同小取较小,小大大小中间找,大大小小解不了.6.(3分)如图,直线l1∥l2,且分别与△ABC的两边AB、AC相交,若∠A=50°,∠1=35°,则∠2的度数为()A.35° B.65° C.85°D.95°考点:平行线的性质;三角形内角和定理.分析:先根据平行线性质求出∠3,再根据三角形内角和定理求出∠4,即可求出答案.解答:解:∵直线l1∥l2,且∠1=35°,∴∠3=∠1=35°,∵在△AEF中,∠A=50°,∴∠4=180°﹣∠3﹣∠A=95°,∴∠2=∠4=95°,故选D.点评:本题考查了平行线的性质和三角形内角和定理,对顶角相等的应用,注意:①两直线平行,同位角相等,②两直线平行,内错角相等,③两直线平行,同旁内角互补.7.(3分)如图,⊙O是△ABC的外接圆,连结OA、OB,且点C、O在弦AB的同侧,若∠ABO=50°,则∠ACB的度数为()A.50° B.45° C.30°D.40°考点:圆周角定理.分析:利用等边对等角求得∠BAO的度数,然后根据三角形内角和定理求得∠AOB的度数,最后根据圆周角定理即可求解.解答:解:∵OA=OB,∴∠BAO=∠ABO=50°,∴∠AOB=180°﹣50°﹣50°=80°.∴∠ACB=∠AOB=40°.故选D.点评:本题考查了等腰三角形的性质定理以及圆周角定理,正确理解定理,求得∠AOB的度数是关键.8.(3分)如图,在平面直角坐标系中,菱形ABCD的顶点C的坐标为(﹣1,0),点B的坐标为(0,2),点A在第二象限.直线y=﹣x+5与x轴、y轴分别交于点N、M.将菱形ABCD沿x轴向右平移m个单位,当点D落在△MON的内部时(不包括三角形的边),则m的值可能是()A. 1 B. 2 C. 4 D.8考点:一次函数综合题.分析:根据菱形的对角线互相垂直平分表示出点D的坐标,再根据直线解析式求出点D 移动到MN上时的x的值,从而得到m的取值范围,再根据各选项数据选择即可.解答:解:∵菱形ABCD的顶点C(﹣1,0),点B(0,2),∴点D的坐标为(﹣2,2),当y=2时,﹣x+5=2,解得x=6,∴点D向右移动2+6=8时,点D在MN上,∵点D落在△MON的内部时(不包括三角形的边),∴2<m<8,∵1、2、4、8中只有4在此范围内,∴m的值可能是4.故选C.点评:本题是一次函数综合题型,主要利用了一次函数图象上点的坐标特征,菱形的性质,比较简单,求出m的取值范围是解题的关键.二、填空题(每小题3分,共18分)9.(3分)计算:﹣2=1.考点:实数的运算.专题:计算题.分析:原式第一项利用平方根定义化简,计算即可得到结果.解答:解:原式=3﹣2=1.故答案为:1.点评:此题考查了实数的运算,熟练掌握运算法则是解本题的关键.10.(3分)某饭店在2014年春节年夜饭的预定工作中,第一天预定了a桌,第二天预定的桌数比第一天多了4桌,则这两天该饭店一共预定了2a+4桌年夜饭(用含a的代数式表示).考点:列代数式.分析:首先求出第二天预定的桌数为(a+4),再进一步与第一天的合并即可.解答:解:a+a+4=2a+4(桌).这两天该饭店一共预定了(2a+4)桌年夜饭.故答案为:2a+4.点评:此题考查列代数式,理清思路,根据题意列出代数式解决问题.11.(3分)一个正方形与一个正六边形如图放置,正方形的一条边与正六边形的一条边完全重合,则∠1的度数为30度.考点:多边形内角与外角.分析:求得正六边形的内角和正方形的内角后相减即可确定答案.解答:解:∵360°÷6=60°,∴正六边形的外角为60°,∴正六边形的内角为120°,∵正方形的内角为90°,∴∠1=120°﹣90°=30°,故答案为:30.点评:本题考查了多边形的内角与外角,解题的关键是确定正六边形的内角的度数.12.(3分)如图,MN是⊙O的直径,矩形ABCD的顶点A、D在MN上,顶点B、C在⊙O 上,若⊙O的半径为5,AB=4,则AD边的长为6.考点:垂径定理;勾股定理;矩形的性质.分析:连接OB,根据矩形性质得出AB=CD=4,∠BAO=∠CDO=90°,根据勾股定理求出AO、DO,即可得出答案.解答:解:连接OB,∵四边形ABCD是矩形,∴AB=CD=4,∠BAO=∠CDO=90°,∵OB=5,∴AO==3,同理DO=3,∴AD=3+3=6,故答案为:6.点评:本题考查了矩形性质,勾股定理的应用,解此题的关键是求出AO和DO的长,题目比较典型,难度不大.13.(3分)如图,已知抛物线y=﹣x2+bx+c的对称轴为直线x=1,且与x轴的一个交点为(3,0),那么它对应的函数解析式是y=﹣x2+2x+3.考点:待定系数法求二次函数解析式.专题:常规题型.分析:首先根据对称轴为1,求得b,然后根据与x轴的一个交点为(3,0)解得c.解答:解:∵抛物线y=﹣x2+bx+c的对称轴为直线x=1,∴=1,解得b=2,∵与x轴的一个交点为(3,0),∴0=﹣9+6+c,解得c=3,故函数解析式为y=﹣x2+2x+3.故答案为:y=﹣x2+2x+3.点评:本题主要考查待定系数求二次函数的解析式的知识点,熟练掌握二次函数的性质,此题难度一般.14.(3分)如图,点A在反比例函数y=(x>0)的图象上,过点A作AD⊥y轴于点D,延长AD至点C,使AD=DC,过点A作AB⊥x轴于点B,连结BC交y轴于点E.若△ABC 的面积为4,则k的值为4.考点:反比例函数系数k的几何意义.专题:计算题.分析:连结BD,利用三角形面积公式得到S△ADB=S△BAC=2,则S矩形OBAD=2S△ADB=4,于是可根据反比例函数的比例系数k的几何意义得到k的值.解答:解:连结BD,如图,∵AD=DC,∴S△ADB=S△BDC=S△BAC=×4=2,∵AD⊥y轴于点D,AB⊥x轴,∴四边形OBAD为矩形,∴S矩形OBAD=2S△ADB=2×2=4,∴k=4.故答案为4.点评:本题考查了反比例函数的比例系数k的几何意义:在反比例函数y=图象中任取一点,过这一个点向x轴和y轴分别作垂线,与坐标轴围成的矩形的面积是定值|k|.三、解答题(本大题10小题,共78分)15.(5分)化简:÷.考点:分式的乘除法.专题:计算题.分析:原式利用除法法则变形,约分即可得到结果.解答:解:原式=•=.点评:此题考查了分式的乘除法,熟练掌握运算法则是解本题的关键.16.(6分)在一个不透明的盒子中放有三张卡片,分别标记为A、B、C,每张卡片除了标记不同外,其余均相同.某同学第一次从盒子中随机抽取一张卡片,卡片放回,第二次又随机抽取一张卡片.请用画树状图(或列表)的方法,求两次抽取的都是A的概率.考点:列表法与树状图法.分析:首先根据题意画出树状图,然后由树状图求得所有等可能的结果与两次抽取的都是A的情况,再利用概率公式即可求得答案.解答:解:画树状图得:∵共有9种等可能的结果,两次抽取的都是A的有1种情况,∴两次抽取的都是A的概率为:.点评:本题考查的是用列表法或画树状图法求概率.注意列表法或画树状图法可以不重复不遗漏的列出所有可能的结果,列表法适合于两步完成的事件,树状图法适合两步或两步以上完成的事件.用到的知识点为:概率=所求情况数与总情况数之比.17.(6分)某车间接到加工200个零件的任务,在加工完40个后,由于改进了技术,每天加工的零件数量是原来的2.5倍,整个加工过程共用了13天完成.求原来每天加工零件的数量.考点:分式方程的应用.分析:设原来每天加工零件的数量是x个,根据整个加工过程共用了13天完成,列出方程,再进行检验即可.解答:解:设原来每天加工零件的数量是x个,根据题意得:+=13,解得:x=8将检验x=8是原方程的解,答:原来每天加工零件的数量是8个.点评:本题考查分式方程的应用,分析题意,找到关键描述语,找到合适的等量关系是解决问题的关键.涉及到的公式:工作时间=工作总量÷工作效率.18.(7分)如图,在矩形ABCD中,以点D为圆心,DA长为半径画弧,交CD于点E,以点A为圆心,AE长为半径画弧,恰好经过点B,连结BE、AE.求∠EBC的度数.考点:矩形的性质;等腰直角三角形.分析:根据题意可得AD=DE,AE=AB,再根据矩形的性质可得∠D=∠ABC=∠DAB=90°,然后根据等腰三角形的性质分别算出∠DAE和∠EAB,再根据叫的和差关系可得答案.解答:解:由题意得:AD=DE,AE=AB,∵四边形ABCD是矩形,∴∠D=∠ABC=∠DAB=90°,∵AD=DE,∴∠DAE=45°,∴∠EAB=45°,∵AE=AB,∴∠EBA=∠AEB==67.5°,∴∠EBC=90°﹣67.5°=22.5°.点评:此题主要考查了矩形的性质,以及等腰三角形的性质,关键是掌握矩形的四个角都是直角.19.(7分)周末,小强在文化广场放风筝.如图,小强为了计算风筝离地面的高度,他测得风筝的仰角为58°,已知风筝线BC的长为10米,小强的身高AB为1.55米.请你帮小强画出测量示意图,并计算出风筝离地面的高度(结果精确到0.1米).(参考数据:sin58°=0.85,cos58°=0.53,tan58°=1.60)考点:解直角三角形的应用-仰角俯角问题.分析:根据题意画出图形,根据sin58°=可求出CE的长,再根据CD=CE+ED即可得出答案.解答:解:如图,过点C作地面的垂线CD,垂足为D,过点B作BE⊥CD于E.在Rt△CEB中,∵sin∠CBE=,∴CE=BC•sin58°=10×0.85≈8.5m,∴CD=CE+ED=8.5+1.55=10.05≈10.1m,答:风筝离地面的高度约为10.1m.点评:本题考查的是解直角三角形的应用﹣仰角俯角问题,根据题意作出辅助线,构造出直角三角形是解答此题的关键.20.(8分)为了了解某市初中学生上学的交通方式,从中随机调查了a名学生的上学交通方式,统计结果如图.(1)求a的值;(2)补全条形统计图并求出乘坐公共汽车上学占上学交通方式百分比的扇形圆心角的度数;(3)该市共有初中学生15000名,请估计其中坐校车上学的人数.考点:条形统计图;用样本估计总体;扇形统计图.分析:(1)用乘坐私家车的人数除以其所占的百分比即可确定a值;(2)总数减去其他交通方式出行的人数即可确定乘坐校车的人数,从而补全统计图;(3)用学生总数乘以乘坐校车的所占的百分比即可.解答:解:(1)观察两种统计图知:乘坐私家车上学的有600人,占20%,∴a=600÷20%=3000人;(2)乘坐校车的有3000﹣600﹣600﹣300﹣300=1200人,统计图为:乘坐公共汽车上学占上学交通方式百分比的扇形圆心角的度数为×360°=120°;(3)初中学生15000名中,坐校车上学的人数有15000×=6000人.点评:本题考查了条形统计图及扇形统计题的知识,解题的关键是从两种统计图中整理出进一步解题的有关信息,难度适中.21.(8分)一辆轿车从甲地驶往乙地,到达乙地后返回甲地,速度是原来的1.5倍,共用t 小时;一辆货车同时从甲地驶往乙地,到达乙地后停止.两车同时出发,匀速行驶.设轿车行驶的时间为x(h),两车到甲地的距离为y(km),两车行驶过程中y与x之间的函数图象如图.(1)求轿车从乙地返回甲地时的速度和t的值;(2)求轿车从乙地返回甲地时y与x之间的函数关系式,并写出自变量x的取值范围;(3)直接写出轿车从乙地返回甲地时与货车相遇的时间.考点:一次函数的应用.分析:(1)利用行驶的速度变化进而得出时间变化,进而得出t的值;(2)利用待定系数法求一次函数解析式进而利用图象得出自变量x的取值范围;(3)利用函数图象交点求法得出其交点横坐标,进而得出答案.解答:解:(1)∵一辆轿车从甲地驶往乙地,到达乙地后返回甲地,速度是原来的1.5倍,∴行驶的时间分别为:=3小时,则=2小时,∴t=3+2=5;∴轿车从乙地返回甲地时的速度是:=120(km/h);(2)∵t=5,∴此点坐标为:(5,0),设轿车从乙地返回甲地时y与x之间的函数关系式为:y=kx+b,∴,解得:,∴轿车从乙地返回甲地时y与x之间的函数关系式为:y=﹣120x+600(3≤x≤5);(3)设货车行驶图象解析式为:y=ax,则240=4a,解得:a=60,∴货车行驶图象解析式为:y=60x,∴当两图象相交则:60x=﹣120x+600,解得:x=,故﹣3=(小时),∴轿车从乙地返回甲地时与货车相遇的时间小时.点评:此题主要考查了一次函数的应用以及待定系数法求一次函数解析式等知识,利用数形结合得出函数解析式是解题关键.22.(9分)如图,在四边形ABCD中,∠ABC=30°,∠ADC=60°,AD=DC,连接AC、BD.在四边形ABCD的外部以BC为一边作等边三角形BCE,连接AE.(1)求证:BD=AE;(2)若AB=2,BC=3,求BD的长.考点:全等三角形的判定与性质;等边三角形的判定与性质.分析:(1)由∠ADC=60°,AD=DC,易得△ADC是等边三角形,又由△BCE是等边三角形,可证得△BDC≌△EAC(SAS),即可得BD=AE;(2)由△BCE是等边三角形,∠ABC=30°,易得∠ABE=90°,然后由勾股定理求得AE的长,即可求得BD的长.解答:(1)证明:∵在△ADC中,AD=DC,∠ADC=60°,∴△ADC是等边三角形,∴DC=AC,∠DCA=60°;又∵△BCE是等边三角形,∴CB=CE,∠BCE=60°,∴∠DCA+∠ACB=∠ECB+∠ACB,即∠DCB=∠ACE,在△BDC和△EAC中,,∴△BDC≌△EAC(SAS),∴BD=AE;(2)解:∵△BCE是等边三角形,∴BE=BC=3,∠CBE=60°.∵∠ABC=30°,∴∠ABE=∠ABC+∠CBE=90°.在Rt△ABE中,AE===,∴BD=AE=.点评:此题考查了全等三角形的判定与性质、等边三角形的判定与性质以及勾股定理.此题难度适中,注意掌握数形结合思想的应用.23.(10分)如图①,在平面直角坐标系中,点A是抛物线y=x2在第一象限上的一个点,连结OA,过点A作AB⊥OA,交y轴于点B,设点A的横坐标为n.【探究】:(1)当n=1时,点B的纵坐标是2;(2)当n=2时,点B的纵坐标是5;(3)点B的纵坐标是n2+1(用含n的代数式表示).【应用】:如图②,将△OAB绕着斜边OB的中点顺时针旋转180°,得到△BCO.(1)求点C的坐标(用含n的代数式表示);(2)当点A在抛物线上运动时,点C也随之运动.当1≤n≤5时,线段OC扫过的图形的面积是2.考点:二次函数综合题.分析:探究;依据直角三角形的射影定理即可求得B点的坐标.应用:(1)依据全等三角形的性质即可求得C点的坐标,(2)通过(1)可求得C1、C2的坐标,从而得出矩形面积和三角形的面积,最后求得当1≤n≤5时,线段OC扫过的图形的面积.解答:解:探究(3)如图1所示:设点A的横坐标为n,点A是抛物线y=x2在第一象限上的一个点;∴A(n,n2);∴AD=n,OD=n2;在Rt△ACB中,AD2=OD•BD;设B点的纵坐标为y1,则n2=n2•(y1﹣n2),解得:y1=n2+1,∴点B的纵坐标是n2+1.应用:(1)点B的纵坐标是n2+1,A点的纵坐标是n2,∴BD=1,根据旋转的定义可知CE=AD=n,OE=BD=1;∴C点的坐标为:(﹣n,1);(2)当n=1时C点的坐标为C1(﹣1,1),当n=5时C点的坐标为C2(﹣5,1),如上图所示;S=S﹣S=×1×5﹣×1×1=2.∴当1≤n≤5时,线段OC扫过的图形的面积是2.点评:本题考查了直角三角形的射影定理的应用,全等三角形的性质,直角坐标系中面积求法是本题的关键.24.(12分)如图,在Rt△ABC中,∠ACB=90°,AC=8cm,AB=10cm.点P从点A出发,以5cm/s的速度从点A运动到终点B;同时,点Q从点C出发,以3cm/s的速度从点C运动到终点B,连结PQ;过点P作PD⊥AC交AC于点D,将△APD沿PD翻折得到△A′PD,以A′P和PB为邻边作▱A′PBE,A′E交射线BC于点F,交射线PQ于点G.设▱A′PBE与四边形PDCQ重叠部分图形的面积为Scm2,点P的运动时间为ts.(1)当t为何值时,点A′与点C重合;(2)用含t的代数式表示QF的长;(3)求S与t的函数关系式;(4)请直接写出当射线PQ将▱A′PBE分成的两部分图形的面积之比是1:3时t的值.考点:相似形综合题;解一元一次不等式组;等腰三角形的判定与性质;勾股定理;平行四边形的性质;相似三角形的判定与性质.专题:压轴题.分析:(1)易证△ADP∽△ACB,从而可得AD=4t,由折叠可得AA′=2AD=8t,由点A′与点C重合可得8t=8,从而可以求出t的值.(2)根据点F的位置不同,可分点F在BQ上(不包括点B)、在CQ上(不包括点Q)、在BC的延长线上三种情况进行讨论,就可解决问题.(3)根据点F的位置不同,可分点F在BQ上(不包括点B)、在CQ上(不包括点Q)、在BC的延长线上三种情况进行讨论,就可解决问题.(4)可分①S△A′PG:S四边形PBEG=1:3,如图7,②S△BPN:S四边形PNEA′=1:3,如图8,两种情况进行讨论,就可解决问题.解答:解:(1)如图1,由题可得:PA′=PA=5t,CQ=3t,AD=A′D.∵∠ACB=90°,AC=8,AB=10,∴BC=6.∵∠ADP=∠ACB=90°,∴PD∥BC.∴△ADP∽△ACB.∴==.∴==.∴AD=4t,PD=3t.∴AA′=2AD=8t.当点A′与点C重合时,AA′=AC.∴8t=8.∴t=1.(2)①当点F在线段BQ上(不包括点B)时,如图1,则有CQ≤CF<CB.∵四边形A′PBE是平行四边形,∴A′E∥BP.∴△CA′F∽△CAB.∴=.∴=.∴CF=6﹣6t.∴3t≤6﹣6t<6.∴0<t≤.此时QF=CF﹣CQ=6﹣6t﹣3t=6﹣9t.②当点F在线段CQ上(不包括点Q)时,如图2,则有0≤CF<CQ.∵CF=6﹣6t,CQ=3t,∴0≤6﹣6t<3t.∴<t≤1.此时QF=CQ﹣CF=3t﹣(6﹣6t)=9t﹣6.③当点F在线段BC的延长线上时,如图3,则有AA′>AC,且AP<AB.∴8t>8,且5t<10.∴1<t<2.同理可得:CF=6t﹣6.此时QF=QC+CF=3t+6t﹣6=9t﹣6.综上所述:当0<t≤时,QF=6﹣9t;当<t<2时,QF=9t﹣6.(3)①当0<t≤时,过点A′作A′M⊥PG,垂足为M,如图4,则有A′M=CQ=3t.∵==,==,∴=,∵∠PBQ=∠ABC,∴△BPQ∽△BAC.∴∠BQP=∠BCA.∴PQ∥AC.∵AP∥A′G.∴四边形APGA′是平行四边形.∴PG=AA′=8t.∴S=S△A′PG=PG•A′M=×8t×3t=12t2.②当<t≤1时,过点A′作A′M⊥PG,垂足为M,如图5,则有A′M=QC=3t,PQ=DC=8﹣4t,PG=AA′=8t,QG=PG﹣PQ=12t﹣8,QF=9t﹣6..∴S=S△A′PG﹣S△GQF=PG•A′M﹣QG•QF=×8t×3t﹣×(12t﹣8)×(9t﹣6)=﹣42t2+72t﹣24.③当1<t<2时,如图6,∵PQ∥AC,PA=PA′∴∠BPQ=∠PAA′,∠QPA′=∠PA′A,∠PAA′=∠PA′A.∴∠BPQ=∠QPA′.∵∠PQB=∠PQS=90°,∴∠PBQ=∠PSQ.∴PB=PS.∴BQ=SQ.∴SQ=6﹣3t.∴S=S△PQS=PQ•QS=×(8﹣4t)×(6﹣3t)=6t2﹣24t+24.综上所述:当0<t≤时,S=12t2;当<t≤1时,S=﹣42t2+72t﹣24:当1<t<2时,S=6t2﹣24t+24.(4)①若S△A′PG:S四边形PBEG=1:3,过点A′作A′M⊥PG,垂足为M,过点A′作A′T⊥PB,垂足为T,如图7,则有A′M=PD=QC=3t,PG=AA′=8t.∴S△A′PG=×8t×3t=12t2.∵S△APA′=AP•A′T=AA′•PD,∴A′T===t.∴S▱PBEA′=PB•A′T=(10﹣5t)×t=24t(2﹣t).∵S△A′PG:S四边形PBEG=1:3,∴S△A′PG=×S▱PBEA′.∴12t2=×24t(2﹣t).∵t>0,∴t=.②若S△BPN:S四边形PNEA′=1:3,如图8,同理可得:∠BPQ=∠A′PQ,BQ=6﹣3t,PQ=8﹣4t,S▱PBEA′=24t(2﹣t).∵四边形PBEA′是平行四边形,∴BE∥PA′.∴∠BNP=∠NPA′.∴∠BPN=∠BNP.∴BP=BN.∵∠BQP=∠BQN=90°,∴PQ=NQ.∴S△BPN=PN•BQ=PQ•BQ=(8﹣4t)×(6﹣3t).∵S△BPN:S四边形PNEA′=1:3,∴S△BPN=×S▱PBEA′.∴(8﹣4t)×(6﹣3t)=×24t(2﹣t).∵t<2,∴t=.综上所述:当射线PQ将▱A′PBE分成的两部分图形的面积之比是1:3时,t的值为秒或秒.点评:本题考查了相似三角形的判定与性质、等腰三角形的判定与性质、平行四边形的性质、解一元一次不等式组、勾股定理等知识,还考查了分类讨论的思想,有一定的综合性.。
北京市朝阳区2014年中考一模化学试题含答案
北京市朝阳区九年级综合练习(一)化 学 试 卷 2014.5学校 班级 姓名 考号可能用到的相对原子质量H 1 Li 7 C 12 O 16 Na 23 S 32 Cl 35.5 Ca 40 Fe 56 Cu 64 一、 选择题(每小题只有1个选项符合题意。
共25个小题,每小题1分,共25分) 1.下列属于化学变化的是A .冰雪融化B .干冰升华C .蜡烛燃烧D .菠萝榨汁 2.下列属于纯净物的是A .洁净空气B .可口可乐C .新鲜牛奶D .蒸馏水 3.下列项目没有列入空气质量监测的是A .N 2B .NO 2C .COD .PM 2.5 4.下列物质中,属于氧化物的是A .NaClB .MnO 2C .NaOHD .H 2SO 45.下列物质在氧气中燃烧,火星四射、生成黑色固体的是A .木炭B .镁条C .红磷D .铁丝 6.下列标志中,与保护环境无关的是A B C D7.不同种元素的本质区别是A .中子数不同B.电子数不同C.质子数不同D.相对原子质量不同 8.下列物质放入水中,能形成无色溶液的是A .高锰酸钾B .蔗糖C .植物油D .硫酸铜 9.下列符号中,表示2个氢原子的是A .H 2B .2HC .2H +D .2H 210.配制500 g 0.9%的生理盐水,不需要的仪器是A.烧杯B.量筒C.蒸发皿D.玻璃棒11.加热胆矾固体的实验过程中,操作正确的是A.取样 B.加药 C.加热 D.熄灭12 下列物质中,含有氧分子的是A.O2 B.H2O C.CO2 D.SO213.Cr2O3可以作某些化学反应的催化剂,其中Cr元素的化合价为A.+1 B.+2 C.+3 D.+614.下列物质敞口放置于空气中,质量会增加的是A.食盐水 B.石灰石 C.浓盐酸 D.浓硫酸15.右图为汞元素的信息,下列说法正确的是A.汞的核电荷数为80B.汞属于非金属元素C.汞的相对原子质量为200.6gD.在化学反应中,汞原子容易得到电子16.从分子的角度分析,下列解释不正确的是A.水结冰体积变大——分子大小发生改变B.氧气加压后贮存在钢瓶中——分子间有间隔C.水通电生成氢气和氧气——分子在化学变化中可分D.湿衣服在太阳下干得快——分子运动速率与温度有关17.金属M与AgNO3溶液反应的化学方程式为:M + 2AgNO3= M(NO3)2+ 2Ag。
