高中立体几何八大定理
立体几何四大公理八大定理

立体几何四大公理八大定理《立体几何四大公理八大定理篇一》立体几何,那可是数学里的一座神秘大山。
说起立体几何四大公理八大定理,就像是在讲述一个神秘组织的规则一样。
先说说这四大公理吧。
公理就像是游戏的基本规则,大家都得默认它是对的,没什么可商量的余地。
就像那“如果一条直线上的两点在一个平面内,那么这条直线在此平面内”这条公理,我刚接触的时候就觉得,这不是理所当然的嘛。
可后来仔细一想,这就像在说一个小蚂蚁在一张纸上爬,如果它的两只脚都在纸上,那它整个身子肯定也在纸上啊。
这就像生活中的一些道理,看似简单,其实蕴含着很深的意义。
再看那八大定理,我的天呐,就像是迷宫里的一道道关卡。
有时候我感觉自己像是在黑暗中摸索的探险家,试图搞清楚这些定理之间的关系。
比如说,线面垂直的判定定理,要证明一条直线垂直一个平面,得找平面内两条相交直线都和这条直线垂直。
我每次做这种题的时候,就像在玩一场“找不同”的游戏,在复杂的图形里找出那两条特殊的相交直线。
我记得有一次考试,有一道立体几何的大题,就是要用到这些公理和定理。
我当时看着那图形,就像看一幅外星来的抽象画一样,完全蒙圈了。
我就想,这公理和定理怎么在这时候就像跟我捉迷藏似的呢?也许是我还不够熟练,就像一个新手厨师,虽然知道菜谱上的步骤,但是真到做的时候就手忙脚乱。
我开始在脑海里拼命回忆那些公理和定理,就像在翻找一个装满杂物的旧箱子,试图找到那个合适的工具。
可是有时候我又觉得这些公理和定理是不是有点太刻板了呢?我就想啊,在现实生活中,有些东西可没这么规规矩矩的。
比如说,我们看到的那些建筑,虽然也是基于立体几何的原理,但有些设计就很奇特,好像有点打破这些公理定理的感觉。
但也许这就是理论和实际的差距吧,理论是基础,实际是在这个基础上的创新。
就像我们学走路,先得学会基本的步伐,然后才能跳出自己的舞步。
这些公理和定理虽然有时候让我头疼得像要炸开一样,但我也知道,它们就像一把把钥匙,能打开立体几何这个神秘世界的大门。
立体几何常考法则概括(八大法则)

立体几何常考法则概括(八大法则)立体几何是数学中的一个分支,研究的是三维空间中的图形和形状。
在解决立体几何问题时,我们可以借助一些常考的法则来简化求解过程。
本文将介绍八大立体几何常考法则,以帮助读者更好地理解和应用。
1. 平行与垂直关系平行关系:- 平面平行关系:两个平面如果没有公共点或平面间的交线平行于平面的截线,则这两个平面是平行的。
- 直线平行关系:如果两条直线在同一平面内,且不相交,则这两条直线是平行的。
垂直关系:- 平面垂直关系:两个平面的法线向量垂直,则这两个平面是垂直的。
- 直线垂直关系:两条直线的斜率之积为-1,则这两条直线是垂直的。
2. 距离和长度关系距离公式:- 两点距离:两点之间的距离可以通过勾股定理求解:$\sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2 + (z_2 - z_1)^2}$长度关系:- 线段等长关系:如果两条线段的长度相等,则这两条线段是等长的。
3. 角度关系直角关系:- 直角:两条相交的直线产生的两个相邻补角之和为90度。
平面角关系:- 互余角:两个角互补或补角相等。
4. 空间图形性质正方体:- 八个顶点、六个面、十二条边。
- 相对面平行、对角面垂直。
- 对边平行且等长、相邻面的边垂直。
正八面体:- 六个顶点、八个面、十二条边。
- 任意两个顶点之间的连线等长。
圆柱体:- 两个圆底面、一个侧面。
- 侧面是矩形、底面圆心连线垂直于侧面。
圆锥体:- 一个圆底面、一个侧面。
- 侧面是扇形、底面圆心连线垂直于侧面。
球体:- 一个面,无棱无角。
- 任意两点之间的连线长度等于球心间距。
以上是八大立体几何常考法则的概括。
通过了解和熟练运用这些法则,我们可以更轻松地解决立体几何相关的问题。
希望本文对读者有所帮助。
高中数学立体几何定理总结

高中数学立体几何定理总结一、线线平行的判定1.定义:在同一平面内,没有公共点的两条直线,记作a∥b。
2.平行于同一条直线的两条直线互相平行。
即a∥b,b∥c,则a∥c。
3.如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线和交线平行。
即l∥m,l∥α,则m∥α。
4.如果两个平行平面同时与第三个平面相交,那么它们的交线平行。
即α∥β,α∩γ=a,β∩γ=b,则a∥b。
5.垂直于同一平面的两条直线平行。
即ba⊥α,ba⊥β,则a∥b。
二、线面平行的判定1.定义:直线与平面无公共点,记作a∥α。
2.如果不在一个平面内的一条直线和平面内的一条直线平行,那么这条直线和这个平面平行。
即l∋α,XXXα,则l∥α。
3.如果在一个平面内的一条直线和这个平面内的一条斜线的射影垂直,则这条直线和这个平面内的任何直线垂直。
即l⊥α,XXX⊥α,则l⊥PA。
三、面面平行的判定1.定义:两个平面没有公共点,记作α∥β。
2.如果一个平面内有两条相交直线分别平行于另一个平面,则这两个平面互相平行。
即a∥β,b∥β,a∩b=A,则α∥β。
3.一个平面内的两条相交直线与另一平面平行,则这两个平面平行。
即a∥α,a∥β,a∩b=A,则α∥β。
垂直判定总结1.定义:两直线所成角为90度。
2.线面垂直的性质:若直线垂直平面,则直线垂直平面内的任何直线。
即l⊥α,XXXα,则XXX。
3.三垂线定理:在平面内的一条直线,如果和这个平面的一条斜线的射影垂直,则它也和这条斜线垂直。
即PA∩α=A,PB⊥α,则PA⊥PB。
4.三垂线定理的逆定理:在平面内的一条直线,如果和这个平面的一条斜线垂直,则它也和这条斜线的射影垂直。
即PA∩α=A,PB⊥AB,则XXX⊥α。
高中数学立体几何定理总结

1、直线与平面平行的判定定理:平面外一条直线与此平面内一条直线平行,则该直线与此平面平行.2、直线与平面平行的性质定理:如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线和交线平行.ba b a a ////⇒⎪⎭⎪⎬⎫=⊂βαβα3、平面与平面平行的判定定理:如果一个平面内的两条相交直线都平行于另一个平面,那么这两个平面平行.4、平面与平面平行的性质定理:①如果两个平面平行,那么某一个平面内的直线与另一个平面平行.βαβα//,//a a ⇒⊂②如果两个平行平面都和第三个平面相交,那么它们的交线平行. b a b a ////⇒⎪⎭⎪⎬⎫==γβγαβα γba βαβαββαα//////⇒⎪⎪⎪⎭⎪⎪⎪⎬⎫=⊂⊂b a P b a b aααα////a b a b a ⇒⎪⎭⎪⎬⎫⊂⊄βαm l如果一条直线和一个平面内的两条相交直线都垂直,那么这条直线垂直这个平面.ααα⊥⇒⎪⎪⎪⎭⎪⎪⎪⎬⎫=⊂⊂⊥⊥l P b a b a b l a l6、直线与平面垂直的性质定理:①如果一条直线与一个平面垂直,那么它就与平面内的任何一条直线垂直.b a b a ⊥⇒⊂⊥αα,②如果两条直线同垂直于一个平面,那么这两条直线平行.ba b a //⇒⎭⎬⎫⊥⊥αα7、平面与平面垂直的判定定理:如果一个平面经过另一个平面的一条垂线,那么这两个平面互相垂直.8、平面与平面垂直的性质定理:如果两个平面互相垂直,那么在一个平面内垂直于他们的交线的直线垂直于另一个平面.ββαβα⊥⇒⎪⎭⎪⎬⎫⊥⊂=b b b a βαβαβα⊥⇒⎪⎪⎭⎪⎪⎬⎫⊥⊂=⊥a b a a b1、直线与平面平行的判定定理:2、直线与平面平行的性质定理:3、平面与平面平行的判定定理:4、平面与平面平行的性质定理:①②6、直线与平面垂直的性质定理:①②7、平面与平面垂直的判定定理:8、平面与平面垂直的性质定理:。
高中数学立体几何中所有定理 高考必背
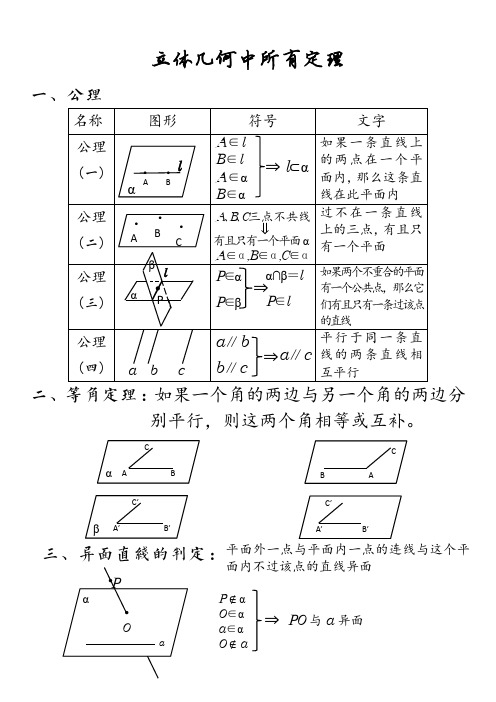
一、公理
名称
图形
符号
文字
公理 (一)
公理 (二) 公理 (三)
· ·l
αA B
· A
· B·
C
βl
α
·
P
公理 (四) a b c
A∈l
如果一条直线上
B∈l A∈α B∈α
⇒ l⊂α
的两点在一个平 面内,那么这条直
线在此平面内
A、B、C三点不共线 过 不 在 一 条 直 线
⇒
上的三点,有且只
它也和这条斜线垂直, 反之亦成立
九、线面垂直的判定
名称 线面垂 直判定 定理
图形 l
a α Ob
线面垂 直的性
a
b
质
α
面面垂
βB
直的性 C A 质定理 α
面面垂
直的性
质
α
a βγ
十、面面垂直的判定
名称
图形
面面垂 直的判
βa
定定理 α
面面垂
α
直的性
β
质
γ
符号
a⊂α b⊂α a∩b=O l⊥a l⊥b
七、面面平行的判定
名称 面面平 行的判 定定理
图形
b
a
αO
β
线面垂 α 直性质 β a
八、线线垂直的判定
符号
a⊂α b⊂α
a∩b=O a∥β b∥β
a⊥α
a⊥β
⇒ α∥β ⇒ α∥β
文字
如果一个平面内有 两条相交直线分别 平行另一个平面, 则这两个平面平行
若一条直线同时与 两个平面垂直,则 这两个平面平行
垂直于同一平面的两 条直线相互平行
2021年高中立体几何八大定理之令狐文艳创作

令狐文艳创作线面位置关系的八大定理令狐文艳一、直线与平面平行的判定定理:文字语言:如果平面外的一条直线与平面内的一条直线平行,则这条直线与平面平行 图形语言: 符号语言:作用:线线平行⇒线面平行二、直线与平面平行的性质定理:文字语言:如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线就和交线平行。
图形语言:符号语言://l l m αβαβ⎫⎪⊂⎬⎪⋂=⎭⇒//l m 作用:线面平行⇒线线平行 三、平面与平面平行的判定定理文字语言:如果一个平面内有两条相交直线都平行于另一个平面,那么这两个平面平行. 图形语言: 符号语言:作用:线线平行⇒ 面面平行 四、平面与平面平行的性质定理:αbalmβα令狐文艳创作文字语言:如果两个平行平面同时和第三个平面相交,那么所得的两条交线平行 图形语言:符号语言:////a a b b αβαγβγ⎫⎪⋂=⇒⎬⎪⋂=⎭作用: 面面平行⇒线线平行五、直线与平面垂直的判定定理:文字语言:如果一条直线和一个平面内的两条相交直线垂直,那么这条直线垂直于这个平面 图形语言:符号语言:作用:线线垂直⇒线面垂直六、直线与平面垂直的性质定理:文字语言:若两条直线垂直于同一个平面,则这两条直线平行 图形语言: 符号语言:作用:线面垂直⇒线线平行七、平面与平面垂直的判定定理:文字语言:如果一个平面经过另一个平面的一条垂线,则这两个平面互相垂直。
图形语言:aβααbanmAαa符号表示:aaααββ⊥⎫⇒⊥⎬⊂⎭注:线面垂直⇒面面垂直八、平面与平面垂直的性质定理:文字语言:如果两个平面互相垂直,那么在一个平面内垂直与它们的交线的直线垂直于另一个平面图形语言:符号语言:lAB ABAB lαβαββα⊥⎫⎪=⎪⇒⊥⎬⊂⎪⎪⊥⎭作用:面面垂直⇒线面垂直BAlβα令狐文艳创作。
立体几何八个定理默写_含答案

2014学年高二数学---1028立体几何“平行、垂直”定理默写给你定理的图形语言,请写出定理的文字语言(即类似原话的叙述)、以及符号语言:文字语言: 符号语言:图形语言:② 面面平行的判定定理——线面平行 则面面平行文字语言: 符号语言: 图形语言:③ 线面平行的性质定理——线面平行 则线线平行文字语言: 符号语言: 图形语言:④ 面面平行的性质定理——面面平行 则线线平行文字语言: 符号语言: 图形语言:▲平行的其它结论:(1) 若面面平行,则一面内任一线平行于另一面。
(2) 等角定理:若两个角的边对应平行,则这两个角相等或互补。
⑤ 线面垂直的判定定理——线线垂直 则线面垂直 文字语言: 符号语言: 图形语言:⑥ 面面垂直的判定定理——线面垂直 则面面垂直文字语言: 符号语言: 图形语言:⑦ 线面垂直的性质定理:(这个还是线面垂直的定义“线面垂直则线线垂直”有用,故用定义代替定理)文字语言: 符号语言: ④ 面面平行的性⑤ 线面垂直的判⑦ 线面垂直的性⑧ 面面垂直的性⑧ 面面垂直的性质定理:面面垂直 则线面垂直文字语言: 符号语言: 图形语言:▲垂直的其它结论:(1)若两平行线中的一条垂直于一面,则另一条也垂直于该面。
(2)若两直线都垂直于一面,则这两直线平行。
(这个是书上的线面垂直性质定理)(3)若两平面垂直,则过一面内一点与另一面垂直的直线,必在该面内。
答案1、八个定理——立体几何的证明的依据、更是证明的思路:① 线面平行的判定定理——线线平行,则线面平行文字语言: 符号语言: 图形语言: 平面外一条直线与此平面 内的一条直线平行,则此直线与此平面平行。
② 面面平行的判定定理——线面平行,则面面平行文字语言: 符号语言: 图形语言: 一个平面内的两条相交 直线与另一个平面平行,则这两个平行平行。
③ 线面平行的性质定理——线面平行,则线线平行文字语言: 符号语言: 图形语言: 一条直线与一个平面平行, 则过这条直线的任一平面与此平面的交线与该直线平行。
立体几何证明8条定理
文字语言
图形语言
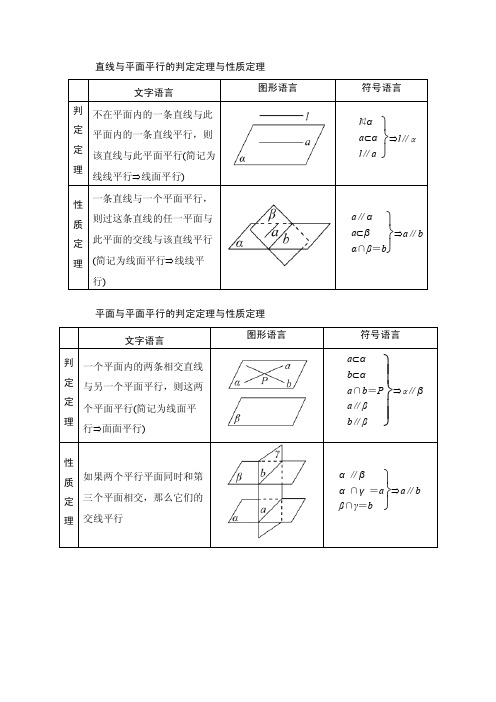
判 一个平面内的两条相交直线
定 与另一个平面平行,则这两 定 个平面平行(简记为线面平 理
行⇒面面平行)
性 质 如果两个平行平面同时和第 定 三个平面相交,那么它们的
理 交线平行
符号语言
l⊄α a⊂α ⇒l∥α l∥a a∥α a⊂β ⇒a∥b α∩β=b
符号语言 a⊂α
b⊂α a∩b=P ⇒α∥β a∥β
直线与平面平行的判定定理与性质定理
文字语言
判 不在平面内的一条直线与此 定 平面内的一条直线平行,则 定 该直线与此平面平行(简记为 理
线线平行⇒线面平行)
图形语言
性 一条直线与一个平面平行, 质 则过这条直线的任一平面与 定 此平面的交线与该直线平行 理 (简记为线面平行⇒线线平
行)
平面与平面平行的判定定理与性质定理
b∥β
α ∥β α ∩γ =a⇒a∥b β∩γ=b
直线与平面垂直的判定定理及性质定理
文字语言
图形语言
判 一条直线与平面内的两条相
定 交直线都垂直,则该直线与此
定 平面垂直
理
性 质 垂直于同一个平面的两条直 定 线平行 理
平面与平面垂直的判定定理及性质定理
文字语言
图形语言
判定 定理
一个平面过另一个平面的一 条垂线,则这两个平面互相垂 直
性质 定理
两个平面互相垂直,则一个平 面内垂直于交线的直线垂直 于另一个平面
符号语言
a,b⊂α
a∩b=O l⊥a
⇒l⊥α
l⊥b
a⊥α b⊥α
⇒a∥b
符号语言
l⊂β l⊥α
⇒α⊥β
α ⊥α
l⊥a
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
令狐采学创作
令狐采学创作
l
m
b
a
线面位置关系的八大定理
令狐采学
一、直线与平面平行的判定定理:
文字语言:如果平面外的一条直线与平面内的一
条直线平行,则这条直线与平面平行
图形语言:
符号语言:
作用:线线平行线面平行
二、直线与平面平行的性质定理:
文字语言:如果一条直线和一个平面平行,经过这条直线的平
面和这个平面相交,那么这条直线就和交线平行。
图形语言:
符号语言:
//l
lm
//lm
作用:线面平行线线平行
三、平面与平面平行的判定定理
文字语言:如果一个平面内有两条相交直线都平行于另一个平
面,那么这两个平面平行.
图形语言:
符号语言:
作用:线线平行 面面平行
四、平面与平面平行的性质定理:
令狐采学创作
令狐采学创作
n
mA
a
b
a
a
文字语言:如果两个平行平面同时和第三个
平面相交,那么所得的两条交线平行
图形语言:
符号语言:
//
//aabb
作用: 面面平行线线平行
五、直线与平面垂直的判定定理:
文字语言:如果一条直线和一个平面内的两条相交直线垂直,
那么这条直线垂直于这个平面
图形语言:
符号语言:
作用:线线垂直线面垂直
六、直线与平面垂直的性质定理:
文字语言:若两条直线垂直于同一个平面,则这两条直
线平行
图形语言:
符号语言:
作用:线面垂直线线平行
七、平面与平面垂直的判定定理:
文字语言:如果一个平面经过另一个平面的一条垂线,则这两
个平面互相垂直。
图形语言:
令狐采学创作
令狐采学创作
B
A
l
符号表示:
aa
注:线面垂直面面垂直
八、平面与平面垂直的性质定理:
文字语言:如果两个平面互相垂直,那么在一个平面内垂
直与它们的交线的直线垂直于另一个平面
图形语言:
符号语言:
lABABABl
作用:面面垂直线面垂直
