2018中考数学总复习考点跟踪突破22 矩形、菱形与正方形
【精品】2018版中考数学:4.6-矩形、菱形、正方形(含答案)

§4.6矩形、菱形、正方形A组2018年全国中考题组一、选择题1.(2018·四川泸州,6,3分)菱形具有而平行四边形不具有的性质是() A.两组对边分别平行B.两组对角分别相等C.对角线互相平分D.对角线互相垂直解析根据菱形的特殊性质可知对角线互相垂直.A.不正确,两组对边分别平行,两者均有此性质;B.不正确,两组对角分别相等,两者均有此性质;C.不正确,对角线互相平分,两者均具有此性质;D.菱形的对角线互相垂直但平行四边形却无此性质.答案D2.(2018·山东日照,6,3分)小明在学习了正方形之后,给同桌小文出了道题,从下列四个条件:①AB=BC,②∠ABC=90°,③AC=BD,④AC⊥BD中选两个作为补充条件,使▱ABCD为正方形(如图),现有下列四种选法,你认为其中错误的是()A.①②B.②③C.①③D.②④解析A.∵四边形ABCD是平行四边形,∴当①AB=BC时,平行四边形ABCD是菱形,当②∠ABC=90°时,菱形ABCD是正方形,故此选项错误;B.∵四边形ABCD是平行四边形,∴当②∠ABC=90°时,平行四边形ABCD是矩形,当AC=BD时,这是矩形的性质,无法得出四边形ABCD是正方形,故此选项正确;C.∵四边形ABCD是平行四边形,∴当①AB=BC时,平行四边形ABCD是菱形,当③AC =BD时,菱形ABCD是正方形,故此选项错误;D.∵四边形ABCD是平行四边形,∴当②∠ABC=90°时,平行四边形ABCD是矩形,当④AC⊥BD时,矩形ABCD是正方形,故此选项错误.答案B3.(2018·山东青岛,7,3分)如图,菱形ABCD的对角线AC,BD相交于O点,E,F分别是AB,BC边上的中点,连结EF.若EF=。
通用版2018年中考数学总复习专题突破预测与详解第五单元四边形专题18矩形菱形和正方形试题新版新人教版
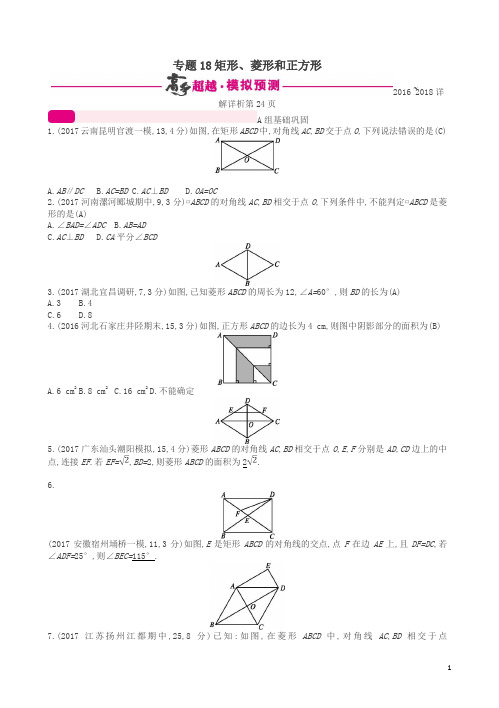
专题18矩形、菱形和正方形2016~2018详解详析第24页A组基础巩固1.(2017云南昆明官渡一模,13,4分)如图,在矩形ABCD中,对角线AC,BD交于点O,下列说法错误的是(C)A.AB∥DCB.AC=BDC.AC⊥BDD.OA=OC2.(2017河南漯河郾城期中,9,3分)▱ABCD的对角线AC,BD相交于点O,下列条件中,不能判定▱ABCD是菱形的是(A)A.∠BAD=∠ADCB.AB=ADC.AC⊥BDD.CA平分∠BCD3.(2017湖北宜昌调研,7,3分)如图,已知菱形ABCD的周长为12,∠A=60°,则BD的长为(A)A.3B.4C.6D.84.(2016河北石家庄井陉期末,15,3分)如图,正方形ABCD的边长为4 cm,则图中阴影部分的面积为(B)A.6 cm2B.8 cm2C.16 cm2D.不能确定5.(2017广东汕头潮阳模拟,15,4分)菱形ABCD的对角线AC,BD相交于点O,E,F分别是AD,CD边上的中点,连接EF.若EF=,BD=2,则菱形ABCD的面积为2.6.(2017安徽宿州埇桥一模,11,3分)如图,E是矩形ABCD的对角线的交点,点F在边AE上,且DF=DC,若∠ADF=25°,则∠BEC=115°.7.(2017江苏扬州江都期中,25,8分)已知:如图,在菱形ABCD中,对角线AC,BD相交于点O,DE∥AC,AE∥BD.(1)求证:四边形AODE是矩形;(2)若AB=4,∠BCD=120°,求四边形AODE的面积.(1)证明∵DE∥AC,AE∥BD,∴四边形AODE是平行四边形.∵在菱形ABCD中,AC⊥BD,∴平行四边形AODE是矩形.(2)解∵∠BCD=120°,AB∥CD,∴∠ABC=180°-120°=60°.∵AB=BC,∴△ABC是等边三角形,∴OA=×4=2.∵在菱形ABCD中,AC⊥BD,∴由勾股定理得OB==2,∵四边形ABCD是菱形,∴OD=OB=2,∴四边形AODE的面积=OA·OD=4.〚导学号92034076〛B组能力提升1.(2017广西贵港平南一模,12,3分)如图,在矩形ABCD中,AB=3,BC=2,点E为AD中点,点F为BC边上任一点,过点F分别作EB,EC的垂线,垂足分别为点G,H,则FG+FH为(D)A.B.C.D.〚导学号92034077〛2.(2018中考预测)如图,正方形ABCD的四个顶点A,B,C,D正好分别在四条平行线l1,l3,l4,l2上.若从上到下每两条平行线间的距离都是2 cm,则正方形ABCD的面积为20 cm2.C组综合创新(2017辽宁营口金桥一模,25,12分)在平行四边形ABCD中,E是AD上一点,AE=AB,过点E作直线EF,在EF上取一点G,使得∠EGB=∠EAB,连接AG.(1)如图①,当EF与AB相交时,若∠EAB=60°,求证:EG=AG+BG;(2)如图②,当EF与CD相交时,且∠EAB=90°,请你写出线段EG,AG,BG之间的数量关系,并证明你的结论.(1)证明作∠GAH=∠EAB交GE于点H.∴∠GAB=∠HAE.∵∠EAB=∠EGB,∠APE=∠BPG,∴∠ABG=∠AEH.在△ABG和△AEH中,∠GAB=∠HAE,AB=AE,∠ABG=∠AEH,∴△ABG≌△AEH(ASA).∴BG=EH,AG=AH.∵∠GAH=∠EAB=60°,∴△AG H是等边三角形.∴AG=HG.∴EG=AG+BG.(2)解 EG=AG-BG.证明:作∠GAH=∠EAB交GE于点H.∴∠GAB=∠HAE.∵∠EGB=∠EAB=90°,∴∠ABG+∠AEG=∠AEG+∠AEH=180°.∴∠ABG=∠AEH.∵AB=AE,∴△ABG≌△AEH(ASA).∴BG=EH,AG=AH.∵∠GAH=∠EAB=90°,∴△AGH是等腰直角三角形.∴AG=HG.∴EG=AG-BG.。
中考数学复习讲义课件 第五单元 四边形 第22讲 矩形、菱形、正方形

▪ 假设正方形边长为1,设CE=x,则BE= 1-x,
EF= 2x.
▪ 如图1,连接AC,交EF于O. ▪ ∵AE=AF,CE=CF, ▪ ∴AC是EF的垂直平分线. ▪ ∴AC⊥EF,OE=OF,∠EAO=∠FAO. ▪ ∵∠EAF=∠BAC=45°, ▪ ∴∠EAO=∠FAO=∠BAE=22.5°. ▪ 又AE=AE,∠ABE=∠AOE=90°,
▪ ∴OA=OB=AB=4.
▪ ∵四边形ABCD是平行四边形,
∴OB=OD=12BD,OA=OC=12AC.
▪ ∴BD=AC=8.
▪ ∴□ABCD是矩形.
▪ (2)求AD的长.
▪ 解:∵□ABCD是矩形,
▪ ∴∠BAD=90°.
∴AD= BD2-AB2= 82-42=4 3.
▪ 1.矩形的判定:首先判定该四边形为平 行四边形,然后找角或对角线的关系.若角 度容易求,则证其一内角为90°,便可判定 是矩形;若对角线容易求,则证其对角线相 等即可判定为矩形.
▪ (2)若CF=2,∠FAC=30°,∠B= 45°,求AB的长. ▪ 解:过点A作AG⊥BC于点G. ▪ 由(1)知四边形AECF是菱形. ▪ 又CF=2,∠FAC=30°, ▪ ∴AF∥EC,AE=CF=2,∠FAE= 2∠FAC=60°.∴∠AEB=∠FAE=60°. ▪ ∵AG⊥BC,∴∠AGB=∠AGE=90°.
▪ ∴△ABE≌△AOE(AAS).
∴AO=AB=1,∴AC= 2=1+OC.
在 Rt△CEF 中,OC=12EF= 22x.
∴1+ 22x= 2,解得 x=2- 2.
∴BEEC=1-(2-2-2 2)=(
2-1)(2+ 2
2)= 22.
▪ ③如图2,△ADF绕点A顺时针旋转90° 得到△ABH,则AF=AH,DF=BH,∠DAF =∠BAH.
2018年云南中考数学一轮复习课件-第5章第2节 矩形、菱形、正方形

第18页
2018中考数学复习课件
(2)解:连接 EF.由(1)知:四边形 AEDF 是菱形. ∵AE+ED+ DF+ AF= 12, ∴AE=ED= DF= AF= 3. ∵对角线 AD 与 EF 互相垂直平分, AD EF 2 2 ∴ 2 + 2 = 32, 2 2 ∴AD +EF = 36. ∵AD+EF= 7,∴AD2+EF2+ 2AD· EF=49, ∴2AD· EF+ 36= 49, 13 ∴AD·EF= . 2 1 1 13 13 ∴菱形 AEDF 的面积 S= AD· EF= × = .,⇨ 2 2 2 4
第9页
2018中考数学复习课件
6.(人教八下 P68 第 8 题改编)如图,在正方形 ABCD 中 ,E,F 分别是 AB,BC 上 的点, 且 AE=BF.求证:CE= DF.
证明:在正方形 ABCD 中, AB= BC=CD, ∠B=∠ BCD=90°.∵AE=BF, ∴AB-AE= BC- BF, 即 BE=CF. 易证△ BCE≌△CDF(SAS), ∴CE=DF.
第16页
2018中考数学复习课件
重难点 2:与菱形有关的证明及计算 4.(2017·云南)如图,△ABC 是以 BC 为底的等腰三角形,AD 是边 BC 上的高, 点 E,F 分别是 AB,AC 的中点. (1)求证:四边形 AEDF 是菱形; (2)如果四边形 AEDF 的周长为 12,两条对角线的和等于 7,求四边形 AEDF 的面积 S.
第11页
2018中考数学复习课件
2.★如图 ,在矩形 ABCD 中,AB= 2,E 是 BC 的 中点 ,AE⊥BD 于点 F, 则 CF 的长是( B ) A. 1 B. 2 C. 3 D.2
第12页
中考数学(浙江)总复习练习:考点跟踪突破22矩形

考点跟踪突破22 矩形、菱形与正方形 A 组 基础闯关一、选择题1.(2017·兰州)如图,矩形ABCD 的对角线AC 与BD 相交于点O ,∠ADB =30°,AB =4,则OC =( B )A .5B .4C .3.5D .3,第1题图) ,第2题图)2.(2016·海南)如图所示,矩形ABCD 的顶点A ,C 分别在直线a ,b 上,且a ∥b ,∠1=60°,则∠2的度数为( C )A .30°B .45°C .60°D .75°3.(2016·雅安)如图,四边形ABCD 的四边相等,且面积为120 cm 2,对角线AC =24 cm ,则四边形ABCD 的周长为( A )A .52 cmB .40 cmC .39 cmD .26 cm,第3题图) ,第4题图)4. (2016·宜宾)如图,点P 是矩形ABCD 的边AD 上的一动点,矩形的两条边AB ,BC 的长分别是6和8,则点P 到矩形的两条对角线AC 和BD 的距离之和是( A )A .4.8B .5C .6D .7.25.(2017·临沂)在△ABC 中,点D 是边BC 上的点(与B ,C 两点不重合),过点D 作DE ∥AC ,DF ∥AB ,分别交AB ,AC 于E ,F 两点,下列说法正确的是( D )A .若AD ⊥BC ,则四边形AEDF 是矩形B .若AD 垂直平分BC ,则四边形AEDF 是矩形C .若BD =CD ,则四边形AEDF 是菱形D .若AD 平分∠BAC ,则四边形AEDF 是菱形二、填空题6.(2017·孝感)如图,四边形ABCD 是菱形,AC =24,BD =10,DH ⊥AB 于点H ,则线段BH 的长度为__5013__.,第6题图) ,第7题图)7.(2017·枣庄)在矩形ABCD 中,∠B 的角平分线BE 与AD 交于点E ,∠BED 的角平分线EF 与DC 交于点F ,若AB =9,DF =2FC ,则BC =__62+3__.(结果保留根号)8.小明在学习了正方形之后,给同桌小文出了道题,从下列四个条件:①AB =BC ,②∠ABC =90°,③AC =BD ,④AC ⊥BD 中选两个作为补充条件,使▱ABCD 成为正方形,所有正确的选择为__①②或①③或②④或③④__.9.如图,矩形ABCD 中,AB =3,BC =4,点E 是BC 边上一点,连结AE ,把∠B 沿AE 折叠,使点B 落在点B′处,当△CEB′为直角三角形时,BE 的长为__3或32__. 三、解答题10.(2017·荆州)如图,在矩形ABCD 中,连结对角线AC ,BD ,将△ABC 沿BC 方向平移,使点B 移动到点C 处,得到△DCE.(1)求证:△ACD ≌△EDC ;(2)请探究△BDE 的形状,并说明理由.解:(1)证明:∵四边形ABCD 是矩形,∴AB =DC ,AC =BD ,AD =BC ,∠ADC =∠ABC =90°.由平移的性质得,DE =AC ,CE =BC ,∠DCE =∠ABC =90°,DC =AB ,∴AD =EC ,在△ACD 和△EDC 中,⎩⎨⎧AD =EC ,∠ADC =∠DCE ,CD =DC ,∴△ACD ≌△EDC (SAS ).(2)△BDE 是等腰三角形.理由如下:∵AC =BD ,DE =AC ,∴BD =DE ,∴△BDE 是等腰三角形.B 组 能力提升11.(2017·泰安)如图,四边形ABCD 是平行四边形,点E 是边CD 上一点,且BC =EC ,CF ⊥BE 交AB 于点F ,P 是EB 延长线上一点,下列结论:①BE 平分∠CBF ;②CF 平分∠DCB ;③BC =FB ;④PF =PC ,其中正确结论的个数为( D )A.1 B.2 C.3 D.4,第11题图),第12题图) 12.(2017·绍兴)如图为某城市部分街道示意图,四边形ABCD为正方形,点G在对角线BD上,GE⊥CD,GF⊥BC,AD=1 500 m,小敏行走的路线为B→A→G→E,小聪行走的路线为B→A→D→E→F.若小敏行走的路程为3 100 m,则小聪行走的路程为__4_600__m.13.如图,在△ABC中,∠ACB=90°,BC的垂直平分线DE交BC于点D,交AB 于点E,F在DE上,并且AF=CE.(1)求证:四边形ACEF是平行四边形;(2)当∠B的大小满足什么条件时,四边形ACEF是菱形?请回答并证明你的结论;(3)四边形ACEF有可能是正方形吗?为什么?解:(1)证明:∵DE垂直平分BC,∠ACB=90°,∴DE∥AC,∴DE为△ABC的中位线,∴E为AB的中点,∴CE=AE=AF.∵DF∥AC,∴∠ECA=∠EAC=∠AEF=∠EFA,从而△AFE≌△EAC,∴EF=AC,∴四边形ACEF为平行四边形.(2)当∠E=30°,四边形ACEF为菱形.理由:∵∠B=30°,∴∠EAC=60°.∵AE=EC,∴△AEC为正三角形,∴AC=EC=AE,∴平行四边形ACEF为菱形.(3)四边形ACEF不可能为正方形.理由:若四边形ACEF为正方形,则∠ACE=90°.又∠ACB=90°,则E,D两点重合,这与DE垂直平分BC矛盾.∴四边形ACEF不可能为正方形.C组拓展培优14.(2017·玉林)如图,在等腰直角三角形ABC中,∠ACB=90°,AC=BC=4,D是AB的中点,E,F分别是AC,BC上的点(点E不与端点A,C重合),且AE=CF,连结EF并取EF的中点O,连结DO并延长至点G,使GO=OD,连结DE,DF,GE,GF.(1)求证:四边形EDFG是正方形;(2)当点E在什么位置时,四边形EDFG的面积最小?并求四边形EDFG面积的最小值.解:(1)证明:连结CD ,∵△ABC 为等腰直角三角形,∠ACB =90°,D 是AB 的中点,∴∠A =∠DCF =45°,AD =CD.在△ADE 和△CDF 中,⎩⎨⎧AE =CF ,∠A =∠DCF ,AD =CD ,∴△ADE ≌△CDF (SAS ),∴DE =DF ,∠ADE =∠CDF.∵∠ADE +∠EDC =90°,∴∠EDC +∠CDF =∠EDF =90°,∴△EDF 为等腰直角三角形.∵O 为EF 的中点,GO =OD ,∴GD ⊥EF ,且GD =2OD =EF ,∴四边形EDFG 是正方形.(2)过点D 作DE′⊥AC 于点E′,∵△ABC 为等腰直角三角形,∠ACB =90°,AC =BC =4,∴DE ′=12BC =2,AB =42,点E′为AC 的中点,∴2≤DE <22,∴4≤S 四边形EDFG =DE 2<8.∴当点E 为线段AC 的中点时,四边形EDFG 的面积最小,该最小值为4.。
【中考数学复习】《22第22讲矩形、菱形、正方形》考点梳理(精练册)PPT课件

B.AC⊥BD
1
2
C.AB=AD
3
4
5
D)
D.AC=BD
6
7
8
9
10
11
12
13
14
第22讲 矩形、菱形、正方形
基础全练
挑战高分
中考创新练
5.(2022·内蒙古呼和浩特)如图,四边形ABCD是菱形,∠DAB=60°,点E是
DA中点,F是对角线AC上一点,且∠DEF=45°,则AF:FC的值是( D )
2
3
4
5
6
7
8
9
10
11
12
13
14
第22讲 矩形、菱形、正方形
基础全练
挑战高分
中考创新练
∠DCF=∠DCO,
(1)证明:在△DCF和△DCO中,
CD=CD,
∠CDF=∠CDO,
∴△DCF≌△DCO(ASA),∴DF=DO,CF=CO,
∵四边形ABCD是矩形,∴OC=OD= AC= BD,
基础全练
挑战高分
中考创新练
9.(2022·黑龙江齐齐哈尔)如图,在四边形ABCD中,AC⊥BD,垂足
为O,AB∥CD,要使四边形ABCD为菱形,应添加的条件是
AB=CD或AD∥BC或OA=OC或OB=OD等
____________________________________.(只需写出一个条件即可)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
第22讲 矩形、菱形、正方形
矩形、菱形、正方形知识点汇总+5大题型解析+例题
一、矩形、菱形、正方形的性质1.矩形的性质①具有平行四边形的一切性质;②矩形的四个角都是直角;③矩形的对角线相等;④矩形是轴对称图形,它有两条对称轴;⑤直角三角形斜边上的中线等于斜边的一半。
2.菱形的性质①具有平行四边形的一切性质;②菱形的四条边都相等;③菱形的两条对角线互相垂直,并且每一条对角线平分一组对角;④菱形是轴对称图形,每条对角线所在的直线都是它的对称轴;⑤菱形的面积=底×高=对角线乘积的一半。
3.正方形的性质正方形具有平行四边形,矩形,菱形的一切性质①边:四边相等,对边平行;②角:四个角都是直角;③对角线:互相平分;相等;且垂直;每一条对角线平分一组对角,即正方形的对角线与边的夹角为45度;④正方形是轴对称图形,有四条对称轴。
例1矩形ABCD中,DE⊥AC于E,且∠ADE:∠EDC=3:2,则∠BDE的度数为()A.36° B.9°C.27° D.18°例2 如图,矩形ABCD中,AE⊥BD于点E,对角线AC与BD 相交于点O,BE:ED=1:3,AB=6cm,求AC的长。
例3如图,O是矩形ABCD 对角线的交点,AE平分∠BAD,∠AOD=120°,求∠AEO 的度数。
例 4 菱形的周长为40cm,两邻角的比为1:2,则较短对角线的长________ 。
例5如图,在正方形ABCD中,G是BC上任意一点,连接AG,DE⊥AG于E,BF∥DE交AG于F,探究线段AF、BF、EF三者之间的数量关系,并说明理由.答案:1:D 2:12cm 3:30° 4:10cm 5:AF=BF+EF二、矩形、菱形、正方形的判定1.矩形的判定①有一个内角是直角的平行四边形是矩形;②对角线相等的平行四边形是矩形;③有三个角是直角的四边形是矩形;④还有对角线相等且互相平分的四边形是矩形。
2.菱形的判定方法①有一组邻边相等的平行四边形是菱形;②对角线互相垂直的平行四边形是菱形;③四条边都相等四边形是菱形;④对角线垂直平分的四边形是菱形。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
考点跟踪突破22 矩形、菱形与正方形
一、选择题
1.(2016·无锡)下列性质中,菱形具有而矩形不一定具有的是( C )
A.对角线相等 B.对角线互相平分
C.对角线互相垂直 D.邻边互相垂直
2.(2016·宁夏)菱形ABCD的对角线AC,BD相交于点O,E,F分别是
AD,CD边上的中点,连接EF,若EF=2,BD=2,则菱形ABCD的面积为
( A )
A.22 B.2 C.62 D.82
,第2题图) ,第3题图)
3.(2016·荆门)如图,在矩形ABCD中(AD>AB),点E是BC上一点,且
DE=DA,AF⊥DE,垂足为点F,在下列结论中,不一定正确的是( B )
A.△AFD≌△DCE B.AF=AD
C.AB=AF D.BE=AD-DF
4.(2016·宜宾)如图,点P是矩形ABCD的边AD上的一动点,矩形的两条
边AB,BC的长分别是6和8,则点P到矩形的两条对角线AC和BD的距离之
和是( A )
A.4.8 B.5 C.6 D.7.2
,第4题图) ,第5题图)
5.(导学号:01262033)(2016·呼和浩特)如图,面积为24的正方形ABCD
中,有一个小正方形EFGH,其中E,F,G分别在AB,BC,FD上.若BF=
6
2
,则小正方形的周长为( C )
A.568 B.566 C.562 D.1063
点拨:∵四边形ABCD是正方形,面积为24,∴BC=
CD=26,∠B=∠C=90°,∵四边形EFGH是正方形,∴∠EFG=90°,∵∠
EFB+∠DFC=90°,∠BEF+∠EFB=90°,∴∠BEF=∠DFC,∵∠EBF=∠C=90°,
∴△BEF∽△CFD,∴EFDF=BFDC,∵BF=62,
CF=362,DF=CD2+CF2=562,∴EF562=6226,∴EF=568,∴正方
形EFGH的周长为562.故选C.
二、填空题
6.(2016·扬州)如图,菱形ABCD的对角线AC,BD相交于点O,E为AD
的中点,若OE=3,则菱形ABCD的周长为__24__.
