电路戴维宁定理
戴维宁定理和诺顿定理
戴维宁定理和诺顿定理戴维宁定理是关于线性有源二端网络的串联型等效电路的定理。
(此处所谓有源二端网络是指含有独立源的二端网络)。
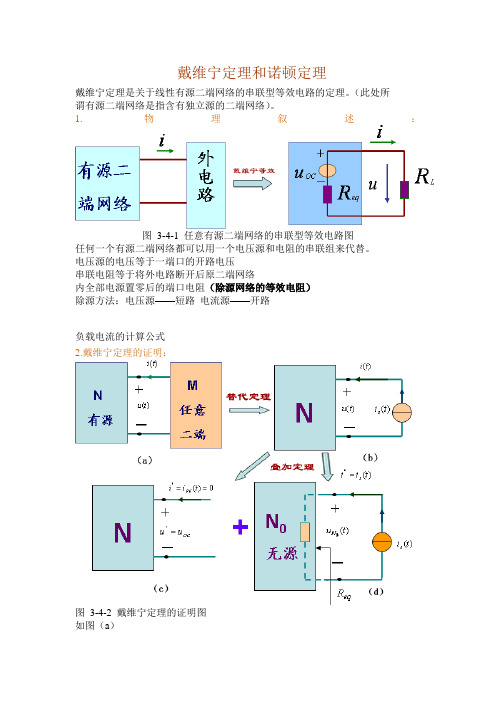
1. 物理叙述:图3-4-1 任意有源二端网络的串联型等效电路图任何一个有源二端网络都可以用一个电压源和电阻的串联组来代替。
电压源的电压等于一端口的开路电压串联电阻等于将外电路断开后原二端网络内全部电源置零后的端口电阻(除源网络的等效电阻)除源方法:电压源——短路电流源——开路负载电流的计算公式2.戴维宁定理的证明:图3-4-2 戴维宁定理的证明图如图(a)(1) 按替代定理用一个电流源代替任意二端网络M ,此电流源的电流(t)等于被代替的二端网络M 的端口电流,二者的参考方向也相同,如图(b)(2) 根据叠加定理,线性有源二端网络的端口电压和端口电流可以看成是两个分量叠加的结果:一个分量是当该网络内部所有独立源共同作用时在网络端口处产生的电压和电流,如图(c),另一个分量是当该网络外部的电流源单独作用时在同一端口处产生的电压和电流,如图(d)。
图(d)中无源网络的等效电阻为,网络可以用一个阻值为的等效电阻元件来代替,则有。
根据叠加定理可以确定原线性有源二端网络的端口电压为根据这个关系可以构造出原线性有源二端网络N的等效电路如图(e)(图中恢复了原任意二端网络M)由此说明有源二端网络可用电压源与电阻的串联组合等效代替:电压=有源二端网络的开路电压电阻=除源网络的等效电阻(除独立源)图3-4-3原线性有源二端网络N的等效电路图3.作用:在有些情况下只需计算一个复杂电路中某一支路(或某一部分)的电流。
我们可以把这个支路(部分)划出,而把其余部分看成是一个有源二端网络,这个有源二端网络对于此支路仅相当于一个供给电流的电源。
只要将这个网络用电压源于电阻的串联组合成电流源与电阻的并联组合等效代替就可以使问题简单化。
4.求解戴维宁定理的关键:1)、求开路电压:几乎用到解复杂电路的各种方法2)、等效电阻:当网络含受控源时方法:①外施电压法、电流②短路电流法例3-4-1诺顿定理是关于线性有源二端网络的并联型等效电路的定理。
戴维宁定理及诺顿定理

二、诺顿定理: 任何一个含独立电源、线性电阻和线性受控源的一 端口,对外电路来说,可以用一个电流源和电导的并联 来等效替代;其中电流源的电流等于该一端口的短路电 流,而电阻Ri等于把该一端口的全部独立电源置零后的 输入电导。 a Isc Gi b
a
A
b
可由戴维宁定理等效电路通过电源等效变换证明
例4-7 求如图所示诺顿等效电路。
20 40V +
解:
40 + 40V -
3A
20 Isc 60V +
Isc
Ri
i SC
60 40 40 3 A 20 40 20
i SC 1 A
1 Ri 8 1 1 1 20 40 20
注意:用戴维宁和诺顿定理求解时,必须画出等效电路图
30 5 R0 4.29 Ω 35
i U0 80 5.6 A R0 R 4.29 10
R0 + U0 -
i R
例4-5
14 + 14V -
如图所示电路,求戴维宁等效电路。 i
14 + 7V + 14 u 或 + 14V 14 + 7V -
i
+ u -
解: 列结点电压方程 1 1 14 7 ( )un1 i 14 14 14 14 un1 u
u 10.5 7i
R0 + U0 -
R0 7 U 0 10.5V
例4-6 已知如图,求UR 。(含受控源)
+ – 9V 3 – 6I1 + I1 + 3 UR – Ri + Uo –
+ 3 UR -
戴维南定理典型例子_戴维南定理解题方法

戴维南定理典型例子_戴维南定理解题方法什么是戴维南定理戴维南定理(又译为戴维宁定理)又称等效电压源定律,是由法国科学家L·C·戴维南于1883年提出的一个电学定理。
由于早在1853年,亥姆霍兹也提出过本定理,所以又称亥姆霍兹-戴维南定理。
其内容是:一个含有独立电压源、独立电流源及电阻的线性网络的两端,就其外部型态而言,在电性上可以用一个独立电压源V和一个松弛二端网络的串联电阻组合来等效。
在单频交流系统中,此定理不仅只适用于电阻,也适用于广义的阻抗。
戴维南定理在多电源多回路的复杂直流电路分析中有重要应用。
戴维南定理(Thevenin‘stheorem):含独立电源的线性电阻单口网络N,就端口特性而言,可以等效为一个电压源和电阻串联的单口网络。
电压源的电压等于单口网络在负载开路时的电压uoc;电阻R0是单口网络内全部独立电源为零值时所得单口网络N0的等效电阻。
戴维南定理典型例子戴维南定理指出,等效二端网络的电动势E等于二端网络开路时的电压,它的串联内阻抗等于网络内部各独立源和电容电压、电感电流都为零时,从这二端看向网络的阻抗Zi。
设二端网络N中含有独立电源和线性时不变二端元件(电阻器、电感器、电容器),这些元件之间可以有耦合,即可以有受控源及互感耦合;网络N的两端ɑ、b接有负载阻抗Z(s),但负载与网络N内部诸元件之间没有耦合,U(s)=I(s)/Z(s)。
当网络N中所有独立电源都不工作(例如将独立电压源用短路代替,独立电流源用开路代替),所有电容电压和电感电流的初始值都为零的时候,可把这二端网络记作N0。
这样,负载阻抗Z(s)中的电流I(s)一般就可以按下式1计算(图2)式中E(s)是图1二端网络N的开路电压,亦即Z(s)是无穷大时的电压U(s);Zi(s)是二端网络N0呈现的阻抗;s是由单边拉普拉斯变换引进的复变量。
和戴维南定理类似,有诺顿定理或亥姆霍兹-诺顿定理。
按照这一定理,任何含源线性时不变二端网络均可等效为二端电流源,它的电流J等于在网络二端短路线中流过的电流,并联内阻抗同样等于看向网络的阻抗。
戴维宁定理典型例题

戴维宁定理典型例题在电路分析中,戴维宁定理是一个非常重要的工具,它能够帮助我们简化复杂的电路,从而更方便地计算电路中的电流、电压等参数。
接下来,我们通过几个典型例题来深入理解戴维宁定理的应用。
例题一:考虑一个电路,其中包含一个电阻R₁=10Ω,一个电感L =2H,以及一个交流电源,电源的电压表达式为 u(t) = 100sin(100t) V。
我们需要求出从电阻 R₁两端看进去的戴维宁等效电路。
首先,我们将电感 L 短路,计算出此时电阻 R₁两端的电压 U₁。
根据欧姆定律,I = U/R₁,而 U = 100sin(100t),所以 I =100sin(100t) / 10 = 10sin(100t) A。
那么,电阻 R₁两端的电压 U₁= I × R₁= 10sin(100t) × 10 =100sin(100t) V。
接下来,计算等效内阻 R₀。
将电源短路,此时电路中只剩下电阻R₁和电感 L。
由于电感在直流情况下相当于短路,所以等效内阻 R₀就是电阻 R₁的阻值,即 R₀=10Ω。
因此,从电阻 R₁两端看进去的戴维宁等效电路是一个电压为100sin(100t) V 的交流电源和一个10Ω 的电阻串联。
例题二:有一个电路,包含两个电阻 R₁=5Ω 和 R₂=10Ω,一个直流电源V =20V。
我们想要计算从电阻R₂两端看进去的戴维宁等效电路。
先将电阻 R₂从电路中断开,此时通过电阻 R₁的电流 I₁= V /R₁= 20 / 5 = 4A。
电阻 R₁两端的电压 U₁= I₁ × R₁= 4 × 5 = 20V。
所以,电阻 R₂两端的开路电压 U₂= U₁= 20V。
然后计算等效内阻 R₀。
将电源短路,此时电阻 R₁和 R₂并联,等效电阻 R₀= R₁ × R₂/(R₁+ R₂) = 5 × 10 /(5 + 10) = 10 /3 Ω。
戴维宁定理求开路电压方法

戴维宁定理求开路电压方法要求解一个节点的开路电压,可以按照以下步骤进行:第一步,选择一个参考节点(接地节点),将其电势设为0V。
第二步,根据戴维宁定理,对于要求解的节点,我们需要找到所有与该节点相连的电阻、电流源、电压源的电流和电压。
第三步,利用欧姆定律和基尔霍夫定律,将电流和电压转化为未知量和已知量的关系。
第四步,建立方程并解方程,从而求解出所需节点的电压。
以下是一个具体的例子,通过该例子来演示戴维宁定理的求解开路电压的方法:假设有如下电路,要求解节点A的开路电压。
```R1R2---/\/\/\----/\/\----A3Ω5Ω```解题步骤如下:Step 1: 选择参考节点将节点A作为参考节点,将其电势设为0V。
Step 2: 找到与节点A相连的元件节点A与电阻R1和电阻R2相连。
Step 3: 利用欧姆定律和基尔霍夫定律,将电流和电压转化为未知量和已知量的关系根据欧姆定律可以得到:V1=I1*R1V2=I2*R2由于节点A是开路的,所以通过节点A的电流为0,即I1=I2=0。
Step 4: 建立方程并解方程由戴维宁定理可知,节点A的电压等于经过电阻R1和R2的电流和电压的乘积之和:0=V1+V2代入欧姆定律的关系,得到:0=I1*R1+I2*R2代入I1=I2=0,得到:0=0+0所以,节点A的开路电压为0V。
通过这个例子,可以看出戴维宁定理在求解开路电压中的作用。
根据戴维宁定理,我们可以通过分析电流和电压的关系,得到节点的电压。
通过实际计算和解方程,我们可以得到准确的结果。
尽管戴维宁定理在求解电路中的开路电压有一定的局限性,但在实际应用中它是非常有用的。
特别是在复杂的电路中,戴维宁定理可以简化计算,并提供快速求解电路节点电压的方法。
电路原理实验报告戴维宁定理或诺顿定理等效电路模拟运行

实验二戴维宁和诺顿等效电路
一.实验目的
(1)熟练运用电路仿真软件,熟练运用电压表电流表以及功率表的运用。
(2)熟练运用戴维宁定理,掌握含受控源电路的戴维宁定理的运行。
(3)利用电路仿真软件验证戴维宁定理的正确性,深刻认识等效电路的变换
二.实验原理
实验原理:一个线性含源一端口电阻网络,对外电路来说,可以用一个电压源和电阻的串联组合来代替。
此电压源的电压等于含源一端口的开路电压Uoc,串联电阻等一一端口内部的全部独立电源置零后的等效电阻Req
二.实验步骤
1.分别从电源库、元件库和指示部件库中调用所需电源、电阻和电压表、电流,如图将电压表接至a,b两端,确定电压表属性中Mode为DC。
打开仿真,记下电压表数据为21.904V
2.如图将电流表接至a,b两端,确定电流表属性中Mode为DC。
打开仿真,记下电流表数据为0.968A。
四.仿真结果
戴维南和诺顿等效电路如图
五.分析现象
不难看出ab两端的开路电压和短路电流的仿真电路结果与理论结果相同。
即戴维宁定理是正确的
六.实验收获
深刻了解戴维宁等效电路的转变方法。
熟练运用Multisim仿真电路分析戴维宁等效电路。
在仿真电路分析中,接地还是不能忘记,电压源和电流源测量的也是直流电。
电路实验指导书 戴维宁定理的研究

电路实验 戴维宁定理的研究一、实验目的1. 通过实验加深对等效概念的理解,验证戴维宁定理。
2. 学习有源线性二端网络的等效电路参数的测试方法。
3. 初步掌握实验电路的设计思路和方法。
二、实验原理1. 戴维宁定理戴维宁定理指出:任何一个有源线性二端网络N ,对外电路而言,都可以用一个理想电压源和一个电阻串联的支路等效,如图2-1所示。
(a )原电路 (b )戴维宁等效电路图2-1 有源线性二端网络的等效等效的理想电压源电压等于原有源二端网络的开路电压,如图2-2(a )所示;等效的串联电阻等于原有源二端网络N 中所有独立电源置零时的无源二端网络N 0的输入电阻,如图2-2(b )所示。
(a )求开路电压(b )求等效内阻图2-2 有源线性二端网络的等效参数的求取2. 有源线性二端网络的等效电阻的测量方法 (1)直接测量法测量时将有源二端网络N 中所有的独立电源置零,用数字式万用表的电阻挡直接测量a 、b 间的电阻值即可。
+-IU +-I OCU 0ROC U 0R 0R(2)开路短路法在如图2-1(a )所示的电路中,当时,测量有源二端网络的开路电压,当时,测量有源二端网络的短路电流,则等效内阻。
(3)加压求流法将有源二端网络N 中的所有独立电源置零,在a 、b 端施加一已知直流电压U ,测量流入二端网络的电流I ,如图2-3所示,则等效内阻。
(4)半电压法电路如图2-4所示,改变值,当负载电压时,负载电阻即为被测有源二端网络的等效电阻值。
图2-3 加压求流法 图2-4 半电压法(5)直线延长法当有源二端网络不允许短路时,先测开路电压,然后按图2-5(a )所示的电路连线,读出电压表读数和电流表读数。
在电压和电流的直角坐标系中标出(,0)(,)两点,如图2-5(b )所示,过这两点作直线,与纵轴的交点为(0,),则,所以,。
(a )电路图 (b )U -I 曲线图2-5 直线延长法L R =∞OC U 0L R =SC I 0OCSCU R I =0U R I=L R 0.5OC U U =ab-OC U 1U 1I OC U 1U 1I SC I 11OC SC OC U I I U U =-101OC U U R I -=(6)两次求压法测量时先测一次开路电压,然后在a 、b 端接入一个已知负载电阻,再测负载电阻两端的电压,则等效内阻。
4.3.1戴维宁定理和诺顿定理 - 戴维宁定理——【江苏大学 电路原理】
人物介绍
戴维宁 (1857-1926)是法国电报工程师。戴维 宁定理1883年发表在法国科学院刊物上,文仅一 页半,是在直流电源和电阻的条件下提出的,然 而由于其证明带有普遍性,它适用于一般电路, 如含独立电源、受控源以及正弦交流、复频域等 电路,戴维宁定理是电路中一个重要的定理。诺 顿定理是戴维宁定理发表的五十年后由美国贝尔 电话实验室工程师诺顿提出的。
2. 戴维宁定理
任何一个线性含有独立电源、线性电阻和受 控源的一端口网络,对外电路来说,可以用一个 电压源和电阻的串联组合来等效置换;此电压源 的电压等于一端口的开路电压Uoc,而电阻等于 一端口中全部独立电源置零后的输入电阻Req。
i
a
a 等效 Req
NS
b i
+ Uoc
-
b
ia
证明: NS
+ –u
1.几个名词
i a
(1) 端口
NS
指电路引出的一对端钮,其中从一
b i
个端钮(如a)流入的电流一定等于从另一端钮(如b)
流出的电流。
(2) 一端口网络 亦称二端网络
网络与外部电路只有一对端钮(或一个端口)连接。
(3) 含源与无源一端口网络
网络内部含有独立电源的称为含源一端口网络(NS)。 网络内部没有独立电源的称为无源一端口网络(N0)。
4 a 6
Rx 6
I 4
解:保留Rx支路,将其余一 端口网络化为戴维宁等
b 10V +–
效电路:
a
I
a
+ – U1
+ U2 –
10V +–
Rx I b
Req
+ Uoc
–
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
电路戴维宁定理
戴维南定理(Thevenin's theorem):含独立电源的线性电阻单口网络N,就端口特性而言,可以等效为一个电压源和电阻串联的单口网络。
电压源的电压等于单口网络在负载开路时的电压uoc;电阻R0是单口网络内全部独立电源为零值时所得单口网络N0的等效电阻。
简介
戴维南定理(又译为戴维宁定理)又称等效电压源定律,是由法国科学家莱昂·夏尔·戴维南于1883年提出的一个电学定理。
由于早在1853年,亥姆霍兹也提出过本定理,所以又称亥姆霍兹-戴维南定理。
其内容是:一个含有独立电压源、独立电流源及电阻的线性网络的两端,就其外部型态而言,在电性上可以用一个独立电压源V和一个松弛二端网络的串联电阻组合来等效。
在单频交流系统中,此定理不仅只适用于电阻,也适用于广义的阻抗。
戴维南定理在多电源多回路的复杂直流电路分析中有重要应用。
对于含独立源,线性电阻和线性受控源的单口网络(二端网络),都可以用一个电压源与电阻相串联的单口网络(二端网络)来等效,这个电压源的电压,就是此单口网络(二端网络)的开路电压,这个串联电阻就是从此单口网络(二端网络)两端看进去,当网络内部所有独立源均置零以后的等效电阻。
uoc 称为开路电压。
Ro称为戴维南等效电阻。
在电子电路中,当单口网络视为电源时,常称此电阻为输出电阻,常用Ro表示;当单口网络视为负载时,则称之为输入电阻,并常用Ri表示。
电压源uoc
和电阻Ro的串联单口网络,常称为戴维南等效电路。
当单口网络的端口电压和电流采用关联参考方向时,其端口电压电流关系方程可表为:u=R0i+uoc
戴维南定理和诺顿定理是最常用的电路简化方法。
由于戴维南定理和诺顿定理都是将有源二端网络等效为电源支路,所以统称为等效电源定理或等效发电机定理。
当研究复杂电路中的某一条支路时,利用电工学中的支路电流法、节点电压法等方法很不方便,此时用戴维南定理来求解某一支路中的电流和电压是很适合的。
