第一章 有理数 单元总结 (解析版)
(完整版)有理数第一章知识点总结,推荐文档

一、正数,负数的定义:大于 0 的数叫做正数;小于 0 的数叫做负数。
注意:1、0 既不是正数也不是负数。2、a 可以表示任意数,当 a 表示正数时,-a 是负数;
当 a 表示负数时,-a 是正数;当 a 表示 0 时,-a 仍是 0
练习:1、带+号的数是正数,带-号的数是负数,对吗?
5…也是奇数。
练习:观察下面 9 个数,并给它们进行分类.
5、5.6、-6、-3.7、0、3、-2、9/3、-1/2、 20 00 、π
整数:
分数:
正数:
负数:
3、数轴:数轴是规定了原点、正方向、单位长度的一条直线. 注意:所有的有理数都可以用数轴上的点表示出来,但数轴上的点不都表示有理数(如, 数轴上的点 π 不是有理数)
c0ba
四、相反数:有符号不同的两个数叫做互为相反数。一般地 a 的相反数是–a 特别:0 的
相反数还是 0
注意:1、互为相反数的两个数一定一正一负或者同时为 0;
2、相反数的和为 0 即
a,b 互为相反数,则 a+b=0
a
3、相反数的商为-1.即 a,b 互为相反数,则 ==
-1(a 0,b
b
练习 1、.在数轴上记出下列各数: -2, -2.5,+2,+1.5,
2、、如图,数轴上所标出的点中,相邻两点间的距离相等,则点 A 表示的数为( )
A、30
B、50
C、60
D、80
3、数轴上到 1 距离 5 个单位长度的点表示的数是( ) A +6 B -4 C+6 或-4
4、有理数 a,b,c 在数轴上的位置如图所示,求 a b c 的值 abc
0))
河南省七年级数学上册第一章有理数知识点总结(超全)

河南省七年级数学上册第一章有理数知识点总结(超全)单选题1、早在两千多年前,中国人就已经开始使用负数,并运用到生产和生活中,比西方早一千多年,下列各式计算结果为负数的是()A.3+(−2)B.3−(−2)C.3×(−2)D.(−3)÷(−2)答案:C分析:各式计算得到结果,即可作出判断.解:A、3+(−2)=1,故选项不符合;B、3−(−2)=5,故选项不符合;C、3×(−2)=-6,故选项符合;,故选项不符合;D、(−3)÷(−2)=32故选C.小提示:此题考查了有理数的混合运算,熟练掌握运算法则是解本题的关键.2、实数a,b在数轴上的对应点的位置如图所示,下列结论中正确的是()A.a<−2B.b<1C.a>b D.−a>b答案:D分析:根据数轴上的点的特征即可判断.解:点a在−2的右边,故a>−2,故A选项错误;点b在1的右边,故b>1,故B选项错误;b在a的右边,故b>a,故C选项错误;由数轴得:−2<a<−1.5,则1.5<−a<2,1<b<1.5,则−a>b,故D选项正确,故选:D.小提示:本题考查了数轴上的点,熟练掌握数轴上点的特征是解题的关键.3、实数a ,b ,c 在数轴上对应点的位置如图所示,如果a +b =0,那么下列结论正确的是( )A .|a |>|c |B .a +c >0C .abc >0D .a b =0答案:B分析:根据a +b =0,确定原点的位置,再根据a ,b ,c 与原点的距离判断选项;解:∵a +b =0,∴a ,b 互为相反数,∴a <0<b <c ;A ,因为|a |=|b |<c ,所以描述错误;B ,c 点离原点的距离大于a 点离原点的距离,结论正确;C ,a <0,abc <0,结论错误;D ,a 不为零,结论错误;故答案选:B小提示:本题考查了数轴上点的位置关系,数轴上右边的点大于左边的点,离原点越远数越大,解决本题的关键是确定原点的位置.4、实数a 的绝对值是54,a 的值是( )A .54B .−54C .±45D .±54答案:D分析:根据绝对值的意义直接进行解答解:∵|a |=54, ∴a =±54. 故选:D .小提示:本题考查了绝对值的意义,即在数轴上,表示一个数的点到原点的距离叫做这个数的绝对值.5、在《九章算术注》中用不同颜色的算筹(小棍形状的记数工具)分别表示正数和负数(白色为正,黑色为负),如图1表示的是+21−32=−11的计算过程,则图2表示的过程是在计算( )A.(−13)+(+23)=10B.(−31)+(+32)=1C.(+13)+(+23)=36D.(+13)+(−23)=−10答案:A分析:根据图1可知,一横表示10,一竖表示1,白色为正,黑色为负,由此即可得出答案.解:由图1可知,一横表示10,一竖表示1,白色为正,黑色为负,则图2表示的过程是在计算(−13)+(+23)=10,故选:A.小提示:本题考查了有理数的加减法,掌握理解每个算筹所表示的数是解题关键.6、小红解题时,将式子(﹣8)+(﹣3)+8+(﹣4)先变成[(﹣8)+8]+[(﹣3)+(﹣4)]再计算结果,则小红运用了()A.加法的交换律B.加法的交换律和结合律C.加法的结合律D.无法判断答案:B分析:根据有理数混合运算律求解即可.解:将式子(﹣8)+(﹣3)+8+(﹣4)先变成[(﹣8)+8]+[(﹣3)+(﹣4)]再计算结果,小红运用了加法的交换律和结合律,故选:B.小提示:本题主要考查有理数的混合运算,解题的关键是掌握有理数的混合运算顺序和运算法则及其运算律.7、为庆祝建党100周年,某党支部制作了精美的纪念章,其质量要求是“50±0.20克”,则下列纪念章质量符合标准的是()A .49.70克B .50.30克C .50.25克D .49.85克答案:D分析:将质量要求50±0.20克化为50−0.20克至50+0.20克,即可求解.解:∵质量要求是50±0.20克,∴质量要求是50−0.20克至50+0.20克,∵50−0.20=49.80,50+0.20=50.20,∴质量要求是49.80克至50.20克,∵49.80<49.85<50.20,∴49.85克符合标准,故选:D .小提示:本题考查正数和负数,解题的关键是将50±0.20克化为50−0.20克至50+0.20克.8、−2020的相反数为( )A .−12020B .2020C .−2020D .12020答案:B−2020的相反数为-(-2020)=2020.故选B .小提示:此题考查了相反数,解题关键是正确理解相反数的定义.9、−(−12)2的倒数是( ) A .-4B .−14C .14D .4 答案:A分析:根据有理数的乘方和倒数定义计算即可.解:−(−12)2=−14,−14的倒数为-4; 故选:A .小提示:本题考查了有理数的乘方和倒数的定义,解题关键是明确倒数的定义,熟练运用相关法则进行计算.10、|−23|的倒数为( )A .23B .32C .−23D .−32 答案:B分析:直接利用绝对值的性质再结合倒数的定义分析得出答案.解:|−23|=23所以23的倒数是:32.故选:B .小提示:此题主要考查了倒数与绝对值,正确把握倒数的定义是解题关键.11、数轴上点A 表示的数是−3,将点A 在数轴上平移7个单位长度得到点B .则点B 表示的数是( )A .4B .−4或10C .−10D .4或−10答案:D分析:根据题意,分两种情况,数轴上的点右移加,左移减,求出点B 表示的数是多少即可.解:点A 表示的数是−3,左移7个单位,得−3−7=−10,点A 表示的数是−3,右移7个单位,得−3+7=4,故选:D .小提示:此题主要考查了数轴的特征和应用,要熟练掌握,解答此题的关键是要明确:数轴上的点右移加,左移减.12、在简便运算时,把24×(−994748)变形成最合适的形式是( )A .24×(−100+148)B .24×(−100−148)C .24×(−99−4748)D .24×(−99+4748)答案:A分析:根据乘法分配律即可求解.24×(−994748)=24×(−100+148)计算起来最简便,故选A .小提示:此题主要考查有理数的运算,解题的关键是熟知乘法分配律的运用.13、数轴上表示整数的点称为整点,某数轴的单位长度为1cm ,若在数轴上随意画出一条长2021cm 长的线段AB ,则线段AB 盖住的的整点有( )个A.2018或2019B.2019或2020C.2022或2023D.2021或2022答案:D分析:分线段AB的端点与整点重合和不重合两种情况考虑,重合时盖住的整点是线段的长度+1,不重合时盖住的整点是线段的长度,由此即可得出结论.解:若线段AB的端点恰好与整点重合,则1厘米长的线段盖住2个整点,若线段AB的端点不与整点重合,则1厘米长的线段盖住1个整点,∵2021+1=2022,∴2021厘米的线段AB盖住2021或2022个整点.故选:D小提示:本题考查了数轴,解题的关键是根据题意得到找出长度为n(n为正整数)的线段盖住n或n+1个整点并注意利用分类讨论思想解答.14、下面是关于0的一些说法,其中正确说法的个数是()①0既不是正数也不是负数;②0的绝对值最小;③0是最小的整数;④0的绝对值、相反数、倒数都是它本身.A.0B.1C.2D.3答案:C分析:根据有理数的分类,绝对值,相反数,倒数的定义逐一判断即可.解:①0既不是正数也不是负数,说法正确,符合题意;②0的绝对值最小,说法正确,符合题意;③0不是最小的整数,说法错误,不符合题意;④0的绝对值、相反数都是它本身,0没有倒数,说法错误,不符合题意;∴说法正确的一共有2个,故选C.小提示:本题主要考查了有理数的分类,绝对值,相反数和倒数,熟知相关定义是解题的关键.15、对于有理数x,y,若xy <0,则|xy|xy+y|y|+|x|x的值是().A.−3B.−1C.1D.3 答案:B分析:由xy<0,可得x,y异号,再分两种情况讨论,当x>0,y<0时,当x<0,y>0时,再化简绝对值即可得到答案.解:∵xy<0,∴x,y异号,∴xy<0,∴|xy|=−xy,当x>0,y<0时,|xy|xy +y|y|+|x|x=−1−1+1=−1,当x<0,y>0时,|xy|xy +y|y|+|x|x=−1+1−1=−1,故选B小提示:本题考查的是绝对值的化简,有理数的乘法与除法的符号确定,除法运算,掌握“绝对值的化简”是解本题的关键.填空题16、如图,在数轴上有A、B两个动点,O为坐标原点.点A、B从图中所示位置同时向数轴的负方向运动,A点运动速度为每秒2个单位长度,B点运动速度为每秒3个单位长度,当运动___________秒时,点O恰好为线段AB中点.答案:45##0.8分析:设经过t秒,点O恰好是线段AB的中点,因为点B不能超过点O,所以0<t<2,经过t秒点A,B表示的数为,-2-2t,6-3t,根据题意可知-2-2t<0,6-3t>0,化简|-2-2t|=|6-3t|,即可得出答案.解:设经过t秒,点O恰好为线段AB中点,根据题意可得,经过t秒,点A表示的数为-2-2t,AO的长度为|-2-2t|,点B表示的数为6-3t,BO的长度为|6-3t|,因为点B不能超过点O,所以0<t<2,则|-2-2t|=|6-3t|,因为-2-2t<0,6-3t>0,所以,-(-2-2t)=6-3t,解得t=45.所以答案是:45.小提示:本题主要考查了数轴和绝对值的意义,解一元一次方程,根据题意列出等式应用绝对值的意义化简是解决本题的关键.17、−12×(14−13+1)+11=_________.答案:0分析:根据有理数的混合计算法则求解即可.解:−12×(14−13+1)+11=−12×14−(−12)×13+(−12)×1+11=−3+4−12+11=0,所以答案是:0.小提示:本题主要考查了有理数的混合计算,熟知相关计算法则是解题的关键.18、若a,b互为相反数,则(a+b﹣1)2016=_____.答案:1分析:根据相反数的性质得a+b=0,再代入进行计算即可.解:∵a,b互为倒数,∴a+b=0,∴(a+b﹣1)2016=(0−1)2016=(−1)2016=1,所以答案是:1.小提示:此题主要考查相反数的性质和有理数的乘方,关键是正确理解相反数的性质.19、大家知道,|5|=|5−0|,它在数轴上的意义是:表示5的点与原点(即表示0的点)之间的距离.又如式子|6−3|,它在数轴上的意义是:表示6的点与表示3的点之间的距离.类似地,式子|a−(−5)|在数轴上的意义是______.答案:表示a的点与表示-5的点之间的距离分析:利用绝对值的意义即可求解.解:因为|5|=|5−0|,它在数轴上的意义是:表示5的点与原点(即表示0的点)之间的距离,式子|6−3|,它在数轴上的意义是:表示6的点与表示3的点之间的距离,所以式子|a−(−5)|在数轴上的意义是表示a的点与表示-5的点之间的距离.小提示:本题考查了绝对值,掌握绝对值的意义是解题的关键.20、在一次数学活动课上,某数学老师将1~10共十个整数依次写在十张不透明的卡片上(每张卡片上只写一个数字,每一个数字只写在一张卡片上,而且把写有数字的那一面朝下).他先像洗扑克牌一样打乱这些卡片的顺序,然后把甲、乙、丙、丁、戊五位同学叫到讲台上,随机地发给每位同学两张卡片,并要求他们把自己手里拿的两张卡片上的数字之和写在黑板上,写出的结果依次是:甲:11;乙:4;丙:15;丁:8;戊:17,则丙同学手里拿的卡片的数字是_________.答案:5和10分析:根据两数之和结果确定,对两个加数的不同情况进行分类讨论,列举出所有可能的结果后,再逐一根据条件进行推理判断,最后确定出正确结果即可.解:由题意可知,一共十张卡片十个数,五个人每人两张卡片,∴每人手里的数字不重复.由甲:11,可知甲手中的数字可能是1和10,2和9,3和8,4和7,5和6;由乙:4,可知乙手中的数字只有1和3;由丙:15,可知丙手中的数字可能是5和10,7和8,6和9;由丁:8,可知丁手中的数字可能是1和7,2和6,3和5;由戊:17,可知戊手中的数字可能是7和10,8和9;∴丁只能是2和6,甲只能是4和7,丙只能是5和10,戊只能是8和9.所以答案是:5和10.小提示:本题考查的是有理数加法的应用,关键是把所有可能的结果列举出来,再进行推理.。
有理数单元小结1

6、比较两个有理数的大小
数轴上两个点表示的数,右边的总比左边的 大;
正数大于0,负数小于0,正数大于负数; 两个负数比较大小,绝对值大的反而小.
7、有理数的加法
同号两数相加,取相同的符号,并把绝对值 相加.
异号两数相加,绝对值相等时和为0;绝对 值不等时,取绝对值较大的加数的符号,并 用较大的绝对值减去较小的绝对值.
14、科学记数法
一般地,一个大于10的数总可以表示为 a 10n
的形式,其中 1 a 10
(n等于原数的整数位数减1)
15、提高运算速度和准确性的方法
灵活运用运算法则、运算律.要灵活运用运 算法则和运算律,首先必须加强对法则和运 算律本身的理解和掌握,要特别注意符号的 确定;
积累运算技巧,提高运算速度; 做到严谨细致,运算后要仔细检查,避免有
11、有理数的乘方
求n个相同因数a的积的运算叫做乘方. 正数的任何次幂都是正数; 负数的奇数次幂是负数,负数的偶数次幂是
正数. 0的任何非零次幂都是0.
12、运算律
加法交换律 加法结合律 乘法交换律 乘法结合律 乘法对加法的分配律
13、有理数的混合运算
先算乘方,再算乘除,最后算加减; 如果有括号,先做括号内的运算. 同级运算,从左到右进行;
4、相反数
如果两个数只有符号不同,那么我们称其中 一个数为另一个数的相反数.
0的相反数为0 . 在数轴上,表示互为相反数的两个点,位于
原点的两侧,并且与原点的距离相等.
5、绝对值
在数轴上,一个数所对应的点与原点的距离 叫做该数的绝对值.
正数的绝对值是它本身; 0 的绝对值是0; 负数的绝对值是它的相反数.
一、知识梳理:
1、有理数的概念
人教版 七年级(上)数学 第一章 有理数 有理数的加减 (含解析)

第 2 讲有理数的加减知识定位讲解用时:3分钟A、适用范围:人教版初一,基础一般;B、知识点概述:本讲义主要用于人教版初一新课,本节课我们要学习有理数的加法,有理数的减法;核心部分是有理数加减法的混合运算。
知识梳理讲解用时:20分钟有理数的加法1.定义:把两个有理数合成一个有理数的运算叫作有理数的加法.2.法则:(1)同号两数相加,取相同的符号,并把绝对值相加;(2)绝对值不相等的异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值.互为相反数的两个数相加得0;(3)一个数同0相加,仍得这个数.3.运算律:有理数加法运算律加法交换律文字语言两个数相加,交换加数的位置,和不变符号语言a+b=b+a加法结合律文字语言三个数相加,先把前两个数相加,或者先把后两个数相加,和不变符号语言(a+b)+c=a+(b+c)要点诠释:交换加数的位置时,不要忘记符号.课堂精讲精练【例题1】我国是最早认识负数,并进行相关运算的国家.在古代数学名著《九章算术》里,就记载了利用算筹实施“正负术”的方法,图1表示的是计算3+(﹣4)的过程.按照这种方法,图2表示的过程应是在计算()A.(﹣5)+(﹣2)B.(﹣5)+2 C.5+(﹣2)D.5+2【答案】C【解析】解:由图1知:白色表示正数,黑色表示负数,所以图2表示的过程应是在计算5+(﹣2),故选:C.讲解用时:3分钟解题思路:由图1可以看出白色表示正数,黑色表示负数,观察图2即可列式.教学建议:引导学生读懂题目信息是解题的关键.1.定义:已知两个数的和与其中一个加数,求另一个加数的运算,叫做减法,减法是加法的逆运算.要点诠释:(1)任意两个数都可以进行减法运算.(2)几个有理数相减,差仍为有理数,差由两部分组成:①性质符号;②数字即数的绝对值.2.法则:减去一个数,等于加这个数的相反数,即有:.要点诠释:将减法转化为加法时,注意同时进行的两变,一变是减法变加法;二变是把减数变为它的相反数”.()a b a b-=+-有理数的减法难度: 3 适应场景:当堂练习例题来源:无【练习1.1】在下列执行异号两数相加的步骤中,错误的是()①求两个有理数的绝对值;②比较两个有理数绝对值的大小;③将绝对值较大数的符号作为结果的符号;④将两个有理数绝对值的和作为结果的绝对值A.①B.②C.③D.④【答案】D【解析】解:执行异号两数相加的步骤:①求两个有理数的绝对值,正确;②比较两个有理数绝对值的大小,正确;③将绝对值较大数的符号作为结果的符号,正确;④将两个有理数绝对值的和作为结果的绝对值,错误.故选:D.讲解用时:2分钟解题思路:根据有理数加法法则:①同号相加,取相同符号,并把绝对值相加.②绝对值不等的异号加减,取绝对值较大的加数符号,并用较大的绝对值减去较小的绝对值,进而判断即可.教学建议:强调有理数加减法的运算法则难度: 3 适应场景:当堂例题例题来源:无【例题2】如图,乐乐将﹣3,﹣2,﹣1,0,1,2,3,4,5分别填入九个空格内,使每行、每列、每条对角线上的三个数之和相等,现在a、b、c分别标上其中的一个数,则a﹣b+c的值为()A.﹣1B.0C.1D.3【答案】C【解析】解:∵5+1﹣3=3,每行、每列、每条对角线上的三个数之和相等,∴a+5+0=33+1+b=3c﹣3+4=3,∴a=﹣2,b=﹣1,c=2,∴a﹣b+c=﹣2+1+2=1,故选:C.讲解用时:3分钟解题思路:根据三个数的和为依次列式计算即可求解.教学建议:根据表格,先求出三个数的和是解题的关键.难度: 3 适应场景:当堂例题例题来源:无【练习2.1】下列说法:①所有有理数都能用数轴上的点表示;②符号不同的两个数互为相反数;③有理数包括整数和分数;④两数相加,和一定大于任意一个加数.()A.3个B.2个C.1个D.0个【答案】B【解析】解:①所有有理数都能用数轴上的点表示,正确;②符号不同的两个数互为相反数,相加为零此时互为相反数,故此选项错误;③有理数包括整数和分数,正确;④两数相加,和一定大于任意一个加数,两负数相加则不同,故此选项错误,故选:B.讲解用时:2分钟解题思路:直接利用互为相反数以及有理数的定义和有理数加减运算法则分别判断得出答案.教学建议:此题主要考查了有理数的加法运算以及相反数的定义等知识,正确掌握运算法则是解题关键.难度: 3 适应场景:当堂练习例题来源:无【例题3】计算:(﹣3)+(+15.5)+(﹣6)+(﹣5)【答案】0【解析】解:原式=(﹣3﹣6)+(15.5﹣5)=﹣10+10=0.讲解用时:3分钟解题思路:原式结合后,相加即可求出值.教学建议:此题考查了有理数的加法,熟练掌握运算法则是解本题的关键.难度: 3 适应场景:当堂练习例题来源:无【练习3.1】已知a为正数,b为负数,且|a|=4,|b|=6,求a+b的值.【答案】﹣2【解析】解:因为a为正数,|a|=4,所以a=4,因为b为负数,|b|=6,所以b=﹣6,所以a+b=4+(﹣6)=﹣2.讲解用时:3分钟解题思路:先依据绝对值的性质求得a、b的值,最后依据加法法则进行计算即可.教学建议:巩固有理数的加法、绝对值的性质,熟练掌握相关法则是解题的关键.难度: 3 适应场景:当堂例题例题来源:无【例题4】下表列出了国外几个城市与北京的时差(带正号的数表示同一时刻比北京的时间早的时数).现在的北京时间是上午8:00.(1)求现在纽约时间是多少?(2)斌斌现在想给远在巴黎的姑妈打电话,你认为合适吗?时差/时纽约﹣13巴黎﹣7东京+1芝加哥﹣14【答案】(1)现在纽约时间是晚上7点;(2)不合适.【解析】解:(1)现在纽约时间是晚上7点;(2)现在巴黎时间是凌晨1点,不合适.讲解用时:3分钟解题思路:(1)根据时差求出纽约时间即可;(2)计算出巴黎的时间,即可做出判断.教学建议:熟练掌握运算法则是解本题的关键.难度: 3 适应场景:当堂例题例题来源:无【练习4.1】在一个3×3的方格中填写了9个数字,使得每行、每列、每条对角线上的三个数之和相等,得到的3×3的方格称为一个三阶幻方.(1)在图1中空格处填上合适的数字,使它构成一个三阶幻方;(2)如图2的方格中填写了一些数和字母,当x+y的值为多少时,它能构成一个三阶幻方.【答案】(1)(2)x+y=13【解析】解:(1)2+3+4=9,9﹣6﹣4=﹣1,9﹣6﹣2=1,9﹣2﹣7=0,9﹣4﹣0=5,如图所示:(2)﹣3+1﹣4=﹣6,﹣6+1﹣(﹣3)=﹣2,﹣2+1+4=3,如图所示:x=3﹣4﹣(﹣6)=5,y=3﹣1﹣(﹣6)=8,x+y=5+8=13.讲解用时:4分钟解题思路:(1)根据三个数的和为2+3+4=9,依次列式计算即可求解;(2)先求出下面中间的数,进一步得到右上面的数,从而得到x、y的值,相加可求x+y的值.教学建议:根据表格,先求出三个数的和是解题的关键,也是本题的突破口.难度: 3 适应场景:当堂练习例题来源:无【例题5】列式计算:(1)已知甲、乙两数之和为﹣2020,其中甲数是﹣7,求乙数;(2)已知x是5的相反数,y比x小﹣7,求x与﹣y的差.【答案】(1)﹣2013;(2)﹣3【解析】解:(1)根据题意知乙数为﹣2020﹣(﹣7)=﹣2020+7=﹣2013;(2)根据题意知x=﹣5,y=x﹣(﹣7)=﹣5+7=2,则x﹣(﹣y)=﹣5﹣(﹣2)=﹣3.讲解用时:3分钟解题思路:(1)根据题意知乙数为﹣2020﹣(﹣7),计算可得;(2)由题意得x=﹣5,y=x﹣(﹣7)=﹣5+7=2,再代入x﹣(﹣y)计算可得.教学建议:本题主要考查有理数的加法,解题的关键是根据题意列出算式并熟练掌握有理数的加减运算法则.难度: 3 适应场景:当堂例题例题来源:无【练习5.1】已知有理数a,b,c在数轴上的位置如图所示,且|a|=1,|b|=2,|c|=4.求3b+2a ﹣c的值.【答案】8.【解析】解:∵a、c在原点的左侧,b在原点的右侧,∴b>0,c<0,a<0,∵|a|=1,|b|=2,|c|=4,∴a=﹣1,b=2,c=﹣4,∴3b+2a﹣c=6﹣2+4=8.讲解用时:3分钟解题思路:根据a 、b 、c 在数轴上的位置可知b >0,c <0,a <0,再根据|a|=1,|b|=2,|c|=4可求出a 、b 、c 的值,代入3b+2a ﹣c 进行计算即可. 教学建议:这题考查的是数轴的特点及绝对值的性质,属较简单题目. 难度: 3 适应场景:当堂练习 例题来源:无【例题6】某单位一周中收支情况如下:524.5+元,274.3-元,490+元,100-元,29.7+元,123.6-元,232.1-元.问该单位这一周,总共收入多少元?总共支出多少元?收支相抵后,余额是多少元?【答案】共收入1044.2元,共支出730元,收支相抵后,余额为314.2元.【解析】()524.5++()490+()+29.7=1044.2+解:共收入为:元,()274.3+-()100-()+123.6-()+232.1730-=- 共支出为:元()2.3147302.1044=-+ 收支相抵为:元.讲解用时:3分钟解题思路:利用收入与支出的概念和有理数的混合运算即可解决教学建议:引导学生理解有理数的加法的实际应用.难度: 3 适应场景:当堂例题 例题来源:无【练习6.1】(1)()()()()()1789614------+--;(2)21513263⎛⎫⎛⎫⎛⎫⎛⎫--+---- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭; (3)()()1112 6.5 6.3625⎛⎫⎡⎤---+--- ⎪⎢⎥⎝⎭⎣⎦. 【答案】(1)8;(2)0;(3) 6.1-.【解析】()()()()()178961417896148------+--=-++-+=(1);215121151155503263332632666⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫--+----=-+-+=--+=-+= ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭(2); ()111112 6.5 6.3612 6.412 6.4 6.12522⎛⎫⎡⎤⎛⎫⎛⎫=---+-=---=-+=- ⎪ ⎪ ⎪⎢⎥⎝⎭⎣⎦⎝⎭⎝⎭原式(3).讲解用时:4分钟 解题思路:利用有理数减法的运算法则即可解决,括号前面是负号时,去括号要注意变号.教学建议:注意跟学生强调变号问题难度: 3 适应场景:当堂练习 例题来源:无【例题7】 如果2113x ⎛⎫+-= ⎪⎝⎭,那么x 等于______. 【答案】322=x 或223x =-. 【解析】2113x ⎛⎫+-= ⎪⎝⎭解:因为,2211233x ⎛⎫=--= ⎪⎝⎭所以, 322=x 223x =-所以或.讲解用时:3分钟解题思路:利用绝对值的代数意义和有理数的加减法运算法则即可求出结果 教学建议:熟练掌握绝对值的代数意义是解本题的关键.难度: 3 适应场景:当堂例题 例题来源:无【练习7.1】若a 、b 互为相反数,c 、d 互为倒数,m 的绝对值为2.(1)直接写出a+b ,cd ,m 的值;(2)求m+cd+的值.【答案】(1)a+b=0,cd=1,m=±2.(2)3或﹣1.【解析】解:(1)∵a 、b 互为相反数,c 、d 互为倒数,m 的绝对值为2, ∴a+b=0,cd=1,m=±2.(2)当m=2时,m+cd+=2+1+0=3; 当m=﹣2时,m+cd+=﹣2+1+0=﹣1. 讲解用时:4分钟解题思路:(1)根据互为相反数的和为0,互为倒数的积为1,绝对值的意义,即可解答;(2)分两种情况讨论,即可解答.教学建议:解决本题的关键是熟记倒数、相反数、绝对值的意义.难度: 3 适应场景:当堂练习 例题来源:无课后作业【作业1】如果规定运算()()23a b a b ⊗=---,求73124⎛⎫⊗- ⎪⎝⎭的值. 【答案】1253- 【解析】7373795=2331241246412⎡⎤⎛⎫⎛⎫⎛⎫⊗--⨯--⨯-=--=- ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦. 讲解用时:4分钟难度: 2 适应场景:练习题 例题来源:无【作业2】计算:123456789101112201720182019+--++--++--+++-.【答案】0.【解析】123456789101112201720182019+--++--++--+++-()()()()504123456789101112201720182019=+--++--++--+++-对括号 45042016=-⨯+20162016=-+0=.讲解用时:4分钟难度: 4 适应场景:练习题 例题来源:无【作业3】 计算:21150543236-+---. 【答案】31. 【解析】211521154543236322=-+--=-+--原式2111543223=-+-= 讲解用时:5分钟难度: 3 适应场景:练习题 例题来源:无。
(完整版)有理数知识点总结.doc

有理数知识点总结(2016 )第一章有理数1.1正数和数一、概念1 、正数:大于零的数,有根据需要在正数前面加“+”(正号)2 、数:在正数前面加上“—(” 号)的数明:一个数前面的“+”“—叫”做它的号,其中“+”有可以省略,但仍然表示正数,有“+”是了它是正数,但“—”号是不能省略的。
3 、0 既不是正数也不是数,它是正数的分界。
明:关于0 的——数,自然数,有理数,整数,非正数,非数,偶数,相反数是本身,没有倒数,是本身,正数分界二、用在解决一些,可以定具有相反意的量的正。
例如:收入正,支出,收支平衡0 零上正,零下,分界 0 向北()走正,向南(西)走,原地不0 加分正,扣分,不加不扣0 逆正,超正,低,准0 地上正,地下,地面基准0 盈余正,空,收支平衡0 水位上升正,水位下降,水平面0 高于平均分正,低于平均分增加正,减少,不增不减0 海平面以上正,以下,海平面0三、易易点1 、-a 一定是数么?答案:不一定,需要分分析解析:当a大于0,-a就是数;当 a 等于 0 , -a0 ;当 a 小于 0 ,-a 是正数因此,a不一定是正数也不一定是数,判断字母的正,需要分,也不能忽略0 的存在。
2 、海拔 0 米并不表示没有海拔,而是海拔中海平面的平均高度0 米。
3、非正数:0和数非数:0和正数1.2有理数一、概念1 、有理数:正整数,0,整数,正分数,分数都可以写成分数(含有限小数和无限循小数)的形式,的数称有理数。
2 、无理数:既不是正数也不是分数,就一定不是有理数。
如无限不循小数π=3.1415926⋯它不能化成分数形式。
二、分1 、按定分;有理数分整数(正整数、0、整数);分数(正分数、分数)2 、按性符号分;有理数分正有理数(正整数、正分数)、0、有理数(整数、分数)三、数1 、定:数是一条可以向两端无限延伸的直定三要素——原点,正方向,位度注意“ 定”二字,是三要素是根据需要定的。
《有理数》章节知识点归纳总结

《有理数》章节知识点归纳总结有理数是数学中的一种基本概念,它包括了整数、分数和零。
有理数可以用分数形式表示,分子是整数,分母是正整数。
一、有理数的定义和性质1.有理数的定义:有理数表示为两个整数的比值,其中分母不为零。
有理数可以用分数形式表示为a/b的形式,其中a是整数,b是正整数。
2.有理数的四则运算法则:加法:同号求和,异号作差,结果的符号跟两个有理数的符号相同。
减法:转化为加法运算,将减法问题转化为加法问题。
乘法:同号得正,异号得负。
除法:将除法转化为乘法,取倒数后将除法问题转换为乘法问题。
3.有理数的乘方运算:有理数的乘方运算是将一个有理数乘以自身若干次。
有理数的乘方运算的结果仍然是有理数。
4.有理数的比较运算:可以通过比较大小符号来比较有理数的大小,如果两个有理数的大小符号相同,则比较绝对值的大小。
5.有理数的约分:可以将一个有理数化简成最简形式,即将分子和分母互质的形式。
二、有理数的绝对值和相反数1.有理数的绝对值:绝对值表示有理数距离零的距离,绝对值是非负的。
正数的绝对值是它本身,负数的绝对值是它的相反数。
2.有理数的相反数:一个有理数的相反数是与它的绝对值相等但符号相反的数。
三、有理数的数轴1.有理数的数轴是一条直线,可以用来表示有理数的大小关系。
2.在数轴上,正数表示为向右的方向,负数表示为向左的方向,原点为零。
3.数轴上,绝对值越大的数离原点越远,绝对值相同的数离原点的距离相等。
四、有理数的运算律1.有理数的加法符合交换律、结合律和分配律。
交换律:a+b=b+a结合律:(a+b)+c=a+(b+c)分配律:a×(b+c)=a×b+a×c2.有理数的乘法符合交换律、结合律和分配律。
交换律:a×b=b×a结合律:(a×b)×c=a×(b×c)分配律:(a+b)×c=a×c+b×c五、有理数的应用1.有理数可以用来表示一些具体问题中的数值,比如表示温度、长度、质量等。
七年级第一章有理数知识点总结

七年级第一章有理数知识点总结有理数知识点总结正数是大于零的数。
负数是在正数前面加上负号“—”的数。
零既不是正数也不是负数,是整数的分界线,是整数的一部分。
需要注意的是,不是所有带“—”号的数都是负数,只有在正数前加“—”的数才是负数。
有理数是整数和分数的统称。
整数包括正整数和负整数,而分数包括正分数和负分数。
有限小数和无限循环小数都是有理数。
需要注意的是,正数和零统称为非负数,负数和零统称为非正数,正整数和零统称为非负整数,负整数和零统称为非正整数。
有理数可以按照正、负性质或者整数、分数分类。
正有理数包括正整数和正分数,负有理数包括负整数和负分数,零是一个特殊的有理数。
在数轴上,右边的数总比左边的数大。
数轴是一个直线,规定了原点、正方向和单位长度。
数轴上的点和有理数是一一对应的。
可以使用数轴求两点之间的距离,两点在原点的同侧作减法,在原点的两侧作加法。
相反数是只有符号不同的两个数。
在数轴上,离原点的距离相等的两个点所表示的数叫做相反数。
若a与b互为相反数,则a+b=0,即a=-b;反之,若a+b=0,则a与b互为相反数。
倒数是乘积为1的两个数互为倒数。
若a与b互为倒数,则a·b=1;反之,若a·b=1,则a与b互为倒数。
若a与b互为负倒数,则a·b=-1;反之,若a·b= -1则a与b互为负倒数。
绝对值是一个数的距离到原点的距离。
一个正数的绝对值是它本身,一个负数的绝对值是它的相反数。
如果两个数的绝对值相等,则这两个数可能相等,也可能互为相反数。
表示为底数的幂,底数为a,指数为n,用a^n表示。
2.乘方法则:⑴同底数幂相乘,底数不变,指数相加。
⑵幂的幂,底数不变,指数相乘。
⑶乘方分配律:一个数的积的幂,等于这个数的每个因数的幂的积。
3.开方法则:⑴一个数的平方根是正数,它的平方等于这个数。
⑵一个非负数的n次方根是非负数,它的n次方等于这个数。
4.指数法则:⑴同底数幂的指数相减,底数不变,指数相减。
第一章 有理数小结
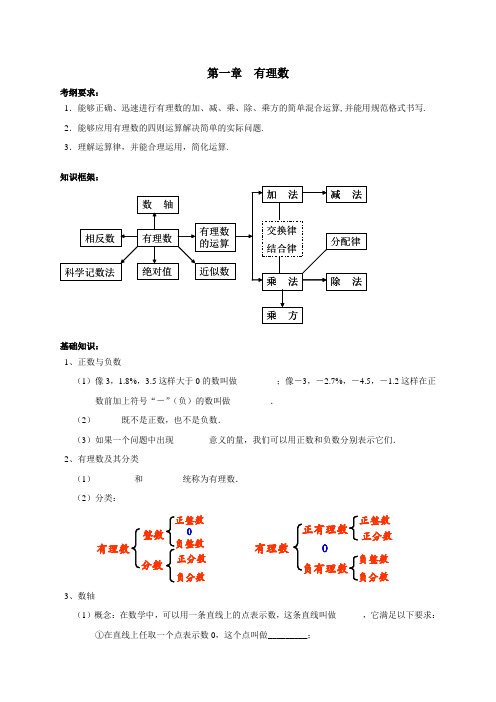
第一章 有理数考纲要求:1.能够正确、迅速进行有理数的加、减、乘、除、乘方的简单混合运算,并能用规范格式书写. 2.能够应用有理数的四则运算解决简单的实际问题. 3.理解运算律,并能合理运用,简化运算.知识框架:基础知识: 1、正数与负数(1)像3,1.8%,3.5这样大于0的数叫做_________;像―3,―2.7%,―4.5,―1.2这样在正数前加上符号“-”(负)的数叫做_________. (2)______既不是正数,也不是负数.(3)如果一个问题中出现________意义的量,我们可以用正数和负数分别表示它们. 2、有理数及其分类(1)_________和_________统称为有理数. (2)分类:正整数0有理数负整数正分数负分数分数整数正有理数负有理数正整数正分数有理数负整数负分数3、数轴(1)概念:在数学中,可以用一条直线上的点表示数,这条直线叫做______,它满足以下要求: ①在直线上任取一个点表示数0,这个点叫做_________;②通常规定直线上从原点向右(或上)为正方向,从原点向左(或下)为负方向; ③选取适当的长度为单位长度,直线上从原点向右,每隔一个单位长度取一个点,依次表示1,2,3,…;从原点向左,用类似方法依次表示-1,-2,-3,…(如图所示).(2)一般地,设a 是一个正数,则数轴上表示数a 的点在原点的_____边,与原点的距离是____个单位长度;表示数a -的点在原点的______边,与原点的距离是_____个单位长度.4、相反数(1)像2和-2,5和-5这样,只有_________不同的两个数叫做互为相反数.(2)一般地,a 和a -互为相反数.特别地,0的相反数是_____.这里,a 表示任意一个数,可以是正数、负数,也可以是0.(3)一般地,设a 是一个正数,数轴上与原点的距离是a 的点有两个,它们分别在原点左右,表示a -和a ,我们就说这两点关于________对称.(4)若a 、b 互为相反数,则=+b a ______. 5、绝对值(1)一般地,数轴上表示数a 的点与原点的距离叫做数a 的绝对值,记作||a .(2)一个正数的绝对值是它本身;一个负数的绝对值是它的相反数;0的绝对值是0.即:____(0)||____(0)____(0)a a a a >⎧⎪==⎨⎪<⎩6、倒数:(1)乘积为______的两个数,叫做互为倒数. (2)一般地,a (a ≠0)的倒数是a1;零没有倒数. (3)若a 、b 互为倒数,则=ab ______. 7、有理数的大小比较(1)数轴法:在数轴上表示表示有理数,它们从左到右的顺序,就是从小到大的顺序,即左边的数________右边的数.(2)定义法:负数<_______<正数.(3)绝对值法:两个负数,绝对值大的反而小.8、有理数的运算 (1)加法:①同号两数相加,取相同的符号,并把绝对值相加.②绝对值不相等异号两数相加,取绝对值较大的数的符号,并用较大的绝对值减去较小的绝对值.互为相反数的两个数相加得0.③一个数同0相加,仍得这个数.(2)减法:减去一个数,等于加这个数的相反数,即()a b a b -=+-. (3)乘法:①两数相乘,同号得正,异号得负,并把绝对值相乘.②零乘以任何数都得零.(4)除法:除以一个不等于0的数,等于乘以这个数的倒数,即a ÷b =a ·1b(b ≠0). (5)乘方:求n 个相同因数的积的运算,叫做乘方,乘方的结果叫做幂.在na 中,a 叫做____,n 叫做_______,当n a 看作a 的n 次方的结果时,也可读作“a 的n 次幂”. (6)运算顺序:先乘方,再乘除,最后加减;同级运算,从左到右进行;如有括号,先做括号内的运算,按小括号、中括号、大括号依次进行.9、有理数的运算律(1)加法交换律:a b b a +=+; (2)加法结合律:()()a b c a b c ++=++; (3)乘法交换律:ab ba =; (4)乘法结合律:()()ab c a bc =; (5)乘法分配律:()a b c ab ab +=+.10、科学记数法:把一个数表示成na 10⨯的形式,其中______<≤||a ______,n 为整数. 11、近似数:将一个数___________________所得到的数.例题剖析:例1(选自人教版七上P3)(1)一个月内,小明体重增加2 kg ,小明体重减少1 kg ,小强体重无变化,写出他们这个月的体重增长值;(2)某年,下列国家的商品进出口总额比上年的变化情况是: 美国减少6.4%, 德国增长1.3%, 法国减少2.4%, 英国减少3.5%, 中国增长7.5%, 意大利增长0.2%.写出这些国家这一年商品进出口总额的增长率.例2(选自人教版七上P13) 比较下列各对数的大小:(1))1(--和)1(+-; (2)218-和73-; (3))30(.--和31-.例3(选自人教版七上P18)计算:(1))9()3(-+-; (2)93)74(..+-.例4(选自人教版七上P19) 计算:)35(24)25(16-++-+.例5(选自人教版七上P20)10袋小麦称后记录如下:91,91,91.5,89,91.2,91.3,88.7,88.8,91.8,91.1.10袋小麦一共多少千克?如果每袋小麦以90kg 为标准,10袋小麦总计超过多少千克或不足多少千克?例6(选自人教版七上P22)计算:(1))5()3(---; (2)70-; (3))84(27..--; (4)415213-⎪⎭⎫ ⎝⎛-.计算:)7()5()3()20(+---++-.例8(选自人教版七上P30)计算:(1)9)3(⨯-; (2))1(8-⨯; (3))2(21-⨯⎪⎭⎫⎝⎛-.例9(选自人教版七上P31) 计算:(1)⎪⎭⎫ ⎝⎛-⨯⎪⎭⎫ ⎝⎛-⨯⨯-415965)3(; (2)41546)5(⨯⎪⎭⎫ ⎝⎛-⨯⨯-.例10(选自人教版七上P33) 用两种方法计算:12216141⨯⎪⎭⎫⎝⎛-+.例11(选自人教版七上P34)计算:(1))36(-÷9; (2)⎪⎭⎫ ⎝⎛-2512÷⎪⎭⎫⎝⎛-53.例12(选自人教版七上P35) 化简下列分数:(1)312-; (2)1245--.例13(选自人教版七上P35)计算:(1)⎪⎭⎫ ⎝⎛-75125÷)5(-; (2)72.-÷85×⎪⎭⎫ ⎝⎛-41.例14(选自人教版七上P36)计算:(1)48+-÷)2(-; (2)90)5()7(--⨯-÷)15(-.计算:(1)3)4(-; (2)4)2(-; (3)332⎪⎭⎫⎝⎛-.例16(选自人教版七上P43)计算:(1)15)3(4)3(23+-⨯--⨯; (2)3)2(-+)3(-×2)4[(-+]2-2)3(-÷)2(-.例17(选自人教版七上P43) 观察下面三行数:―2, 4, ―8, 16, ―32, 64,… ; ① 0, 6, ―6, 18, ―30, 66,… ; ② ―1, 2, ―4, 8, ―16, 32,… . ③ (1)第①行数按什么规律排列?(2)第②③行数与第①行数分别有什么关系? (3)取每行数的第10个数,计算这三个数的和.例18(选自人教版七上P45)用科学记数法表示下列各数:(1)1 000 000; (2)57 000 000; (3)-123 000 000 000.例19(选自人教版七上P46)按括号内的要求,用四舍五入法对下列各数取近似数:(1)01580.(精确到0010.); (2)35304.(精确到个位); (3)8041.(精确到10.); (4)8041.(精确到010.).每日一题:(改编自人教版七上第24页“探究”)在数轴上,点A ,B 分别表示数a ,b ,利用有理数减法,分别计算下列情况下点A ,B 之间的距离: (1)①当2a =,6b =时,AB =__________; ②当6a =-,2b =-时,AB =__________;③当a =_______,b =________时,AB =__________;(写一组符合要求的即可) (2)用含a 、b 的式子表示AB ;(3)式子|32|-或|23|-的几何意义可以是:数轴上表示3与2的两点之间的距离.试解释: ①1|05|6-的几何意义:_______________________________________________________ ②|25|+的几何意义:_________________________________________________________。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第一章 有理数 单元总结 【思维导图】
【知识要点】 知识点一 有理数基础概念 有理数(概念理解) 有理数的分类(两种)(见思维导图) 数轴 规定了原点、正方向、单位长度的直线叫做数轴。 ✓ 数轴的三要素:原点、正方向、单位长度(重点) 任何有理数都可以用数轴上的点表示,有理数与数轴上的点是一一对应的。 ✓ 数轴上的点表示的数从左到右依次增大;原点左边的数是负数,原点右边的数是正数. 相反数 只有符号不同的两个数叫做互为相反数.(绝对值相等,符号不同的两个数叫做互为相反数) 绝对值 正数的绝对值是它本身;负数的绝对值是它的相反数;0的绝对值是0。(互为相反数的两个数的绝对值相等。) 比较大小 (1)数轴上两个点表示的数,右边的总比左边的大。正数大于0,负数小于0,正数大于负数。 (2)方法总结: 两个正数比较大小,与小学一致; 正数与零比较,正数大于零; 正数与负数比较,正数大于负数; 负数与零比较,负数小于零; 两个负数比较,绝对值大的反而小。
【典例分析】 1.x=7,则x=___7或-7____. 【解析】绝对值概念的理解。 2.按从小到大的顺序用“<”号把下列各数连接起来:_-3<-1.6<0<1.6<3___. 1.6,﹣1.6,0,3,﹣3. 【解析】 方法一:在数轴上标出,右边的数字大于左边的。 方法二:利用绝对值比较大小(注意两个负数如何比较大小)。 3.若∣2x-4∣+(3y+9)2=0,则x+y=_____-1________ 【解析】本题考查非负数的应用及代数式的求值。根据已知条件可知,2x-4=0和3y+9=0,求得x,y的值。 4.当m=___-1___时,代数式3m-1与2(1-m)的值互为相反数。 【解析】本题考查相反数的概念和解一元一次方程,根据已知条件,列出方程求解即可。
知识点二 有理数的加减法 有理数的加法(重点) 有理数的加法法则:(先确定符号,再算绝对值) 同号两数相加,取相同的符号,并把绝对值相加; 异号两数相加,绝对值不相等时,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值; 互为相反数的两个数相加得0;(如果两个数的和为0,那么这两个数互为相反数) 一个数同0相加,仍得这个数。 有理数的加法运算律: 两个数相加,交换加数的位置,和不变。即abba; 三个数相加,先把前两个数相加,或者先把后两个数相加,和不变。即abcabc。 有理数的减法 有理数的减法法则: 减去一个数等于加上这个数的相反数。即abab。 注:两个变化:减号变成加号;减数变成它的相反数。 有理数的加减混合运算 规则:运用减法法则将加减混合运算统一为加法进行运算 步骤:(1)减法化加法; (2)省略括号和加号; (3)运用加法运算律使计算简便; (4)运用有理数加法法则进行计算。 注:运用加法运算律时,可按如下几点进行: (1)同号的先结合; (2)同分母的分数或者比较容易通分的分数相结合; (3)互为相反数的两数相结合; (4)能凑成整数的两数相结合; (5)带分数一般化为假分数或者分为整数和分数两部分,再分别相加。 【典例分析】 1.若 |a |3, |b| 1 ,且 a b ,那么 a b 的值是( D ) A.4 B.2 C.4 D.4或2 【解析】本题考查了学生对绝对值的性质及有理数减法的理解,关键在绝对值等于一个正数的值有两个。 【详解】有题意可得,a=±3,b=±1 而a>b 所以分两种情况: 1) a=3,b=1,所以a-b=2 2) a=3,b=-1,所以a-b=4 所以选D 2.将 6-(+3)+(-2) 改写成省略括号的和的形式是( A ) A.632 B.632 C.63+2 D.6+32 【解析】本题考察了有理数加减混合运算,将算式写成省略括号的形式必须统一成加法后,才能省略括号和加号。
知识点三 有理数的乘除法 有理数的乘法(重点) 有理数的乘法法则: (1)两数相乘,同号得正,异号得负,并把绝对值相乘。 (2)任何数同0相乘,都得0.
倒数:乘积是1的两个有理数互为倒数。0没有倒数。(数0aa的倒数是1a) 多个有理数相乘的法则及规律: (1)几个不是0的数相乘,负因数的个数是奇数时,积是负数; 负因数的个数是偶数时,积是正数。确定符号后,把各个因数的绝对值相乘。
(2)几个数相乘,有一个因数为0,积为0;反之,如果积为0,那么至少有一个因数是0. 注:带分数与分数相乘时,通常把带分数化成假分数,再与分数相乘。 有理数的乘法运算律 乘法交换律:两个数相乘,交换因数的位置,积相等。 即abba。 乘法结合律:三个数相乘,先把前两个数相乘,或者先把后两个数相乘,积相等。 即abcabc。 乘法分配律:一个数同两个数的和相乘,等于把这个数分别同这两个数相乘,再把积相加。 即abcabac。 有理数的除法 有理数除法法则:
(1)除以一个不为0的数,等于乘以这个数的倒数。即10ababb。 (2)两数相除(被除数不为0),同号得正,异号得负,并把绝对值相除。 0除以任何不为0的数,都得0。 步骤:先确定商的符号,再算出商的绝对值。 有理数的乘除混合运算 运算顺序:从左往右进行,将除法化成乘法后,进行约分计算。 (注:带分数应首先化为假分数进行运算) 有理数的四则混合运算 运算顺序:先乘除,后加减,有括号要先算括号里面的。 注:除法一般先化为乘法,带分数化为假分数,合理使用运算律 【典例分析】 1.(2019·黑龙江初一期末)计算
(1)215132824
(2)2241
233
【答案】1.(1)-19;(2)13.
【分析】 (1)原式利用除法法则变形,再利用乘法分配律计算即可求出值; (2)原式先计算乘方运算,再计算乘除运算即可求出值. 【详解】
(1)原式=215328
×24=-16+12-15=-19;
(2)原式=3114493. 知识点四 有理数的乘方 乘方(重点)
一般地,n个相同的因数a相乘,即𝑎×𝑎×𝑎⋯×𝑎⏟ 𝑛个,记作na,读作a的n次方。求n个相同因数的积的运算,叫做乘方,乘方的结果叫做幂。 在na中,a叫做底数,n叫做指数。na读作a的n次方,也可以读作a的n次幂。 乘方的规律: 负数的奇次幂是负数,负数的偶次幂是正数。 正数的任何次幂都是正数,0的任何正整数次幂都是0. 有理数的混合运算 运算顺序:(1)先乘方,再乘除,最后加减; (2)同级运算,从左到右进行; (3)如有括号,先算括号里的,按小括号、中括号、大括号的顺序。 科学记数法 把一个大于10的数记成10na的形式,其中a是整数数位只有一位的数(即110a),n是正整数,这样的记数方法叫科学记数法。(用科学记数法表示一个数时,10的指数比原数的整数位数少1.)
把10na还原成原数时,只需把a的小数点往前移动n位。 近似数和有效数字 在实际问题中,由“四舍五入”得到的数或大约估计的数都是近似数。(近似数小数点后的末位数是0的,不能去掉0.)
一个近似数从左边第一位非0的数字起,到末位数字止,所有的数字都是这个数的有效数字。一个近似数有几个有效数字,就称这个近似数保留几个有效数字。
精确度:表示一个近似数与准确数的接近程度。一个近似数,四舍五入到哪一位,就称这个数精确到哪一位。 【典例分析】 1.下列等式正确的是 ( C ) ∣0.000126=1.26×10-4 ∣3.10×104=31000 ∣1.1×10-5=0.000011 ∣12600000=1.26×106 A.∣∣ B.∣∣ C.∣∣∣ D.∣∣∣ 【解析】试题分析:根据科学记数法的意义,能够把较大或较小的数用科学记数法表示,或把科学记数法表示的数,还原即可,由0.000126=1.26×10-4,故∣正确;3.10×104=31000,故∣正确;1.1×10-5=0.000011,故∣正确;
12600000=1.26×107,故∣不正确.
故选:C 【点睛】此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.
2.2.30×610
精确到______位,有____个有效数字 【答案】万 3 【分析】 用科学记数法表示的a×10n的形式,它的有效数字只与前面的a有关,与10的多少次方无关; 精确度只需看a的末位数字实际在哪一位,则精确到了哪一位. 【详解】 近似数2.30×106精确到的位数为万位,有效数字的个数为三个,分别是2、3、0. 故答案为:万,3. 【点睛】 此题主要考查了确定近似数的精确度和有效数字.对于用科学记数法表示的数,有效数字的计算方法以及与精确到哪一位是需要识记的内容.
3.计算:
0114(1)()2
.
【答案】5 【分析】先去掉绝对值符号、对负整数指数幂、零指数幂分别进行计算,然后根据实数的运算法则求得计算结果.
【详解】解:原式4125. 【点睛】 本题主要考查了实数的综合运算能力,是各地中考题中常见的计算题型.解决此类题目的关键是熟练掌握负整数指数幂、零指数幂、绝对值考点的运算.
4.计算:(﹣1)1001+(π﹣2)0+(12)2. 【答案】14
【分析】直接利用零指数幂的性质以及指数幂的性质分别化简得出答案.
