(完整版)三角形的外角练习题及答案
三角形外角和--基础练习[下学期]--深港版
![三角形外角和--基础练习[下学期]--深港版](https://img.taocdn.com/s3/m/5dd1e85b52ea551811a68720.png)
7、如图,D为BC上一点,∠1=∠2, ∠3=∠4, ∠A=50°求∠EDF的度数。
A
E
1
F
4
B
2 3C
D
8、如图,∠BOC=138°,∠B=36° ∠C=30°,求∠A的度数。
A
O
B
C
9、如图,P是⊿ABC内任意一点 求证:∠BPC>∠A A
三角形外角和 练习
华师中山附中 聂少林
1、如图∠BDC是 的外角, 基
∠BDC=
+
础
∠EFC是
的外角,
训 练
∠EFC=
+
∠BFC是 和 的外角,A
∠BFC>
>
D
B
FE C
2、在⊿ABC中, ∠A等于和它相邻的 外角的四分之一,这个外角等于∠B 的2倍,那么∠A= 度,∠B = 度,∠C= 度。
3、如图,∠1=27.5°,∠2=95°, ∠3=38.5°,则∠4的大小是
D 1
B
C
10、如图,⊿ABC中,AD⊥BC
于D,AE平分∠BAC ,∠B=80°
∠C=46°求∠DAE的度数。 A
B
DE
C
下 课 喽!
6、如图, ⊿ABC的一个角 A
B
被纸挡住了,请你根据以
下问题中的条件填空:
⑴若∠A=35°∠B=55°则⊿ABC 是 角三角形。
⑵若∠A=48°∠B=43°则⊿ABC 是 角三角形。
⑶若∠A=37°∠B=52°则⊿ABC 是 角三角形。
A
⑷若∠A、∠B都大于45°
B
则⊿ABC是 角三角形。
⑸若∠A、∠B都小于45°,则⊿ABC 是 角三角形。
八年级数学上册三角形的外角精选练习题

八年级数学上册三角形的外角精选练习题一、选择题:1.CD‖AB,∠ 1 = 120 °, ∠ 2=80°,则∠ e是a.40°b.60°c.80°d.120°2.将三角形板的直角顶点放在正方形的一侧,∠ 1=30°,以及∠ 2=50°,则∠ 3是a.80b.]50c.30d.203.已知ab‖CD的程度,∠ EBA=45°,∠ e+∠ D是a.30°b.60°c.90°d.45°4.如果图中有四条不平行的直线L1、L2、L3和L4,则七个角将被切割。
关于这七个角的度关系,以下哪项是正确的a.∠2=∠4+∠7b.∠3=∠1+∠6c.∠1+∠4+∠6=180°d.∠2+∠3+∠5=360°5.一对三角形板有两个直角三角形。
如果它们叠在一起∠ α什么是a.165°b.120°c.150°d.135°6.直线ab‖CD,∠ a=70°,∠ C=40°,则∠ e等于a.30°b.40°c.60°d.70°7.以下四种形式:,∠ 1 = ∠ 2一定是真的a.b.c.d.8.企业规模关系∠ A.∠ 1.∠ 2是a.∠a>∠1>∠2b.∠2>∠1>∠ac.∠a>∠2>∠1d.∠2>∠a>∠1二、填空9.将一副常规的三角尺按如方式放置,则中∠aob的度数为________10.L‖m,等腰直角三角形ABC的直角顶点C在直线m上,如果∠ 那么β=20°∠ α是________11.若三角形的外角中有一个是锐角,则这个三角形是________三角形.12.在△ ABC,如果∠ C-∠ B=∠ a、外角中的最小角度△ 或“钝角”13.x=______.14.在△ 美国广播公司,∠ a=45°,∠ B=60°,然后是外角∠ ACD=度15.已知△abc是等边三角形,点b、c、d、e在同一直线上,且cg=cd,df=de,则∠e=_________ 度.16.放置一对直角三角形板,使30°角三角形板的一个直角侧与45°α=的三角形板的一个直角侧重合。
八上三角形外角经典题型

人教版八年级上册三角形的外角经典题训练一.选择题1.如图,在△ABC中,∠A=50°,∠C=70°,则外角∠ABD的度数是()A.110°B.120°C.130°D.140°2.如图,在△ABC中,∠A=45°,△ABC的外角∠CBD=75°,则∠C的度数是()A.30°B.45°C.60°D.75°3.如图,直线AB∥CD,∠A=70°,∠C=40°,则∠E等于()A.30°B.40°C.60°D.70°4.如图所示,∠1=∠2=145°,则∠3=()A.80°B.70°C.60°D.50°5.如图,CE是△ABC的外角∠ACD的平分线,若∠B=35°,∠ACE=60°,则∠A=()A.35°B.95°C.85°D.75°°,∠ACP=50°,则∠A+∠P=()A.70°B.80°C.90°D.100°二.填空题7.如图,根据三角形的有关知识可知图中的x的值是.8.一副三角板如图放置,若∠1=90°,则∠2的度数为.9.如图,∠BCD=150°,则∠A+∠B+∠D的度数为.10.已知:如图,在△ABC中,∠A=55°,H是高BD、CE的交点,则∠BHC=度.11.将一副直角三角板按如图放置,使两直角重合,则∠1的度数为.15°,∠ACP=50°,则∠P=°.三.解答题13.如图所示,在△ABC中,D是BC边上一点,∠1=∠2,∠3=∠4,∠BAC=63°,求∠DAC的度数.14.如图,CE是△ABC的外角∠ACD的平分线,且CE交BA的延长线于点E,∠B=25°,∠E=30°,求∠BAC的度数.15.如图,△ABC中,∠ABC=∠C=70°,BD平分∠ABC,求∠ADB的度数.16.已知:如图,△ABC的两个外角的平分线交于点P,如果∠A=40°,求∠BPC的度数.17.如图,在△ABC中,AD是高,∠DAC=10°,AE是∠BAC外角的平分线,BF平分∠ABC交AE于点F,若∠ABC=46°,求∠AFB的度数.18.如图①,在△ABC中,∠ABC与∠ACB的平分线相交于点P.(1)如果∠A=80°,求∠BPC的度数;(2)如图②,作△ABC外角∠MBC,∠NCB的角平分线交于点Q,试探索∠Q、∠A 之间的数量关系.(3)如图③,延长线段BP、QC交于点E,△BQE中,存在一个内角等于另一个内角的2倍,求∠A的度数.参考答案一.选择题1.解:由三角形的外角性质的,∠ABD=∠A+∠C=50°+70°=120°.故选:B.2.解:∵∠A=45°,△ABC的外角∠CBD=75°,∴∠C=∠CBD﹣∠A=75°﹣45°=30°,故选:A.3.解:如图,∵AB∥CD,∠A=70°,∴∠1=∠A=70°,∵∠1=∠C+∠E,∠C=40°,∴∠E=∠1﹣∠C=70°﹣40°=30°.故选:A.4.解:∵∠1、∠2、∠3是△ABC的三个外角,∴∠1+∠2+∠3=360°,∵∠1=∠2=145°,∴∠3=360°﹣145°×2=70°,故选:B.5.解:∵CE是△ABC的外角∠ACD的平分线,∠ACE=60°,∴∠ACD=2∠ACE=120°,∵∠ACD=∠B+∠A,∴∠A=∠ACD﹣∠B=120°﹣35°=85°,故选:C.6.解:∵BP是△ABC中∠ABC的平分线,CP是∠ACB的外角的平分线,∵∠ABP=20°,∠ACP=50°,∴∠ABC=2∠ABP=40°,∠ACM=2∠ACP=100°,∴∠A=∠ACM﹣∠ABC=60°,∠ACB=180°﹣∠ACM=80°,∴∠BCP=∠ACB+∠ACP=130°,∵∠PBC=20°,∴∠P=180°﹣∠PBC﹣∠BCP=30°,∴∠A+∠P=90°,故选:C.二.填空题7.解:根据三角形的外角性质得:x+80=x+20+x,解得:x=60,故答案为:60.8.解:由题意得:∠B=30°,∠A=45°,∵∠1=90°,∴∠A+∠3=90°,∴∠3=45°,∴∠4=45°,∵∠B=30°,∴∠2=45°+30°=75°,故答案为:75°.9.解:延长DC交AB于E,∠CEB是△ADE的一个外角,∴∠CEB=∠A+∠D,同理,∠BCD=∠CEB+∠B,∴∠A+∠B+∠D=∠CEB+∠B=∠BCD=150°,故答案为:150°.10.解:在△ABD中,∵BD⊥AC,∴∠ABD=90°﹣∠A=35°,∴∠BHC=90°+35°=125°.11.解:如图,由题意知,∠CAD=60°,∠B=90°﹣45°=45°,∴∠CAB=120°,∴∠1=∠B+∠CAB=45°+120°=165°.故答案为:165°.12.解:∵BP是△ABC中∠ABC的平分线,∠ABP=15°,∴∠CBP=∠ABP=15°,∵CP是∠ACB的外角的平分线,∠ACP=50°,∴∠PCM=∠ACP=50°,∴∠P=∠PCM﹣∠CBP=50°﹣15°=35°,故答案为:35.三.解答题13.解:设∠1=∠2=x,则∠3=∠4=2x.因为∠BAC=63°,所以∠2+∠4=117°,即x+2x=117°,所以x=39°;所以∠3=∠4=78°,∠DAC=180°﹣∠3﹣∠4=24°.14.解:∵∠B=25°,∠E=30°,∴∠ECD=∠B+∠E=55°.∵CE是∠ACD的平分线,∴∠ACE=∠ECD=55°.∴∠BAC=∠ACE+∠E=85°.15.解:∵∠ABC=∠C=70°,BD平分∠ABC,∴∠DBC=35°,∴∠ADB=∠C+∠DBC=70°+35°=105°.16.解:∵∠A=40°,∴∠ABC+∠ACB=180°﹣40°=140°,∴∠EBC+∠FCB=360°﹣140°=220°,∵BP、CP是△ABC的外角平分线,∴∠PBC=∠EBC,∠PCB=∠FCB,∴∠PBC+∠PCB=(∠EBC+∠FCB)=110°,∴∠BPC=180°﹣(∠PBC+∠PCB)=70°.17.解:∵AD是高,∴∠ADB=90°,∴∠BAD=90°﹣∠ABC=44°,又∠DAC=10°,∴∠BAC=54°,∴∠MAC=126°,∵AE是∠BAC外角的平分线,∴∠MAE=∠MAC=63°,∵BF平分∠ABC,∴∠ABF=∠ABC=23°,∴∠AFB=∠MAE﹣∠ABF=40°.18.(1)解:∵∠A=80°.∴∠ABC+∠ACB=100°,∵点P是∠ABC和∠ACB的平分线的交点,∴∠P=180°﹣(∠ABC+∠ACB)=180°﹣×100°=130°,(2)∵外角∠MBC,∠NCB的角平分线交于点Q,∴∠QBC+∠QCB=(∠MBC+∠NCB)=(360°﹣∠ABC﹣∠ACB)=(180°+∠A)=90°+∠A∴∠Q=180°﹣(90°+∠A)=90°﹣∠A;(3)延长BC至F,∵CQ为△ABC的外角∠NCB的角平分线,∴CE是△ABC的外角∠ACF的平分线,∴∠ACF=2∠ECF,∵BE平分∠ABC,∴∠ABC=2∠EBC,∵∠ECF=∠EBC+∠E,∴2∠ECF=2∠EBC+2∠E,即∠ACF=∠ABC+2∠E,又∵∠ACF=∠ABC+∠A,∴∠A=2∠E,即∠E=∠A;∵∠EBQ=∠EBC+∠CBQ=∠ABC+∠MBC=(∠ABC+∠A+∠ACB)=90°.如果△BQE中,存在一个内角等于另一个内角的2倍,那么分四种情况:①∠EBQ=2∠E=90°,则∠E=45°,∠A=2∠E=90°;②∠EBQ=2∠Q=90°,则∠Q=45°,∠E=45°,∠A=2∠E=90°;③∠Q=2∠E,则90°﹣∠A=∠A,解得∠A=60°;④∠E=2∠Q,则∠A=2(90°﹣∠A),解得∠A=120°.综上所述,∠A的度数是90°或60°或120°.。
2020--2021学年人教版八年级数学上册11.2 ;三角形的外角性质 练习题
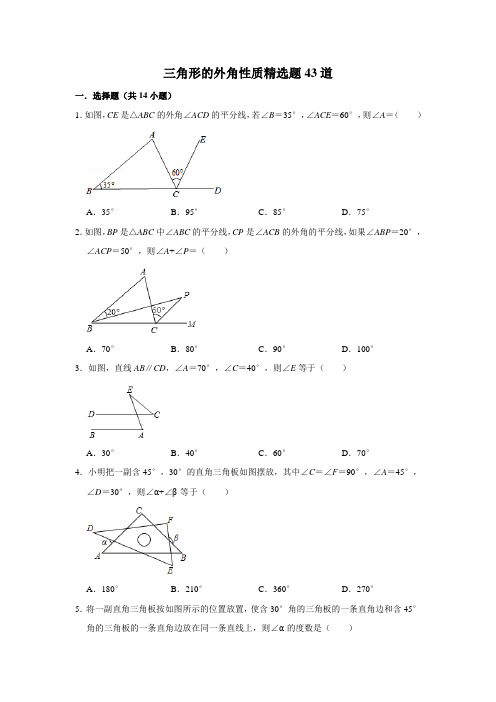
三角形的外角性质精选题43道一.选择题(共14小题)1.如图,CE是△ABC的外角∠ACD的平分线,若∠B=35°,∠ACE=60°,则∠A=()A.35°B.95°C.85°D.75°2.如图,BP是△ABC中∠ABC的平分线,CP是∠ACB的外角的平分线,如果∠ABP=20°,∠ACP=50°,则∠A+∠P=()A.70°B.80°C.90°D.100°3.如图,直线AB∥CD,∠A=70°,∠C=40°,则∠E等于()A.30°B.40°C.60°D.70°4.小明把一副含45°,30°的直角三角板如图摆放,其中∠C=∠F=90°,∠A=45°,∠D=30°,则∠α+∠β等于()A.180°B.210°C.360°D.270°5.将一副直角三角板按如图所示的位置放置,使含30°角的三角板的一条直角边和含45°角的三角板的一条直角边放在同一条直线上,则∠α的度数是()A.45°B.60°C.75°D.85°6.如图,在△ABC中,∠A=50°,∠C=70°,则外角∠ABD的度数是()A.110°B.120°C.130°D.140°7.将一副直角三角板如图放置,使含30°角的三角板的短直角边和含45°角的三角板的一条直角边对齐,则∠1的度数为()A.30°B.45°C.60°D.75°8.如图,在△ABC中,BE是∠ABC的平分线,CE是外角∠ACM的平分线,BE与CE相交于点E,若∠A=60°,则∠BEC是()A.15°B.30°C.45°D.60°9.如图,点D在△ABC边AB的延长线上,DE∥BC.若∠A=35°,∠C=24°,则∠D 的度数是()A.24°B.59°C.60°D.69°10.将一副三角板按如图所示的位置摆放在直尺上,则∠1的度数为()A.60°B.65°C.75°D.85°11.如图在△ABC中,BO,CO分别平分∠ABC,∠ACB,交于O,CE为外角∠ACD的平分线,BO的延长线交CE于点E,记∠BAC=∠1,∠BEC=∠2,则以下结论①∠1=2∠2,②∠BOC=3∠2,③∠BOC=90°+∠1,④∠BOC=90°+∠2正确的是()A.①②③B.①③④C.①④D.①②④12.如图,在△ABC中,∠ABC=∠ACB,BD是△ABC内角∠ABC的平分线,AD是△ABC 外角∠EAC的平分线,CD是△ABC外角∠ACF的平分线,以下结论不正确的是()A.AD∥BC B.∠ACB=2∠ADBC.∠ADC=90°﹣∠ABD D.BD平分∠ADC13.将一副三角尺按如图所示的方式摆放,则∠α的大小为()A.85°B.75°C.65°D.60°14.如图,直线AB∥CD,∠B=50°,∠D=20°,则∠E的度数是()A.20°B.30°C.50°D.70°二.填空题(共19小题)15.如图,BP是△ABC中∠ABC的平分线,CP是∠ACB的外角的平分线,如果∠ABP=20°,∠ACP=50°,则∠P=°.16.将一副直角三角板,按如图所示叠放在一起,则图中∠α的度数是.17.如图,∠BCD=150°,则∠A+∠B+∠D的度数为.18.如图,已知△ABC的两条高BD、CE交于点F,∠ABC的平分线与△ABC外角∠ACM 的平分线交于点G,若∠BFC=8∠G,则∠A=°.19.如图,在△ABC中,∠A、∠B的平分线相交于点I,若∠C=70°,则∠AIB=度,若∠AIB=155°,则∠C=度.20.如图,CE是△ABC的外角∠ACD的平分线,若∠B=35°,∠ACE=60°,则∠A =.21.小明将一副三角板中的两块直角三角尺的直角顶点C按如图所示的方式叠放在一起,当∠ACE<180°且点E在直线AC的上方时,他发现若∠ACE=,则三角板BCE有一条边与斜边AD平行.(写出所有可能情况)22.如图,△ADC是45°的直角三角板,△ABE是30°的直角三角板,若CD与BE交于点F,则∠DFB的度数为.23.一副三角板如图放置,若∠1=90°,则∠2的度数为.24.如图,∠ABC=∠ACB,AD、BD、CD分别平分△ABC的外角∠EAC、内角∠ABC、外角∠ACF,以下结论:①AD∥BC;②∠ACB=2∠ADB;③∠ADC=90°﹣∠ABC;④∠BDC=∠BAC.其中正确的结论有(填序号).25.三角形三个内角的比为2:3:4,则这个三角形最大的外角是度.26.已知:如图,在△ABC中,∠A=55°,H是高BD、CE的交点,则∠BHC=度.27.如图,已知△OAB中,∠AOB=70°,∠OAB的角平分线与△OBA的外角∠ABN的平分线所在的直线交于点D,则∠ADB的大小为.28.将一副直角三角板如图放置,使两直角重合,则∠1=度.29.如图,根据三角形的有关知识可知图中的x的值是.30.如图,CE平分∠ACD,交AB于点E,∠A=40°,∠B=30°,∠D=104°,则∠BEC 的度数为.31.将一副三角板如图所示放置(其中含30°角的三角板的一条较短直角边与另一块三角板的斜边放置在一直线上),那么图中∠1=度.32.如图,AB∥CD,∠B=68°,∠E=20°,则∠D的度数为度.33.如图,已知△ABC中,∠A=60°,点O为△ABC内一点,且∠BOC=140°,其中O1B平分∠ABO,O1C平分∠ACO,O2B平分∠ABO1,O2C平分∠ACO1,…,O n B平分∠ABO n﹣1,O n C平分∠ACO n﹣1,…,以此类推,则∠BO1C=°,∠BO2017C =°.三.解答题(共10小题)34.如图所示,在△ABC中,D是BC边上一点,∠1=∠2,∠3=∠4,∠BAC=63°,求∠DAC的度数.35.如图①,在△ABC中,∠ABC与∠ACB的平分线相交于点P.(1)如果∠A=80°,求∠BPC的度数;(2)如图②,作△ABC外角∠MBC,∠NCB的角平分线交于点Q,试探索∠Q、∠A之间的数量关系.(3)如图③,延长线段BP、QC交于点E,△BQE中,存在一个内角等于另一个内角的2倍,求∠A的度数.36.如图,在Rt△ABC中,∠ACB=90°,∠A=40°,△ABC的外角∠CBD的平分线BE 交AC的延长线于点E.(1)求∠CBE的度数;(2)过点D作DF∥BE,交AC的延长线于点F,求∠F的度数.37.认真阅读下面关于三角形内外角平分线所夹角的探究片段,完成所提出的问题.探究1:如图1,在△ABC中,O是∠ABC与∠ACB的平分线BO和CO的交点,通过分析发现∠BOC=90°+,理由如下:∵BO和CO分别是∠ABC和∠ACB的角平分线∴∴又∵∠ABC+∠ACB=180°﹣∠A∴∴∠BOC=180°﹣(∠1+∠2)=180°﹣(90°﹣∠A)=探究2:如图2中,O是∠ABC与外角∠ACD的平分线BO和CO的交点,试分析∠BOC 与∠A有怎样的关系?请说明理由.探究3:如图3中,O是外角∠DBC与外角∠ECB的平分线BO和CO的交点,则∠BOC 与∠A有怎样的关系?(只写结论,不需证明)结论:.38.如图,在Rt△ABC中,∠ACB=90°,∠A=40°,△ABC的外角∠CBD的平分线BE 交AC的延长线于点E,点F为AC延长线上的一点,连接DF.(1)求∠CBE的度数;(2)若∠F=25°,求证:BE∥DF.39.(1)探究:如图1,求证:∠BOC=∠A+∠B+∠C.(2)应用:如图2,∠ABC=100°,∠DEF=130°,求∠A+∠C+∠D+∠F的度数.40.如图,已知D为△ABC边BC延长线上一点,DF⊥AB于F交AC于E,∠A=35°,∠D=42°,求∠ACD的度数.41.如图,△ABC中,∠ABC=∠C=70°,BD平分∠ABC,求∠ADB的度数.42.如图①,在△ABC中,∠ABC与∠ACB的平分线相交于点P.(1)如果∠A=80°,求∠BPC的度数;(2)如图②,作△ABC外角∠MBC、∠NCB的平分线交于点Q,试探索∠Q、∠A之间的数量关系.(3)如图③,延长线段BP、QC交于点E,△BQE中,存在一个内角等于另一个内角的3倍,请直接写出∠A的度数.43.如图,在△ABC中,AD是高,∠DAC=10°,AE是∠BAC外角的平分线,BF平分∠ABC交AE于点F,若∠ABC=46°,求∠AFB的度数.三角形的外角性质精选题43道参考答案与试题解析一.选择题(共14小题)1.如图,CE是△ABC的外角∠ACD的平分线,若∠B=35°,∠ACE=60°,则∠A=()A.35°B.95°C.85°D.75°【分析】根据三角形角平分线的性质求出∠ACD,根据三角形外角性质求出∠A即可.【解答】解:∵CE是△ABC的外角∠ACD的平分线,∠ACE=60°,∴∠ACD=2∠ACE=120°,∵∠ACD=∠B+∠A,∴∠A=∠ACD﹣∠B=120°﹣35°=85°,故选:C.【点评】本题考查了三角形外角性质,角平分线定义的应用,注意:三角形的一个外角等于和它不相邻的两个内角的和.2.如图,BP是△ABC中∠ABC的平分线,CP是∠ACB的外角的平分线,如果∠ABP=20°,∠ACP=50°,则∠A+∠P=()A.70°B.80°C.90°D.100°【分析】根据角平分线的定义以及一个三角形的外角等于与它不相邻的两个内角和,可求出∠A的度数,根据补角的定义求出∠ACB的度数,根据三角形的内角和即可求出∠P 的度数,即可求出结果.【解答】解:∵BP是△ABC中∠ABC的平分线,CP是∠ACB的外角的平分线,∵∠ABP=20°,∠ACP=50°,∴∠ABC=2∠ABP=40°,∠ACM=2∠ACP=100°,∴∠A=∠ACM﹣∠ABC=60°,∠ACB=180°﹣∠ACM=80°,∴∠BCP=∠ACB+∠ACP=130°,∵∠PBC=20°,∴∠P=180°﹣∠PBC﹣∠BCP=30°,∴∠A+∠P=90°,故选:C.【点评】本题考查了角平分线的定义,一个三角形的外角等于与它不相邻的两个内角和以及补角的定义以及三角形的内角和为180°,难度适中.3.如图,直线AB∥CD,∠A=70°,∠C=40°,则∠E等于()A.30°B.40°C.60°D.70°【分析】先根据两直线平行,同位角相等求出∠1,再利用三角形的外角等于和它不相邻的两个内角的和即可求出∠E的度数.【解答】解:如图,∵AB∥CD,∠A=70°,∴∠1=∠A=70°,∵∠1=∠C+∠E,∠C=40°,∴∠E=∠1﹣∠C=70°﹣40°=30°.故选:A.【点评】本题考查的是平行线的性质及三角形外角的性质,熟知两直线平行,同位角相等是解答此题的关键.4.小明把一副含45°,30°的直角三角板如图摆放,其中∠C=∠F=90°,∠A=45°,∠D=30°,则∠α+∠β等于()A.180°B.210°C.360°D.270°【分析】根据三角形的外角的性质分别表示出∠α和∠β,计算即可.【解答】解:∠α=∠1+∠D,∠β=∠4+∠F,∴∠α+∠β=∠1+∠D+∠4+∠F=∠2+∠D+∠3+∠F=∠2+∠3+30°+90°=210°,故选:B.【点评】本题考查的是三角形外角的性质,掌握三角形的一个外角等于和它不相邻的两个内角的和是解题的关键.5.将一副直角三角板按如图所示的位置放置,使含30°角的三角板的一条直角边和含45°角的三角板的一条直角边放在同一条直线上,则∠α的度数是()A.45°B.60°C.75°D.85°【分析】先根据三角形的内角和得出∠CGF=∠DGB=45°,再利用∠α=∠D+∠DGB 可得答案.【解答】解:如图,∵∠ACD=90°、∠F=45°,∴∠CGF=∠DGB=45°,则∠α=∠D+∠DGB=30°+45°=75°,故选:C.【点评】本题主要考查三角形的外角的性质,解题的关键是掌握三角形的内角和定理和三角形外角的性质.6.如图,在△ABC中,∠A=50°,∠C=70°,则外角∠ABD的度数是()A.110°B.120°C.130°D.140°【分析】根据三角形的一个外角等于与它不相邻的两个内角的和列式计算即可得解.【解答】解:由三角形的外角性质的,∠ABD=∠A+∠C=50°+70°=120°.故选:B.【点评】本题考查了三角形的一个外角等于与它不相邻的两个内角的和的性质,熟记性质是解题的关键.7.将一副直角三角板如图放置,使含30°角的三角板的短直角边和含45°角的三角板的一条直角边对齐,则∠1的度数为()A.30°B.45°C.60°D.75°【分析】根据三角形的内角和求出∠2=45°,再根据对顶角相等求出∠3=∠2,然后根据三角形的一个外角等于与它不相邻的两个内角的和计算即可.【解答】解:∵∠2=90°﹣45°=45°(直角三角形两锐角互余),∴∠3=∠2=45°,∴∠1=∠3+30°=45°+30°=75°.故选:D.【点评】本题考查的是三角形外角的性质,熟知三角形的一个外角等于与它不相邻的两个内角的和是解答此题的关键.8.如图,在△ABC中,BE是∠ABC的平分线,CE是外角∠ACM的平分线,BE与CE相交于点E,若∠A=60°,则∠BEC是()A.15°B.30°C.45°D.60°【分析】根据角平分线的定义得到∠EBM=∠ABC、∠ECM=∠ACM,根据三角形的外角性质计算即可.【解答】解:∵BE是∠ABC的平分线,∴∠EBM=∠ABC,∵CE是外角∠ACM的平分线,∴∠ECM=∠ACM,则∠BEC=∠ECM﹣∠EBM=×(∠ACM﹣∠ABC)=∠A=30°,故选:B.【点评】本题考查的是三角形的外角性质、角平分线的定义,掌握三角形的一个外角等于和它不相邻的两个内角的和是解题的关键.9.如图,点D在△ABC边AB的延长线上,DE∥BC.若∠A=35°,∠C=24°,则∠D 的度数是()A.24°B.59°C.60°D.69°【分析】根据三角形外角性质求出∠DBC,根据平行线的性质得出即可.【解答】解:∵∠A=35°,∠C=24°,∴∠DBC=∠A+∠C=59°,∵DE∥BC,∴∠D=∠DBC=59°,故选:B.【点评】本题考查了三角形外角性质和平行线的性质,能熟练地运用性质进行推理是解此题的关键.10.将一副三角板按如图所示的位置摆放在直尺上,则∠1的度数为()A.60°B.65°C.75°D.85°【分析】利用三角形外角性质(三角形的一个外角等于不相邻的两个内角和)解题或利用三角形内角和解题皆可.【解答】解:如图:∵∠BCA=60°,∠DCE=45°,∴∠2=180°﹣60°﹣45°=75°,∵HF∥BC,∴∠1=∠2=75°,故选:C.【点评】主要考查了一副三角板所对应的角度是60°,45°,30°,90°和三角形外角的性质.本题容易,解法很灵活.11.如图在△ABC中,BO,CO分别平分∠ABC,∠ACB,交于O,CE为外角∠ACD的平分线,BO的延长线交CE于点E,记∠BAC=∠1,∠BEC=∠2,则以下结论①∠1=2∠2,②∠BOC=3∠2,③∠BOC=90°+∠1,④∠BOC=90°+∠2正确的是()A.①②③B.①③④C.①④D.①②④【分析】依据角平分线的性质以及三角形外角性质,即可得到∠1=2∠2,∠BOC=90°+∠1,∠BOC=90°+∠2.【解答】解:∵CE为外角∠ACD的平分线,BE平分∠ABC,∴∠DCE=∠ACD,∠DBE=∠ABC,又∵∠DCE是△BCE的外角,∴∠2=∠DCE﹣∠DBE,=(∠ACD﹣∠ABC)=∠1,故①正确;∵BO,CO分别平分∠ABC,∠ACB,∴∠OBC=ABC,∠OCB=∠ACB,∴∠BOC=180°﹣(∠OBC+∠OCB)=180°﹣(∠ABC+∠ACB)=180°﹣(180°﹣∠1)=90°+∠1,故②、③错误;∵OC平分∠ACB,CE平分∠ACD,∴∠ACO=∠ACB,∠ACE=ACD,∴∠OCE=(∠ACB+∠ACD)=×180°=90°,∵∠BOC是△COE的外角,∴∠BOC=∠OCE+∠2=90°+∠2,故④正确;故选:C.【点评】本题考查了三角形的内角和定理,三角形的一个外角等于与它不相邻的两个内角的和的性质,以及角平分线的定义.12.如图,在△ABC中,∠ABC=∠ACB,BD是△ABC内角∠ABC的平分线,AD是△ABC 外角∠EAC的平分线,CD是△ABC外角∠ACF的平分线,以下结论不正确的是()A.AD∥BC B.∠ACB=2∠ADBC.∠ADC=90°﹣∠ABD D.BD平分∠ADC【分析】A、由AD平分△ABC的外角∠EAC,求出∠EAD=∠DAC,由三角形外角得∠EAC=∠ACB+∠ABC,且∠ABC=∠ACB,得出∠EAD=∠ABC,利用同位角相等两直线平行得出结论正确.B、由AD∥BC,得出∠ADB=∠DBC,再由BD平分∠ABC,所以∠ABD=∠DBC,∠ABC=2∠ADB,得出结论∠ACB=2∠ADB,C、在△ADC中,∠ADC+∠CAD+∠ACD=180°,利用角的关系得∠ADC+∠CAD+∠ACD=∠ADC+2∠ABD+∠ADC=2∠ADC+2∠ABD=180°,得出结论∠ADC=90°﹣∠ABD;D、用排除法可得结论.【解答】解:A、∵AD平分△ABC的外角∠EAC,∴∠EAD=∠DAC,∵∠EAC=∠ACB+∠ABC,且∠ABC=∠ACB,∴∠EAD=∠ABC,∴AD∥BC,故A正确.B、由(1)可知AD∥BC,∴∠ADB=∠DBC,∵BD平分∠ABC,∴∠ABD=∠DBC,∴∠ABC=2∠ADB,∵∠ABC=∠ACB,∴∠ACB=2∠ADB,故B正确.C、在△ADC中,∠ADC+∠CAD+∠ACD=180°,∵CD平分△ABC的外角∠ACF,∴∠ACD=∠DCF,∵AD∥BC,∴∠ADC=∠DCF,∠ADB=∠DBC,∠CAD=∠ACB∴∠ACD=∠ADC,∠CAD=∠ACB=∠ABC=2∠ABD,∴∠ADC+∠CAD+∠ACD=∠ADC+2∠ABD+∠ADC=2∠ADC+2∠ABD=180°,∴∠ADC+∠ABD=90°∴∠ADC=90°﹣∠ABD,故C正确;不妨设,D选项正确,可以推出AB=AD=AC,推出∠ACB=∠ACD=∠DCF=60°,显然不可能,故D错误.故选:D.【点评】本题主要考查了三角形的内角和,平行线的判定和性质,三角形外角的性质等知识,解题的关键是正确找各角的关系.13.将一副三角尺按如图所示的方式摆放,则∠α的大小为()A.85°B.75°C.65°D.60°【分析】利用三角形外角的性质解答即可.【解答】解:如图所示,∠α=∠E+∠ACB=30°+45°=75°,故选:B.【点评】本题考查的是三角形外角的性质,熟知性质定理是解答此题的关键.14.如图,直线AB∥CD,∠B=50°,∠D=20°,则∠E的度数是()A.20°B.30°C.50°D.70°【分析】根据平行线的性质,得出∠BMD=∠B=50°,再根据∠BMD是△CDE的外角,即可得出∠E.【解答】解:∵AB∥CD,∴∠BMD=∠B=50°,又∵∠BMD是△CDE的外角,∴∠E=∠BMD﹣∠D=50°﹣20°=30°.故选:B.【点评】本题主要考查了平行线的性质以及三角形外角性质的运用,解题时注意:两直线平行,内错角相等.二.填空题(共19小题)15.如图,BP是△ABC中∠ABC的平分线,CP是∠ACB的外角的平分线,如果∠ABP=20°,∠ACP=50°,则∠P=30°.【分析】根据角平分线的定义以及一个三角形的外角等于与它不相邻的两个内角和,可求出∠P的度数.【解答】解:∵BP是△ABC中∠ABC的平分线,CP是∠ACB的外角的平分线,∴∠ABP=∠CBP=20°,∠ACP=∠MCP=50°,∵∠PCM是△BCP的外角,∴∠P=∠PCM﹣∠CBP=50°﹣20°=30°,故答案为:30°.【点评】本题考查了三角形外角性质以及角平分线的定义,解题时注意:一个三角形的外角等于与它不相邻的两个内角的和.16.将一副直角三角板,按如图所示叠放在一起,则图中∠α的度数是75°.【分析】先根据直角三角形两锐角互余求出∠1,再根据三角形的一个外角等于与它不相邻的两个内角的和列式计算即可得解.【解答】解:如图,∠1=90°﹣60°=30°,∴∠α=30°+45°=75°.故答案为:75°.【点评】本题考查了直角三角形两锐角互余的性质,三角形的一个外角等于与它不相邻的两个内角的和的性质,是基础题,熟记性质是解题的关键.17.如图,∠BCD=150°,则∠A+∠B+∠D的度数为150°.【分析】延长DC交AB于E,先根据三角形的外角性质求出∠CEB=∠A+∠D,再根据三角形的外角性质计算,得到答案.【解答】解:延长DC交AB于E,∠CEB是△ADE的一个外角,∴∠CEB=∠A+∠D,同理,∠BCD=∠CEB+∠B,∴∠A+∠B+∠D=∠CEB+∠B=∠BCD=150°,故答案为:150°.【点评】本题考查的是三角形的外角性质,掌握三角形的一个外角等于和它不相邻的两个内角的和是解题的关键》18.如图,已知△ABC的两条高BD、CE交于点F,∠ABC的平分线与△ABC外角∠ACM 的平分线交于点G,若∠BFC=8∠G,则∠A=36°.【分析】首先根据三角形的外角性质求出∠G=∠A,结合三角形的高的知识得到∠G 和∠A之间的等量关系,进而求出∠A的度数.【解答】解:由三角形的外角性质得,∠ACM=∠A+∠ABC,∠GCM=∠G+∠GBC,∵∠ABC的平分线与∠ACM的平分线交于点G,∴∠GBC=∠ABC,∠GCM=∠ACD,∴∠G+∠GBC=(∠A+∠ABC)=∠A+∠GBC,∴∠G=∠A,∵∠BFC=8∠G,且BD⊥AC,CE⊥AB,∴∠BFC+∠A=180°,∴8∠G+∠A=180°,∴5∠A=180°,∴∠A=36°,故答案为36.【点评】本题主要考查了三角形的外角性质,解题的关键是证明出∠A=2∠G,此题有一定的难度.19.如图,在△ABC中,∠A、∠B的平分线相交于点I,若∠C=70°,则∠AIB=125度,若∠AIB=155°,则∠C=130度.【分析】作出辅助线,构造三角形的外角解答.【解答】解:连接CI并延长交AB于P.∵AI平分∠CAP,∴∠1=∠2.∵BI平分∠CBP,∴∠3=∠4,∴∠1+∠3=(∠CAB+∠CBA)=×(180°﹣70°)=55°,∴∠7+∠8=∠1+∠3+∠5+∠6=55°+70°=125°.∵∠AIB=155°,∴∠2+∠4=180°﹣155°=25°,又∵∠CAP、∠CBP的平分线,相交于点I,∴∠CAP+∠CBP=2×25°=50°,∴∠ACB=180°﹣50°=130°.【点评】解答此题要多次利用三角性内角和外角的关系,以建立起各角之间的联系.20.如图,CE是△ABC的外角∠ACD的平分线,若∠B=35°,∠ACE=60°,则∠A=85°.【分析】根据角平分线定义求出∠ACD,根据三角形的外角性质得出∠ACD=∠A+∠B,即可求出答案.【解答】解:∵∠ACE=60°,CE是△ABC的外角∠ACD的平分线,∠ACD=2∠ACE=120°,∵∠ACD=∠A+∠B,∠B=35°,∴∠A=∠ACD﹣∠B=85°,故答案为:85°【点评】本题考查了三角形的外角性质的应用,能根据三角形的外角性质得出ACD=∠A+∠B是解此题的关键.21.小明将一副三角板中的两块直角三角尺的直角顶点C按如图所示的方式叠放在一起,当∠ACE<180°且点E在直线AC的上方时,他发现若∠ACE=30°或120°或165°,则三角板BCE有一条边与斜边AD平行.(写出所有可能情况)【分析】分三种情形画出图形分别求解即可解决问题;【解答】解:有三种情形:①如图1中,当AD∥BC时.∵AD∥BC,∴∠D=∠BCD=30°,∵∠ACE+∠ECD=∠ECD+∠DCB=90°,∴∠ACE=∠DCB=30°.②如图2中,当AD∥CE时,∠DCE=∠D=30°,可得∠ACE=90°+30°=120°.③如图2中,当AD∥BE时,延长BC交AD于M.∵AD∥BE,∴∠AMC=∠B=45°,∴∠ACM=180°﹣60°﹣45°=75°,∴∠ACE=75°+90°=165°,综上所述,满足条件的∠ACE的度数为30°或120°或165°.故答案为30°或120°或165°.【点评】本题考查旋转变换、平行线的判定和性质、三角形内角和定理等知识,解题的关键是学会用分类讨论的首先思考问题,属于中考常考题型.22.如图,△ADC是45°的直角三角板,△ABE是30°的直角三角板,若CD与BE交于点F,则∠DFB的度数为15°.【分析】利用三角形的外角的性质即可解决问题.【解答】解:∵∠ADC=45°,∠B=30°,∴∠DFB=∠ADC﹣∠B=15°,故答案为15°.【点评】本题考查特殊三角形的性质,三角形内角和定理,三角形外角的性质等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.23.一副三角板如图放置,若∠1=90°,则∠2的度数为75°.【分析】首先根据三角板可得∠B=30°,∠A=45°,再根据三角形内角和可得∠3=45°,然后再根据三角形内角与外角的关系可得∠2=∠B+∠4,进而得到答案.【解答】解:由题意得:∠B=30°,∠A=45°,∵∠1=90°,∴∠A+∠3=90°,∴∠3=45°,∴∠4=45°,∵∠B=30°,∴∠2=45°+30°=75°,故答案为:75°.【点评】此题主要考查了三角形内角和定理,以及三角形内角与外角的关系,关键是掌握三角形的一个外角等于和它不相邻的两个内角的和.24.如图,∠ABC=∠ACB,AD、BD、CD分别平分△ABC的外角∠EAC、内角∠ABC、外角∠ACF,以下结论:①AD∥BC;②∠ACB=2∠ADB;③∠ADC=90°﹣∠ABC;④∠BDC=∠BAC.其中正确的结论有①②④(填序号).【分析】根据角平分线定义得出∠ABC=2∠ABD=2∠DBC,∠EAC=2∠EAD,∠ACF =2∠DCF,根据三角形的内角和定理得出∠BAC+∠ABC+∠ACB=180°,根据三角形外角性质得出∠ACF=∠ABC+∠BAC,∠EAC=∠ABC+∠ACB,根据已知结论逐步推理,即可判断各项.【解答】解:∵AD平分∠EAC,∴∠EAC=2∠EAD,∵∠EAC=∠ABC+∠ACB,∠ABC=∠ACB,∴∠EAD=∠ABC,∴AD∥BC,∴①正确;∵AD∥BC,∴∠ADB=∠DBC,∵BD平分∠ABC,∠ABC=∠ACB,∴∠ABC=∠ACB=2∠DBC,∴∠ACB=2∠ADB,∴②正确;∵AD平分∠EAC,CD平分∠ACF,∴∠DAC=∠EAC,∠DCA=∠ACF,∵∠EAC=∠ACB+∠ACB,∠ACF=∠ABC+∠BAC,∠ABC+∠ACB+∠BAC=180°,∴∠ADC=180°﹣(∠DAC+∠ACD)=180°﹣(∠EAC+∠ACF)=180°﹣(∠ABC+∠ACB+∠ABC+∠BAC)=180°﹣(180°+∠ABC)=90°﹣∠ABC,∴③错误;∵∠ACF=2∠DCF,∠ACF=∠BAC+∠ABC,∠ABC=2∠DBC,∠DCF=∠DBC+∠BDC,∴∠BAC=2∠BDC,∴④正确;故答案为:①②④【点评】本题考查了三角形外角性质,角平分线定义,平行线的判定,三角形内角和定理的应用,主要考查学生的推理能力,有一定的难度.25.三角形三个内角的比为2:3:4,则这个三角形最大的外角是140度.【分析】根据三角形的内角和是180度和三角形内角和相邻外角的和是180°即可求解.【解答】解:这个三角形最大的外角=180°﹣,故答案为:140.【点评】本题考查了三角形的内角和定理,理解定理是关键.26.已知:如图,在△ABC中,∠A=55°,H是高BD、CE的交点,则∠BHC=125度.【分析】根据直角三角形的两个锐角互余,可求得∠ABD.再根据三角形的一个外角等于和它不相邻的两个内角和,进而求出∠BHC.【解答】解:在△ABD中,∵BD⊥AC,∴∠ABD=90°﹣∠A=35°,∴∠BHC=90°+35°=125°.【点评】运用了直角三角形的两个锐角互余以及三角形的内角和定理的推论.27.如图,已知△OAB中,∠AOB=70°,∠OAB的角平分线与△OBA的外角∠ABN的平分线所在的直线交于点D,则∠ADB的大小为35°.【分析】根据三角形的外角的性质得到∠ABN﹣∠OAB=∠AOB=70°,根据角平分线的定义计算即可.【解答】解:∠ABN﹣∠OAB=∠AOB=70°,∵AD平分∠OAB,BC平分∠ABN,∴∠ABC=∠ABN,∠BAD=∠OAB,∴∠ADB=∠ABC﹣∠BAD=35°,故答案为:35°.【点评】本题考查的是三角形的外角的性质、角平分线的定义,掌握三角形的一个外角等于和它不相邻的两个内角的和是解题的关键.28.将一副直角三角板如图放置,使两直角重合,则∠1=165度.【分析】由题意得出∠CAD=60°、∠B=45°、∠CAB=120°,根据∠1=∠B+∠CAB 可得答案.【解答】解:如图,由题意知,∠CAD=60°,∠B=45°,∴∠CAB=120°,∴∠1=∠B+∠CAB=45°+120°=165°,故答案为:165.【点评】本题主要考查三角形外角的性质,解题的关键是掌握三角形的一个外角等于和它不相邻的两个内角的和.29.如图,根据三角形的有关知识可知图中的x的值是60.【分析】根据三角形外角性质得出关于x的方程,求出即可.【解答】解:根据三角形的外角性质得:x+80=x+20+x,解得:x=60,故答案为:60.【点评】本题考查了三角形外角性质的应用,能根据三角形的外角性质得出关于x的方程是解此题的关键,注意:三角形的一个外角等于和它不相邻的两个内角的和.30.如图,CE平分∠ACD,交AB于点E,∠A=40°,∠B=30°,∠D=104°,则∠BEC 的度数为57°.【分析】延长CD交AB于F,根据三角形的外角性质、角平分线的定义计算即可.【解答】解:延长CD交AB于F,∵∠BDC是△BFD的一个外角,∴∠BFD=∠BDC﹣∠B=104°﹣30°=74°,∵∠BFD是△AFC的一个外角,∴∠ACF=∠BFD﹣∠A=74°﹣40°=34°,∵CE平分∠ACD,∴∠ACE=∠FCE=∠ACF=17°,∵∠BEC是△AEC的一个外角,∴∠BEC=∠ACE+∠A=17°+40°=57°,故答案为:57°.【点评】本题考查的是三角形的外角性质,掌握三角形的一个外角等于和它不相邻的两个内角的和是解题的关键.31.将一副三角板如图所示放置(其中含30°角的三角板的一条较短直角边与另一块三角板的斜边放置在一直线上),那么图中∠1=105度.【分析】根据三角形的外角定理,即可得出∠1的度数.【解答】解:由题意可得,∠2=60°,∠3=45°,由三角形外角定理,∠1=∠2+∠3=60°+45°=105°.故答案为105.【点评】本题主要考查了三角形的内角和为180°,熟练掌握三角形的内角和性质是解题的关键,难度适中.32.如图,AB∥CD,∠B=68°,∠E=20°,则∠D的度数为48度.【分析】根据平行线的性质得∠BFD=∠B=68°,再根据三角形的一个外角等于与它不相邻的两个内角和,得∠D=∠BFD﹣∠E,由此即可求∠D.【解答】解:∵AB∥CD,∠B=68°,∴∠BFD=∠B=68°,而∠D=∠BFD﹣∠E=68°﹣20°=48°.故答案为:48.【点评】此题主要运用了平行线的性质以及三角形的一个外角等于和它不相邻的两个内角和.33.如图,已知△ABC中,∠A=60°,点O为△ABC内一点,且∠BOC=140°,其中O1B平分∠ABO,O1C平分∠ACO,O2B平分∠ABO1,O2C平分∠ACO1,…,O n B平分∠ABO n﹣1,O n C平分∠ACO n﹣1,…,以此类推,则∠BO1C=100°,∠BO2017C=(60+)°.【分析】根据三角形内角和定理可求得∠ABO+∠ACO的度数,再根据角平分线的定义和三角形内角和定理即可求出∠BO1C的度数;用n°的代数式表示出∠O1BC+∠O1CB 的度数的和,再根据三角形的内角和定理得出结论算出∠BO2017C的度数即可.【解答】解:∵∠BOC=140°,∴∠1+∠2=180°﹣140°=40°.∴∠ABO+∠ACO=180°﹣60°﹣40°=80°∵点O1是∠ABC与∠ACB的角平分线的交点,∴∠BO1C=180°﹣(×80°+40°)=100°.∴∠BO2C=180°﹣[120°﹣(∠ABO2+∠ACO2)=180°﹣[120°﹣(××80°+40°)=80°.∠BO2017C=180°﹣[120°﹣()2017×80°]=60°+()2017×80°=(60+)°故答案为:100,(60+).【点评】本题考查了三角形内角和定理,角平分线定义的应用,注意:三角形的内角和等于180°.三.解答题(共10小题)34.如图所示,在△ABC中,D是BC边上一点,∠1=∠2,∠3=∠4,∠BAC=63°,求∠DAC的度数.【分析】△ABD中,由三角形的外角性质知∠3=2∠2,因此∠4=2∠2,从而可在△BAC 中,根据三角形内角和定理求出∠4的度数,进而可在△DAC中,由三角形内角和定理求出∠DAC的度数.【解答】解:设∠1=∠2=x,则∠3=∠4=2x.因为∠BAC=63°,所以∠2+∠4=117°,即x+2x=117°,所以x=39°;所以∠3=∠4=78°,∠DAC=180°﹣∠3﹣∠4=24°.【点评】此题主要考查了三角形的外角性质以及三角形内角和定理的综合应用.35.如图①,在△ABC中,∠ABC与∠ACB的平分线相交于点P.(1)如果∠A=80°,求∠BPC的度数;(2)如图②,作△ABC外角∠MBC,∠NCB的角平分线交于点Q,试探索∠Q、∠A之间的数量关系.(3)如图③,延长线段BP、QC交于点E,△BQE中,存在一个内角等于另一个内角的2倍,求∠A的度数.【分析】(1)运用三角形的内角和定理及角平分线的定义,首先求出∠1+∠2,进而求出∠BPC即可解决问题;(2)根据三角形的外角性质分别表示出∠MBC与∠BCN,再根据角平分线的性质可求得∠CBQ+∠BCQ,最后根据三角形内角和定理即可求解;(3)在△BQE中,由于∠Q=90°﹣∠A,求出∠E=∠A,∠EBQ=90°,所以如果△BQE中,存在一个内角等于另一个内角的2倍,那么分四种情况进行讨论:①∠EBQ =2∠E=90°;②∠EBQ=2∠Q=90°;③∠Q=2∠E;④∠E=2∠Q;分别列出方程,求解即可.【解答】(1)解:∵∠A=80°.∴∠ABC+∠ACB=100°,∵点P是∠ABC和∠ACB的平分线的交点,∴∠P=180°﹣(∠ABC+∠ACB)=180°﹣×100°=130°,(2)∵外角∠MBC,∠NCB的角平分线交于点Q,∴∠QBC+∠QCB=(∠MBC+∠NCB)=(360°﹣∠ABC﹣∠ACB)=(180°+∠A)=90°+∠A∴∠Q=180°﹣(90°+∠A)=90°﹣∠A;(3)延长BC至F,∵CQ为△ABC的外角∠NCB的角平分线,∴CE是△ABC的外角∠ACF的平分线,∴∠ACF=2∠ECF,∵BE平分∠ABC,∴∠ABC=2∠EBC,∵∠ECF=∠EBC+∠E,∴2∠ECF=2∠EBC+2∠E,即∠ACF=∠ABC+2∠E,又∵∠ACF=∠ABC+∠A,∴∠A=2∠E,即∠E=∠A;∵∠EBQ=∠EBC+∠CBQ=∠ABC+∠MBC=(∠ABC+∠A+∠ACB)=90°.如果△BQE中,存在一个内角等于另一个内角的2倍,那么分四种情况:①∠EBQ=2∠E=90°,则∠E=45°,∠A=2∠E=90°;②∠EBQ=2∠Q=90°,则∠Q=45°,∠E=45°,∠A=2∠E=90°;③∠Q=2∠E,则90°﹣∠A=∠A,解得∠A=60°;④∠E=2∠Q,则∠A=2(90°﹣∠A),解得∠A=120°.综上所述,∠A的度数是90°或60°或120°.【点评】本题是三角形综合题,考查了三角形内角和定理、外角的性质,角平分线定义等知识;灵活运用三角形的内角和定理、外角的性质进行分类讨论是解题的关键.36.如图,在Rt△ABC中,∠ACB=90°,∠A=40°,△ABC的外角∠CBD的平分线BE 交AC的延长线于点E.(1)求∠CBE的度数;(2)过点D作DF∥BE,交AC的延长线于点F,求∠F的度数.【分析】(1)先根据直角三角形两锐角互余求出∠ABC=90°﹣∠A=50°,由邻补角定义得出∠CBD=130°.再根据角平分线定义即可求出∠CBE=∠CBD=65°;(2)先根据三角形外角的性质得出∠CEB=90°﹣65°=25°,再根据平行线的性质即可求出∠F=∠CEB=25°.【解答】解:(1)∵在Rt△ABC中,∠ACB=90°,∠A=40°,∴∠ABC=90°﹣∠A=50°,∴∠CBD=130°.∵BE是∠CBD的平分线,∴∠CBE=∠CBD=65°;(2)∵∠ACB=90°,∠CBE=65°,∴∠CEB=90°﹣65°=25°.∵DF∥BE,∴∠F=∠CEB=25°.【点评】本题考查了三角形内角和定理,三角形外角的性质,平行线的性质,邻补角定义,角平分线定义.掌握各定义与性质是解题的关键.37.认真阅读下面关于三角形内外角平分线所夹角的探究片段,完成所提出的问题.探究1:如图1,在△ABC中,O是∠ABC与∠ACB的平分线BO和CO的交点,通过分析发现∠BOC=90°+,理由如下:∵BO和CO分别是∠ABC和∠ACB的角平分线∴∴又∵∠ABC+∠ACB=180°﹣∠A∴∴∠BOC=180°﹣(∠1+∠2)=180°﹣(90°﹣∠A)=探究2:如图2中,O是∠ABC与外角∠ACD的平分线BO和CO的交点,试分析∠BOC 与∠A有怎样的关系?请说明理由.探究3:如图3中,O是外角∠DBC与外角∠ECB的平分线BO和CO的交点,则∠BOC 与∠A有怎样的关系?(只写结论,不需证明)结论:∠BOC=90°﹣∠A.【分析】(1)根据提供的信息,根据三角形的一个外角等于与它不相邻的两个内角的和,用∠A与∠1表示出∠2,再利用∠O与∠1表示出∠2,然后整理即可得到∠BOC与∠A 的关系;(2)根据三角形的一个外角等于与它不相邻的两个内角的和以及角平分线的定义表示出∠OBC与∠OCB,然后再根据三角形的内角和定理列式整理即可得解.【解答】解:(1)探究2结论:∠BOC=∠A,理由如下:∵BO和CO分别是∠ABC和∠ACD的角平分线,∴∠1=∠ABC,∠2=∠ACD,又∵∠ACD是△ABC的一外角,∴∠ACD=∠A+∠ABC,∴∠2=(∠A+∠ABC)=∠A+∠1,∵∠2是△BOC的一外角,∴∠BOC=∠2﹣∠1=∠A+∠1﹣∠1=∠A;(2)探究3:∠OBC=(∠A+∠ACB),∠OCB=(∠A+∠ABC),∠BOC=180°﹣∠0BC﹣∠OCB,=180°﹣(∠A+∠ACB)﹣(∠A+∠ABC),=180°﹣∠A﹣(∠A+∠ABC+∠ACB),结论∠BOC=90°﹣∠A.【点评】本题考查了三角形的外角性质与内角和定理,熟记三角形的一个外角等于与它不相邻的两个内角的和是解题的关键,读懂题目提供的信息,然后利用提供信息的思路也很重要.38.如图,在Rt△ABC中,∠ACB=90°,∠A=40°,△ABC的外角∠CBD的平分线BE 交AC的延长线于点E,点F为AC延长线上的一点,连接DF.(1)求∠CBE的度数;(2)若∠F=25°,求证:BE∥DF.【分析】(1)先根据直角三角形两锐角互余求出∠ABC=90°﹣∠A=50°,由邻补角定义得出∠CBD=130°.再根据角平分线定义即可求出∠CBE=65°;(2)先根据三角形外角的性质得出∠CEB=90°﹣65°=25°,再根据∠F=25°,即可得出BE∥DF.【解答】解:(1)∵在Rt△ABC中,∠ACB=90°,∠A=40°,∴∠ABC=90°﹣∠A=50°,∴∠CBD=130°.∵BE是∠CBD的平分线,∴∠CBE=∠CBD=65°;(2)∵∠ACB=90°,∠CBE=65°,∴∠CEB=90°﹣65°=25°.又∵∠F=25°,∴∠F=∠CEB=25°,∴DF∥BE.【点评】本题考查了三角形内角和定理,三角形外角的性质,平行线的性质,邻补角定义,角平分线定义.掌握各定义与性质是解题的关键.39.(1)探究:如图1,求证:∠BOC=∠A+∠B+∠C.。
11.2与三角形有关的角第3课时 三角形的外角

2 . (4 分 ) 如图 , 在△ ABC 中 , ∠ A = 50° , ∠ C = 外角∠ABD的度数是( B ) A.110° B.120° C.130° D.140°
3.(4分)(2016· 乐山)如图,CE是△ABC的外角∠AC 若∠B=35°,∠ACE=60°,则∠A的度数为( A.35° B.95° C.85° D.75°
8 . (4 分 ) 在△ ABC 中 , 如果∠ A , ∠ B , ∠ C 的相邻 4∶2∶3,那么∠A的度数为( A ) A.20° B.40° C.70° D.80°
9.(8分)如图,在五角星ABCDE中,试说明:∠A+∠
+∠E=180°.
解:设BE与AC,AD分别交于点G,F,∵∠AGF=∠
4.(4分)若三角形的一个外角等于和它相邻的内角
形是( B )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.都有可能
5.(8分)如图,点D,B,C在同一直线上 ,∠A=6
50°,∠D=25°,求∠1的度数.
解:∵∠A+∠ABC+∠C=180°,∠A=60°,∠
∴∠ABC=180°-∠A-∠C=180°-60°-50°
第十一章 三角形
11.2 与三角形有关的角
第3课时 三角形的外角
1.三角形的一边与另一边的延长线组成的角叫做三角
2.三角形的外角等于与__________ 它不相邻 的两个内角的__ 和
三角形的外角
1 . (4 分 ) 如图 , 在∠ 1 , ∠ 2 , ∠ 3 和∠ 4 这四个角中
的外角的有( A )
∠AFG=∠B+∠D,且∠A+∠AGF+∠AFG=180° ∠B+∠C+∠D+∠E=180°
三角形的内、外角和三线综合练习题

三角形的内、外角和三线综合练习题三角形的内、外角和三线综合练习题一.解答题(共30小题)1.(2010•玉溪)平面内的两条直线有相交和平行两种位置关系(1)如图a,若AB∥CD,点P在AB、CD外部,则有∠B=∠BOD,又因∠BOD是△POD的外角,故∠BOD=∠BPD+∠D,得∠BPD=∠B﹣∠D.将点P移到AB、CD内部,如图b,以上结论是否成立?若成立,说明理由;若不成立,则∠BPD、∠B、∠D之间有何数量关系?请证明你的结论;(2)在图b中,将直线AB绕点B逆时针方向旋转一定角度交直线CD于点Q,如图c,则∠BPD﹑∠B﹑∠D﹑∠BQD之间有何数量关系?(不需证明)(3)根据(2)的结论求图d中∠A+∠B+∠C+∠D+∠E+∠F的度数.2.(2006•浙江)已知:如图,AB∥CD,直线EF分别交AB、CD于点E、F,∠BEF的平分线与∠DFE的平分线相交于点P.求证:∠P=90°.3.(2000•内蒙古)如图,已知在三角形ABC中,∠C=∠ABC=2∠A,BD是AC边上的高,求∠DBC的度数.4.(2013•响水县一模)探究与发现:探究一:我们知道,三角形的一个外角等于与它不相邻的两个内角的和.那么,三角形的一个内角与它不相邻的两个外角的和之间存在何种数量关系呢?已知:如图1,∠FDC与∠ECD分别为△ADC的两个外角,试探究∠A与∠FDC+∠ECD的数量关系.探究二:三角形的一个内角与另两个内角的平分线所夹的钝角之间有何种关系?已知:如图2,在△ADC中,DP、CP分别平分∠ADC和∠ACD,试探究∠P与∠A的数量关系.探究三:若将△ADC改为任意四边形ABCD呢?已知:如图3,在四边形ABCD中,DP、CP分别平分∠ADC和∠BCD,试利用上述结论探究∠P与∠A+∠B的数量关系.探究四:若将上题中的四边形ABCD改为六边形ABCDEF(图4)呢?请直接写出∠P与∠A+∠B+∠E+∠F的数量关系:_________.5.如图,△ABC中,∠A=40°,∠B=72°,CE平分∠ACB,CD⊥AB于D,DF⊥CE交CE于F,求∠CDF的度数.6.如图1,点O为直线AB上一点,过点O作射线OC,使∠AOC=60°.将一直角三角板的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方.(1)将图1中的三角板绕点O顺时针旋转至图2,使一边OM在∠BOC的内部,且恰好平分∠BOC,求∠CON的度数;(2)将图1中的三角板绕点O按每秒10°的速度沿顺时针方向旋转一周,在旋转的过程中,第t秒时,直线ON恰好平分锐角∠AOC,则t的值为_________秒(直接写出结果);(3)将图1中的三角板绕点O顺时针旋转至图3,使ON在∠AOC的内部,请探究∠AOM与∠NOC之间的数量关系,并说明理由.7.如图,AD、BC交于O点,且∠A=∠B,∠C=∠D.求证:AB∥CD.8.如图,已知点A,D,B在同一直线上,∠1=∠2,∠3=∠E.求证:DE∥BC.9.如图,∠D=∠1,∠E=∠2,DC⊥EC.求证:AD∥BE.10.如图,若∠CAB=∠CED+∠CDE,求证:AB∥CD.11.直线AB、CD被直线EF所截,EF分别交AB、CD于M,N,∠EMB=50°,MG平分∠BMF,MG交CD于G.(1)如图1,若AB∥CD,求∠1的度数.(2)如图2,若∠MNC=140°,求∠1的度数.12.如图,四边形ABCD中,∠B=∠D=90°,AE平分∠BAD,若AE∥CF,∠BCF=60°,请你求出∠DCF的度数.并说明你的理由.13.已知AB∥CD,直线l与AB、CD分别交于点E、F,点P是直线CD上的一个动点(点P不与F重合),点M 在EF上,且∠FMP=∠FPM,(1)如图1,当点P在射线FC上移动时,若∠AEF=60°,则∠FPM=_________;假设∠AEF=a,则∠FPM= _________;(2)如图2,当点P在射线FD上移动时,猜想∠FPM与∠AEF有怎样的数量关系?请你说明理由.14.如图(1)直线GC∥HD,EF交CG、HD于A、B,三条直线把EF右侧的平面分成①、②、③三个区域,(规定:直线上各点不属于任何区域).将一个透明的直角三角尺放置在该图中,使得30°角(即∠P)的两边分别经过点A、B,当点P落在某个区域时,连接PA、PB,得到∠PBD、∠PAC两个角.(1)如图(1),当点P落在第②区域时,求∠PAC+∠PBD的度数;(2)如图(2),当点P落在第③区域时,∠PAC﹣∠PBD=_________度(3)如图(3),当点P落在第①区域时,直接写出∠PAC、∠PBD之间的等量关系.15.如图,直线a∥b,直线AC分别交a、b于点B、点C,直线AD交a于点D.若∠1=20°,∠2=65°,求∠3的度数.16.(1)如图(1),AB∥CD,点P在AB、CD外部,若∠B=40°,∠D=15°,则∠BPD=_________.(2)如图(2),AB∥CD,点P在AB、CD内部,则∠B,∠BPD,∠D之间有何数量关系?证明你的结论;(3)在图(2)中,将直线AB绕点B按逆时针方向旋转一定角度交直线CD于点M,如图(3),若∠BPD=90°,∠BMD=40°,求∠B+∠D的度数.17.(2012•樊城区模拟)下面是有关三角形内外角平分线的探究,阅读后按要求作答:探究1:如图(1),在△ABC中,O是∠ABC与∠ACB的平分线BO和CO的交点,通过分析发现:∠BOC=90°+∠A(不要求证明).探究2:如图(2)中,O是∠ABC与外角∠ACD的平分线BO和CO的交点,试分析∠BOC与∠A有怎样的数量关系?请说明理由.探究3:如图(3)中,O是外角∠DBC与外角∠ECB的平分线BO和CO的交点,则∠BOC与∠A有怎样的数量关系?(只写结论,不需证明).结论:_________.18.(2011•宜兴市二模)操作示例如图1,△ABC中,AD为BC边上的中线,则S△ABD=S△ADC.实践探究(1)在图2中,E、F分别为矩形ABCD的边AD、BC的中点,则S阴和S矩形ABCD之间满足的关系式为_________(2)在图3中,E、F分别为平行四边形ABCD的边AD、BC的中点,则S阴和S平行四边形ABCD之间满足的关系式为_________;(3)在图4中,E、F分别为任意四边形ABCD的边AD、BC的中点,则S阴和S四边形ABCD之间满足的关系式为_________;解决问题:(4)在图5中,E、G、F、H分别为任意四边形ABCD的边AD、AB、BC、CD的中点,并且图中阴影部分的面积为20平方米,求图中四个小三角形的面积和,即S1+S2+S3+S4=_________.19.如图,在△BCD中,BE平分∠DBC交CD于F,延长BC至G,CE平分∠DCG,且EC、DB的延长线交于A 点,若∠A=33°,∠DFE=63°.(1)求证:∠DFE=∠A+∠D+∠E;(2)求∠E的度数;(3)若在上图中作∠CBE与∠GCE的平分线交于E1,作∠CBE1与∠GCE1的平分线交于E2,作∠CBE2与∠GCE2的平分线于E3,以此类推,∠CBE n与∠GCE n的平分线交于E n+l,请用含有n的式子表示∠E n+l的度数(直接写答案).20.已知:△ABC中,AD⊥BC,AE平分∠BAC,请根据题中所给的条件,解答下列问题:(1)如图1,若∠BAD=60°,∠EAD=15°,求∠ACB的度数.(2)通过以上的计算你发现∠EAD和∠ACB﹣∠B之间的关系应为:_________.(3)在图2的△ABC中,∠ACB>90°,那么(2)中的结论仍然成立吗?为什么?21.如图(甲),D是△ABC的边BC的延长线上一点.∠ABC、∠ACD的平分线相交于P1.(1)若∠ABC=80°,∠ACB=40°,则∠P1的度数为_________;(2)若∠A=α,则∠P1的度数为_________;(用含α的代数式表示)(3)如图(乙),∠A=α,∠ABC、∠ACD的平分线相交于P1,∠P1BC、∠P1CD的平分线相交于P2,∠P2BC、∠P2CD的平分线相交于P3依此类推,则∠Pn的度数为_________(用n与α的代数式表示)22.在△ABC中,∠C>∠B,AE是△ABC中∠BAC的平分线;(1)若AD是△ABC的BC边上的高,且∠B=30°,∠C=70°(如图1),求∠EAD的度数;(2)若F是AE上一点,且FG⊥BC,垂足为G(如图2),求证:;(3)若F是AE延长线上一点,且FG⊥BC,G为垂足(如图3),②中结论是否依然成立?请给出你的结论,并说明理由.23.已知,如图,在△ABC中,AD平分∠BAC,DE,DF分别是△ADC的高和角平分线(∠C>∠DAC),若∠B=80°,∠C=40°.(1)求∠DAE的度数;(2)试猜想∠EDF、∠C与∠DAC有何关系?并说明理由.24.如图,在△ABC中,已知∠ACB=67°,BE是AC上的高,CD是AB上的高,F是BE和CD的交点,∠DCB=45°,求∠ABE和∠BFC的度数.25.如图,已知△ABC中,∠B=40°,∠C=62°,AD是BC边上的高,AE是∠BAC的平分线.求:∠DAE的度数.(写出推导过程)26.已知△ABC中,∠BAC=90°,∠C=30°,点D为BC边上一点,连接AD,作DE⊥AB于点E,DF⊥AC于点F.(1)若AD为△ABC的角平分线(如图1),图中∠1、∠2有何数量关系?为什么?(2)若AD为△ABC的高(如图2),求图中∠1、∠2的度数.27.如图,(1)在△ABC中,∠A=52°,∠ABC与∠ACB的角平分线交于D1,∠ABD1与∠ACD1的角平分线交于点D2,依此类推,∠ABD4与∠ACD4的角平分线交于点D5,则∠BD5C的度数是_________.(2)在△ABC中,∠ABC与∠ACB的角平分线交于D1,∠ABD1与∠ACD1的角平分线交于点D2,∠ABD2与∠ACD2的角平分线交于点D3,若∠BD3C的度数是n°,则∠A的度数是_________(用含n的代数式表示).28.已知△ABC.(1)若∠BAC=40°,画∠BAC和外角∠ACD的角平分线相交于O1点(如图①),求∠BO1C的度数;(2)在(1)的条件下,再画∠O1BC和∠O1CD的角平分线相交于O2点(如图②),求∠BO2C的度数;(3)若∠BAC=n°,按上述规律继续画下去,请直接写出∠BO2012C的度数.29.(1)如图1,在锐角△ABC中,BD、CE分别是AC、AB边上的高线,BD与CE相交于点P,若已知∠A=50°,∠BPC的度数为多少;(2)如图2,在钝角△ABC中,BD、CE分别是AC、AB边上的高线,BD与EC的延长线相交于点P,若已知∠A=50°,则∠BPC的度数为多少;(3)在△ABC中,若∠A=α,请你探索AB、AC边上的高线(或延长线)相交所成的∠BPC的度数.(可以用含α的代数式表示)30.如图(1),△ABC中,AD是角平分线,AE⊥BC于点E.(1).若∠C=80°,∠B=50°,求∠DAE的度数.(2).若∠C>∠B,试说明∠DAE=(∠C﹣∠B).(3).如图(2)若将点A在AD 上移动到A´处,A´E⊥BC于点E.此时∠DAE变成∠DA´E,(2)中的结论还正确吗?为什么?三角形的内、外角和三线综合练习题参考答案与试题解析一.解答题(共30小题)1.(2010•玉溪)平面内的两条直线有相交和平行两种位置关系(1)如图a,若AB∥CD,点P在AB、CD外部,则有∠B=∠BOD,又因∠BOD是△POD的外角,故∠BOD=∠BPD+∠D,得∠BPD=∠B﹣∠D.将点P移到AB、CD内部,如图b,以上结论是否成立?若成立,说明理由;若不成立,则∠BPD、∠B、∠D之间有何数量关系?请证明你的结论;(2)在图b中,将直线AB绕点B逆时针方向旋转一定角度交直线CD于点Q,如图c,则∠BPD﹑∠B﹑∠D﹑∠BQD之间有何数量关系?(不需证明)(3)根据(2)的结论求图d中∠A+∠B+∠C+∠D+∠E+∠F的度数.分析:(1)延长BP交CD于E,根据两直线平行,内错角相等,求出∠PED=∠B,再利用三角形的一个外角等于和它不相邻的两个内角的和即可说明不成立,应为∠BPD=∠B+∠D;(2)作射线QP,根据三角形的外角性质可得;(3)根据三角形的外角性质,把角转化到四边形中再求解.解答:解:(1)不成立.结论是∠BPD=∠B+∠D延长BP交CD于点E,∵AB∥CD∴∠B=∠BED又∵∠BPD=∠BED+∠D,∴∠BPD=∠B+∠D.(2)结论:∠BPD=∠BQD+∠B+∠D.(3)连接EG并延长,根据三角形的外角性质,∠AGB=∠A+∠B+∠E,又∵∠AGB=∠CGF,在四边形CDFG中,∠CGF+∠C+∠D+∠F=360°,∴∠A+∠B+∠C+∠D+∠E+∠F=360°.2.(2006•浙江)已知:如图,AB∥CD,直线EF分别交AB、CD于点E、F,∠BEF的平分线与∠DFE的平分线相交于点P.求证:∠P=90°.分析:由AB∥CD,可知∠BEF与∠DFE互补,由角平分线的性质可得∠PEF+∠PFE=90°,由三角形内角和定理可得∠P=90度.解答:证明:∵AB∥CD,∴∠BEF+∠DFE=180°.又∵∠BEF的平分线与∠DFE的平分线相交于点P,∴∠PEF=∠BEF,∠PFE=∠DEF,∴∠PEF+∠PFE=(∠BEF+∠DFE)=90°.∵∠PEF+∠PFE+∠P=180°,∴∠P=90°.3.(2000•内蒙古)如图,已知在三角形ABC中,∠C=∠ABC=2∠A,BD是AC边上的高,求∠DBC的度数.分析:根据三角形的内角和定理与∠C=∠ABC=2∠A,即可求得△ABC三个内角的度数,再根据直角三角形的两个锐角互余求得∠DBC的度数.解答:解:∵∠C=∠ABC=2∠A,∴∠C+∠ABC+∠A=5∠A=180°,∴∠A=36°.则∠C=∠ABC=2∠A=72°.又BD是AC边上的高,则∠DBC=90°﹣∠C=18°.4.(2013•响水县一模)探究与发现:探究一:我们知道,三角形的一个外角等于与它不相邻的两个内角的和.那么,三角形的一个内角与它不相邻的两个外角的和之间存在何种数量关系呢?已知:如图1,∠FDC与∠ECD分别为△ADC的两个外角,试探究∠A与∠FDC+∠ECD的数量关系.探究二:三角形的一个内角与另两个内角的平分线所夹的钝角之间有何种关系?已知:如图2,在△ADC中,DP、CP分别平分∠ADC和∠ACD,试探究∠P与∠A的数量关系.探究三:若将△ADC改为任意四边形ABCD呢?已知:如图3,在四边形ABCD中,DP、CP分别平分∠ADC和∠BCD,试利用上述结论探究∠P与∠A+∠B的数量关系.探究四:若将上题中的四边形ABCD改为六边形ABCDEF(图4)呢?请直接写出∠P与∠A+∠B+∠E+∠F的数量关系:∠P=(∠A+∠B+∠E+∠F)﹣180°.分析:探究一:根据三角形的一个外角等于与它不相邻的两个内角的和可得∠FDC=∠A+∠ACD,∠ECD=∠A+∠ADC,再根据三角形内角和定理整理即可得解;探究二:根据角平分线的定义可得∠PDC=∠ADC,∠PCD=∠ACD,然后根据三角形内角和定理列式整理即可得解;探究三:根据四边形的内角和定理表示出∠ADC+∠BCD,然后同理探究二解答即可;探究四:根据六边形的内角和公式表示出∠ADC+∠BCD,然后同理探究二解答即可.解答:解:探究一:∵∠FDC=∠A+∠ACD,∠ECD=∠A+∠ADC,∴∠FDC+∠ECD=∠A+∠ACD+∠A+∠ADC=180°+∠A;探究二:∵DP、CP分别平分∠ADC和∠ACD,∴∠PDC=∠ADC,∠PCD=∠ACD,∴∠DPC=180°﹣∠PDC﹣∠PCD,=180°﹣∠ADC﹣∠ACD,=180°﹣(∠ADC+∠ACD),=180°﹣(180°﹣∠A),=90°+∠A;探究三:∵DP、CP分别平分∠ADC和∠BCD,∴∠PDC=∠ADC,∠PCD=∠BCD,∴∠DPC=180°﹣∠PDC﹣∠PCD,=180°﹣∠ADC﹣∠BCD,=180°﹣(∠ADC+∠BCD),=180°﹣(360°﹣∠A﹣∠B),=(∠A+∠B);探究四:六边形ABCDEF的内角和为:(6﹣2)•180°=720°,∵DP、CP分别平分∠ADC和∠ACD,∴∠P=∠ADC,∠PCD=∠ACD,∴∠P=180°﹣∠PDC﹣∠PCD,=180°﹣∠ADC﹣∠ACD,=180°﹣(∠ADC+∠ACD),=180°﹣(720°﹣∠A﹣∠B﹣∠E﹣∠F),=(∠A+∠B+∠E+∠F)﹣180°,即∠P=(∠A+∠B+∠E+∠F)﹣180°.5.如图,△ABC中,∠A=40°,∠B=72°,CE平分∠ACB,CD⊥AB于D,DF⊥CE交CE于F,求∠CDF的度数.分析:首先根据三角形的内角和定理求得∠ACB的度数,再根据CE平分∠ACB求得∠ACE的度数,则根据三角形的外角的性质就可求得∠CED=∠A+∠ACE,再结合CD⊥AB,DF⊥CE就可求解.解答:解:∵∠A=40°,∠B=72°,∴∠ACB=180°﹣40°﹣72°=68°,∵CE平分∠ACB,∴∠ACE=∠BCE=34°,∴∠CED=∠A+∠ACE=74°,∴∠CDE=90°,DF⊥CE,∴∠CDF+∠ECD=∠ECD+∠CED=90°,∴∠CDF=74°.6.如图1,点O为直线AB上一点,过点O作射线OC,使∠AOC=60°.将一直角三角板的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方.(1)将图1中的三角板绕点O顺时针旋转至图2,使一边OM在∠BOC的内部,且恰好平分∠BOC,求∠CON的度数;(2)将图1中的三角板绕点O按每秒10°的速度沿顺时针方向旋转一周,在旋转的过程中,第t秒时,直线ON恰好平分锐角∠AOC,则t的值为12或30秒(直接写出结果);(3)将图1中的三角板绕点O顺时针旋转至图3,使ON在∠AOC的内部,请探究∠AOM与∠NOC之间的数量关系,并说明理由.分析:(1)由角的平分线的定义和等角的余角相等求解;(2)由∠BOC=120°可得∠AOC=60°,则∠AON=30°或∠NOR=30°,即顺时针旋转300°或120°时ON平分∠AOC,据此求解;(3)因为∠MON=90°,∠AOC=60°,所以∠AOM=90°﹣∠AON、∠NOC=60°﹣∠AON,然后作差即可.解答:解:(1)已知∠AOC=60°,∴∠BOC=120°,又OM平分∠BOC,∠COM=∠BOC=60°,∴∠CON=∠COM+90°=150°;(2)延长NO,∵∠BOC=120°∴∠AOC=60°,当直线ON恰好平分锐角∠AOC,∴∠AOD=∠COD=30°,即顺时针旋转300°时NO延长线平分∠AOC,由题意得,10t=300°∴t=30,当NO平分∠AOC,∴∠NOR=30°,即顺时针旋转120°时NO平分∠AOC,∴10t=120°,∴t=12,∴t=12或30;(3)∵∠MON=90°,∠AOC=60°,∴∠AOM=90°﹣∠AON、∠NOC=60°﹣∠AON,∴∠AOM﹣∠NOC=(90°﹣∠AON)﹣(60°﹣∠AON)=30°,所以∠AOM与∠NOC之间的数量关系为:∠AOM﹣∠NOC=30°.7.如图,AD、BC交于O点,且∠A=∠B,∠C=∠D.求证:AB∥CD.分析:证两直线平行,需证得两直线的内错角相等.结合已知,可用△AOB和△COD的外角∠AOC为媒介,证得∠A=∠D或∠B=∠C,由此来证得AB∥CD.解答:证明:∵∠AOC=∠A+∠B,∠A=∠B,∴∠AOC=2∠B.∵∠AOC=∠C+∠D,∠C=∠D,∴∠AOC=2∠C.∴∠C=∠B.∴AB∥CD.8.如图,已知点A,D,B在同一直线上,∠1=∠2,∠3=∠E.求证:DE∥BC.分析:由∠1=∠2,∠AOE=∠COD可证得∠CDO=∠E;再由∠3=∠E得∠CDO=∠3,即得DE∥BC(内错角相等,两直线平行).解答:证明:∵∠1=∠2,∠AOE=∠COD(对顶角相等),∴在△AOE和△COD中,∠CDO=∠E(三角形内角和定理);∵∠3=∠E,∴∠CDO=∠3,∴DE∥BC(内错角相等,两直线平行).9.如图,∠D=∠1,∠E=∠2,DC⊥EC.求证:AD∥BE.分析:根据DC⊥EC,得∠1+∠2=90°,再结合已知条件,得∠D+∠1+∠E+∠2=180°,利用三角形的内角和定理就可求得∠A+∠B的值,从而证明结论.解答:证明:∵DC⊥EC,∴∠1+∠2=90°,又∠D=∠1,∠E=∠2,∴∠D+∠1+∠E+∠2=180°.根据三角形的内角和定理,得∠A+∠B=180°,∴AD∥BE.10.如图,若∠CAB=∠CED+∠CDE,求证:AB∥CD.分析:利用三角形的内角和定理得∠C+∠CED+∠CDE=180°,已知∠CAB=∠CED+∠CDE,所以∠C+∠CAB=180°,根据同旁内角互补,两直线平行可证AB∥CD.解答:证明:在△ECD中∵∠C+∠CED+∠CDE=180°(三角形内角和定理),又∵∠CAB=∠CED+∠CDE(已知),∴∠C+∠CAB=180°(等量代换),∴AB∥CD(同旁内角互补,两直线平行).11.直线AB、CD被直线EF所截,EF分别交AB、CD于M,N,∠EMB=50°,MG平分∠BMF,MG交CD于G.(1)如图1,若AB∥CD,求∠1的度数.(2)如图2,若∠MNC=140°,求∠1的度数.分析:(1)根据两角互补及角平分线的性质可求出∠BMG的度数,再根据平行线的性质即可求解;(2)先根据两角互补及角平分线的性质可求出∠NMG的度数,再由三角形内角与外角的性质及∠MNC=140°即可求出∠1的度数.解答:解:(1)∵∠BMF+∠EMB=180°,∴∠BMF=180°﹣∠EMB,∵∠EMB=50°,∴∠BMF=180°50°=130°,(2分)∵MG平分∠BMF,∴∠BMG=∠GMN=∠BMF=65°,(4分)∵AB∥CD,∴∠1=∠BMG=65°;(5分)(2)∵∠MNC=∠1+∠GMN,∴∠1=∠MNC﹣∠GMN,(7分)∵∠MNC=140°,∠GMN=65°,∴∠1=140°﹣65°=75°.(8分)12.如图,四边形ABCD中,∠B=∠D=90°,AE平分∠BAD,若AE∥CF,∠BCF=60°,请你求出∠DCF的度数.并说明你的理由.解答:解:∠DCF=60°,理由如下:∵∠B=90°∴∠1+∠BCF=90°∵∠BCF=60°∴∠1=30度.∵AE∥CF∴∠2=∠1=30度∵AE平分∠BAD∴∠3=∠2=30度又∵∠D=90°∴∠3+∠4=90°∴∠4=60°∵AE∥CF∴∠DCF=∠4=60°.13.已知AB∥CD,直线l与AB、CD分别交于点E、F,点P是直线CD上的一个动点(点P不与F重合),点M 在EF上,且∠FMP=∠FPM,(1)如图1,当点P在射线FC上移动时,若∠AEF=60°,则∠FPM=30°;假设∠AEF=a,则∠FPM=α;(2)如图2,当点P在射线FD上移动时,猜想∠FPM与∠AEF有怎样的数量关系?请你说明理由.分析:(1)根据两直线平行,同旁内角互补以及△PFM的内角和是180°填空;(2)根据两直线平行,内错角相等和三角形的内角和为180度,易得∠FPM=90°﹣∠AEF.解答:解:(1)∵AB∥CD,∴∠AEF+∠MFP=180°.∵∠MFP+∠FMP+∠FPM=180°,∴∠FMP+∠FPM=∠AEF;∵∠FMP=∠FPM,∴∠FPM=∠AEF;∴若∠AEF=60°,则∠FPM=30°;若∠AEF=a,则∠FPM=α;(2)∠FPM=90°﹣∠AEF.理由:∵AB∥CD,∴∠AEF=∠MFP(两直线平行,内错角相等).∵∠MFP+∠FMP+∠FPM=180°,∴∠FMP+∠FPM=180°﹣∠MFP=180°﹣∠AEF;∵∠FMP=∠FPM,∴∠FPM=90°﹣∠AEF.14.如图(1)直线GC∥HD,EF交CG、HD于A、B,三条直线把EF右侧的平面分成①、②、③三个区域,(规定:直线上各点不属于任何区域).将一个透明的直角三角尺放置在该图中,使得30°角(即∠P)的两边分别经过点A、B,当点P落在某个区域时,连接PA、PB,得到∠PBD、∠PAC两个角.(1)如图(1),当点P落在第②区域时,求∠PAC+∠PBD的度数;(2)如图(2),当点P落在第③区域时,∠PAC﹣∠PBD=30度(3)如图(3),当点P落在第①区域时,直接写出∠PAC、∠PBD之间的等量关系.分析:解答:(1)过点P作PQ∥GC,则由平行线的性质求出∠PAC+∠PBD=∠P,从而得出答案.(2)由GC∥HD,得∠EAC=∠EBD,再由外角的性质得出∠PAE=∠P+∠ABP,从而得出∠PAC=∠PBD+∠P;(3)由GC∥HD,得∠1=∠PBD,再由外角的性质得出∠1=∠P+∠CAP,从而得出∠PBD=∠PAC+∠P.解:(1)过点P作PQ∥GC,∴∠PAC=∠APQ,∠BPQ=∠PBD,∴∠PAC+∠PBD=∠APQ+∠QPB,即∠PAC+∠PBD=∠P,∵∠P=30°,∴∠PAC+∠PBD=30°.(2)∵GC∥HD,∴∠EAC=∠EBD,∵∠PAE=∠P+∠ABP,∴∠PAC=∠PBD+∠P,∴∠PAC﹣∠PBD=30°;(3)∵GC∥HD,∴∠1=∠PBD,∵∠1=∠P+∠CAP,∴∠PBD=∠PAC+∠P,即∠PBD﹣∠PAC=∠P.∴∠P=30°.15.如图,直线a∥b,直线AC分别交a、b于点B、点C,直线AD交a于点D.若∠1=20°,∠2=65°,求∠3的度数.分析:根据两直线a∥b推知,内错角∠2=∠4;然后由三角形的外角性质及等量代换求得∠3的度数即可.解答:解:∵a∥b,∴∠2=∠4(两直线平行,内错角相等),又∵∠4=∠1+∠3(外角定理),∠1=20°,∠2=65°,∴∠3=∠2﹣∠1=45°,即∠3=45°.16.(1)如图(1),AB∥CD,点P在AB、CD外部,若∠B=40°,∠D=15°,则∠BPD=25°.(2)如图(2),AB∥CD,点P在AB、CD内部,则∠B,∠BPD,∠D之间有何数量关系?证明你的结论;(3)在图(2)中,将直线AB绕点B按逆时针方向旋转一定角度交直线CD于点M,如图(3),若∠BPD=90°,∠BMD=40°,求∠B+∠D的度数.分析:(1)由AB∥CD,∠B=40°,根据两直线平行,内错角相等,即可求得∠BOD的度数,又由三角形外角的性质,可求得∠BPD的度数;(2)首先过点P作PE∥AB,由AB∥CD,可得AB∥PE∥CD,然后由两直线平行,内错角相等,即可证得∠BPD=∠1+∠2=∠B+∠D;(3)首先延长BP交CD于点E,利用三角形外角的性质,即可求得∠B+∠D的度数.解答:解:(1)∵AB∥CD,∠B=40°,∴∠BOD=∠B=40°,∴∠P=∠BOD﹣∠D=40°﹣15°=25°.故答案为:25°;(2)∠BPD=∠B+∠D.证明:过点P作PE∥AB,∵AB∥CD,∴AB∥PE∥CD,∴∠1=∠B,∠2=∠D,∴∠BPD=∠1+∠2=∠B+∠D.(3)延长BP交CD于点E,∵∠1=∠BMD+∠B,∠BPD=∠1+∠D,∴∠BPD=∠BMD+∠B+∠D,∵∠BPD=90°,∠BMD=40°,∴∠B+∠D=∠BPD﹣∠BMD=90°﹣40°=50°.17.(2012•樊城区模拟)下面是有关三角形内外角平分线的探究,阅读后按要求作答:探究1:如图(1),在△ABC中,O是∠ABC与∠ACB的平分线BO和CO的交点,通过分析发现:∠BOC=90°+∠A(不要求证明).探究2:如图(2)中,O是∠ABC与外角∠ACD的平分线BO和CO的交点,试分析∠BOC与∠A有怎样的数量关系?请说明理由.探究3:如图(3)中,O是外角∠DBC与外角∠ECB的平分线BO和CO的交点,则∠BOC与∠A有怎样的数量关系?(只写结论,不需证明).结论:∠BOC=90°﹣∠A.分析:(1)根据提供的信息,根据三角形的一个外角等于与它不相邻的两个内角的和,用∠A与∠1表示出∠2,再利用∠O与∠1表示出∠2,然后整理即可得到∠BOC与∠O的关系;(2)根据三角形的一个外角等于与它不相邻的两个内角的和以及角平分线的定义表示出∠OBC与∠OCB,然后再根据三角形的内角和定理列式整理即可得解.解答:解:(1)探究2结论:∠BOC=∠A,理由如下:∵BO和CO分别是∠ABC和∠ACD的角平分线,∴∠1=∠ABC,∠2=∠ACD,又∵∠ACD是△ABC的一外角,∴∠ACD=∠A+∠ABC,∴∠2=(∠A+∠ABC)=∠A+∠1,∵∠2是△BOC的一外角,∴∠BOC=∠2﹣∠1=∠A+∠1﹣∠1=∠A;(2)探究3:∠OBC=(∠A+∠ACB),∠OCB=(∠A+∠ABC),∠BOC=180°﹣∠0BC﹣∠OCB,=180°﹣(∠A+∠ACB)﹣(∠A+∠ABC),=180°﹣∠A﹣(∠A+∠ABC+∠ACB),结论∠BOC=90°﹣∠A.18.(2011•宜兴市二模)操作示例如图1,△ABC中,AD为BC边上的中线,则S△ABD=S△ADC.实践探究(1)在图2中,E、F分别为矩形ABCD的边AD、BC的中点,则S阴和S矩形ABCD之间满足的关系式为;(2)在图3中,E、F分别为平行四边形ABCD的边AD、BC的中点,则S阴和S平行四边形ABCD之间满足的关系式为;(3)在图4中,E、F分别为任意四边形ABCD的边AD、BC的中点,则S阴和S四边形ABCD之间满足的关系式为;;解决问题:(4)在图5中,E、G、F、H分别为任意四边形ABCD的边AD、AB、BC、CD的中点,并且图中阴影部分的面积为20平方米,求图中四个小三角形的面积和,即S1+S2+S3+S4=20.分析:(1)利用E、F分别为矩形ABCD的边AD、BC的中点,分别求得S阴和S矩形ABCD即可.(2)利用E、F分别为平行四边形ABCD的边AD、BC的中点,分别求则S阴和S平行四边形ABCD即可.(3)利用E、F分别为任意四边形ABCD的边AD、BC的中点,分别求得则S阴和S四边形ABCD即可.(4)先设空白处面积分别为:x、y、m、n由上得,,分别求得S1、S2、S3、S4.然后S1+S2+S3+S4=S阴即可.解答:解:(1)由E、F分别为矩形ABCD的边AD、BC的中点,得S阴=BF•CD=BC•CD,S矩形ABCD=BC•CD,所以;(2)同理可得;;(3)同理可得;;(4)设空白处面积分别为:x、y、m、n(见右图),由上得,,∴S1+x+S2+S3+y+S4=.S1+m+S4+S2+n+S3=,∴(S1+x+S2+S3+y+S4)+(S1+m+S4+S2+n+S3)=S四边形ABCD.∴(S1+x+S2+S3+y+S4)+(S1+m+S4+S2+n+S3)=S1+x+S2+n+S3+y+S4+m+S阴∴S1+S2+S3+S4=S阴=20.故答案分别为:(1);(2);(3);(4)20.19.如图,在△BCD中,BE平分∠DBC交CD于F,延长BC至G,CE平分∠DCG,且EC、DB的延长线交于A 点,若∠A=33°,∠DFE=63°.(1)求证:∠DFE=∠A+∠D+∠E;(2)求∠E的度数;(3)若在上图中作∠CBE与∠GCE的平分线交于E1,作∠CBE1与∠GCE1的平分线交于E2,作∠CBE2与∠GCE2的平分线于E3,以此类推,∠CBEn与∠GCEn的平分线交于En+l,请用含有n的式子表示∠En+l的度数(直接写答案).分析:(1)根据三角形的一个外角等于和它不相邻的两个内角的和,得出∠DCE=∠A+∠D,∠DFE=∠DCE+∠E,将第一式代入第二式即可得证;(2)根据角平分线及三角形外角的性质得出∠ECG=∠DCG=(∠D+∠DBC),∠ECG=∠E+∠EBC=∠E+∠DBC,则∠D=2∠E,再利用上题结论∠DFE=∠A+∠D+∠E,将已知条件代入,即可求出∠E的度数;(3)先根据角平分线及三角形外角的性质得出∠E1=∠E,同理得出∠E2=∠E1,则∠E2=∠E=∠E,由此得出规律∠E n+l=∠E.解答:(1)证明:∵∠DCE=∠A+∠D,∠DFE=∠DCE+∠E,∴∠DFE=∠A+∠D+∠E;(2)解:∵∠DCG=∠D+∠DBC,CE平分∠DCG,∴∠ECG=∠DCG=(∠D+∠DBC),∵BE平分∠DBC,∴∠EBC=∠DBC,∵∠ECG=∠E+∠EBC=∠E+∠DBC,∴∠E+∠DBC=(∠D+∠DBC),∴∠E=∠D,∴∠D=2∠E.∵∠DFE=63°,∠A=33°,∠DFE=∠A+∠D+∠E,∴∠D+∠E=∠DEF﹣∠A=63°﹣33°=30°,∴2∠E+∠E=30°,∴∠E=10°;(3)∵∠ECG=∠E+∠EBC,CE1平分∠ECG,∴∠E1CG=∠ECG=(∠E+∠EBC).∵BE1平分∠EBC,∴∠E1BC=∠EBC.∵∠E1CG=∠E1+∠E1BC=∠E1+∠EBC,∴∠E1+∠EBC=(∠E+∠EBC),∴∠E1=∠E.同理:∠E2=∠E1,∴∠E2=∠E=∠E,∴∠E n+l=∠E.20.已知:△ABC中,AD⊥BC,AE平分∠BAC,请根据题中所给的条件,解答下列问题:(1)如图1,若∠BAD=60°,∠EAD=15°,求∠ACB的度数.(2)通过以上的计算你发现∠EAD和∠ACB﹣∠B之间的关系应为:∠ACB﹣∠B=2∠EAD.(3)在图2的△ABC中,∠ACB>90°,那么(2)中的结论仍然成立吗?为什么?分析:(1)先求出∠BAE=∠BAD﹣∠EAD=45°,再根据角平分线的定义,得出∠BAC=90°,则根据三角形内角和定理得出∠ACB=90°﹣∠B,故求出∠B的度数即可.而在直角△ABD中,∠B=90°﹣∠BAD=30°;(2)由(1)的计算发现∠EAD和∠ACB﹣∠B之间的关系应为:∠ACB﹣∠B=2∠EAD;(3)先根据三角形内角和定理及垂直的定义,得出∠ACB﹣∠B=∠BAD﹣∠CAD,再由角平分线的定义得出结论∠ACB﹣∠B=2∠EAD.解答:解:(1)∵∠BAD=60°,∠EAD=15°,∴∠BAE=∠BAD﹣∠EAD=45°,∵AE平分∠BAC,∴∠BAC=2∠BAE=90°.∵AD⊥BC,∠BAD=60°,∴∠B=30°,∴∠ACB=90°﹣30°=60°;(2)∵(1)中∠EAD=15°,∠ACB﹣∠B=60°﹣30°=30°,发现∠ACB﹣∠B=2∠EAD,∴推测∠ACB﹣∠B=2∠EAD;(3)在图2的△ABC中,∠ACB>90°,那么(2)中的结论仍然成立.理由如下:∵在△ABC中,AD⊥BC,AE平分∠BAC,∴∠ADC=∠ADB=90°,∠BAE=∠CAE,∴∠ACB﹣∠B=90°﹣∠CAD﹣(90°﹣∠BAD)=∠BAD﹣∠CAD,又∵∠BAD=∠BAE+∠EAD,∠CAD=∠CAE﹣∠EAD,∴∠ACB﹣∠B=2∠EAD.21.如图(甲),D是△ABC的边BC的延长线上一点.∠ABC、∠ACD的平分线相交于P1.(1)若∠ABC=80°,∠ACB=40°,则∠P1的度数为30°;(2)若∠A=α,则∠P1的度数为α;(用含α的代数式表示)(3)如图(乙),∠A=α,∠ABC、∠ACD的平分线相交于P1,∠P1BC、∠P1CD的平分线相交于P2,∠P2BC、∠P2CD的平分线相交于P3依此类推,则∠Pn的度数为()nα(用n与α的代数式表示)分析:由∠P1CD=∠P1+∠P1BC,∠ACD=∠ABC+∠A,而P1B、P1C分别平分∠ABC和∠ACD,得到∠ACD=2∠P1CD,∠ABC=2∠P1BC,于是有∠A=2∠P1,同理可得∠P1=2∠P2,即∠A=22∠P2,因此找出规律.解答:解:∵P1B、P1C分别平分∠ABC和∠ACD,∴∠ACD=2∠P1CD,∠ABC=2∠P1BC,而∠P1CD=∠P1+∠P1BC,∠ACD=∠ABC+∠A,∴∠A=2∠P1,∴∠P1=∠A,(1)∵∠ABC=80°,∠ACB=40°,∴∠A=60°,∴∠P1=30°;(2)∵∠A=α,∴∠P1的度数为α;(3)同理可得∠P1=2∠P2,即∠A=22∠P2,∴∠A=2n∠P n,∴∠Pn=()nα.故答案为:30°,α,()nα.22.在△ABC中,∠C>∠B,AE是△ABC中∠BAC的平分线;(1)若AD是△ABC的BC边上的高,且∠B=30°,∠C=70°(如图1),求∠EAD的度数;(2)若F是AE上一点,且FG⊥BC,垂足为G(如图2),求证:;(3)若F是AE延长线上一点,且FG⊥BC,G为垂足(如图3),②中结论是否依然成立?请给出你的结论,并说明理由.分析:(1)根据三角形内角和定理得∠A=180°﹣30°﹣70°=80°,再根据角平分线定义得∠EAC=×80°=40°,由AD是△ABC的BC边上的高,得∠ADC=90°,计算出∠DAC=90°﹣70°=20°,则∠EAD=∠EAC﹣∠DAC=40°﹣20°=20°;(2)根据三角形内角和定理得∠A=180°﹣∠B﹣∠C,再根据角平分线定义得∠EAC=(180°﹣∠B﹣∠C)=90°﹣(∠B+∠C),而∠DAC=90°﹣∠C,可计算得∠EAD=∠EAC﹣∠DAC=90°﹣(∠B+∠C)﹣90°﹣∠C=(∠C﹣∠B),然后利用平行线的性质得到结论;(3)与(2)证明方法一样.解答:(1)解:∵∠B=30°,∠C=70°,∴∠A=180°﹣30°﹣70°=80°,∵AE是△ABC中∠BAC的平分线,∴∠EAC=×80°=40°,∵AD是△ABC的BC边上的高,∴∠ADC=90°,∴∠DAC=90°﹣70°=20°,∴∠EAD=∠EAC﹣∠DAC=40°﹣20°=20°;(2)证明:过A点作高AD,如图,∠A=180°﹣∠B﹣∠C,∵AE是△ABC中∠BAC的平分线,∴∠EAC=(180°﹣∠B﹣∠C)=90°﹣(∠B+∠C),而∠DAC=90°﹣∠C,∴∠EAD=∠EAC﹣∠DAC=90°﹣(∠B+∠C)﹣90°﹣∠C=(∠C﹣∠B),∵FG⊥BC,∴∠EFG=∠EAD,∴∠EFG=(∠C﹣∠B);(3)②中结论依然成立.理由如下:过A点作高AD,如图,在(2)中得到∠EAD=(∠C﹣∠B),∵FG⊥BC,∴∠EFG=∠EAD,∴∠EFG=(∠C﹣∠B).23.已知,如图,在△ABC中,AD平分∠BAC,DE,DF分别是△ADC的高和角平分线(∠C>∠DAC),若∠B=80°,∠C=40°.(1)求∠DAE的度数;(2)试猜想∠EDF、∠C与∠DAC有何关系?并说明理由.分析:(1)先根据三角形内角和定理求出∠BAC的度数,再根据三角形的角平分线的定义即可求出∠DAE 的度数;(2)先根据三角形内角和定理及角平分线的定义求出∠CDF=(180°﹣∠DAC﹣∠C),再由直角三角形两锐角互余得出∠CDE=90°﹣∠C,则根据∠EDF=∠CDF﹣∠CDE即可得出∠EDF=(∠C﹣∠DAC).解答:解:(1)∵在△ABC中,∠B=80°,∠C=40°,∴∠BAC=180°﹣80°﹣40°=60°,∵AD平分∠BAC,∴∠DAE=∠BAC=30°;(2)∠EDF=(∠C﹣∠DAC).理由如下:在△DAC中,∵∠ADC+∠DAC+∠C=180°,∴∠ADC=180°﹣∠DAC﹣∠C,∵DF平分∠ADC,∴∠CDF=∠ADC=(180°﹣∠DAC﹣∠C),∵DE是△ADC的高,∴∠CDE=90°﹣∠C,∴∠EDF=∠CDF﹣∠CDE=(180°﹣∠DAC﹣∠C)﹣(90°﹣∠C)=(∠C﹣∠DAC).故∠EDF=(∠C﹣∠DAC).24.如图,在△ABC中,已知∠ACB=67°,BE是AC上的高,CD是AB上的高,F是BE和CD的交点,∠DCB=45°,求∠ABE和∠BFC的度数.分析:根据三角形高的定义得到∠CDB=90°,∠BEC=90°,先利用三角形内角和定理得∠DBC=180°﹣90°﹣45°=45°,∠EBC=180°﹣∠ECB﹣∠BEC=180°﹣67°﹣90°=23°,则∠ABE=∠ABC﹣∠EBC=45°﹣23°=22°,然后利用三角形外角性质可计算∠BFC=22°+90°=112°.解答:解:∵CD是AB上的高,∴∠CDB=90°,∵∠CDB+∠DBC+∠DCB=180°,∴∠DBC=180°﹣90°﹣45°=45°,∵BE是AC上的高,∴∠BEC=90°,∴∠EBC=180°﹣∠ECB﹣∠BEC=180°﹣67°﹣90°=23°,∴∠ABE=∠ABC﹣∠EBC=45°﹣23°=22°;∵∠BFC=∠FDB+∠DBF,∴∠BFC=22°+90°=112°.25.如图,已知△ABC中,∠B=40°,∠C=62°,AD是BC边上的高,AE是∠BAC的平分线.求:∠DAE的度数.(写出推导过程)分析:根据三角形的内角和定理,可求得∠BAC的度数,由AE是∠BAC的平分线,可得∠EAC的度数;在直角△ADC中,可求出∠DAC的度数,所以∠DAE=∠EAC﹣∠DAC,即可得出.解答:解:∵△ABC中,∠B=40°,∠C=62°,∴∠BAC=180°﹣∠B﹣∠C=180°﹣40°﹣62°=78°,∵AE是∠BAC的平分线,∴∠EAC=∠BAC=39°,∵AD是BC边上的高,∴在直角△ADC中,∠DAC=90°﹣∠C=90°﹣62°=28°,∴∠DAE=∠EAC﹣∠DAC=39°﹣28°=11°.26.已知△ABC中,∠BAC=90°,∠C=30°,点D为BC边上一点,连接AD,作DE⊥AB于点E,DF⊥AC于点F.(1)若AD为△ABC的角平分线(如图1),图中∠1、∠2有何数量关系?为什么?(2)若AD为△ABC的高(如图2),求图中∠1、∠2的度数.分析:(1)根据已知得出∠1=∠DAC,∠2=∠DAB,以及AD平分∠BAC,即可得出∠1=∠2;(2)首先得出DE∥AC,再利用∠1=∠ADB﹣∠BDE=30°,进而求出∠FDC=180°﹣∠DFC﹣∠C=60°,即可求出∠2=∠ADC﹣∠FDC的度数.解答:解:(1)∠1=∠2,理由如下:∵DE⊥AB,DF⊥AC,∴∠DEB=∠DFC=∠BAC=90°,∴DE∥AC,DF∥AB,∴∠1=∠DAC,∠2=∠DAB,∵AD平分∠BAC,∴∠DAC=∠DAB,∴∠1=∠2;(2)∵DE⊥AB,DF⊥AC,AD⊥BC,∴∠ADB=∠ADC=∠DEB=∠DFC=∠BAC=90°,∴DE∥AC,∴∠BDE=∠C=30°,∴∠1=∠ADB﹣∠BDE=30°,∵∠FDC=180°﹣∠DFC﹣∠C=60°,∴∠2=∠ADC﹣∠FDC=60°.27.如图,(1)在△ABC中,∠A=52°,∠ABC与∠ACB的角平分线交于D1,∠ABD1与∠ACD1的角平分线交于点D2,依此类推,∠ABD4与∠ACD4的角平分线交于点D5,则∠BD5C的度数是56°.(2)在△ABC中,∠ABC与∠ACB的角平分线交于D1,∠ABD1与∠ACD1的角平分线交于点D2,∠ABD2与∠ACD2的角平分线交于点D3,若∠BD3C的度数是n°,则∠A的度数是(用含n的代数式表示).分析:(1)根据角平分线的性质可得到:∠ABD1=∠CBD1=∠ABC,∠ACD1=∠BCD1=∠ACB,再根据三角形的内角和定理可得:∠BD1C的度数,再根据∠ABD1与∠ACD1的角平分线交于点D2,可得∠D2BC=∠ABC,∠D2CB=∠ACB,进而求出∠BD2C=180°﹣(∠ABC+∠ACB),以此类推可得到:∠BD5C=180°﹣(∠ABC+∠ACB),再次利用三角形内角和代入∠ABC+∠ACB=180°﹣∠A,即可求出答案.(2)根据(1)中所求即可得出答案.解答:解:(1)∵∠A=52°,∴∠ABC+∠ACB=180°﹣52°=128°,又∠ABC与∠ACB的角平分线交于D1,∴∠ABD1=∠CBD1=∠ABC,∠ACD1=∠BCD1=∠ACB,∴∠CBD1+∠BCD1=(∠ABC+∠ACB)=×128°=64°,∴∠BD1C=180°﹣(∠ABC+∠ACB)=180°﹣64°=116°,同理∠BD2C=180°﹣(∠ABC+∠ACB)=180°﹣96°=84°,依此类推,∠BD5C=180°﹣(∠ABC+∠ACB)=180°﹣124°=56°.故答案为:56°;(2)由(1)可得:∠BD3C=180°﹣(∠ABC+∠ACB)=180°﹣(180°﹣∠A)=n°.解得:∠A=.故答案为:.28.已知△ABC.(1)若∠BAC=40°,画∠BAC和外角∠ACD的角平分线相交于O1点(如图①),求∠BO1C的度数;(2)在(1)的条件下,再画∠O1BC和∠O1CD的角平分线相交于O2点(如图②),求∠BO2C的度数;(3)若∠BAC=n°,按上述规律继续画下去,请直接写出∠BO2012C的度数.分析:由∠O1CD=∠O1+∠O1BC,∠ACD=∠ABC+∠A,而O1B、O1C分别平分∠ABC和∠ACD,得到∠ACD=2∠O1CD,∠ABC=2∠O1BC,于是有∠A=2∠O1,同理可得∠O1=2∠O2,即∠A=22∠O2,因此找出规律.解答:解:∵O1B、O1C分别平分∠ABC和∠ACD,∴∠ACD=2∠O1CD,∠ABC=2∠O1BC,而∠O1CD=∠O1+∠O1BC,∠ACD=∠ABC+∠A,∴∠A=2∠01=40°,∴∠O1=20°,同理可得∠O1=2∠O2,即∠A=22∠02=40°,∴∠O2=10°,∴∠A=2n∠A n,∴∠A n=n°×()n.则∠BO2012C=0.29.(1)如图1,在锐角△ABC中,BD、CE分别是AC、AB边上的高线,BD与CE相交于点P,若已知∠A=50°,∠BPC的度数为多少;(2)如图2,在钝角△ABC中,BD、CE分别是AC、AB边上的高线,BD与EC的延长线相交于点P,若已知∠A=50°,则∠BPC的度数为多少;(3)在△ABC中,若∠A=α,请你探索AB、AC边上的高线(或延长线)相交所成的∠BPC的度数.(可以用含α的代数式表示)分析:(1)根据直角三角形两锐角互余求出∠ABD,再根据三角形的一个外角等于与它不相邻的两个内角的和列式进行计算即可得解;(2)根据直角三角形两锐角互余可得∠A+∠ACE=90°,∠BPC+∠PCD=90°,再根据∠ACE和∠PCD是对顶角解答即可;。
三角形内角和、外角定理(含详细解答)

三角形内角和、外角定理(含详细解答)-CAL-FENGHAL-(YICAI)-Company One 1三角形内角和、外角和定理选择题(共10小题)(2013?泉州〉在AABC 中,Z A=20\ Z B=60\ 则△ ABC 的形状是(等边三角形 B・锐角三角形 C.直角三角形(2012?河源)如图,在折纸活动中,小明制作了一张△ABC纸片.点D、E分别是边AB. AC上,将△ ABC沿着DE折叠压平,小£重合,若Z A=75\则Z 1+Z 2=()4. (2012?云南〉如图,在AABC 中,Z 6=67% Z C=33%C.105°D 75°A 40°45°B・C.50°D 55°A ABC中,Z C=70%若沿图中虚线截去ZC,则Z 1+Z 2=(5. (2012?南通)如图,250°B・C. 180" D 140°6. (2012?桶州)如图,AE是^ ABC的角平分线,AD丄BC于点D.若Z BAC=128\ Z C=36\则Z DAE的度数是1.A 钝角三角形2.A(2012?滨州〉一个三角形三个内角的度数之比为2:3:等腰三角形 B・直角三角形 C.锐角三角形7,D这个三角形一定是(钝角三角形3-AD是AABC的角平分线,则ZCAD的度数为(A 10°B・12°C・15°D 18°已知宜线 AB II CD, Z8125°,Z A=45\那么Z E的大小为(7. (2011?日照〉如图,80°C.90°D 100°& (2011?台湾〉列何者正确(如图中有四条互相不平行的直线Li、L2、L3、L4所截出的七个角.关于这七个角的度数关系,下A Z 2=Z 4+Z 7 B・ Z 3=Z 1+Z 6 C・ Z 1+Z 4+Z 6=1 D Z 2+Z 3+Z 5=380° • 60°9.A (2011?台湾)若A ABC中,2(Z A+ZC) =3Z B,则ZB的外角度数为何(36 B・ 72 C. 108 D 14410. A (2011?台湾)若钝角三角形ABC中,Z A=27\则下列何考不可能是Z B的度数(37 B・ 57 C. 77 D 97填空题(共4小题)(2014?抚顺)将正三角形、正四边形、正五边形按如图所示的位這摆放-如果Z 3=32。
三角形内角和、外角定理(含详细解答)

三角形内角和、外角定理(含详细解答)-CAL-FENGHAI.-(YICAI)-Company One1三角形内角和、外角和定理一.选择题(共10小题)1.(2013?泉州)在△ABC中,∠A=20°,∠B=60°,则△ABC的形状是()A .等边三角形B.锐角三角形C.直角三角形D.钝角三角形2.(2012?滨州)一个三角形三个内角的度数之比为2:3:7,这个三角形一定是()A .等腰三角形B.直角三角形C.锐角三角形D.钝角三角形3.(2012?河源)如图,在折纸活动中,小明制作了一张△ABC纸片,点D、E分别是边AB、AC上,将△ABC沿着DE折叠压平,A与A′重合,若∠A=75°,则∠1+∠2=()A .150°B.210°C.105°D.75°4.(2012?云南)如图,在△ABC中,∠B=67°,∠C=33°,AD是△ABC的角平分线,则∠CAD的度数为()A .40°B.45°C.50°D.55°5.(2012?南通)如图,△ABC中,∠C=70°,若沿图中虚线截去∠C,则∠1+∠2=()A .360°B.250°C.180°D.140°6.(2012?梧州)如图,AE是△ABC的角平分线,AD⊥BC于点D,若∠BAC=128°,∠C=36°,则∠DAE的度数是()A .10°B.12°C.15°D.18°7.(2011?日照)如图,已知直线AB∥CD,∠C=125°,∠A=45°,那么∠E的大小为()A .70°B.80°C.90°D.100°8.(2011?台湾)如图中有四条互相不平行的直线L1、L2、L3、L4所截出的七个角.关于这七个角的度数关系,下列何者正确()A .∠2=∠4+∠7B.∠3=∠1+∠6C.∠1+∠4+∠6=180°D.∠2+∠3+∠5=360°9.(2011?台湾)若△ABC中,2(∠A+∠C)=3∠B,则∠B的外角度数为何()A .36B.72C.108D.14410.(2011?台湾)若钝角三角形ABC中,∠A=27°,则下列何者不可能是∠B的度数()A .37B.57C.77D.97二.填空题(共4小题)11.(2014?抚顺)将正三角形、正四边形、正五边形按如图所示的位置摆放.如果∠3=32°,那么∠1+∠2= _________度.12.(2013?河池)如图,点O是△ABC的两条角平分线的交点,若∠BOC=118°,则∠A的大小是_________.13.(2008?安徽)如图,已知a∥b,∠1=70°,∠2=40°,则∠3=_________度.14.(2003?金华)如图,平面镜A与B之间夹角为120°,光线经过平面镜A反射后射在平面镜B上,再反射出去,若∠1=∠2,则∠1=_________度.三.解答题(共16小题)15.(2014?六盘水)(1)三角形内角和等于_________.(2)请证明以上命题.16.(2001?海南)如图,在△ABC中,已知∠ABC=46°,∠ACB=80°,延长BC至D,使CD=CA,连接AD,求∠BAD的度数.17.(2000?内蒙古)如图,已知在△ABC中,∠C=∠ABC=2∠A,BD是AC边上的高,求∠DBC的度数.18.(2011?青海)认真阅读下面关于三角形内外角平分线所夹角的探究片段,完成所提出的问题.探究1:如图1,在△ABC中,O是∠ABC与∠ACB的平分线BO和CO的交点,通过分析发现∠BOC=90°+,理由如下:∵BO和CO分别是∠ABC和∠ACB的角平分线∴∴又∵∠ABC+∠ACB=180°﹣∠A∴∴∠BOC=180°﹣(∠1+∠2)=180°﹣(90°﹣∠A)=探究2:如图2中,O是∠ABC与外角∠ACD的平分线BO和CO的交点,试分析∠BOC与∠A有怎样的关系请说明理由.探究3:如图3中,O是外角∠DBC与外角∠ECB的平分线BO和CO的交点,则∠BOC与∠A有怎样的关系(只写结论,不需证明)结论:_________.19.(2010?玉溪)平面内的两条直线有相交和平行两种位置关系(1)如图a,若AB∥CD,点P在AB、CD外部,则有∠B=∠BOD,又因∠BOD是△POD的外角,故∠BOD=∠BPD+∠D,得∠BPD=∠B﹣∠D.将点P移到AB、CD内部,如图b,以上结论是否成立若成立,说明理由;若不成立,则∠BPD、∠B、∠D之间有何数量关系请证明你的结论;(2)在图b中,将直线AB绕点B逆时针方向旋转一定角度交直线CD于点Q,如图c,则∠BPD﹑∠B﹑∠D﹑∠BQD之间有何数量关系(不需证明)(3)根据(2)的结论求图d中∠A+∠B+∠C+∠D+∠E+∠F的度数.20.(2013?响水县一模)探究与发现:探究一:我们知道,三角形的一个外角等于与它不相邻的两个内角的和.那么,三角形的一个内角与它不相邻的两个外角的和之间存在何种数量关系呢已知:如图1,∠FDC与∠ECD分别为△ADC的两个外角,试探究∠A与∠FDC+∠ECD的数量关系.探究二:三角形的一个内角与另两个内角的平分线所夹的钝角之间有何种关系已知:如图2,在△ADC中,DP、CP分别平分∠ADC和∠ACD,试探究∠P与∠A的数量关系.探究三:若将△ADC改为任意四边形ABCD呢已知:如图3,在四边形ABCD中,DP、CP分别平分∠ADC和∠BCD,试利用上述结论探究∠P与∠A+∠B的数量关系.探究四:若将上题中的四边形ABCD改为六边形ABCDEF(图4)呢请直接写出∠P与∠A+∠B+∠E+∠F的数量关系:_________.21.已知:如图,在△ABC中,D为BC上一点,∠1=∠2,∠3=∠4,∠BAC=120°,求∠DAC的度数.22.如图,求∠A+∠B+∠C+∠D+∠E的度数和.23.如图,在△ABC中,D为BC上一点,∠1=∠2,∠3=∠4,∠BAC=63°,试求∠DAC,∠ADC的度数.24.已知:如图所示,∠ABC=66°,∠ACB=54°,BE是AC边上的高,CF是AB边上的高,H是BE和CF的交点,求:∠ABE,∠ACF和∠BHC的度数.25.如图,△ABC中,AD是高,AE、BF是角平分线,它们相交于点O,∠A=50°,∠C=60°,求∠DAC及∠BOA.26.如图,AF是△ABC的高,AD是△ABC的角平分线,∠B=36°,∠C=76°,求∠DAF的度数.27.一个零件的形状如图,按规定∠A=90°,∠C=25°,∠B=25°,检验已量得∠BDC=150°,就判断这个零件不合格,运用三角形的有关知识说明零件不合格的理由.28.一个零件的形状如图所示,按规定∠A应等于90°,∠B、∠C应分别是30°和20°,李叔叔量得∠BDC=142°,就判定这个零件不合格,你能说出其中的道理吗29.如图所示,求∠A+∠B+∠C+∠D+∠E+∠F的度数.30.如图,在三角形ABC中,∠A=35°,求∠1+∠2+∠3+∠4的度数和.三角形内角和、外角和定理参考答案与试题解析一.选择题(共10小题)1.(2013?泉州)在△ABC中,∠A=20°,∠B=60°,则△ABC的形状是()A .等边三角形B.锐角三角形C.直角三角形D.钝角三角形考点:三角形内角和定理.分析:根据三角形的内角和定理求出∠C,即可判定△ABC的形状.解答:解:∵∠A=20°,∠B=60°,∴∠C=180°﹣∠A﹣∠B=180°﹣20°﹣60°=100°,∴△ABC是钝角三角形.故选D.点评:本题考查了三角形的内角和定理,比较简单,求出∠C的度数是解题的关键.2.(2012?滨州)一个三角形三个内角的度数之比为2:3:7,这个三角形一定是()A .等腰三角形B.直角三角形C.锐角三角形D.钝角三角形考点:三角形内角和定理.专题:方程思想.分析:已知三角形三个内角的度数之比,根据三角形内角和定理,可求得三角的度数,由此判断三角形的类型.解答:解:三角形的三个角依次为180°×=30°,180°×=45°,180°×=105°,所以这个三角形是钝角三角形.故选:D.点评:本题考查三角形的分类,这个三角形最大角为180°×>90°.本题也可以利用方程思想来解答,即2x+3x+7x=180,解得x=15,所以最大角为7×15°=105°.3.(2012?河源)如图,在折纸活动中,小明制作了一张△ABC纸片,点D、E分别是边AB、AC上,将△ABC沿着DE折叠压平,A与A′重合,若∠A=75°,则∠1+∠2=()A .150°B.210°C.105°D.75°考点:三角形内角和定理;翻折变换(折叠问题).专题:压轴题.分析:先根据图形翻折变化的性质得出△ADE≌△A′DE,∠AED=∠A′ED,∠ADE=∠A′DE,再根据三角形内角和定理求出∠AED+∠ADE及∠A′ED+∠A′DE的度数,然后根据平角的性质即可求出答案.解答:解:∵△A′DE是△ABC翻折变换而成,∴∠AED=∠A′ED,∠ADE=∠A′DE,∠A=∠A′=75°,∴∠AED+∠ADE=∠A′ED+∠A′DE=180°﹣75°=105°,∴∠1+∠2=360°﹣2×105°=150°.故选A.点评:本题考查的是图形翻折变换的性质,即折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.4.(2012?云南)如图,在△ABC中,∠B=67°,∠C=33°,AD是△ABC的角平分线,则∠CAD的度数为()A .40°B.45°C.50°D.55°考点:三角形内角和定理.分析:首先利用三角形内角和定理求得∠BAC的度数,然后利用角平分线的性质求得∠CAD的度数即可.解答:解:∵∠B=67°,∠C=33°,∴∠BAC=180°﹣∠B﹣∠C=180°﹣67°﹣33°=80°∵AD是△ABC的角平分线,∴∠CAD=∠BAC=×80°=40°故选A.点评:本题考查了三角形的内角和定理,属于基础题,比较简单.三角形内角和定理在小学已经接触过.5.(2012?南通)如图,△ABC中,∠C=70°,若沿图中虚线截去∠C,则∠1+∠2=()A .360°B.250°C.180°D.140°考点:三角形内角和定理;多边形内角与外角.分析:先利用三角形内角与外角的关系,得出∠1+∠2=∠C+(∠C+∠3+∠4),再根据三角形内角和定理即可得出结果.解答:解:∵∠1、∠2是△CDE的外角,∴∠1=∠4+∠C,∠2=∠3+∠C,即∠1+∠2=∠C+(∠C+∠3+∠4)=70°+180°=250°.故选B.点评:此题主要考查了三角形内角和定理及外角的性质,三角形内角和是180°;三角形的任一外角等于和它不相邻的两个内角之和.6.(2012?梧州)如图,AE是△ABC的角平分线,AD⊥BC于点D,若∠BAC=128°,∠C=36°,则∠DAE的度数是()A .10°B.12°C.15°D.18°考点:三角形内角和定理;三角形的角平分线、中线和高.分析:根据直角三角形两锐角互余求出∠CAD,再根据角平分线定义求出∠CAE,然后根据∠DAE=∠CAE ﹣∠CAD,代入数据进行计算即可得解.解答:解:∵AD⊥BC,∠C=36°,∴∠CAD=90°﹣36°=54°,∵AE是△ABC的角平分线,∠BAC=128°,∴∠CAE=∠BAC=×128°=64°,∴∠DAE=∠CAE﹣∠CAD=64°﹣54°=10°.故选A.点评:本题考查了三角形的内角和定理,三角形的角平分线,高线的定义,准确识图,找出各角度之间的关系并求出度数是解题的关键.7.(2011?日照)如图,已知直线AB∥CD,∠C=125°,∠A=45°,那么∠E的大小为()A .70°B.80°C.90°D.100°考点:三角形内角和定理;平行线的性质.专题:计算题.分析:根据两直线平行,同旁内角互补,求得∠EFA=55°,再利用三角形内角和定理即可求得∠E的度数.解答:解:∵AB∥CD,∠C=125°,∴∠EFB=125°,∴∠EFA=180﹣125=55°,∵∠A=45°,∴∠E=180°﹣∠A﹣∠EFA=180°﹣45°﹣55°=80°.故选B.点评:本题应用的知识点为:两直线平行,同旁内角互补;三角形内角和定理.8.(2011?台湾)如图中有四条互相不平行的直线L1、L2、L3、L4所截出的七个角.关于这七个角的度数关系,下列何者正确()A .∠2=∠4+∠7B.∠3=∠1+∠6C.∠1+∠4+∠6=180°D.∠2+∠3+∠5=360°考点:三角形内角和定理;对顶角、邻补角;三角形的外角性质.分析:根据对顶角的性质得出∠1=∠AOB,再用三角形内角和定理得出∠AOB+∠4+∠6=180°,即可得出答案.解答:解:∵四条互相不平行的直线L1、L2、L3、L4所截出的七个角,∵∠1=∠AOB,∵∠AOB+∠4+∠6=180°,∴∠1+∠4+∠6=180°.故选C.点评:此题主要考查了对顶角的性质以及三角形的内角和定理,正确的应用三角形内角和定理是解决问题的关键.9.(2011?台湾)若△ABC中,2(∠A+∠C)=3∠B,则∠B的外角度数为何()A .36B.72C.108D.144考点:三角形内角和定理;解二元一次方程组;对顶角、邻补角.专题:计算题.分析:由∠A+∠B+∠C=180°,得到2(∠A+∠C)+2∠B=360°,求出∠B=72°,根据∠B的外角度数=180°﹣∠B即可求出答案.解答:解:∵∠A+∠B+∠C=180°,∴2(∠A+∠B+∠C)=360°,∵2(∠A+∠C)=3∠B,∴∠B=72°,∴∠B的外角度数是180°﹣∠B=108°,故选C.点评:本题主要考查对二元一次方程组,三角形的内角和定理,邻补角等知识点的理解和掌握,能根据三角形的内角和定理求出∠B的度数是解此题的关键.10.(2011?台湾)若钝角三角形ABC中,∠A=27°,则下列何者不可能是∠B的度数()A .37B.57C.77D.97考点:三角形内角和定理.专题:推理填空题.分析:根据钝角三角形有一内角大于90°且三角形内角和为180°,①∠C>90°,②∠B>90°,分类讨论解答.解答:解:∵钝角三角形△ABC中,∠A=27°,∴∠B+∠C=180°﹣27°=153°,又∵△ABC为钝角三角形,有两种可能情形如下:①∠C>90°,∴∠B<153°﹣90°=63°,∴选项A、B合理;②∠B>90°,∴选项D合理,∴∠B不可能为77°.故选C.点评:本题考查了钝角三角形的定义及三角形的内角和定理,体现了分类讨论思想.二.填空题(共4小题)11.(2014?抚顺)将正三角形、正四边形、正五边形按如图所示的位置摆放.如果∠3=32°,那么∠1+∠2=70度.考点:三角形内角和定理;多边形内角与外角.专题:几何图形问题.分析:分别根据正三角形、正四边形、正五边形各内角的度数及平角的定义进行解答即可.解答:解:∵∠3=32°,正三角形的内角是60°,正四边形的内角是90°,正五边形的内角是108°,∴∠4=180°﹣60°﹣32°=88°,∴∠5+∠6=180°﹣88°=92°,∴∠5=180°﹣∠2﹣108° ①,∠6=180°﹣90°﹣∠1=90°﹣∠1 ②,∴①+②得,180°﹣∠2﹣108°+90°﹣∠1=92°,即∠1+∠2=70°.故答案为:70°.点评:本题考查的是三角形内角和定理,熟知正三角形、正四边形、正五边形各内角的度数是解答此题的关键.12.(2013?河池)如图,点O是△ABC的两条角平分线的交点,若∠BOC=118°,则∠A的大小是56°.考点:三角形内角和定理.分析:先根据三角形内角和定理求出∠1+∠2的度数,再根据角平分线的定义求出∠ABC+∠ACB的度数,由三角形内角和定理即可得出结论.解答:解:∵△BOC中,∠BOC=118°,∴∠1+∠2=180°﹣118°=62°.∵BO和CO是△ABC的角平分线,∴∠ABC+∠ACB=2(∠1+∠2)=2×62°=124°,在△ABC中,∵∠ABC+∠ACB=124°,∴∠A=180°﹣(∠ABC+∠ACB)=180°﹣124°=56°.故答案为:56°.点评:本题考查的是角平分线的定义,三角形内角和定理,即三角形的内角和是180°.13.(2008?安徽)如图,已知a∥b,∠1=70°,∠2=40°,则∠3=70度.考点:三角形内角和定理;平行线的性质.专题:计算题.分析:把∠2,∠3转化为△ABC中的角后,利用三角形内角和定理求解.解答:解:由对顶角相等可得∠ACB=∠2=40°,在△ABC中,由三角形内角和知∠ABC=180°﹣∠1﹣∠ACB=70°.又a∥b,∴∠3=∠ABC=70°.点评:本题考查了平行线与三角形的相关知识.14.(2003?金华)如图,平面镜A与B之间夹角为120°,光线经过平面镜A反射后射在平面镜B上,再反射出去,若∠1=∠2,则∠1=30度.考点:三角形内角和定理;角平分线的定义.专题:压轴题.分析:因为入射角等于反射角,所以∠1=∠2=(180°﹣120°)÷2.解答:解:如图所示,作出入射光线的法线,根据“入射角等于反射角”可知∠1=∠3,∠2=∠4,∵∠1=∠2,∠AOB=120°,∴1=∠2=(180°﹣120°)÷2=30°.故答案为:30°.点评:此题由题意得出“入射角等于反射角”是关键.三.解答题(共16小题)15.(2014?六盘水)(1)三角形内角和等于180°.(2)请证明以上命题.考点:三角形内角和定理;平行线的性质.专题:证明题.分析:(1)直接根据三角形内角和定理得出结论即可;(2)画出△ABC,过点C作CF∥AB,再根据平行线的性质得出∠2=∠A,∠B+∠BCF=180°,再通过等量代换即可得出结论.解答:解:(1)三角形内角和等于180°.故答案为:180°;(2)已知:如图所示的△ABC,求证:∠A+∠B+∠C=180°.证明:过点C作CF∥AB,∵CF∥AB,∴∠2=∠A,∠B+∠BCF=180°,∵∠1+∠2=∠BCF,∴∠B+∠1+∠2=180°,∴∠B+∠1+∠A=180°,即三角形内角和等于180°.点评:本题考查的是三角形内角和定理,熟知三角形的内角和等于180°是解答此题的关键.16.(2001?海南)如图,在△ABC中,已知∠ABC=46°,∠ACB=80°,延长BC至D,使CD=CA,连接AD,求∠BAD的度数.考点:三角形内角和定理;三角形的外角性质;等腰三角形的性质.分析:要求∠BAD的度数,只要求出∠C的度数就行了,根据三角形内角和为180°,求出∠BAD的度数,根据三角形内角和外角关系及等腰三角形性质,易求∠C的度数.解答:解:∵∠ACB=80°∴∠ACD=180°﹣∠ACB=180°﹣80°=100°又∵CD=CA∴∠CAD=∠D∵∠ACD+∠CAD+∠D=180°∴∠CAD=∠D=40°在△ABC内∴∠BAD=180°﹣∠ABC﹣∠D=180°﹣46°﹣40°=94°.点评:此题主要考三角形内角与外角的关系及等腰三角形的性质;找出角之间的关系利用内角和求解是正确解答本题的关键.17.(2000?内蒙古)如图,已知在△ABC中,∠C=∠ABC=2∠A,BD是AC边上的高,求∠DBC的度数.考点:三角形内角和定理.专题:数形结合.分析:根据三角形的内角和定理与∠C=∠ABC=2∠A,即可求得△ABC三个内角的度数,再根据直角三角形的两个锐角互余求得∠DBC的度数.解答:解:∵∠C=∠ABC=2∠A,∴∠C+∠ABC+∠A=5∠A=180°,∴∠A=36°.则∠C=∠ABC=2∠A=72°.又BD是AC边上的高,则∠DBC=90°﹣∠C=18°.点评:此题主要是三角形内角和定理的运用.三角形的内角和是180°.18.(2011?青海)认真阅读下面关于三角形内外角平分线所夹角的探究片段,完成所提出的问题.探究1:如图1,在△ABC中,O是∠ABC与∠ACB的平分线BO和CO的交点,通过分析发现∠BOC=90°+,理由如下:∵BO和CO分别是∠ABC和∠ACB的角平分线∴∴又∵∠ABC+∠ACB=180°﹣∠A∴∴∠BOC=180°﹣(∠1+∠2)=180°﹣(90°﹣∠A)=探究2:如图2中,O是∠ABC与外角∠ACD的平分线BO和CO的交点,试分析∠BOC与∠A有怎样的关系请说明理由.探究3:如图3中,O是外角∠DBC与外角∠ECB的平分线BO和CO的交点,则∠BOC与∠A有怎样的关系(只写结论,不需证明)结论:∠BOC=90°﹣∠A.考点:三角形的外角性质;三角形内角和定理.专题:压轴题.分析:(1)根据提供的信息,根据三角形的一个外角等于与它不相邻的两个内角的和,用∠A与∠1表示出∠2,再利用∠O与∠1表示出∠2,然后整理即可得到∠BOC与∠A的关系;(2)根据三角形的一个外角等于与它不相邻的两个内角的和以及角平分线的定义表示出∠OBC与∠OCB,然后再根据三角形的内角和定理列式整理即可得解.解答:解:(1)探究2结论:∠BOC=∠A,理由如下:∵BO和CO分别是∠ABC和∠ACD的角平分线,∴∠1=∠ABC,∠2=∠ACD,又∵∠ACD是△ABC的一外角,∴∠ACD=∠A+∠ABC,∴∠2=(∠A+∠ABC)=∠A+∠1,∵∠2是△BOC的一外角,∴∠BOC=∠2﹣∠1=∠A+∠1﹣∠1=∠A;(2)探究3:∠OBC=(∠A+∠ACB),∠OCB=(∠A+∠ABC),∠BOC=180°﹣∠0BC﹣∠OCB,=180°﹣(∠A+∠ACB)﹣(∠A+∠ABC),=180°﹣∠A﹣(∠A+∠ABC+∠ACB),结论∠BOC=90°﹣∠A.点评:本题考查了三角形的外角性质与内角和定理,熟记三角形的一个外角等于与它不相邻的两个内角的和是解题的关键,读懂题目提供的信息,然后利用提供信息的思路也很重要.19.(2010?玉溪)平面内的两条直线有相交和平行两种位置关系(1)如图a,若AB∥CD,点P在AB、CD外部,则有∠B=∠BOD,又因∠BOD是△POD的外角,故∠BOD=∠BPD+∠D,得∠BPD=∠B﹣∠D.将点P移到AB、CD内部,如图b,以上结论是否成立若成立,说明理由;若不成立,则∠BPD、∠B、∠D之间有何数量关系请证明你的结论;(2)在图b中,将直线AB绕点B逆时针方向旋转一定角度交直线CD于点Q,如图c,则∠BPD﹑∠B﹑∠D﹑∠BQD之间有何数量关系(不需证明)(3)根据(2)的结论求图d中∠A+∠B+∠C+∠D+∠E+∠F的度数.考点:三角形的外角性质;平行线的性质;三角形内角和定理.专题:综合题;压轴题.分析:(1)延长BP交CD于E,根据两直线平行,内错角相等,求出∠PED=∠B,再利用三角形的一个外角等于和它不相邻的两个内角的和即可说明不成立,应为∠BPD=∠B+∠D;(2)作射线QP,根据三角形的外角性质可得;(3)根据三角形的外角性质,把角转化到四边形中再求解.解答:解:(1)不成立.结论是∠BPD=∠B+∠D延长BP交CD于点E,∵AB∥CD∴∠B=∠BED又∵∠BPD=∠BED+∠D,∴∠BPD=∠B+∠D.(2)结论:∠BPD=∠BQD+∠B+∠D.(3)连接EG并延长,根据三角形的外角性质,∠AGB=∠A+∠B+∠E,又∵∠AGB=∠CGF,在四边形CDFG中,∠CGF+∠C+∠D+∠F=360°,∴∠A+∠B+∠C+∠D+∠E+∠F=360°.点评:本题是信息给予题,利用平行线的性质和三角形的一个外角等于和它不相邻的两个内角的和解答.20.(2013?响水县一模)探究与发现:探究一:我们知道,三角形的一个外角等于与它不相邻的两个内角的和.那么,三角形的一个内角与它不相邻的两个外角的和之间存在何种数量关系呢已知:如图1,∠FDC与∠ECD分别为△ADC的两个外角,试探究∠A与∠FDC+∠ECD的数量关系.探究二:三角形的一个内角与另两个内角的平分线所夹的钝角之间有何种关系已知:如图2,在△ADC中,DP、CP分别平分∠ADC和∠ACD,试探究∠P与∠A的数量关系.探究三:若将△ADC改为任意四边形ABCD呢已知:如图3,在四边形ABCD中,DP、CP分别平分∠ADC和∠BCD,试利用上述结论探究∠P与∠A+∠B的数量关系.探究四:若将上题中的四边形ABCD改为六边形ABCDEF(图4)呢请直接写出∠P与∠A+∠B+∠E+∠F的数量关系:∠P=(∠A+∠B+∠E+∠F)﹣180°.考点:三角形的外角性质;三角形内角和定理.专题:探究型.分析:探究一:根据三角形的一个外角等于与它不相邻的两个内角的和可得∠FDC=∠A+∠ACD,∠ECD=∠A+∠ADC,再根据三角形内角和定理整理即可得解;探究二:根据角平分线的定义可得∠PDC=∠ADC,∠PCD=∠ACD,然后根据三角形内角和定理列式整理即可得解;探究三:根据四边形的内角和定理表示出∠ADC+∠BCD,然后同理探究二解答即可;探究四:根据六边形的内角和公式表示出∠ADC+∠BCD,然后同理探究二解答即可.解答:解:探究一:∵∠FDC=∠A+∠ACD,∠ECD=∠A+∠ADC,∴∠FDC+∠ECD=∠A+∠ACD+∠A+∠ADC=180°+∠A;探究二:∵DP、CP分别平分∠ADC和∠ACD,∴∠PDC=∠ADC,∠PCD=∠ACD,∴∠DPC=180°﹣∠PDC﹣∠PCD,=180°﹣∠ADC﹣∠ACD,=180°﹣(∠ADC+∠ACD),=180°﹣(180°﹣∠A),=90°+∠A;探究三:∵DP、CP分别平分∠ADC和∠BCD,∴∠PDC=∠ADC,∠PCD=∠BCD,∴∠DPC=180°﹣∠PDC﹣∠PCD,=180°﹣∠ADC﹣∠BCD,=180°﹣(∠ADC+∠BCD),=180°﹣(360°﹣∠A﹣∠B),=(∠A+∠B);探究四:六边形ABCDEF的内角和为:(6﹣2)180°=720°,∵DP、CP分别平分∠ADC和∠ACD,∴∠P=∠ADC,∠PCD=∠ACD,∴∠P=180°﹣∠PDC﹣∠PCD,=180°﹣∠ADC﹣∠ACD,=180°﹣(∠ADC+∠ACD),=180°﹣(720°﹣∠A﹣∠B﹣∠E﹣∠F),=(∠A+∠B+∠E+∠F)﹣180°,即∠P=(∠A+∠B+∠E+∠F)﹣180°.点评:本题考查了三角形的外角性质,三角形的内角和定理,多边形的内角和公式,此类题目根据同一个解答思路求解是解题的关键.21.已知:如图,在△ABC中,D为BC上一点,∠1=∠2,∠3=∠4,∠BAC=120°,求∠DAC的度数.考点:三角形的外角性质;三角形内角和定理.分析:根据三角形的内角和定理和三角形的外角性质即可解决.解答:解:∵∠BAC=120°,∴∠2+∠3=60°①∵∠1=∠2,∴∠4=∠3=∠1+∠2=2∠2②把②代入①得:3∠2=60°,∠2=20°.∴∠DAC=120°﹣20°=100°.点评:注意三角形的内角和定理以及推论的运用,还要注意角之间的等量代换.22.如图,求∠A+∠B+∠C+∠D+∠E的度数和.考点:三角形的外角性质;三角形内角和定理.分析:由三角形的一个外角等于与它不相邻的两个内角的和,得∠4=∠A+∠2,∠2=∠D+∠C,进而利用三角形的内角和定理求解.解答:解:如图可知:∵∠4是三角形的外角,∴∠4=∠A+∠2,同理∠2也是三角形的外角,∴∠2=∠D+∠C,在△BEG中,∠B+∠E+∠4=180°,即∠B+∠E+∠A+∠D+∠C=180°.点评:本题考查三角形外角的性质及三角形的内角和定理,解答的关键是沟通外角和内角的关系.23.如图,在△ABC中,D为BC上一点,∠1=∠2,∠3=∠4,∠BAC=63°,试求∠DAC,∠ADC的度数.考点:三角形的外角性质;三角形内角和定理.分析:由三角形的内角和是180°,和三角形的一个外角等于与它不相邻的两个内角的和,可求∠1=39°,∠3=78°,所以∠DAC=24°,∠ADC=∠3=78°.解答:解:∵∠1=∠2,∴∠3=∠1+∠2=2∠1=∠4,∴2∠3+∠CAD=2∠1+2∠2+∠BAC﹣∠1=4∠1+63°﹣∠1=3∠1+63°=180°,∴∠1=39°=∠2,∠3=∠4=78°,∴∠DAC=63°﹣∠1=63°﹣39°=24°,∠ADC=∠3=78°.点评:本题考查三角形外角的性质及三角形的内角和定理.求角的度数常常要用到“三角形的内角和是180°”这一隐含的条件;以及三角形的一个外角等于与它不相邻的两个内角的和.24.已知:如图所示,∠ABC=66°,∠ACB=54°,BE是AC边上的高,CF是AB边上的高,H是BE和CF的交点,求:∠ABE,∠ACF和∠BHC的度数.考点:三角形的外角性质;三角形内角和定理.分析:由三角形的内角和是180°,可求∠A=60°.又因为BE是AC边上的高,所以∠AEB=90°,所以∠ABE=30°.同理,∠ACF=30度,又因为∠BHC是△CEH的一个外角,所以∠BHC=120°.解答:解:∵∠ABC=66°,∠ACB=54°,∴∠A=180°﹣∠ABC﹣∠ACB=180°﹣66°﹣54°=60°.又∵BE是AC边上的高,所以∠AEB=90°,∴∠ABE=180°﹣∠BAC﹣∠AEB=180°﹣90°﹣60°=30°.同理,∠ACF=30°,∴∠BHC=∠BEC+∠ACF=90°+30°=120°.点评:本题考查三角形外角的性质及三角形的内角和定理,求角的度数常常要用到“三角形的内角和是180°”这一隐含的条件;三角形的外角通常情况下是转化为内角来解决.25.如图,△ABC中,AD是高,AE、BF是角平分线,它们相交于点O,∠A=50°,∠C=60°,求∠DAC及∠BOA.考点:三角形的外角性质;三角形内角和定理.专题:计算题.分析:先利用三角形内角和定理可求∠ABC,在直角三角形ACD中,易求∠DAC;再根据角平分线定义可求∠CBF、∠EAF,然后利用三角形外角性质,可先求∠AFB,再次利用三角形外角性质,容易求出∠BOA.解答:解:∵∠A=50°,∠C=60°∴∠ABC=180°﹣50°﹣60°=70°,又∵AD是高,∴∠ADC=90°,∴∠DAC=180°﹣90°﹣∠C=30°,∵AE、BF是角平分线,∴∠CBF=∠ABF=35°,∠EAF=25°∴∠AFB=∠C+∠CBF=60°+35°=95°,∴∠BOA=∠EAF+∠AFB=25°+95°=120°,∴∠DAC=30°,∠BOA=120°.点评:本题考查了三角形内角和定理、角平分线定义、三角形外角性质.关键是利用角平分线的性质解出∠EAF、∠CBF,再运用三角形外角性质求出∠AFB.26.如图,AF是△ABC的高,AD是△ABC的角平分线,∠B=36°,∠C=76°,求∠DAF的度数.考点:三角形的外角性质;角平分线的定义;三角形内角和定理.分析:在△ADF中,由三角形的外角性质知:∠ADF=∠B+∠BAC,所以∠B+∠BAC+∠FAD=90°,联立△ABC中,由三角形内角和定理得到的式子,即可推出∠DAF,∠B,∠C的关系,再代值求解即可.解答:解:由三角形的外角性质知:∠ADF=∠B+∠BAC,故∠B+∠BAC+∠DAF=90°;①△ABC中,由三角形内角和定理得:∠C+∠B+∠BAC=180°,即:∠C+∠B+∠BAC=90°,②②﹣①,得:∠DAF=(∠C﹣∠B)=20°.点评:此题主要考查了三角形的外角性质、角平分线的性质以及三角形内角和定理等知识,熟记此题的结论在解选择和填空题时会加快解题效率.27.一个零件的形状如图,按规定∠A=90°,∠C=25°,∠B=25°,检验已量得∠BDC=150°,就判断这个零件不合格,运用三角形的有关知识说明零件不合格的理由.考点:三角形的外角性质.分析:根据三角形外角的性质求出∠BDC的度数,与测量所得的度数对比即可得出结论.解答:解:如图,∠CDE是△ADC的外角,∠BDE是△ABD的外角,∵∠CDE=∠C+∠CAD,∠BDE=∠B+∠DAB,∴∠BDC=∠CDE+∠BDE=∠C+∠CAD+∠B+∠DAB,即∠BDC=∠B+∠C+∠A=25°+25°+90°=140°.检验已量得∠BDC=150°,就判断这个零件不合格.点评:考查了三角形的外角性质,三角形的外角等于和它不相邻的两个内角的和.28.一个零件的形状如图所示,按规定∠A应等于90°,∠B、∠C应分别是30°和20°,李叔叔量得∠BDC=142°,就判定这个零件不合格,你能说出其中的道理吗考点:三角形的外角性质.分析:连接AD并延长,根据三角形的一个外角等于和它不相邻的两个内角的和求出∠1=∠B+∠BAD,∠2=∠C+∠CAD,然后求出∠1+∠2的度数,根据零件规定数据,只有140°才是合格产品.解答:解:如图,连接AD并延长,∴∠1=∠B+∠BAD,∠2=∠C+∠CAD,∵∠A=90°,∠B=30°,∠C=20°,∴∠BDC=∠1+∠2,=∠B+∠BAD+∠DAC+∠C,=∠B+∠BAC+∠C,=30°+90°+20°,=140°,∵140°≠142°,∴这个零件不合格.点评:本题主要利用三角形的一个外角等于和它不相邻的两个内角的和的性质,熟练掌握性质是解题的关键.29.如图所示,求∠A+∠B+∠C+∠D+∠E+∠F的度数.考点:三角形的外角性质;三角形内角和定理.分析:连接BE,由三角形内角和外角的关系可知∠C+∠D=∠CBE+∠DEB,由四边形内角和是360°,即可求∠A+∠ABC+∠C+∠D+∠DEF+∠F=360°.解答:解:如图连接BE.∵∠1=∠C+∠D,∠1=∠CBE+∠DEB,∴∠C+∠D=∠CBE+∠DEB,∴∠A+∠ABC+∠C+∠D+∠DEF+∠F=∠A+∠ABC+∠CBE+∠DEB+∠DEF+∠F=∠A+∠ABE+∠BEF+∠F.又∵∠A+∠ABE+∠BEF+∠F=360°,∴∠A+∠ABC+∠C+∠D+∠DEF+∠F=360°.点评:本题考查的是三角形内角与外角的关系,涉及到四边形及三角形内角和定理,比较简单.30.如图,在三角形ABC中,∠A=35°,求∠1+∠2+∠3+∠4的度数和.考点:三角形的外角性质;三角形内角和定理.分析:根据三角形的内角和是180°,可分别求出∠1+∠2=∠3+∠4=145°,即可求出∠1+∠2+∠3+∠4的度数和.解答:解:∵∠A=35°,在△ABC中,∠A+∠1+∠2=180°,∴∠1+∠2=180°﹣∠A=145°,同理可证∠3+∠4=145°,∴∠1+∠2+∠3+∠4=290°.点评:本题考查了三角形的内角和定理,求角的度数常常要用到“三角形的内角和是180°”这一隐含的条件.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
7.2.2 三角形的外角
基础过关作业
1.若三角形的外角中有一个是锐角,则这个三角形是________三角形.
2.△ABC中,若∠C—∠B=∠A,则△ABC的外角中最小的角是______(填“锐角”、“直角”或“钝角”).3.如图1,x=______.
(1)(2) (3)
4.如图2,△ABC中,点D在BC的延长线上,点F是AB边上一点,延长CA到E,连EF,则∠1,∠2,∠3的大小关系是_________.
5.如图3,在△ABC中,AE是角平分线,且∠B=52°,∠C=78°,求∠AEB的度数.
6.如图,在△ABC中,∠A=60°,BD、CE分别是AC、AB上的高,H是BD、•CE的交点,求∠BHC的度数.
综合创新作业
7.如图所示,在△ABC中,AB=AC,AD=AE,∠BAD=60°,则∠EDC=______.
8.一个零件的形状如图7-2-2—6所示,按规定∠A应等于90°,∠B、∠D应分别是30°和20°,李叔叔量得∠BCD=142°,就断定这个零件不合格,你能说出道理吗?
9.(1)如图7-2—2—7(1),求出∠A+∠B+∠C+∠D+∠E+∠F的度数;
(2)如图7—2—2-7(2),求出∠A+∠B+∠C+∠D+∠E+∠F的度数.
10.(易错题)三角形的三个外角中最多有_______个锐角.
培优作业
11.(探究题)(1)如图,BD、CD分别是△ABC的两个外角∠CBE、∠BCF•的平分线,试探索∠BDC与∠A之间的数量关系.
(2)如图,BD为△ABC的角平分线,CD为△ABC的外角∠ACE的平分线,它们相交于点D,试探索∠BDC与∠A之间的数量关系.
12.(趣味题)如图,在绿茵场上,足球队员带球进攻,总是向球门AB冲近,说明这是为什么?
数学世界
七桥问题
18世纪在哥尼斯堡城的普莱格尔河上有七座桥,将河中的两个岛和河岸连接.如图所示.城中的居民经常沿河过桥散步,于是就提出一个问题:•能否一次不重复地把这七座桥走遍?可是,走来走去,这个愿望还是无法实现.该怎样走才好呢?•这就是著名的哥尼斯堡七桥问题.••好奇的人把这个问题拿给当时的大数学家欧拉(1707~1783).欧拉以深邃的洞察力很快证明了这样的走法不存在.
你知道欧拉是根据什么道理证明的吗?
答案:
1.钝角
2.直角点拨:∵∠C-∠B=∠A,∴∠C=∠A+∠B.
又∵(∠A+∠B)+∠C=180°,∴∠C+∠C=180°,∴∠C=90°,
∴△ABC的外角中最小的角是直角.
3.60 点拨:由题意知x+80=x+(x+20).解得x=60.
4.∠1〉∠2>∠3
点拨:∵∠1是∠2的外角,∠2是∠3的外角,∴∠1〉∠2〉∠3.
5.解:∠BAC=180°—(∠B+∠C)=180°-(52°+78°)=50°.
∵AE是∠BAC的平分线,
∴∠BAE=∠CAE=1
2
∠BAC=25°.
∴∠AEB=∠CAE+∠C=25°+78°=103°.
6.解:在△ACE中,∠ACE=90°-∠A=90°-60°=30°.而∠BHC是△HDC的外角,
所以∠BHC=∠HDC+∠ACE=90°+30°=120°.
7.30°点拨:设∠CAD=2a,由AB=AC知∠B=1
2
(180°-60°—2a)=60°—•a,•
∠ADB=180°—∠B-60°=60°+a,由AD=AE知,∠ADE=90°—a,所以∠EDC=180°-∠ADE—∠ADB=30°.
8.解法1:如答图1,延长BC交AD于点E,
则∠DEB=∠A+∠B=90°+30°=•120°,
从而∠DCB=∠DEB+∠D=120°+20°=140°.
若零件合格,∠DCB应等于140°.
李叔叔量得∠BCD=142°,
因此可以断定该零件不合格.
(1) (2) (3)
点拨:也可以延长DC与AB交于一点,方法与此相同.
解法2:如答图2,连接AC并延长至E,则∠3=∠1+∠D,∠4=∠2+∠B,
因此∠DCB=∠1+∠D+∠2+∠B=140°.以下同方法1.
解法3:如答图3,过点C作EF∥AB,交AD于E,
则∠DEC=90°,∠FCB=∠B=•30°,所以∠DCF=∠D+∠DEC=110°,
从而∠DCB=∠DCF+∠FCB=140°.以下同方法1.
说明:也可以过点C作AD的平行线.
点拨:上述三种解法应用了三角形外角的性质:三角形的一个外角等于它不相邻的两个内角的和.9.解:(1)由图知∠A+∠F=∠OQA,∠B+∠C=∠QPC,∠D+∠E=∠EOP.
而∠OQA、•∠QPC、∠EOP是△OPQ的三个外角.
∴∠OQA+∠QPC+∠EOP=360°.
∴∠A+∠B+∠C+∠D+∠E+∠F=∠OQA+∠QPC+∠EOP=360°.
(2)360°点拨:方法同(1).
10.1 点拨:本题易因混淆内角、外角的概念,而误填为3.
11.解:(1)∠BDC=90°-1
2
∠A.
理由:∠ABC+∠ACB=180°—∠A.
∠EBC+∠FCB=(180°—∠ABC)+(180°-∠ACB)=360°-(∠ABC+∠ACB)=180°+∠A.∵BD、CD分别为∠EBC、∠FCB的平分线,
∴∠CBD=1
2
∠EBC,∠BCD=
1
2
∠FCB.
∴∠CBD+∠BCD=1
2
(∠EBC+∠FCB)=
1
2
×(180°+∠A)
=90°+1
2
∠A.
在△BDC中,∠BDC=180°—(∠CBD+∠BCD)=180°—(90°+1
2
∠A)=90°-
1
2
∠A.
(2)∠BDC=1
2
∠A.
理由:∵∠ACE是△ABC的外角,
∴∠ACE=∠A+∠ABC,
∵CD是∠ACE的平分线,BD是∠ABC的平分线,
∴∠DCE=1
2
∠ACE=
1
2
∠A+
1
2
∠ABC,∠DBC=
1
2
∠ABC.
∵∠DCE是△BCD的外角,
∴∠BDC=∠DCE-∠DBC=1
2
∠A+
1
2
∠ABC—
1
2
∠ABC=
1
2
∠A.
12.解:如图,设球员接球时位于点C,他尽力向球门冲近到D,
此时不仅距离球门近,射门更有力,而且对球门AB的张角也扩大,球就更容易射中.
理由说明如下:
延长CD到E,则∠ADE>∠ACE,∠BDE〉∠BCE,
∴∠ADE+∠BDE>∠ACE+∠BCE,即∠ADB〉∠ACB.
点拨:解此题关键是将生活中的问题抽象为数学问题.
数学世界答案:
欧拉将七桥布局转化为图所示的简单图形,于是七桥问题就变成一个一笔画的问题.这个图形显然无法一笔画出,也就是说,•要想一次无重复地走遍这七座桥是办不到的.。
