《旋转与角》课时练
2022秋四年级数学上册 第二单元 线与角第4课时 旋转与角习题课件 北师大版

第4课时 旋转与角
1、纪律是集体的面貌,集体的声音,集体的动作,集体的表情,集体的信念。 2、知之者不如好之者,好之者不如乐之者。 3、反思自我时展示了勇气,自我反思是一切思想的源泉。 4、在教师手里操着幼年人的命运,便操着民族和人类的命运。一年之计,莫如树谷;十年之计,莫如树木;终身之计,莫如树人。 5、诚实比一切智谋更好,而且它是智谋的基本条件。 6、做老师的只要有一次向学生撒谎撒漏了底,就可能使他的全部教育成果从此为之失败。2022年1月2022/1/312022/1/312022/1/311/31/2022 7、凡为教者必期于达到不须教。对人以诚信,人不欺我;对事以诚信,事无不成。2022/1/312022/1/31January 31, 2022 8、教育者,非为已往,非为现在,而专为将来。2022/1/312022/1/312022
《旋转与角》(教案)四年级上册数学北师大版

《旋转与角》(教案)四年级上册数学北师大版一、导入情境引入:同学们,你们在生活中有没有遇到过旋转的现象呢?比如,转动的风车、旋转的陀螺等。
二、新课导入1. 角的认识(1)出示直角、锐角、钝角,让学生观察并说出它们的特点。
(2)学生举例说明生活中哪些物体可以组成角。
2. 角的度量(1)认识量角器,学生动手操作,量一量直角、锐角、钝角。
(2)比较量角器度数的大小,让学生体会量角器在生活中的作用。
三、随堂练习1. 完成课本第3页“做一做”第1题。
2. 比一比,哪个角大,哪个角小。
四、例题讲解1. 例题:一个角是直角,另一个角是钝角,它们组成的图形是什么?解答:直角是90度,钝角是大于90度小于180度的角,所以它们组成的图形是钝角三角形。
2. 例题:一个三角形,一个角是直角,另一个角是锐角,这个三角形是什么三角形?解答:直角三角形有一个角是直角,锐角三角形有一个角是锐角,所以这个三角形是直角三角形。
五、课堂小结今天我们学习了角的认识和角的度量,知道了直角、锐角、钝角的特点,以及如何使用量角器测量角的大小。
六、课后反思本节课,通过生活实例引入,让学生感受到数学与生活的联系。
在教学过程中,注重学生的动手操作和合作探究,使学生在实践中掌握知识,提高解决问题的能力。
七、拓展延伸1. 让学生收集生活中旋转的例子,并画出相应的图形。
2. 让学生尝试用不同的方法测量一个角的大小。
八、作业设计1. 完成课本第3页“做一做”第2题。
2. 比一比,哪个角是直角,哪个角是钝角。
九、课后反思及拓展延伸课后反思:通过本节课的学习,学生对角的认识有了进一步的提高,能够运用所学知识解决一些实际问题。
在拓展延伸环节,学生积极参与,充分发挥了他们的想象力和创造力。
拓展延伸:让学生在课后收集更多关于旋转的例子,并尝试用不同的方法测量角的大小,进一步提高他们的实践能力。
同时,鼓励学生将所学知识运用到生活中,提高他们的数学素养。
重点和难点解析:在《旋转与角》的教学中,有几个细节是需要我重点关注的。
人教版小学五年级数学下册旋转第一课时练习
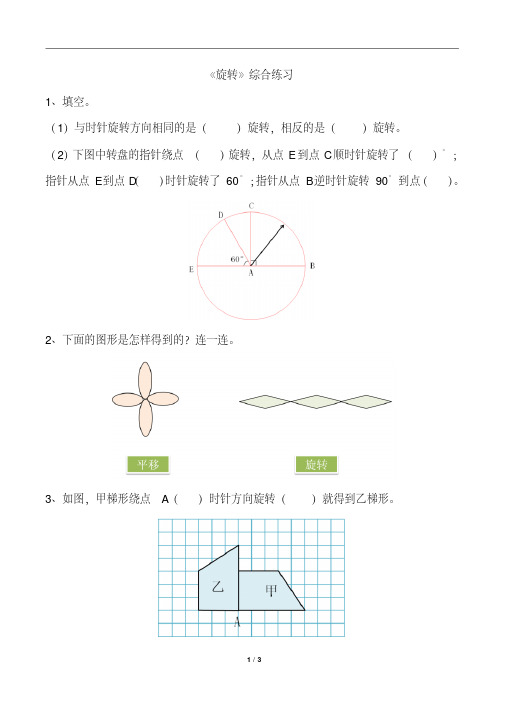
《旋转》综合练习
1、填空。
(1)与时针旋转方向相同的是()旋转,相反的是()旋转。
(2)下图中转盘的指针绕点()旋转,从点E到点C顺时针旋转了()°;指针从点E到点D()时针旋转了60°;指针从点B逆时针旋转90°到点()。
2、下面的图形是怎样得到的?连一连。
3、如图,甲梯形绕点A()时针方向旋转()就得到乙梯形。
4、将平行四边形绕点A顺时针旋转90°,将三角形绕点B逆时针旋转90°。
5、按要求画一画。
(1)将直角三角形绕点A逆时针旋转90°。
(2)将等腰三角形绕点O顺时针旋转90°。
(3)长方形是由原来的长方形绕着点B逆时针旋转90°得到的,画出原来的长方形。
6、通过旋转把方格中的两个三角形变成一个长方形,并用文字叙述旋转过程。
《旋转与角》综合习题

《旋转与角》综合习题引领思路
1、填一填。
夯实基础
2、下面的角各是什么角?请在括号里写出它们的名字。
3、填一填。
4、下面钟面上时针和分针各组成什么角?分别是多少度?说说你是怎样得到这些度数的。
(提示:分针每走一大格是30°)
提升能力
5、画出下面钟表中的分针,使时针与分针形成相应的角,并在括号里写出时间。
参考答案
引领思路
1、填一填。
夯实基础
2、下面的角各是什么角?请在括号里写出它们的名字。
3、填一填。
4、下面钟面上时针和分针各组成什么角?分别是多少度?说说你是怎样得到这些度数的。
(提示:分针每走一大格是30°)
提升能力
5、画出下面钟表中的分针,使时针与分针形成相应的角,并在括号里写出时间。
略。
新北师大版四年级数学上册《旋转与角》优质教学课件

(教材P23T5)
5.分别剪出一个三角形和平行四边形纸片。把三角形的各个 角撕下来拼在一起,与同伴说一说,你发现了什么?把平行 四边形的各个角撕下来拼在一起呢?
拼成一个平角
拼成一个周角
补充练习
1. 填一填。 (1)3时整,分针和时针所形成的较小角是( 直 )角。 (2)6时整,分针和时针所形成的角是( 平 )角。 (3)12时整,分针和时针所形成的角是( 周 )角。 (4)从3时到4时,分针旋转所形成的角是( 周 )角。
2. 我是小法官。(对的画“√”,错的画“✕”) (1)平角就是一条直线,周角就是一条射线。( ✕ ) (2)周角只有一条边。 ( ✕ )
课堂小结
你学会了 哪些知识?
1.角的大小与两边开口的大小有关,角的开口越大, 角越大。
2.锐角:大于0°,小于90°的角。 直角:等于90°的角。 钝角:大于90°,小于180°的角。 平角:等于180°的角。 周角:等于360°的角。
3.锐角<直角<钝角<平角<周角。
课堂总结
学完这课,你收获了什么?有什 么样的感悟?与同学相互交流讨 论。
1. 从课后习题中选取; 2. 完成练习册本课时的习题.
教师寄语
我们在生活中要站得挺拔,坐得端正,读 得响亮,说得大方。要做一个有精神的小 学生!
结束语
大千世界,充满着无数的奥秘, 希望同学们能遇事独立,积极探索 钻研,解决更多的难题。
2.观察每个钟面,并写出时针和分针所形成的角 的名称。
锐角
直角
钝角 平角
(教材P23T3)
3.在点子图上分别画出一个锐角、直角、钝角和平角。
(画法不唯一)
(教材P23T4)
4.折一折。和同桌比一比、说一说,你们 折得一样大吗?
2021年北师大版数学四年级上册2.4旋转与角练习卷(2)
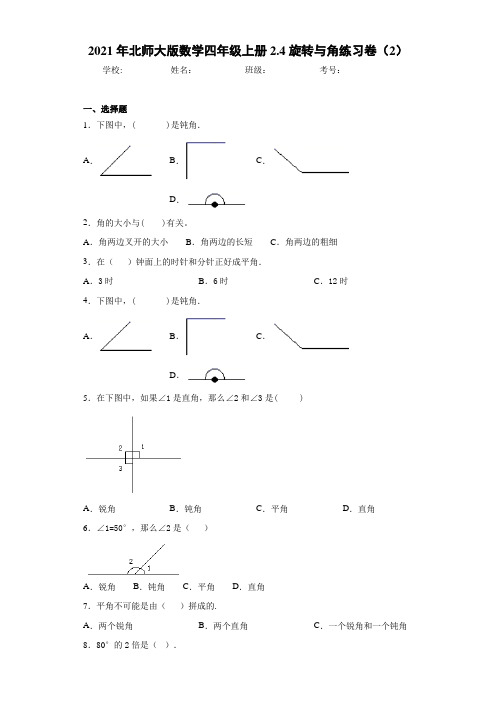
2021年北师大版数学四年级上册2.4旋转与角练习卷(2)学校:___________姓名:___________班级:___________考号:___________一、选择题1.下图中,( )是钝角.A.B.C.D.2.角的大小与( )有关。
A.角两边叉开的大小B.角两边的长短C.角两边的粗细3.在()钟面上的时针和分针正好成平角.A.3时B.6时C.12时4.下图中,( )是钝角.A.B.C.D.5.在下图中,如果∠1是直角,那么∠2和∠3是( )A.锐角B.钝角C.平角D.直角6.∠1=50°,那么∠2是()A.锐角B.钝角C.平角D.直角7.平角不可能是由()拼成的.A.两个锐角B.两个直角C.一个锐角和一个钝角8.80°的2倍是().A.锐角B.平角C.钝角9.黑板上的直角比三角尺上的直角()A.大B.小C.相等10.下图中一共有()个角。
A.1B.2C.3二、填空题11.一个角有________个顶点,________条边,比直角小的角是________,比直角大的角是________.12.钟面上6时整,时针和分针形成(______)角.13.求图中∠1、∠2的度数.(1)∠1=________°(2)∠2=________°14.直角三角形的一个锐角是35°,另一个锐角是________度.15.平角等于________度,周角等于________度.16.一个周角是一个平角的________倍,是一个直角的________倍.17.如图,已知∠AOB=155°,∠AOC=∠BOD=90°,则∠COD=________°.18.平角等于________度,周角等于________度.19.如下图∠1=13°,∠2=15°,那么∠3=________度.20.周角是________度,平角是________度,直角是________度.三、解答题21.标出下面图形中的角,说一说哪些是钝角,哪些是直角,哪些是锐角。
人教版数学九年级上学期课时练习-《旋转》全章复习与巩固(知识讲解)(人教版)
专题23.7《旋转》全章复习与巩固(知识讲解)【学习目标】1、通过具体实例认识旋转,探索它的基本性质,理解对应点到旋转中心的距离相等、对应点与旋转中心连线所成的角彼此相等的性质;2、通过具体实例认识中心对称,探索它的基本性质,理解对应点所连线段被对称中心平分的性质,了解平行四边形、圆是中心对称图形;3、能够按要求作出简单平面图形旋转后的图形,欣赏旋转在现实生活中的应用;4、探索图形之间的变化关系(轴对称、平移、旋转及其组合),灵活运用轴对称、平移和旋转的组合进行图案设计.【要点梳理】要点一、旋转1.旋转的概念:把一个图形绕着某一点O转动一个角度的图形变换叫做旋转..点O叫做旋转中心,转动的角叫做旋转角(如∠AO A′),如果图形上的点A经过旋转变为点A′,那么,这两个点叫做这个旋转的对应点.特别说明:旋转的三个要素:旋转中心、旋转方向和旋转角度.2.旋转的性质: (1)对应点到旋转中心的距离相等(OA=OA′);(2)对应点与旋转中心所连线段的夹角等于旋转角;''').(3)旋转前、后的图形全等(△ABC≌△A B C特别说明:图形绕某一点旋转,既可以按顺时针旋转也可以按逆时针旋转.3.旋转的作图:在画旋转图形时,首先确定旋转中心,其次确定图形的关键点,再将这些关键沿指定的方向旋转指定的角度,然后连接对应的部分,形成相应的图形.作图的步骤:(1)连接图形中的每一个关键点与旋转中心;(2)把连线按要求(顺时针或逆时针)绕旋转中心旋转一定的角度(旋转角);(3)在角的一边上截取关键点到旋转中心的距离,得到各点的对应点;(4)连接所得到的各对应点.要点二、特殊的旋转—中心对称1.中心对称:把一个图形绕着某一个点旋转180°,如果它能够与另一个图形重合,那么就说这两个图形关于这个点对称或中心对称,这个点叫做对称中心.这两个图形中的对应点叫做关于中心的对称点.特别说明:(1)有两个图形,能够完全重合,即形状大小都相同;(2)位置必须满足一个条件:将其中一个图形绕着某一个点旋转180°能够与另一个图形重合 (全等图形不一定是中心对称的,而中心对称的两个图形一定是全等的) .2.中心对称图形:把一个图形绕着某一个点旋转180°,如果旋转后的图形能够与原来的图形重合,那么这个图形叫做中心对称图形,这个点就是它的对称中心.特别说明:(1)中心对称图形指的是一个图形;(2)线段,平行四边形,圆等等都是中心对称图形.要点三、平移、轴对称、旋转平移、轴对称、旋转之间的对比【典型例题】类型一、旋转三要素1.如图,E是正方形ABCD的边AB上任意一点(不与点A,B重合),DAE△按逆时针方向旋转后恰好能够与DCF重合.(1)旋转中心是________,旋转角为________;(2)请你判断DFE△的形状,并说明理由.【答案】(1) 点D ;90° (2) 等腰直角三角形,理由见分析 【分析】(1)由已知可知,旋转中心为点D ,旋转角∠ADC = 90°,即可求解; (2)由旋转的性质可得DE = DF ,∠EDF = ∠ADC = 90,可得结论. (1)解:由题意得:旋转中心是点D ;旋转角为∠ADC ,在正方形ABCD 中,∠ADC =90°, ∠旋转角为90°; 故答案为:点D ;90°(2)解:根据题意得:DE DF =,90EDF ADC ∠=∠=︒,∠DEF 是等腰直角三角形.【点拨】本题考查了旋转的性质,正方形的性质,掌握旋转的性质是解题的关键. 举一反三:【变式1】在ABC 中,30B ACB ∠+∠=︒,4AB =,ABC 逆时针旋转一定角度后与ADE 重合,且点C 恰好成为AD 中点,如图. (1) 旋转中心是点______,AE =______; (2) 求直线BC 与直线DE 的夹角.【答案】(1) A ,AC (2)30 【分析】(1)根据旋转后A 点与自身对应,则旋转中心为点A ,进而根据12AC AD =,可知AE 与AC 对应,即可求解;(2)延长BC 交ED 于点F ,取AB 中点G ,连接EG ,证明AEG △是等边三角形,进而求得1,120,902EG AB BG EGB BEA ==∠=︒∠=︒在EBF △中,根据三角形内角和定理求得EFB ∠,即直线BC 与直线DE 的夹角.(1)解:∠旋转后A 点与自身对应,∠旋转中心为点A , 12AC AD =,则AC 旋转后与AD 不对应,则AC 与AE 对应 故答案为:A ,AC(2)延长BC 交ED 于点F ,取AB 中点G ,连接EG ,30ABC ACB ∠+∠=︒,4AB =,180150BAC B ACB ∴∠=︒-∠-∠=︒∴ABC 逆时针旋转150︒后与ADE 重合, ∴150CAE BAC ∠=∠=︒,BCA DEA ∠=∠36060EAG EAC DAB ∴∠=︒-∠-∠=︒ G 是AB 的中点,122AG AB ∴== 1,22AD AB AC AD === ∴2AE AC ==∴AEG 是等边三角形60AGE ∴∠=︒ 120EGB ∴∠=︒又2EG AG AE BG ====30∴∠=∠=︒GBE GEB∴∠=∠+∠=︒90BEA BEG GEABEF中∠+∠FBE BEF=∠+∠+∠+∠CBA ABE BEA AED=∠+∠+∠+∠ABE BEA CBA AED()==︒+︒︒12030150∴∠=︒EFB30即直线BC与直线DE的夹角为30【点拨】本题考查了旋转的性质,等边三角形的判定,三角形内角和定理,掌握旋转的性质是解题的关键.【变式2】如图,点P是正方形ABCD内一点,连接P A,PB,PC,将∠ABP绕点B 顺时针旋转到∠CBP′的位置.(1)旋转中心是点__________,旋转角度是__________.(2)连接PP′,∠BPP′的形状是__________ 三角形.(3)若P A=2,PB=4,∠APB=135°,求PC的长.【答案】(1)B,90°;(2)等腰直角;(3)6【分析】(1)根据旋转的定义解答;(2)根据旋转的性质可得BP=BP′,又旋转角为90°,然后根据等腰直角三角形的定义判定;(3)∠根据勾股定理列式求出PP′,先根据旋转的性质求出∠BP′C=135°,再求出∠PP′C=90°,然后根据勾股定理列式进行计算即可得解.解:(1)∠P是正方形ABCD内一点,∠ABP绕点B顺时针旋转到∠CBP′的位置,∠旋转中心是点B,点P旋转的度数是90度,故答案为:B ,90°;(2)根据旋转的性质BP=BP′,旋转角为90°,∠∠BPP′是等腰直角三角形; 故答案为:等腰直角;(3)在等腰Rt ∠BPP '中,∠PB =BP '=4,∠PP ′= ∠∠BP ′C =∠BP A =135°,∠∠PP ′C =∠BP ′C -∠BP ′P =135°-45°=90°, ∠P 'C =P A =2 在Rt ∠PP ′C 中,PC 6==【点拨】本题考查旋转的性质,勾股定理,正方形的性质,等腰直角三角形的判定和性质,解题的关键是熟练掌握旋转的性质和正方形的性质.类型二、利用旋转性质求值或证明2.如图,点E 是正方形ABCD 内一点,将BEC △绕点C 顺时针旋转90°至DFC △. (1) 若30EBC ∠=︒,80BCE ∠=︒,求DFC ∠; (2) 若3CE =,求CEF △的面积.【答案】(1) 70DFC ∠=︒ (2) CEF △的面积为92【分析】(1)根据三角形内角和定理,先算出70BEC ∠=︒,根据旋转性质,得出70DFC BEC ∠=∠=︒;(2)根据旋转性质得出90ECF ∠=︒,3CF CE ==,即可算出∠CEF 的面积. (1)解:∠30EBC ∠=︒,80BCE ∠=︒,∠18070BEC EBC BCE ∠=︒-∠-∠=︒,∠将BEC △绕点C 顺时针旋转90°至DFC △, ∠70DFC BEC ∠=∠=︒.(2)∠将BEC △绕点C 顺时针旋转90°至DFC △, ∠90ECF ∠=︒,3CF CE ==, ∠11933222CEF S CE CF ∆=⨯⨯=⨯⨯=.【点拨】本题主要考查了三角形内角和定理,旋转的性质,根据旋转得出90ECF ∠=︒,3CF CE ==,是解题的关键.举一反三:【变式1】已知在Rt ABC △中,90ACB ∠=︒,AC BC =,CD AB ⊥于点D .在边BC 上取一点E ,连接DE ,将线段DE 绕点E 顺时针旋转90°得到线段EF ,连接AF ,交线段CD 于点G .(1) 如图,若点E 与点C 重合,求证:FCG ADG △△≌; (2) 探究线段AG 与GF 之间满足的数量关系,并说明理由;(3) 若10AB =,请直接写出点C 与点F 之间的最小距离,不必写解答过程. 【答案】(1)见分析(2)AG =GF ,理由见分析(3)5 【分析】(1)根据题意,∠ABC 是等腰直角三角形,CD ∠AB ,所以CD =AD ,根据旋转的性质,CD =CF ,所以CF =AD ,又因为∠GCF =∠GDA =90°,∠CGF =∠DGA ,所以FCG ADG △△≌(ASA );(2)作EH ∠BC ,交CD 于点H ,连接FH ,则可证明∠FEH ≌∠CED (SAS ),得到FH =DC =AD ,∠EHF =∠ECD =45°,从而证明∠FHG =90°,又因为对顶角相等,可证明∠FGH≌∠AGD (AAS ),所以AG =GF ;(3)根据(2)中的结论,CF ,所以当CE 取最小值0时CF有最小值5.解:(1)根据题意,∠ABC 是等腰直角三角形,∠CD AB ⊥∠CD 是斜边AB 的中线 ∠CD =AD∠线段DE 绕点E 顺时针旋转90°得到线段EF ∠∠FCG =∠ADG =90°,CD =CF ∠AD =CF在△FCG 和ADG 中FCG ADG CF ADFGC AGD ∠=∠⎧⎪=⎨⎪∠=∠⎩∠FCG ADG △△≌(ASA ) (2)AG =GF ,理由如下:作EH ∠BC ,交CD 于点H ,连接FH ,如图,∠∠ABC 是等腰直角三角形,CD ∠AB∠∠BCD =12ACB ∠=45°,CD =AD =12AB∠EH ∠BC∠∠EHC =∠BCD =45° ∠CE =HE∠∠FED +∠DEH =∠DEH +∠HEC ∠∠FEH =∠DEC 又∠EF =ED∠∠FEH ≌∠CED (SAS )∠FH =DC =AD ,∠EHF =∠ECD =45° ∠∠CHF =∠CHE +∠EHF =45°+45°=90° ∠∠FHG =90°=∠ADG 又∠∠FGH =∠AGD ∠∠FGH ≌∠AGD (AAS ) ∠AG =GF (3)连接CF ,∠FH =AD =12AB =11052⨯=,CH∠CF当CE 最小时CF 最小,CE 最小值为0,∠CF 5=点C 与点F 之间的最小距离为5.【点拨】本题考查全等三角形的判定与性质,旋转的性质,勾股定理,熟练掌握等腰直角三角形的性质和全等三角形的判定与性质是解题的关键.【变式2】如图,P 是等边ABC 内的一点,且5,4,3PA PB PC ===,将APB △绕点B 逆时针旋转,得到CQB △.(1) 旋转角为_____度; (2) 求点P 与点Q 之间的距离;(3)求BPC∠的度数;S.(4)求ABC的面积ABC【答案】+9.【分析】(1)根据∠QCB是∠P AB绕点B逆时针旋转得到,可知∠ABC为旋转角即可得出答案,(2)连接PQ,根据等边三角形得性质得∠ABC=60°,BA=BC,由旋转的性质得BP =BQ,∠PBQ=∠ABC=60°,CQ=AP=5,BP=BQ=4,∠PBQ=60°,于是可判断∠PBQ 是等边三角形,所以PQ=PB=4;(3)先利用勾股定理的逆定理证明∠PCQ是直角三角形,且∠QPC=90°,再加上∠BPQ =60°,然后计算∠BPQ+∠QPC即可.(4)由直角三角形的性质可求CH,PH的长,由勾股定理和三角形的面积公式可求解.解:(1)∠∠ABC是等边三角形,∠∠ABC=60°,∠∠QCB是∠P AB绕点B逆时针旋转得到的,∠旋转角为60°故答案为:60;(2)连接PQ,如图1,∠∠ABC是等边三角形,∠∠ABC=60°,BA=BC,∠∠QCB是∠P AB绕点B逆时针旋转得到的,∠∠QCB∠∠P AB,∠BP=BQ,∠PBQ=∠ABC=60°,CQ=AP=5,∠BP=BQ=4,∠PBQ=60°,∠∠PBQ是等边三角形,∠PQ=PB=4;(3)∠QC =5,PC =3,PQ =4, 而32+42=52, ∠PC 2+PQ 2=CQ 2,∠∠PCQ 是直角三角形,且∠QPC =90°, ∠∠PBQ 是等边三角形, ∠∠BPQ =60°,∠∠BPC =∠BPQ +∠QPC =60°+90°=150°; (4)如图2,过点C 作CH ∠BP ,交BP 的延长线于H , ∠∠BPC =150°, ∠∠CPH =30°, ∠CH 12=PC 32=,PH=, ∠BH =4 ∠BC 2=BH 2+CH 2232⎛⎫=+ ⎪⎝⎭2425⎛+ ⎝⎭= ∠S △ABC =2, ∠S △ABC 25=+=9.【点拨】本题考查了旋转的性质,等边三角形的判定与性质,全等三角形的性质,勾股定理的逆定理,掌握旋转的性质是本题的关键.类型三、中心对称图形与轴对称图形3、如图,在平面直角坐标系中,ABC 为格点三角形(顶点为网格线的交点),∠ABC =90°,点A 的坐标为(1,4).已知ABC 与DEF 关于点(),0a 成中心对称(点D ,E ,F 分别为A ,B ,C 的对应点,0a ≥且4a ≠).连接AF ,CD .(1) 若0a =,画出此时DEF 的位置;(2) 线段AF 与CD 的位置和大小关系是______;(3) 若四边形AFDC 是一个轴对称图形,则a 的值为______. 【答案】(1)见分析(2)AF CD ∥,且AF CD =(3)1 【分析】(1)当0a =时,点(a ,0)即为原点,作出ABC 关于原点成中心对称的图形即可;(2)设对称中心为点P (a ,0),根据中心对称的性质,即可得出结论; (3)当四边形AFDC 是菱形或矩形时,可得出a 的值. (1)如图,DEF 即为所画;(2)如图所示,AF CD ∥,且AF CD =故答案为:AF CD ∥,且AF CD =(3)∠ABC 是直角三角形,且B (1,0),∠ABC 与DEF 关于点()1,0成中心对称时,四边形AFDC 是菱形,如图,∠1,a = 故答案为:1【点拨】本题考查作图-中心对称、轴对称等知识,解题的关键是理解题意,灵活运用所学知识解决问题.举一反三:【变式1】已知:BD 是ABC 的角平分线,点E ,F 分别在BC AB ,上,且DE AB ,BE AF =.(1) 如图1,求证:四边形ADEF 是平行四边形;(2) 如图2,若ABC 为等边三角形,在不添加辅助线的情况下,请你直接写出所有是轴对称但不是中心对称的图形.【答案】(1)证明见分析(2)等边ABC ,等边BEF ,等边CDE ,等腰BDE ,等腰梯形ABED ,等腰梯形ACEF【分析】(1)由角平分线可知ABD CBD ∠=∠,由平行可知BDE ABD ∠=∠,可得CBD BDE ∠=∠,DE BE AF ==,进而结论得证;(2)由题意可得四边形ADEF 是菱形,,,D E F 是等边三角形的中点,然后根据在平面内,把一个图形绕着某个点旋转180°,如果旋转后的图形能与原来的图形重合,那么这个图形叫做中心对称图形;在平面内,一个图形沿一条直线折叠,直线两旁的部分能够完全重合的图形叫做轴对称图形;对图中的三角形与四边形的对称性进行判断即可.(1)证明:∠BD 是ABC 的角平分线∠ABD CBD ∠=∠ ∠DE AB ∥ ∠BDE ABD ∠=∠ ∠CBD BDE ∠=∠ ∠DE BE AF == ∠DE AF ∥,DE AF = ∠四边形ADEF 是平行四边形.(2)解:由(1)知四边形ADEF 是平行四边形∠EF AC∠ABC 是等边三角形 ∠60EFB C B ∠=∠=∠=︒ ∠BE EF DE == ∠四边形ADEF 是菱形 ∠,,AF BF BE CE CD AD === ∠,,D E F 是等边三角形的中点 ∠,BG EF BD EF ⊥⊥∠由轴对称图形与中心对称图形的定义可知,是轴对称图形但不是中心对称图形的有:等边ABC ,等边 BEF ,等边CDE △,等腰BDE ,等腰梯形ABED ,等腰梯形ACEF .【点拨】本题考查了角平分线,等腰三角形的判定与性质,等边三角形的判定性质,平行四边形的判定与性质,菱形的判定与性质,轴对称图形,中心对称图形等知识.解题的关键在于对知识的熟练掌握与灵活运用.【变式2】 在边长为1个单位长度的正方形网格中建立如图所示的平面直角坐标系,ABC 的顶点都在格点上,请解答下列问题:(1)作出ABC 向左平移4个单位长度后得到的111A B C △,并写出点1C 的坐标; (2)作出ABC 关于原点O 对称的222A B C △,并写出点2C 的坐标;222A B C △可看作111A B C △以点(________,________)为旋转中心,旋转________°得到的.(3)已知ABC 关于直线l 对称的333A B C △的顶点3A 的坐标为()4,2--,请直接写出直线l 的函数解析式________.【答案】(1)图见详解,C 1(-1,2);(2)图见详解,C 2(-3,-2),(-2,0),180;(3)y =-x【分析】(1)根据平移的性质即可画出ABC 向左平移4个单位后的111A B C △;(2)根据中心对称的性质即可作出ABC 关于原点O 对称的222A B C △,再根据旋转的性质即可得出结论;(3)根据轴对称的性质,可以知道直线必过点(-1,1),即可求出解析式. 解:(1)如图所示,点C 1的坐标(-1,2);(2)如图所示,点C 2的坐标(-3,-2),222A B C △可看作111A B C △以点(-2,0)为旋转中心,旋转180°得到的;(3)因为A 的坐标为(2,4),A 3的坐标为(-4,-2),所以直线必过点(-1,1),所以直线的解析式为y =-x .【点拨】本题主要考查了平移,轴对称,中心对称的作图,熟练其概念准确的画出图形是解决本题的关键.类型四、直角坐标系中的中心对称图形4、已知∠ABC的三个顶点的坐标分别为A(-5,0)、B(-2,3)、C(-1,0).(1)画出∠ABC关于坐标原点O成中心对称的∠A′B′C′;(2)将∠ABC绕坐标原点O顺时针旋转90°,画出对应的∠A′′B′′C′′;(3)若以A′、B′、C′、D′为顶点的四边形为平行四边形,则在第四象限中的点D′坐标为.【答案】(1)见分析(2)见分析(3)(6,-2)【分析】(1)根据关于原点对称的点的横坐标与纵坐标都互为相反数解答;(2)根据网格结构找出点A、B、C绕坐标原点O顺时针旋转90°的点A″、B″、C″的坐标,然后顺次连接即可;(3)根据平行四边形的对边平行且相等解答.(1)如图所示,∠A′B′C′就是求作的图形;(2)如图所示,∠A′′B′′C′′就是求作的三角形;(3)如图所示,点D′坐标为(6,-2);【点拨】本题考查了利用旋转变换作图,平行四边形的性质,熟练掌握网格结构准确找出对应点的位置是解题的关键.举一反三:【变式1】如图,△ABC 三个顶点的坐标分别是A (1,1),B (4,2),C (3,4).(1) 若ABC 经过平移后得到111A B C △,已知点C 的对应点1C 的坐标为()2,4-,画出111A B C △;(2) 请画出△ABC 关于原点对称的△A 2B 2C 2. 【答案】(1)见分析(2)见分析 【分析】(1)根据C 点的平移方式依次得到A 点和B 点的对应点的位置,顺次相连即可; (2)根据中心对称的定义确定对应点的位置后顺次连接即可. (1)如图,△A 1B 1C 1即为所求. (2)如图,△A 2B 2C 2即为所求.【点拨】本题考查了平面直角坐标系内的图形的平移和中心对称,解题关键是牢记平移作图与中心对称图形的作图方法.【变式2】 已知抛物线y =﹣2x 2+8x ﹣7.(1) 二次函数的图象与已知抛物线关于y 轴对称,求它的解析式;(2) 二次函数y =ax 2+bx +c 的图象与已知抛物线关于原点对称,求a ,b ,c 的值. 【答案】(1)y =﹣2x 2﹣8x ﹣7(2)a =2,b =8,c =7 【分析】(1)抛物线y =﹣2x 2+8x ﹣7的图象关于y 轴对称的抛物线x 互为相反数,y 不变进行求解即可;(2)抛物线y =﹣2x 2+8x ﹣7的图象关于原点对称的抛物线x 、y 均互为相反数进行求解即可;(1)解:抛物线y =﹣2x 2+8x ﹣7的图象关于y 轴对称的抛物线x 互为相反数,y 不变,∠y =﹣2(﹣x )2+8(﹣x )﹣7=﹣2x 2﹣8x ﹣7;(2)抛物线y =﹣2x 2+8x ﹣7的图象关于原点对称的抛物线x 、y 均互为相反数,∠﹣y =﹣2(﹣x )2+8(﹣x )﹣7=﹣2x 2﹣8x ﹣7, 即y =2x 2+8x +7∠二次函数y =ax 2+bx +c 中的a =2,b =8,c =7.【点拨】本题主要考查二次函数的图象及性质,掌握二次函数的图象及性质是解题的关键.类型五、旋转几何综合拓展5、∠ABC 和∠DEC 是等腰直角三角形,90ACB DCE ∠=∠=︒,AC BC =,CD CE =.(1)【观察猜想】当∠ABC 和∠DEC 按如图1所示的位置摆放,连接BD 、AE ,延长BD 交AE 于点F ,猜想线段BD 和AE 有怎样的数量关系和位置关系.(2)【探究证明】如图2,将∠DCE 绕着点C 顺时针旋转一定角度()090αα︒<<︒,线段BD 和线段AE 的数量关系和位置关系是否仍然成立?如果成立,请证明:如果不成立,请说明理由.(3)【拓展应用】如图3,在∠ACD 中,45ADC ∠=︒,CD =4=AD ,将AC 绕着点C 逆时针旋转90°至BC ,连接BD ,求BD 的长.【答案】(1)BD AE = ,BD AE ⊥(2)成立,理由见分析(3)【分析】(1)通过证明BCD ACE ≅,即可求证;(2)通过证明BCD ACE ≅,即可求证;(3)过点C 作CH CD ⊥,垂足为C ,交AD 于点H ,根据旋转的性质,等腰直角三角形的性质,勾股定理,即可求解.解:(1)BD AE = ,BD AE ⊥,证明如下:在BCD △和ACE 中,90ACB DCE ∠=∠=︒,AC BC =,CD CE =,BCD ACE ∴≅,,BD AE CBD CAE ∴=∠=∠,90ACB ∠=︒,90CBD BDC ∴∠+∠=︒,BDC ADF ∠=∠,90CAE ADF ∴∠+∠=︒,BD AE ∴⊥;(2)成立,理由如下:∠ACB DEC ∠=∠,∠ACB ACD DCE ACD ∠+∠=∠+∠,即BCD ACE ∠=∠,在BCD △和ACE 中,∠AC BC =,BCD ACE ∠=∠,CD CE =,∠BCD ACE ≌,∠BD AE =,CBD CAE ∠=∠,∠BGC AGF ∠=∠,∠CBD BGC CAE AGF ∠+∠=∠+∠,∠90ACB ∠=︒,∠90CBD BGC ∠+∠=︒,∠90CAE AGF ∠+∠=︒,∠90AFB ∠=︒,∠BD AE ⊥;(3)如图,过点C 作CH CD ⊥,垂足为C ,交AD 于点H ,由旋转性质可得:90ACB ∠=︒,AC BC =,∠CH CD ⊥,∠90DCH ∠=︒,∠90ADC CHD ∠+∠=︒,且45ADC ∠=︒,∠45CHD ∠=︒,∠CHD ADC ∠=∠,∠CD CH ==在Rt DCH 中:2DH =,∠90ACB DCH ∠=∠=︒,∠ACB ACH DCH ACH ∠+∠=∠+∠,即ACD BCH ∠=∠,在ACD △和BCH 中,∠AC BC =,ACD BCH ∠=∠,CD CH =,∠ACD BCH ≌△△,∠4BH AD ==,CBH DAC ∠=∠,∠12CBH DAC ∠+∠=∠+∠,∠90ACB ∠=︒,∠190CBH ∠+∠=︒,∠290DAC ∠+∠=︒,∠90∠=°,BHA∠BH AD⊥,∠BHD△是直角三角形,在Rt BDH中,BD=【点拨】本题考查了全等三角形的判定和性质,勾股定理,旋转的性质,等腰直角三角形的性质等,熟练掌握知识点是解题的关键.举一反三:【变式1】如图1,在∠ABC中,∠C=90°,∠ABC=30°,AC=1,D为∠ABC内部的一动点(不在边上),连接BD,将线段BD绕点D逆时针旋转60°,使点B到达点F的位置;将线段AB绕点B顺时针旋转60°,使点A到达点E的位置,连接AD,CD,AE,AF,BF,EF.(1)求证:∠BDA∠∠BFE;(2)∠CD+DF+FE的最小值为;∠当CD+DF+FE取得最小值时,求证:AD∠BF.(3)如图2,M,N,P分别是DF,AF,AE的中点,连接MP,NP,在点D运动的过程中,请判断∠MPN的大小是否为定值.若是,求出其度数;若不是,请说明理由.【答案】(1)见解答;(2);∠见解答;(3)是,∠MPN=30°.【分析】(1)由旋转60°知,∠ABD=∠EBF、AB=AE、BD=BF,故由SAS证出全等即可;(2)∠由两点之间,线段最短知C、D、F、E共线时CD+DF+FE最小,且CD+DF+FE 最小值为CE,再由∠ACB=90°,∠ABC=30°,AC=1求出BC和AB,再由旋转知AB=BE,∠CBE=90°,最后根据勾股定理求出CE即可;∠先由∠BDF 为等边三角形得∠BFD =60°,再由C 、D 、F 、E 共线时CD +DF +FE 最小,∠BFE =120°=∠BDA ,最后ADF =∠ADB -∠BDF =120°-60°=60°,即证;(3)由中位线定理知道MN ∠AD 且PN ∠EF ,再设∠BEF =∠BAD =α,∠P AN =β,则∠PNF =60°-α+β,∠FNM =∠F AD =60°+α-β,得∠PNM =120°.(1)证明:∠∠DBF =∠ABE =60°,∠∠DBF -∠ABF =∠ABE -∠ABF ,∠∠ABD =∠EBF ,在∠BDA 与∠BFE 中,BD BF ABD EBF AB BE ⎧⎪∠∠⎨⎪⎩===,∠∠BDA ∠∠BFE (SAS );(2)∠∠两点之间,线段最短,即C 、D 、F 、E 共线时CD +DF +FE 最小,∠CD +DF +FE 最小值为CE ,∠∠ACB =90°,∠ABC =30°,AC =1,∠BE =AB =2,BC∠∠CBE =∠ABC +∠ABE =90°,∠CE=∠证明:∠BD =BF ,∠DBF =60°,∠∠BDF 为等边三角形,即∠BFD =60°,∠C 、D 、F 、E 共线时CD +DF +FE 最小,∠∠BFE =120°,∠∠BDA ∠∠BFE ,∠∠BDA =120°,∠∠ADF =∠ADB -∠BDF =120°-60°=60°,∠∠ADF =∠BFD ,∠AD ∠BF ;(3)∠MPN 的大小是为定值,理由如下:如图,连接MN ,∠M ,N ,P 分别是DF ,AF ,AE 的中点,∠MN ∠AD 且PN ∠EF ,∠AB =BE 且∠ABE =60°,∠∠ABE 为等边三角形,设∠BEF =∠BAD =α,∠P AN =β,则∠AEF =∠APN =60°-α,∠EAD =60°+α,∠∠PNF =60°-α+β,∠FNM =∠F AD =60°+α-β,∠∠PNM =∠PNF +∠FNM =60°-α+β+60°+α-β=120°,∠∠BDA ∠∠BFE ,∠MN =12AD =12FE =PN , ∠∠MPN =12(180°-∠PNM )=30°. 【点拨】本题是三角形与旋转变换的综合应用,熟练掌握旋转的性质、三角形全等的判定与性质、平行线的判定、勾股定理的应用、中位线的性质及等腰、等边三角形的判定与性质是解题关键 .【变式2】 如图1,正方形ABCD 的边长为4,点P 在边AD 上(P 不与,A D 重合),连接,PB PC .将线段PB 绕点P 顺时针旋转90°得到PE ,将线段PC 绕点P 逆时针旋转90°得到PF .连接EF EA FD ,,.(1)求证:∠PDF ∆的面积212S PD =; ∠EA FD =;(2)如图2,EA FD.的延长线交于点M,取EF的中点N,连接MN,求MN的取值范围.【答案】(1)∠见详解;∠见详解;(2)4≤MN<【分析】≌,即可得到结论;(1)∠过点F作FG∠AD交AD的延长线于点G,证明PFG CPD∠过点E作EH∠DA交DA的延长线于点H,证明PEH BPA≌,可得≌,结合PFG CPDGD=EH,同理:FG=AH,从而得AHE FGD≌,进而即可得到结论;(2)过点F作FG∠AD交AD的延长线于点G,过点E作EH∠DA交DA的延长线于点EF,HG= 2AD=8,EH+FG= AD=4,然后求出当点P与点D重H,可得∠AMD=90°,MN=12合时,EF最大值=P与AD的中点重合时,EF最小值= HG=8,进而即可得到答案.解:(1)∠证明:过点F作FG∠AD交AD的延长线于点G,∠∠FPG+∠PFG=90°,∠FPG+∠CPD=90°,∠∠FPG=∠CPD,又∠∠PGF=∠CDP=90°,PC=PF,∠PFG CPD ≌(AAS ),∠FG =PD ,∠PDF ∆的面积21122S PD FG PD =⋅=; ∠过点E 作EH ∠DA 交DA 的延长线于点H ,∠∠EPH +∠PEH =90°,∠EPH +∠BP A =90°,∠∠PEH =∠BP A ,又∠∠PHE =∠BAP =90°,PB =PE ,∠PEH BPA ≌(AAS ),∠EH =P A ,由∠得:FG =PD ,∠EH +FG =P A +PD =AD =CD ,由∠得:PFG CPD ≌,∠PG =CD ,∠PD +GD = CD = EH +FG ,∠FG + GD = EH +FG ,∠GD =EH ,同理:FG =AH ,又∠∠AHE =∠FGD ,∠AHE FGD ≌,∠EA FD =;(2)过点F 作FG ∠AD 交AD 的延长线于点G ,过点E 作EH ∠DA 交DA 的延长线于点H ,≌,由(1)得:AHE FGD∠∠HAE=∠GFD,∠∠GFD+∠GDF=90°,∠∠HAE+∠GDF=90°,∠∠HAE=∠MAD,∠GDF=∠MDA,∠∠MAD+∠MDA=90°,∠∠AMD=90°,∠点N是EF的中点,EF,∠MN=12∠EH=DG=AP,AH=FG=PD,∠HG=AH+DG+AD=PD+AP+AD=2AD=8,EH+FG=AP+PD=AD=4,当点P与点D重合时,FG=0,EH=4,HG=8,此时EF最大值当点P与AD的中点重合时,FG=2,EH=2,HG=8,此时EF最小值= HG=8,【点拨】本题主要考查全等三角形的判定和性质,正方形的性质,勾股定理,旋转的性质,添加辅助线,构造直角全等的直角三角形,是解题的关键.。
《旋转与角》(教案)北师大版四年级数学上册
第二单元线与角·第4课时旋转与角·教案班级:课时:课型:一、学情分析学生在二年级对“角”已经有了初步认识,知道锐角、直角、钝角。
本课时进一步认识角,拓展角的概念。
通过纸条旋转的过程,建立角的“动态表象”,将平角、周角与射线、直线区分开来,同时直观感受角之间的大小关系。
二、教学目标1.结合操作“活动角”的过程,从旋转的角度进一步认识角。
2.认识平角和周角,了解各种角之间的大小关系。
三、重点难点【教学重点】认识平角和周角。
【教学难点】知道平角和周角是如何形成的。
四、教学过程设计第一板块【复习旧知引入新课】师:同学们,还记得我们学过的角吗?角是由什么组成的?生:一个顶点和两条边。
小结:由一个点引出两条射线所组成的图形叫做角。
师:你能说出这些角的名字吗?生:锐角、直角、钝角。
师:它们之间谁最大?谁最小?生:钝角>直角>锐角师:这节课我们继续研究有关角的知识。
(教师板书课题)设计意图:复习学过的角的知识,唤起学生已有的学习经验,为接下来更深入学习角的知识作铺垫。
第二板块【合作交流探索新知】1.做一个活动角师:拿出课前准备好的两张硬纸条,我们一起来做一个活动角。
学生带领学生一起操作:先把两张硬纸条的一端钉在一起;再固定其中一张硬纸条,旋转另一张硬纸条。
师:在操作过程中,请同学们思考以下三个问题:(1)旋转过程中,你有什么发现?(2)随着开口越大,角如何变化?(3)角的大小与什么有关?学生操作完成后,汇报:生1:有很多很多角,角越来越大了。
生2:开口越大,角越大。
……讨论:角的大小与什么有关?师:分享你的观点并验证一下。
生:我和同桌做的角重合在一起之后,角一样大,但是边的长短不一样。
教师用课件演示一个角的两条边不断延长,但角的开口没有变化。
师:所以角的大小与什么有关?与什么无关?谁能完整地说一下?生:角的大小与边的长短无关,与角的两条边的开口有关,开口越大,所形成的角越大。
2.认识平角和周角(1)观察旋转过程中所形成的角,认一认,说一说。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《旋转与角》课时练
⒈填一填。
⑴一条射线围绕它的端点旋转而成的图形叫做( )。
⑵下午六时整时,时针与分针所成的角是( )。
⑶一个角有( )个顶点和( )条边。
⑷互相垂直的两条直线相交所构成的直角有( )个。
⑸一个三角尺共有( )个角,其中有( )个直角和( )个锐角。
⑹当角的两条边成一条直线时,这样的角叫( )。
⒉下面的角都是什么角?请在括号里写出它们的名字。
⑴ ⑵
( ) ( )
⑶ ⑷
( ) ( )
⑸ ⑹
( ) ( )
⒊选择(将正确答案的序号填在括号内)。
⑴角的两边分别是两条( )。
A 直线 B 射线 C 线段
⑵3时整时,时针和分针所成的角是( )。
A 锐角 B 直角 C 钝角
⑶三角板中没有( )角。
A 锐角 B 直角 C 钝角
⑷一个三角形中,至少有( )个锐角。
A 1 B 2 C 3
⒋画出下面钟表中的时针,使时针与分针形成各种角,并在括号里写出时间。
锐角 直角 钝角
( )时 ( )时 ( )时
平角 周角
( )时 ( )时
⒌我会数。
⑴下图中共有( )个直角。 ⑵下图中共有( )个角。
答案:
1.(1)角(2)平角(3)1;2(4)4(5)3,1,2(6)平角
2. 钝角,锐角;直角,平角;钝角,周角
3.B,B,C,B
4. 略
5. 3;10
