浙江省金华市2018年中考科学试题含参考答案
(完整版)2018年浙江省宁波市中考科学试卷-答案

hing at a time and All things in their being are good for somethin
和非特异性免疫
4.【答案】A 【解析】A 柴火烧水是通过热传递的方式改变内能的;
BCD 压缩空气发热、搓手取暖、钻木取火都是做功使物体的内能增加的;
显然 A 选项与其它三个选项改变物体内能的方式不同。
NaOH+HCl NaCl+H2O ,
40
36.5
20g 10%
x 7.3%
40 = 36.5 20g 10% x 7.3%
x=25g ,
恰好完全反应时溶液质量为: 20g 25g=45g ,该选项对应关系不正确;
B 由 A 中计算可知,恰好完全反应时消耗盐酸质量是 25 g,溶液质量是 45 g,该选项对应关系正确;
故选:A。
【考点】热传递改变物体内能.
5.【答案】C
6.【答案】C 【解析】由题意可知,电磁弹射器的弹射车与飞机前轮连接,并处于强磁场中,当弹射车内的导体通以强电流
时,即可受到强大的推力,由此可知其原理是通电导体在磁场中受力而运动。
A 电铃是利用电磁继电器来工作的,故 A 不符合题意;
B 发电机的工作原理是电磁感应现象,故 B 不符合题意;
没有脊椎骨组成的脊柱;
5 / 15
hing at a time and All things in their being are good for somethin
(2)蛋白质是大分子物质,必须经消化后才能被吸收,蛋白质的消化是从胃开始的,当食物中的蛋白质进入胃 以后,在胃液的作用下进行初步消化后进入小肠,小肠里的胰液和肠液含有消化糖类、脂肪和蛋白质的酶, 在这些酶的作用下,蛋白质被彻底消化为氨基酸;所以鱼肉中富含蛋白质等营养物质,蛋白质在人体消化道 内被消化成氨基酸,才能被人体吸收进入血液。 故答案为:(1)体内有无脊柱;(2)氨基酸。 【考点】食物的消化和营养物质的吸收过程,动物的分类. 17.【答案】(1)神经 (2)舒张 (3)静脉 【解析】(1)酒精具有麻醉作用,会使人体的大脑的反应速度减慢。人体若摄入过量酒精 (乙醇)后,会引起 中枢神经系统由兴奋转入抑制的毒性生理反应(即“醉酒”),导致人体定向功能和判断能力下降。 (2)人在平静状态下呼气时,膈肌舒张,膈顶部上升,肋间外肌同时舒张,肋骨向下向内移动,这样,胸廊的容积 就缩小,肺随之回缩,肺内气体通过呼吸道排出体外。 (3)当绑扎人体上臂后,由于静脉血管的功能是将血液从全身各处输送到心脏去,而前臂被绑住了,血液无法 从手臂运回心脏,于是就在手臂上出现了一条条隆起的“青筋”,这些“青筋”实际上是鼓起的静脉血管。 因此在抽血时,护士会用一根橡皮软管将上臂扎紧,一会前臂靠近肘关节处的血管膨胀,该血管是静脉。 故答案为:(1)神经;(2)舒张;(3)静脉 【考点】血管的结构、功能和保健,呼气和吸气,酗酒对人体健康的危害 18.【答案】缩小 抽水。 【解析】(1)由图可知,物距大于像距,并且能在光屏上成实像,所以物距一定是在二倍焦距之外,所以成的是 倒立、缩小的实像; (2)向左移动蜡烛,即此时的物距变大,像距应该变小,即光屏应该向左移动,才能使得像清晰,但若保持光屏 和透镜不变,仍使得像成在光屏上,即需要让凸透镜的会聚能力减弱,即需要让凸透镜变薄,故应该向外抽水。
浙江省金华市2018年中考科学试题物理部分

2018年浙江省金华市初中毕业生学业考试物理试题考生须知:1. 全卷共四大题,38小题,满分为160分。
考试时间为120分钟。
2. 全卷分为卷Ⅰ<选择题)和卷Ⅱ<非选择题)两部分,全部在“答题纸”上作答。
卷Ⅰ的答案必须用2B铅笔填涂;卷Ⅱ的答案必须用黑色字迹钢笔或签字笔写在“答题纸”的相应位置上。
S2sNGOA8k23. 请用黑色字迹钢笔或签字笔在“答题纸”上先填写姓名和准考证号。
5.本卷计算中g取10牛/千克。
卷Ⅰ说明:本卷共有一大题,20小题,共60分。
请用2B铅笔在“答题纸”上将你认为正确的选项对应的小方框涂黑、涂满。
S2sNGOA8k2一、选择题<本大题共有20小题,每小题3分,共60分。
每小题只有一个选项是正确的,不选、多选、错选均不给分)S2sNGOA8k23.下列所描述的现象中,属于液化的是A.铁块熔成铁水 B.湿衣服晾干C.河水结成冰 D.沸水上方出现“白气”5.杠杆在生产生活中普遍使用。
下列工具在使用过程中,属于省力杠杆的是10.某品牌的微型电脑吸尘器有两个开关,开关S1控制照明灯L 和吸尘电动机M ,开关S2只控制吸尘电动机M 。
下列电路图符合要求的是S2sNGOA8k2138人,张老师因此被誉为“最美女教师”。
对上述有关情境的分析,错误的是S2sNGOA8k2A .冲向学生的客车具有较大的动能 B .“客车冲向学生”——以客车为参照物 C .被压在车轮下的双腿受到很大的压力 D .学生被推出说明力能改变物体的运动状态17.小金设计了一个如图所示的线圈指南针,将它放入盛有食盐水的水槽中<水构成了化学电池,铜片为正极,锌片为负极),浮在液面上的线圈就能指示方向了。
关于该装置的分析错误的是 A .线圈周围的磁场与条形磁铁的磁场相似 B .线圈能够指示方向是因为存在地磁场 C .利用该装置可以判断磁铁的南北极 D .交换铜片和锌片位置不会改变线圈的磁极A. 天平 C. 钓鱼竿 D. 铡刀B. 铁锹 第5题图第10题第17题食盐水铜片泡沫塑料20.在做“探究滑动摩擦力大小与哪些因素有关”实验时,某同学用弹簧测力计拉着同一木块在水平木板上做匀速直线运动,实验记录如下表。
2018年浙江省金华市中考数学试卷(包含答案解析版)
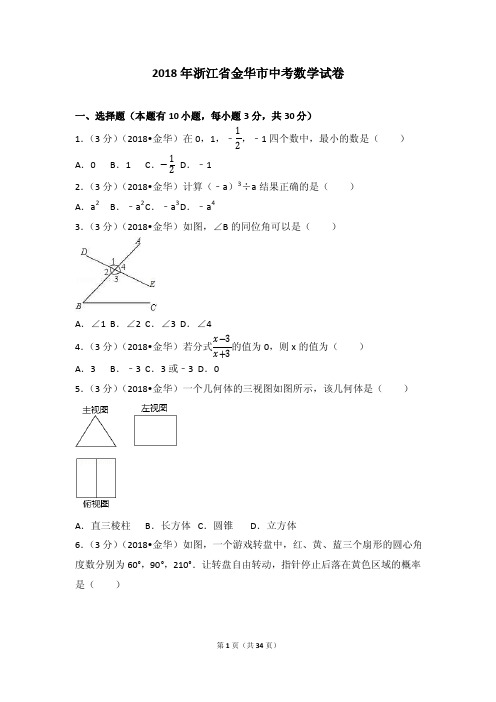
2018年浙江省金华市中考数学试卷一、选择题(本题有10小题,每小题3分,共30分)1.(3分)(2018•金华)在0,1,﹣12,﹣1四个数中,最小的数是()A.0 B.1 C.−12D.﹣12.(3分)(2018•金华)计算(﹣a)3÷a结果正确的是()A.a2B.﹣a2 C.﹣a3 D.﹣a43.(3分)(2018•金华)如图,∠B的同位角可以是()A.∠1 B.∠2 C.∠3 D.∠44.(3分)(2018•金华)若分式x−3x+3的值为0,则x的值为()A.3 B.﹣3 C.3或﹣3 D.05.(3分)(2018•金华)一个几何体的三视图如图所示,该几何体是()A.直三棱柱B.长方体C.圆锥D.立方体6.(3分)(2018•金华)如图,一个游戏转盘中,红、黄、蓝三个扇形的圆心角度数分别为60°,90°,210°.让转盘自由转动,指针停止后落在黄色区域的概率是()A .16B .14C .13D .7127.(3分)(2018•金华)小明为画一个零件的轴截面,以该轴截面底边所在的直线为x 轴,对称轴为y 轴,建立如图所示的平面直角坐标系.若坐标轴的单位长度取1mm ,则图中转折点P 的坐标表示正确的是( )A .(5,30)B .(8,10)C .(9,10)D .(10,10)8.(3分)(2018•金华)如图,两根竹竿AB 和AD 斜靠在墙CE 上,量得∠ABC=α,∠ADC=β,则竹竿AB 与AD 的长度之比为( )A .tanαtanβB .sinβsinαC .sinαsinβD .cosβcosα9.(3分)(2018•金华)如图,将△ABC 绕点C 顺时针旋转90°得到△EDC .若点A ,D ,E 在同一条直线上,∠ACB=20°,则∠ADC 的度数是( )A .55°B .60°C .65°D .70°10.(3分)(2018•金华)某通讯公司就上宽带网推出A,B,C三种月收费方式.这三种收费方式每月所需的费用y(元)与上网时间x(h)的函数关系如图所示,则下列判断错误的是()A.每月上网时间不足25h时,选择A方式最省钱B.每月上网费用为60元时,B方式可上网的时间比A方式多C.每月上网时间为35h时,选择B方式最省钱D.每月上网时间超过70h时,选择C方式最省钱二、填空题(本题有6小题,每小题4分,共24分)11.(4分)(2018•金华)化简(x﹣1)(x+1)的结果是.12.(4分)(2018•金华)如图,△ABC的两条高AD,BE相交于点F,请添加一个条件,使得△ADC≌△BEC(不添加其他字母及辅助线),你添加的条件是.13.(4分)(2018•金华)如图是我国2013~2017年国内生产总值增长速度统计图,则这5年增长速度的众数是.14.(4分)(2018•金华)对于两个非零实数x ,y ,定义一种新的运算:x*y=a x +by.若1*(﹣1)=2,则(﹣2)*2的值是 .15.(4分)(2018•金华)如图2,小靓用七巧板拼成一幅装饰图,放入长方形ABCD 内,装饰图中的三角形顶点E ,F 分别在边AB ,BC 上,三角形①的边GD 在边AD 上,则AB BC的值是 .16.(4分)(2018•金华)如图1是小明制作的一副弓箭,点A ,D 分别是弓臂BAC 与弓弦BC 的中点,弓弦BC=60cm .沿AD 方向拉动弓弦的过程中,假设弓臂BAC 始终保持圆弧形,弓弦不伸长.如图2,当弓箭从自然状态的点D 拉到点D 1时,有AD 1=30cm ,∠B 1D 1C 1=120°.(1)图2中,弓臂两端B 1,C 1的距离为 cm .(2)如图3,将弓箭继续拉到点D 2,使弓臂B 2AC 2为半圆,则D 1D 2的长为 cm .三、解答题(本题有8小题,共66分,各小题都必须写出解答过程) 17.(6分)(2018•金华)计算: 8+(﹣2018)0﹣4sin45°+|﹣2|.18.(6分)(2018•金华)解不等式组: x3+2<x2x +2≥3(x −1)19.(6分)(2018•金华)为了解朝阳社区20~60岁居民最喜欢的支付方式,某兴趣小组对社区内该年龄段的部分居民展开了随机问卷调查(每人只能选择其中一项),并将调查数据整理后绘成如下两幅不完整的统计图.请根据图中信息解答下列问题:(1)求参与问卷调查的总人数. (2)补全条形统计图.(3)该社区中20~60岁的居民约8000人,估算这些人中最喜欢微信支付方式的人数.20.(8分)(2018•金华)如图,在6×6的网格中,每个小正方形的边长为1,点A 在格点(小正方形的顶点)上.试在各网格中画出顶点在格点上,面积为6,且符合相应条件的图形.21.(8分)(2018•金华)如图,在Rt △ABC 中,点O 在斜边AB 上,以O 为圆心,OB 为半径作圆,分别与BC ,AB 相交于点D ,E ,连结AD .已知∠CAD=∠B . (1)求证:AD 是⊙O 的切线.(2)若BC=8,tanB=12,求⊙O 的半径.22.(10分)(2018•金华)如图,抛物线y=ax 2+bx (a <0)过点E (10,0),矩形ABCD 的边AB 在线段OE 上(点A 在点B 的左边),点C ,D 在抛物线上.设A (t ,0),当t=2时,AD=4. (1)求抛物线的函数表达式.(2)当t 为何值时,矩形ABCD 的周长有最大值?最大值是多少?(3)保持t=2时的矩形ABCD 不动,向右平移抛物线.当平移后的抛物线与矩形的边有两个交点G ,H ,且直线GH 平分矩形的面积时,求抛物线平移的距离.23.(10分)(2018•金华)如图,四边形ABCD 的四个顶点分别在反比例函数y=m x与y=n x(x >0,0<m <n )的图象上,对角线BD ∥y 轴,且BD ⊥AC 于点P .已知点B 的横坐标为4. (1)当m=4,n=20时.①若点P 的纵坐标为2,求直线AB 的函数表达式.②若点P 是BD 的中点,试判断四边形ABCD 的形状,并说明理由.(2)四边形ABCD 能否成为正方形?若能,求此时m ,n 之间的数量关系;若不能,试说明理由.24.(12分)(2018•金华)在Rt △ABC 中,∠ACB=90°,AC=12.点D 在直线CB 上,以CA ,CD 为边作矩形ACDE ,直线AB 与直线CE ,DE 的交点分别为F ,G .(1)如图,点D在线段CB上,四边形ACDE是正方形.①若点G为DE中点,求FG的长.②若DG=GF,求BC的长.(2)已知BC=9,是否存在点D,使得△DFG是等腰三角形?若存在,求该三角形的腰长;若不存在,试说明理由.2018年浙江省金华市中考数学试卷参考答案与试题解析一、选择题(本题有10小题,每小题3分,共30分)1.(3分)(2018•金华)在0,1,﹣12,﹣1四个数中,最小的数是()A.0 B.1 C.−12D.﹣1【考点】18:有理数大小比较.【专题】1 :常规题型;511:实数.【分析】根据有理数的大小比较法则(正数都大于0,负数都小于0,正数大于一切负数,两个负数,其绝对值大的反而小)比较即可.【解答】解:∵﹣1<﹣12<0<1,∴最小的数是﹣1,故选:D.【点评】本题考查了对有理数的大小比较法则的应用,用到的知识点是正数都大于0,负数都小于0,正数大于一切负数,两个负数,其绝对值大的反而小.2.(3分)(2018•金华)计算(﹣a)3÷a结果正确的是()A.a2B.﹣a2 C.﹣a3 D.﹣a4【考点】48:同底数幂的除法.【专题】11 :计算题.【分析】直接利用幂的乘方运算法则以及同底数幂的除法运算法则分别化简求出答案【解答】解:(﹣a)3÷a=﹣a3÷a=﹣a3﹣1=﹣a2,故选:B.【点评】此题主要考查了幂的乘方运算以及同底数幂的除法运算,正确掌握运算法则是解题关键.3.(3分)(2018•金华)如图,∠B的同位角可以是()A.∠1 B.∠2 C.∠3 D.∠4【考点】J6:同位角、内错角、同旁内角.【专题】1 :常规题型.【分析】直接利用两条直线被第三条直线所截形成的角中,若两个角都在两直线的同侧,并且在第三条直线(截线)的同旁,则这样一对角叫做同位角,进而得出答案.【解答】解:∠B的同位角可以是:∠4.故选:D.【点评】此题主要考查了同位角的定义,正确把握定义是解题关键.4.(3分)(2018•金华)若分式x−3x+3的值为0,则x的值为()A.3 B.﹣3 C.3或﹣3 D.0【考点】63:分式的值为零的条件.【专题】11 :计算题.【分析】根据分式的值为零的条件可以求出x的值.【解答】解:由分式的值为零的条件得x﹣3=0,且x+3≠0,解得x=3.故选:A.【点评】本题考查了分式值为0的条件,具备两个条件:(1)分子为0;(2)分母不为0.这两个条件缺一不可.5.(3分)(2018•金华)一个几何体的三视图如图所示,该几何体是()A .直三棱柱B .长方体C .圆锥D .立方体【考点】U3:由三视图判断几何体. 【专题】55:几何图形.【分析】根据三视图的形状可判断几何体的形状. 【解答】解:观察三视图可知,该几何体是直三棱柱. 故选:A .【点评】本题考查了几何体的三视图和结构特征,根据三视图的形状可判断几何体的形状是关键.6.(3分)(2018•金华)如图,一个游戏转盘中,红、黄、蓝三个扇形的圆心角度数分别为60°,90°,210°.让转盘自由转动,指针停止后落在黄色区域的概率是( )A .16B .14C .13D .712【考点】X5:几何概率. 【专题】543:概率及其应用.【分析】求出黄区域圆心角在整个圆中所占的比例,这个比例即为所求的概率. 【解答】解:∵黄扇形区域的圆心角为90°, 所以黄区域所占的面积比例为90360=14,即转动圆盘一次,指针停在黄区域的概率是14,故选:B.【点评】本题将概率的求解设置于转动转盘游戏中,考查学生对简单几何概型的掌握情况,既避免了单纯依靠公式机械计算的做法,又体现了数学知识在现实生活、甚至娱乐中的运用,体现了数学学科的基础性.用到的知识点为:概率=相应的面积与总面积之比.7.(3分)(2018•金华)小明为画一个零件的轴截面,以该轴截面底边所在的直线为x轴,对称轴为y轴,建立如图所示的平面直角坐标系.若坐标轴的单位长度取1mm,则图中转折点P的坐标表示正确的是()A.(5,30)B.(8,10)C.(9,10)D.(10,10)【考点】D3:坐标确定位置.【专题】11 :计算题.【分析】先求得点P的横坐标,结合图形中相关线段的和差关系求得点P的纵坐标.【解答】解:如图,过点C作CD⊥y轴于D,∴BD=5,CD=50÷2﹣16=9,OA=OD﹣AD=40﹣30=10,∴P(9,10);故选:C.【点评】此题考查了坐标确定位置,根据题意确定出CD=9,AD=10是解本题的关键.8.(3分)(2018•金华)如图,两根竹竿AB 和AD 斜靠在墙CE 上,量得∠ABC=α,∠ADC=β,则竹竿AB 与AD 的长度之比为( )A .tanαtanβB .sinβsinαC .sinαsinβD .cosβcosα【考点】T8:解直角三角形的应用. 【专题】552:三角形.【分析】在两个直角三角形中,分别求出AB 、AD 即可解决问题; 【解答】解:在Rt △ABC 中,AB=AC sinα,在Rt △ACD 中,AD=AC sinβ,∴AB :AD=AC sinα:AC sinβ=sinβsinα,故选:B .【点评】本题考查解直角三角形的应用、锐角三角函数等知识,解题的关键是学会利用参数解决问题,属于中考常考题型.9.(3分)(2018•金华)如图,将△ABC 绕点C 顺时针旋转90°得到△EDC .若点A ,D ,E 在同一条直线上,∠ACB=20°,则∠ADC 的度数是( )A .55°B .60°C .65°D .70°【考点】R2:旋转的性质.【专题】55:几何图形.【分析】根据旋转的性质和三角形内角和解答即可.【解答】解:∵将△ABC绕点C顺时针旋转90°得到△EDC.∴∠DCE=∠ACB=20°,∠BCD=∠ACE=90°,AC=CE,∴∠ACD=90°﹣20°=70°,∵点A,D,E在同一条直线上,∴∠ADC+∠EDC=180°,∵∠EDC+∠E+∠DCE=180°,∴∠ADC=∠E+20°,∵∠ACE=90°,AC=CE∴∠DAC+∠E=90°,∠E=∠DAC=45°在△ADC中,∠ADC+∠DAC+∠DCA=180°,即45°+70°+∠ADC=180°,解得:∠ADC=65°,故选:C.【点评】此题考查旋转的性质,关键是根据旋转的性质和三角形内角和解答.10.(3分)(2018•金华)某通讯公司就上宽带网推出A,B,C三种月收费方式.这三种收费方式每月所需的费用y(元)与上网时间x(h)的函数关系如图所示,则下列判断错误的是()A.每月上网时间不足25h时,选择A方式最省钱B.每月上网费用为60元时,B方式可上网的时间比A方式多C.每月上网时间为35h时,选择B方式最省钱D.每月上网时间超过70h时,选择C方式最省钱【考点】E6:函数的图象.【专题】532:函数及其图像;533:一次函数及其应用.【分析】A、观察函数图象,可得出:每月上网时间不足25 h时,选择A方式最省钱,结论A正确;B、观察函数图象,可得出:当每月上网费用≥50元时,B方式可上网的时间比A方式多,结论B正确;C、利用待定系数法求出:当x≥25时,y A与x之间的函数关系式,再利用一次函数图象上点的坐标特征可求出当x=35时y A的值,将其与50比较后即可得出结论C正确;D、利用待定系数法求出:当x≥50时,y B与x之间的函数关系式,再利用一次函数图象上点的坐标特征可求出当x=70时y B的值,将其与120比较后即可得出结论D错误.综上即可得出结论.【解答】解:A、观察函数图象,可知:每月上网时间不足25 h时,选择A方式最省钱,结论A正确;B、观察函数图象,可知:当每月上网费用≥50元时,B方式可上网的时间比A 方式多,结论B正确;C、设当x≥25时,y A=kx+b,将(25,30)、(55,120)代入y A=kx+b,得:25k+b=3055k+b=120,解得:k=3b=−45,∴y A=3x﹣45(x≥25),当x=35时,y A=3x﹣45=60>50,∴每月上网时间为35h时,选择B方式最省钱,结论C正确;D、设当x≥50时,y B=mx+n,将(50,50)、(55,65)代入y B=mx+n,得:50m+n=5055m+n=65,解得:m=3n=−100,∴y B=3x﹣100(x≥50),当x=70时,y B=3x﹣100=110<120,∴结论D错误.故选:D.【点评】本题考查了函数的图象、待定系数法求一次函数解析式以及一次函数图象上点的坐标特征,观察函数图象,利用一次函数的有关知识逐一分析四个选项的正误是解题的关键.二、填空题(本题有6小题,每小题4分,共24分)11.(4分)(2018•金华)化简(x﹣1)(x+1)的结果是x2﹣1.【考点】4F:平方差公式.【专题】11 :计算题.【分析】原式利用平方差公式计算即可得到结果.【解答】解:原式=x2﹣1,故答案为:x2﹣1【点评】此题考查了平方差公式,熟练掌握平方差公式是解本题的关键.12.(4分)(2018•金华)如图,△ABC的两条高AD,BE相交于点F,请添加一个条件,使得△ADC≌△BEC(不添加其他字母及辅助线),你添加的条件是AC=BC.【考点】KB:全等三角形的判定.【专题】1 :常规题型.【分析】添加AC=BC,根据三角形高的定义可得∠ADC=∠BEC=90°,再证明∠EBC=∠DAC,然后再添加AC=BC可利用AAS判定△ADC≌△BEC.【解答】解:添加AC=BC,∵△ABC的两条高AD,BE,∴∠ADC=∠BEC=90°,∴∠DAC+∠C=90°,∠EBC+∠C=90°,∴∠EBC=∠DAC,在△ADC和△BEC中∠BEC=∠ADC ∠EBC=∠DAC AC=BC,∴△ADC≌△BEC(AAS),故答案为:AC=BC.【点评】此题主要考查了三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.13.(4分)(2018•金华)如图是我国2013~2017年国内生产总值增长速度统计图,则这5年增长速度的众数是 6.9%.【考点】W5:众数.【专题】11 :计算题.【分析】根据众数的概念判断即可.【解答】解:这5年增长速度分别是7.8%、7.3%、6.9%、6.7%、6.9%,则这5年增长速度的众数是6.9%,故答案为:6.9%.【点评】本题考查的是众数的确定,掌握一组数据中出现次数最多的数据叫做众数是解题的关键.14.(4分)(2018•金华)对于两个非零实数x,y,定义一种新的运算:x*y=ax+by.若1*(﹣1)=2,则(﹣2)*2的值是﹣1.【考点】2C :实数的运算.【专题】11 :计算题;36 :整体思想. 【分析】根据新定义的运算法则即可求出答案. 【解答】解:∵1*(﹣1)=2, ∴a1+b −1=2即a ﹣b=2 ∴原式=a−2+b2=−12(a ﹣b )=﹣1 故答案为:﹣1【点评】本题考查代数式运算,解题的关键是熟练运用整体的思想,本题属于基础题型.15.(4分)(2018•金华)如图2,小靓用七巧板拼成一幅装饰图,放入长方形ABCD 内,装饰图中的三角形顶点E ,F 分别在边AB ,BC 上,三角形①的边GD 在边AD 上,则AB BC的值是 2+14.【考点】LB :矩形的性质;IM :七巧板. 【专题】556:矩形菱形正方形.【分析】设七巧板的边长为x ,根据正方形的性质、矩形的性质分别表示出AB ,BC ,进一步求出AB BC的值.【解答】解:设七巧板的边长为x ,则 AB=12x +22x ,BC=12x +x +12x=2x ,AB BC =12x + 22x 2x = 2+14.故答案为:2+1 4.【点评】考查了矩形的性质,七巧板,关键是熟悉七巧板的特征,表示出AB,BC的长.16.(4分)(2018•金华)如图1是小明制作的一副弓箭,点A,D分别是弓臂BAC与弓弦BC的中点,弓弦BC=60cm.沿AD方向拉动弓弦的过程中,假设弓臂BAC始终保持圆弧形,弓弦不伸长.如图2,当弓箭从自然状态的点D拉到点D1时,有AD1=30cm,∠B1D1C1=120°.(1)图2中,弓臂两端B1,C1的距离为303cm.(2)如图3,将弓箭继续拉到点D2,使弓臂B2AC2为半圆,则D1D2的长为105﹣10cm.【考点】M3:垂径定理的应用;KU:勾股定理的应用;M5:圆周角定理.【专题】559:圆的有关概念及性质.【分析】(1)如图1中,连接B1C1交DD1于H.解直角三角形求出B1H,再根据垂径定理即可解决问题;(2)如图3中,连接B1C1交DD1于H,连接B2C2交DD2于G.利用弧长公式求出半圆半径即可解决问题;【解答】解:(1)如图2中,连接B1C1交DD1于H.∵D1A=D1B1=30∴D1是B1AC1的圆心,∵AD1⊥B1C1,∴B1H=C1H=30×sin60°=153,∴B1C1=303∴弓臂两端B1,C1的距离为303(2)如图3中,连接B1C1交DD1于H,连接B2C2交DD2于G.设半圆的半径为r,则πr=120⋅π⋅30180,∴r=20,∴AG=GB2=20,GD1=30﹣20=10,在Rt△GB2D2中,GD2=302−202=105∴D1D2=105﹣10.故答案为303,105﹣10,【点评】本题考查垂径定理的应用、勾股定理、弧长公式等知识,解题的关键是学会添加常用辅助线,构造直角三角形解决问题,属于中考填空题中的压轴题.三、解答题(本题有8小题,共66分,各小题都必须写出解答过程)17.(6分)(2018•金华)计算:8+(﹣2018)0﹣4sin45°+|﹣2|.【考点】2C:实数的运算;6E:零指数幂;T5:特殊角的三角函数值.【专题】11 :计算题.【分析】根据零指数幂和特殊角的三角函数值进行计算.【解答】解:原式=22+1﹣4×2 2+2=22+1﹣22+2=3.【点评】本题考查了实数的运算:实数的运算和在有理数范围内一样,值得一提的是,实数既可以进行加、减、乘、除、乘方运算,又可以进行开方运算,其中正实数可以开平方.18.(6分)(2018•金华)解不等式组: x3+2<x2x +2≥3(x −1)【考点】CB :解一元一次不等式组.【专题】11 :计算题;524:一元一次不等式(组)及应用. 【分析】首先分别解出两个不等式的解集,再求其公共解集即可. 【解答】解:解不等式x3+2<x ,得:x >3,解不等式2x +2≥3(x ﹣1),得:x ≤5, ∴不等式组的解集为3<x ≤5.【点评】此题主要考查了不等式组的解法,关键是熟练掌握不等式组解集的确定:同大取大;同小取小;大小小大中间找;大大小小找不到.19.(6分)(2018•金华)为了解朝阳社区20~60岁居民最喜欢的支付方式,某兴趣小组对社区内该年龄段的部分居民展开了随机问卷调查(每人只能选择其中一项),并将调查数据整理后绘成如下两幅不完整的统计图.请根据图中信息解答下列问题:(1)求参与问卷调查的总人数. (2)补全条形统计图.(3)该社区中20~60岁的居民约8000人,估算这些人中最喜欢微信支付方式的人数.【考点】VC :条形统计图;V5:用样本估计总体;VB :扇形统计图. 【专题】542:统计的应用.【分析】(1)根据喜欢支付宝支付的人数÷其所占各种支付方式的比例=参与问卷调查的总人数,即可求出结论;(2)根据喜欢现金支付的人数(41~60岁)=参与问卷调查的总人数×现金支付所占各种支付方式的比例﹣15,即可求出喜欢现金支付的人数(41~60岁),再将条形统计图补充完整即可得出结论;(3)根据喜欢微信支付方式的人数=社区居民人数×微信支付所占各种支付方式的比例,即可求出结论.【解答】解:(1)(120+80)÷40%=500(人).答:参与问卷调查的总人数为500人.(2)500×15%﹣15=60(人).补全条形统计图,如图所示.(3)8000×(1﹣40%﹣10%﹣15%)=2800(人).答:这些人中最喜欢微信支付方式的人数约为2800人.【点评】本题考查了条形统计图、扇形统计图以及用样本估计总体,解题的关键是:(1)观察统计图找出数据,再列式计算;(2)通过计算求出喜欢现金支付的人数(41~60岁);(3)根据样本的比例×总人数,估算出喜欢微信支付方式的人数.20.(8分)(2018•金华)如图,在6×6的网格中,每个小正方形的边长为1,点A在格点(小正方形的顶点)上.试在各网格中画出顶点在格点上,面积为6,且符合相应条件的图形.【考点】N4:作图—应用与设计作图. 【专题】13 :作图题.【分析】利用数形结合的思想解决问题即可; 【解答】解:符合条件的图形如图所示:【点评】本题考查作图﹣应用与设计,三角形的面积,平行四边形的性质等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.21.(8分)(2018•金华)如图,在Rt △ABC 中,点O 在斜边AB 上,以O 为圆心,OB 为半径作圆,分别与BC ,AB 相交于点D ,E ,连结AD .已知∠CAD=∠B . (1)求证:AD 是⊙O 的切线.(2)若BC=8,tanB=12,求⊙O 的半径.【考点】ME :切线的判定与性质;T7:解直角三角形. 【专题】55A :与圆有关的位置关系.【分析】(1)连接OD,由OD=OB,利用等边对等角得到一对角相等,再由已知角相等,等量代换得到∠1=∠3,求出∠4为90°,即可得证;(2)设圆的半径为r,利用锐角三角函数定义求出AB的长,再利用勾股定理列出关于r的方程,求出方程的解即可得到结果.【解答】(1)证明:连接OD,∵OB=OD,∴∠3=∠B,∵∠B=∠1,∴∠1=∠3,在Rt△ACD中,∠1+∠2=90°,∴∠4=180°﹣(∠2+∠3)=90°,∴OD⊥AD,则AD为圆O的切线;(2)设圆O的半径为r,在Rt△ABC中,AC=BCtanB=4,根据勾股定理得:AB=42+82=45,∴OA=45﹣r,在Rt△ACD中,tan∠1=tanB=1 2,∴CD=ACtan∠1=2,根据勾股定理得:AD2=AC2+CD2=16+4=20,在Rt△ADO中,OA2=OD2+AD2,即(45﹣r)2=r2+20,解得:r=35 2.【点评】此题考查了切线的判定与性质,以及勾股定理,熟练掌握切线的判定与性质是解本题的关键.22.(10分)(2018•金华)如图,抛物线y=ax2+bx(a<0)过点E(10,0),矩形ABCD的边AB在线段OE上(点A在点B的左边),点C,D在抛物线上.设A (t,0),当t=2时,AD=4.(1)求抛物线的函数表达式.(2)当t为何值时,矩形ABCD的周长有最大值?最大值是多少?(3)保持t=2时的矩形ABCD不动,向右平移抛物线.当平移后的抛物线与矩形的边有两个交点G,H,且直线GH平分矩形的面积时,求抛物线平移的距离.【考点】HF:二次函数综合题.【专题】15 :综合题;535:二次函数图象及其性质;558:平移、旋转与对称.【分析】(1)由点E的坐标设抛物线的交点式,再把点D的坐标(2,4)代入计算可得;(2)由抛物线的对称性得BE=OA=t,据此知AB=10﹣2t,再由x=t时AD=﹣14t2+52t,根据矩形的周长公式列出函数解析式,配方成顶点式即可得;(3)由t=2得出点A、B、C、D及对角线交点P的坐标,由直线GH平分矩形的面积知直线GH必过点P,根据AB∥CD知线段OD平移后得到的线段是GH,由线段OD的中点Q平移后的对应点是P知PQ是△OBD中位线,据此可得.【解答】解:(1)设抛物线解析式为y=ax(x﹣10),∵当t=2时,AD=4,∴点D的坐标为(2,4),∴将点D坐标代入解析式得﹣16a=4,解得:a=﹣1 4,抛物线的函数表达式为y=﹣14x2+52x;(2)由抛物线的对称性得BE=OA=t , ∴AB=10﹣2t ,当x=t 时,AD=﹣14t 2+52t ,∴矩形ABCD 的周长=2(AB +AD ) =2[(10﹣2t )+(﹣14t 2+52t )]=﹣12t 2+t +20 =﹣12(t ﹣1)2+412,∵﹣12<0,∴当t=1时,矩形ABCD 的周长有最大值,最大值为412;(3)如图,当t=2时,点A 、B 、C 、D 的坐标分别为(2,0)、(8,0)、(8,4)、(2,4), ∴矩形ABCD 对角线的交点P 的坐标为(5,2),当平移后的抛物线过点A 时,点H 的坐标为(4,4),此时GH 不能将矩形面积平分;当平移后的抛物线过点C 时,点G 的坐标为(6,0),此时GH 也不能将矩形面积平分;∴当G 、H 中有一点落在线段AD 或BC 上时,直线GH 不可能将矩形的面积平分, 当点G 、H 分别落在线段AB 、DC 上时,直线GH 过点P 必平分矩形ABCD 的面积, ∵AB ∥CD ,∴线段OD 平移后得到的线段GH ,∴线段OD 的中点Q 平移后的对应点是P , 在△OBD 中,PQ 是中位线, ∴PQ=12OB=4,所以抛物线向右平移的距离是4个单位.【点评】本题主要考查二次函数的综合问题,解题的关键是掌握待定系数法求函数解析式、二次函数的性质及平移变换的性质等知识点.23.(10分)(2018•金华)如图,四边形ABCD 的四个顶点分别在反比例函数y=m x与y=n x(x >0,0<m <n )的图象上,对角线BD ∥y 轴,且BD ⊥AC 于点P .已知点B 的横坐标为4. (1)当m=4,n=20时.①若点P 的纵坐标为2,求直线AB 的函数表达式.②若点P 是BD 的中点,试判断四边形ABCD 的形状,并说明理由.(2)四边形ABCD 能否成为正方形?若能,求此时m ,n 之间的数量关系;若不能,试说明理由.【考点】GB :反比例函数综合题. 【专题】15 :综合题.【分析】(1)①先确定出点A ,B 坐标,再利用待定系数法即可得出结论; ②先确定出点D 坐标,进而确定出点P 坐标,进而求出PA ,PC ,即可得出结论; (2)先确定出B (4,m 4),进而得出A (4﹣t ,m 4+t ),即:(4﹣t )(m 4+t )=m ,即可得出点D (4,8﹣m4),即可得出结论.【解答】解:(1)①如图1,∵m=4,∴反比例函数为y=4 x ,当x=4时,y=1,∴B(4,1),当y=2时,∴2=4 x ,∴x=2,∴A(2,2),设直线AB的解析式为y=kx+b,∴2k+b=2 4k+b=1,∴k=−1 2b=3,∴直线AB的解析式为y=﹣12x+3;②四边形ABCD是菱形,理由如下:如图2,由①知,B(4,1),∵BD∥y轴,∴D(4,5),∵点P是线段BD的中点,∴P(4,3),当y=3时,由y=4x得,x=43,由y=20x得,x=203,∴PA=4﹣43=83,PC=203﹣4=83,∴PA=PC,∵PB=PD,∴四边形ABCD为平行四边形,∵BD⊥AC,∴四边形ABCD 是菱形;(2)四边形ABCD 能是正方形,理由:当四边形ABCD 是正方形,记AC ,BD 的交点为P , ∴PA=PB=PC=PD ,(设为t ,t ≠0), 当x=4时,y=m x=m4,∴B (4,m4),∴A (4﹣t ,m 4+t ),C (4+t ,m4+t ),∴(4﹣t )(m 4+t )=m ,∴t=4﹣m 4, ∴C (8﹣m4,4), ∴(8﹣m 4)×4=n ,∴m +n=32,∵点D 的纵坐标为m4+2t=m4+2(4﹣m 4)=8﹣m4,∴D (4,8﹣m4),∴4(8﹣m4)=n ,∴m +n=32.【点评】此题是反比例函数综合题,主要考查了待定系数法,平行四边形的判定,菱形的判定和性质,正方形的性质,判断出四边形ABCD是平行四边形是解本题的关键.24.(12分)(2018•金华)在Rt△ABC中,∠ACB=90°,AC=12.点D在直线CB 上,以CA,CD为边作矩形ACDE,直线AB与直线CE,DE的交点分别为F,G.(1)如图,点D在线段CB上,四边形ACDE是正方形.①若点G为DE中点,求FG的长.②若DG=GF,求BC的长.(2)已知BC=9,是否存在点D,使得△DFG是等腰三角形?若存在,求该三角形的腰长;若不存在,试说明理由.【考点】LO :四边形综合题. 【专题】152:几何综合题.【分析】(1)①只要证明△ACF ∽△GEF ,推出FG AF =EG AC,即可解决问题;②如图1中,想办法证明∠1=∠2=30°即可解决问题;(2)分四种情形:①如图2中,当点D 中线段BC 上时,此时只有GF=GD ,②如图3中,当点D 中线段BC 的延长线上,且直线AB ,CE 的交点中AE 上方时,此时只有GF=DG ,③如图4中,当点D 在线段BC 的延长线上,且直线AB ,EC 的交点中BD 下方时,此时只有DF=DG ,如图5中,当点D 中线段CB 的延长线上时,此时只有DF=DG ,分别求解即可解决问题;【解答】解:(1)①在正方形ACDE 中,DG=GE=6, 中Rt △AEG 中,AG= AE 2+EG 2=6 5, ∵EG ∥AC , ∴△ACF ∽△GEF , ∴FG AF =EG AC ,∴FG AF =612=12,∴FG=13AG=2 5.②如图1中,正方形ACDE 中,AE=ED ,∠AEF=∠DEF=45°, ∵EF=EF ,∴△AEF ≌△DEF ,∴∠1=∠2,设∠1=∠2=x , ∵AE ∥BC , ∴∠B=∠1=x , ∵GF=GD , ∴∠3=∠2=x ,在△DBF 中,∠3+∠FDB +∠B=180°, ∴x +(x +90°)+x=180°,解得x=30°,∴∠B=30°,∴在Rt △ABC 中,BC=AC tan 30°=12 3.(2)在Rt △ABC 中,AB= AC 2+BC 2= 122+92=15,如图2中,当点D 中线段BC 上时,此时只有GF=GD ,∵DG ∥AC ,∴△BDG ∽△BCA ,设BD=3x ,则DG=4x ,BG=5x ,∴GF=GD=4x ,则AF=15﹣9x ,∵AE ∥CB ,∴△AEF ∽△BCF ,∴AE BC =AF BF , ∴9−3x 9=15−9x9x ,整理得:x 2﹣6x +5=0,解得x=1或5(舍弃)∴腰长GD 为=4x=4.如图3中,当点D 中线段BC 的延长线上,且直线AB ,CE 的交点中AE 上方时,此时只有GF=DG ,设AE=3x ,则EG=4x ,AG=5x ,∴FG=DG=12+4x ,∵AE ∥BC ,∴△AEF ∽△BCF ,∴AE BC =AF BF , ∴3x 9=9x +129x +27,解得x=2或﹣2(舍弃),∴腰长DG=4x +12=20.如图4中,当点D 在线段BC 的延长线上,且直线AB ,EC 的交点中BD 下方时,此时只有DF=DG ,过点D 作DH ⊥FG .设AE=3x ,则EG=4x ,AG=5x ,DG=4x +12,∴FH=GH=DG•cos ∠DGB=(4x +12)×45=16x +485,∴GF=2GH=32x +965, ∴AF=GF ﹣AG=7x +965,∵AC ∥DG , ∴△ACF ∽△GEF ,∴AC EG =AF FG ,∴124x =7x +96532x +965, 解得x=12 147或﹣12 147(舍弃), ∴腰长GD=4x +12=84+48 147,如图5中,当点D 中线段CB 的延长线上时,此时只有DF=DG ,作DH ⊥AG 于H . 设AE=3x ,则EG=4x ,AG=5x ,DG=4x ﹣12,∴FH=GH=DG•cos ∠DGB=16x−485, ∴FG=2FH=32x−965, ∴AF=AG ﹣FG=96−7x 5, ∵AC ∥EG ,∴△ACF ∽△GEF ,∴AC EG =AF FG ,∴124x =96−7x 532x−965, 解得x=12 147或﹣12 147(舍弃), ∴腰长DG=4x ﹣12=−84+48 147,综上所述,等腰三角形△DFG 的腰长为4或20或84+48 147或−84+48 147.【点评】本题考查四边形综合题、正方形的性质、矩形的性质、相似三角形的判定和性质、锐角三角函数、平行线的性质、勾股定理等知识,解题的关键是学会用分类讨论的思想思考问题,属于中考压轴题.。
浙江省宁波市2018年中考科学真题试卷及答案(word版)

浙江省宁波市2018年中考科学真题试卷及答案(word版)宁波市2018年初中学业水平考试科学试题考生须知:1.全卷分试题卷I、试题卷I和答题卷。
试题卷共8页,有4个大题,33个小题。
满分为180分,考试时间为120分钟。
2.请将姓名、准考证号分别填写在试题卷和答题卷的规定位置上。
3.答题时,把试题卷I的答案在答题卷I上对应的选项位置用2B铅笔涂黑、涂满。
将试题卷Ⅱ答案用黑色字迹的钢笔或签宇笔书写,答案必须按照题号顺序在答题卷各题目规定区域内作答,做在试题卷上或超出答题区域书写的答案无效。
4. 本卷可能用到的相对原子质量:H:1 C:12 N:14 0:16 Na:23 C1:35.5 Fe:56 Cu:64 Ag:108本卷g取10N/kg试题卷I一、选择题(本题共15小题.第1-10小题,每小题4分,第11-15小题,每小题3分,共55分。
请选出每小题中一个符合题意的选项,不选错选均不给分)1.树立和践行”绿水青山就是金山银山”的理念建设美国宁波。
下列做法不符合...该理念的是()A.对河道开展清淤保洁工作B. 提们步行或骑单车等出行B.燃煤电厂安装脱硫农置 D. 现们焚烧枯杆增加土壤肥力2.在粗盐提纯的实验中,下列操作不.规.范.的是()3. 甲型流行性感冒是甲型流感病毒引起的人禽共患的传染病。
下列有关说法正确的是()A.甲型流感病毒是该病的病原体B.甲型流感病毒具有完整的细胞结构C.甲型流感病毒性状由体内蛋白质控制D.接种流感疫苗获得的免疫是非特异性免疫4. 下列事例中,改变物体内能的途径与其他三项不同..的是()5. 2018年1月31日晚,我国大部分地区能观察到罕见的“月全食+超级月亮+蓝月亮”三最合一的天文奇观。
下列说法正确的是()A.月相变化的周期为27.3日B.当天是我国的农历初一C.当天太阳直射点位于地球的南半球D.月全食时月亮处于地球和太阳之间6. 我国未来的航母将采用自行研制的电磁弹射器。
浙江省金华市2018年中考化学真题试题(含答案)

浙江省金华市2018年中考化学真题试题一、选择题(本大题共有15小题,每小题3分,共45分。
每小题只有一个选项是正确的,不选、多选、错选均不给分)6.如图是微信热传的“苯宝宝表情包”,苯(化学式C6H6)、六氯苯(化学式C6Cl6)都是重要的化工原料,下列有关说法正确的是()A.苯分子由碳、氢两种元素组成B.苯中氢元素的质量分数小于10%C.六氯苯中碳氯两种元素的质量比为1:1D.六氯苯由6个碳原子和6个氯原子构成8.“丹砂烧之成水银”中的“丹砂”指的是硫化汞。
该反应的微观示意图如下,有关说法正确的是()A.“●”代表非金属单质汞B.此反应遵循质量守恒定律C.反应前后原子的种类发生改变D.反应前后各元素的化合价都不变12.20℃时,在各盛有100克水的烧杯中,分别加入10克甲、乙、丙三种纯净物(不含结晶水,不与水反应),充分溶解后,结果如图。
下列说法正确的是()A.所得溶液可能都是饱和溶液B.20℃时,乙溶液的溶质质量最小C.溶液溶质的质量分数:甲>丙>乙D.升高温度,溶液溶质的质量分数一定变大14.用所给实验器材(规格和数量不限),就能顺利完成相应实验的是()19.中国是全球第一个实现在海域“可燃冰”试开采中获得连续稳定产气的国家。
“可燃冰”是甲烷和水在低温、高压条件下形成的水合物(CH4·nH2O)。
(1)在常温常压下,“可燃冰”会发生反应:CH4·nH2O=CH4+nH2O,该反应属于(填基本反应类型);(2)甲烷可制成合成气(CO、H2),再制成甲醇(CH3OH),代替日益供应紧张的燃油。
由合成气制甲醇的反应方程式为:CO+2H2一定条件CH3OH,由甲烷制成合成气有两种方法:①CH4+H2O一定条件CO+3H2②2CH4+O2一定条件2CO+4H2从原料配比角度比较方法①和②,更适宜用于合成甲醇的方法是(填序号)。
23.A、B、C、D是初中科学常见的四种物质,其中A、B属于相同物质类别的化合物,C、D物质类别不同,它们之间的转化和反应关系如图。
浙江省金华市2018年中考数学试卷(Word版-含答案)

2018年浙江省金华市中考数学试卷一、选择题(本题有10小题,每小题3分,共30分)1.(3分)在0,1,﹣,﹣1四个数中,最小的数是()A.0 B.1 C.D.﹣12.(3分)计算(﹣a)3÷a结果正确的是()A.a2B.﹣a2 C.﹣a3 D.﹣a43.(3分)如图,∠B的同位角可以是()A.∠1 B.∠2 C.∠3 D.∠44.(3分)若分式的值为0,则x的值为()A.3 B.﹣3 C.3或﹣3 D.05.(3分)一个几何体的三视图如图所示,该几何体是()A.直三棱柱B.长方体C.圆锥D.立方体6.(3分)如图,一个游戏转盘中,红、黄、蓝三个扇形的圆心角度数分别为60°,90°,210°.让转盘自由转动,指针停止后落在黄色区域的概率是()A.B.C.D.7.(3分)小明为画一个零件的轴截面,以该轴截面底边所在的直线为x轴,对称轴为y轴,建立如图所示的平面直角坐标系.若坐标轴的单位长度取1mm,则图中转折点P的坐标表示正确的是()A.(5,30)B.(8,10)C.(9,10)D.(10,10)8.(3分)如图,两根竹竿AB和AD斜靠在墙CE上,量得∠ABC=α,∠ADC=β,则竹竿AB与AD的长度之比为()A.B.C.D.9.(3分)如图,将△ABC绕点C顺时针旋转90°得到△EDC.若点A,D,E在同一条直线上,∠ACB=20°,则∠ADC的度数是()A.55°B.60°C.65°D.70°10.(3分)某通讯公司就上宽带网推出A,B,C三种月收费方式.这三种收费方式每月所需的费用y(元)与上网时间x(h)的函数关系如图所示,则下列判断错误的是()A.每月上网时间不足25 h时,选择A方式最省钱B.每月上网费用为60元时,B方式可上网的时间比A方式多C.每月上网时间为35h时,选择B方式最省钱D.每月上网时间超过70h时,选择C方式最省钱二、填空题(本题有6小题,每小题4分,共24分)11.(4分)化简(x﹣1)(x+1)的结果是.12.(4分)如图,△ABC的两条高AD,BE相交于点F,请添加一个条件,使得△ADC≌△BEC(不添加其他字母及辅助线),你添加的条件是.13.(4分)如图是我国2013~2017年国内生产总值增长速度统计图,则这5年增长速度的众数是.14.(4分)对于两个非零实数x,y,定义一种新的运算:x*y=+.若1*(﹣1)=2,则(﹣2)*2的值是.15.(4分)如图2,小靓用七巧板拼成一幅装饰图,放入长方形ABCD内,装饰图中的三角形顶点E,F分别在边AB,BC上,三角形①的边GD在边AD上,则的值是.16.(4分)如图1是小明制作的一副弓箭,点A,D分别是弓臂BAC与弓弦BC 的中点,弓弦BC=60cm.沿AD方向拉弓的过程中,假设弓臂BAC始终保持圆弧形,弓弦不伸长.如图2,当弓箭从自然状态的点D拉到点D1时,有AD1=30cm,∠B1D1C1=120°.(1)图2中,弓臂两端B1,C1的距离为cm.(2)如图3,将弓箭继续拉到点D2,使弓臂B2AC2为半圆,则D1D2的长为cm.三、解答题(本题有8小题,共66分,各小题都必须写出解答过程)17.(6分)计算:+(﹣2018)0﹣4sin45°+|﹣2|.18.(6分)解不等式组:19.(6分)为了解朝阳社区20~60岁居民最喜欢的支付方式,某兴趣小组对社区内该年龄段的部分居民展开了随机问卷调查(每人只能选择其中一项),并将调查数据整理后绘成如下两幅不完整的统计图.请根据图中信息解答下列问题:(1)求参与问卷调查的总人数.(2)补全条形统计图.(3)该社区中20~60岁的居民约8000人,估算这些人中最喜欢微信支付方式的人数.20.(8分)如图,在6×6的网格中,每个小正方形的边长为1,点A在格点(小正方形的顶点)上.试在各网格中画出顶点在格点上,面积为6,且符合相应条件的图形.21.(8分)如图,在Rt△ABC中,点O在斜边AB上,以O为圆心,OB为半径作圆,分别与BC,AB相交于点D,E,连结AD.已知∠CAD=∠B.(1)求证:AD是⊙O的切线.(2)若BC=8,tanB=,求⊙O的半径.22.(10分)如图,抛物线y=ax2+bx(a≠0)过点E(10,0),矩形ABCD的边AB在线段OE上(点A在点B的左边),点C,D在抛物线上.设A(t,0),当t=2时,AD=4.(1)求抛物线的函数表达式.(2)当t为何值时,矩形ABCD的周长有最大值?最大值是多少?(3)保持t=2时的矩形ABCD不动,向右平移抛物线.当平移后的抛物线与矩形的边有两个交点G,H,且直线GH平分矩形的面积时,求抛物线平移的距离.23.(10分)如图,四边形ABCD的四个顶点分别在反比例函数y=与y=(x >0,0<m<n)的图象上,对角线BD∥y轴,且BD⊥AC于点P.已知点B的横坐标为4.(1)当m=4,n=20时.①若点P的纵坐标为2,求直线AB的函数表达式.②若点P是BD的中点,试判断四边形ABCD的形状,并说明理由.(2)四边形ABCD能否成为正方形?若能,求此时m,n之间的数量关系;若不能,试说明理由.24.(12分)在Rt△ABC中,∠ACB=90°,AC=12.点D在直线CB上,以CA,CD 为边作矩形ACDE,直线AB与直线CE,DE的交点分别为F,G.(1)如图,点D在线段CB上,四边形ACDE是正方形.①若点G为DE中点,求FG的长.②若DG=GF,求BC的长.(2)已知BC=9,是否存在点D,使得△DFG是等腰三角形?若存在,求该三角形的腰长;若不存在,试说明理由.参考答案与试题解析一、选择题(本题有10小题,每小题3分,共30分)1.D.2.B.3.D.4.A.5.A.6.B.7.C.8.B.9.C.10.D.二、填空题(本题有6小题,每小题4分,共24分)11.x2﹣112.AC=BC.13. 6.9%.14.﹣115..16.30,10﹣10,三、解答题(本题有8小题,共66分,各小题都必须写出解答过程)17.解:原式=2+1﹣4×+2=2+1﹣2+2=3.18.解:解不等式+2<x,得:x>3,解不等式2x+2≥3(x﹣1),得:x≤5,∴不等式组的解集为3<x≤5.19.解:(1)(120+80)÷40%=500(人).答:参与问卷调查的总人数为500人.(2)500×15%﹣15=60(人).(3)8000×(1﹣40%﹣10%﹣15%)=2800(人).答:这些人中最喜欢微信支付方式的人数约为2800人.20.解:符合条件的图形如图所示;21.(1)证明:连接OD,∵OB=OD,∴∠3=∠B,∵∠B=∠1,∴∠1=∠3,在Rt△ACD中,∠1+∠2=90°,∴∠4=180°﹣(∠2+∠3)=90°,∴OD⊥AD,则AD为圆O的切线;(2)设圆O的半径为r,在Rt△ABC中,AC=BCtanB=4,根据勾股定理得:AB==4,∴OA=4﹣r,在Rt△ACD中,tan∠1=tanB=,∴CD=ACtan∠1=2,根据勾股定理得:AD2=AC2+CD2=16+4=20,在Rt△ADO中,OA2=OD2+AD2,即(4﹣r)2=r2+20,解得:r=.22.解:(1)设抛物线解析式为y=ax(x﹣10),∵当t=2时,AD=4,∴点D的坐标为(2,4),∴将点D坐标代入解析式得﹣16a=4,解得:a=﹣,抛物线的函数表达式为y=﹣x2+x;(2)由抛物线的对称性得BE=OA=t,∴AB=10﹣2t,当x=t时,AD=﹣t2+t,∴矩形ABCD的周长=2(AB+AD)=2[(10﹣2t)+(﹣t2+t)]=﹣t2+t+20=﹣(t﹣1)2+,∵﹣<0,∴当t=1时,矩形ABCD的周长有最大值,最大值为;(3)如图,当t=2时,点A、B、C、D的坐标分别为(2,0)、(8,0)、(8,4)、(2,4),∴矩形ABCD对角线的交点P的坐标为(5,2),当平移后的抛物线过点A时,点H的坐标为(4,4),此时GH不能将矩形面积平分;当平移后的抛物线过点C时,点G的坐标为(6,0),此时GH也不能将矩形面积平分;∴当G、H中有一点落在线段AD或BC上时,直线GH不可能将矩形的面积平分,当点G、H分别落在线段AB、DC上时,直线GH过点P必平分矩形ABCD的面积,∵AB∥CD,∴线段OD平移后得到的线段GH,∴线段OD的中点Q平移后的对应点是P,在△OBD中,PQ是中位线,∴PQ=OB=4,所以抛物线向右平移的距离是4个单位.23.解:(1)①如图1,∵m=4,∴反比例函数为y=,当x=4时,y=1,∴B(4,1),当y=2时,∴2=,∴x=2,∴A(2,2),设直线AB的解析式为y=kx+b,∴,∴,∴直线AB的解析式为y=﹣x+3;②四边形ABCD是菱形,理由如下:如图2,由①知,B(4,1),∵BD∥y轴,∴D(4,5),∵点P是线段BD的中点,∴P(4,3),当y=3时,由y=得,x=,由y=得,x=,∴PA=4﹣=,PC=﹣4=,∴PA=PC,∵PB=PD,∴四边形ABCD为平行四边形,∵BD⊥AC,∴四边形ABCD是菱形;(2)四边形ABCD能是正方形,理由:当四边形ABCD是正方形,∴PA=PB=PC=PD,(设为t,t≠0),当x=4时,y==,∴B(4,),∴A(4﹣t,+t),∴(4﹣t)(+t)=m,∴t=4﹣,∴点D的纵坐标为+2t=+2(4﹣)=8﹣,∴D(4,8﹣),∴4(8﹣)=n,∴m+n=32.24.解:(1)①在正方形ACDE中,DG=GE=6,中Rt△AEG中,AG==6,∵EG∥AC,∴△ACF∽△GEF,∴=,∴==,∴FG=AG=2.②如图1中,正方形ACDE中,AE=ED,∠AEF=∠DEF=45°,∵EF=EF,∴△AEF≌△DEF,∴∠1=∠2,设∠1=∠2=x,∵AE∥BC,∴∠B=∠1=x,∵GF=GD,∴∠3=∠2=x,在△DBF中,∠3+∠FDB+∠B=180°,∴x+(x+90°)+x=180°,解得x=30°,∴∠B=30°,∴在Rt△ABC中,BC==12.(2)在Rt△ABC中,AB===15,如图2中,当点D中线段BC上时,此时只有GF=GD,∵DG∥AC,∴△BDG∽△BCA,设BD=3x,则DG=4x,BG=5x,∴GF=GD=4x,则AF=15﹣9x,∵AE∥CB,∴△AEF∽△BCF,∴=,∴=,整理得:x2﹣6x+5=0,解得x=1或5(舍弃)∴腰长GD为=4x=4.如图3中,当点D中线段BC的延长线上,且直线AB,CE的交点中AE上方时,此时只有GF=DG,设AE=3x,则EG=4x,AG=5x,∴FG=DG=12+4x,∵AE∥BC,∴△AEF∽△BCF,∴=,∴=,解得x=2或﹣2(舍弃),∴腰长DG=4x+12=20.如图4中,当点D在线段BC的延长线上,且直线AB,EC的交点中BD下方时,此时只有DF=DG,过点D作DH⊥FG.设AE=3x,则EG=4x,AG=5x,DG=4x+12,∴FH=GH=DG•cos∠DGB=(4x+12)×=,∴GF=2GH=,∴AF=GF﹣AG=,∵AC∥DG,∴△ACF∽△GEF,∴=,∴=,解得x=或﹣(舍弃),∴腰长GD=4x+12=,如图5中,当点D中线段CB的延长线上时,此时只有DF=DG,作DH⊥AG于H.设AE=3x,则EG=4x,AG=5x,DG=4x﹣12,∴FH=GH=DG•cos∠DGB=,∴FG=2FH=,∴AF=AG﹣FG=,∵AC∥EG,∴△ACF∽△GEF,∴=,∴=,解得x=或﹣(舍弃),∴腰长DG=4x﹣12=,综上所述,等腰三角形△DFG的腰长为4或20或或.。
2023年浙江省金华市中考科学真题(含答案)

浙江省2023年初中学业水平考试(金华卷)科学试题卷卷Ⅰ一、选择题(本大题共有15小题,每小题3分,共45分.每小题只有一个选项是正确的,不选、多选、错选均不给分)1.每年的6月5日是世界环境日.今年我国的主题是“建设人与自然和谐共生的现代化”,尊重自然、顺应自然、保护自然是这一主题的内在要求。
下列行为不符合这一主题的是()A.垃圾分类处理,做到变废为宝B.工业废气直接排放,提高经济效益C.建立自然保护区,保护生物多样性D.合理使用化肥农药,提高粮食产量2.某些高层建筑的玻璃幕墙会产生强烈的镜面反射,造成光污染。
下列各图中光学现象的原理与玻璃幕墙发生镜面反射的原理相同的是()A.林中光束B.拱桥倒影C.水中铅笔D.人手影子3.地球是人类赖以生存的家园。
下列关于地球的认识正确的是()A.地球自转的方向为自东向西B.地球是一个正球体C.火山和地震多发生在板块内部D.地球从内到外分为地核、地幔、地壳三层4.“健康生活,珍爱生命”。
下列关于健康生活的叙述错误的是()A.坚持体育锻炼,养成良好习惯B.不与异性交往,保持身心健康C.学会与人相处,乐观开朗合群D.远离毒品,不要吸烟、酗酒5.实验规范操作是实验成功的关键。
粗盐提纯实验中,下列实验操作正确的是()A.称量B.溶解C.过滤D.蒸发6.分布在地球各处的水处于不断运动和相互转化之中。
如图为部分水循环的示意图,下列有关水循环说法正确的是()A.图中环节②代表水汽输送,环节②代表降水B.水会不断地循环,无需提倡节约用水C.地球上的水,大部分以气态形式存在于大气中D.水循环中,水仅在固液两态之间相互转化7.如图为我国首列永磁磁浮列车“兴国号”运行的照片。
“兴国号”列车利用永磁体和水磁轨道之间的排斥力,能“悬挂”在空中行驶,大大减轻了城市交通压力。
下列说法正确的是()A.列车转弯时,水平方向受到平衡力的作用B.以行驶的列车为参照物,永磁轨道是静止的C.“兴国号”与传统火车相比,减少了行驶时与轨道间的摩擦力D.列车刹车后继续向前滑行,是因为受到惯性力的作用8.观察和实验是学习科学的重要方法。
浙江省宁波市2018年中考科学真题试卷及答案版

XX市2018年初中学业水平考试科学试题XX号考生须知:1.全卷分试题卷I、试题卷I和答题卷。
试题卷共8页,有4个大题,33个小题。
总分值为180分,考试时间为120分钟。
2.请将XX、XX号分别填写在试题卷和答题卷的规定位置上。
3.答题时,把试题卷I的答案在答题卷I上对应的选项位置用2B铅笔涂黑、涂满。
将试题卷Ⅱ答案用黑色字迹的钢笔或签宇笔书写,答案必须按照题号顺序在答题卷各题目规定区域内作答,做在试题卷上或超出答题区域书写的答案无效。
4. 本卷可能用到的相对原子质量:H:1 C:12 N:14 0:16 Na:23 C1:35.5 Fe:56 Cu:64 Ag:108本卷g取10N/kg试题卷I一、选择题(此题共15小题.第1-10小题,每题4分,第11-15小题,每题3分,共55分。
请选出每题中一个符合题意的选项,不选错选均不给分)该理念的1.树立和践行〞绿水青山就是金山银山〞的理念建立美国XX。
以下做法不符合...是〔〕A.对河道开展清淤保洁工作B.提们步行或骑单车等出行B.燃煤电厂安装脱硫农置D. 现们燃烧枯杆增加土壤肥力的是〔〕2.在粗盐提纯的实验中,以下操作不.标准..3.甲型流行性感冒是甲型流感病毒引起的人禽共患的传染病。
以下有关说法正确的选项是〔〕A.甲型流感病毒是该病的病原体B.甲型流感病毒具有完整的细胞构造C.甲型流感病毒性状由体内蛋白质控制D.接种流感疫苗获得的免疫是非特异性免疫的是〔〕4.以下事例中,改变物体内能的途径与其他三项不同..5. 2018年1月31日晚,我国大局部地区能观察到罕见的“月全食+超级月亮+蓝月亮〞三最合一的天文奇观。
以下说法正确的选项是〔〕A.月相变化的周期为27.3日B.当天是我国的农历初一C.当天太阳直射点位于地球的南半球D.月全食时月亮处于地球和太阳之间6.我国未来的航母将采用自行研制的电磁弹射器。
电磁弹射器的弹射车与飞机前轮连接,并处于强磁场中,当弹射车内的导体通以强电流时,舰载机受到强大的推力而快速起飞。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2018年浙江金华中考真题科学卷 一、选择题 1.2018年中国环境日主题为“美丽中国,我是行动者”为共建天蓝,地绿、水清的美丽金华,下列措施不可取的是 A.加大空气质量检测,改善环境状况 B.生活垃圾分类回收,垃圾资源化 C.大量使用农药化肥,提高粮食产量 D.大力开展五水共治,保护水资源 2.每年4〜5月有些桂花树上长着紫蓝色的果子(如图)。桂果是一种中药原材料,有润肺止疼等功效。桂花树在分类上属于
A.被子植物 B.裸子植物 C.蕨类植物 D.苔藓植物 3.下列关于家庭电路及安全用电的说法正确的是 A.只要人体接触火线都会发生触电亊故 B.低于36伏的电压对人体一定是安全的 C.测电笔可用于检测物体带正电还是带负电 D.使用三脚插头是为防止触电而采取的安全措施 4.地球上的水处于不停地运动之中,下列不属于水循环主要环节的是 A.蒸发 B.径流 C.太阳辑射 D.水汽输送 5.如图是微信热传的“苯宝宝表情包”,苯(化学式C6H6),六氯苯(化学式C6Cl4)都是重要的化工原料,下列有关说法正确的是
A.苯分子由碳、氢两种元素组成 B.苯中氢元素的质量分数小于10% C.六氯苯中碳氯两种元素的质量比为1:1 D.六氯苯由6个磷原子和6个氯原子构成 6.松材线虫病被称为“松树痛症”,松材线虫通过松褐天牛传播,寄生在木质部,破坏细胞,导致松树枯死。如图为松树茎的横切面,松材线虫寄生的部位是 A.甲 B.乙 C.丙 D. 丁 7.限于活动范围,人们通常无法直接观察地球的形状,但可通过身边某些现象和事件找到地球是球体的证据,下列现象和事件不能作为证据的是 A.麦哲伦环球航行 B.太空拍摄的地球照片 C.铅笔在篮球和木板上移动的位置变化 D.海面上远去的船只船身比桅杆先消失 8.“丹砂烧之成水银”中的“丹砂”指的是硫化汞,该反应的微观示意图如下,有关说法正确的是
A.“”代表非金属单质汞 B.此反应遵循质量守恒定律 C.反应前后原子的种类发生改变 D.反应前后各元素的化合价都不变 9.岸上景物在湖水中形成清晰的倒影(如图),下列有关“水中倒影”的说法正确的是
A.是光的反射形成的虚像 B.是光的折射形成的虚像 C.是光沿直线传播形成的影子 D,“水中倒彩”比岸上景物大一些 10.血液流经人体器官b时,血液中某种物质含量的变化用曲线表示,如图。下列说法错误的是
A.若是O2含量的变化,b代表肺 B.若是CO2含量的变化,b可代表脑 C.若是尿素含量的变化,b代表肾脏 D.若是饭后葡萄糖含量的变化,b代表小肠 11.2018年3月月14日,患有“渐冻症”的杰出物理学家斯带芬·金去世。“渐冻症”是由于传出神经元受损引起的。在一个以肌肉为效应器的反射弧中,假如传出神经受损,其它结构正常,当感受器接受信息刺激后将会 A.有感觉但不能运动 B.失去感觉但能运动 C.既有感觉又能运动 D.失去感觉同时不能运动 12.20℃时,在各盛有100克水的烧杯中,分别加入10克甲、乙、丙三种纯净物(不含结晶水,不与水反应),充分溶解后,结果如图。下列说法正确的是
A.所得溶液可能都是饱和溶液 B.20℃时,乙溶液的溶质质量最小 C.溶液溶质的质量分数:甲>丙>乙 D.升高温度,溶液溶质的质量分数一定变大 13.2018年2月22日,在短道速滑男子500米决赛中,武大靖为中国赢得平昌冬奥会首枚金牌。下列说法正确的是 A.把冰刀磨得很锋利,是为了增大摩擦力 B.冲过终点后不能立即停止滑行,是因为运动员具有惯性 C.以滑行中的运动员作为参照物,观众是静止的 D.运动员用力蹬冰面就会向前运动,说明力是维持物体运动的原因 14.用所给实验器材(规格和数量不限),就能顺利完成相应实验的是 选项 相应实验 实验器材(省略夹持装置) A 硫酸铜晶体的制备和生长 烧杯、玻璃棒、蒸发皿、量筒 B 分离氯化钾和二氧化锰的混合物 烧杯、玻璃棒、胶头滴管、滤纸 C 用固体氯化钠配制5%的溶液 烧杯、玻璃、胶头滴管、量筒 D 用pH试纸测定溶液的酸碱性强弱 烧杯、玻璃棒、pH试纸、标准比色卡 A.A B.B C.C D.D 15.如图,用刻度均匀的匀质杠杆进行“杠杆平衡条件”的实验(每个钩码重为0.5牛)。下列说法正确的是
A.实验前出现图甲所示情况,应将杠杆的平衡螺母向左调 B.图乙,在AB处各增加一个钩码,杠杆仍然能保持平衡 C.图丙,弹簧测力计从a位置转到b,为保持杠杆在水平位置平衡,其示数需变大 D.图丁,用弹簧测力计在c点向上拉杠杆,为保持杠杆在水平位置平衡,其示数小于3牛 二、填空题 16.小科在实验室发现一枚钢针,为能快速利用小磁针判断:①钢针是否有磁性,②若有磁性则磁极如何分布,小科画出思维导图,请补充完整:
17.2018年5月29日(农历四月十五),这一天金华市昼______夜(填“长于”或“短于”),当天的月相最接近下图中的______(填字母)。
A.下弦月 B.新月 C.上弦月 D.满月 18.小科在观察洋葱表皮细胞实验的过程中,观察到下列物像(如图):
(1)制作装片时,先要在洁净的载玻片中央滴一滴______。 (2)观察时,看到了物像D,在此之前看到的物像依次是____________。 19.中国是全球第一个实现在海域“可燃冰”试开采中获得连续稳定产气的国家。“可燃冰”是甲烷和水在低温、高压条件下形成的水合物(CH4·nH2O), (1)在常温常压下,“可燃冰”会发生反应:CH4·NH2O== CH4+nH2O,该反应属于______(填基本反应类型); (2)甲烷可制成合成气(CO,H2),再制成甲醇(CH3OH),代替日益供应紧张的燃油,由合
成气制甲醇的反应方程式为:232COHCHOH+一定条件,由甲烷制成合成气有两种方法: ①4223CHHOCOH+一定条件+
②422224CHOCOH+一定条件+ 从原料配比角度比较方法①和②,更适宜用于合成甲醇的方法是______(填序号)。 20.杯子放在水平桌面上,放入茶叶,再倒入开水,茶叶先漂浮在水面上,过一段时间,茶叶逐渐下沉到杯底。
()茶叶漂浮在水面,是因为浮力______重力(填“大于”、“小于”或“等于"); (2)茶叶匀速下沉阶段(不考虑水的蒸发),茶杯对桌面的压力将______(填“变大”、“变小”或“不变”)。 21.2017年11月27日、12月5日,克隆猴“中中”、“华华”相继在中科院某研究所诞生,它们是采用同一只猴的体细胞克隆的,这标志着中国率先开启以体细胞克隆猴作为实验动物的新时代。猴的克隆过程(如图),请回答:
(1)克隆猴的生殖方式属于______。 (2)“中中”、“华华”的生物性状由DNA分子上的______控制。 22.在一个玻璃瓶里放一些湿棉花,将浸泡过的蚕豆种子摆放在瓶壁和湿棉花之间(如图)。将玻璃瓶放置在温暖的地方数天,观察种子的萌发情况。
(1)该实验可以探究植物根的______性; (2)放置湿棉花是考虑到种于萌发需要____________。 23.A,B,C,D是初中科学常见的四种物质,其中A,B属于相同物质类别的化合物,C,D物质类别不同,它们之间的转化和反应关系如图。图中“→”表示某一种物质经一步反 应可转化为另一种物质,“一”表示相连两物质能发生化学反应,部分反应物、生成物及反应条件已略去,请回答:
(1)若C是二氧化碳,B是氢氧化钙,则B→A的化学方程式是____________; (2)若C是锌,A和B都属于酸,写出D可能的化学式____________(物质类别不同的两种即可) 24.用如图所示的电路图研究“电流与电阻的关系”.电流表量程为“0~0.6A",电压表量程为“0~3V”,滑动变阻器的规格为“50Ω 1A”,电源电压3伏恒定不变。在AB间分别接入阻值不同的电阻R,移动滑动变阻器的滑片,使电压表示数保持2伏不变,读出电流表示数并记录。
(1)分析表中数据,可得出的实验结论是_____________________。 (2)为了使实验结论更可靠,控制AB间电压2伏不变,再多测几组数据,AB间允许接入电阻R的取值范围是_______欧。 25.有一包白色固体可能含有碳酸钠、硫酸钠、硝酸钡、氢氧化钠中的一种或几种.某个科学兴趣小组为探究其成分做了以下实验: ①取少量固体于烧杯中,加足量的水溶解,烧杯内有固体残留并得到无色溶液甲; ②取少量无色溶液甲于试管中,滴加酚酞溶液,溶液不变色; ③继续向①的烧杯中滴加稀硝酸并不断搅拌,烧杯内固体的质量随加入稀硝酸质量的变化如图所示。
(1)仅通过①可以得出的结论是:原白色固体中一定有______________; (2)无色溶液甲中一定不存在的物质是( )(填字母) A.碳酸钠 B.硫酸钠 C.硝酸钡 D.氢氧化钠 三、实验探究题 6.小巧同学发现她家种的牵牛花,早晨为红色,大阳出来后颜色逐渐加深,中午呈紫色。她很好奇,于是设计实验进行探究。 【提出问题】花瓣颜色变化是否与光照有关? 【实验步骤】①早晨,她选取两组生长状况相同,且均开红花的牵牛花,编号A和B;②A组放在阳光下,B组遮光处理,其它条件相同且适宜;③中午,观察花的颜色、记录实验现象:A组为紫色,B组为红色;④得出实验结论。请回答: (1)实验中的变量是_______; (2)上述实验得出的结论是______________; 【拓展反思】查找资料发现:牵牛花的细胞液中含有花青素,它在酸性条件下显红色、中性条件下显紫色;细胞液的酸碱性强弱受其中的二氧化碳含量影响。 (3)从植物生理活动的角度分析,牵牛花花瓣从红色变为紫色的原因是_____________________。 27,相关资料表明,大部分重大交通事故是因为汽车超载超速造成的。兴趣小组决定对超载超速问题进行一次模拟探究,经讨论后认为,可以用小球作为理想模型,代替汽车作为研究对象。如图,将小球从高度为h的同一斜面上由静止开始滚下,推动同一小木块向前移动一
