样本 2015-2016学年度第二学期五周练习
【最新】岭南版美术教案五年级下册
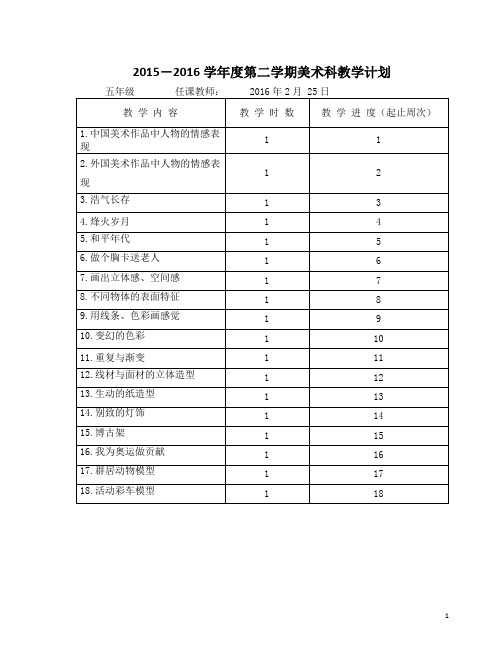
2015-2016学年度第二学期美术科教学计划2015——2016学年度第二学期第十册美术教案1、中国美术作品中人物的情感表现教学目标:1. 知识与技能感知中国美术作品种人物的面部情感及动态表现;2. 了解中国美术作品的相关历史知识及艺术表现的形式美重点、难点:1.从作品的人物造型、动态、表情,理解人物的真实情感,从而更好地理解作品的内涵。
2.如何解决作品的丰富内涵与学生的生活阅历及审美经验的差距。
课前准备:准备人物情感的图片、美术作品教学活动:一、导入千百年来,艺术家们通过无数优秀的作品表达了人类的丰富情感,我们可以从中感受到人生的喜怒哀乐。
让我们先看看中国的艺术家是怎样通过美术语言来表达人物情感的。
二、欣赏活动1. 活动一:观察与思考——《流民图》A.谈谈对《流民图》的第一印象或总体印象。
B .中国画独特的长卷形式与人物画技法的简要介绍。
C.作品的时代背景与场景气氛。
D.画家和画家的创作动机介绍。
E.对作品中人物身份、年龄、性别、衣着、道具等方面的分析。
F.作品中人物造型、肢体动作、五官描写与情感表达的关系。
G.作品如何通过人物情感的表达来解释作品的主题。
2. 活动二:观察与思考——《说唱俑》赏析A.作品第艺术形式与诞生年代。
B.人物身份、动态分析。
C.作品人物表达了什么情感?作者是通过那些造型要素来表现情感的?D.用对比手法谈谈对《说唱俑》与《流民图》的不同观感。
3. 活动三:体验与评价A.举例说明美术作品通过那些方面来表现情感?B.用恰当词汇表达欣赏某幅人物作品的感受,如欢乐、悲伤、轻松……C.画出生活中人物某种情感的头像,或临摹他人作品。
三、板书设计中国美术作品中人物的情感表现《流民图》《说唱俑》课后反思:2、外国美术作品中人物的情感表现教学目标:1. 欣赏感受外国美术作品中的任务造型及情感表现;2. 初步了解外国美术作品的性观历史知识及艺术美。
教学重点、难点:从欣赏中了解外国美术作品的情感表现,主要通过人物造型、动态、表情,了解人物的真实情感。
人教版数学八年级下册—第二学期新课程素质能力测试

-------------------------------------------------------------------奋斗没有终点任何时候都是一个起点----------------------------------------------------- 信达 初中数学试卷 2015—2016学年度第二学期新课程素质能力测试八年级(下)
数学试题 第二十章 数据的分析测试题 时限.100分钟 满分.120分 命题人:周艺 班级____姓名_____得分_____ 一.选择题(本大题共12个小题,每小题3分,共36分。在每小题给出的四个选项中,只有一项是满足题目要求的,请把其代号填在答题栏中相应题号的下面)。
题号 1 2 3 4 5 6 7 8 9 10 11 12 答案 1.数据5,3,2,1,4的平均数是 A. 2 B. 5 C. 4 D. 3 2.六个学生进行投篮比赛,投进的个数分别为2,3,3,5,10,13,这六个数的中位数是 A.3 B.4 C.5 D.6 3.10名学生的体重分别是41,48,50,53,49,53,53,51,67(单位:kg),这组数据的众数是
A.67 B.53 C.50 D.49 4.人数相等的甲.乙两班学生参加了同一次数学测验,班平均分和方差分别为 =82分,82-------------------------------------------------------------------奋斗没有终点任何时候都是一个起点----------------------------------------------------- 信达 分, 245分190分那么成绩较为整齐的是 A.甲班 B.乙班 C.两班一样整齐 D.无法确定 5.某电视台举办的青年歌手电视大奖赛上,六位评委给3号选手的评分如下:90,96, 91,96,95,94,这组数据的中位数是
【中小学资料】广东省北京师范大学东莞石竹附属学校2015-2016学年八年级生物下学期期中试题(无答案) 新人

广东省北京师范大学东莞石竹附属学校2015-2016学年八年级生物下学期期中试题单项选择题(每题2分,共100分,请把正确答案填在答题卡的答案栏中)关节的基本结构包括关节头,关节囊和关节腔误的是( )A .病毒第二次侵入后,人体内产生的抗体大量增多B .人体所产生的抗体只能对该种病毒有免疫作用C .第一次侵染后所形成的免疫功能属于非特异性免疫D .人体内能够产生抗体的细胞属于血液中白细胞的一种6、夏季是细菌性痢疾的多发季节,为预防该传染病的发生与流行,防疫部门严禁学校食堂二次销售部分剩余饭菜,该传染病的类型和防疫.A.植物组织培养 B.大棚黄瓜嫁接 C.克隆羊多莉的培育D.“试管婴儿”的培育A.分子生物学为判断各种生物之间的亲缘关系提供了依据B.与人类亲缘关系最近的生物是黑猩猩 C.与人类亲缘关系最远的动物是金枪鱼D.各种生物细胞色素C含量不同,说明他们的原始祖先不同12.如图是四种动物之间亲缘关系的图解,下列有关解释正确的是()A.小熊猫和熊猫的亲缘关系最近B.熊猫和熊食性差别较大,亲缘关系较远C.四种“熊”体细胞内的染色体数目和形态不同D.海豚与四种“熊”的生殖发育特点不同13.在寿光蔬菜博览园内,每年都有大量的蔬菜新品种展出,新品种的培育与广泛推广极大丰富了人们的菜篮子,同时根本上丰富了()A.遗传的多样性 B.物种的多样性C.生态系统的多样性 D.植物种类的多样性14. 培养细菌和真菌的一般方法通常包括以下步骤,正确的排列顺序是()①高温灭菌②配制培养基③将接种后的培养基放在适宜的温度下培养④接种.A.③①②④ B.②④③① C.①④③② D.②①④③15.在“检测不同环境中的细菌和真菌”的探究实验中,下列有关说法不正确的是()A.用无菌棉棒擦取手心后在培养基上轻轻涂抹,就是接种B.培养用的培养皿和培养基,在接种前必须进行高温灭菌处理C.本实验需要设置对照实验 D.接种后的培养基应再次进行高温灭菌处理16. “秋风起,食腊味”,广式腊味选在气候干燥的秋季进行晒制,其主要目的是A.脱去肉内的水分 B.使肉的色泽金黄好看C.使蛋白质分解为氨基酸 D.让肉发酵,产生独特香味.17.下列实例应用了转基因技术的是()A.克隆羊 B.高产抗倒伏小麦 C.试管婴儿 D.生产胰岛素的大肠杆菌18.下列生物中,没有细胞结构的是()A.大肠杆菌 B.变形虫 C.酵母菌 D.绿脓杆菌噬菌体19.如图表示Ⅰ、Ⅱ两种生物之间的关系.下列各组生物的关系不符合图示曲线的是()A.地衣中的真菌与藻类 B.豆科植物与根瘤菌C.草食动物与胃肠内的纤维细菌 D.人与链球菌20. 在人体内,艾滋病病毒只有寄生在淋巴细胞内才可繁殖,分析其原因在于()A.艾滋病病毒的组成物质中没有蛋白质 B.艾滋病病毒的组成物质中没有遗传物质C.艾滋病病毒不是生命体 D.艾滋病病毒没有细胞结构21.都属于无脊椎动物的一组是A、海马、海蜇B、蜜蜂、蜂鸟C、章鱼、带鱼D、蜘蛛、蜘蛛蟹22.下列各种动物结构与生理功能相适应的叙述,错误的是A. 兔牙齿的分化,与植食性相适应 B.鲫鱼有鳃,与水中呼吸相适应C.家鸽有坚硬角质喙,与飞行相适应 D.蛇体表覆盖角质鳞片,与减少体内水分散失相适应23.华枝睾吸虫、绦虫、蛔虫等寄生虫结构简单及结构特别发达的器官分别是()A.运动器官;消化器官 B.消化器官;生殖器官C.生殖器官;运动器官 D.消化器官;呼吸器官24.下列动物中,属于环节动物的是:()①蜈蚣②水螅③蛔虫④蚯蚓⑤小麦线虫⑥丝虫⑦水蛭⑧沙蚕.A.①②④ B.④⑦⑧ C.③⑤⑦ D.②⑤⑥25.下列不属于蟹、虾、蜈蚣、蜘蛛、蝗虫共同特征的是()A.身体分为头、胸、腹三部分 B.体表有外骨骼C.身体由许多体节构成 D.附肢分节26.在生长着许多水生植物的池塘中养鱼,经常可以看到鱼在黎明时浮头,甚至跳起.有下面几种猜测,你认为哪种更合理?()A.鱼喜欢阳光刺激B.鱼要在水面觅食 C.池水中含氧量较低D.池塘表面水较温暖27.青蛙是田园卫士,是人类的好朋友,我们要保护青蛙.下列有关青蛙的叙中,错误的是()A.幼体生活在水中,成体水陆两栖 B.幼体用鳃呼吸,成体主要用肺呼吸C.雌雄异体,受精作用在体内进行 D.幼体与成体差异很大,其发育过程为变态发育.爬行动物是真正的陆生脊椎动物,其身体表面能减少水分蒸发的结构是(①体表有羽毛②用肺呼吸并用气囊辅助呼吸③体温恒定④通过产卵繁殖后代A.兔的牙齿有分化,提高了摄取食物和对食物的消化能力B.蜥蜴的体表有角质的鳞片,可以防止体内水分的蒸发C.鱼鳃内含有丰富的毛细血管,有利于鱼在水中呼吸D.家鸽每呼吸一次,要在肺和气囊中各进行一次气体交换31. 保护生物的根本措施是()①保护生物的栖息地②保护生态系统的多样性③保护草原生态系统④保护家养动物、栽培植物和野生亲缘种的.A.①② B.①③ C.②③ D.③④32.如图表示四种动物的足印,请根据足印来判断哪种动物与狗的亲缘关系最近()33. 柑橘黄龙病是由严重危害柑橘类果树的黄龙病病毒引起的,这种病可以摧毁整个柑橘园。
合唱社团活动计划表

第十五周
6、6--------6、10 Nhomakorabea复习第十六周
6、13-----6、17
复习
第十七周
6、20------6、24
复习,总结
迎宾路小学少先大队部
第五周
3、28----4、1
合唱曲练习
在演唱时学生们表现很好,精神注意力集中。
学生有个别记不住歌词的现象。
第七周
4、5------4、8
合唱的基本功练习
学生运用科学的呼吸方法进行歌唱,并能按要求来进行呼吸练习,掌握正确的呼吸方法。
学生有个别记不住歌词的现象。需要教师加强督促。
第八周
4、11-----4、15
小学学生社团活动计划表
社团名称:风韵悠扬(2015 --2016)学年度第二学期
辅导教师:刘淑芬
周次
起止时间
活动内容
完成情况
出入原因
第一周
2、29------3、4
合唱的基本功练习
学生明白参加合唱队的目的、了解合唱队的功能
学生自制能力差,不能严格按老师的要求去做。
第二周
3、7-------3、11
合唱的基本功练习及歌曲合排
学生演唱时的呼吸,情绪需要加强练习。
第十一周
5、9-----5、13
合唱的基本功练习
部分同学不能遵循老师的讲解去练习
学生演唱时的呼吸,情绪需要加强练习。
第十二周
5、16------5、20
合唱的基本功练习
部分同学不能遵循老师的讲解去练习
第十三周
5、23------5、27
合唱的基本功练习
第十四周
5、30-------6、3
合唱的基本功练习
北京市海淀区2015-2016学年高一下期末练习数学试题含答案

海淀区高一年级第二学期期末练习数 学 2016.7学校 班级 姓名 成绩本试卷共100分.考试时间90分钟.一.选择题:本大题共8小题,每小题4分,共32分. 在每小题给出的四个选项中,只有一项是符合题目要求的.1. 不等式2230x x +-<的解集为 ( ) A. {|31}x x x <->或 B. {|13}x x x <->或 C. {|13}x x -<< D. {|31}x x -<<2. 若等差数列{}n a 中,33=a ,则{}n a 的前5项和5S 等于 ( )A .10B .15C .20D . 303.当3a =,5b =,7c =时,执行如图所示的程序框图,输出的m 值为 ( )A .12B .12-C .32D . 32-4.设,,a b c ∈R 且a b >,则下列不等式成立的是( ) A .b c a c -<- B .22ac bc >C .11a b <D .1ba<5.若向面积为2的ABC ∆内任取一点P ,并连接PB ,PC ,则PBC ∆的面积小于1的概率为 ( )A.14 B. 12 C. 23 D. 346.某小型服装厂生产一种风衣,日销售量x (件)与单价P (元)之间的关系为P =160-2x ,生产x 件所需成本为C (元),其中C =500+30x 元,若要求每天获利不少于1300元,则日销量x 的取值范围是 ( )A. 20≤x ≤30B. 20≤x ≤45C. 15≤x ≤30D. 15≤x ≤45 7. 在ABC ∆中,A ∠,B ∠,C ∠所对应的边分别为a ,b ,c . 若30C ∠=︒,2a c =,则B∠等于 ( ) A. 45︒ B. 105︒C. 15︒或105︒D. 45︒或135︒8.某校为了了解学生近视的情况,对四个非毕业年级各班的近视学生人数做了统计,每个年级都有7个班.如果某个年级的每个班的近视人数都不超过5人,则认定该年级为“学生视力保护达标年级”.这四个年级各班近视学生人数情况统计如下表:初一年级 平均值为2,方差为2 初二年级 平均值为1,方差大于0 高一年级 中位数为3,众数为4 高二年级平均值为3,中位数为4从表中数据可知:一定是“学生视力保护达标年级”的是 ( )A. 初一年级B.初二年级C.高一年级D.高二年级二.填空题:本大题共6小题,每小题4分,共24分.9.若实数,a b 满足02a <<,01b <<,则a b -的取值范围是 . 10.公比为2的等比数列{}n a 中,若123a a +=,则34a a +的值为 .11.如图,若5=N ,则输出的S 值等于_________.12.函数24()(0)x x f x x x-+-=>的最大值为_________, 此时x 的值为_________.13.高一某研究性学习小组随机抽取了100名年龄在10岁到60岁的市民进行问卷调查,并制作了频率分布直方图(如图),从图中数据可知a = .现从上述年龄在20岁到50岁的市民中按年龄段采用分层抽样的方法抽取30人,则在[)20,30年龄段抽取的人数应为_________.14.设数列{}n a 使得10a =,且对任意的*n ∈N ,均有1||n n a a n +-=,则3a 所有可能的取值构成的集合为 ;64a 的最大值为 .三.解答题:本大题共4小题,共44分. 解答应写出文字说明,证明过程或演算步骤. 15. (本小题满分12分)已知公差不为零的等差数列{}n a 满足11a =,2a 是1a 与5a 的等比中项(Ⅰ)求数列{}n a 的通项公式; (Ⅱ)设2n a nb =,判断数列{}n b 是否为等比数列. 如果是,求数列{}n b 的前n 项和n S ,如果不是,请说明理由.16. (本小题满分12分)如图,在ABC ∆中,点D 在BC 边上,60ADC ∠=︒,=2CD .(Ⅰ)若3AD BD ==,求ABC ∆的面积; (Ⅱ)若=2AD ,=4BD ,求sin B 的值.17. (本小题满分12分)某家电专卖店试销A 、B 、C 三种新型空调,连续五周销售情况如表所示:第一周 第二周 第三周 第四周 第五周 A 型数量/台 12 8 15 22 18 B 型数量/台 7 12 10 10 12 C 型数量/台C 1C 2C 3C 4C 5(Ⅰ)求 A 型空调平均每周的销售数量;(Ⅱ)为跟踪调查空调的使用情况,从该家电专卖店第二周售出的A 、B 型空调销售记录中,随机抽取一台,求抽到B 型空调的概率;(III )已知C 型空调连续五周销量的平均数为7,方差为4,且每周销售数量C 1,C 2,C 3,C 4,C 5互不相同,求C 型空调这五周中的最大销售数量.(只需写出结论)18. (本小题满分8分)高一某班级在学校数学嘉年华活动中推出了一款数学游戏,受到大家的一致追捧.游戏规则如下:游戏参与者连续抛掷一颗质地均匀的骰子,记第i次得到的点数为i x,若存在正整数n,使得126 nx x x+++=,则称n为游戏参与者的幸运数字.(Ⅰ)求游戏参与者的幸运数字为1的概率;(Ⅱ)求游戏参与者的幸运数字为2的概率.海淀区高一年级第二学期期末练习参考答案2016.7数 学阅卷须知:1.评分参考中所注分数,表示考生正确做到此步应得的累加分数.2.其它正确解法可以参照评分标准按相应步骤给分.一、选择题:本大题共8小题,每小题4分,共32分.1.D2.B3.B4.A5.D6.B7.C8.A二、填空题:本大题共6小题,每小题4分,共24分.(有两空的小题每空2分)9. (1,2)- 10. 12 11.5612. 3-, 2 13. 035.0 , 10 14. {3,1,1,3}-- , 2016三、解答题: 本大题共4小题,共44分.15.解:(Ⅰ)设等差数列{}n a 的公差为d (0≠d ),则由11a =得211a a d d =+=+;51414a a d d =+=+.--------------------------2分因为2a 是1a 与5a 的等比中项,所以2215a a a =⋅,即2(1)14d d +=+, --------------------------4分解得0d =(舍)或2d =, --------------------------5分 故数列{}n a 的通项公式为1(1)21n a a n d n =+-⋅=-.--------------------------6分(Ⅱ)由2n a nb =,得(1)当1n =时,11220a b ==≠--------------------------7分(2)当2n ≥时,12123122422n n a n n a n n b b ----===--------------------------9分 故数列{}n b 为以2为首项,4为公比的等比数列,有()111422411143n n n n q S b q --=⋅=⋅=⨯---.-------------------------12分16. (Ⅰ)解法一:当3AD BD ==时,ABD ∆的面积11393sin 332224ABD S AD BD ADB ∆=⋅⋅⋅∠=⋅⋅⋅=-----------2分 ACD ∆的面积11333sin 322222ACD S AD CD ADC ∆=⋅⋅⋅∠=⋅⋅⋅=-----------4分 ABC ∆的面积9333153424ABC ABD ACD S S S ∆∆∆=+=+=-----------5分解法二:当3AD BD ==时,过点A 作BC AE ⊥于点E ,如上图所示,--------2分因为060=∠ADC ,所以23360sin 3sin 0=⨯=∠=ADE AD AE .----------4分 又因为=2CD ,所以5=+=CD BD BC .所以ABC ∆的面积431521=⋅=∆AE BC S ABC .---------5分(Ⅱ)解法一:当2AD =,4BD =时,180120ADB ADC ∠=︒-∠=︒ ----------6分 在ADB ∆中,由余弦定理ADB BD AD BD AD AB ∠⋅-+=cos 2222 -----------7分 28214224222=⎪⎭⎫⎝⎛-⨯⨯⨯-+= 故27AB =. -----------9分 在ADB ∆中,由正弦定理得sin sin AB ADADB B=∠∠, -----------10分 即272sin 32B =∠,整理得3212sin 147B ∠==. -----------12分解法二:当2AD =,4BD =时,过点A 作BC AE ⊥于点E ,如图所示, -----------6分 因为060=∠ADC ,所以360sin 2sin 0=⨯=∠=ADE AD AE .---------7分160cos 2cos 0=⨯=∠=ADE AD DE , -----------9分 又因为4BD =,所以5=+=DE BD BE .所以7222=+=BE AE AB . -----------10分 所以321sin 1427AE B AB ===-----------12分17.解:(Ⅰ)A 型空调平均每周的销售数量12+8+15+22+18=155(台); ----------4分(Ⅱ)设“随机抽取一台,抽到B 型空调”为事件D , ----------5分 则事件D 包含12个基本事件, ----------6分 而所有基本事件个数为81220+=, ----------7分所以()123205P D ==; ----------8分(III )10台. ------------12分18.解:(Ⅰ)设“游戏参与者的幸运数字为1 ”为事件A -------------1分 由题意知61=x ,抛掷了1次骰子,相应的基本事件空间为{}6,5,4,3,2,1=ΩA ,共有6个基本事件, -------------2分 而{}6=A ,只有1个基本事件, ------------3分 所以61)(=A P ------------4分(Ⅱ)设“游戏参与者的幸运数字为2”为事件B , ------------5分 由题意知621=+x x ,抛掷了2次骰子,相应的基本事件空间为(){}N N ∈∈≤≤≤≤=Ω212121,,61,61,x x x x x x B , 共有36个基本事件, -----------6分而{})1,5(),2,4(),3,3(),4,2(),5,1(=B ,共有5个基本事件, ----------7分 所以365)(=B P . -----------8分注:第8题、第14题、第17题(Ⅲ)参考解答见第8题、第14题、第17题(Ⅲ)参考解答8.解:根据题目要求,如果符合“学生视力保护达标年级”,则需要该年级7个班的近视人数都不超过5人.为了便于说明,不妨设某年级各班的近视人数分别为)(7i 1≤≤i x ,并且1i x +≤i x .A. 初一年级:平均值为2,方差为2. 易知1471=∑=i ix且14)2(712=-∑=i i x .由于14<16,所以42<-i x ,由于只有7个样本且都为整数,所以可以把14分解成以下两种形式: ①22212314++=; ②222221122214++++=对于情况①,只能有一种情况:0,1,2,2,2,2,5;而情况②中可以有0,0,2,2,3,3,4和0,1,1,2,2,4,4这两种情况.B. 初二年级:平均值为1,方差大于0.如果出现的不符合的情况,在满足各班人数和为7的前提下,除了7x ,其他各班都尽量小即可,本选项的反例有以下两种:0,0,0,0,0,0,7;0,0,0,0,0,1,6.C. 高一年级:中位数为3,众数为4.易知34=x ,由于众数为4,可知765x x x ,,三个中至少有两个为4,如果出现的不符合的情况,则需要,465==x x 且57>x 即可,由于众数为4,所以其他每班的人数必须各不相同,所以本项的反例前六个班的近视人数只有0,1,2,3,4,4一种.D. 高二年级:平均值为3,中位数为4.易知44=x ,如果出现的不符合的情况,需要让321,,x x x 尽量小,所以令0321===x x x ,同时为了让7x 尽量的大,则只需令465==x x ,由已知可知2171=∑=i ix,所以此时97=x ,当然,对于本选项的反例还可以举出如下几种:0,0,1,4,4,4,8;0,0,0,4,4,5,8;0,0,2,4,4,4,7;0,1,1,4,4,4,7;0,0,0,4,4,6,7;0,0,0,4,5,5,7; 0,0,1,4,4,5,7;0,0,3,4,4,4,6;0,1,2,4,4,4,6;1,1,1,4,4,4,6;0,0,0,4,5,6,6;0,0,1,4,4,6,6; 0,0,1,4,5,5,6;0,0,2,4,4,5,6;0,1,1,4,4,5,6.综上,本项所涉及的三种情况均符合班的近视人数都不超过5人,所以初一年级符合“学生视力保护达标年级”.14. 设数列{}n a 使得10a =,且对任意的*n ∈N ,均有1||n n a a n +-=,则3a 所有可能的取值构成的集合为 ;64a 的最大值为 .解析: 设1n n n a a b +-=,则(1)若11b =, 22b =,则33a =若11b =-,22b =,则31a = 若11b =, 22b =-,则31a =- 若11b =-,12b =-,则33a =-(2)6411263a a b b b -=++⋅⋅⋅+注意到10a =,||n b n =,得 6412632016a ≤++⋅⋅⋅+=17.(Ⅲ)解:由于C 型空调的每周销售数量54321,,,,C C C C C 互不相同, 所以不妨设54321C C C C C <<<<,因为C 型空调连续五周销量的平均数为7,方差为4, 所以3551i i=∑=C,20)7-(51i 2i =∑=C .为了让C 型空调这五周中的最大周销售数量最大,即只需让5C 最大即可 , 由于20)7-(51i 2i=∑=C,所以易知115≤C , 当115=C 时,由于3551i i=∑=C,20)7-(51i 2i =∑=C ,所以2441i i=∑=C,421(7)4i i C =-=∑此时必然有64321====C C C C ,而与题目中所要求的每周销售数量54321,,,,C C C C C 互不相同矛盾,故115≠C . 当105=C 时,由于3551i i=∑=C,20)7-(51i 2i =∑=C ,所以2541i i=∑=C,11)7-(41i 2i =∑=C ,且37-i ≤C ,若不存在37-i =C 的情况,则∑=41i 2i)7-(C的最大值为11101144<=+++,所以必有37-1=C ,即41=C ,而此时2142i i=∑=C,2)7-(42i 2i =∑=C , 易知8,7,6432===C C C ,符合题意,故C 型空调的五周中的最大周销售数量为10台.。
方差分析1实验报告

.. . . . .实验报告课程名称生物医学统计分析实验名称方差分析1专业班级姓名学号实验日期实验地点2015—2016学年度第 2 学期组内38.842 20 1.942总数85.340 24分析:表2是方差分析的统计结果,由此可知,F=5.986,P=0.002〈0.01,可认为5个品种猪存在极显著差异,故须进行多重比较。
表3 5个品种猪增重的多重比较(LSD法)(I) 品种(J) 品种均值差 (I-J) 标准误显著性95% 置信区间下限上限LSD 1 2 3.0000*.8046 .001 1.322 4.6783 1.8667*.8439 .039 .106 3.6274 .5417 .8996 .554 -1.335 2.4185 3.5417*.8996 .001 1.665 5.4182 1 -3.0000*.8046 .001 -4.678 -1.3223 -1.1333 .8439 .194 -2.894 .6274 -2.4583*.8996 .013 -4.335 -.5825 .5417 .8996 .554 -1.335 2.4183 1 -1.8667*.8439 .039 -3.627 -.1062 1.1333 .8439 .194 -.627 2.8944 -1.3250 .9348 .172 -3.275 .6255 1.6750 .9348 .088 -.275 3.6254 1 -.5417 .8996 .554 -2.418 1.3352 2.4583*.8996 .013 .582 4.3353 1.3250 .9348 .172 -.625 3.2755 3.0000*.9854 .006 .944 5.0565 1 -3.5417*.8996 .001 -5.418 -1.6652 -.5417 .8996 .554 -2.418 1.3353 -1.6750 .9348 .088 -3.625 .2754 -3.0000*.9854 .006 -5.056 -.944*. 均值差的显著性水平为 0.05。
丰城中学-下学期高四周练试卷.docx
高中数学学习材料马鸣风萧萧*整理制作丰城中学2015-2016学年下学期高四周练试卷命题人:熊文宏审题人:高四文科数学备课组 2016.3.8一、选择题1、若偶函数的图像关于对称,且当时,,则函数的零点个数为()(A)(B)(C)(D)2、函数在区间 [0,]上的最大值为5,最小值为1,则的取值范围是()A .B . [0,2]C .( D. [2,4]3、若直线交抛物线于A,B两点,且线段AB中点到轴的距离为3,则( )A、12B、10C、8 D、64、已知函数f(x)=的图象与直线y=x恰有三个公共点,则实数m的取值范围是()A.(﹣∞,﹣1] B.[﹣1,2) C.[﹣1,2] D.[2,+∞)5、直线过点(-1,2)且与以点 (-3,-2)、 (4,0)为端点的线段恒相交,则的斜率取值范围是()A.[-,5] B.[-,0)∪(0,2] C.(-∞,-]∪[5,+∞) D.(-∞,-]∪[2,+∞)6、.在平面内,过定点P的直线与过定点Q的直线相交于点M,则的最大值为()A. B. C. 10 D.57、如图,已知A(4,0)、B(0,4),从点P(2,0)射出的光线经直线AB反射后再射到直线OB上,最后经直线OB反射后又回到P点,则光线所经过的路程是( ) A.2 B.6 C.3D.28、将函数图象上各点的横坐标伸长到原的2倍,再向左平移个单位,纵坐标不变,所得函数图象的一条对称轴的方程是()A. B. C. D.9、若向量且若则的值为( )A. B. C.D.10、在中,角A,B,C所对的边分别是,若,且则的面积等于A. B. C. D.11、已知函数的图像过原点,且在原点处的切线斜率是-3,则不等式组所确定的平面区域在内的面积为A.B.C.D.12、不等式ax2﹣2x+1<0的解集非空的一个必要而不充分条件是()A.a<1 B.a<0 C.0<a<1 D.a≤1二填空题13、在各项均为正数的等比数列中,若,则的最小值是.14、从集合中取两个不同的数,则的概率为.15、将边长为1的正方形ABCD沿对角线AC折起,使得平面ADC⊥平面ABC,在折起后形成的三棱锥D﹣ABC中,给出下列三个命题:①△DBC是等边三角形;②AC⊥BD;③三棱锥D﹣ABC的体积是.其中正确命题的序号是.(写出所有正确命题的序号)16、对五个样本点(1,2.98),(2,5.01),(3,m),(4,8.99),(6,13)分析后,得到回归直线方程为y=2x+1,则样本点中m为________.丰城中学2015-2016学年下学期高四周练答题卡班级: _____ 姓名:__________学号:_______ 得分:_______一、选择题(本大题共12个小题,每小题5分,共60分)题号1 2 3 4 5 6 7 8 9 10 11 12答案二、填空题(本大题共有5小题,每小题4分共20分.把答案填在题中横线上)13. 14. 15. 16.三、解答题:17、已知函数;(1)求函数的图象在点处的切线方程;(2)函数,若在定义域内恒成立,求k的最大值。
2015年下半年周次表
周次
日
一
二
三
四
五
六
备注
第一周
30
十七
31
十八
1/9
十九
2
廿
3
廿一
4
廿二
5
廿三
胜利日
第二周
6
廿四
7
廿五
8
廿六
9
廿七
10
廿八
11
廿九
12
三十
教师节
第三周
13
八月大
14
初二
15
初三
16
初四
17
初五
18
初六
19
初七
第四周
20
初八
21
初九
22
初十
23
初一
24
十二
25
十三
26
4
廿三
5
廿四
第十五周
6
廿五
7
廿六
8
廿七
9
廿八
10
廿九
11
十一月大
12
初二
第十六周
13
初三
14
初四
15
初五
16
初六
17
初七
18
初八
19
初九
第十七周
20
初十
21
十一
22
十二
23
十三
24
十四
25
十五
26
十六
第十八周
27
十七
28
十八
29
十九
30
廿
湖北省武汉市第二中学2015-2016学年高二数学上学期期末考试试题-理
武汉二中2015-2016学年度上学期期末考试高二理科数学试卷一、选择题: (本大题共12小题; 每小题5分, 共60分. 在每小题给出的四个选项中, 只有一个选项是符合题目要求的, 把正确选项的代号填在答题卡上. ) 1.两个事件对立是两个事件互斥的( )A.充分非必要条件B.必要非充分条件C.充要条件D.既不充分又不必要条件2.设某大学的女生体重y (单位:kg)与身高x (单位:cm)具有线性相关关系, 根据一组样本数据(x i , y i )(i =1,2, …, n ), 用最小二乘法建立的回归方程为y ^=0.85x -85.71, 则下列结论中不.正确的是( )A .y 与x 具有正的线性相关关系B .回归直线过样本点的中心(x , y )C .若该大学某女生身高增加1 cm, 则其体重约增加0.85 kgD .若该大学某女生身高为170 cm, 则可断定其体重必为58.79 kg 3.下列命题正确的是( ) A.若p , q 为两个命题, 则“p 且q 为真”是“p 或q 为真”的必要不充分条件; B.若p 为:2,20x R x x ∃∈+≤, 则p ⌝为:2,20x R x x ∀∈+>;C.命题p 为真命题, 命题q 为假命题。
则命题()p q ⌝∧, ()p q ⌝∨都是真命题;D.命题“若p ⌝, 则q ”的逆否命题是“若p , 则q ⌝”.4.从2003件产品中选取50件, 若采用下面的方法选取:先用简单随机抽样从2003件产品中剔除3件, 剩下的2000件再按系统抽样的方法抽取, 则每件产品被选中的概率 ( )A.不都相等B.都不相等C.都相等, 且为200350 D.都相等, 且为4015.在下列命题中: ①若向量a b 、共线, 则向量a b、所在的直线平行; ②若向量a b 、所在的直线为异面直线, 则向量a b 、不共面;③若三个向量a b c 、、两两共面, 则向量a b c、、共面; ④已知空间不共面的三个向量a b c 、、, 则对于空间的任意一个向量p, 总存在实数,,x y z , 使得p x a y b z c=++;其中正确的命题的个数是( ) A .0B . 1C . 2D . 36. 一个三位自然数百位、十位、个位上的数字依次为,,a b c , 当且仅当其中有两个数字的和等于第三 个数字时称为“有缘数”(如213, 341等). 若{},,1,2,3,4a b c ∈, 且,,a b c 互不相同, 任取一个三位 自然数, 则它是“有缘数”的概率是( )A.12B.13C.23D.347. 如果ξ~B ,1⎛⎫20 ⎪3⎝⎭, 则使P (ξ=k )取最大值时的k 值为( )A .5或6B .6或7C .7或8D .以上均错8. 已知实数[]1,9x ∈, 执行如图所示的程序框图, 则输出的x 小于55的概率为( )A.58B.38C.23D.139. 若()52ax x y++的展开式的各项系数和为243,则52x y 的系数为( )A.10B.20C.30D.6010. 若某同学连续三次考试的名次(第一名为1,第二名为2,依次类推且可以有名次并列情况)均不超过3,则称该同学为班级的尖子生.根据甲、乙、丙、丁四位同学过去连续三次考试的名次数据, 推断一定不是尖子生的是( ) A.甲同学:均值为2, 中位数为2 B.乙同学:均值为2, 方差小于1 C.丙同学:中位数为2, 众数为2 D.丁同学:众数为2, 方差大于1 11. 设甲、乙两人每次射击命中目标的概率分别为34和45, 且各次射击相互独立, 若按甲、乙、甲、乙……的次序轮流射击, 直到有一人击中目标就停止射击, 则停止射击时, 甲射击了两次的概率是( )A .380B .920C .925 D .1940012. 已知双曲线的左、右焦点分别是12F F 、,过2F 的直线交双曲线的右支于P Q 、两点,若112PF F F =,且2232PF QF =,则该双曲线的离心率为( )A.43 B.103C.2D.75二、填空题: (本大题共有4个小题, 每小题5分, 共20分. 把正确答案填在答题卡的相应位置. )13. 有5名数学实习老师,现将他们分配到高二年级的三个班实习,每班至少1名,最多2名,则不同的分配方案有 种(用数字作答).14.甲、乙两个小组各10名学生的英语口语测试成绩的茎叶图如图所示.现从这20名学生中随机抽取一人, 将“抽出的学生为甲小组学生”记为事件A ;“抽出的学生英语口语测试成绩不低于85分”记为事件B .则()P AB 的值是________.第14题 第15题15. 在一个正方体1111D C B A ABCD -中, P 为正方形1111D C B A 四边上的动点, O 为底面正方形ABCD 的中心,N M ,分别为BC AB ,的中点, 点Q 为平面ABCD 内一点, 线段Q D 1与OP 互相平分, 则满足MN MQ λ=的实数λ的值有_____个16. 已知圆224P x y y +=:及抛物线28S x y =:,过圆心P 作直线l ,此直线与上述两曲线的四个交点自左向右顺次记为A BC D 、、、,如果线段AB BC CD 、、的长度按此顺序构成一个等差数列,则直线l 的斜率为____________三、解答题: (本大题共6个小题, 共70分. 解答应写出文字说明、证明过程或推演步骤. )17. (本小题满分10分)已知命题p :方程11222=--m y m x 表示焦点在y 轴上的椭圆;命题q :双曲线1522=-mx y 的离心率)2,1(∈e , 若p 、q 有且只有一个为真, 求m 的取值范围.18. (本小题满分12分)设函数c bx x x f ++=2)(, 其中,b c 是某范围内的随机数, 分别在下列条件下, 求事件A “(1)5f ≤且(0)3f ≤”发生的概率. (1) 若随机数,{1,2,3,4}b c ∈;(2) 已知随机函数Rand()产生的随机数的范围为{}10≤≤x x , ,b c 是算法语句4Rand()b =*和4Rand()c =*的执行结果.(注: 符号“*”表示“乘号”)19. (本小题满分12分) 如图, 在三棱柱111ABC A B C -中, AB AC ⊥,顶点1A 在底面ABC 上的射影恰为点B , 且1 2.AB AC A B ===(1) 证明:平面1A AC ⊥平面1;AB B (2) 求棱1AA 与BC 所成的角的大小;(3) 若点P 为11B C 的中点, 并求出二面角1P AB A --的平面角的余弦值.20.(本小题满分12分)某市一高中经过层层上报, 被国家教育部认定为2015年全国青少年足球特色学校.该校成立了特色足球队, 队员来自高中三个年级, 人数为50人.视力对踢足球有一定的影响, 因而对这50人的视力作一调查.测量这50人的视力(非矫正视力)后发现他们的视力全部介于4.75和5.35之间, 将测量结果按如下方式分成6组:第一组[)4.75,4.85, 第二组[)4.85,4.95, …,第6组[]5.25,5.35,下图是按上述分组方法得到的频率分布直方图.又知:该校所在的省中, 全省喜爱足球的高中生视力统计调查数据显示:全省100000名喜爱足球的高中生的视力服从正态分布()5.01,0.0064N .⑴试评估该校特色足球队人员在全省喜爱足球的高中生中的平均视力状况;⑵求这50名队员视力在5.15以上(含5.15)的人数;⑶在这50名队员视力在5.15以上(含5.15)的人中任意抽取2人, 该2人中视力排名(从高到低)在全省喜爱足球的高中生中前130名的人数记为ξ,求ξ的数学期望.参考数据:若ξ~N(μ, σ 2), 则()P μσξμσ-<≤+= 0.6826,()220.9544P μσξμσ-<≤+=,()330.9974P μσξμσ-<≤+=21. (本小题满分12分)已知椭圆2222:1(0)x y C a b a b +=>>的离心率为3以原点O 为圆心, 椭圆C 的长半轴这半径的圆与直线260x +=相切. (1)求椭圆C 标准方程;(2)已知点,A B 为动直线(2)(0)y k x k =-≠与椭圆C 的两个交点, 问:在x 轴上是否存在点E , 使2EA EA AB +⋅为定值?若存在, 试求出点E 的坐标和定值, 若不存在, 说明理由.22. (本小题满分12分)在平面直角坐标系xOy 中, 已知点(1,2),Q P 是动点, 且三角形POQ 的三边所在直线的斜率满足111.OP OQ PQk k k += (1)求点P 的轨迹C 的方程;(2)过点D(1,0)任作两条互相垂直的直线12,l l , 分别交轨迹C 于点,A B 和M, N, 设线段,AB MN 的中点分别为,,E F求证:直线EF 恒过一定点.武汉二中2015-2016学年度上学期期末考试高二理科数学参考答案一、选择题:1-5 ADBCB 6-10 ABBCD 11-12 DD 二、填空题 13. 90 14. 5915.2 16. 三、解答题:17. 解:将方程11222=--m y m x 改写为11222=-+my m x , 只有当,021>>-m m 即310<<m 时,方程表示的曲线是焦点在y 轴上的椭圆,所以命题p 等价于310<<m ;………………………………………………………………………4分 因为双曲线1522=-mx y 的离心率)2,1(∈e , 所以0>m ,且1455<+<m,解得150<<m ,…………………………………6分 所以命题q 等价于150<<m ; ……………………………………………………8分 若p 真q 假,则∅∈m ;若p 假q 真,则1531<≤m 综上:m 的取值范围为1531<≤m ………………………………………………………10分 18.解:由c bx x x f ++=2)(知,事件A “(1)5f ≤且(0)3f ≤”,即4.3b c c +≤⎧⎨≤⎩ 1分(1) 因为随机数,{1,2,3,4}b c ∈,所以共等可能地产生16个数对(,)b c ,列举如下:(1,1),(1,2),(1,3),(1,4),(2,1),(2,2),(2,3),(2,4),(3,1),(3,2),(3,3),(3,4), (4,1),(4,2),(4,3),(4,4). 4分事件A :43b c c +≤⎧⎨≤⎩包含了其中6个数对(,)b c ,即:(1,1),(1,2),(1,3),(2,1),(2,2),(3,1).所以63()168P A ==,即事件A 发生的概率为3.8·············· 7分 (2) 由题意,,b c 均是区间[0,4]中的随机数,产生的点(,)b c 均匀地分布在边长为4的正方形区域Ω中(如图),其面积16)(=ΩS . ····························· 8分事件A :43b c c +≤⎧⎨≤⎩所对应的区域为如图所示的梯形(阴影部分),其面积为:115()(14)322S A =⨯+⨯=.10分所以15()152()()1632S A P A S ===Ω,即事件A 的发生概率为15.3212分 19.解:⑴证明:1A B ABC ⊥ 面,1A B AC ∴⊥,又AB AC ⊥,1AB A B B = ,1AC AB B ∴⊥面,1AC A AC ⊂ 面,1AB B ∴⊥1平面A AC 平面. 4分⑵以A 为原点建立如图所示的空间直角坐标系,则()()()12,0,0,0,2,0,0,2,2C B A ,()10,4,2B ,()12,2,2C , ()10,2,2AA = ,()112,2,0BC B C ==-,1111cos ,2AA BC AA BC AA BC===- , 故1AA 与棱BC 所成的角是3π. 8分 ⑶因为P 为棱11B C 的中点,故易求得()1,3,2P .设平面PAB 的法向量为()1,,n x y z =,则110,0n AP n AB ⎧=⎪⎨=⎪⎩,由()()1,3,20,2,0AP AB ⎧=⎪⎨=⎪⎩ ,得32020x y z y ++=⎧⎨=⎩,令1z =,则()12,0,1n =- , 而平面1ABA 的法向量()21,0,0n = .则121212cos ,5n n n n n n ===- . 由图可知二面角1P AB A --为锐角,故二面角1P AB A --的平面角的余弦值是5分 20.解:⑴由频率分布直方图知,该校特色足球队人员平均视力为4.8⨯0.1+4.9⨯0.2+5.0⨯0.3+5.1⨯0.2+5.2⨯0.1+5.3⨯0.1=5.03 高于全省喜爱足球的高中生的平均值5.01. 4分⑵由频率分布直方图知,后两组队员的视力在5.15以上(含5.15),其频率为0.2,人数为0.2⨯50=10,即这50名队员视力在5.15以上(含5.15)的人数为10人. 6分⑶()5.0130.08 5.0130.080.9974P ξ-⨯<≤+⨯= ,即()4.77 5.250.9974P ξ<≤=,()10.99745.250.00132P ξ-∴≥==,0.0013100000130⨯=. 8分 所以全省喜爱足球的高中生中前130名的视力在5.25以上.这50人中视力在5.25以上的有0.1⨯50=5人,这50名队员视力在5.15以上(含5.15)的人分为两部分:5人在5.25以上,5人在5.15 5.25. 9分 ∴随机变量ξ可取0,1,2,于是()252101020459C P C ξ====,()11552102551459C C P C ξ====,()252101022459C P C ξ====.2520121999E ξ∴=⨯+⨯+⨯=. 12分21. 解答.(1)由36=e 得36=a c ,即a c 36=① ………1分 又以原点O 为圆心,椭圆C 的长轴长为半径的圆为222a y x =+ 且与直线0622=+-y x 相切, 所以6)2(2622=-+=a 代入①得c=2, ………2分所以2222=-=c a b .所以椭圆C 的标准方程为12622=+y x ………4分 (2)由⎪⎩⎪⎨⎧-==+)2(12622x k y y x 得061212)31(2222=-+-+k x k x k ………6分 设()()1122,,,A x y B x y ,所以2221222131612,3112k k x x k k x x +-=+=+ ………8分根据题意,假设x 轴上存在定点E(m,0),使得⋅=⋅+=⋅+)(2为定值.则()()()21212211)(,,y y m x m x y m x y m x EB EA +--=-⋅-=⋅………9分 =()()()()()()22222221221231610123421km k m mmk x x m k x x k +-++-=++++-+ 要使上式为定值,即与k 无关,()631012322-=+-m m m , ………10分得37=m . ……11分 此时, 95622-=-=⋅+m , 所以在x 轴上存在定点E(37,0) 使得AB EA EA ⋅+2为定值,且定值为95-. ……12分22.解:⑴设点P 的坐标为(),P x y ,则OP y k x =,2OQ k =,21PQ y k x -=-,由111.OP OQ PQk k k += 得1122x x y y -+=-.整理得点P 的轨迹的方程为.()240,2y x y y =≠≠. 4分 ⑵设点,A B 的坐标为()11,A x y ,()22,B x y ,则点E 的坐标为1212,22x x y y ++⎛⎫⎪⎝⎭. 由题意可设直线1l 的方程为()()10y k x k =-≠由()241y x y k x ⎧=⎪⎨=-⎪⎩消去y 得()2222240k x k x k -++=,()224224416160k k k ∆=+-=+> 因为直线1l 与抛物线交于A,B 两点,所以12242x x k +=+,()121242y y k x x k+=+-=, 所以点E 的坐标为2221,k k ⎛⎫+⎪⎝⎭. 由题知,直线2l 的斜率为1k-,同理可得F 的坐标为()212,2k k +-. 当1k ≠±时,有222112k k+≠+.此时直线EF 的斜率为:2222221112EF kk k k k k k+==-+--所以直线EF 的方程为()222121k y k x k k +=---,整理得()231k y x k=--. 于是直线EF 恒过定点()3,0,当1k =±时,直线EF 的方程为3x =,也过点()3,0.综上所述,直线EF 恒过定点()3,0. 12分。
花样跳绳校本教案.(精选)
花样跳绳校本计划2015—2016 学年度第二学期 )一、指导思想:为全面贯彻素质教育的指导方针,使学生的德、智、体得到发展,使学生的智力、体力得到充分的自由的发挥,并根据学生身心发展的情况,特制定跳绳活动计划。
二、活动目标通过一定的培养,使学生更好的了解跳绳这项活动,能更好的热爱这项活动,使得跳的次数达到要求,并能形成良好的行为习惯,最后达到增强体质、促进身心发展的目标。
三、活动措施1、训练要求①必须严格遵守时间和训练内容。
②教师关注全体学生的训练。
③教师应进行科学训练,及时总结并做好记录。
④训练中注意安全,积极预防运动损伤的发生。
2、训练时间安排每周周四校本课程时间。
3、场地器材安排学校操场2 号场地。
器材方面:短绳由学生自备,长绳2 根由学校统一准备。
四、活动中应注意的问题:活动的目的是强身健体,因此在活动中,不能强行让学生跳绳,坚持自愿的原则,带伤的、有病的、身体不适应的学生不能参加。
五、活动内容安排孝直中学花样跳绳校本课时计划名称:花样跳绳辅导教师:展爱菊word.孝直中学花样跳绳校本课时计划名称:花样跳绳辅导教师:展爱菊word.孝直中学花样跳绳校本课时计划名称:花样跳绳辅导教师:展爱菊word.孝直中学花样跳绳校本课时计划名称:花样跳绳辅导教师:展爱菊word.名称:花样跳绳辅导教师:展爱菊名称:花样跳绳辅导教师:展爱菊名称:花样跳绳辅导教师:展爱菊名称:花样跳绳辅导教师:展爱菊名称:花样跳绳辅导教师:展爱菊孝直中学花样跳绳校本课时计划名称:花样跳绳辅导教师:展爱菊word.孝直中学花样跳绳校本课时计划名称:花样跳绳辅导教师:展爱菊word.孝直中学花样跳绳校本课时计划名称:花样跳绳辅导教师:展爱菊word.孝直中学花样跳绳校本课时计划名称:花样跳绳辅导教师:展爱菊word.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
复习课2015-2016学年度第二学期第五周复习题 作业布置 语文:1-3单元课下解释复习&文言文复习 地理:第六章复测题 生物:复习题
练习试题
七年级地理(第六章 认识大洲·单元测评) 一、选择题: “我们亚洲,山是高昂的头;我们亚洲,河像热血流„”听到这首《亚洲雄风》歌曲,我们的脑海中会涌现出一幅壮丽山河的画卷.据此回答1﹣2题. 1.“我们亚洲,山是高昂的头”,这里的“山”如果是世界的“头”那么这座山是指( ) A.天山 B.阿尔卑斯山 C.青藏高原 D.珠穆朗玛峰 2.“我们亚洲,河像热血流”是说亚洲河流众多,奔流不息,下列关于亚洲河流的叙述正确的是( ) A.大河都发源于中部高原、山地,呈放射状流入太平洋和印度洋 B.中南半岛河流自西向东流,说明地势西高东低 C.鄂毕河、叶尼塞河自南向北流,注入北冰洋 D.印度河主要流经印度,注入孟加拉湾 3.人类是世界的创造者,没有人类就没有现在这样多姿多彩的世界,然而世界人口分布是不平衡的,你知道现在什么地方人最多吗?如果从大洲和国家来看分别是( ) A.亚洲 印度 B.拉丁美洲 俄罗斯C.亚洲 中国 D.非洲 中国 4.羚羊在狂奔,长颈鹿伸着脖子吃树梢上的嫩枝绿叶,成群的斑玛向水草地迁移,凶猛的狮子和豹紧追其后,赶上落后的斑马,饱餐一顿.这种景观出现在撒哈拉以南非洲的( ) A.热带沙漠中 B.热带草原上 C.热带雨林中 D.温带草原上 5.东南亚流经国家最多的河流是( )A.伊洛瓦底江 B.萨尔温江 C.湄南河 D.湄公河 6.在欧洲分布最广泛而在亚洲缺失的气候类型是( ) A.温带海洋性气候 B.温带季风气候C.地中海气候 D.高山气候 7.亚洲东部季风气候典型的原因是( )A.地形复杂多样B.海陆差异大 C.纬度范围广 D.经度跨度大 8.世界最高和最低处都在亚洲,其中最低处在( )A.里海湖面 B.咸海湖面 C.死海湖面 D.青海湖面 9.混血人种比重最高的大洲是( )A.亚洲 B.北美洲 C.南美洲 D.大洋洲 10.下列关于非洲的世界之最的叙述,不正确的是( ) A.尼罗河是世界第一大河B.刚果盆地是世界上面积最大的盆地 C.撒哈拉沙漠是世界最大沙漠D.东菲裂谷带是世界陆地最长裂谷带 11.南北美洲的分界线是( ) A.美国与墨西哥的国界线B.中美地峡的巴拿马运河C.北冰洋与太平洋之间的白令海峡D.横贯美洲大陆的赤道 12.世界最大淡水湖群五大湖的形成原因是( )A.流水侵蚀B..地壳断裂C.、火山喷发 D..冰川侵蚀 13.新加坡,马来西亚,印度尼西亚等,终年高温多雨,这里的气候是( ) A.亚热带季风 B.热带季风 C.热带草原 D.热带雨林 14.乞力马扎罗山成为“赤道雪峰”的主要原因是( )A.地形因素 B.海陆因素 C.纬度因素 D.人为因素 15.有“非洲屋脊”之称的高原( )A.埃塞俄比亚高原 B.撒哈拉沙漠C.东非高原 D.南非高原 16.北冰洋与太平洋之间的通道是( )A.中美地峡 B.直布罗陀海峡 C.白令海峡 D.麦哲伦海峡 17.拉丁美洲居民主要通行的语言是( )A.汉语 B.英语C.西班牙语和葡萄牙语 D.俄语 18.小明在某一网站上搜到有关亚洲的地理知识,他认为其中有一处是错误的,请你找出来( ) A.亚洲称为“亚细亚”是世界上面积最大、人口最多的大洲 B.亚洲北、东、南、西分别临北冰洋、太平洋、印度洋和大西洋 C.亚洲地形以高原、山地为主,地面起伏大,高低悬殊,地势中部高,四周低 D.气候复杂多样,季风气候典型,气候的大陆性特征显著 19.亚洲和欧洲都有分布的气候类型是( ) ①温带季风气候②温带大陆性气候③地中海气候④热带草原气候. A.①② B.②③ C.①③ D.②④ 20.下列关于非洲的叙述,错误的是( ) A.非洲绝大部分位于低纬度,五带中以热带为主B.赤道跨非洲中部,东濒印度洋,西临大西洋 C.非洲在陆地上与亚欧两洲相邻,是世界古人类和古文明的发祥地 D.非洲长期受殖民统治,二战前只有三个独立国家 21.下列称号不符合非洲的是( )A.高原大陆 B.热带大陆 C.富饶大陆 D.湿热大陆 22.下列关于美洲的说法,错误的是( ) A.美洲又称阿美利加洲,地理大发现结束了亚、非、欧洲与美洲相互隔绝的局面 B.美洲最狭窄的地方是南北美洲的界线 C.美国以南的美洲叫拉丁美洲,拉丁美洲居民以黄色人种为主D.美洲西部(包括中美洲)多火山地震 23.下列关于美洲地形的说法,错误的是( ) A.科迪勒拉山系是世界上最长的山系,安第斯山是世界上最长的山脉 B.落基山脉是北美洲最长的山脉,亚马孙平原是南美洲最大的平原 C.南美洲西部是高大的安第斯山,东部高原与平原相间分布 D.美洲板块和太平洋板块碰撞形成科迪勒拉山系诸山脉 24.关于南美洲气候的叙述,错误的是( ) A.南美洲以热带气候为主,没有寒带B.南美洲主要的气候类型有热带雨林气候和热带草原气候 C.南美洲大部分地区年降水量在1000毫米以上,是世界上最湿润的大洲D.南美洲缺乏干燥的沙漠气候 25.关于美洲居民的说法,错误的是( ) A.美洲的土著居民因纽特人和印第安人都是黄色人种B.美洲的黑人是由欧洲殖民者当做奴隶从非洲贩运到美洲的C.南美洲人种复杂,美洲居民主要信仰基督教D.北美洲居民通用英语,拉丁美洲居民通用葡萄牙语 26.“亚细亚”意为( )A.日落之地 B.日出之地 C.东方日出之地 D.西方世界 27.世界上各种气候类型中,在亚洲没有分布的是( ) A.温带季风气候 B.温带海洋性气候C.地中海气候 D.热带雨林气候 28.除南极洲外,世界上海拔最高的大洲是( )A.南极洲 B.非洲 C.亚洲 D.欧洲 29.亚洲河网分布特点的叙述,正确的是( ) A.大河顺地势由中部高原山地呈放射状向四周奔流B.亚洲部分只有小面积的无流区 C.亚洲内流区面积广大,主要内流河有注入咸海的锡尔河和阿姆河D.高原山地区河网密,平原丘陵区河网疏 30.下列关于亚洲及欧洲人口的叙述,正确的是( ) A.在各大洲中,亚洲人口最多,欧洲人口密度最小B.目前欧洲是世界上人口分布最均匀的大洲 C.除南极洲外,欧洲是世界上人口最少的大洲D.世界上人口超过1亿的国家,大多数在亚洲和欧洲 31.二战前夕,非洲只有埃及、埃塞俄比亚、( )三个国家独立. A.南非 B.利比亚 C.利比里亚 D.肯尼亚 32.下列关于非洲气候类型分布的叙述,正确的是( ) A.气温高 B.季风气候显著C.干燥地区广大 D.气候带南北对称分布 33.世界上面积最大的热带草原分布在( )A.亚洲 B.欧洲 C.南美洲 D.非洲 34.下列关于非洲资源的说法,错误的是( ) A.矿产资源种类多,储量大B.桃花木、檀木、花梨木是热带雨林区的珍贵树种 C.大型野生动物的种类和数量均居世界各大洲之首D.金刚石、黄金、石油的储量和产量居世界首位 35.以下世界之最位于非洲的是( ) A.世界上最大的高原B.世界上最长的裂谷带C.世界上最大最典型的弧形群岛D.世界上面积最大的岛屿 36.美洲面积最大的国家是( )A.美国 B.加拿大 C.巴西 D.俄罗斯 37.关于南、北美洲气候和资源的比较,正确的是( ) A.西部沿海地区的气候类型都相同B.两洲都有大面积温带大陆性气候 C.东部高原都蕴藏着丰富的煤、铁资源D.两大洲气候都具有暖温的特征 38.好望角位于( )A.欧洲西南端 B.南美洲南端 C.非洲南端 D.亚洲东南端 39.下列四国中,北回归线和北极圈都穿过的国家是( )A.美国 B.中国 C.俄罗斯 D.加拿大 40.南美洲工业最发达的国家是( )A.巴西 B.阿根廷 C.智利 D.委内瑞拉 41.亚洲与北美洲的洲界线、俄罗斯与美国的国界线和日界线,“三线”穿过的海峡是( ) A.马六甲海峡 B.直布罗陀海峡 C.白令海峡 D.黑海海峡 42.南美洲和北美洲的分界线是( )A.巴拿马运河 B.白令海峡 C.苏伊士运河 D.乌拉尔山 43.以下别称所描述的地理事物都位于非洲的是( ) A.“地球之巅”、北半球的“寒极”B.“富饶大陆”、“赤道雪峰” C.世界人种大熔炉”、“高原大陆D.“玉米的故乡”、“热带大陆” 44.世界上最湿润的大洲是( )A.亚洲 B.欧洲 C.非洲 D.南美洲 45.世界上最长的山脉是什么,位于哪儿( ) A.喜马拉雅山脉,亚洲 B.落基山,北美洲C.安第斯山脉,南美洲 D.阿尔卑斯山脉,欧洲 46.来自撒哈拉以南的一位非洲游客介绍家乡情况,你认为不可信的是( ) A.我的家乡是世界上黑种人的故乡B.我的家乡自然资源丰富,南非的黄金产量居世界之首 C.我的家乡长期受殖民统治,经济非洲水平比较低,现在有的国家还未独立 D.你吃过香蕉吗?喝过咖啡吗?告诉你,它们的原产地就在我的家乡 47.按地理方位,将亚洲分为六个地区,我们所在的地区是( ) A.南亚地区 B.东亚地区 C.西亚地区 D.中亚地区 48.一艘油轮从波斯湾出发到西欧大西洋沿岸,它不可能经过的是( ) A.土耳其海峡 B.霍尔木兹海峡 C.苏伊士运河 D.直布罗陀海峡 49.下列说法,不正确的是( ) A.世界上最长的山脉是安第斯山脉B.拉丁美洲最早的居民是印第安人 C.拉丁美洲的大多数国家通用葡萄牙语D.东南亚的气候以热带雨林气候和温带大陆性气候为主 50.下面是世界上人口超过1亿的国家示意图,其中亚洲人口最多的两个国家是( ) A.中国 印尼 B.中国 日本 C.中国 印度 D.中国 巴西 51.有关亚洲的叙述,错误的是( ) A.地形类型复杂多样,以高原和山地为主 B.亚洲的分布最广的气候类型是温带大陆性气候 C.亚洲是世界上人口最多的大洲 D.亚洲的发达国家有日本、伊拉克、沙特阿拉伯
二、综合题 52.读非洲轮廓图,完成下列各题: (1)在图中适当位置填出地中海、几内亚湾南、北回归线及赤道的名称; (2)写出图中字母所代表的地理事物名称: ①国家:A__________、D__________; ②海域:B__________; (3)C是__________沙漠,它是世界上最大的沙 漠,该地是__________气候; E是__________河流,它流经世界最大的__________盆地,该地是__________气候; (4)从图中可以看出,非洲大部分位于__________带(温度带),所以它被称为__________. 53.读材料和图,完成下列要求. 材 料 2008年以来,索马里沿海经常发生海盗袭击事件,引起国际社会广泛关注.我国护航舰艇于2008年12月26日下午13时45分从海南三亚(海南最南端)启航经南海、马六甲海峡穿越印度洋,在2009年1月6日抵达亚丁湾执行护航任务. (1)填出下列半岛的名称:A__________,B__________. (2)填出下列半岛的主要气候类型名称:A__________,B__________.
