快速傅里叶变换ftt晶体
FFT快速傅里叶变换(蝶形算法)详解概要

5.4 按频率抽取的基2-FFT算法
算法原理
先把输入按n的顺序分成前后两半 再把输出X(k)按k的奇偶分组 设序列长度为N=2L,L为整数 前半子序列x(n) 后半子序列 x(n
nk x ( n ) W N
N 1
rk k rk x1 (r )W N WN x ( r ) W 2 N 2 2
k X 1 (k ) WN X 2 (k )
式中,X1(k)和X2(k)分别是x1(n)和x2(n)的N/2的DFT。
另外,式中k的取值范围是:0,1, …,N/2-1 。
N 2M , 第L级:
r WN W2jL , j 0,1,2,,2 L1 1
2 L 2 M 2 LM N 2 LM
W W
r N j N 2 L M
e
j
2 N 2 L M
j
e
j
2 j 2 M L N
W
j 2 M L N
r WN
的确定
25
序列的逆序排列
序列的逆序排列
由于 x(n) 被反复地按奇、偶分组,所以流图输入端的 排列不再是顺序的,但仍有规律可循: 因为 N=2M , 对于任意 n(0≤n ≤N-1),可以用M个 二进制码表示为:
n( DEC) (nM 1nM 2 n2 n1n0 ) ( BIN )
(2)周期性 (3)可约性 另外,
( n N ) k n( k N ) nk WN WN WN
mnk nk WmN WN
nk nk / m WN WN /m
( k N / 2) k WN WN
N /2 WN 1
8
快速傅里叶变换FFT算法及其应用

快速傅里叶变换FFT算法及其应用快速傅里叶变换(Fast Fourier Transform, FFT)是一种高效的计算离散傅里叶变换(Discrete Fourier Transform, DFT)的算法,它可以将一个时间域上的信号转换为频域上的表示。
FFT算法的提出改变了信号处理、图像处理、音频处理等领域的发展,广泛应用于各种科学与工程领域。
FFT算法的基本思想是将一个N点的DFT分解为多个较小规模的DFT,然后再通过合并子问题的解来得到原问题的解。
这种分治思想使得FFT算法的时间复杂度从O(N^2)降低到了O(NlogN),大大提高了计算效率。
FFT算法主要利用了DFT的对称性和周期性质,通过递归和迭代的方式,以分离出DFT的实部和虚部的形式计算出频域上的信号。
FFT算法的应用非常广泛。
在通信领域中,FFT算法常被用于信号的频谱分析、频域滤波、信号调制解调等方面。
在图像处理中,FFT算法可用于图像增强、滤波、噪声去除等。
在音频处理中,FFT算法可以用于音频压缩、声音合成等。
此外,FFT算法还广泛应用于科学计算、数字信号处理、雷达信号处理、语音识别、生物信息学等领域。
以音频处理为例,使用FFT算法可以将音频信号从时域转换到频域表示,使得我们可以对音频信号进行频谱分析。
通过FFT计算,我们可以获取音频信号的频率分量、频谱特征、能量分布等信息。
这对于音频的压缩、降噪、音频增强、音频特征提取等操作非常有帮助。
例如,在音频压缩中,我们可以根据音频信号的频谱特性,选择性地保留主要的频率成分,从而实现压缩效果。
而在音频增强中,我们可以通过FFT计算,去除或减弱一些频率上的噪声,提高音频的质量。
在实际应用中,为了提高计算效率和减少计算量,通常会使用基于FFT算法的快速卷积、快速滤波等技术。
这些技术可以利用FFT算法的高效性质,实现更快速、更准确的计算。
此外,也可以采用多线程、并行计算等技术,进一步提高FFT算法的性能。
FFT快速傅里叶变换(蝶形算法)详解 ppt课件

N / 21
N 1
x(n)WNnk
x(n)WNnk
n0
nN /2
N / 21
x(n)WNnk
n0
N / 21
x(n
n0
N 2
(n
)WN
因为 N=2M ,对于任意 n(0≤n ≤N-1),可以用M个 二进制码表示为:
n(DEC) (nM 1nM 2 n2 n1n0 ) (BIN)
nM 1, nM 2 ,, n2 , n1, n0
0 1
n 反复按奇、偶分解时,即按二进制码的“0” “1” 分解。
ppt课件
26
倒位序的树状图(N=8)
DFT运算量的比较 按时间抽取的FFT算法的特点 按时间抽取FFT算法的其它形式流程图
ppt课件
5.3.1 算法原理
设N=2L,将x(n)按 n 的奇偶分为两组:
x(2r) x1(r) x(2r 1) x2 (r)
r =0,1,…,N 1
2
则
N 1
X (k) DFT[x(n)] x(n)WNnk
r 0
r 0
N
N
1
1
2
2
x1
(r
)W
rk N
WNk
x2
(r
)W
rk N
r 0
2
r 0
2
X 1 (k ) WNk X 2 (k )
式中,X1(k)和X2(k)分别是x1(n)和x2(n)的N/2的DFT。 另外,式中k的取值范围是:0,1, …,N/2-1 。
ppt课件
64 4049 192
快速傅里叶变换

快速傅⾥叶变换快速傅⾥叶变换快速傅⾥叶变换(FFT )是根据计算量的最⼩化原理来设计和实施离散傅⾥叶变换(DFT)计算的⽅法。
1965年,库利(T.W.Cooley )和图基(J.W.tukey )发表了著名的《计算机计算傅⾥叶级数的⼀种算法》论⽂。
从此掀起了快速傅⾥叶变换计算⽅法研究的热潮。
快速傅⾥叶变换(FFT )的出现,实现了快速、⾼效的信号分析和信号处理,为离散傅⾥叶变换(DFT)的⼴泛应⽤奠定了基础。
1.1离散傅⾥叶变换(DFT)的计算设x(n)是⼀个长度为M 的有限长序列,则定义x(n)的N 点离散傅⾥叶变换为∑-===10)()]([)(N n kn NW n x n x DFT k X 其中由于计算⼀个X(k)值需要N 次复乘法和(N-1)次复数加法,因⽽计算N 个X(k)值,共需N2次复乘法和N(N-1)次复加法。
每次复乘法包括4次实数乘法和2次实数加法,每次复加法包括2次实数加法,因此计算N 点的DFT 共需要4N2次实数乘法和(2N2+2N ·(N-1))次实数加法。
当N 很⼤时,这是⼀个⾮常⼤的计算量。
1.2减少DFT 计算量的⽅法减少DFT 的计算量的主要途径是利⽤k N W 的性质和计算表达式的组合使⽤,其本质是减少DFT 计算的点数N 以便减少DFT 的计算量。
k N W 的性质:(1)对称性: (2)周期性: (3) 可约性: (4) 特殊点:选择其中⼀个证明N N j k N j N k N j N k N e e e W 222)2(22πππ--+-+==ππj k N j e e --=2k N j e π2--=k N W -=FFT 算法是基于可以将⼀个长度为N 的序列的离散傅⾥叶变换逐次分解为较短的离散傅⾥叶变换来计算这⼀基本原理的。
这⼀原理产⽣了许多不同的算法,但它们在计算速度上均取得了⼤致相当的改善。
0,1,,1k N =-()*nk nk N N W W -=()()nk N n k n N k N N NW W W ++==nk mnk N mN W W =//nk nk m N N mW W =01N W =/21N N W =-(/2)k N k N NW W +=-在这⾥讨论两类基本的FFT 算法。
快速傅里叶变换(FFT)的原理及公式
快速傅里叶变换(FFT)的原理及公式原理及公式非周期性连续时间信号x(t)的傅里叶变换可以表示为式中计算出来的是信号x(t)的连续频谱。
但是,在实际的控制系统中能够得到的是连续信号x(t)的离散采样值x(nT)。
因此需要利用离散信号x(nT)来计算信号x(t)的频谱。
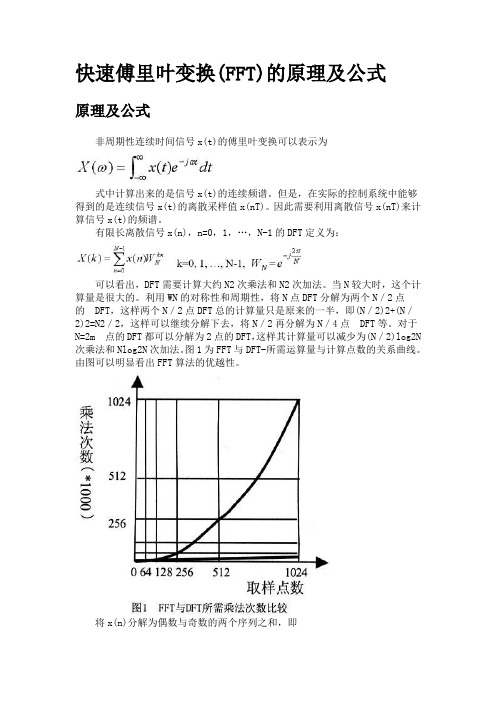
有限长离散信号x(n),n=0,1,…,N-1的DFT定义为:可以看出,DFT需要计算大约N2次乘法和N2次加法。
当N较大时,这个计算量是很大的。
利用WN的对称性和周期性,将N点DFT分解为两个N/2点的DFT,这样两个N/2点DFT总的计算量只是原来的一半,即(N/2)2+(N/2)2=N2/2,这样可以继续分解下去,将N/2再分解为N/4点DFT等。
对于N=2m点的DFT都可以分解为2点的DFT,这样其计算量可以减少为(N/2)log2N 次乘法和Nlog2N次加法。
图1为FFT与DFT-所需运算量与计算点数的关系曲线。
由图可以明显看出FFT算法的优越性。
将x(n)分解为偶数与奇数的两个序列之和,即x1(n)和x2(n)的长度都是N/2,x1(n)是偶数序列,x2(n)是奇数序列,则其中X1(k)和X2(k)分别为x1(n)和x2(n)的N/2点DFT。
由于X1(k)和X2(k)均以N/2为周期,且WN k+N/2=-WN k,所以X(k)又可表示为:上式的运算可以用图2表示,根据其形状称之为蝶形运算。
依此类推,经过m-1次分解,最后将N点DFT分解为N/2个两点DFT。
图3为8点FFT的分解流程。
FFT算法的原理是通过许多小的更加容易进行的变换去实现大规模的变换,降低了运算要求,提高了与运算速度。
FFT不是DFT的近似运算,它们完全是等效的。
关于FFT精度的说明:因为这个变换采用了浮点运算,因此需要足够的精度,以使在出现舍入误差时,结果中的每个组成部分的准确整数值仍是可辨认的。
为了FFT的舍入误差,应该允许增加几倍log2(log2N)位的二进制。
快速傅里叶变换FFT算法及其应用_————

快速傅里叶变换FFT算法及其应用_————快速傅里叶变换(Fast Fourier Transform,简称FFT)是一种高效的计算傅里叶变换的算法,广泛应用于信号处理、图像处理、语音识别、音频压缩等领域。
它的优点是能够大幅度减少计算量,提高算法的运行速度。
FFT算法的核心思想是将复杂度为O(n^2)的DFT(离散傅里叶变换)转化为复杂度为O(nlogn)的运算。
它通过利用分治的思想,将一个规模为n的DFT分解为多个规模为n/2的子问题,然后再将子问题进一步分解,最终得到一系列规模为1的问题,即基本DFT。
然后通过计算每个基本DFT的结果,再经过一系列合并操作,得到最终的DFT结果。
FFT算法的步骤如下:1.将输入的序列进行位逆序排列。
通过位逆序排列可以将基本DFT的计算顺序优化成一定的规律,方便后续的计算。
2.对序列进行迭代式的分解和合并操作。
首先将序列拆分成两个长度为n/2的子序列,然后对子序列进行递归的FFT计算,再将两个子序列合并为一个序列的DFT结果。
3.重复以上步骤,直到计算得到最终的DFT结果。
FFT算法的应用非常广泛。
以下是一些常见的应用场景:1.信号处理:FFT算法在信号处理中广泛应用于频谱分析、滤波器设计、波形合成等方面。
它可以将信号从时间域转化到频域,方便分析信号的频谱特性。
2.图像处理:在图像处理中,FFT算法常用于图像增强、去噪、边缘检测等方面。
通过将图像转换到频域,可以更好地处理图像中的频域信息。
3.音频压缩:FFT算法在音频压缩中起到了至关重要的作用。
通过将音频信号转换到频域,可以将音频信号中的冗余信息去除,以达到音频压缩的目的。
4.语音识别:在语音识别中,FFT算法用于提取语音信号的频谱特征,以便进行语音识别算法的进一步处理。
5.通信系统:FFT算法在OFDM(正交频分复用)通信系统中得到了广泛的应用。
通过将信号转换到频域,可以减小不同子载波之间的干扰,提高通信系统的容量和可靠性。
第4章 快速傅里叶变换(FFT)

本章主要内容
直接计算DFT的问题及改进的途径 按时间抽取的基2-FFT算法 按频率抽取的基2-FFT算法 快速傅里叶逆变换(IFFT)算法
2
4.1 引言
DFT在实际应用中很重要: 可以计算信号 的频谱、功率谱和线性卷积等。
直接按DFT变换进行计算,当序列长度N很
5.4 512 262 144 2 304 113.8
8.0 1024 1 048 576 5 120 204.8
12.8 2048 4 194 304 11 264 372.4
64 4049 192
21.4
24
4.2.5 按频率抽取的基2-FFT算法
算法原理
先把输入按n的顺序分成前后两半
再把输出X(k)按k的奇偶分组
所以 整个N点DFT运算共需要: 实数乘法次数: 4 N2
实数加法次数: N×2(2N-1)= 2N(2N-1)
6
DFT运算量的结论
N点DFT的复数乘法次数举例
N
N2
N
N2
2
4
64
4049
4
16
128
16384
8
64
256
65 536
16
256
512
262 144
32
1028
1024
1 048 576
N / 21
x(n)WNnk
n0
N / 21
x(n
n0
N 2
(n N )k
)WN 2
N / 21 x(n)
n0
x(n
N 2
fft快速傅里叶变换得到的结果

fft快速傅里叶变换得到的结果FFT(快速傅里叶变换)是一种常用的数学算法,用于将时域信号转换为频域信号。
通过FFT,我们可以得到信号的频谱分布,从而分析信号的频率成分和特征。
傅里叶变换是一种将时域信号转换为频域信号的数学工具。
它将一个复杂的信号分解成多个简单的正弦和余弦函数的叠加。
傅里叶变换的结果是一个包含频率和振幅信息的频谱图。
然而,传统的傅里叶变换算法计算复杂度较高,需要O(N^2)的计算量,这在处理大量数据时效率较低。
为了提高计算效率,Cooley和Tukey在1965年提出了FFT算法。
FFT通过利用信号的对称性和周期性,将傅里叶变换的计算复杂度降低到O(NlogN)。
这使得FFT成为处理大规模数据的重要工具,广泛应用于信号处理、图像处理、音频处理等领域。
在FFT算法中,信号被表示为一个复数序列,其中实部表示信号的幅度,虚部表示信号的相位。
通过对这个复数序列进行递归分解和合并操作,可以得到频谱图。
FFT算法的核心思想是将一个长度为N的信号分解为两个长度为N/2的子信号,然后再将这两个子信号分别继续进行分解。
这个过程一直持续下去,直到最后得到长度为1的子信号。
接着,将这些子信号通过合并操作逐步恢复为原始信号的频谱图。
FFT算法的关键步骤是蝶形运算。
蝶形运算是一种基于旋转因子的复数运算,它能够将两个复数进行合并操作。
通过多次蝶形运算,可以将子信号逐步合并为原始信号的频谱图。
FFT算法的优点不仅在于其高效的计算速度,还在于其对称性和周期性的利用。
这使得FFT算法能够应用于各种类型的信号处理问题。
例如,在音频处理中,FFT可以用于音频信号的频谱分析、滤波器设计和音频合成等方面。
在图像处理中,FFT可以用于图像的频域滤波、图像去噪和图像压缩等方面。
然而,FFT算法也存在一些限制。
首先,FFT算法要求信号长度必须是2的幂次,这在某些情况下可能会导致数据的丢失或填充。
其次,FFT算法对信号的稳定性和周期性有一定的要求,对非周期信号或不稳定信号的处理效果可能不理想。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
快速傅里叶变换ftt晶体
傅里叶变换(FTT)是一种十分重要的信号处理技术,广泛运用于
许多领域,尤其在晶体学研究中发挥着至关重要的作用。
本文将生动
地介绍FTT的原理、应用和指导意义。
首先,我们来了解一下FTT的原理。
傅里叶变换是一种将时域信
号转换为频域信号的方法。
它基于一个基本原理,即任何一个周期信
号都可以由不同频率的正弦波组合而成。
通过FTT,我们可以将信号分解为不同频率的频谱,从而更好地理解信号的特征和组成。
在晶体学研究中,FTT被广泛应用于晶体结构分析和晶格参数测定。
晶体学家通常使用X射线衍射技术来研究晶体结构,通过将衍射图案
进行FTT,可以获得晶体中原子的空间分布信息。
这对于确定晶体的晶胞参数、晶格对称性以及晶格畸变等方面非常关键。
其次,FTT在晶体学中还有许多其他的应用。
例如,在材料科学领域中,研究人员可以使用FTT来分析材料的晶格缺陷、晶体生长过程
中的畸变行为等问题。
而在生物医学领域,FTT可以用于分析生物分子的结构和动态变化,帮助研究人员了解生物体系的性质和功能。
除了应用于研究,FTT在实际应用中也具有重要的指导意义。
例如,在晶体材料的制备和加工过程中,FTT可以用来监测晶体的质量和纯度。
通过对晶体的衍射图案进行FTT分析,可以及时发现晶体中的缺陷和
杂质,从而改进制备工艺,提高材料性能。
此外,FTT在信号处理和通信领域也有广泛的应用。
例如,在音频和视频数据的处理中,FTT可以用来分析和提取音频和视频中的频谱特征,从而实现音频和视频的压缩、传输和重建。
在通信系统中,FTT可以用来对信号进行频域滤波,提高信号传输的可靠性和带宽利用率。
综上所述,快速傅里叶变换(FTT)作为一种重要的信号处理技术,在晶体学研究和其他领域中发挥着巨大的作用。
它不仅可以帮助我们
更好地理解信号的特征和组成,还可以为晶体结构分析、晶格参数测定、材料科学和生物医学研究等提供重要的指导意义。
因此,熟练掌
握和应用FTT技术对于科学研究和工程应用都具有重要的价值。
