高一数学算法案例3
高中数学 1.3 算法案例课件 新人教A版必修3

例2:已知一个五次多项式为 f (x) 1+x+0.5x2 0.16667x3 0.04167x4 0.00833x5 用秦九韶算法求这个多项式当x=-0.2的值。
解答: 将多项式变形:
f (x) ((((0.00833x 0.04167)x 0.16667)x 0.5)x 1)x 1
=3125+625+125+25+5+1
=3906
算法2: f(5)=55+54+53+52+5+1
=5×(54+53+52+5+1)+1 =5×(5×(53+52+5+1)+1)+1 =5×(5×(5×(52+5+1)+1)+1)+1 =5×(5×(5×(5×(5+1)+1)+1)+1)+1
思考2 两种算法各用了几次乘法运算和几次加法运算?
用秦九韶算法求f(5)的值.
解:f(x)=((((5x+2)x+3.5)x-2.6)x+1.7)x-0.8 v1=5×5+2=27; v2=27×5+3.5=138.5; v3=138.5×5-2.6=689.9; v4=689.9×5+1.7=3451.2; v5=3451.2×5-0.8=17255.2.
a1x a0
对该多项式按下面的方式进行改写:
f ( x) an xn an1xn1
(an xn1 an1xn2
a1x a0
a1)x a0
((an a0
( (an x an1)x an2 )x a1)x a0
解答: 算法一共做了1+2+3+4=10次乘法运算,5次加法运算。 算法二共做了4次乘法运算,5次加法运算。 通过对比,很明显,算法二比算法一优越,这种算法就是秦九 韶算法。
高一数学算法案例3

上海自仪 http://www.sh/新款耐腐蚀磷化泵后期维护手册!金属材料表面涂装前经磷化处理可以显著提高涂层的附着力和耐腐蚀性,因此耐腐蚀磷化泵在各行业得到了广泛应用,耐腐蚀磷化泵可以将磷化渣及时从槽液中清除,从而保障了磷化液的清洁,延长其使用寿命。 泵浦安装工具泵浦配件防护衣安全鞋防护手套 1、检查耐腐蚀磷化泵管路及结合处有无松动现象。用手转动耐腐蚀磷化泵,试看耐腐蚀磷化泵是否灵活。2、向轴承体内加入轴承润滑机油,观察油位应在油标的中心线处,润滑油应及时更换或补充。3、拧下耐腐蚀磷化泵泵体的引水螺塞,灌注引水(或引浆)。4、关好出水管路的闸阀和出口压力 建筑桩基检测实战桩基检测承载力标准值与特征值区别,合格数值多大 桩基检测仪枕块、槽钢、压力表,重型吊车 1、清理基槽,平整桩基周围,桩基套护筒。吊车吊装枕块,千斤顶安装。 2、桩基检测仪安装,这时给千斤顶加压,设置控制荷载。 例:控制荷载为9800KN.(单桩承载力特征值) 3、定时观察实际荷载数值(单桩承载力标椎值);单桩承载力标准值不小于2倍单桩承载力特征值。例:实际荷载为9823KN合格 空调不制冷的原因分析返回暂停重播播放x世界如此简单61条相关空调不制冷怎么办 妙招好生活怎样检查冰箱的制冷效果如... 文文龚出品空调只吹风不制冷维修(空... 妙招好生活空调外机结冰怎么办 妙招好生活夏天空调为什么不能制冷以... 妙招好生活冬天冰箱不制冷的解决方法 妙招好生活冰箱灯亮不制冷没声音 妙招好生活冰箱不冷冻的原因 妙招好生活冰箱加氟图解步骤 妙招好生活爱奇艺如何调整解码方... 题库在线加载更多~1366785人看了这个1、电源电压故障,电压低或者电源输入不良; 2、电气控制系统输出不良; 3、制冷系统缺氟,管路有漏点; 4、压机运转不良,压机电容或者压机本身不良; 5、内外机通风不良 万用表 压力表 温度表 十字花螺丝刀 尖嘴钳 1、通电能否开机,判断电源及内机控制是否良好 2、检查外机运转状况,判断内机信号输出及压机是否正常 3、检测系统压力,判断制冷剂是否正常 电冰箱打压检漏的技巧打压检漏是电冰箱维修中必不可少的关键一个步骤,也是不易操作的一个步骤, 要想彻底的将冰箱的漏点区分是哪个部位内漏,就要进行分体打压,具体技巧如下: 真空泵一台氮气瓶一只压力表三块手提焊炬 1、将压缩机上面的高低压管用割刀从里压缩机2-3cm处割开,将过滤器与毛细管接头处离过滤器2-5cm处用钳子剪断,2、用焊炬将毛细管和过滤器的断口处焊死,3、用焊炬将从压缩机上断开的高低压管子的端口处各焊接上一块压力表,4、把电冰箱冷冻室的盘管从冰箱里面拆开网外拉出来一些, 空调漏氟怎么检测空调漏氟的检测方法基本有两点,一是看,二是直接用压力表测试。 压力表,制冷剂输液管,手套,活扳手空调 1、用眼睛看,观察空调外机二通阀和三通阀是否有明显的油渍,如图:2、像上图一样很明显空调漏氟了,如果有非常顽固的灰尘落在了上面,那么说明这个接口处是有轻微的泄漏。用手指摸一下会明显的闻到一股机油的味道,这也说明是制冷剂泄漏。3、如果二通阀和三通阀没有明显的痕迹, 以上就是判断和检测空调漏氟的方法,个人的实践经验。
高中数学 算法案例课件 新人教A版必修3

为了区分不同的进位制,常在数的右下角标明基数, 十进制一般不标注基数. 七进制的13,写成13(7);二进制的10,写成10(2)
一般地,若k是一个大于1的整数,那么以k 为基数的k进制数可以表示为一串数字连写在一起 的形式:
anan1 a1a0(k)(0 an k,0 an1, ,a1,a0 k).
2 11 0
25 1
从下到上排列,
22 1
21 0 01
得到89=1011001(2)
可以推广为把十进制数化为k进制 训练题2 把156化为八进制数
89=324(5) 156 234(8)
思考:把 11011(2)化为四,八进制数表示
思路:利用十进制作为中间桥梁转化
其它进制数化成十进制数公式
16
适应训练
将下列数化为十进制 1. 101011 (2) 2. 1234 (5) 3. 1021 (8)
Key :43, 194, 529
17
十进制数化为其它进制数:
解例:5
把89化为二进制数。
除2取余法
余数
2 89
1.最后一步商为0,
2 44 1
2 22 0
2.把上式各步所得的余数
例如:3721 表示有:1个1,2个十, 7个百即7个10的 平方, 3个千即3个10的立方 于是,我们可以得到下面这个式子
3721 3103 7 102 2101 1100
与十位制类似,其他的进位制也可以按照 位置原则计数,也可以表示成不同位上数 字与基数的幂的乘积之和的形式。
13
你能类比十位制数的表示方法表示其他进 制的数吗?
3
在商代的甲骨文中,已经有了一、二、三、
四、五、六、七、八、九、十、百、千、万
高一数学必修3:算法案例

1.3 算法案例双基达标(限时20分钟) 1.利用秦九韶算法求P (x )=a n x n +a n -1x n -1+…+a 1x +a 0,当x =x 0时P (x 0)的值,需做加法和乘法的次数分别为 ( )A .n ,nB .n ,n (n +1)2C .n,2n +1D .2n +1,n (n +1)2解析 由秦九韶算法知P (x 0)=(…((a n x 0+a n -1)x 0+a n -2)x 0+…+a 1)x 0+a 0,上式共进行了n 次乘法运算和n 次加法运算.答案 A2.两个二进制数101(2)与110(2)的和用十进制数表示为 ( ).A .12B .11C .10D .9解析 101(2)=22+0×21+1×20=5,110(2)=1×22+1×21+0×20=6.答案 B3.4 830与3 289的最大公约数为 ( ).A .23B .35C .11D .13解析 4 830=1×3 289+ 1 541;3 289=2×1 541+207;1 541=7×207+92;207=2×92+23;92=4×23;∴23是4 830与3 289的最大公约数.答案 A4.用更相减损术求36与134的最大公约数,第一步应为________.解析 ∵36与134都是偶数,∴第一步应为:先除以2,得到18与67.答案 先除以2,得到18与675.将八进制数127(8)化成二进制数为________(2).解析 将127(8)化为十进制:127(8)=1×82+2×8+7=64+16+7=87,再将十进制数87化为二进制数为:∴87=1010111(2).答案10101116.用秦九韶算法求多项式f(x)=7x7+6x6+5x5+4x4+3x3+2x2+x当x=3时的值.解f(x)=((((((7x+6)x+5)x+4)x+3)x+2)x+1)x,所以v0=7v1=7×3+6=27v2=27×3+5=86v3=86×3+4=262v4=262×3+3=789v5=789×3+2=2 369v6=2 369×3+1=7 108v7=7 108×3=21 324,故x=3时,多项式f(x)=7x7+6x6+5x5+4x4+3x3+2x2+x的值为21 324.综合提高(限时25分钟)7.用秦九韶算法求多项式f(x)=7x6+6x5+3x2+2,当x=4时的值时,先算的是().A.4×4=16 B.7×4=28C.4×4×4=64 D.7×4+6=34解析因为f(x)=a n x n+a n-1x n-1+…+a1x+a0=(…((a n x+a n-1)x+a n-2)x+…+a1)x+a0,所以用秦九韶算法求多项式f(x)=7x6+6x5+3x2+2当x=4时的值时,先算的是7×4+6=34.答案 D8.下列各数中最小的数是().A .101 010(2)B .210(8)C .1 001(16)D .81解析 101010(2)=1×25+0×24+1×23+0×22+1×21+0×20=42.210(8)=2×82+1×81+0×80=136,1001(16)=1×163+0×162+0×16+1×160=4 097,故选A.答案 A9.用更相减损术求459和357的最大公约数,需要减法的次数为________.解析 使用更相减损术有:459-357=102;357-102=255;255-102=153;153-102=51;102-51=51,共作了5次减法.答案 510.用秦九韶算法求函数f (x )=1+2x +x 2-3x 3+2x 4,当x =-1的值时,v 2的结果是________.解析 此题的n =4,a 4=2,a 3=-3,a 2=1,a 1=2,a 0=1,由秦九韶算法的递推关系式⎩⎪⎨⎪⎧v 0=a n ,v k =v k -1x +a n -k (k =1,2,…,n ),得v 1=v 0x +a 3=2×(-1)-3=-5.v 2=v 1x +a 2=-5×(-1)+1=6.答案 611.把“三进制”数2 101 211(3)转化为“八进制”的数.解 先将三进制化为十进制,再将十进制化为八进制.2 101 211(3)=2×36+1×35+1×33+2×32+1×31+1×30=1 458+243+27+18+3+1=1 750(10),所以2 101 211(3)=3 326(8).12.(创新拓展)用秦九韶算法计算多项式f(x)=x6-12x5+60x4-160x3+240x2-192x+64当x=2时的值.解将f(x)改写为f(x)=(((((x-12)x+60)x-160)x+240)x-192)x+64由内向外依次计算一次多项式当x=2时的值,v0=1,v1=1×2-12=-10,v2=-10×2+60=40,v3=40×2-160=-80,v4=-80×2+240=80,v5=80×2-192=-32,v6=-32×2+64=0.∴f(2)=0,即x=2时,原多项式的值为0.。
高一数学算法案例3

高中数学必修3 1.3.1算法案例(辗转相除法)(z)
思考1:从上面的两个例子可以 看出计算的规律是什么? S1:用大数除以小数
S2:除数变成被除数,余数变成除 显然37是148和37的最大 数 S3:重复S1,直到余数为0 公约数,也就是8251和 6105的最大公约数
练习1:利用辗转相除法求两数4081与 20723的最大公约数. (53) 20723=4081×5+318;
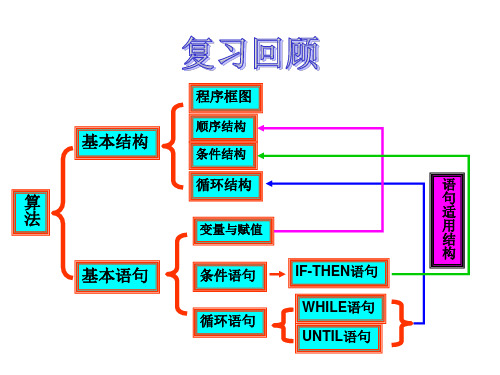
程序框图
顺序结构
基本结构
条件结构
循环结构
算 法 基本语句
变量与赋值
语 句 适 用 结 构 IF-THEN语句 WHILE语句 UNTIL语句
条件语句 循环语句Fra bibliotek1.3
算法案例
我们这节课就利用基本的算法程序来 解决一些实际问题,进一步体会算法的 程序思想。
案例1.辗转相除法与更相减损术
在初中,我们已经学过求最大公约数的知 识,你能求出18与30的最大公约数吗?
辗转相除法是一个反复执行直到余数等于0停止 的步骤,这实际上是一个循环结构。m = n × q + r
用程序框图表示出右边的过程 8251=6105×1+2146 6105=2146×2+1813 2146=1813×1+333
r=m MOD n
m=n
n=r r=0? 否
1813=333×5+148
2
3
18 9 3
互质
30 15 5
所以,18和30的最大公约数是:2×3=6 但是,当我们处理较大数(如:8251 与6105)的最大公因数时,如果利用这种 方法可能计算量比较大,步骤比较多。下 面我们介绍一种古老而有效的算法——辗 转相除法
辗转相除法
1.3算法案例 课件-高一数学人教A版必修3
用秦九韶算法求这个多项式当x=5时的值。
解:根据秦九韶算法,把多项式改写成如下 形式:
f (x) ((((4x 2)x 3.5)x 2.6)x 1.7)x 0.8
按照从内到外的顺序,依次计算一次多项式当 x=5时的值:
WHILE d<>n
IF d>n THEN m=d
ELSE m=n
n=d
END IF d=m-n WEND d=2^k*d
PRINT d
END
问题2:怎样求多项式 f (x) x5 x4 x3 x2 x 1当x=5 的值呢?
方法1:把5代入多项式,计算各项的值,然后把它们加 起来。这时共做了1+2+3+4=10次乘法运算,5 次加法运算。
例1:用更相减损术求98与63的最大公约数。
解:由于63不是偶数,把98和63以大数减小数, 并辗转相减得,如图所示:
98-63=35 63-35=28 35-28=7 28-7=21 21-7=14 14-7=7
所以,98和63的最大公约数等于7。
思考:把更相减损术与辗转相除法比较,你有什么
发现?你能根据更相减损术设计程序,求两个正数的 最大公约数吗?
v1 an x an1
然后由内向外逐层计算一次多项式的值,即
v2 v1 x an2 ,
v3 v2 x an3 ,
vn vn1 x a0 ,
这样,求n次多项式f(x)的值就转化为求n个一次多项 式的值。
上述方法称为秦九韶算法。直到今天, 这种算法仍是 多项式求值比较先进的算法。
例2、已知一个5次多项式为
⑤十进制化k进制
