(完整版)七年级尖子班讲义第1讲平行线四大模型

平行线四大模型

平行线的判定与性质

l、平行线的判定

根据平行线的定义，如果平面内的两条直线不相交，就可以判断这两条直线平行，但是，由于直线无限延伸，检验它们是否相交有困难，所以难以直接根据定义来判断两条直线是否平行，这就需要更简单易行的判定方法来判定两直线平行．

判定方法l：

两条直线被第三条直线所截，如果同位角相等，那么这两条直线平行．

简称：同位角相等，两直线平行．

判定方法2：

两条直线被第三条直线所截，如果内错角相等，那么这两条直线平行．

简称：内错角相等，两直线平行，

判定方法3：

两条直线被第三条直线所截，如果同旁内角互补，那么这两条直线平行．

简称：同旁内角互补，两直线平行，

如上图：

若已知∠1=∠2，则AB∥CD（同位角相等，两直线平行）；

若已知∠1=∠3，则AB∥CD（内错角相等，两直线平行）；

若已知∠1+ ∠4= 180°，则AB∥CD（同旁内角互补，两直线平行）．

另有平行公理推论也能证明两直线平行：

平行公理推论：如果两条直线都与第三条直线平行，那么这两条直线也互相平行．

2、平行线的性质

利用同位角相等，或者内错角相等，或者同旁内角互补，可以判定两条直线平行．反过来，如果已知两条直线平行，当它们被第三条直线所截，得到的同位角、内错角、同

旁内角也有相应的数量关系，这就是平行线的性质．

性质1：

两条平行线被第三条直线所截，同位角相等．

简称：两直线平行，同位角相等

性质2：

两条平行线被第三条直线所截，内错角相等.

简称：两直线平行，内错角相等

性质3：

两条平行线被第三条直线所截，同旁内角互补．

简称：两直线平行，同旁内角互补

本讲进阶平行线四大模型

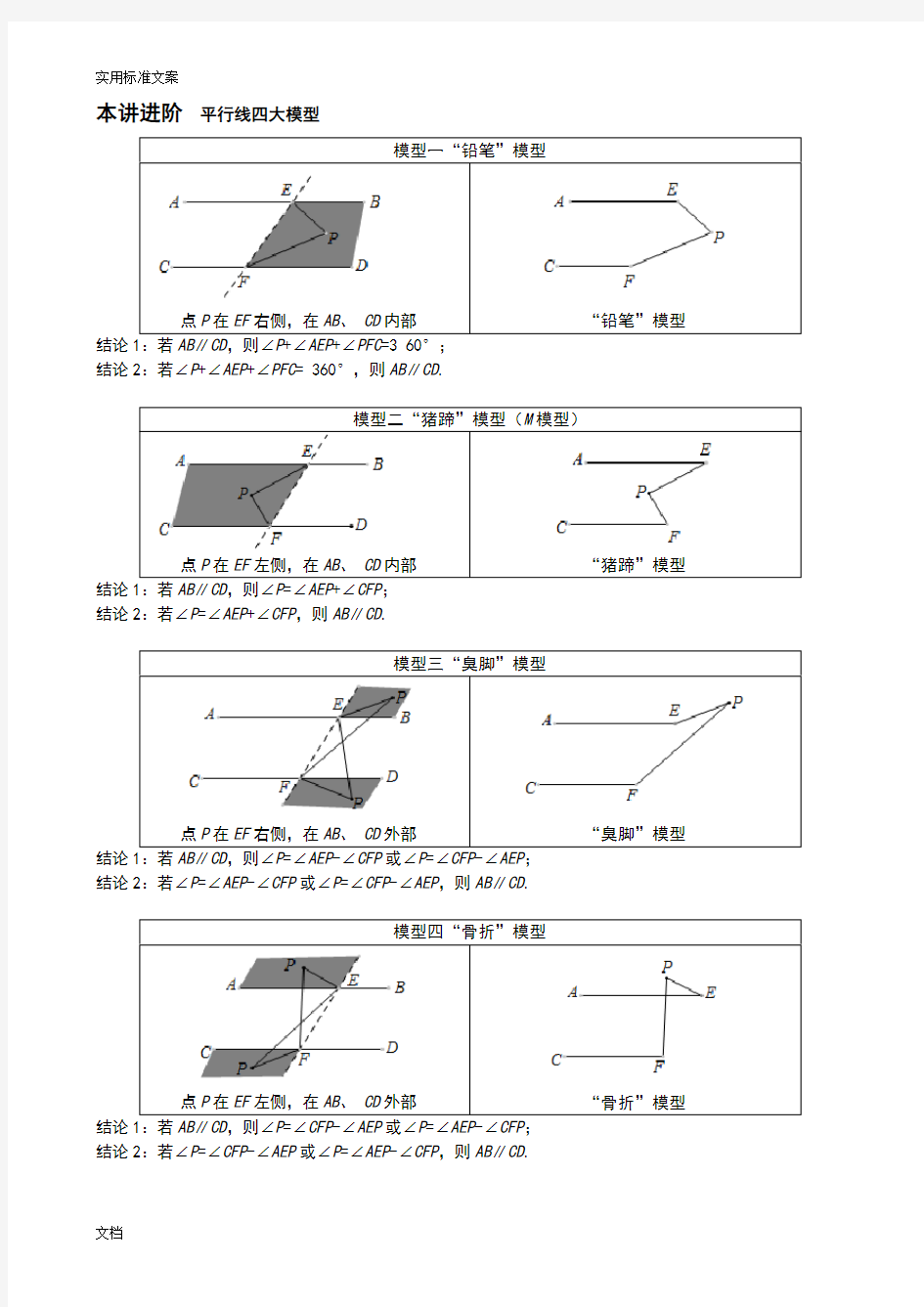
模型一“铅笔”模型

点P在EF右侧，在AB、CD内部“铅笔”模型结论1：若AB∥CD，则∠P+∠AEP+∠PFC=3 60°；

结论2：若∠P+∠AEP+∠PFC= 360°，则AB∥CD.

模型二“猪蹄”模型（M模型）

点P在EF左侧，在AB、CD内部“猪蹄”模型结论1：若AB∥CD，则∠P=∠AEP+∠CFP；

结论2：若∠P=∠AEP+∠CFP，则AB∥CD.

模型三“臭脚”模型

点P在EF右侧，在AB、CD外部“臭脚”模型结论1：若∥，则∠=∠-∠或∠=∠-∠；

结论2：若∠P=∠AEP-∠CFP或∠P=∠CFP-∠AEP，则AB∥CD.

模型四“骨折”模型

点P在EF左侧，在AB、CD外部“骨折”模型结论1：若∥，则∠=∠-∠或∠=∠-∠；

结论2：若∠P=∠CFP-∠AEP或∠P=∠AEP-∠CFP，则AB∥CD.

（1）已知AE // CF ,求证∠P +∠AEP +∠PFC = 360°

.（2）已知∠P=∠AEP+∠CFP，求证AE∥CF．

（3）已知AE∥CF，求证∠P=∠AEP-∠CFP.

（4）已知∠P= ∠CFP -∠AEP ,求证AE //CF .

例1

（1）如图，a∥b,M、N分别在a、b上，P为两平行线间一点，那么∠l+∠2+∠3= ．

(2)如图，AB∥CD，且∠A=25°，∠C=45°，则∠E的度数是．

(3)如图，已知AB∥DE，∠ABC=80°，∠CDE =140°，则∠BCD= .

(4) 如图，射线AC∥BD，∠A= 70°，∠B= 40°，则∠P= ．

练

(1)如图所示，AB∥CD，∠E=37°，∠C= 20°，则∠EAB的度数为．

(2) （七一中学2015-2016七下3月月考）

如图，AB∥CD，∠B=30°，∠O=∠C．则∠C= .

例2

如图，已知AB ∥DE ，BF 、 DF 分别平分∠ABC 、∠CDE ，求∠C 、 ∠F 的关系.

练

如图，已知AB ∥DE ，∠FBC =

n 1∠ABF ，∠FDC =n

∠FDE . (1)若n =2,直接写出∠C 、∠F 的关系； (2)若n =3，试探宄∠C 、∠F 的关系；

(3)直接写出∠C 、∠F 的关系（用含n 的等式表示）.

例3

如图，已知AB ∥CD ，BE 平分∠ABC ，DE 平分∠ADC ．求证：∠E = 2 (∠A +∠C ) .

练

如图，己知AB ∥DE ，BF 、DF 分别平分∠ABC 、∠CDE ，求∠C 、∠F 的关系.

例4

如图，∠3==∠1+∠2，求证：∠A+∠B+∠C+∠D= 180°．

练

（武昌七校 2015-2016 七下期中）如图，AB⊥BC，AE平分∠BAD交BC于E，AE⊥DE，∠l+∠2= 90°，M、N分别是BA、CD的延长线上的点，∠EAM和∠EDN的平分线相交于点F则∠F的度数为（）．

A. 120°

B. 135°

C. 145°

D. 150°

模块二平行线四大模型构造

例5

如图，直线AB∥CD，∠EFA= 30°，∠FGH= 90°，∠HMN=30°，∠CNP= 50°，则

∠GHM= .

练

如图，直线AB∥CD，∠EFG =100°，∠FGH =140°，则∠AEF+ ∠CHG= .

例6

已知∠B =25°，∠BCD=45°，∠CDE =30°，∠E=l0°，求证：AB∥EF．

练

已知AB∥EF，求∠l-∠2+∠3+∠4的度数.

(1)如图(l)，已知MA1∥NA n，探索∠A1、∠A2、…、∠A n，∠B1、∠B2…∠B n-1之间的

关系．

(2)如图(2)，己知MA1∥NA4，探索∠A1、∠A2、∠A3、∠A4，∠B1、∠B2之间的关系．

(3)如图(3)，已知MA1∥NA n，探索∠A1、∠A2、…、∠A n之间的关系．

如图所示，两直线AB∥CD平行，求∠1+∠2+∠3+∠4+∠5+∠6．

挑战压轴题

（粮道街2015—2016 七下期中）

如图1，直线AB ∥CD ，P 是截线MN 上的一点，MN 与CD 、AB 分别交于E 、F ． (1) 若∠EFB =55°，∠EDP = 30°，求∠MPD 的度数；

(2) 当点P 在线段EF 上运动时，∠CPD 与∠ABP 的平分线交于Q ,问：DPB

∠∠是否为定值？若是定值，请求出定值；若不是，说明其范围；

(3) 当点P 在线段EF 的延长线上运动时，∠CDP 与∠ABP 的平分线交于Q ，问DPB

∠∠的值足否定值，请在图2中将图形补充完整并说明理由．

第一讲平行线四大模型（课后作业）

1.如图，AB // CD // EF , EH ⊥CD 于H ,则∠BAC +∠ACE +∠CEH 等于( ).

A . 180°

B . 270°

C . 360°

D . 450° 2．（武昌七校2015-2016七下期中）若AB ∥CD ，∠CDF =

32∠CDE ，∠ABF =3

∠ABE ，则∠E ：∠F =( )．

A ．2:1

B ．3:1

C ．4:3

D ．3:2

3.如图3，己知AE ∥BD ，∠1=130°，∠2=30°，则∠C = .

4.如图，已知直线AB ∥CD ，∠C =115°，∠A = 25°，则∠E = ．

5．如阁所示，AB ∥CD ，∠l =l l 0°，∠2=120°，则∠α= .

6．如图所示，AB ∥DF ，∠D =116°，∠DCB =93°，则∠B = .

7．如图，将三角尺的直角顶点放在直线a上，a∥b.∠1=50°，∠2 =60°，则∠3的度数为 .

8．如图，AB∥CD，EP⊥FP, 已知∠1=30°，∠2=20°．则∠F的度数为．

9.如图，若AB∥CD，∠BEF=70°，求∠B+∠F+∠C的度数.

10．已知，直线AB∥CD．

(1)如图l，∠A、∠C、∠AEC之间有什么关系？请说明理由；

（2）如图2，∠AEF、∠EFC、∠FCD之间有什么关系？请说明理由；

(3)如图3，∠A、∠E、∠F、∠G、∠H、∠O、∠C之间的关是 .

三角形计算四大模型

D C B A G F E D C B A “铅笔头模型” 例(1）如图①，AB ∥ＣD,则∠A+∠C= 。如图②,AB ∥CD,则∠Ａ＋∠E ＋∠C= 。如图③,A Ｂ∥CD,则∠A ＋∠E ＋∠F ＋∠C= 。如图④，AB ∥C Ｄ,则∠Ａ＋∠E+∠F+∠Ｇ+∠C ＝。 (2）如图⑤，AB ∥CD,则∠A ＋∠Ｅ+∠F+…+∠C= 。 (3)利用上述结论解决问题:如图已知AB ∥CD,∠B ＡE 和∠ＤCE 的平分线相交于F ，∠E=１40°，求∠ＡFC 的度数。图① 图② 图③ 图 ④ “锯齿模型” 例3.如图，AB ∥CD ，猜想∠BED 与∠B 、∠D 的大小关系,并说明理由。 E D C B A 如图，已知AB ∥E Ｆ，BC ⊥ＣＤ于点Ｃ，若∠A ＢC ＝3０°,∠D ＥF =45°,则∠C ＤE 等于( ) E D C B A F E D C B A n 个点 F E B

如图，直线AB 平行CD, ∠ＥFA=３0，∠F ＧH ＝90,∠H ＭN=30，∠CN Ｐ＝50,则∠GH Ｍ的大小是多少( ） 2.如图,已知ＡＢ∥CD ，∠ＥAF ＝ 41∠E ＡB,∠ＥCF ＝4 1 ∠ECD ，试∠AEC 与∠ＡF Ｃ之间的关系式。 “８字型” 如图,俩直线AB ，CD 平行，则,∠１+∠2+∠３+∠4+∠5+∠6= “飞镖模型” 例1.如图 2,40,15,35,B C A B C D ∠=?∠=?∠=?∠=则______＿ __; F E D C B A C A B D

变式训练：１.如图,已知?=∠27A ,?=∠96CBE ,?=∠30C . 求：ADE ∠的大小. ２.如图,五角星AB ＣＤE ，求E D C B A ∠+∠+∠+∠+∠的度数. 变式训练： 1．探索三角形的内角和外角角平分线(平分三角形外角的射线角外角角平分线,如图（2）,AEC ∠是ABC ?的外角,C Ｏ平分ACE ∠,那么射线CO 就是外角平分线） (1）如图（1)，在ABC ?中，两内角角平分线BO,C Ｏ相交于点O,若 50=∠A ，则=∠BOC _＿______＿__；此时A ∠与BOC ∠有怎样的关系? （2）如图（2）,在ABC ?中，一内角平分线BO 与一外角平分线CO 相交于点O ， 50=∠A ，则=∠BOC _____＿_＿___；此时A ∠与BOC ∠有怎样的关系？（3)如图（3），在ABC ?中，两外角EBC ∠、FCB ∠的平分线,B Ｏ,CO 相交于点Ｏ，若 50=∠A ,则=∠BOC _＿＿_＿______;此时A ∠与BOC ∠有怎样的关系？

小高奥数几何-三角形五大模型及例题解析 (1)

三角形五大模型【专题知识点概述】本讲复习以前所学过的有关平面几何方面的知识，旨在提高学生对该部分知识的综合运用能力。重点模型重温一、等积模型 ①等底等高的两个三角形面积相等； ②两个三角形高相等，面积比等于它们的底之比；两个三角形底相等，面积比等于它们的高之比；如右图12::S S a b = ③夹在一组平行线之间的等积变形，如右图ACD BCD S S =△△；反之，如果ACD BCD S S =△△，则可知直线AB 平行于CD ． ④等底等高的两个平行四边形面积相等(长方形和正方形可以看作特殊的平行四边形)； ⑤三角形面积等于与它等底等高的平行四边形面积的一半； ⑥两个平行四边形高相等，面积比等于它们的底之比；两个平行四边形底相等，面积比等于它们的高之比．二、等分点结论（“鸟头定理”）如图，三角形AED 占三角形ABC 面积的 23×14=16 三、任意四边形中的比例关系（“蝴蝶定理”） ① S 1︰S 2=S 4︰S 3 或者S 1×S 3=S 2×S 4 ② ②AO ︰OC=（S 1+S 2）︰（S 4+S 3） D C B A b

梯形中比例关系（“梯形蝴蝶定理”） ① S 1︰S 3=a 2︰b 2 ②S 1︰S 3︰S 2︰S 4= a 2︰b 2︰ab ︰ab ; ③S 的对应份数为（a+b ）2 模型四：相似三角形性质如何判断相似 (1)相似的基本概念：两个三角形对应边城比例，对应角相等。 (2)判断相似的方法： ①两个三角形若有两个角对应相等则这两个三角形相似； ②两个三角形若有两条边对应成比例，且这两组对应边所夹的角相等则两个三角形相似。 h h H c b a C B A a c b H C B A ① a b c h A B C H === ; ② S 1︰S 2=a 2︰A 2 模型五：燕尾定理

平行线有关模型汇总

直线平行的条件和性质 1. 猪蹄模型已知：如图，AB ∥CD ，求证：∠B+∠D=∠BED 。 2. 铅笔模型如图,已知: CD AB ∥,求证: ∠+B ∠D +∠=BED 360°. (至少用三种方法) 3. 其他 4. 角平分线如图1，在ABC ?中,BE 平分,ABC CE ∠平分ACB ∠.若80A ∠=?，则BEC ∠= ;若A n ∠=?，求BEC ∠用含n 的代数式表示)

如图3，在ABC ?中，BO 平分外角,CBD CO ∠平分外角BCE ∠.若A n ∠=?，求BOC ∠. 如图5，在ABC ?中，BE 平分ABC ∠, CE 平分外角ACM ∠.若A n ∠=?，求BEC ∠. 5. “8”字形如图b 所示的“ ”字型，其也存在着一个等式：1+2=3+4∠∠∠∠，请证明； 6. “A ”字型如图a 所示的“”字型，我们可称其为“A 字型”或“塔形”，其存在一个等式： 1+2=3+4∠∠∠∠，请证明；

7. 燕尾形如图c所示，其也存在着如下等式：D A B C ∠=∠+∠+∠，请证明一．考点：平行线的性质，角度的计算与证明．二．重难点：常见的几种两条直线平行的结论 1．两条平行线被第三条直线所截，一组同位角的角平分线平行； 2．两条平行线被第三条直线所截，一组内错角的角平分线平行； 3．两条平行线被第三条直线所截，一组同旁内角的角平分线垂直．三．易错点： 1．性质是由图形的“位置关系”决定“数量关系”； 2．两条平行线之间的距离其实可看成点到直线的距离．题型一：猪蹄模型例1. 如图，直线a∥b，直角三角形ABC的顶点B在直线a上，∠C=90°，∠β=55°，则∠α的度数为（） A． 15° B． 25° C． 35° D． 55° 题型二：铅笔模型 ∠+∠+∠+∠=（）例2. 如图，AB∥CD，A E F C

五年级下册数学竞赛试题- 14讲图形-五大模型全国通用(含答案)

五年下册奥数试题-图形-五大模型（一）姓名得分【名师解析】一、等积变换模型 1、等底等高的两个三角形面积相等。 2、两个三角形高相等，面积比等于它们的底之比。 3、两个三角形底相等，面积比等于它的的高之比。二、共角定理模型（共角定理）两个三角形中有一个角相等或互补，这两个三角形叫做共角三角形。共角三角形的面积比等到于对应角（相等角或互补角）两夹边的乘积之比。如：依次称之为A 字型鸟头、X 字型鸟头、歪脖型鸟头、直脖型鸟头。如图在ABC △中，,D E 分别是,AB AC 上的点如图(或D 、E 分别在BA 、CA 延长线上。则有：ADE ABC S AD AE AD AE S AB AC AB AC ?=?=?△△ 三、蝴蝶定理模型（风筝模型）（说明：任意四边形与四边形、长方形、梯形，连接对角线所成四部的比例关系是一样的。）四、相似三角形模型（沙漏模型）五、燕尾定理模型【例题精讲】例1、三角形ABC 中，BD 是DC 的2倍，AE 是EC 的3倍。三角形DEC 的面积为3平方厘米，求三角形ABC 的面积是多少平方厘米？ E A D C B 练习、在下图中，已知CF=2DF ，DE=EA ，△BCF 的面积为2，四边形BFDE 的面积为4，求△ABE 的面积。

F E D C B A 例2、(1)在下图中，2AB BD AC CE ==，，如果29ADE S cm D =，求ABC S D ？ E D C B A 练习、如图在ABC △中，D 在BA 的延长线上，E 在AC 上，且:5:2AB AD =， :3:2AE EC =，12ADE S =△平方厘米，求ABC △的面积． D E A B C 例3、正方形ABCD 边长为6 厘米，BC CF AC AE 3131 == ，．三角形DEF 的面积为多少平方厘米？ A B C D E F 练习、如图，1ABC S =△，5BC BD =，4AC EC =，DG GS SE ==，AF FG =．求F G S S ．

平行线知识点+四大模型

平行线四大模型平行线的判定与性质 l 、平行线的判定根据平行线的定义，如果平面的两条直线不相交，就可以判断这两条直线平行，但是，由于直线无限延伸，检验它们是否相交有困难，所以难以直接根据定义来判断两条直线是否平行，这就需要更简单易行的判定方法来判定两直线平行．判定方法l：两条直线被第三条直线所截，如果同位角相等，那么这两条直线平行．简称：同位角相等，两直线平行．判定方法2：两条直线被第三条直线所截，如果错角相等，那么这两条直线平行．简称：错角相等，两直线平行，判定方法3：两条直线被第三条直线所截，如果同旁角互补，那么这两条直线平行．简称：同旁角互补，两直线平行，如上图：若已知/ 1 = / 2,贝U AB// CD （同位角相等，两直线平行）; 若已知/仁/3,贝U AB / CD （错角相等，两直线平行）; 若已知/ 1+ / 4= 180。，则AB // CD （同旁角互补，两直线平行）. 另有平行公理推论也能证明两直线平行：平行公理推论：如果两条直线都与第三条直线平行,那么这两条直线也互相平行. 2、平行线的性质利用同位角相等,或者错角相等,或者同旁角互补,可以判定两条直线平行.反过来,如果已知两条直线平行,当它们被第三条直线所截,得到的同位角、错角、同旁角也有相应的数量关系,这就是平行线的性质. 性质1 ：两条平行线被第三条直线所截,同位角相等. 简称：两直线平行,同位角相等性质2：两条平行线被第三条直线所截,错角相等. 简称：两直线平行,错角相等性质3：两条平行线被第三条直线所截,同旁角互补. 简称：两直线平行,同旁角互补本讲进阶平行线四大模型

三角形四大模型

三角形的四大模型一、三角形的重要概念和性质 1、三角形的内角和定理：三角形的内角和等于180° 2、三角形的外角和定理：三角形的一个外角等于和它不相邻的两个内角的和 3、三角形角平分线（角分线）中线（分面积等）高（直角三角形两锐角互余）二、八字模型：证明结论：∠A＋∠B＝∠C＋∠D 三、飞镖模型：证明结论：1．∠BOC＝∠A＋∠B＋∠C 四、角分线模型：如图，BD、CD分别是∠ABC和∠ACB的角平分线，BD、CD相交于点D，之间的数量关系，并证明你的结论．试探索∠A与∠D

n 如图，△ABC 两个外角（∠CAD 、∠ACE ）的平分线相交于点P ．探索∠P 与∠B 有怎样的数量关系，并证明你的结论．题型一、三角形性质等应用 1．如图，小亮从A 点出发前进10m ，向右转15°，再前进10m ，又向右转15°，这样一直走下去，他第一次回到出发点A 时，一共走了米数是（）A ．120 B ．150 C ．240 D ．360 2．如图所示是重叠的两个直角三角形．将其中一个直角三角形沿BC 方向平移得到△DEF ．如果AB=8cm ，BE=4cm ，DH=3cm ，则图中阴影部分面积为 cm 2 ． 3．如图，在△ABC 中，已知点D ，E ，F 分别为边BC ，AD ，CE 的中点，且S △ABC =4cm 2，则S 阴影= cm 2． 4． A 、B 、C 是线段A 1B ，B 1C ，C 1A 的中点，S △ABC 的面积是1，则S △A 1B 1C 1的面积． 5．一个四边形截去一个角后，剩下的部分可能是什么图形？画出所有可能的图形，并分别说出内角和和外角和变化情况． 6．如图，直线AC ∥BD ，连接AB ，直线AC ，BD 及线段AB 把平面分成①、②、③、④四个部分，规定：线上各点不属于任何部分．当动点P 落在某个部分时，连接PA ，PB ，构成∠PAC ，∠APB ，∠PBD 三个角．（提示：有公共端点的两条重合的射线所组成的角是0°角）（1）当动点P 落在第①部分时，求证：∠APB=∠PAC+∠PBD ；（2）当动点P 落在第②部分时，∠APB=∠PAC+∠PBD 是否成立？（直接回答）（3）当动点P 在第③部分时，全面探究∠PAC ，∠APB ，∠PBD 之间的关系，并写出

小学思维数学讲义：平面五大模型之三角形等高模型与鸟头模型(二)-带详解

三角形等高模型与鸟头模型（二）板块一三角形等高模型我们已经知道三角形面积的计算公式：三角形面积=底?高2÷ 从这个公式我们可以发现：三角形面积的大小，取决于三角形底和高的乘积．如果三角形的底不变，高越大(小)，三角形面积也就越大(小)；如果三角形的高不变，底越大(小)，三角形面积也就越大(小)；这说明当三角形的面积变化时，它的底和高之中至少有一个要发生变化．但是，当三角形的底和高同时发生变化时，三角形的面积不一定变化．比如当高变为原来的3倍，底变为原来的1 3 ，则三角形面积与原来的一样．这就是说：一个三角形的面积变化与否取决于它的高和底的乘积，而不仅仅取决于高或底的变化．同时也告诉我们：一个三角形在面积不改变的情况下，可以有无数多个不同的形状．在实际问题的研究中，我们还会常常用到以下结论： ①等底等高的两个三角形面积相等； ②两个三角形高相等，面积比等于它们的底之比；两个三角形底相等，面积比等于它们的高之比；如左图12::S S a b = s 2s 1b a D C B A ③夹在一组平行线之间的等积变形，如右上图ACD BCD S S =△△；反之，如果ACD BCD S S =△△，则可知直线AB 平行于CD ． ④等底等高的两个平行四边形面积相等(长方形和正方形可以看作特殊的平行四边形)； ⑤三角形面积等于与它等底等高的平行四边形面积的一半； ⑥两个平行四边形高相等，面积比等于它们的底之比；两个平行四边形底相等，面积比等于它们的高之比．板块二鸟头模型两个三角形中有一个角相等或互补，这两个三角形叫做共角三角形．共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比．如图在ABC △中，,D E 分别是,AB AC 上的点如图 ⑴(或D 在BA 的延长线上，E 在AC 上)，则:():()ABC ADE S S AB AC AD AE =??△△ E D C B A D E C B A 图⑴ 图⑵ 【例 1】如图在ABC △中，,D E 分别是,AB AC 上的点，且:2:5AD AB =，:4:7AE AC =，16ADE S =△平方厘米，求ABC △的面积．例题精讲

专题四平行线模型归纳

专题四平行线模型归纳基本模型归纳：基本模型的运用：基础过关： 1.将两张矩形纸片如图所示摆放，使其中一张矩形纸片的一个顶点恰好落在另一张矩形纸片的一边上，求∠1+∠2的度数。

2. 如图，直线a//b ，求∠A 的度数。 3. 如图，已知AB//CD,∠1=100°，∠2=120°，求∠3的度数。 4. 如图，已知AB//CD,∠ABC=80°，∠CDE=140°，求∠BCD 的度数。 5. 如图，已知l//m ，∠1=115°，∠2=95°，求∠3的度数。 6. 如图，已知直线AB//CD ，∠C=115°，∠A=25°，求∠E 的度数。 7. 如图，已知FC//AB//DE ，∠1：∠D:∠B=2：3：4，求∠1，∠D ，∠B 的度数。 E A D B

8. 如图，已知∠BFM=∠1+∠2，求证：AB//CD 。能力提升 1.已知AB//CD,∠AEC=90°。（1）如图1，当CE 平分∠ACD 时，求证：AE 平分∠BAC （2）如图2，移动直角顶点E ，使∠MCE=∠ECD,求证：2∠BAE=∠MCG G A B A 2.如图，已知CD//EF ，∠ 1+∠2=∠ABC ，求证：AB//GF 。 F A 3.如图已知AB//CD ，∠ABE 和∠CDE 的平分线相交于F ，∠E=140°，求∠BFD 的度数。 E D C E B

4.如图，直线AB//CD,∠1=30°，∠2=90°，∠3=30°，∠4=50°求∠5的度数。 D C B A 5.如图，已知 AD//CE ，∠BCF=∠BCG ，CF 与∠BAH 的平分线交于点F ，若∠F 的余角等于2∠B 的补角，求∠BAH 的度数。 D C E G 6.如图，直线AC ∥BD ，连接AB ，直线AC 、BD 及线段AB 把平面分成①、②、③、④四个部分，规定：线上各点不属于任何部分．当动点P 落在某个部分时，连接PA 、PB ，构成∠PAC 、∠APB 、∠PBD 三个角．（提示：有公共端点的两条重合的射线所组成的角是0°）（1）当动点P 落在第①部分时，有∠ APB=∠PAC+∠PBD ，请说明理由；（2）当动点P 落在第②部分时，∠APB=∠PAC+∠PBD 是否成立？若不成立，试写出∠PAC 、∠APB 、∠PBD 三个角的等量关系（无需说明理由）；（3）当动点P 在第③④部分时，探究∠PAC 、∠APB 、∠PBD 之间的关系，写出你发现的结论并加以说明．

七年级三角形四大模型

2016年01月07日liwei的初中数学组卷一．选择题（共5小题） 1．（2015春?扬中市校级期末）如图1，一副三角板的两个直角重叠在一起，∠A=30°，∠C=45°△COD固定不动，△AOB绕着O 点逆时针旋转α°（0°＜α＜180° ）（1）若△AOB绕着O点旋转图2的位置，若∠BOD=60°，则 ∠AOC=；（2）若0°＜α＜90°，在旋转的过程中∠BOD+∠AOC的值会发生变化吗？若不变化，请求出这个定值；（3）若90°＜α＜180°，问题（2）中的结论还成立吗？说明理由；（4）将△AOB绕点O逆时针旋转α度（0°＜α＜180°），问当α为多少度时，两个三角形至少有一组边所在直线垂直？（请直接写出所有答案）． 2．（2014?赤峰）如图1，E是直线AB，CD内部一点，AB∥CD，连接EA，ED．

（1）探究猜想： ①若∠A=30°，∠D=40°，则∠AED等于多少度？ ②若∠A=20°，∠D=60°，则∠AED等于多少度？ ③猜想图1中∠AED，∠EAB，∠EDC的关系并证明你的结论．（2）拓展应用：如图2，射线FE与矩形ABCD的边AB交于点E，与边CD交于点F，①②③④分别是被射线FE隔开的4个区域（不含边界，其中区域③、④位于直线AB上方，P是位于以上四个区域上的点，猜想：∠PEB，∠PFC，∠EPF的关系（不要求证明）． 3．（2013秋?微山县期中）如图，若∠DBC=∠D，BD平分∠ABC，∠ABC=50°，则∠BCD的大小为（） A．50°B．100° C．130°D．150°

4．（2013春?连云区校级月考）如图，小亮从A点出发前进10m，向右转15°，再前进10m，又向右转15°，这样一直走下去，他第一次回到出发点A时，一共走了米数是（） A．120 B．150 C．240 D．360 5．如图，在△ABC中，∠A=42°，∠ABC和∠ACB的三等分线分别交于点D，E，则∠BDC的度数是（） A．67°B．84°C．88°D．110° 二．填空题（共3小题） 6．（2007?遵义）如图所示是重叠的两个直角三角形．将其中一个直角三角形沿BC方向平移得到△DEF．如果AB=8cm，BE=4cm，DH=3cm，则图中阴影部分面积为cm2．

几何五大模型汇总

小学平面几何五大模型一、共角定理两个三角形中有一个角相等或互补，这两个三角形叫做共角三角形．共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比．如图在ABC △中，,D E分别是, AB AC上的点如图⑴(或D在BA的延长线上，E在AC上)，则:():() S S AB AC AD AE =?? △△ 证明：由三角形面积公式S=1/2*a*b*sinC可推导出若△ABC和△ADE中， ∠BAC=∠DAE 或∠BAC+∠DAE=180°，则 ADE ABC S S ? ? = AE AD AC AB ? ? 二、等积模型 ①等底等高的两个三角形面积相等； ②两个三角形高相等，面积比等于它们的底之比；两个三角形底相等，面积比等于它们的高之比；如下图 12 :: S S a b = ③夹在一组平行线之间的等积变形，如右图 ACD BCD S S= △△ ；反之，如果 ACD BCD S S = △△ ，则可知直线AB平行于CD． ④等底等高的两个平行四边形面积相等(长方形和正方形可以看作特殊的平行四边形)； ⑤三角形面积等于与它等底等高的平行四边形面积的一半； ⑥两个平行四边形高相等，面积比等于它们的底之比；两个平行四边形底相等，面积比等于它们的高之比． b a S2 S1 D C B A

三、蝶形定理 1、任意四边形中的比例关系(“蝶形定理”)： ①1243::S S S S =或者1324S S S S ?=? ②()()1243::AO OC S S S S =++ 速记：上×下=左×右蝶形定理为我们提供了解决不规则四边形的面积问题的一个途径．通过构造模型，一方面可以使不规则四边形的面积关系与四边形内的三角形相联系；另一方面，也可以得到与面积对应的对角线的比例关系． 2、梯形中比例关系(“梯形蝶形定理”)： ①2213::S S a b = ②221324::::::S S S S a b ab ab =； ③S 的对应份数为()2a b +．四、相似模型 (一)金字塔模型 (二) 沙漏模型 G F E A B C D A B C D E F G ①AD AE DE AF AB AC BC AG ===； ②22:ADE ABC S S AF AG =△△：．相似三角形，就是形状相同，大小不同的三角形(只要其形状不改变，不论大小怎样改变它们都相似)，与相似三角形相关的常用的性质及定理如下： ⑴相似三角形的一切对应线段的长度成比例，并且这个比例等于它们的相似比； ⑵相似三角形的面积比等于它们相似比的平方； A B C D O b a S 3 S 2 S 1S 4 S 4 S 3 S 2 S 1O D C B A

小学奥数-几何五大模型(等高模型)

模型一三角形等高模型已经知道三角形面积的计算公式：三角形面积=底?高2÷ 从这个公式我们可以发现：三角形面积的大小，取决于三角形底和高的乘积．如果三角形的底不变，高越大(小)，三角形面积也就越大(小)；如果三角形的高不变，底越大(小)，三角形面积也就越大(小)；这说明当三角形的面积变化时，它的底和高之中至少有一个要发生变化．但是，当三角形的底和高同时发生变化时，三角形的面积不一定变化．比如当高变为原来的3倍，底变为原来的1 3 ，则三角形面积与原来的一样．这就是说：一个三角形的面积变化与否取决于它的高和底的乘积，而不仅仅取决于高或底的变化．同时也告诉我们：一个三角形在面积不改变的情况下，可以有无数多个不同的形状．在实际问题的研究中，我们还会常常用到以下结论： ①等底等高的两个三角形面积相等； ②两个三角形高相等，面积比等于它们的底之比；两个三角形底相等，面积比等于它们的高之比；如图 12::S S a b = b a S 2S 1 D C B A ③夹在一组平行线之间的等积变形，如右上图ACD BCD S S =△△；反之，如果ACD BCD S S =△△，则可知直线AB 平行于CD ． ④等底等高的两个平行四边形面积相等(长方形和正方形可以看作特殊的平行四边形)； ⑤三角形面积等于与它等底等高的平行四边形面积的一半； ⑥两个平行四边形高相等，面积比等于它们的底之比；两个平行四边形底相等，面积比等于它们的高之比．三角形等高模型与鸟头模型

【例 1】你有多少种方法将任意一个三角形分成：⑴ 3个面积相等的三角形；⑵ 4个面积相等的三角形；⑶ 6个面积相等的三角形。【解析】 ⑴ 如下图，D 、E 是BC 的三等分点，F 、G 分别是对应线段的中点，答案不唯一： C E D B A F C D B A G D B A ⑵ 如下图，答案不唯一，以下仅供参考： ⑸ ⑷⑶⑵⑴ ⑶如下图，答案不唯一，以下仅供参考：【例 2】如图，BD 长12厘米，DC 长4厘米，B 、C 和D 在同一条直线上。 ⑴ 求三角形ABC 的面积是三角形ABD 面积的多少倍？ ⑵ 求三角形ABD 的面积是三角形ADC 面积的多少倍？【解析】因为三角形ABD 、三角形ABC 和三角形ADC 在分别以BD 、BC 和DC 为底时，它们的高都是从A 点向BC 边上所作的垂线，也就是说三个三角形的高相等。于是：三角形ABD 的面积12=?高26÷=?高三角形ABC 的面积124=+?（）高28÷=?高三角形ADC 的面积4=?高22÷=?高所以，三角形ABC 的面积是三角形ABD 面积的 4 3 倍；三角形ABD 的面积是三角形ADC 面积的3倍。【例 3】如右图，ABFE 和CDEF 都是矩形，AB 的长是4厘米，BC 的长是3厘米，那么图中阴影部分的面积是平方厘米。【解析】图中阴影部分的面积等于长方形ABCD 面积的一半，即4326?÷=(平方厘米)。【巩固】(2009年四中小升初入学测试题)如图所示，平行四边形的面积是50平方厘米，则阴影部分的面积是平方厘米。 C D B A

苏版七年级平行线和全等三角形模型(拓展提优)

平面图形（二）&全等三角形模型汇编平行线四大模型：结论1 结论2：若∠P+∠AEP+∠PFC= 360°，则AB∥CD. 结论1 结论2：若∠P=∠AEP+∠CFP，则AB∥CD. 结论1：若∥，则∠=∠-∠或∠=∠-∠；结论2：若∠P=∠AEP-∠CFP或∠P=∠CFP-∠AEP，则AB∥CD. 结论1 结论2：若∠P=∠CFP-∠AEP或∠P=∠AEP-∠CFP，则AB∥CD. 巩固练习平行线四大模型证明（1）已知AE // CF ,求证∠P +∠AEP +∠PFC = 360° . （2）已知∠P=∠AEP+∠CFP，求证AE∥CF．（3）已知AE∥CF，求证∠P=∠AEP-∠CFP. （4）已知∠P= ∠CFP -∠AEP ,求证AE //CF . 模块一平行线四大模型应用例1 （1）如图，a∥b,M、N分别在a、b上，P为两平行线间一点，那么∠l+∠2+∠3= ．

(2)如图，AB ∥CD ，且∠A =25°，∠C =45°，则∠E 的度数是． (3)如图，已知AB ∥DE ，∠ABC =80°，∠CDE =140°，则∠BCD = . (4) 如图，射线AC ∥BD ，∠A = 70°，∠B = 40°，则∠P = ．练如图所示，AB ∥CD ，∠E =37°，∠C = 20°，则∠EAB 的度数为．（七一中学2015-2016七下3月月考）如图，AB ∥CD ，∠B =30°，∠O =∠C ．则∠C = . 例2如图，已知AB ∥DE ，BF 、 DF 分别平分∠ABC 、∠CDE ，求∠C 、 ∠F 的关系. 练如图，已知AB ∥DE ，∠FBC =n 1∠ABF ，∠FDC =n 1∠FDE . (1)若n =2,直接写出∠C 、∠F 的关系； (2)若n =3，试探宄∠C 、∠F 的关系； (3)直接写出∠C 、∠F 的关系（用含n 的等式表示）. 例3 如图，已知AB ∥CD ，BE 平分∠ABC ，DE 平分∠ADC ．求证：∠E = 2 (∠A +∠C ) . 练如图，己知AB ∥DE ，BF 、DF 分别平分∠ABC 、∠CDE ，求∠C 、∠F 的关系. 例4如图，∠3==∠1+∠2，求证：∠A +∠B +∠C +∠D = 180° 练（武昌七校 2015-2016 七下期中）如图，AB ⊥BC ，AE 平分∠BAD 交BC 于E ，AE ⊥DE ，∠l +∠2= 90°，M 、N 分别是BA 、 CD 的延长线上的点，∠EAM 和∠EDN 的平分线相交于点 F 则∠F 的度数为（）． A . 120° B . 135° C . 145° D . 150° 模块二平行线四大模型构造

小学奥数-几何五大模型(蝴蝶模型)知识讲解

小学奥数-几何五大模型(蝴蝶模型)

模型三蝴蝶模型（任意四边形模型）任意四边形中的比例关系(“蝴蝶定理”)： S 4 S 3 S 2 S 1O D C B A ①1243::S S S S =或者1324S S S S ?=? ②()()1243::AO OC S S S S =++ 蝴蝶定理为我们提供了解决不规则四边形的面积问题的一个途径。通过构造模型，一方面可以使不规则四边形的面积关系与四边形内的三角形相联系；另一方面，也可以得到与面积对应的对角线的比例关系。【例 1】 (小数报竞赛活动试题)如图，某公园的外轮廓是四边形ABCD ，被对角线AC 、BD 分成四个部分，△AOB 面积为1平方千米，△BOC 面积为2平方千米，△COD 的面积为3平方千米，公园由陆地面积是6．92平方千米和人工湖组成，求人工湖的面积是多少平方千米？ O D C B A 【分析】根据蝴蝶定理求得312 1.5AOD S =?÷=△平方千米，公园四边形ABCD 的面积是 123 1.57.5+++=平方千米，所以人工湖的面积是7.5 6.920.58-=平方千米【巩固】如图，四边形被两条对角线分成4个三角形，其中三个三角形的面积已知，求：⑴三角形BGC 的面积；⑵:AG GC =？任意四边形、梯形与相似模型

B 【解析】 ⑴根据蝴蝶定理，123BGC S ?=?V ，那么6BGC S =V ； ⑵根据蝴蝶定理，()():12:361:3AG GC =++=． (？？？) 【例 2】四边形ABCD 的对角线AC 与BD 交于点O (如图所示)。如果三角形ABD 的面积等于三角形BCD 的面积的1 3 ，且2AO =，3DO =，那么CO 的长度是DO 的长度的_________倍。 A B C D O H G A B C D O 【解析】在本题中，四边形ABCD 为任意四边形，对于这种”不良四边形”，无外乎两种处理方法：⑴利用已知条件，向已有模型靠拢，从而快速解决；⑵通过画辅助线来改造不良四边形。看到题目中给出条件:1:3ABD BCD S S =V V ，这可以向模型一蝴蝶定理靠拢，于是得出一种解法。又观察题目中给出的已知条件是面积的关系，转化为边的关系，可以得到第二种解法，但是第二种解法需要一个中介来改造这个”不良四边形”，于是可以作AH 垂直BD 于H ，CG 垂直BD 于G ，面积比转化为高之比。再应用结论：三角形高相同，则面积之比等于底边之比，得出结果。请老师注意比较两种解法，使学生体会到蝴蝶定理的优势，从而主观上愿意掌握并使用蝴蝶定理解决问题。解法一：∵::1:3ABD BDC AO OC S S ??==， ∴236OC =?=， ∴:6:32:1OC OD ==．解法二：作AH BD ⊥于H ，CG BD ⊥于G ． ∵1 3 ABD BCD S S ??=， ∴13 AH CG =， ∴13 AOD DOC S S ??=， ∴13 AO CO =， ∴236OC =?=， ∴:6:32:1OC OD ==．【例 3】如图，平行四边形ABCD 的对角线交于O 点，CEF △、OEF △、ODF △、BOE △的面积依次是2、4、4和6。求：⑴求OCF △的面积；⑵求GCE △的面积。

奥数几何三角形五大模型带解析

三角形五大模型【专题知识点概述】本讲复习以前所学过的有关平面几何方面的知识，旨在提高学生对该部分知识的综合运用能力。重点模型重温一、等积模型 ①等底等高的两个三角形面积相等； ②两个三角形高相等，面积比等于它们的底之比；两个三角形底相等，面积比等于它们的高之比；如右图12::S S a b = ③夹在一组平行线之间的等积变形，如右图ACD BCD S S =△△；反之，如果ACD BCD S S =△△，则可知直线平行于CD ． ④等底等高的两个平行四边形面积相等( 长方形和正方形可以看作特殊的平行四边形)； ⑤三角形面积等于与它等底等高的平行四边形面积的一半； ⑥两个平行四边形高相等，面积比等于它们的底之比；两个平行四边形底相等，面积比等于它们的高之比．二、等分点结论（“鸟头定理”） D C B A b a s 2 s 1

如图，三角形AED 占三角形ABC 面积的23×14=1 6 三、任意四边形中的比例关系（“蝴蝶定理”） ① S 1︰S 2=S 4︰S 3 或者S 1×S 3=S 2×S 4 ② ②AO ︰OC=（S 1+S 2）︰（S 4+S 3）梯形中比例关系（“梯形蝴蝶定理”） ① S 1︰S 3=a 2︰b 2 ②S 1︰S 3︰S 2︰S 4= a 2︰b 2︰ab ︰ab ; ③S 的对应份数为（a+b ）2 模型四：相似三角形性质如何判断相似 (1)相似的基本概念：两个三角形对应边城比例，对应角相等。 (2)判断相似的方法： ①两个三角形若有两个角对应相等则这两个三角形相似； ②两个三角形若有两条边对应成比例，且这两组对应边所夹的角相等则两个 S 4 S 3 s 2 s 1O D C B A S 4 S 3s 2 s 1 b a

三角形的四大模型

三角形的四大模型令狐采学一、三角形的重要概念和性质 1、三角形的内角和定理：三角形的内角和等于180° 2、三角形的外角和定理：三角形的一个外角等于和它不相邻的两个内角的和 3、三角形角平分线（角分线）中线（分面积等）高（直角三角形两锐角互余）二、八字模型：证明结论：∠A＋∠B＝∠C＋∠D 三、飞镖模型：证明结论：1．∠BOC＝∠A＋∠B＋∠C 四、角分线模型：如图，BD、CD分别是∠ABC和∠ACB的角平分线，BD、CD相交于点D，试探索∠A与∠D之间的数量关系，并证明你的结论．如图，△ABC两个外角（∠CAD、∠ACE）的平分线相交于点P．探索∠P与∠B有怎样的数量关系，并证明你的结论．题型一、三角形性质等应用

1．如图，小亮从A点出发前进10m，向右转15°，再前进10m，又向右转15°，这样一直走下去，他第一次回到出发点A时，一共走了米数是（） A．120 B．150 C．240 D．360 2．如图所示是重叠的两个直角三角形．将其中一个直角三角形沿BC方向平移得到△DEF．如果AB=8cm，BE=4cm，DH=3cm，则图中阴影部分面积为cm2． 3．如图，在△ABC中，已知点D，E，F分别为边BC，AD，CE的中点，且S△ABC=4cm2，则S阴影=cm2． 4．A、B、C是线段A1B，B1C，C1A的中点，S△ABC的面积是1，则S△A1B1C1的面积． 5．一个四边形截去一个角后，剩下的部分可能是什么图形？画出所有可能的图形，并分别说出内角和和外角和变化情况．6．如图，直线AC∥BD，连接AB，直线AC，BD及线段AB把平面分成①、②、③、④四个部分，规定：线上各点不属于任何部分．当动点P落在某个部分时，连接PA，PB，构成∠PAC，∠APB，∠PBD三个角．（提示：有公共端点的两条重合的射线所组成的角是0°角）（1）当动点P落在第①部分时，求证：∠APB=∠PAC+∠PBD；

七年级：三角形三线合一性质专题

F E D C B A E D C B A B ' C B A 专题四（第九讲）：三角形三线性质金牌数学专题系列导入知识要点知识点1 ：三角形的重要线段意义图形 > 表示法三角形的高线从三角形的一个顶点向它的对边所在的直线作垂线,顶点和垂足之间的线段 D C B A 是△ABC 的BC 上的高线. ⊥BC 于D. 3.∠ADB=∠ADC=90°. 三角形的中线 / 三角形中,连结一个顶点和它对边中的线段 D C B A 是△ABC 的BC 上的中线. =EC= 12 BC. 三角形的角平分线三角形一个内角的平分线与它的对边相交,这个角顶点与交点之间的线段 21 D C B A 是△ABC 的∠BAC 的平分线. · 2.∠1=∠2=1 2 ∠BAC. 双基练习一、选择题： 1.如图1所示,在△ABC 中,∠ACB=90°,把△ABC 沿直线AC 翻折180°,使点B 落在点B ′的位置,则线段AC 具有性质( ) A.是边BB ′上的中线 B.是边BB ′上的高 C.是∠BAB ′的角平分线 D.以上三种性质合一） (1) (2) (3) 2.如图2所示,D,E 分别是△ABC 的边AC,BC 的中点,则下列说法正确的是( ) 是△BCD 的中线是△ABC 的中线 =DC,BD=EC D.∠C 的对边是DE 3.如图3所示,在△ABC 中,已知点D,E,F 分别为边BC,AD,CE 的中点, 且S △ABC =4cm 2,则S 阴影等于( ) A.2cm 2 .1cm 2 C 12 14 小学时上课爱睡觉。一次语文课老师布置作业写一篇作文，题目是《假如我是蜘蛛》。下课了问了同学，晚上在家绞尽脑汁，写了一篇轰动全校的《假如我是只猪》

相似三角形模型分析大全(非常全面经典)

相似三角形模型分析大全一、相似三角形判定的基本模型认识（一）A字型、反A字型（斜A字型） B （平行） B （不平行）（二）8字型、反8字型 B C B C （蝴蝶型）（平行）（不平行）（三）母子型 B

（四）一线三等角型：三等角型相似三角形是以等腰三角形（等腰梯形）或者等边三角形为背景（五）一线三直角型：（六）双垂型：

二、相似三角形判定的变化模型旋转型：由A 字型旋转得到。 8字型拓展 C B E D A 共享性 G A B C E F 一线三等角的变形一线三直角的变形第二部分相似三角形典型例题讲解

母子型相似三角形例1：如图，梯形ABCD 中，AD ∥BC ，对角线AC 、BD 交于点O ，BE ∥CD 交CA 延长线于E ．求证：OE OA OC ?=2 ．例2：已知：如图，△ABC 中，点E 在中线AD 上, ABC DEB ∠=∠．求证：（1）DA DE DB ?=2 ；（2）DAC DCE ∠=∠．例3：已知：如图，等腰△ABC 中，AB ＝AC ，AD ⊥BC 于D ，CG ∥AB ，BG 分别交AD 、AC 于E 、F ．求证：EG EF BE ?=2 ． A C D E B

相关练习： 1、如图，已知AD 为△ABC 的角平分线，EF 为AD 的垂直平分线．求证：FC FB FD ?=2 ． 2、已知：AD 是Rt △ABC 中∠A 的平分线，∠C=90°，EF 是AD 的垂直平分线交AD 于M ，EF 、BC 的延长线交于一点N 。求证：(1)△AME ∽△NMD; (2)ND 2 =NC ·NB 3、已知：如图，在△ABC 中，∠ACB=90°，CD ⊥AB 于D ，E 是AC 上一点，CF ⊥BE 于F 。求证：EB ·DF=AE ·DB

学而思寒假七年级尖子班讲义第1讲平行线四大模型

目录 Contents 第1讲平行线四大模型 (1) 第2讲实数三大概念 (17) 第3讲平面直角坐标系 (33) 第4讲坐标系与面积初步 (51) 第5讲二元—次方程组进阶 (67) 第6讲含参不等式（组） (79)

1平行线四大模型知识目标目标一熟练掌握平行线四大模型的证明目标二熟练掌握平行线四大模型的应用目标三掌握辅助线的构造方法，熟悉平行线四大模型的构造秋季回顾平行线的判定与性质 l、平行线的判定根据平行线的定义，如果平面内的两条直线不相交，就可以判断这两条直线平行，但是，由于直线无限延伸，检验它们是否相交有困难，所以难以直接根据定义来判断两条直线是否平行，这就需要更简单易行的判定方法来判定两直线平行．判定方法l：两条直线被第三条直线所截，如果同位角相等，那么这两条直线平行．简称：同位角相等，两直线平行．判定方法2：两条直线被第三条直线所截，如果内错角相等，那么这两条直线平行．简称：内错角相等，两直线平行，判定方法3：两条直线被第三条直线所截，如果同旁内角互补，那么这两条直线平行．简称：同旁内角互补，两直线平行，如上图：若已知∠1=∠2，则AB∥CD（同位角相等，两直线平行）；若已知∠1=∠3，则AB∥CD（内错角相等，两直线平行）；若已知∠1+ ∠4= 180°，则AB∥CD（同旁内角互补，两直线平行）．另有平行公理推论也能证明两直线平行：平行公理推论：如果两条直线都与第三条直线平行，那么这两条直线也互相平行． 2、平行线的性质利用同位角相等，或者内错角相等，或者同旁内角互补，可以判定两条直线平行．反过来，如果已知两条直线平行，当它们被第三条直线所截，得到的同位角、内错角、同旁内角也有相应的数量关系，这就是平行线的性质．性质1：