最值宝典第第七讲：定角对定边类问题

第七讲：定角对定边类问题

【定边定角模型】如图：∠A =θ(定角)，角固定不变，BC =a （定值），则点A 在△ABC 的外接圆上运动. 【模型原理】

① 定边定角定三角形外接圆

O ;由正弦定理：

2sin sin a a R A θ

==（初中可推导） 可见，当BC 和∠A 确定时，△ABC 的外接圆O 的半径R 也是确定的，即△ABC 外接

圆唯一.

② 同圆等圆中同弧所对的圆周角相等；如果将BC 视为BC 所夹的一条弦，满足∠A =θ的所有圆周角都在△ABC 的外接圆上，故点A 在△ABC 的外接圆上运动； 【一般结论】：当点A 位于BAC 中点时，△ABC 的面积最大，此时△ABC 的高

h OA OE =+，()

11

()(22

ABC MAX S

BC OA OE a r =?+=??+弦心距） 【核心提炼】

① 定边对定角，三点确定外接圆 ②确定圆心位置，计算外接圆半径。 ② 求出外接圆圆心至定弦的距离（弦心距） ④计算最值

【基本模型】定边定角的探究

已知线段AB =6，平面内一点C ，满足90ACB ∠= 问题一：根据以上信息，如何确定点C 的运动轨迹？ 问题二：求C 点的运动路径长？ 问题三：求△ABC 面积的最大值？ 【分析】问题一：点C 的运动轨迹是一个圆

问题二：点C 的运动路径长为△ABC 外接圆的周长：6π

问题三：当点C 运动到ACB 中点时，△ABC 面积的最大值，最大面积为9．

a O

A

C

说理：∵OA+OE≥AE , h≤AE ， ∴h≤OA+OE （仅当A,O,E 三点共线时取等号）

C

A

B

a

h a

h O E (D )

D

O

E A

C

C

B

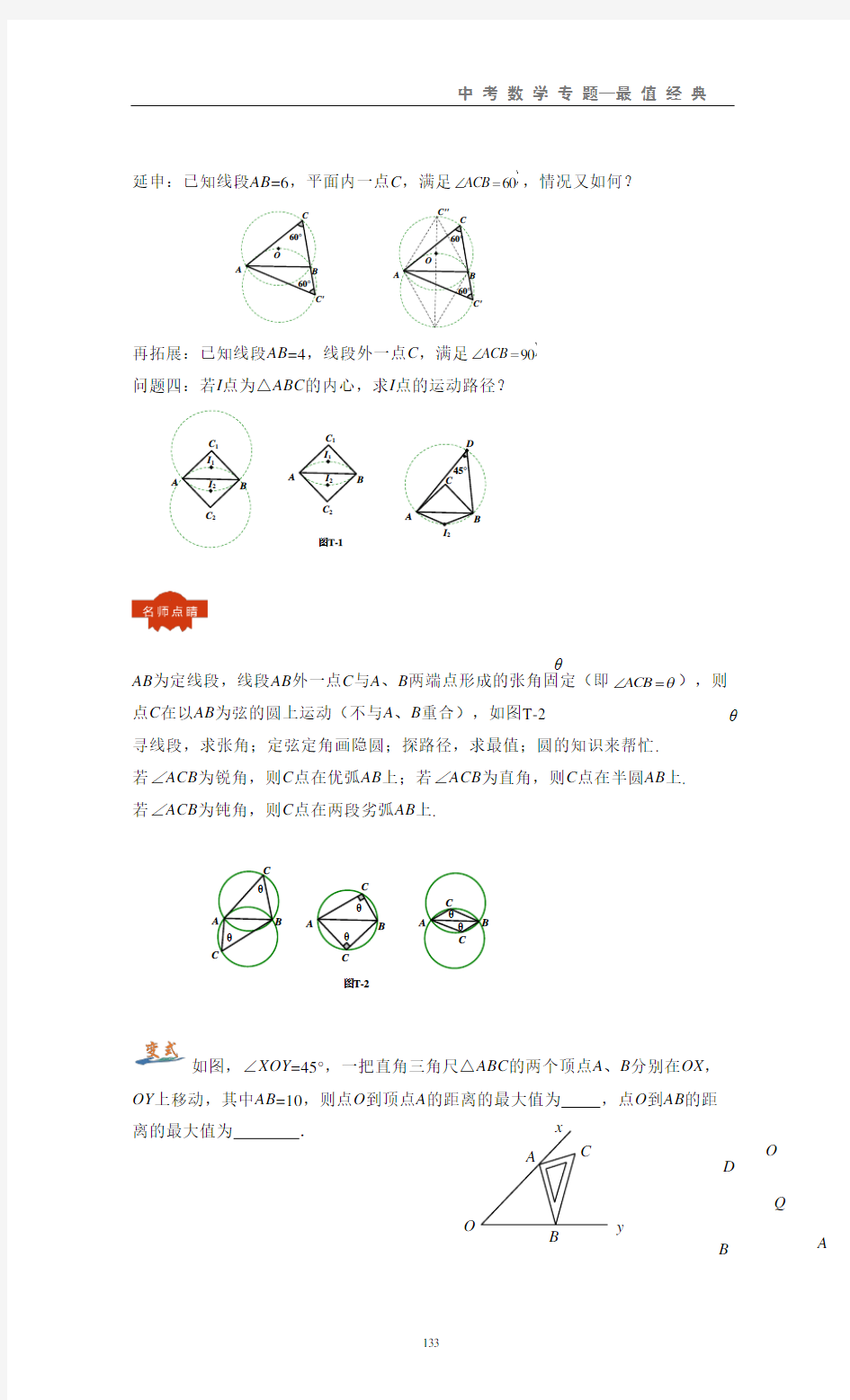
60，情况又如何？

90

如图，∠XOY=45°，一把直角三角尺△ABC的两个顶点A、B分别在OX，

OY上移动，其中AB=10，则点O到顶点A的距离的最大值为，点O到AB的距

离的最大值为．

Q

O

A

x

45sin AB AO

=2,AB 如图，∠MON =90°，已知△ABC ，AC =BC =5，AB =6，三角形ABC 的顶点A 、

B 分别在边OM ，ON 上当B 在边ON 上运动时，A 随之在边OM 上运动，三角形AB

C 的形状保持不变，在运动过程中，点C 到点O 的最大距离为 ．

【解答】解：如图，取AB 的中点D ，连接CD ．

∵AC =BC =5，AB =6．∵点D 是AB 边中点，∴BD =

AB =3

∴CD =

；连接OD ，OC ，有OC ≤OD +DC 当O 、D 、C 共线时，OC 有最大值，最大值是OD +CD 又∵△AOB 为直角三角形，D 为斜边AB 的中点，∴OD =

AB =3， ∴OD +CD =3+4=7，即OC =7．故答案为：7．

如图，∠MON =90°，矩形ABCD 的顶点A 、B 分别在边OM ，ON 上，当B 在边ON 上运动时，A 随之在边OM 上运动，矩形ABCD 的形状保持不变，其中AB =8，BC =3，运动过程中，点D 到点O 的最大距离为 ．

【解答】解：如图，取AB 的中点E ，连接OE 、DE 、OD ，

Q

O D

B

A

M P F

E D C B

A A

B C D （E ）M

D '

G

（F ）O

N

M

C

A A

B

C

M

N

N M

O D C

B A A

B C

D

O M N

E

P

E D A

A D （E ）N

M O

D

C B A A

B

C D O

M

N

E

O

∵OD ≤OE +DE ，∴当O 、D 、E 三点共线时，点D 到点O 的距离最大 此时，∵AB =8，BC =3，∴OE =AE =AB =4

∴DE =

，∴OD 的最大值为：5+4=9；故答案为：9．

如图，△ABC 中，AC ＝3，BC ＝，∠ACB ＝45°，D 为△ABC 内一动点，

⊙O 为△ACD 的外接圆，直线BD 交⊙O 于P 点，交BC 于E 点，弧AE ＝CP ，则AD 的最小值为（ ）

A.1

B.2

C.

D.

解：∵∠CDP ＝∠ACB ＝45° ∴∠BDC ＝135°（定弦定角最值）

如图，当AD 过O ′时，AD 有最小值

∵∠BDC ＝135° ∴∠BO ′C ＝90° ∴△BO ′C 为等腰直角三角形

∴∠ACO ′＝45°＋45°＝90° ∴AO ′＝5，

又O ′B ＝O ′C ＝4，∴AD ＝.

【基本模型】定边定角与点圆最值

如图，正方形ABCD 中，AB =4，动点E 从点A 出发向点D 运动，同时动点F 从点D 出发向点C 运动，点E 、F 运动的速度相同，当它们到达各自终点时停止运动，运动过程中线段AF 、BE 相交于点P ，M 是线段BC 上任意一点，则MD +MP 的最小值为

．

【解答】解：如上图作点D 关于BC 的对称点D ′，连接PD ′，

由轴对称的性质可知：MD =D ′M ，CD =CD ′=4，∴PM +DM =PM

+MD ′=PD ′ 过点P 作PE 垂直DC ，垂足为G ，易证AF ⊥BE ，故可知P 的轨迹为以AB 为直径的四分之一圆弧上，当点E 与点D 重合，点F 与点C 重合时，PG 和GD ′均最短，

∴此时，PD ′最短．∵四边形ABCD 为正方形，∴PG =AD =2，GC =DC =2．

2422441 O P D C B A O '

M E A

B

D C

O O '

M

P

F E D C

B A

A B M D '

P

A

O C

D

A E E

A B

O '

P

O E

D

C

B

A A

B C D （E ）

M

D 'G

（F ）

∴GD ′=6．在Rt △PGD ′中，由勾股定理得：

．

如图，AC ＝3，BC ＝5，且∠BAC ＝90°，D 为AC 上一动点，以AD 为直径

作圆，连接BD 交圆于E 点，连CE ，则CE 的最小值为（ ） A. B. C.5 D.

解：连接AE ，∵AD 为⊙O 的直径 ∴∠AEB ＝∠AED ＝90°， ∴E 点在以AB 为直径的圆上运动，当CE 过圆心O ′时，CE 有最小值为

.

如图，在△ABC 中，AC ＝3，BC ＝，∠ACB ＝45°，AM //BC ，点P 在射线AM

上运动，连BP 交

△APC 的外接圆于D ，则AD 的最小值为（ ） A.1 B.2 C. D ．

解：连接CD ， ∴∠P AC ＝∠PDC ＝∠ACB ＝45° ∴∠BDC ＝135°，如图，当AD 过圆心

O ′时， AD 有最小值，∵∠BDC ＝135°，∴∠BO ′C ＝90°， ∴O ′B ＝O ′C ＝4，又∠ACO ′＝90°，∴AO ′＝5 ∴AD 的最小值为

如图，⊙O 的半径为2，弦AB 的长为，点P 为优弧AB 上一动点，

交直线PB 于点C ，则的面积的最大值是（ ） A. B. C. D.

解析：构造直径BE ，易求要使△ABC 的最大面积，则点C 到AB 的距离最大，点C 在⊙M 上，且

当点C 为优弧AB 的中点时，点C 到AB 的距离最大，此时△ABC 为等腰三角形， 213-213+9

16O

P

D

C

B

A O 'M

M P

O D

C

B

A

C

2422432AP AC ⊥ABC ?3612+336+3312+346+y

x M

F

E C D B A A B D C E

F M x y

M

M

故选B

如图，A (1，0)、B (3，0)，以AB 为直径作⊙M ，射线OF 交⊙M 于E 、F 两

点，C 为弧AB 的中点，D 为EF 的中点．当射线绕O 点旋转时，CD 的最小值为_____

解：连接DM ∵D 是弦EF 的中点

∴DM ⊥EF ∴点D 在以A 为圆心的，OM 为直径的圆上运动 当CD 过圆心A 时，CD 有最小值，连接CM ∵C 为弧AB 的中点∴CM ⊥AB ∴CD 的最小值为

如图，AB 是⊙O 的直径，AB ＝2，∠ABC ＝60°，P 是上一动点，D 是AP 的

中点，连接CD ，则CD 的最小值为_____

解：连接OD ，∵D 为弦AP 的中点，∴OD ⊥AP ，∴点D 在以AO 为直径的圆上运动，当CD 过圆心O ′时，CD 有最小值，过点C 作CM ⊥AB 于M

∵OB ＝OC ，∠ABC ＝60°，∴△OBC 为等边三角形 ∴OM ＝，CM ＝∴O ′C ＝

∴CD 的最小值为

.

【基本模型】折叠类遇定边定角的探究

如图1，P 是⊙O 外的一点，直线

PO

分别交⊙O 于点A ，B ，则P A 是点P 到⊙O 上的点的最短距离． （1）探究一：如图2，在Rt △ABC 中，∠ACB =90°，AC =BC =2，以BC 为直径的半圆交AB 于D ，P 是上的一个动点，连接AP ，则AP 的最小值是．

（2）探究二：如图3，在边长为2的菱形ABCD 中，∠A =60°，M 是AD 边的中点，N 是AB 边上一动点，将△AMN 沿MN 所在的直线翻折得到△A ′MN ，连接A ′C ，请求出A ′C 长度的最小值．

（3）探究三，在正方形ABCD 中，点E ，F 分别从D ，C 两点同时出发，以相同的

x

F E P D

C B A 图4

A 'N

M

C D B A 图3P O B A B

P D

C

A 图1

图2B

A

B

A

CD 1

速度在直线DC ，CB 上移动，连接AE 和DF 交于点P ，由于点E ，F 的移动，使得点P 也随之运动，若AD =4，试求出线段CP 的最小值．

【解答】解：（1）找到BC 的中点E ，连接AE ，交半圆于P 2，在半圆上任取P 1，连接AP 1，EP 1，可见，AP 1+EP 1＞AE ，即AP 2是AP 的最小值． 在Rt △ABC 中，∠ACB =90°，AC =BC =2，CE =BC =1∴AE =

，

∵P 2E =1，∴AP 2=

．故答案为：

．

（2）如图所示：因为点M 是AD 的中点， ∴AM =MA ′=

AD =1，由于△AMN 沿MN 所在的直线翻折得到△A ′MN

∴MA ′=AM =1是定值，当点A ′在MC 上时，A ′C 长度最小．过点M 作ME ⊥DC 于点E ，∵在边长为2的菱形ABCD 中，∠A =60°，M 为AD 中点， ∴2MD =AD =CD =2，∠EDM =60°，∴∠EMD =30°， ∴ED =MD =

，∴EM =DM ×cos 30°=

，

∴MC =

，∴

．

答：A ′C 长度的最小值为

．

（3）∵四边形ABCD 是正方形，

∴AD =DC =4，∠ADC =∠C =90°．在△ADE 和△DCF 中，，

∴△ADE ≌△DCF （SAS ）．∴AE =DF ，∠DAE =∠CDF ， 由于∠CDF +∠ADF =90°，∴∠DAE +∠ADF =90°．∴AE ⊥DF ；

由于点P 在运动中保持∠APD =90°，∴点P 的路径是一段以AD 为直径的弧， 设AD 的中点为Q ，连接QC 交弧于点P ，此时CP 的长度最小， 在Rt △QDC 中，QC =，

∴

．

F E

P

D

C B A

图4

A 'N

M C

D

B A 图3P

B

B

P D

C

A

图1

图2

F E

P D C B A

图4A '

N M C D B

A

图3

答：线段CP 的最小值为

．

【基本模型】定边定角的综合应用

（1）如图①，△ABC 是等边三角形，AB ＝12，若点O 是△ABC 的内心，则OA 的长为

；

问题探究

（2）如图②，在矩形ABCD 中，AB ＝12，AD ＝18，如果点P 是AD 边上一点，且AP ＝3，那么BC 边上是否存在一点Q ，使得线段PQ 将矩形ABCD 的面积平

分？若存在，求出PQ 的长；若不存在，请说明理由．

问题解决

（3）某城市街角有一草坪，草坪是由△ABM 草地和弦AB 与其所对的劣弧围成的草地组成，如图③所示．管理员王师傅在M 处的水管上安装了一喷灌龙头，以后，他想只用喷灌龙头来给这块草坪浇水，并且在用喷灌龙头浇水时，既要能确保草坪的每个角落都能浇上水，又能节约用水，于是，他让喷灌龙头的转角正好等于∠AMB （即每次喷灌时喷灌龙头由MA 转到MB ，然后再转回，这样往复喷灌．）同时，再合理设计好喷灌龙头喷水的射程就可以了．

如图③，已测出AB ＝24m ，MB ＝10m ，△AMB 的面积为96m 2；过弦AB 的中点D 作DE ⊥AB 交于点E ，又测得DE ＝8m ．

请你根据以上信息，帮助王师傅计算喷灌龙头的射程至少多少米时，才能实现他的想法？为什么？（结果保留根号或精确到0.01米）

【解答】解：（1）如图1，过O 作OD ⊥AC 于D ，则AD ＝

AC ＝×12＝6，

∵O 是内心，△ABC 是等边三角形，∴∠OAD ＝∠BAC ＝×60°＝30°， 在Rt △AOD 中，cos ∠OAD ＝cos 30°＝，∴OA ＝， 故答案为：； F E P D C

B A O P 'P

E O D

C

A B D C B A

D B A C D B A C 图3图2图1N

M E D C

B

A

A '

E D F

C

P Q

A

B

A

C D

B

P 1

P 2AB O

H N M

F E

D C B A G

M

Q P

O D C B A 图3

图1图2O C

D

B A ③

图图②

图①

C B

A

D

C

B

A

E

B

A

D M

（2）存在，如图2，连接AC 、BD 交于点O ，连接PO 并延长交BC 于Q ，则线段PQ 将矩形ABCD 的面积平分，

∵点O 为矩形ABCD 的对称中心，∴CQ ＝AP ＝3， 过P 作PM ⊥BC 于点M ，则PM ＝AB ＝12，MQ ＝，

由勾股定理得：PQ ＝

；

（3）如图3，作射线ED 交AM 于点C ∵AD ＝DB ，ED ⊥AB ，

是劣弧，∴

所在圆的圆心在射线DC 上，

假设圆心为O ，半径为r ，连接OA ，则OA ＝r ，OD ＝r ﹣8，AD ＝AB ＝12，

在Rt △AOD 中，

，解得：r ＝13，∴OD ＝5，

过点M 作MN ⊥AB ，垂足为N ，∵S △ABM ＝96，AB ＝24，∴ A B ?MN ＝96，

×24×MN ＝96，∴MN ＝8，NB ＝6，AN ＝18， ∵CD ∥MN ，∴△ADC ∽△ANM ，∴，∴

，∴DC ＝，

∴OD ＜CD ，∴点O 在△AMB 内部， ∴连接MO 并延长交于点F ，则MF 为草坪上的点到M 点的最大距离，

∵在

上任取一点异于点F 的点G ，连接GO ，GM ，

∴MF ＝OM +OF ＝OM +OG ＞MG ，

即MF ＞MG ，过O 作OH ⊥MN ，垂足为H ，则OH ＝DN ＝6，MH ＝3， ∴OM ＝

，∴MF ＝OM +r ＝

+13≈19.71（米），

答：喷灌龙头的射程至少为19.71米．

（1）如图①，在△ABC 中，AB ＝AC ＝10，BC ＝12，点O 是△ABC 的外接圆的圆心，则OB 的长为 .

问题探究 （2）如图②，已知矩形ABCD ，AB ＝4，AD ＝6，点E 为AD 的中点，以BC 为

直径作半圆O ，点P 为半圆O 上一动点，求E 、P 之间的最大距离； 问题解决

（3）某地有一块如图③所示的果园，果园是由四边形ABCD 和弦CB 与其所对的劣弧场地组成的，果园主人现要从入口D 到上的一点P 修建一条笔直的小

O C

B A O E

C D

B A F E D

C

A B 图图图O H N F

E

D C B

A

G

M

Q P O D

C

B A

图3

图1

图2

O C

D

B

A

BC

路DP ．已知AD //BC ，∠ADB ＝45°，BD ＝米，BC ＝160米，过弦BC 的中点E 作EF ⊥BC 交于点F ，又测得EF ＝40米．修建小路平均每米需要40元（小路宽度不计），不考虑其他因素，请你根据以上信息，帮助果园主人计算修建这条小路最多要花费多少元？

【解答】解：（1）如图，若AO 交BC 于K ，

∵点O 是△ABC 的外接圆的圆心，AB ＝AC ，∴AK ⊥BC ，BK ＝，

∴AK ＝

，

在Rt △BOK 中，OB 2＝BK 2+OK 2，设OB ＝x ， ∴， 解得x ＝

，∴OB ＝

；故答案为：

．

（2）如图，连接EO ，延长EO 交半圆于点P ，可求出此时E 、P 之间的距离最大， ∵在

是任意取一点异于点P 的P ′，连接OP ′，P ′E ，

∴EP ＝EO +OP ＝EO +OP ′＞EP ′，即EP ＞EP ′， ∵AB ＝4，AD ＝6，∴EO ＝4，OP ＝OC ＝

，

∴EP ＝OE +OP ＝7，∴E 、P 之间的最大距离为7． （3）作射线FE 交BD 于点M ， ∵BE ＝CE ，EF ⊥BC ，是劣弧，

∴

所在圆的圆心在射线FE 上，

假设圆心为O ，半径为r ，连接OC ，则OC ＝r ，OE ＝r ﹣40， BE ＝CE ＝

，

在Rt △OEC 中，r 2＝802+（r ﹣40）2，解得：r ＝100， ∴OE ＝OF ﹣EF ＝60，

过点D 作DG ⊥BC ，垂足为G ，

∵AD ∥BC ，∠ADB ＝45°，∴∠DBC ＝45°， 在Rt △BDG 中，DG ＝BG ＝

，在Rt △BEM 中，ME ＝BE ＝80，

∴ME ＞OE ，∴点O 在△BDC 内部，

2120BC

C

B

C

D A F

E D

C

A

B ③

图图②图

①

①

图②

图A B E O

C

P '

②

图A

B

D C

E O P '

图③

B A D

E

F H

O M

G

P '

P

图③

B

∴连接DO 并延长交于点P ，则DP 为入口D 到

上一点P 的最大距离，

∵在

上任取一点异于点P 的点P ′，连接OP ′，P ′D ，

∴DP ＝OD +OP ＝OD +OP ′＞DP ′，即DP ＞DP ′，过点O 作OH ⊥DG ， 垂足为H ，，则OH ＝EG ＝40，DH ＝DG ﹣HG ＝DG ﹣OE ＝60， ∴

，∴DP ＝OD +r ＝

+100，

∴修建这条小路最多要花费元．.

问题提出

（1）如图①，在等腰Rt △ABC 中，斜边AC ＝4，点D 为AC 上一点，连接BD ，则BD 的最小值为 2 ； 问题探究

（2）如图②，在△ABC 中，AB ＝AC ＝5，BC ＝6，点M 是BC 上一点，且BM ＝4，点P 是边AB 上一动点，连接PM ，将△BPM 沿PM 翻折得到△DPM ，点D 与点B 对应，连接AD ，求AD

的最小值； 问题解决

（3）如图③，四边形ABCD 是规划中的休闲广场示意图，其中∠BAD ＝∠ADC ＝135°，∠DCB ＝30°，AD ＝ m m ，AB ＝3mm ，点M 是BC 上一点，MC ＝4mm ．现计划在四边形ABCD 内选取一点P ，把△DCP 建成商业活动区，其余部分建成景观绿化区．为方便进入商业区，需修建小路BP 、MP ，从实用和美观的角度，要求满足∠PMB ＝∠ABP ，且景观绿化区面积足够大，即△DCP 区域面积尽可能小．则在四边形ABCD 内是否存在这样的点P ？若存在，请求出△DCP 面积的最小值；若不存在，请说明理由．

【解答】解：（1）当BD ⊥AC 时，如图1， ∵AB ＝BC ，∴D 是AC 的中点，∴BD ＝AC ＝×4＝2， 即BD 的最小值是2；故答案为：2；

22O D C

B A 图1图2A B

C

D P

M E D 'A B C D M

图3Q G H P P

'F

E D

A

C

B

①

图P

D C

B

A ②

图图③

O D C B A 图1图2B C D P M E D 'A B C M 图G P P F

O

图2A

B C D P M E D 'A B C

D M

图

Q

G H P P 'F E

（2）如图2，由题意得：DM ＝MB ，

∴点D 在以M 为圆心，BM 为半径的⊙M 上，连接AM 交⊙M 于点D '， 此时AD 值最小，过A 作AE ⊥BC 于E ，∵AB ＝AC ＝5， ∴BE ＝EC ＝

BC ＝

，由勾股定理得：AE ＝，

∵BM ＝4，∴EM ＝

，∴AM ＝

，

∵D 'M ＝BM ＝4，∴AD '＝AM ﹣D 'M ＝

，即线段AD 长的最小值是

；

（3）如图3，假设在四边形ABCD 中存在点P ， ∵∠BAD ＝∠ADC ＝135°，∠DCB ＝30°， ∴

，

∵∠PMB ＝∠ABP ， ∴

，

以BM 为边向下作等边△BMF ，作△BMF 的外接圆⊙O ，

∵∠BFM +∠BPM ＝60°+120°＝180°，则点P 在上，过O 作OQ ⊥CD 于Q ，

交⊙O 于点P ， 设点P '是

上任意一点，连接OP '，过P '作P 'H ⊥CD 于H ，可得OP '+P 'H ≥OQ

＝OP +PQ ，即P 'H ≥PQ ，

∴P 即为所求的位置，延长CD ，BA 交于点E ，

∵∠BAD ＝∠ADC ＝135°，∠DCB ＝30°，∠ABC ＝60°，∴∠E ＝90°，∠EAD ＝∠EDA ＝45°，∵AD ＝，∴AE ＝DE ＝2，∴BE ＝AE +AB ＝5，BC ＝2BE ＝10，CE ＝

，∴BM ＝

＝6，CD ＝

，

过O 作OG ⊥BM 于G ，∵∠BOM ＝2∠BFM ＝120°，OB ＝OM ，∴∠OBM ＝30°， ∴∠ABO ＝∠ABM +∠MBO ＝90°，OB ＝，

∴∠E ＝∠ABO ＝∠OQE ＝90°，

∴四边形OBEQ 是矩形，∴OQ ＝BE ＝5，∴，

∴

，

∴存在点P ，使得△DCP 的面积最小，△DCP 面积的最小值是（

）mm 2． O

A B

C

D M

图3

Q G H P P 'F E

已知AC、BD为四边形ABCD的对角线，BC=2，CD=2AC，∠DCA=60°，

∠DAB=135°，则线段BD的最大值为_____．

【解答】：如图T6-1,∵CD=2AC，∠DCA=60°

∴△ADC是含30°、60°、90°的直角三角形

经过以上六个类型问题分析，我们不难得到解决这类问题思维模式。具体如下：

①让主动点动一下，观察从动点的运动轨迹，发现从动点的运动轨迹是一段弧。

②寻找不变的张角（这个时候一般是找出张角的补角，这个补角一般为45°、60°或者一个确定的三角函数的对角等）

③找张角所对的定弦，根据三点确定隐形圆。

④确定圆心位置，计算隐形圆半径。

⑤求出隐形圆圆心至所求线段定点的距离。

⑥计算最值：在此基础上，根据点到圆的距离求最值（最大值或最小值）

1.学习与探究：

（1）请在图1的正方形ABCD中，作出使∠APB=90°的所有点P，并简要说明做法．我们可以这样解决问题：利用直径所对的圆周角等于90°，作以AB为直径的圆，则正方形ABCD内部的半圆上所有点（A、B除外）为所求．

（2）请在图2的正方形ABCD内（含边），画出使∠APB=60°的所有的点P，尺规作图，不写作法，保留痕迹；

图T6-1

（3）如图3，已知矩形ABCD 中，AB =4，AC =3，请在矩形内（含边），画出∠APB =60°的所有的点P ，尺规作图，不写作法，保留痕迹．

【解答】解：（1）在以AB 为直径的半圆上，A ，B 两点除外；

（2）如图②，

作△ABP 的外接圆⊙O ，分别与AD 、BC 交于点E 、F ，弧EF 上所有的点均可．

理由：同圆中同弧所对的圆周角相等， （3）如图③，画法如图： ①连接AC ；

②以AB 为边作等边△ABE ；

③作等边△ABE 的外接圆O ，交AC 于点P ； ④在AC 上截取AP '=CP ．则点P 、P ′为所求． （评卷时，作图准确，无画法的不扣分）

2.问题提出

（1）如图①，请在正方形ABCD 内画出一个以C 为顶点、BC 为腰长的等腰三角形CBP ． 问题探究

（2）如图②，△ABC 中，AB =AC =10，BC =8，P 为△ABC 内一点且∠BPC =90°，求△PBC 面积的最大值． 问题解决

（3）如图③，正方形ABCD 边长为8，点P 在其内部（包括边界），且CB =CP ，作PH ⊥BC 于H ，M 为△PHC 的内心，试问DC +DM 是否存在最小值？若存在，请求出这个值；若不存在，请说明理由．

F E P D C B A O P 'P

E

O D C A B D C B

A

D B

A

C

D

B

A

C 图3

图2

图1

E E

③

【解答】解：（1）如图①中，以C 为顶点、BC 为腰长的等腰三角形CBP 如图所示．

（2）如图②中，取BC 的中点O ，连接PO ，作PH ⊥BC 于H ．

∵S △PBC =?BC ?PH ，∵OB =OC ，∴OP =

BC =4，∵PH ≤OP ，

∴当PH =OP 时，△PBC 的面积最大，面积的最大值为16． （3）存在．

理由：如图③中，连接CM 、BM 、PM ． ∵CP =CB ，∠MCP =∠MCB ，CM =CM ， ∴∠MCP ≌△MCB ， ∴∠BMC =∠CMP ，

∴△PHC 是直角三角形，M 是内心， ∴∠CMP =135°， ∴∠BMC =135°

∴点M 的运动轨迹是以O 为圆心，OB 为半径的弧BC 上运动，且△BOC 是等腰直角三角形，作OH ⊥AD 于H ，连接OD 交⊙O 于M ′，此时OM ′的长度最短， 在Rt △OHD 中，DO =，

∵OB =OC =，∴DM ′=

，∴DC +DM 的最小值为

．

3.问题提出

（1）如图1，已知等腰△ABC ，BA =BC ，∠ABC =80°，试在△ABC 所在的平面内找

M P

H

O

D C

B

A M '图图

H O

P

C

B

A P

D C

B

A 图

①

图②

图图③

D

C

B

A

P

C

B

A

D

C

B

A M

H

P B

②图H O P

C

B

A P D C B

A ①

图M H

O

C

B

M '③

图②

图H O P C

B

A

M P H

O

D

C B

A

M '

③图

一点P ，使得∠APC =40°： 问题探究

（2）如图2，在△ABC 中，BC =4，∠A =60°，求△ABC 面积的最大值 与周长的最大值； 问题解决

（3）如图3，正方形ABCD 是张叔叔家菜地示意图，其中AB =200米，张叔叔计划在菜地中修建一个鱼塘（四边形CEFG ），已知点E 为AB 中点，点F 在边AD 上，∠CEF =90°，∠CGF =120°，为了容纳更多的垂钓者，要求这个鱼塘的周长和面积尽可能大，你认为张叔叔的想法是否能实现？若能，求出这个四边形CEFG 周长的最大值；若不能，请说明理由．

【解答】解：（1）如图1中，以B 为圆心，BC 长为半径作⊙B ．

在优弧AC 上取一点P ，连接P A 、PC ，则∠APC 即为所求； （2）如图2中，作线段BC 的垂直平分线，在BC 的垂直平分线上取一点O ，使得

∠BOC =120°，以O 为圆心，OB 长为半径作⊙O 交BC 的垂直平分线于． ∵∠BAC =∠B C =60°，当点A 与点重合时，△ABC 的面积最大， 此时△A ′BC 是等边三角形，面积的最大值=．

如图3中，作等边三角形△O 1BC ，以O 1为圆心，O 1B 为半径作⊙O 1．延长BA 交⊙O 1于D ，连接CD ， ∵∠D =

∠BO 1C =30°，∠BAC =∠D +∠ACD =60°，

∴∠D =∠ACD =30°，∴AC =AD ， ∴AB +AC =AB +AD =BD ，

∴BD 的值最大时．△ABC 的周长最大，

A 1F E D

C

B A 图3G H O D

C B A

O 1图3P

A

B

A

C B

A

C

B

A

F

E

D

C

B

A 图3

图2

图

1

F E D C

B A 图3

G H O

D C B A

O 1图3

图1F

E

B

A G H

∴当BD 是为直径时，△ABC 的周长最大， 此时点A 与O 1重合，△ABC 是等边三角形，

∴△ABC 为等边三角形时，周长最大，最大值为12． （3）能实现．理由如下：

如图，连接CF ，作GH ⊥CF 于H ． ∵∠A =∠B =∠FEC =90°，

∴∠AEF +∠BEC =90°，∠BEC +∠BCE =90°， ∴∠AEF =∠BCE ，∴△AEF ∽△BCE ， ∴

，∴

， ∴AF =50，∴EF =，EC =

，CF =250，∴△EFC 的形状大小不变，周长，

面积是定值，∵要使得四边形EFGC 的面积、周长最大，

∴只要△GFC 的面积最大，周长最大即可，由（2）可知，当GF =GC 时，△GFC 的面积最大，周长最大，∵GF =GC ，GH ⊥CF ，∠FGC =120°，∴FH =HC =125，∠GCH =30°∴GC =GF =，∴这个四边形CEFG 周长的

最大值=（m ）

4.问题提出

（1）如图①，已知△ABC ，请画出△ABC 关于直线AC 对称的三角形． 问题探究

（2）如图②，在矩形ABCD 中，AB =4，AD =6，AE =4，AF =2，是否在边BC 、CD 上分别存在点G 、H ，使得四边形EFGH 的周长最小？若存在，求出它周长的最小值；若不存在，请说明理由． 问题解决

（3）如图③，有一矩形板材ABCD ，AB =3米，AD =6米，现想从此板材中裁出一个面积尽可能大的四边形EFGH 部件，使∠EFG =90°，EF =FG =米，∠EHG =45°，经研究，只有当点E 、F 、G 分别在边AD 、AB 、BC 上，且AF ＜BF ，并满足点H 在矩形ABCD 内部或边上时，才有可能裁出符合要求的部件，试问能否裁得符合要求的面积尽可能大的四边形EFGH 部件？若能，求出裁得的四边形EFGH 部件的面积；若不能，请说明理由．

【解答】解：（1）如图1，△ADC 即为所求；

（2）存在，理由：作E 关于CD 的对称点E ′，作F 关于BC 的对称点F ′，连接E ′F ′，5E D 'E

D A ③

图图②

图①

C

B A

F E

D

C

B

A G

F

E

D

C

B

A F

E D

C

B

A 图3

G H

交BC 于G ，交CD 于H ，连接FG ，EH ，则=FG ，E ′H =EH ，则此时四边形

EFGH 的周长最小， 由题意得：=BF =AF =2，=DE =2，∠A =90°，

∴

=6，

=8，∴

=10，EF =

，

∴四边形EFGH 的周长的最小值=EF +FG +GH +HE =EF +E ′F ′=

+10，

∴在边BC 、CD 上分别存在点G 、H ，使得四边形EFGH 的周长最小， 最小值为

+10；

（3）能裁得，理由：∵EF =FG =

，∠A =∠B =90°，∠1+∠AFE =∠2+∠AFE =90°，

∴∠1=∠2，在△AEF 与△BGF 中，，∴△AEF ≌△BGF ，

∴AF =BG ，AE =BF ，设AF =x ，则AE =BF =，∴，

解得：x =1，x =2（不合题意，舍去），∴AF =BG =1，BF =AE =2，∴DE =4，CG =5， 连接EG ，作△EFG 关于EG 的对称△EOG ，则四边形EFGO 是正方形，∠EOG =90°， 以O 为圆心，以OE 为半径作⊙O ，∵CE =CG =5，则∠EHG =45°的点在⊙O 上， 连接FO ，并延长交⊙O 于H ′，则H ′在EG 的垂直平分线上，连接EH ′、GH ′，则∠EH ′G =45°，∵△EFG 的面积是定值，EG 也定值，要裁到的四边形EFGH 的面积最大，只要△EGH 的面积最大， 即：

上一点到EG 的距离最大，而FH '⊥EG 于M ，∴点H '到EG 的距离最大，

∴如图3所示，四边形EFGH ′是要想裁得符合要求的面积最大的， ∴C 在线段EG 的垂直平分线上，∴点F ，O ，H ′，C 在一条直线上， ∵EG =

，∴OF =EG =

，∵CF =2

，∴OC =

，

∵OH ′=OE =FG =，∴OH ′＜OC ，∴点H ′在矩形ABCD 的内部，

∴可以在矩形ABCD 中，裁得符合条件的面积最大的四边形EFGH ′部件， 这个部件的面积=

，

∴当所裁得的四边形部件为四边形EFGH ′时，裁得了符合条件的最大部件，这个部件的面积为（

）m 2．

5．问题提出：

（1）如图1，已知△ABC ，试确定一点D ，使得以A ，B ，C ，D 为顶点的四边形

A D A E

B D C

B A

图1

H G

F E D C

B A

E '

F '

M

G

F E C

D

B

A H '

1

2图3

图2

为平行四边形，请画出这个平行四边形； 问题探究：

（2）如图2，在矩形ABCD 中，AB ＝4，BC ＝10，若要在该矩形中作出一个面积最大的△BPC ，且使∠BPC ＝90°，求满足条件的点P 到点A 的距离； 问题解决：

（3）如图3，有一座塔A ，按规定，要以塔A 为对称中心，建一个面积尽可能大的形状为平行四边形的景区BCDE ．根据实际情况，要求顶点B 是定点，点B 到塔A 的距离为50米，∠CBE ＝120°，那么，是否可以建一个满足要求的面积最大的平行四边形景区BCDE ？若可以，求出满足要求的平行四边形BCDE 的最大面积；若不可以，请说明理由．（塔A 的占地面积忽略不计）

【分析】（1）利用平行四边形的判定方法画出图形即可．

（2）以点O 为圆心，OB 长为半径作⊙O ，⊙O 一定于AD 相交于P 1，P 2两点，

点P 1，P 2即为所求． （3）可以，如图所示，连接BD ，作△BDE 的外接圆⊙O ，则点E 在优弧上，取的中点E ′，连接E ′B ，E ′D ，四边形BC ′DE ′即为所求． 【解答】解：（1）如图记为点D 所在的位置． （2）如图，∵AB ＝4，BC ＝10，∴取BC 的中点O ，则OB ＞AB ．

∴以点O 为圆心，OB 长为半径作⊙O ，⊙O 一定于AD 相交于P 1，P 2两点，

连接BP 1，P 1C ，P 1O ，∵∠BPC ＝90°，点P 不能再矩形外；

∴△BPC 的顶点P 1或P 2位置时，△BPC 的面积最大，

作P 1

E ⊥BC ，垂足为E ，则OE ＝3，∴AP 1

＝BE ＝，

由对称性得AP 2＝8．

（3）可以，如图所示，连接BD ，

C B

A B P 图图

图C B A

D 1D 2D 3图1O

E D C B A P 2

P 1222345图2

F E D

C B A E 'C '

图3

图3图2

图1

C

B

A D C

B

A E

BD BED C

B A C

B A A B P O 图

图图

图1O E D C B A P 2P 1222

345图F E D C B A E 'C '图

C

B A

A B P

O

图

图

D C B A P 2P 1

22245图2F C B A C '图

∵A 为?BCDE 的对称中心，BA ＝50，∠CBE ＝120°，∴BD ＝100，∠BED ＝60° 作△BDE 的外接圆⊙O ，则点E 在优弧上，取的中

点E ′，连接E ′B ，E ′D ，

则E ′B ＝E ′D ，且∠BE ′D ＝60°，∴△BE ′D 为正三角形． 连接E ′O 并延长，经过点A 至C ′，使E ′A ＝AC ′，连接BC ′，DC ′，∵E ′A ⊥BD ，∴四边形E ′D 为菱形，且∠C ′BE ′＝

120°，作EF ⊥BD ，垂足为F ，连接EO ，则EF ≤EO +OA ﹣E ′O +OA ＝E ′A ， ∴，

∴

（m 2）

所以符合要求的?BCDE 的最大面积为m 2．

F E

D

C B

A E 'C '

图3