直线、射线、线段 导学案

七年级数学导学案
4.2直线、射线、线段导学案
执教者:金峰初中吴盛兵
【学习目标】
1、掌握“两点确定一条直线”的基本事实.
2、进一步认识直线、射线、线段,掌握直线、射线、线段的表示方法.
3、初步体会几何语言的应用.
【学习重点】探究“两点确定一条直线”的基本事实;直线、射线、线段的表示方法.【学习难点】图形语言与文字语言的相互转化.
【学习过程】
★创设情景,导入新课
线段、射线、直线有哪些区别与联系?
区别:
联系:1、将线段向无限延伸可得到射线;
2、将线段向无限延伸可得到直线;
3、线段和射线都是的一部分.
★学习语言,探究新知
问题1.动手画一画并回答下列问题
(1)经过一点A能画出几条直线?
(2)经过两点B、C 能画几条直线?
一、直线的基本性质:
;
可以简单说成:.
1、直线:记作
或记作
2记作
或记作
3记作
或记作
趁热打铁
1.判断下列几何语句是否正确
①记作:直线A ()
②记作:射线AB ()
③记作:线段FE ()
A
B
C
A B
l
l
O A
A B
A
E F ——1——
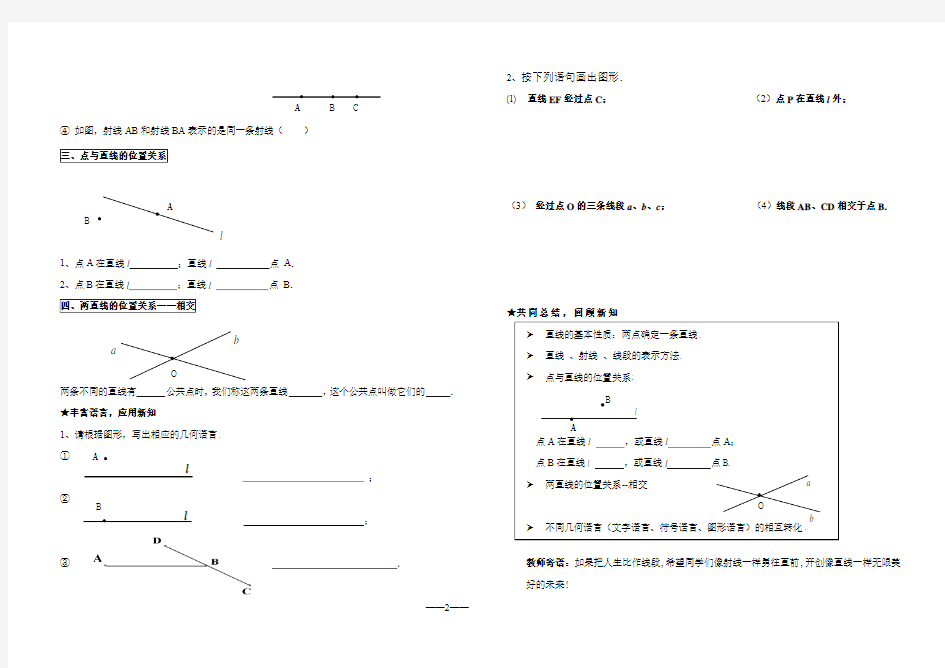
④ 如图,射线AB 和射线BA 表示的是同一条射线( )
1、点A 在直线l ;直线l 点 A .
2、点B 在直线l ;直线l 点 B .
两条不同的直线有 公共点时,我们称这两条直线 ,这个公共点叫做它们的 . ★丰富语言,应用新知
1、请根据图形,写出相应的几何语言. ①
; ②
;
③ .
2、按下列语句画出图形.
(1) 直线EF 经过点C ; (2)点P 在直线l 外;
(3) 经过点O 的三条线段a 、b 、c ; (4)线段AB 、CD 相交于点B.
教师寄语:如果把人生比作线段,希望同学们像射线一样勇往直前,开创像直线一样无限美好的未来!
C
A
B
l
B
l
A
l B
——2——
线段直线射线导学案
【课题】 4.1 线段、射线、直线 【学习目标】 1、在现实情境中进一步理解线段、射线、直线,并会用不同的方式表示。 2、通过操作活动,了解“两点确定一条直线”的几何事实,积累数学活动经验。 3、能够运用几何事实解释和解决具体情境中的实际问题。 【重点、难点、考点】 重点:1、线段、射线、直线的符号表示方法。 2、掌握“两点确定一条直线”的几何事实。 难点:线段、射线、直线之间的区别与联系。 考点:线段、射线、直线的符号表示方法及直线性质的运用。 知识铺垫: 1. 2. ①将线段就形成了射线;②将线段就形成了直线。 联系:都是直线的一部分。 新知讲解: 1.直线的表示方法(用一个小写字母表示或用两个大写字母表示) (1)如图的直线可记作直线______或记作直线_______. m 射线和线段都是直线的一部分,类似直线的表示,我们一起来探究射线和线段的表示方法:2.射线的表示方法:(用一个小写字母表示或用两个大写字母表示) 如图就是一条射线,记作射线或记作射线. a 注意:射线有个端点,向个方向无限延伸.用两个大写字 母表示时,端点O应写在M的前面。 在下面的图中画射线AB、射线EF E 3.线段的表示方法:(用一个小写字母表示或用两个大写字母表示) a 如图就是一条线段,记作线段或记作线段.
A B 练一练: 指出下图中的直线、射线、线段,并表示出来 小组探讨课本第107页“做一做”。 (1) 过一点A可以画几条直线? (2) 过两点A,B可以画几条直线? 探究:经过一点可以画直线,经过两点能画直线,只能画。 (3) 如果你想将一根细木条固定在墙上,至少需要几个钉子? 猜想:如果将细木条抽象成直线,将钉子抽象为点,你可以得出什么结论? 结论:直线的性质:经过两点直线,简称“两点直线” 小试牛刀: 1、木匠师傅锯木料时,一般先在木板上画出两个点,然后过这两点能弹出一条笔直的墨线,而且只能弹出一条这样的墨线,这是为什么? 2、在一个平面内,经过一个点可以画条直线;经过两点可以画条直线;经过三点中的任两点可以画条直线;经过四点中的任两点可以画直线,最少可以画条直线、最多可以画条直线。 3、如图,已知平面上三点A 、B 、C. (1) 画直线AC ;(2)画射线BA ;(3)画线段BC. A . B . . C 当堂检测: 1、下列说法正确的是 ( ) A.经过两点有且只有一条线段 B.经过两点有且只有一条直线 C.经过两点有且只有一条射线 D.经过两点有无数条直线 2、下图中共有几条射线?能用图中字母表示的射线有几条?分别表示出来. 3、用一个钉子把一根细木条钉在墙上,木条可以绕着钉子转动,这是因为___________,要想钉稳木条,至少要钉_____________个钉子,这是因为_____________. 4、表示一个点可用_____________来表示,表示一条直线可用_____________小写字母表示,也可以用它上面任意_____________个点的大写字母表示. 5、三条直线每两条都相交,则最多有_____________个交点,最少有__________个交点.
直线、射线、线段 导学案 教案
知识点:线段、射线、直线及其表示方法 问题情境1:判断几何语言表述是否正确 问题模型:判断直线、射线、线段、点的表示方法是否正确 求解模型: 例题:下列语句准确规范的是( ) A.直线a 、b 相交于一点m B.延长直线AB C.反向延长射线AO(O 是端点) D.延长线段AB 到C,使BC=AB 分析:A 选项中的点不可以用一个小写字母表示,B 选项中直线不可以延长,C 选项中表示射线端点的字母要写在前面,故排除A 、B 、C 。 答案:D 练习:1. 下列说法中,错误的是 ( ) A .经过一点的直线可以有无数条 B .经过两点的直线只有一条 C .一条直线只能用一个字母表示 D .线段CD 和线段DC 是同一条线段 答案:C 2. 延长线段AB 到C ,下列说法中正确的是( ) A.点C 在线段AB 上 B.点C 在直线AB 上 C.点C 不在直线AB 上 D.点C 在直线AB 的延长线上 答案:B 3. 下列语句和图形相符的是( ) A.语句:点C 在直线AB 的延长线上 B.语句:线段AB 与直线a 不相交 C.语句:直线a 、b 、c 相交于点O 直线 表示方法:1.两个大写字母;2.一个小写字母 直线不可以延长,只可以延伸 直线上一点及其一旁的部分是一条射线;直 线上两点之间的部分 是一条线段 射线 表示方法:1.两个大写字母(表示端点的字母在前);2.一个小写字 母 射线不可以延长,只可以反 向延长 线段 表示方法:1.两个大写字母;2.一个小写 字母 线段不可以延伸,只可以延 长或反向延长
D.语句:反向延伸线段AB 为射线BA 答案: D. 问题情境2:根据作图语句画直线与点 问题模式:已知一点与一条直线的位置关系,画出图形 求解模型: 例题: 读出下列语句,并按照这些语句画出图形 (1)两条直线n 、6,相交于点P . (2)直线l 经过A 、B 、C 三点,点C 在点A 与点B 之间. (3)直线a 经过点A 、B ,点P 不在直线a 上. 分析:体会点与直线的关系. 答案: 练习:1. 如图,已知三点A 、B 、C , (1)画直线AB ; (2)画射线AC ; (3)连接BC . 答案:略 2.根据下列语句画出图形. (1)直线l 与直线m 相交于点A,直线m 与直线n 相交于点C,直线n 与直线l 相交于点B ; (2)点M 在直线l 外,点A 、B 、N 在直线l 上,并且点N 在A 、B 两点之间. 解:(1)如图 (2)如图 根据题意确定已知点与直线的位置关系 先确定点,再经过该点的直线或不经过该点的直线 C A B l A B C n m A N B .M
直线、射线、线段 导学案
七年级数学导学案 4.2直线、射线、线段导学案 执教者:金峰初中吴盛兵 【学习目标】 1、掌握“两点确定一条直线”的基本事实. 2、进一步认识直线、射线、线段,掌握直线、射线、线段的表示方法. 3、初步体会几何语言的应用. 【学习重点】探究“两点确定一条直线”的基本事实;直线、射线、线段的表示方法.【学习难点】图形语言与文字语言的相互转化. 【学习过程】 ★创设情景,导入新课 线段、射线、直线有哪些区别与联系? 区别: 联系:1、将线段向无限延伸可得到射线; 2、将线段向无限延伸可得到直线; 3、线段和射线都是的一部分. ★学习语言,探究新知 问题1.动手画一画并回答下列问题 (1)经过一点A能画出几条直线? (2)经过两点B、C 能画几条直线? 一、直线的基本性质: ; 可以简单说成:. 1、直线:记作 或记作 2记作 或记作 3记作 或记作 趁热打铁 1.判断下列几何语句是否正确 ①记作:直线A () ②记作:射线AB () ③记作:线段FE () A B C A B l l O A A B A E F ——1——
④ 如图,射线AB 和射线BA 表示的是同一条射线( ) 1、点A 在直线l ;直线l 点 A . 2、点B 在直线l ;直线l 点 B . 两条不同的直线有 公共点时,我们称这两条直线 ,这个公共点叫做它们的 . ★丰富语言,应用新知 1、请根据图形,写出相应的几何语言. ① ; ② ; ③ . 2、按下列语句画出图形. (1) 直线EF 经过点C ; (2)点P 在直线l 外; (3) 经过点O 的三条线段a 、b 、c ; (4)线段AB 、CD 相交于点B. 教师寄语:如果把人生比作线段,希望同学们像射线一样勇往直前,开创像直线一样无限美好的未来! C A B l B l A l B ——2——
浙教版-数学-七年级上册-《线段、射线和直线》导学案
6.2 线段、射线和直线 【学习目标】 1、进一步认识线段、射线和直线的概念. 2、会用字母表示线段、射线和直线. 3、理解经过两点有且只有一条直线. 4、会用直尺画经过两个已知点的直线. 【重点难点】 1、重点:线段、射线和直线的概念和表示法. 2、难点:射线的表示法以及两点确定一条直线的实际应用. 【课前自学、课中交流】 阅读课文P145-146内容,完成下列问题 【知识链接】 1、在小学已经学过了直线、射线、线段.请你画出一条直线、一条射线、一条线段? 直线 射线 线段 2、如图:给出的直线、射线、线段.根据它们的性质,能相交的是 【自主探究】 1、线段的表示方法: 记作: 或 或 · a · B A
练习: A B C 图中共有 条线段,分别是 . (每条线段只需用一种方法表示) 2、射线的表示方法: 记作: 记作: 注意:用两个大写字母表示射线时,表示 的字母一定要写在前面. 练习: (1)射线AC 与射线AB 是同一射线吗?为什么? (2)射线AB 与射线BD 呢?为什么? 判断两条射线是同一射线的必须具备的条件: (1) (2) 3、直线的性质 (1)如果你想将一根细木条固定在墙上,至少需要几个钉子? 答: (2)经过一个已知点O 的直线,可以画多少条直线?请画图说明. 答: O · (3)经过两个已知点画直线,可以画多少条直线?请画图试试. · · 答: A B 猜想:如果将细木条抽象成直线,将钉子抽象为点,你可以得到什么结论? 直线的基本性质: 经过两点有 条直线,并且 条直线; A B ·
简述为: 举例说明直线的性质在日常生活中的应用: (1)在挂窗帘时,只要在两边钉两颗钉子扯上线即可,这是因为______________ (2)建筑工人在砌墙时拉参照线,木工师傅锯木板时,用墨盒弹墨线,都是根据 (3)你还能从生活中举出应用直线的基本性质的例子吗?试试看: 4、直线有两种表示方法:①用一个小写字母表示;②用两个大写字母表示. 记作: 记作: 或 5、平面上一个点与一条直线的位置有什么关系? ①点在直线______;②点在直线______. 当两条直线有一个共公点时,我们就称这两条直线 ,这个公共点叫做它们的 . 6、如图,已知三点A 、B 、C , (1)画直线AB (2)画射线CA (3)连接BC ,在线段BC 上取一点D 【课堂小结】 1、三种图形的联系(请在横线上填上三者的变化) ______和______都是直线的一部分. B A · · a B A C
七年级数学上册 6.1 线段、射线、直线导学案(1)(无答案) 苏科版
班级 学号 姓名 学习目标: 1通过课本中的议一议,试一试,结合日常生活经验,感受两点之间,线段最短,了解距离的含义。 2.初步了解直线,射线,线段,尝试用符号表示直线,射线,线段。 3.思考直线,线段的表示方法与射线的表示方法的差异。 学习重点:直线,线段的表示方法与射线的表示。 学习难点:直线,线段的表示方法与射线的表示。 一、知识梳理: 1.认识“直线”、“射线”、“线段”(如图1) ① ② ③ (1)图①是 ,有 个端点, (填能或不能)测量长度。这个长度被称为 。 (2)图②是 ,有 个端点, (填能或不能)测量长度。 (3)图③是 ,有 个端点, (填能或不能)测量长度。 2.线段的表示方法和性质(如图2) (1)用线段的两个端点来表示:点A 和点 B 为两个 点,图形可记作 或 。 (2)用一个小写字母表示 。 (3)性质:连接两点的所有线中, 最短。 3.直线的表示方法和性质(如图3) (1)用直线上的任意两点 和 ,直线可记作 或 。 (2)用一个小写字母表示 。 (3)性质:经过两点有 条直线,并且只有 条直线 4. 射线的表示方法和性质(如图4) (1)性质:射线有 个端点,它可以向 个方向 。 图1 图2 A B · · · A · A B B 图4 · B a A · 图3 · · ·
(2)图中的射线端点分别为: ,它们分别记作: 。 例题精讲: 例1.如图,平面内4个点A 、B 、 C 、 D ,根据下列要求画图。 (1)画射线AB ,直线AC,线段BC ; (2)连接点C 、D 和点A 、D ; (3)延长线段AD 到点E,使DE=CD ; (4)反向延长线段BC. 例2.如图,数一数,图中共有多少条线段? 三、尝试练习 1.下列说法中,错误的是 ( ) A 一条线段只有两个端点 B 射线有两个端点 C 在连接两点的所有线中,线段最短 D 直线AB 与直线BA 表示同一条直线 2.平面上三条直线两两相交,最少有 个交点,最多有 个交点。 3.在一条直线上取三个点,最多可以确定 条直线。 4.如图,线段AB 上有C 、D 两点,则图中共有 条线段。它们是 A A B C D F 例2图 · · · · D A C B C 第4题
6.1线段、射线、直线 (1)导学案
6.1线段、射线、直线 (1)学案 姓名:__________ 学习目标: 1.能正确区分“线段、射线、直线”,掌握其表示方法,理解并能运用相关性质、 公理; 2.感受美妙多变的图形世界中,培养观察、分析、比较、探究等能力; 3.通过小组合作、组间竞争等形式,培养团结合作精神,增强进取意识,激发良好的数学学习情感。 学习重点: 通过操作活动,感受图形世界的丰富多彩,积累操作活动的经验。 学习难点: 掌握用字母表示“线段、射线、直线”的方法。 一、自主学习: 1. 阅读课本P148~P149,写出疑问: 2. 读下列语句,并画出图形: ⑴过两点B A 、分别画一条直线; ⑵经过两点B A 、画一条直线。 二、探索活动: 1. 情景创设: 为了吃到骨头,小狗可能走的路线有几条?你认为小狗选择的哪条路线是最短路线?请说明你的理由。 2.生活常识告诉我们: 两点之间的所有连线中,__________________最短。 ______________________________________,叫做这两点之间的距离. 3做一做: 请大家观察P147地图,由火车站到汽车站,你可以走哪些路线,其中你认为哪条路线是最短的?为什么
4.(1)如图:线段可以用表示端点的两个大写字母来表示,也可以用一个小写字母来表示。 那么图(1)的线段可以记作_____或_____或_____。 (2)射线可以用表示端点和射线上另一个点的大写字母来表示。 (表示端点的字母必须写在前面) 那么图(2)的射线可以记作_____ (3)直线可以用表示直线上任意两个点的大写字母来表示,也可以用一个小写字母 来表示。 那么图(3)的直线可以记作_____或_____ 5.议一议: (1)图中以A 为端点的线段有多少条?以B 为端点的线段有多少条?以C 为端点的 线段有条?以D 为端点的线段有多少条?图中一共有多少条线段? A B C D (2)下图中各有多少条线段?你发现了什么规律?(用含n 的代数式表示) …… 三、巩固练习: 课本P 149 练一练 四、课堂总结: 今天你学到了什么? A B a A B 图1 图2 A B 图3 m
秋七年级数学上册 4.2 直线、射线、线段 第1课时 直线、射线、线段学案
几何图形初步 4.2 直线、射线、线段 第1课时直线、射线、线段 学习目标:1.了解直线、射线、线段的联系和区别,掌握它们的表示方法. 2.了解两点确定一条直线的性质,并能初步应用. 3.会用几何语句描述几何图形,能根据几何语句画出相应的几何图形. 学习重点:1.直线、射线、线段的表示方法. 2.建立几何语句与几何图形之间的联系. 学习难点:建立几何语句与几何图形之间的联系. 使用要求:1.阅读课本P128-P129; 2.尝试完成教材P129练习题; 3.限时15分钟完成本导学案(合作或独立完成均可); 4.课前在小组内交流展示. 一、自主学习: 1.学校总务处为解决下雨天学生雨伞的存放问题,决定在每个班级教室外钉一根2米长的装有挂钩的木条.本校三个年级,每个年级10个班,问至少需要买几颗钉子?你能帮总务处的老师算一算吗? 2.P128的探究.
(1)在墙上固定一根木条,至少要几个钉子?动手试一试. (2)动手作图试试: ①过一点O可以作________直线. ②过A、B两点________(能或不能)作直线,能作_________直线. 再过下面的C、D以及E、F两点作直线试试看 注意:直线没有端点,是向两方无限延伸的,画直线时要画出向两方无限延伸的部分.3.直线公理: 直线公理在生活中有广泛的应用,你能举出几个例子吗? 二、合作探究: 1.直线有几种表示方法? (1)如图的直线可记作直线______或记作直线_______.(2)用几何语言描述右面的图形,我们可以说: 点P在直线AB______,点A、B都在直线AB_____.(3)如图,点O既在直线m上,又在直线n上,我们称直线 m、n 相交,交点为O. 想一想,如果两条直线相交,会有几个交点,作图试试.m m
人教版数学七年级上册导学案:4.2 直线、射线、线段(1)
第4学时4.2 直线、射线、线段(1) 学习目标:1.了解直线、射线、线段的联系和区别,掌握它们的表示方法. 2.了解两点确定一条直线的性质,并能初步应用. 3.会用几何语句描述几何图形,能根据几何语句画出相应的几何图形. 学习重点:1.直线、射线、线段的表示方法. 2.建立几何语句与几何图形之间的联系. 学习难点:建立几何语句与几何图形之间的联系. 一、自主学习: 1.学校总务处为解决下雨天学生雨伞的存放问题,决定在每个班级教室外钉一根2米长的装有挂钩的木条.本校三个年级,每个年级10个班,问至少需要买几颗钉子?你能帮总务处的老师算一算吗? 2.探究. (1)在墙上固定一根木条,至少要几个钉子?动手试一试. (2)动手作图试试: ①过一点O可以作________直线. ②过A、B两点________(能或不能)作直线,能作_________直线. 再过下面的C、D以及E、F两点作直线试试看 注意:直线没有端点,是向两方无限延伸的,画直线时要画出向两方无限延伸的部分.3.直线公理:
直线公理在生活中有广泛的应用,你能举出几个例子吗? 二、合作探究: 1.直线有几种表示方法? (1)如图的直线可记作直线______或记作直线_______. (2)用几何语言描述右面的图形,我们可以说: 点P 在直线AB______,点A 、B 都在直线AB_____. (3)如图,点O 既在直线m 上,又在直线n 上,我们称直线 m 、n 相交,交点为O . 想一想,如果两条直线相交,会有几个交点,作图试试. (4)读下面的几何语句,画出图形. ① 点A 在直线a 外 ② 直线AB 、CD 相交于点B ,点E 在直线CD 上. 2.在直线上取点O ,把直线分成两个部分,去掉一边的一个部分,保留点0和另一部分 就得到一条射线, 如图就是一条射线,记作射线OM 或记作射线a . 注意:射线有一个端点,向一方无限延伸. 在下面的图中画射线AB 、射线EF m P m a
《直线、射线、线段》导学案
《直线、射线、线段》导学案 江夏四中----蔡晚荣 [教学目标] 1.了解直线、射线、线段的联系和区别,掌握它们的表示方法. 2.了解两点确定一条直强的性质并能初步应用. 3.会用几位语言描述几何图形,能根据几何语句画出相应的几何图形。 [学习重点] 1.直线、射线、线段的表示方法。 2.建立几何语句与几何图形之间的联系。 [学习难点] 直线、射线、线段的表示方法及三种几何语言之间的转换。 一、情境引入,目标导学 [课堂前置·进门测] 1.直线、射线、线段的区别 2.直线、射线、线段的联系。 二、提出问题,合作探究。 1.问题1:经过点A能画几条直线? 经过两点A、B能画几条直线?
2.由此可以得出一个基本事实: (1)经过两点有条直线,并且只有条直线。 简单说成 (2)在生产生活中还有哪些应用“两点确定一条直线”原理的例子。 (3)直线的表示方法: ① ② (2)点和直线的位置关系。 (3)当直线遇到直线: (4)你能用适当的语句表述下图中点 与直线的关系吗? 4.线段、射线的表示方法: (1)线段的表示方法:
记作:线段AB记作:线段a (2)射线的表示方法: 记作:射线OP记作:射线b 5.判断对错: ①记作:直线A() ②记作:射线BA() ③记作:直线ab() ④记作:线段BA() ⑤画一条2cm的直线。() ⑥如图,直线AB和直线AC表示的是同一条直线() ⑦如上图,射线AB和射线BA 表示的是同一条射线.() 6.我说你画:已知点O、P、Q(如图) ①画线段PQ②画射线op③画直线OQ 三、初用新知,小试牛刀。
し (一)按下列语句画出图形。 (1)直线EF经过点C (2)点P在直线外。 (3)线段AB、CD相交于点B (二)讲一讲:请用适当的语言表述图中的关系。 四、当堂检测,达标反馈。 1.表示下列图形;: (1)(2)(3) 2.按下列语言作图 (1)连接AB.CD (2)作直线AD (3)作射线CB,交直线AD于点O (4)过点O作一条直线,交线段AB于M.交线段CD于N. 3.在同一平面内,有三点A、B、C,每过两点画直线,可以画几条? 4.指出下图中线段、射线、直线分别有多少条?
沪教版七年级数学上册导学案 线段、射线、直线
相关资料 4.2 线段、射线、直线 学习目标: 1、能在图形中找出线段、射线、直线并会用符号表示。 2、通过操作活动,知道两点确定一条直线等事实,积累操作活动经验。 3、初步应用几何知识解决生活中的实际问题,体会研究几何图形的意义。 学习重点:线段、射线、直线的符号表示方法。 学习难点:培养学生学会一些几何语言,培养学生的空间观念。 学习过程: 一、知识回顾: 1.在小学已经学过了直线、射线、线段.请你画出一条直线、一条射线、一条线段? 2、填写下列表格: 二、自主探究: 1.生活中的、都可以近似的看成线段,线段有 个端点。 2.将线段就形成了射线,、 所射出的光线都可以近似的看做射线,射线有个端点,可向延伸。 3.将线段就形成了直线, 可以近似的看做直线,直线有个端点,可向延伸。 综上所述:1.线段有个端点,长度有限,可以度量 2.射线有个端点,长度无限,无法度量 3.直线有个端点,长度无限,无法度量 线段、射线、直线的表示方法(3 分钟)
1.线段的表示方法: <1>一条线段用它的两个端点的大写字母表示,记作或。 <2>一条线段可以用一个小写字母来表示。记作 2.射线的表示方法: 用两个大写字母表示,记作 3.直线的表示方法 <1>用这条直线上的两个点表示,记作或; <2>用一个小写字母表示,可记作。 三、归纳总结: 四、随堂练习: 1.直线有个端点,可向延伸,度量。 射线有个端点,可向延伸,度量。 线段有个端点,度量。 2、.下图的直线可以表示为或。 A B a 3、1.读下列语句,并画出相应的图形。 (1)经过两点 M、N 画出一条直线 (2)经过点 O 的三条线段 a、b、c. (3)点A 在直线 l 外 (4)线段 AB、CD 相交于点 B 4、下图中有多少条线段,分别用两个大写字母表示出来。
直线射线线段导学案
4.2直线射线线段(第三课时)执笔:陈墩增审核:道标审批:编号: 授课人:授课时间:姓名:小组: 学习目标:1.理解线段的中点它是线段中有关计算的条件。 2?在理解线段的中点的基础上明白三等分点、四等分点……..知道线段之间的比例关系。熟练掌握求线段长度的计算方法。 学习重点:禾U用线段的和、差、倍、分求线段的长度。 学习难点:理解数学思想与线段长度的求法关系。 知识连接:线段的和、差、倍、分的概念以及线段的中点、等分点的性质。 体会线段是可度量的,如何求线段的长度是我们必须掌握的基本功。自主学习:阅读课本例题。 学法指导:合作探究反思提升 合作探究: 探究1、利用线段的和差求长度 如图已知线段AB=12cm线段AB上有一点C且BC=4cm,M是AC的中点,求线段AM的长度. A, _________ B 解:由题意可知AC= _______ = _______________ = _______ cm因为点M是AC的中点, 所以AM= __________ AC= ____________ = _____________ cm 那么如果画b-a呢?或者a+2b 2a-b等请同学们回去以后完成。 达标测评: 1、如果线段AB=5cm,BC=4cm,且A.B.C 三点在同一条直线上,那么线段AC的长 是_____ 。_ 2、如图,已知点B、C是线段AD上的两点,E是AB的中点,F是CD的中点,若线段AB是线段CD的2倍,线段AE比线段CF长4, BC=7,求线段AD的长度。 A, ,E ,B ,C ,F ,D 3、如图,点C在线段AB上,AC=8cm,CB=6cm,点M、N分别是AC、BC的中点 探究2、利用方程思想求线段的长度 如图,已知线段AB=2cm延长AB到C使BC=3/2AB , D是线段AB的中点。 (1) (2) (3) 求线段CD的长度。 线段AC是线段DB的几倍? 线段AD是线段BC的几分之几? A, ,D ,B ,C 解: (1)设BC=3xcm , 则AB= ,因为AB=2cm,所以,解得x= 所以BC= 。 又因为D是AB的中点,所以AD= ,即CD= = cm. ⑵由(1)知AC=- cm,BD= cm,所以AC= DB. ⑶由(1)知BC= cm,AD= cm,所以AD= BC. A, _______ B a)求线段MN的长。 b)若C为线段AB上任一点,满足AC+CB=a cm,其他条件不变,你能猜想MN的长度吗?并说明理由。 c)若点C在线段AB的延长线上,且满足AC-BC=b cm,M、N分别为AC、BC 的中点,你能猜想MN的长度吗?请画出图形,写出你的结论,并说明理由。 总结感悟:求线段长度的方法: 学案整理: 探究3、尺规作图 如图,已知线段a和b,请画一条线段使它等于a+b.
线段、直线、射线导学案
线段、直线和射线 教学内容 义务教育课程标准实验教科书(西师版)四年级上册第60~63页。 教学目标 1、通过自主学习知道什么是线段、直线和射线,能正确区分线段、直线和射线。 2、体会两点间所有连线中线段最短,知道两点间的距离。 3、经历认识线段、直线和射线的过程,培养学生的观察能力和分析能力,发展学生的空间观念。 教学重难点:知道什么是线段、直线和射线,能正确区分线段、直线和射线 教学准备:课件和题卡 教学过程 一、引导学生观察单元主题图。 教师:你从图中看见了哪些数学现象? 学生观察后相互说一说,然后抽几个学生汇报。 教师:对了,这幅图中有很多线和角,生活中也有很多线和角。这节课我们就先来研究线。板书:线。谈话引入新课师:同学们都看过《西游记》吧!还记得齐天大圣孙悟空手里那根金箍棒吗?它能小成一根针藏在他的耳朵里,也能无限的变长,上天入地,可神奇啦!今天老师也给大家请来了几位朋友,它们有的也有这样的本领,同学们想认识它们吗?(想)让学生充满好奇感进入新课。 二、自主学习探究: 学生自主学习教材61和62页完成下表: 1.检查线段情况。 (1)出示幅电线图。 教师:同学们看一看两根电线杆之间的一段电线。将一段电线画在黑板上,并明确:这就是线段。 (2)结合电线引导学生认识线段的基本特征:有2个端点、直的(先让学生观察、口说,在集体归纳) (3)能说一说生活中看到过哪些线段吗? 学生回答略。 (4)引导学生在两点之间画线(指名板演,其余学生在纸片上画),让学生思考:你发现了什么? 指名回答,结合黑板上的板演图(教师可以作适当的补充)进行集体交流:在两点之间可以画很多条线,其中线段最短,线段的长度就是两点之间的距离。
新人教版四年级上册数学第三单元《线段、直线、射线和角》导学案
第三单元《线段、直线、射线和角》 第1课时:直线、射线和角 学习目标: 1、使学生进一步认识线段,认识射线和直线,知道三者之的和别。 2、使学生认识角和角的表示方法,知道角的各部分名称。 3、培养学生关于线段、射线、直线和角的空间观念 学习重点:正确建立射线的概念。 学习难点:使学生理解角的边是两条射线。 一、自主学习 1、认识射线、直线和线段 (1)、生活中射线的例子(手电筒、汽车灯、太阳射出的光线)。 注意射线的端点、方向,长度 (2)、直线(电视画面上向远方无限延伸的铁轨) 注意直线的端点、方向,长度 (3)、要求学生画一条射线和一条直线。 (4)、线段(注意线段的端点、方向,长度) 2、学生讨论:直线、射线和线段之间有什么联系和区别并分别画出2条以上的直线、射线和线段。 二、合作探究、归纳展示画直线、射线和线段方法: (小组合作完成,一组展示,其余补充、评价)友情提示:画射线的方法先点一点,再沿着尺的一边画射线 名称端点方向长度图例 直线
射线 线段 三、认识角 1、角的定义及相关概念 2、角用什么符号表示 3、角的画法:在练习本上练习①画出一点,从这一点引出一条射线;②从这一点再引出另一条射线;③写出各部分名称。用∠1表示。 四、过关检测: 1、p36页做一做 2、p39页练习四第1、2题 3、把5厘米长的线段,向两端无限延长,得到的是一条()。 A:直线B:线段C:射线 提示:想一想:直线、线段和射线各有什么特点? 直线、线段和射线有什么联系和区别? 4、一条射线长100厘米。A:正确B:不正确 提示:想一想:射线的长度是有限的吗? 课后总结:
线段射线直线导学案
4.1线段、射线、直线 课型:新授课课时:第1课时设计者:沈建 【学习目标】——导向 1.在现实情境中了解线段、射线、直线的描述性定义和表示方法,理解直线的性质,充分感受生活中所蕴含的丰富多彩的几何图形. 2.通过识图、辨析、观察、猜测、验证等数学探究过程,发展几何意识、合情推理和探究意识. 3.在解决问题的过程中发展类比、联想、猜想等思维能力,培养解决问题的积极性和主动性. 【学习重点】 线段、射线、直线的描述性定义和表示方法,理解其性质。 【学习难点】 线段、射线、直线的描述性定义和表示方法,理解其性质。 【导学过程】——导法 一、问题 用3分钟仔细阅读课本106页的内容,完成自学检测一 1.生活中的、都可以近似的看成线段,线段有个端点。 2.将线段就形成了射线,、 所射出的光线都可以近似的看做射线,射线有个端点,可向延伸。 3.将线段就形成了直线, 二、探究: 探究1: 1、线段、射线、直线的概念 线段作图: 线段:_________________________________________________________________________ 射线作图: 射线:_________________________________________________________________________ 直线作图: 直线:_________________________________________________________________________ 2、思考: ⑴线段、射线、直线之间有什么的联系? _______________________________________________________________________________
七年级数学上册 4_1 线段、射线、直线导学案(新版)北师大版
第一节线段、射线和直线 【学习目标】 1.使学生在了解直线概念的基础上,理解射线和线段的概念,并能理解它们的区别与联系.2.通过直线、射线、线段概念的教学,培养几何想象能力和观察能力,用运动的观点看待几何图形.3.培养对几何图形的兴趣,提高学习几何的积极性. 【学习重难点】重点:直线、射线、线段的概念. 难点:对直线的“无限延伸”性的理解. 【学习方法】小组合作学习 【学习过程】 模块一预习反馈 一、解读教材 1、分组活动一:阅读教材第106页第一、第二段,并观察两个图形,完成下面问题。 绷紧的琴弦、人行横道线都可以近似看做线段,线段有 端点,将线段向一个方向无 限延长就形成了。它有端点,将线段向两个方向无限延长就形成了。它有端点。生活中哪些物体可以近似地看做线段、射线、直线? 看哪个小组举例最精彩、形象; 2、线段射线和直线的比较 概念图形表示方法 向几个方 向延伸端点数 可否度量 线段
直线 即时练习:判断下列说法是否正确,正确的在括号内打“√”,错误的打“×” (1)直线A B和直线BA是同一条直线。……………………( ) 师生备注 (2)射线AB和射线BA是同一条射线。……………………( ) (3)线段AB和线段BA是同一条线段。……………………( ) 二、自主学习(P106——107) 5、探究:(1)经过一个已知点A画直线,可以画多少条? (2)经过两个已知点A、B画直线,可以画多少条? (3)如果你想将一根细木条固定在墙上,至少需要几枚钉子? 解: 归纳:经过两点有且(“有”表示“存在性”,“只有”表示“唯一性”) 模块二合作探究 (1)直线l上有一个点则线段有条,射线有条; (2)直线l上有二个点则线段有条,射线有条; (3)直线l上有三个点则线段有条,射线有条; (4)直线l上有四个点则线段有条,射线有条; (5)直线l上有n个点则线段有条,射线有条. 3、典例示范:根据条件作图,如图,A、B、C三点不在同一直线上,按要求画图。 (1)画线段AB;(2)画射线BC;(3)画直线CA;(4)经过点A画直线a与线段BC交于点D。
直线、射线、线段导学案
《直线、射线、线段》导学案 学习目标: 1、会用字母表示直线、射线、线段; 2、理解直线、射线、线段的区别和联系; 3、理解并掌握直线的性质; 4、会根据语言描述画出图形。 学习过程: 1、直线、射线、线段的表示方法。 分别画一条直线、射线、线段,并用两种方法表示。 2、直线、射线、线段的区别与联系: 联系:。
3、画出点和直线的所有位置关系。 .O .A .B 归纳:点和直线共有种位置关系,分别是:。 4、直线的性质: 画一画:(1)经过一点O可以画几条直线? (2)经过两点A、B可以画直线吗?如果可以,可以画几条? 做一做:如果你想将一根小木条固定在木板上,至少需要几个钉子? 归纳:直线的性质: 思考:经过三点能不能画直线?四点呢? 练习: 1、建筑工人在砌墙的时候经常在两个墙角分别立一根标杆,在两根标杆之间拉一根参照线,这根参照线就是直的,这其中的道理是:。 2、判断下列说法是否正确: (1)线段AB和射线AB都是直线AB的一部分; (2)直线AB和直线BA是同一条直线; (3)射线AB和射线BA是同一条射线; (4)把线段向一个方向无限延伸可得到射线,向两个方向无限延伸可得到直线; (5)延长直线AB; 3、按下列语句画出图形: A . D . (1)连接BD、AD; C . (2)画直线AB,CD,它们相交于点E. B . (3)做射线AC,与线段BD相交于点O。
4、(1)直线EF 经过点C ; (2)点A 在直线a 外; (3)经过点O 的三条直线a 、b 、c ; (4)线段AB ,CD 相交于点B. 3、指出右图中线段、射线、直线分别有多少条? 4、观察下图,判断下列说法是否正确: (1)直线OM 和直线MN 是同一条直线.( ) (2)射线NM 和射线NO 是同一条射线.( ) (3)射线OM 和射线ON 是同一条射线.( ) (4)射线NO 比线段NM 短. ( ) 6、如图,(1)点C 在直线AB______; (2)点O 在直线BD____, (3)过点A 的直线共有____条,它们分别是 。 1.下面几种表示直线的写法中,错误的是( ) A. 直线a B. 直线Ma C. 直线MN D. 直线MO 2.下列四个图中的线段(或直线、射线)能相交的是( ) A.(1) B.(2) C.(3) D.(4) 4.下列语句正确的是( ) A .点a 在直线l 上 B .直线ab 过点p 1() C D 2() D 3() D B 4() D
线段、射线、直线导学案(新)
4.1《线段、射线、直线》导学案 【学习目标】 1、在现实情境中进一步理解线段、射线、直线,并会用不同的方式表示。 2、通过操作活动,了解“两点确定一条直线”的几何事实,积累数学活动经验。 3、能够运用几何事实解释和解决具体情境中的实际问题。 4、通过从事观察、比较、概括等活动,发展抽象的思维能力和有条理的数学表达能力。 【学习重点】线段、射线、直线的区别和联系,会正确表示线段、射线、和直线。【学习难点】“两点确定一条直线”的发现、理解和运用。 【学习方法】自主学习、合作交流、师生互动相结合。 【教学过程】Array一、自主学习 1、请同学们自学课本106-107页; 2、预习检测: 谈谈你对线段、射线、直线的认识(填 表) 二、探究新知 1、线段、射线、直线的联系 (1)、把线段可得到射线;(2)、把线段可得到直线。 由直线也可得到线段、射线: 线段是直线上; 射线是直线上的。 2、线段、射线、直线的画法 请你分别画出一条线段、射线、直线: 线段射线直线 3、线段、射线、直线的表示方法:
线段有两种表示方法: (1).用表示它的两个端点的大写字母表示,记为 ; (2).用一个小写字母表示:记为 。 射线的表示方法: 射线:用它的端点字母和射线方向上的另外任意一点的字母表示,记为 。 直线有两种表示方法:(1).用它上面任意两点的大写字母表示,记为 ;(2).用一个小写字母表示 。 注意:(1)表示线段、射线、直线的时候,都要在字母前注明“线段” “射线 ” “直线”. (2)用两个大写字母表示直线或线段时,两个字母可以交换位置,表示射线的两个大写字母不能交换位置,必须把端点字母放在前面. 跟踪训练: 1.下列给线段取名正确的是( ) A .线段M B.线段m C.线段Mm D.线段mn 2.如图,若射线A B 上有一点C,下列与射线AB 是同一条射线的是 ( ) A.射线BA B.射线AC C.射线BC D.射线CB 3.下列语句中正确的个数有 ( ) O A a B A 直线AB · · a 直线a A B C
直线射线线段导学案3
4.2 直线、射线、线段(3) 【学习目标】 1、利用直线、线段的性质解决相关实际问题; 2、利用线段的中点定义解决相关计算问题. 【学习过程】 一、预习探究 复习:⑴某村庄和小学分别位于两条交叉的大路边,可是有些人不爱惜庄稼, 每年冬天麦田里总会走出一条小路来,其中的数学道理是________________________. ⑵读出下列语句,并按照语句画出图形. ① 点C 在直线AB 上,而点D 在直线AB 外; ② 直线AB 和直线BC 相交于B ; ③ 经过点A 的四条直线a ,b ,c ,d ; ④ 延长线段AB 到C,使AC=3AB . 二、课堂学习 1、已知线段AB=10㎝, C 是线段AB 上任意一点,E 、F 分别是AC 、BC 的中点,求线段EF 的长? 课堂练习1:⑴已知线段AB 及一点P ,若AP+PB=AB ,则点P 在 ⑵. 已知C 是线段AB 上的一点,D 是CB 的中点,DB=2cm ,AC=8cm ,则AB=__ cm. ⑶ 如图,C 、D 是线段AB 上的两点,且AC=CB ,CD=DB ,则线段AB 的中点是点___,点D 是线段____的中点,AC=__DB ,DB=__AB. ⑷ 已知线段AB =10, 点C 在直线AB 上,且AC =4,若点D 是AB 的中点,求DC 的长. 2、已知C 、D 是线段AB 上的两点,且AC ︰CD ︰DB=2︰3︰4,E 、F 分别是AC 、DB 的中点,如果EF=12㎝,求线段AB 的长? 小结 三、反馈练习: 1、 在同一个学校上学的小明、小伟、小红三位同学住在A 、B 、C 三个住宅区,如图2所示, A 、 B 、 C 三点共线,且AB=60米,BC=100米,他们打算合租一辆接送车去上学,由于车位紧张,准备在此之间只设一个停靠点,为使三位同学步行到停靠点的路程之和最小,你认为停靠点应该设在何处? E C A F E C B A F D
数学:4.2《直线、射线、线段(2)》 精品导学案(人教版七年级上)
数学:4.2《直线、射线、线段(2)》学案(人教版七年级 上) 【学习目标】:1、会用尺规画一条线段等于已知线段; 2、会比较两条线段的长短; 3、理解线段中点的概念,了解“两点之间,线段最短”的性质。 【学习重点】:线段的中点概念,“两点之间,线段最短”的性质是重点; 【学习难点】:画一条线段等于已知线段是难点。 【导学指导】 一、温故知新 1、过A 、B 、C 三点作直线,小明说有三条,小颖说有一条,小林说不是一条就是三条,你认为 的说法是对的。 二、自主学习 问题:现有一根长木棒,如何从它上面截下一段,使截下的木棒等于另一根木棒的长? 上面的实际问题可以转化为下面的数学问题: 已知线段a,画一条线段等于已知线段。 1.作一条线段等于已知线段 现在我们来解决这个问题。 作法: (1)作射线AM (2)在AM 上截取AB= a 。 则线段AB 为所求。 应用:已知线段a 、b ,求作线段AB=a+b 。 解:(1)作射线AM ; (2)在AM 上顺次截取AC=a ,CB= b 。 则AB= a+b 为所求。 a M B · · A a b
做一做:作线段AB=a-b 。 2、比较两条线段的长短 两条线段可能相等,也可能不相等,那么怎样比较两条线段的长短呢? 我们先来回答下面的问题。 怎样比较两个同学的身高? 一是用尺子测量;二是站在一起比(脚在同一高度)。 如果把两个同学看成两条线段,那么比较两条线段就有两种方法。 (1)度量法:用刻度尺分别量出两条线段的长度从而进行比较。 ( 2)把一条线段移到另一条线段上,使一端对齐,从而进行比较,我们称为叠合法。(如图) AB <CD AB >CD AB=CD 3、线段的中点及等分点 如图(1),点M 把线段AB 分成相等的两条线段AM 与BM ,点M 叫做线段AB 的中点; 记作AM=MB 或AM=MB=1/2AB 或2AM=2MB=AB 。 如图(2),点M 、N 把线段AB 分成相等的三段AM 、MN 、NB ,点M 、N 叫做线段AB 的三等分点。类似地,还有四等分点,等等。 4、线段的性质 请同学们思考课本131页的思考? 结论: 两点所连的线中, 简单地说成:___________________________________ 你能举出这条性质在生活中的一些应用吗? 两点间的距离的定义:___________________________________ 注意:距离是用“数”来度量的,它是线段的长度,而不是线段本身。 A (C ) B (D ) A ( C ) ( D ) B A (C ) B (D ) ( A B M A B M N (1) (2) M B · · A C
《直线、射线、线段》导学案
、自学平台一一课前利用微课自学: 1、分别画一条直线、射线、线段,并用两种方法表示 2、归纳直线、射线、线段的区别: 说说它们的联系: 3、判别是否同一条射线要满足哪些条件? 4、如图所示,判断下列说法是否正确: 直线AB与直线BA是同一条直线;( 线段AB与线段BA是同一条线段;( (3) 射线O B与射线AB是同一条射线;( 射线AB与射线A O是同一条射线;( (5) 射线O B与射线O A是同一条射线;( 5、手电筒发出的光线,给我们的形象似■ 6、下列语句正确的是() A.点a在直线m上B .直线ab过点D. C.延长直线AB到C D .延长线段AB到C,使AB=BC. 7、画出一个点和一条直线的所有位置关系 归纳:点和直线共有种位置关系,分别是:
学习目标: 1会用字母表示直线、射线、线段;理解它们的区别和联系; 2、理解并掌握直线的性质; 3、掌握点和直线的两种位置关系. 4、会根据语言描述画出图形. 学习过程: 、交流平台 疑难探究 1、创设情境、探究新知: 为了把抹布晾挂起来,班主任决定在墙上固定一根装有挂钩的木条, 几颗钉子?(小组合作,动手探究) 把上述问题抽象成数学问题,画图并思考: (1)经过一点O 可以画几条直线? (2)经过两点A 、B 可以画直线吗?如果可以,可以画几条? ;简单说成: 2、联系生活、应用新知: (1)建筑工人在砌墙时,经常在两个墙角分别立一根标杆 ,在两根标杆之间拉一根线, 然后沿线砌墙,砌出的墙就是直的,其中的道理是 _______________ . _________ 问至少需要 归纳:
3、如图,我说你画: (1) ⑵ ⑶ 连接BD 画直线AD CB相交于点E; 作射线 AC,与线段BD相交于点O . .B 4 、 我说你画: (1) 直线I经过点C;点A在直线I外; 线段AB CD相交于点B. 5 、 我画你说: 如图,⑴点C在直线AB ⑵点O在直线BD (3)点O是直 线 的交点; 三、展示平台 --- 亮我风米 下列说法错误的是() 过一点可以作无数条直线过已知三点可以画一条直线 一条直线通过无数个点 两点确定一条直线下列四个图中的线段(或直线、射 线)能相交的是( 1 、 B 、 C 、 2 、 * ------ * A B (3) A B (1) A B (2) A (4)B A.(1) B.(2 ) C.(3) D.(4 )
