勾股定理与面积计算
勾股定理与面积计算
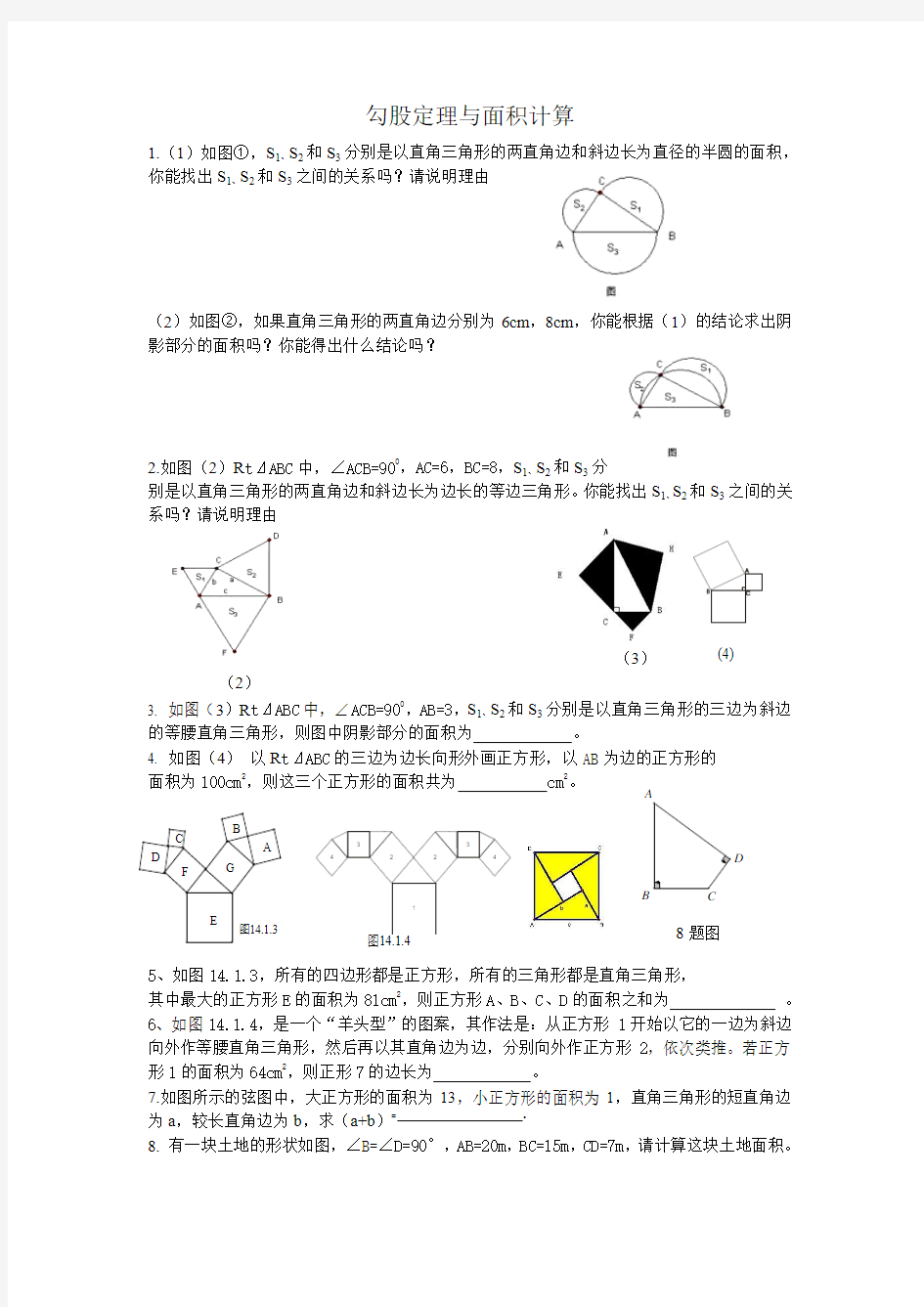
1.(1)如图①,S 1、S 2和S 3分别是以直角三角形的两直角边和斜边长为直径的半圆的面积,你能找出S 1、S 2和S 3之间的关系吗?请说明理由
(2)如图②,如果直角三角形的两直角边分别为6cm ,8cm ,你能根据(1)的结论求出阴影部分的面积吗?你能得出什么结论吗?
2.如图(2)R t ⊿ABC 中,∠ACB=900,AC=6,BC=8,S 1、S 2和S 3分
别是以直角三角形的两直角边和斜边长为边长的等边三角形。你能找出S 1、S 2和S 3之间的关系吗?请说明理由
3. 如图(3)R t ⊿ABC 中,∠ACB=900,AB=3,S 1、S 2和S 3分别是以直角三角形的三边为斜边的等腰直角三角形,则图中阴影部分的面积为 。
4. 如图(4) 以R t ⊿ABC 的三边为边长向形外画正方形,以AB 为边的正方形的 面积为100cm 2,则这三个正方形的面积共为 cm 2。 5、如图14.1.3,所有的四边形都是正方形,所有的三角形都是直角三角形, 其中最大的正方形E 的面积为81cm 2,则正方形A 、B 、C 、D 的面积之和为 。
6、如图14.1.4,是一个“羊头型”的图案,其作法是:从正方形1开始以它的一边为斜边向外作等腰直角三角形,然后再以其直角边为边,分别向外作正方形2,依次类推。若正方
形1的面积为64cm 2,则正形7的边长为 。 7.如图所示的弦图中,大正方形的面积为13,小正方形的面积为1,直角三角形的短直角边
为a ,较长直角边为b ,求(a+b )=
。
8. 有一块土地的形状如图,
∠B=∠D=90°,AB=20m ,BC=15m ,CD=7m ,请计算这块土地面积。 (2) (3)
(4) 1242334图14.1.4B 8题图
7.解题技巧专题:勾股定理与面积问题
解题技巧专题:勾股定理与面积问题 ——全方位求面积,一网搜罗 ◆类型一 三角形中利用面积法求高 1.直角三角形的两条直角边的长分别为5cm ,12cm ,则斜边上的高线的长为( ) A.8013cm B .13cm C.132cm D.6013cm 2.(2017·乐山中考)点A 、B 、C 在格点图中的位置如图所示,格点小正方形的边长为1,则点C 到线段AB 所在直线的距离是________. ◆类型二 结合乘法公式巧求面积或长度 3.已知Rt △ABC 中,∠C =90°,若a +b =12cm ,c =10cm ,则Rt △ABC 的面积是( ) A .48cm 2 B .24cm 2 C .16cm 2 D .11cm 2 4.若一个直角三角形的面积为6cm 2,斜边长为5cm ,则该直角三角形的周长是( ) A .7cm B .10cm C .(5+37)cm D .12cm 5.(2017·襄阳中考)“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲.如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形,设直角三角形较长直角边长为a ,较短直角边长为b ,若(a +b)2=21,大正方形的面积为13,则小正方形的面积为( ) A .3 B .4 C .5 D .6 ◆类型三 巧妙利用割补法求面积 6.如图,已知AB =5,BC =12,CD =13,DA =10,AB ⊥BC ,求四边形ABCD 的面积. 7.如图,∠B =∠D =90°,∠A =60°,AB =4,CD =2,求四边形ABCD 的面积.【方
勾股定理与面积计算
勾股定理与面积计算 1.(1)如图①,S 1、S 2和S 3分别是以直角三角形的两直角边和斜边长为直径的半圆的面积,你能找出S 1、S 2和S 3之间的关系吗?请说明理由 (2)如图②,如果直角三角形的两直角边分别为6cm ,8cm ,你能根据(1)的结论求出阴影部分的面积吗?你能得出什么结论吗? 2.如图(2)R t ⊿ABC 中,∠ACB=900,AC=6,BC=8,S 1、S 2和S 3分 别是以直角三角形的两直角边和斜边长为边长的等边三角形。你能找出S 1、S 2和S 3之间的关系吗?请说明理由 3. 如图(3)R t ⊿ABC 中,∠ACB=900,AB=3,S 1、S 2和S 3分别是以直角三角形的三边为斜边的等腰直角三角形,则图中阴影部分的面积为 。 4. 如图(4) 以R t ⊿ABC 的三边为边长向形外画正方形,以AB 为边的正方形的 面积为100cm 2,则这三个正方形的面积共为 cm 2。 5、如图14.1.3,所有的四边形都是正方形,所有的三角形都是直角三角形, 其中最大的正方形E 的面积为81cm 2,则正方形A 、B 、C 、D 的面积之和为 。 6、如图14.1.4,是一个“羊头型”的图案,其作法是:从正方形1开始以它的一边为斜边向外作等腰直角三角形,然后再以其直角边为边,分别向外作正方形2,依次类推。若正方 形1的面积为64cm 2,则正形7的边长为 。 7.如图所示的弦图中,大正方形的面积为13,小正方形的面积为1,直角三角形的短直角边 为a ,较长直角边为b ,求(a+b )= 。 8. 有一块土地的形状如图, ∠B=∠D=90°,AB=20m ,BC=15m ,CD=7m ,请计算这块土地面积。 (2) (3) (4) 1242334图14.1.4B 8题图
人教版八年级数学下册 第17章 勾股定理中最短路径问题专题
勾股定理中最短路径问题专题 一、同步知识梳理 1、勾股数:满足a2+b2=c2的3个正整数a、b、c称为勾股数. (1)由定义可知,一组数是勾股数必须满足两个条件: ①满足a2+b2=c2 ②都是正整数.两者缺一不可. (2)将一组勾股数同时扩大或缩小相同的倍数所得的数仍满足a2+b2=c2 (但不一定是勾股数),例如:3、4、5是一组勾股数,但是以0.3 cm、0.4 cm、0.5 cm为边长的三个数就不是勾股数。 二、同步题型分析 1、等腰三角形的周长是20 cm,底边上的高是6 cm,求它的面积. 2、(1)在△ABC中,∠C=90°,AB=6,BC=8,DE垂直平分AB,求BE的长. (2)在△ABC中,∠C=90°,AB=6,BC=8,AE平分∠CAE,ED⊥AB,求BE的长. (3)如图,折叠长方形纸片ABCD,是点D落在边BC上的点F处,折痕为AE,AB=CD=6,AD=BC=10,试求EC的长度. 一、专题精讲 知识总结:长方体: (1)长方体的长、宽、高分别为a、b、c;(2)求如图所示的两个对顶点的最短距离d。 E D A C B D E A C B
A B A 1B 1D C D 1C 1214 (2)长方体盒子表面小虫爬行的最短路线d 是22c b a ++)(、22b c a ++)(、2 2a c b ++)( 中最小者的值。 圆柱体: (1)圆柱体的高是h 、半径是r ;(2)要求圆柱体的对顶点的最短距离。 圆柱体盒子外小虫爬行的最短路线d ; 两条路线比较:其一、AC+BC 即高+直径 ; 其二、圆柱表面展开后线段AB=2 2r h +的长. 题型二、长方体 例题1、如图,一只蚂蚁从实心长方体的顶点A 出发,沿长方体的表面爬到对角顶点C 1处(三条棱长如图所示),问怎样走路线最短?最短路线长为 . 例题2、如图,长方体的长为15,宽为10,高为20,点B 离点C 的距离为5,一只蚂蚁如果要沿着长方体的表面从点A 爬到点B ,需要爬行的最短距离是 。 B A A B
勾股定理与面积计算
图14.1.3G F E D C B A 勾股定理与面积计算 1.(1)如图①,S 1、S 2和S 3分别是以直角三角形的两直 角边和斜边长为直径的半圆的面积,你能找出S 1、S 2和S 3之间的关 系吗请说明 理由 (2)如图②,如果直角三角形的两直角边分别为6cm ,8cm ,你能根据(1)的结论求出阴影部分的面积吗你能得出什么结论吗 2.如图(2)Rt ⊿ABC 中,∠ACB=900,AC=6,BC=8,S 1、S 2和S 3分 别是以直角三角形的两直角边和斜边长为边长的等边三角形。你能找出S 1、S 2和S 3之间的关系吗请说明理由 3. 如图(3)Rt ⊿ABC 中,∠ACB=900,AB=3,S 1、S 2和S 3分别是以直角三角形的三边为斜边 的等腰直角三角形,则图中阴影部分的面积为 。 4. 如图(4) 以Rt ⊿ABC 的三边为边长向形外画正方形,以AB 为边的正方形的 面积为100cm 2,则这三个正方形的面积共为 cm 2。 (2) (3) (41 242334图14.1.4 B 8题图
5、如图,所有的四边形都是正方形,所有的三角形都是直角三角形, 其中最大的正方形E的面积为81cm2,则正方形A、B、C、D的面积之和为。 6、如图14.1.4,是一个“羊头型”的图案,其作法是:从正方形1开始以它的一边为斜边向外作等腰直角三角形,然后再以其直角边为边,分别向外作正方形2,依次类推。若正方形1的面积为64cm2,则正形7的边长为。 7.如图所示的弦图中,大正方形的面积为13,小正方形的面积为1,直角三角形的短直角边为a,较长直角边为b,求(a+b)= 。 8. 有一块土地的形状如图,∠B=∠D=90°,AB=20m,BC=15m,CD=7m,请计算这块土地面积。
勾股定理之归纳1最短路径问题与勾股定理
归纳1:最短路径问题与勾股定理 原题1:如图,一条河同一侧的两村庄A、B,其中A、B 到河岸最短距离分别为AC=1km,BD=2km,CD=4km,现欲在河岸上建一个水泵站向A、B两村送水,当建在河岸上何处时,使到A、B两村铺设水管总长度最短,并求出最短距离。 原题2:如图所示,圆柱体的底面直径为6cm,高AC为12cm,一只蚂蚁从A点出发,沿着圆柱的侧面爬行到点B,试求出爬行的最短路程.(π取3) 原题3:如图,有一个长方体的长、宽、高分别是3、2、1,在底面A处有一只蚂蚁,它想吃正方体B处的食物,需要爬行的最短路程是多少? 变式1:正方形ABCD的边长为8,M在DC上,且DM=2,N是AC上的一动点,DN+MN的最小值为多少。 变2:如图(1),A、B两单位分别位于一条封闭街道的两旁(直线l1、l2是街道两边沿),现准备合作修建一座过街人行天桥. (1)天桥应建在何处才能使由A经过天桥走到B的路程最短?在图(2)中作出此时桥PQ的位置,简要叙述作法并保留作图痕迹.(注:桥的宽度忽略不计,桥必须与街道垂直). (2)根据图(1)中提供的数据计算由A经过天桥走到B的最短路线的长.(单位:米) 变3:有一圆形油罐底面圆的周长为24m,高为6m,一只老鼠从距底面1m的A处爬行到对角B处吃食物,它爬行的最短路线长为多少? 变4:有一圆柱形油罐,要以A点环绕油罐建旋梯,正好到A点的正上方B点,问旋梯最短要多少米?(己知油罐周长是12米,高AB是5米) 变5:如图,圆柱底面半径为2cm,高为9π,A、B分别是圆柱底面圆周上的点,且A、B在同一母线上,用一棉线从A顺着圆柱侧面绕3圈到B,求棉线最短距离。 变6:如图, 透明的圆柱形容器( 容器厚度忽略不计) 的高为12cm ,底面周长为10cm ,在容器内壁离容器底部3cm 的点 B 处有一饭粒,此时一只蚂蚁正好在容器外壁,且离容器上沿3cm 的点 A 处,则蚂蚁吃到饭粒需爬行的最短路径是多少? 变7:如图,长方体的长为15 cm,宽为10 cm,高为20 cm,点B离点C 5 cm,一只蚂蚁如果要沿着长方体的表面从点A爬到点B,需要爬行的最短距离是多少?
从勾股定理到图形面积关系的拓展定稿版
从勾股定理到图形面积 关系的拓展 HUA system office room 【HUA16H-TTMS2A-HUAS8Q8-HUAH1688】
从勾股定理到图形面积的拓展 教学目标: 1.通过观察图形,探索图形间的关系,发展学生的拓展性思维. 2.在将实际问题抽象成数学问题的过程中,提高分析问题、解决问题的能力及渗透数学建模的思想. 3.在利用勾股定理解决实际问题的过程中,体验数学学习的实用性.感受数学学习的魅力 教学重点:利用勾股定理,解决实际问题 教学难点:通过体验图形的变式,学会分析问题解决问题的能力及数学建模思想。 教学过程: 一、 向外拓展正方形 如图,在Rt △ ABC ,∠C=090中,AB=c,AC=b,BC=a, 分别以a,b,c 三边为边做正四边形,那么有132s s s =+ 证明:∵ 22b s =,23a s =,21c s = 根据勾股定理:222c b a =+ ∴ 132s s s =+
拓展练习: 1、如图,是一些由正方形和直角三角形拼合成的图形, 其中最大的正方形的边长为7cm.你能求出正方形A、B、 C、D的面积之和吗?请试一试. 2、如图,在四边形ABCD中,∠DAB=∠BCD=90°,分别以四边形的四条边为边向外 作四个正方形,若S 1+S 4 =100,S 3 =36, 则S 2 =() 3、如图,直线L上有三个正方形a,b,c,若a,c的面积分别为5和11.求正 方形b的面积. 4、如图,已知1号、4号两个正方形的面积和为7,2号,3号两个正方形的面积为4则A,B,C三个正方形的面积和为多少?
专题:勾股定理与面积问题 含答案
专题:勾股定理与面积问题 ——全方位求面积,一网搜罗 ◆类型一三角形中利用面积法求高 1.直角三角形的两条直角边的长分别为5cm,12cm,则斜边上的高线的长为() A. 80 13cm B.13cm C. 13 2cm D. 60 13 cm 2.(2017·乐山中考)点A、B、C在格点图中的位置如图所示,格点小正方形的边长为1,则点C到线段AB所在直线的距离是________. ◆类型二结合乘法公式巧求面积或长度 3.已知Rt△ABC中,∠C=90°,若a+b=12cm,c=10cm,则Rt△ABC的面积是() A.48cm2B.24cm2C.16cm2D.11cm2 4.若一个直角三角形的面积为6cm2,斜边长为5cm,则该直角三角形的周长是() A.7cm B.10cm C.(5+37)cm D.12cm 5.(2017·襄阳中考)“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲.如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形,设直角三角形较长直角边长为a,较短直角边长为b,若(a+b)2=21,大正方形的面积为13,则小正方形的面积为() A.3 B.4 C.5 D.6 ◆类型三巧妙利用割补法求面积 6.如图,已知AB=5,BC=12,CD=13,DA=10,AB⊥BC,求四边形ABCD的面积.
7.如图,∠B=∠D=90°,∠ A=60°,AB=4,CD=2,求四边形ABCD的面积.【方法6】 ◆类型四利用“勾股树”或“勾股弦图”求面积 8.如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方 形的边长为9cm,则正方形A ,B,C,D的面积之和为________cm2. 9.在我国古算书《周髀算经》中记载周公与商高的谈话,其中就有勾股定理的最早文字记录,即“勾三股四弦五”,亦被称作商高定理.如图①是由边长相等的小正方形和直角三角形构成的,可以用其面积关系验证勾股定理.图②是将图①放入长方形内得到的,∠BAC =90°,AB=3,AC=4,则D,E,F,G,H,I都在长方形KLMJ的边上,那么长方形KLMJ 的面积为________.
勾股定理最短距离问题
蚂蚁爬行的最短路径 正方体 4.如图,一只蚂蚁从正方体的底面 A 点处沿着表面爬行到点上面的 B 点处,它爬行的最短 路线是( ) 解:根据两点之间线段最短可知选 A. 故选A. 2.如图,边长为1的正方体中,一只蚂蚁从顶点 A 出发沿着正方体的外表面爬到顶点 最短距离是 解:如图将正方体展开,根据“两点之间,线段最短”知,线段 AB 即为最短路线. 2, BC 的中点为 M, —只蚂蚁从 A 点爬行到 M 点的最短距离 解:将正方体展开,连接 M D1, 根据两点之间线段最短, MD=MC+CD=1+2=3 A? Q? B C . A? R? B D A? S? B 为 第7题
解:将长方体展开,连接 MD= MD 2 DD 12 .32 22 , 13 . 5.如图,点A 的正方体左侧面的中心,点 蚂蚁从点A 沿其表面爬到点 所以最短路径长为 5cm 用时最少:5十2=秒. 长方体 10. (2009?恩施州)如图,长方体的长为 15,宽为10,高为20,点B 离点C 的距离为5, 一只蚂蚁如果要沿着长方体的表面从点 A 爬到点B,需要爬行的最短距离是 B 是正方体的一个顶点,正方体的棱长为 2, B 的最短路程是( ) 9. 如图所示一棱长为 3cm 的正方体,把所有的面均分成 3X3个小正方形.其边长都为1cm, 2cm,则它从下底面点 A 沿表面爬行至侧面的 B 点,最少要用 秒钟. ,故分情况分别计算,进行大、小比较,再从各个路线中确定最: (1)展开前面右面由勾股定理得 AB= -::':=门 cm; (2)展开底面右面由勾股定理得 AB= J- ' I I.J ' =5cm ; 10 .故选 c. 的路 A
勾股定理与面积法
17 16 C A B D 勾股定理与面积法 学习目标:熟练应用勾股定理和面积法列方程解决求值问题。培养化归思想和方程思想。 学习过程: 例1学习:如图,Rt △ABC 的两直角边为3,4。求斜边上的高CD 。 3 4 A B D 归纳:我们有Rt △ABC 的两种面积表示方法 BC AC ?2 1 和 。 像这样,用两种面积表示方法表示同一图形的面积,从而建立方程来解决问题的方法叫面积法..... 练习:如图,Rt △ABC 的一直角边为5,斜边长13。求斜边上的高CD 。 5 C A B D 例2学习:如图,等腰三角形的三边为17㎝,17㎝,16㎝。求腰上的高CD 。 分析:由CD 为高想到此三角形的面积可以表示为CD AB ?21 ,如果知道BC 边上的高,就可以用面积法建立方程求出CD 。 解:作BC 边上的高AE 。 ∵AE 为等腰三角形底边上的高 ∴AE 为底边BC 的中线 ( ) ∴CE= 练习:如图,等腰三角形的腰长为17㎝,底边上的高AE 为15㎝。求腰上的高CD 。
C B B C A B 例3学习:等腰三角形的腰长为5,面积为12。求它的底边BC 的长。 首先我们想到:根据面积可以求出腰上的高,但是腰上的高是在三角形的内部还是外部呢?看来我们要分两种情况。先求出CD=4.8,然后求出AD= 再求出BD= 或 最后求出BC= 或 接下来我们想一想等腰三角形三线合一的性质,我们可以作底边的高构造直角三角形,就不需要分类了。 我们可以根据面积列一个方程,还可以根据勾股定理列一个方程。由方程组可以解决这个问题。 解:作BC 边上的高AE 。 ∵AE 为等腰三角形底边上的高 ∴AE 为底边BC 的中线 ( ) 设BE=x=CE,AE=y. (注意2x 的值才是要 求的答案) 由Rt △AEC 得 =+22y x 由三角形面积得 =xy 练习: 1.设直角三角形的三边为a ,b ,c ,斜边c 上的高为h 。 (1)a=6,b=8,求h (2)a=5,c=13,求h (3)b=24,c=25,求h 2.三角形的三边长如图所示,求BC 边上的高。 3.三角形ABC 中,AB=24,AC=13,∠B=30度。求BC 的长。(先把图形画出来) B C E 4 A C B
勾股定理中的最短距离经典题型
最短距离: 1.(本小题10分)如图,这是一个供滑板爱好者使用的U型池,该U型池可以看作是一个长方体去掉一个“半圆柱”而成,中间可供滑行部分的截面是半径为3的半圆,其边缘AB=CD=16,点E在CD上,CE=4,一滑板爱好者从A点滑到E点,则他滑行的最短距离为( )(π按3计算) A. 15 B. C. D. 21 2.如图,圆柱底面半径为,高为9cm,点A,B分别是圆柱两底面圆周上的点,且点A,B在同一母线上,用一根棉线从点A点顺着圆柱侧面绕3圈到B点,则这根棉线的长度最短为( ) A. 12cm B. C. 15cm D. 3. 如图是一个三级台阶,它的每一级的长,宽和高分别为50寸,30寸和10寸,A和B是这个台阶的两个相对端点,A点上有一只蚂蚁想到B点去吃可口的食物,则它所走的最短路线长是( ) A. 13寸 B. 40寸 C. 130寸 D. 169寸 4. 如图,一只蚂蚁从长、宽都是6,高是16的长方体纸箱的A点沿纸箱爬到B点,那么它所爬行 的最短路线的长为( ) A. 20 B. 22 C. 28 D. 18 5. 如图,一个直径为8cm的杯子,在它的正中间竖直放一根筷子,筷子露出杯子外1cm.当筷子倒向杯壁时(筷子底端不动),若筷子顶端刚好触到杯口,则筷子长度和杯子的高度分别为( )cm.
A. 8,7 B. 8.5,7.5 C. 9,8 D. 10,9 6. 如图,将一根木棒垂直或倾斜的放进长、宽、高分别为12cm,4cm,3cm的水箱中,能放入水箱内木棒的最大长度为( )cm. A. 13 B. 12 C. 15 D. 16 7. 一辆卡车装满货物后宽3.2米,这辆卡车要通过如图所示的隧道(上方是一个半圆,下方是边长为4米的正方形),则装满货物后卡车的最大高度为( )米. A. 5.2 B. 5.8 C. 7.6 D. 5.4 8.某工厂大门形状如图所示,其上部分为半圆,工厂门口的道路为双行道(双行道中间隔离带忽略不计).要想使宽为1.5米,高为3.1米的卡车安全通过,那么此大门的宽度至少应增加 多少米? 9. 如图,一圆柱体的底面周长为24cm,高AB为16cm,BC是上底面的直径.一只昆虫从点A出发,沿着圆柱的侧面爬行到点C,则昆虫爬行的最短路程为____cm. 10. 如图,长方体的长、宽、高分别为4cm,2cm,5cm.若一只蚂蚁从P点开始经过4个
勾股定理知识点与常见题型总结
第18章勾股定理复习 一?知识归纳 1?勾股定理 内容:直角三角形两直角边的平方和等于斜边的平方; 表示方法:如果直角三角形的两直角边分别为 a , b ,斜边为 c ,那么a 2 b 2 c 2 勾股定理的由来:勾股定理也叫商高定理,在西方称为毕达哥拉斯定理.我国古代把直角三角形中较 短的直角边称为勾,较长的直角边称为股,斜边称为弦.早在三千多年前,周朝数学家商高就提出了 勾 三,股四,弦五”形式的勾股定理,后来人们进一步发现并证明了直角三角形的三边关系为:两直角边的 平方和等于斜边的平方 2.勾股定理的证明 勾股定理的证明方法很多,常见的是拼图的方法 用拼图的方法验证勾股定理的思路是 ① 图形进过割补拼接后,只要没有重叠,没有空隙,面积不会改变 ② 根据同一种图形的面积不同的表示方法,列出等式,推导出勾股定理 常见方法如下: A 方法一:4S S 正方形EFGH S 正方形ABCD ,4 — ab (b a) c ,化简可证. 2 四个直角三角形的面积与小正方形面积的和等于大正方形的面积. 四个直角三角形的面积与小正方形面积的和为 S 4 — ab c 2 2ab c 2 2 大正方形面积为 S (a b)2 a 2 2ab b 2 所以a 2 b 2 c 2 方法 b a
3 .勾股定理的适用范围 勾股定理揭示了直角三角形三条边之间所存在的数量关系,它只适用于直角三角形,对于锐角三角形和钝 角三角形的三边就不具有这一特征,因而在应用勾股定理时,必须明了所考察的对象是直角三角形 4. 勾股定理的应用 ① 已知直角三角形的任意两边长,求第三边 在 ABC 中, C 90,则 c ■. a 2 b 2 , b . c 2 a 2 , a . c 2 b 2 ② 知道直角三角形一边,可得另外两边之间的数量关系 ③ 可运用勾股定理解决一些实际问题 5. 勾股定理的逆定理 如果三角形三边长a , b , c 满足a 2 b 2 c 2,那么这个三角形是直角三角形,其中 c 为斜边 ① 勾股定理的逆定理是判定一个三角形是否是直角三角形的一种重要方法,它通过 数转化为形”来确定 三角形的可能形状,在运用这一定理时,可用两小边的平方和 a 2 b 2与较长边的平方c 2作比较,若它们相 等时,以a , b , c 为三边的三角形是直角三角形;若 a 2 b 2 c 2,时,以a , b , c 为三边的三角形是钝 角三角形;若a 2 b 2 c 2,时,以a , b , c 为三边的三角形是锐角三角形; ② 定理中a , b , c 及a 2 b 2 c 2只是一种表现形式,不可认为是唯一的,如若三角形三边长 a , b , c 满足a 2 c 2 b 2,那么以a , b , c 为三边的三角形是直角三角形,但是 b 为斜边 ③ 勾股定理的逆定理在用问题描述时,不能说成:当斜边的平方等于两条直角边的平方和时,这个三角 形是直角三角形 6 .勾股数 ① 能够构成直角三角形的三边长的三个正整数称为勾股数,即 a 2 b 2 c 2中,a , b , c 为正整数时, 称a , b , c 为一组勾股数 ② 记住常见的勾股数可以提高解题速度,如 3,4,5 ; 6,8,10 ; 5,12,13 ; 7,24,25等 ③ 用含字母的代数式表示 n 组勾股数: 2 2 n 1,2n,n 1 ( n 2, n 为正整数); 2n 1,2n 2n,2n 2n 1 ( n 为正整数) m 2 n 2,2mn,m 2 n 2 ( m n, m , n 为正整数) 7.勾股定理的应用 勾股定理能够帮助我们解决直角三角形中的边长的计算或直角三角形中线段之间的关系的证明问题?在使 用勾股定理时,必须把握直角三角形的前提条件,了解直角三角形中,斜边和直角边各是什么,以便运用 勾股定理进行计算,应设法添加辅助线(通常作垂线) ,构造直角三角形,以便正确使用勾股定理进行求 解 . 方法三: S 梯形 —(a b) (a b), S 梯形 2S ADE 2 S ABE 2 — ab ■- c ,化简得证 2 2
面积法与勾股定理
面积法与勾股定理 例.如图,在⊿ABC 中,∠ACB=900,AB=5cm,BC=3cm,CD ⊥AB 与D,求: (1),AC 的长;(2)⊿ABC 的面积;(3)CD 的长。 (7分) 解:在Rt △ABC 中,4352222=-=-=BC AB AC 6342 121=??=?=?BC AC S ABC 面积法: 652121=??=?= ?CD CD AB S ABC ∴512=CD 练习1.如图,Rt △ABC 中,∠ACB=90°,CD ⊥AB ,若AC=12,BC=5,则CD= . 解:在Rt △ABC 中,135122222=+=+=BC AC AB CD AB BC AC S ABC ?=?=?2 121 面积法:∴CD 13512=? ∴1360= CD 练习2、如图,长方形长AB=24,宽AD=10。(1)求BD 的长;(2)求点C 到BD 的距离。 解:在Rt △DAB 中,2624102222=+=+= AB AD BD 根据△DCB 中,CE DB CD BC ?=?2121,CE ?=?262410,13 120=CE 练习3.等腰三角形底边长为8cm,腰长为5 cm,则腰上的高为 .
解:求得底边上的高为3,面积法h 52 13821?=??,8.4=h 例2.已知:如图,△ABC 中,∠C = 90°,点O 为△ABC 的三条角平分线的交点,OD ⊥BC ,OE ⊥AC ,OF ⊥AB ,点D 、E 、F 分别是垂足,且BC = 8cm ,CA = 6cm ,则点O 到三边AB ,AC 和BC 的距离分别等于 cm 面积法 10862222=+=+=BC AC AB OD BC OF AB OE AC BC AC ?+?+?=?2 1212121 x x x 810686++=?,2=x 练习2、如图,△ABC 中,∠B=90°,两直角边AB=7,BC=24,三角形内有一点P 到各边的距离相等,则这个距离是( ) (A )1 (B)3 (C)4 (D)5 C O A B D E F 第18题图 A B P C
勾股定理中的最短距离(经典题型)
最短距离: 令狐采学 1.(本小题10分) 如图,这是一个供滑板爱好者使用的U型池,该U型池可以看作是一个长方体去掉一个“半圆柱”而成,中间可供滑行部分的截面是半径为3的半 圆,其边缘AB=CD=16,点E在CD上, CE=4,一滑板爱好者从A点滑到E点, 则他滑行的最短距离为( )(π按3计算)A. 15B. C. D. 21 2.如图,圆柱底面半径为,高为9cm,点A,B分别是圆柱两底面圆周上的点,且点A,B在同一母线上,用一根棉 线从点A点顺着圆柱侧面绕3圈到B点,则这根棉线的 长度最短为( )A. 12cmB. C. 15cmD. 3. 如图是一个三级台阶,它的每一级的长,宽和高分别为 50寸,30寸和10寸,A和B是这个台阶的两个相对端点, A点上有一只蚂蚁想到B点去吃可口的食物,则它所走的最短路线长是( ) A. 13寸 B. 40寸 C. 130寸 D. 169寸 4.如图,一只蚂蚁从长、宽都是6,高是16的长方体纸箱的A 点沿纸箱爬到B点,那么它所爬行的最短路线的长为( ) A. 20 B. 22 C. 28 D. 18
5.如图,一个直径为8cm的杯子,在它的正中间竖直放一根筷子,筷子露出杯子外1cm.当筷子倒向杯壁时(筷子底端不动),若筷子顶端刚好触到杯口,则筷子长度和杯子的高度分别为( )cm. A. 8,7 B. 8.5,7.5 C. 9,8 D. 10,9 6. 如图,将一根木棒垂直或倾斜的放进长、 宽、高分别为12cm,4cm,3cm的水箱中, 能放入水箱内木棒的最大长度为( )cm. A. 13 B. 12 C. 15 D. 16 7. 一辆卡车装满货物后宽3.2米,这辆卡车要通过如图所示的隧道(上方是一个半圆,下方是边长为4米的正方 形),则装满货物后卡车的最大高度为( )米. A. 5.2 B. 5.8 C. 7.6 D. 5.4 8.某工厂大门形状如图所示,其上部分为半圆,工 厂门口的道路为双行道(双行道中间隔离带忽略 不计).要想使宽为1.5米,高为3.1米的卡车安全通过, 那么此大门的宽度至少应增加多少米? 9. 如图,一圆柱体的底面周长为24cm,高AB为16cm, BC是上底面的直径.一只昆虫从点A出发,沿着圆柱 的侧面爬行到点C,则昆虫爬行的最短路程为____cm. 10. 如图,长方体的长、宽、高分别为4cm,2cm,5cm.若 一只蚂蚁从P点开始经过4个侧面爬行一圈到达Q点,
从勾股定理到图形面积关系的拓展
从勾股定理到图形面积的拓展 教学目标: 1. 通过观察图形,探索图形间的关系,发展学生的拓展性思维. 2. 在将实际问题抽象成数学问题的过程中,提高分析问题、解决问题的能力及渗透数学建模的思想. 3. 在利用勾股定理解决实际问题的过程中,体验数学学习的实用性?感受数学学习的魅力教学重点:利用勾股定理,解决实际问题教学难点:通过体验图形的变式,学会分析问题解决 问题的能力及数学建模思想。 教学过程: 一、向外拓展正方形 如图,在心△ ABC , Z C= 90°中, AB=c,ACgBUa,分别以a,b,c三边为边做正四边 形,那么有S2+s3 =S l 证明:T S?= / , S3=U2f S l = C2 ? ? 矢+ $3 = S] 根据勾股定理:CΓ+IΓ=C2 2、如图,在四边形ABCD中,ZDAB=ZBCD=90°,分别以四边形的四条边 为边向外作四个正方形,若Sι+S4=100, S3=36,
则S2=( ) 3、如图,直线L上有三个正方形a,b,c,若a,c的面积分别为5和11.求正方 形b的面积. 52 +6 =T(^ +bI) 9根据勾股定理/ +b2 "得》+$3 =粹= 艮卩:S2 + S3 = S1 三、向外拓展正五边形 如图以直角三角形的三边为边长做正五边形, 求证:s2+s5 = S l
证明:如图连接正五边形的中心O与一边端点的连线构成一个等腰三角形,并做岀等腰三角形底边上的高 h, h C ? COt α =— , ?? /1 =— C Ot Ct f C 2 2 1 C5 φ c ??S[ = —c?-cotα<5 = —c ?cotα? 2 2 4 5 . 5 7 同理:S I = -Ir?cotα , Sy = —cr?cottz , ?4 4 即:s1 +s3 = S I 通过上而的证明我们就得到了“以任意直角三角形的三边为边长做边数相等的正多边形,以斜边边长为 边的正多边形的面积等于以直角边边长为边的两正多边形的面积之和?” 四、向外拓展半圆 同样我们还能得到以“任意直角三角形的三边为直径做半圆(或圆),以斜边边长为直径的半圆(或 圆)的面积等于以直角边为直径的两个半圆(或圆)的面积之和” ? 下而我们来看证明: 已知:如图,直角三角形的两直角边为a,b,斜边为c,分别以a,b,c 为直径做半圆. 、 S3
勾股定理求最短距离问题
课题利用勾股定理求最短问题 学习目标:利用勾股定理知识与其他知识的综合应用解决图形中最短距离问题。 学习重点:勾股定理及其逆定理的综合应用。 学习难点:数形结合法分析问题。 学习过程: 一、复习回顾 (1)勾股定理:如果直角三角形的两直角边长分别为a、b,斜边长为c,那么。(2)逆定理:如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形是三角形。(3)如图一个圆柱,延其一条与轴平行的曲面上一条直线展开侧面图是。 二、学以致用 例1、如图,是一个三级台阶,它的每一级的长、宽和高分别等于5cm,3cm和1cm,A和B是这个台阶的两个相对的端点,A点上有一只蚂蚁,想到B点去吃可口的食物.请你想一想,这只蚂蚁从A点出发,沿着台阶面爬到B点,最短线路是多少? 例2、有一圆形油罐底面圆的周长为24m,高为6m,一只老鼠从距底面1m的A处爬行到对角B处吃食物,它爬行的最短路线长为多少? 例3、如图,边长为1的正方体中,一只蚂蚁从顶点A出发沿着正方体的外表面爬到顶点B的最短距离是()(A)3 (B)√5 (C)2 (D)1 例4、如图,一只蚂蚁从实心长方体的顶点A出发,沿长方体的表面爬到对角顶点C1处(三条棱长如图所示),问怎样走路线最短?最短路线长为多少? 例5、如图,长方体的长为15cm,宽为10cm,高为20cm,点B到点C的距离为5cm,一只蚂蚁如果要沿着长方体的表面从A点爬到B点,需要爬行的最短距离是多少?
三、巩固练习 1. 如图,一圆柱高8cm,底面半径2cm,一只蚂蚁从点A爬到点B处吃食,要爬行的最短路程是多少?( 取3) B 8 2.已知长方体的长为2cm、宽为1cm、高为4cm,一只蚂蚁如果沿长方体的表面从A点爬到B点, 那么沿哪条路最近,最短的路程是多少? 3.如图所示,圆柱形玻璃容器,高18 cm,底面周长为60 cm,在外侧距下底1 cm,点S处有一蜘蛛, 与蜘蛛相对的圆柱形容器的上口外侧距开口处1 cm的点F处有一苍蝇,试求急于捕获苍蝇充饥的蜘蛛, 所走的最短路线的长度。 4. 如右图,有一个长方体盒子,它的长是70cm,宽和高都是50cm。在A点处有一只蚂蚁,它想吃到 B点处的食物,那么它爬行的最短路程是多少? 5.如图是一个三级台阶,它的每一级的长、宽和高分别为20dm、3dm、2dm,A和B是这个台阶两个相 对的端点,A点有一只蚂蚁,想到B点去吃可口的食物,则蚂蚁沿着台阶面爬到B点的最短路程是 多少? 20 3 2 A B 6.如图,铁路上A,B两点相距25km,C,D为两村庄,DA⊥AB于A,CB⊥AB于B,已知DA=15km,CB=10km, 现在要在铁路AB上建一个土特产品收购站E,使得(1)若C,D两村到E站的距离相等,则E站应建 在离A站多少km处? (2)若E站到C,D站的距离之和最短,则 E站应建在离 A站多少km处? A D E B C
勾股定理与面积中考试题荟萃
勾股定理典型练习题 1、勾股定理是几何中的一个重要定理.在我国古算书《周髀算经》中就有“若勾三,股四,则弦五”的记载.如图1是由 边长相等的小正方形和直角三角形构成的,可以用其面积关系验证勾股定理.图2是由图1放入矩形内得到的,∠BAC=90°,AB=3,AC=4,点D ,E ,F ,G ,H ,I 都在矩形KLMJ 的边上,则矩形KLMJ 的面积为( ) A 、90 B 、100 C 、110 D 、 121 2、如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形.若正方形A ,B ,C ,D 的边长分别是3,5,2,3,则最大正方形E 的面积是( ) A 、13 B 、26 C 、47 D 、94 3、如图,在边长为4的等边三角形ABC 中,AD 是BC 边上的高,点E ,F 是AD 上的两点,则图中阴影部分的面积是( ) A 、34 B 、33 C 、32 D 、3 4、如图,直线l 上有三个正方形a ,b ,c ,若a ,c 的面积分别为5和11,则b 的面积为( ) A 、 4 B 、6 C 、16 D 、55 5、如图,分别以直角△ABC 的三边AB 、BC 、CA 为直径向外作半圆,设直线AB 左边阴影部分面积为S 1,右边阴影部分面积为S 2,则( ) A .S1=S2 B .S1<S2 C .S1>S2 D .无法确定 6.已知:如图,以Rt△ABC 的三边为斜边分别向外作等腰直角三角形.若斜边AB=3,则图中阴影部分的面积为_____。 7.如图,以AB 为直径画一个大半圆,BC=2AC ,分别以AC ,CB 为直径在大半圆内部画两个小半圆,那么阴影部分的面积与大半圆面积的比等于 ______。 8.如图,直角三角形ABC 中,∠ABC=90°,AB=6,以AB 为直径画半圆,若阴影部分的面积S1-S2= 2 π ,则BC= _____。 9、如图,Rt△ABC 中,∠ACB=90°.在AB 的同侧分别以AB 、BC 、AC 为直径作三个半圆.图中阴影部分的面积分别记作为S1和S2. (1)求证:S1+S2=S△ABC; (2)若Rt△ABC 的周长是 62+,斜边长为2,求图中阴影部分面积的和. 10、(1)如图4,在梯形ABCD 中,AD∥BC,∠ABC+∠BCD=90°,BC=2AD ,分别以AB 、CD 、AD 为边向梯形外作正方形,其面积分别为S1、S2、S3,则S1、S2、S3之间的数量关系式为 ________。请说明理由。 (2)如图,在梯形ABCD 中,AB∥DC,∠ADC+∠BCD=90°,且DC=2AB ,分别以DA 、BC 、DC 为边向梯形外作正方形,其面积分别为S1、S2、S3,则S1、S2、S3之间数量的关系是( ) A .S 1+S 2=S 3 B 、S 1+S 2= 2 1S 3 C 、S 1+S 2= 31S 3 D 、S 1 +S 2 =4 1S 3 11、(a )如图(1)分别以直角三角形ABC 三边为直径向外作三个半圆,其面积分别用表示 S1、S2、S3则它们有 _________ 2题 3题 4题
勾股定理的应用-最短距离
数学八年级下北师大新课标第一章第二节《勾股定理的应用-最短距离问题》教学设计 西安市第70中学范聪聪 内容和内容解析: 本节是义务教育课程标准北师大版教科书八年级(上)第一章《勾 股定理》第三节.具体内容是运用勾股定理解决简单的立体图形上的最 短距离问题,进一步发展应用意识。本节课是七年级图形的展开与折叠 知识的延续,需要把立体图形展开成平面图形后,利用两点之间线段最 短在平面上找到最短距离,并运用勾股定理求出最短距离。同时本节课 从圆柱(侧面)中来又回到圆柱(内部)中去,最后也为九年级要学习 的视图与投影埋下伏笔。 目标和目标解析: 本节课的重点是利用勾股定理解决立体图形上的最短距离问题,难 点是如何寻找和计算最短距离。设计“蚂蚁怎样走最近?”这个有趣的 实际情景,让学生了解实际问题可以转化成数学问题,让学生体验数学 源于生活,又应用于生活;在经历寻找和计算“最短距离”的过程中, 让学生理解,为什么要把立体图形展开成平面图形,使学生逐渐形成思 维上的转化思想,进一步体会数学的应用价值;学生要探究并掌握立体 图形转化成平面图形后,最短距离的寻找方法和利用勾股定理的计算方 法,这也使学生积累利用数学知识解决日常生活中实际问题的经验和方 法,逐步形成积极参与数学活动的意识。 教学问题诊断分析: 学情分析:学生在七年级已学习过图形的展开与折叠,并了解两点
之间线段最短,有一定基础。本节课要求学生在实际问题中自己寻找并计算最短距离,而八年级学生审题能力,审题方法,数学思维习惯已逐渐养成,但解决实际问题的能力仍需培养; 内容预设:一,本节课学生可能遇到的第一个问题,在寻找“最短距离”的过程中,在展开后的平面图形上不能准确找到蚂蚁或食物所在的“点”,而找不准“关键点”的原因:缺乏空间想象能力;懒于动手操作实践;没能完全感受到立体图形展成平面图形带来的好处;习惯养成问题(审题意识,审题方法)。二,极个别学生在计算最短距离时出问题,究其原因:缺乏利用数学知识解决实际问题的能力;对勾股定理的掌握不够扎实;缺乏由点(蚂蚁和食物)到线(最短距离)再到面(直角三角形)的意识。三,在探究长方体表面的最短距离问题时,展开方式“找不全”,容易遗漏。究其原因:没有真正理解展开的原因,展开后的好处;考虑问题不够全面,急于求成; 教学支持条件分析: 根据教学问题的诊断,将蚂蚁的移动路线;食物所在的“点”;由点到线生成的最短距离;以及最短距离所在的面的生成都利用多媒体演示,直观,生动,并将练习题用多媒体呈现,提高课堂效率
勾股定理与面积法
16C B 勾股定理与面积法 学习目标:熟练应用勾股定理和面积法列方程解决求值问题。培养化归思想和方程思想。 学习过程: 例1学习:如图,Rt △ABC 的两直角边为3,4。求斜边上的高CD 。 A B D 归纳:我们有Rt △ABC 的两种面积表示方法BC AC ?21和 。 像这样,用两种面积表示方法表示同一图形的面积,从而建立方程来解决问题的方法叫面积法..... 练习:如图,Rt △ABC 的一直角边为5,斜边长13。求斜边上的高CD 。 C A B D 例2学习:如图,等腰三角形的三边为17㎝,17㎝,16㎝。求腰上的高CD 。 分析:由CD 为高想到此三角形的面积可以表示为CD AB ?21,如果知道BC 边上的高,就可以用面积法建立方程求出CD 。 解:作BC 边上的高AE 。 ∵AE 为等腰三角形底边上的高 ∴AE 为底边BC 的中线 ( ) ∴CE= 练习:如图,等腰三角形的腰长为17㎝,底边上的高AE 为15㎝。求腰上的高CD 。
C B B C A B 例3学习:等腰三角形的腰长为5,面积为12。求它的底边BC 的长。 首先我们想到:根据面积可以求出腰上的高,但是腰上的高是在三角形的内部还是外部呢?看 来我们要分两种情况。先求出CD=4.8,然后求出AD= 再求出BD= 或 最后求出BC= 或 接下来我们想一想等腰三角形三线合一的性质,我们可以作底边的高构造直角三角形,就不需要分类了。 我们可以根据面积列一个方程,还可以根据勾股定理列一个方程。由方程组可以解决这个问题。 解:作BC 边上的高AE 。 ∵AE 为等腰三角形底边上的高 ∴AE 为底边BC 的中线 ( ) 设BE=x=CE,AE=y. (注意2x 的值才是要 求的答案) 由Rt △AEC 得 =+22y x 由三角形面积得 =xy 练习: 1.设直角三角形的三边为a ,b ,c ,斜边c 上的高为h 。 (1)a=6,b=8,求h (2)a=5,c=13,求h (3)b=24,c=25,求h 2.三角形的三边长如图所示,求BC 边上的高。 3.三角形ABC 中,AB=24,AC=13,∠B=30度。求BC 的长。(先把图形画出来) B C E 4A C B
(完整版)勾股定理解决最短路径问题及折叠问题
勾股定理解决最短路径问题及折叠问题 1、如图,长方体的长为15,宽为10,高为20,点B离点C的距离为5,一只蚂蚁如果要沿着长方体的表面从点A爬到点B,需要爬行的最短距离是多少? 2、如图,长方体的底面边长分别为1cm和3cm,高为6cm.如果用一根细线从点A开始经过4个侧面缠绕一圈到达点B,那么所用细线最短需要_________cm;如果从点A 开始经过4个侧面缠绕n圈到达点B,那么所用细线最短需要_________cm. 3、如图,长方体的长为15cm,宽为10cm,高为20cm,点B到点C的距离为5cm,一只蚂蚁如果要沿着长方体的表面从A点爬到B点,需要爬行的最短距离是多少?
4、如图所示,正方形ABCD 的面积为12,ABE △是等边三角形,点E 在正方形ABCD 内,在对角线AC 上有一点P ,使PD PE 的和最小,求这个最小值 5、恩施州自然风光无限,特别是以“雄、奇、秀、幽、险”著称于世.著名的恩施大峡谷 (A )和世界级自然保护区星斗山(B )位于笔直的沪渝高速公路X 同侧,AB =50km ,A 、B 到直线X 的距离分别为10km 和40km ,要在沪渝高速公路旁修建一服务区P ,向A 、B 两景区运送游客.小民设计了两种方案,图1是方案一的示意图(AP 与直线X 垂直,垂足为P ),P 到A 、B 的距离之和S 1=PA +PB ,图2是方案二的示意图(点A 关于直线X 的对称点是A ′,连接BA ′交直线X 于点P ),P 到A 、B 的距离之和S 2=PA +PB . (1)求S 1、S 2,并比较它们的大小; (2)请你说明S 2=PA +PB 的值为最小; (3)拟建的恩施到张家界高速公路Y 与沪渝高速公路垂直,建立如图3所示的直角坐标系,B 到直线Y 的距离为30km ,请你在X 旁和Y 旁各修建一服务区P 、Q ,使P 、A 、 B 、Q 组成的四边形的周长最小.并求出这个最小值. B A P X 图1 C C B A P X A ′ 图2 M A D E P B C
