非线性时间序列 第五章

127

第五章 非参数密度估计

5.1 引论

在非参数函数估计中，平滑是最基本的方法之一，通常被称为一维散点图平滑和密度估计. 在多维框架下，平滑是建立非参数估计的有用的构建模块. 平滑首先从时间序列中的谱密度估计中产生. 在对Bartlett （1946）的富有创新的文章的讨论中，Henry E. Daniels 指出，谱密度估计的一个可能的修正可以通过平滑周期图来实现. 然后，这一问题的理论和方法由Bartlett （1948，1950）系统地发展起来. 这样，早在半个世纪以前，平滑方法便已是时间序列分析的一个重要部分.

平滑问题在时间序列分析的各个方面经常出现. 平滑方法为概述一个给定的时间序列的边缘分布提供了有用的图解工具. 它们还可用于估计和消除慢变时间趋势. 这就产生了时域平滑. 研究一个时间序列和它的延迟序列联系的需要产生了状态域平滑. 这些方法能够容易地推广到估计一个时间序列的条件方差（波动性）. 为了检验周期形式和别的特征，比如时间序列的功率谱，平滑方法常常用来估计谱密度. 在拟合一个时间序列数据时，一个重要的问题是拟合模型的残差的行为是否像白噪声. 对这类非参数拟合优度检验，非参数函数估计提供了有用的工具. 这个内容将本章和下一章中讨论.

最简单的非参数函数估计问题可能是密度估计. 这种简单结构对理解非参数建模和推断中更复杂的问题提供了有用的工具. 这就是我们在本章中讨论非参数密度估计的目的.

5.2 核密度估计

国库券收益的分布是什么？直方图是回答这类问题的经典的方法. 核密度估计是对直方图方法的改善. 它用来验证数据集合的所有分布特征. 这些包括密度峰和谷的数目和位置以及密度的对称性. 它是揭示非参数函数估计基本特性的最简单的工具. 对密度估计和它的应用的全面的讨论在Devroye 和Gy ?rfi （1985），Silverman （1986）以及Scott （1992）给出.

给定T 个数据点1,,T X X ，通过对每一个观测点乘以量1/T 可得到这些数据点的

经验分布函数：

1

1()()T

t t F x I X x T ==≤∑.

这个累积分布函数是非降的，对验证给定分布的全面的结构不是太有用的. 当人们论及分布时，其脑海里常常有密度函数. 然而，经验分布函数的密度是不存在的. 对经验分布函

128

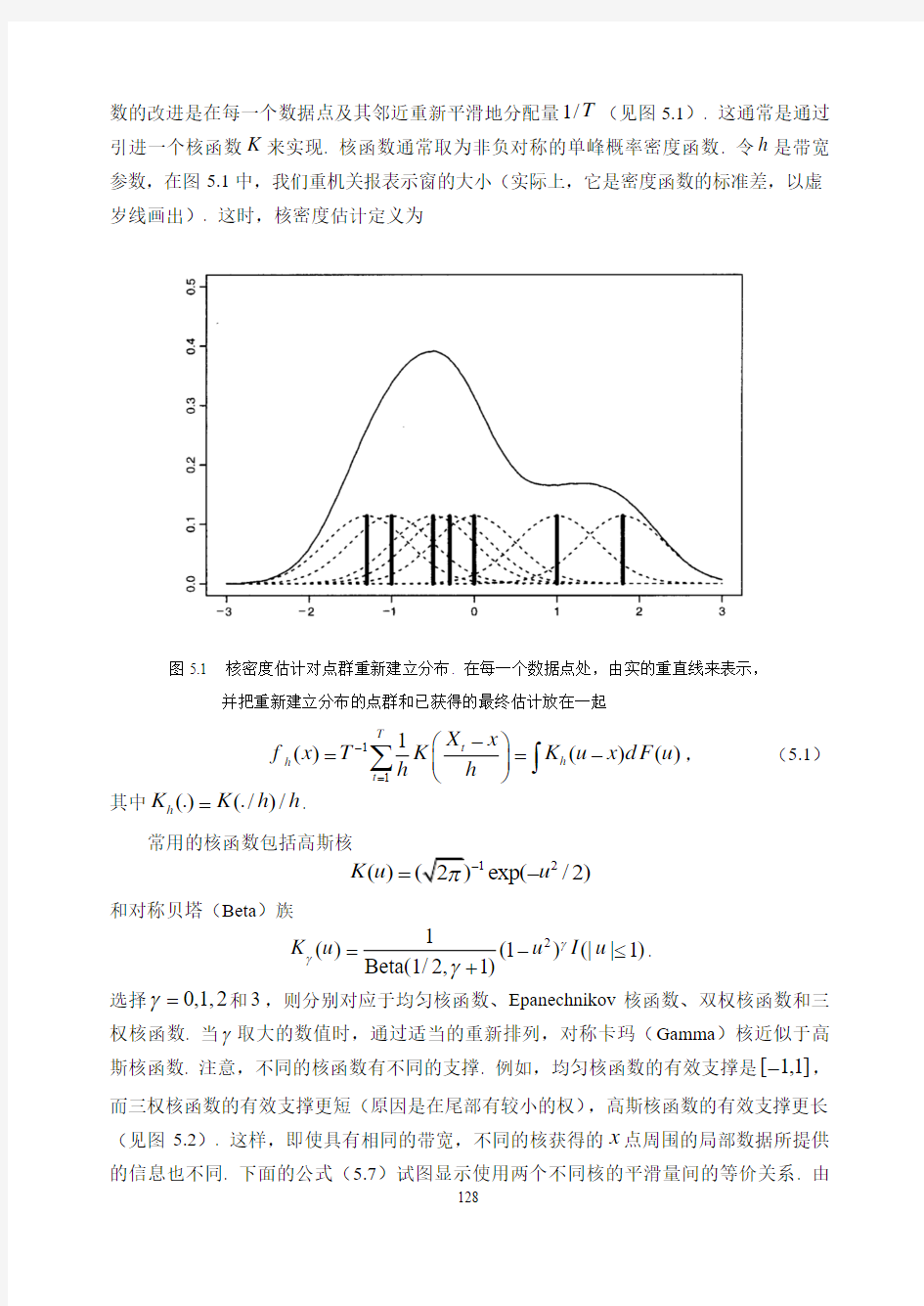
数的改进是在每一个数据点及其邻近重新平滑地分配量1/T （见图5.1）. 这通常是通过引进一个核函数K 来实现. 核函数通常取为非负对称的单峰概率密度函数. 令h 是带宽参数，在图5.1中，我们重机关报表示窗的大小（实际上，它是密度函数的标准差，以虚岁线画出）. 这时，核密度估计定义为

图5.1 核密度估计对点群重新建立分布. 在每一个数据点处，由实的重直线来表示，

并把重新建立分布的点群和已获得的最终估计放在一起

1

1

1()()()T

t h h t X x f x T

K K u x d F u h h -=-??==- ???∑?， （5.1） 其中()(/)/h K K h h ?=?.

常用的核函数包括高斯核

12()exp(/2)K u u -=-

和对称贝塔（Beta ）族

21

()(1)(||1)Beta(1/2,1)

K u u I u γγγ=

-≤+.

选择0,1,2γ=和3，则分别对应于均匀核函数、Epanechnikov 核函数、双权核函数和三权核函数. 当γ取大的数值时，通过适当的重新排列，对称卡玛（Gamma ）核近似于高斯核函数. 注意，不同的核函数有不同的支撑. 例如，均匀核函数的有效支撑是[1,1]-，而三权核函数的有效支撑更短（原因是在尾部有较小的权），高斯核函数的有效支撑更长（见图5.2）. 这样，即使具有相同的带宽，不同的核获得的x 点周围的局部数据所提供的信息也不同. 下面的公式（5.7）试图显示使用两个不同核的平滑量间的等价关系.

由

129

Marron 和Nolan （1988）引入的经典核的概念减弱了这个问题.

图5.2 常用的核函数. 它们被标准化使得最大高度为1，以便于表示. 粗曲线是高斯核， 它比别的核有更长的有效支撑

为了使用核密度估计，人们需要选择核函数和带宽. 众所周知，对核密度估计，无论是从经验的角度，还是从理论的角度，核函数的选择都不是太重要的. 只要它们是对称和单峰的，当带宽h 是最优选择时，所得核密度估计的表现几乎都相同. 见§5.4中的表5.1. 这样，正如图5.3所示，在一个大的带宽h 下，得到一个过度平滑的估计，遗漏一些可能的细节，比如多峰情形和所得的估计密度低于峰值. 换句话说，使用大的带宽可能导致估计产生大的偏差. 当使用较小的带宽时，没有太多的局部数据点被使用，从而减少了估计的方差，其结果可能产生一条摆动的曲线. 为了得到满意的结果，我们需要反复试验. 带宽的数据驱动选择可以帮助我们确定最优的平滑量（更多的细节参阅§5.4）.

如图5.3所示，描绘了用带宽分别为0.61/3,0.61h =和30.61?的高斯核所得的3个月期国库券收益的分布估计. S-Plus 函数“density ”被用来计算核密度估计. 带宽

0.61h =通过下面（5.9）所述的标准参考的带宽来选择，显然，小的带宽导致平滑不足

的估计，产生一个具有不自然摆动样式的密度函数，而大的带宽则给出一条过度平滑的曲线，使得原来分布好的结构变得模糊. 虽然所得的曲线稍微出现过度平滑，但简单的供参考带宽0.61h =通常被认为是对h 的一个初步选择.

正如在图5.3中所看到的那样，利率的分布有长的右尾. 分布的中位数和众数大约是5.34%，而均值是5.97%. 在1980年代初，利率高达

15%.

130

图5.3 用带宽分别为0.61/3h =（短划线），0.61（实线）和30.61?（长划线）的高斯核所得的3个 月期国库券收益（按百分率）密度估计. 因子3是有意用来解释平滑不足和平滑过度的影响

5.3 加窗和白化

如果数据1{}T t t X -是来自具有边缘密度f 的平稳过程的实现，则通过变量变换，我们有

()()

()()

h t h E f x EK X x K u f u hx du +∞-∞

=-=+?

. （5.2） 这样，估计的偏度()()h E f x f x -不依赖于数据的相依结构，就如同于独立样本那样. 然而，估计的方差却受数据相依结构的影响.

为了获得得进一步的认识，我们考虑K 有有界支撑[1,1]-的情形. 这时，核密度估计（5.1）仅用了在局部窗x h ±内的局部数据点：

1

()

1

()()J

h t j h j f x T

K X

x -==-∑，

其中()t j 是落在x h ±中的第j 个数据点，J 是局部数据点的总数. 当原始序列中的数据高相关时，在x 周围的局部窗内，新序列(){,1,,}j t j Y X j J ==的相依性可能相对很弱.

这归因于这样的事实，即时间序列{(),1,

,}t j j J =相对于小的带宽h 来说不得相隔很

远. 作为一个图例，参见5.4. 加拿大山猫数据的一步延迟自相关比局部窗2.70.2±内的那些数据相对很强. 实际上，局部数据看起来就像是来自一个独立样本的数据. 因此，当某种混合条件被使用时，人们将期望核密度估计的渐近方差如同独立观测情形那样. 这种直觉知识由Hart （1996）给予阐明. 由于在状态域中通过局部加窗所得的白化性质，使得混合过程的核密度估计所表现的行为非常像独立样本的情形. 因此，

对独立样本的所有方

131

法都可推广到混合平稳过程. 在§5.6中，我们将给出一些基本理论. 相依结构对核密度估计的影响最近由Claeskens 和Hall （2002）作了详尽的研究.

图 5.4 （a ）加拿大山猫数据的延迟为1的散点图；（b ）落在局部领域2.70.2±中那些数据

{,1,,}j Y j J =的延迟为1的散点图，它是点()t j X 相对于(1)t j X -画出的，用数()t j 表示点

(1)()(,)t j t j X X -；（c ）用带宽0.14h =（实线）和0.23（虚线）所得的加拿大山猫数据的密度估计

5.4 带宽选择

当数据{}t X 是来自平稳过程的实现时，由下面的定理5.1，对f 支撑的内点x ，核密度估计的均方误差（MSE ）能够表示为

2MSE(){()()}h x E f x f x ≡-

{}

2

2

2

421

()

(){()}()4

f x u K u du

f x h K u du Th

+∞+∞-∞

-∞

''≈

+?

?

（5.3）

这里及以后，“≈”意味着两边有相同的主项. 这是一个逐点度量.

通过使用平均平方积

132

分误差（MISE ），可获得全局度量如下：

2MISE {()()}h E f x f x dx +∞-∞

≡-?

{}

22242

11(){()}()4u K u du f x dxh K u du Th

+∞+∞+∞-∞-∞-∞''≈+???. （5.4） 调整带宽参数h 来极小公渐近MISE ，得到一个带宽，称为渐近最优带宽，或简单地，最

优带宽，它由下式给出

2/51/

o p t 2()||||h K f

T α--

''=，

（5.5） 其中222||||()g g u du +∞-∞

=

?

是2L 范数，22()()K u K u du μ+∞-∞

=?

是K 的方差，

2/52/522()()||||K K K αμ-=

是已知常数. 相对于这个渐近最优带宽，最优的MISE 是

2/54/5

25()||()||4

K f x T β-''， （5.6） 其中

2/58/522()()||||K K K βμ=.

由（5.5）得到，对两个不同的核函数1K 和2K ，最优带宽满足

1opt 1opt 22()

()()()

K h K h K K αα=

，

其中opt 1()h K 和opt 2()h K 分别是与核函数1K 和2K 相对应的最优带宽. 下面的表5.1对几个常用的核函数列出了这些有用的函数的值. 从该表可见，对使用最优带宽核函数的不同选择，它们执行的结果几乎完全相同（见表中()K β所在的行）. 因此，核2K 用带宽2h 的执行的结果几乎和核1K 用如下带宽执行的结果相同

1122()

()

K h h K αα=

. （5.7）

这就是经典核概念的思想（Marron 和Nolan 1988）. 它允许两个研究者比较平滑的量，即使他们用的是两个不同的核.

表5.1 一些与核函数相关的有用的常数

泛函

高斯 均匀 Epanechnikov 双权 三权 2()K μ

1 0.3333 0.2000 0.1429 0.1111 22||||K

0.2821 0.5000 0.0600 0.7143 0.8159 ()K α 0.7764 1.3501 1.7188 2.0362 2.3122 ()K β

0.3633

0.3701

0.3491

0.3508

0.3529

最优带宽（5.5）不是直接可用的，这是因为它依赖于未知的参数2||||f ''. 当f 是具

133

有标准差σ的高斯密度时，人们能够容易地由（5.5）推导出

1/51/5

o p t ,(/3)()T h K T

ασ-=. （5.8） 正态参考带宽选择（例如见Bickel 和Doksum, 1977及Silverman （1986））是通过在（5.8）中用样本标准差s 代替未知参数σ来获得得的. 特别地，在数值地计算了常数()K α后，我们有下列正态参考带宽选择

1/5o p t ,1/5

1.06,

2.34,E p a n e c h n i k o v n sT

h sT

--??=???对高斯核,对核. （5.9） 通过在高斯密度周围对f 作Edgeworth 展开可获得得一个改良的带宽选择. 这个带

宽选择由Hjort 和Jones （1996b ）提供，由下式给出

1/5

*22opt,opt,43435

35385148321024T

T h

h γγγ-??=+++ ?

??

，

其中3γ和4γ分别是样本斜度和峰度，其定义为

1

3331(1)

()/T

t

t T X

X s γ-==--∑，

14441

(1)()/3T

t t T X X x γ-==---∑.

正态参考宽选择只是一个简单的经验方法. 当数据接近高斯分布时，它是一个好的选择，而且在许多应用中，常常是适当的. 然而，当真实分布是非对称或多峰时，它可能导致过度平滑. 在此情形，人们或者主观地调整带宽，或者用更精细的带宽选择方法来选择所要的带宽. 人们带可以先对数据做变换，使其分布接近于正态，然后，用正态参考带宽选择估计密度，再应用逆变换获得原始数据的密度估计. 这个方法被称为变换法. 见下面（5.12）. 对由图5.3说明的非对称分布，正态参考带宽选择给出径微的过度平滑估计. 对图5.4（c ）中的双峰数据，正态参考带宽选择是0.23h =，这导致一个过度平滑估计. 因此，址到获得一个适当的估计（图5.4中的实线）时，我们才减少平滑量.

有为数不多的几个重要的带宽选择方法，诸如cross-validation （CV ）和plug-in 带宽选择. 理论上合理、经验上执行良好的概念上简单的方法是plug-in 方法. 该方法依赖于

在（5.5）中寻找泛函2

2||||f ''的一个估计. 这个方法的一个好的补充由Sheather 和Jones

（1991）提出. 带宽选择进展的一个总结可在Jones, Marron 和Sheather （1996）中找到. 还可参阅§6.3.5.

5.5 边界修正

在许多情况中，已知密度f 有一个有界的支撑. 例如，利率不能小于零. 一个自然的假定是利率有支撑[0,)∞. 事实上，过去的四十多年中，最低短期利率是2.11%，而最高利率是16.76%. 因此，假定短期利率有支撑区间[2%，17%]不是没有道理的. 然而，因为

134

核密度估计在观测数据点的周围平滑地散布点团，所以靠近支撑边界的一些点会分布在密度支撑之外（见图5.3）. 故而核密度估计是在边界范围里估计密度. 如在图5.3所见，对大的带宽和对密度有高峰的左边界，问题更严重. 因此，做一些矫正是必需的. 为了获得一些进一步的知识，不失一般性，我们假定密度函数f 有有界的支撑[0,1]，并在左边界处理密度估计. 为简单起见，假设K 有支撑[1,1]-. 则点(01)x ch c =≤<是左边界点. 易见，当0h →时，

()()()(0)()h c

c

E f ch f ch hu K u du f

K u du o ∞∞

--=

+=+?

?

. （5.10）

特别地，对对称核，(0)(0)/2(1)h E f f o =+. 另一方面，在左边界点，所得密度估计仅估计了真实密度的一半. 为了通过图例说明此点，我们从标准指数分布()e x p ()(0f x x I x =-≥抽取容量为200的随机样本，从（5.9）获得带宽0.344，用具有该带宽的高斯构成核密度估计，对密度进行估计. 明显地，在点0x =处的估计仅是真实值的一半.

有几个方法可以用来处理边界点的密度估计. 可能的方法包括边界核、反射、变换和局部多项式拟合. 这里我们介绍两个简单的方法：反射和变换方法. 反射方法是基于反射数据{,1,,}t X t T -=和原始数据{,1,,}t X t T =来构造核密

度估计. 所得的估计为

*

111()()(),0T T

h t h t h t t f x K X x K X x x T ==??

=-+--≥????

∑∑. （5.11）

注意，当x 偏离边界时，（5.11）中的第二项实际上是可被忽略的. 因此，仅需要修正边界附近的估计. 见Schuster （1985）及Hall 和Wehrly （1991）. 这个估计是基于合成数据

{,1,,}t X t T ±=的两次核密度估计，一般地，如果左边界点是0x （代替0），则合成数据是

0{(),,1,

,}t t X x X t T --=，

所得的估计为

*

00111()()(),T T

h t h t h t t f x K X x K x X x x x T ==??

=-+--≥????

∑∑.

图5.5给出模拟数据，图5.6（a ）描绘了基于这个方法给出的估计. 所用的核为高斯核，带宽为0.344.

另一个简单的方法是先对数据做如下变换

(),1,

,i t Y g X i n ==，

其中g 是从-∞到∞的单调增函数. 现在，应用核密度估计（5.1）到这个变换数据集，获得估计()Y f y ，再应用逆变换得到所要的X 的密度. 这就导致如下结果

1

1()()(())()(()())T

h t

X Y t f x g x f g x g x T K g x g X -=''==-∑

， （5.12）

135

图5.5 来自标准指数分布的容量为200n

=随机样本的核密度估计. 实线——真实曲线；

虚线——估计的曲线. 边界影响可被容易地看到

这里()g '?是()g ?的导函数. 图5.6（b ）用对图5.5中的数据使用对数变换来说明这一想法. 我们首先应用核密度估计变换后的数据{log(),1,

,200}t X t -=，以获得()Y f y .

对变换数据使用高斯核，由高斯参考带宽选择得到0.344h =. 因此，所得密度估计是()(log )/X Y f x f x x =，

或(exp())exp()()X Y f x x f x =-. 这样，相对于exp()()Y x f x -画exp()x ，可得所要的密度估计. 在点0x =处的密度对应变换数据密度的尾部，注意到

log(0)=-∞，由于在尾部缺乏数据的原因，通常密度不能被很好地估计. 除了在这一点

处，变换方法有很好的表现.

图5.6 （a ）用反射方法所得的核密度估计；（b ）用变换方法所得的核密度估计. 实线——真实曲线； 虚线——估计的曲线

136

5.6 渐近结果*

我们现在给出当样本容量T →∞时，核密度估计的渐近偏度和方差. 必然地，带宽h 要依赖于T ，而且趋于零. 用在这里的想法能够推广到更复杂的结构，比如非参数回归. 我们从一个简单的引理开始，它对导出渐近偏度是有用的.

引理 5.1 令f 在其支撑的内点x 有连续的有界p 阶导数. 假定函数K 满足

|()|p u K u du +∞-∞

<∞?

. 则当0h →，我们有

()0

()()()()/!()p

i i p i i f x hu K u du K f x h i o h μ+∞-∞

=+=+∑?

，

其中()()i i K u K u du μ+∞-∞

=

?

.

证明 令()0()()()()/!p i i i i D f x hu K u du K f x h i μ+∞=-∞

=

+-∑?

，则

()0

{()()()/!}()p

i i i D f x hu f x hu i K u du +∞-∞

==+-∑?

.

由泰勒展开可得，

()(){()()}()!

p p p p

h D f x T f x u K u du p ξ+∞-∞=+-?， 其中T ξ介于0和hu 之间. 勒贝格控制收敛定理的简单应用可得

/0,0p D h h →→.

这就完成了证明.

注意，当核函数K 有有界支撑时，以上积分取值范围仅是x 的一个邻域. 因此，只需假定密度f 在点x 处有连续的p 阶导数. 鉴于这个原因，为简单的缘故，常假定K 有有界支撑. 去掉这个假定将以冗长的论证作为代价. 特别地，高斯核被允许作为核函数. 使用以上引理和（5.2），对满足下式的核函数

()1,

()0K u du uK u du +∞+∞-∞

-∞

==?

?

，

在f 有连续的二阶导数的条件下，我们即得核密度估计的偏倚为

222()

()()2

K f x h o h μ''+.

如果f 有更高阶的导数，通过要求以下条件，可得偏倚的阶为()p O h

0()1,()

0,1,,1j K K j p μμ===-， （5.13）

但是，所得结论通常对实际的样本大小不是本质的. 满足（5.13）的核称为p 阶核. 当

2p >时，由于2()0K μ=，K 不能再是非负的.

现在，我们返回到计算方差分量. 为此，我们假定过程{}t X 是有α混合系数()k α的

137

平稳过程. 进一步，令(,)g x y l 是1X 和1X +l 的联合密度.

定理 5.1 令{}t X 是一个具有混合系数|()|C βα-≤l l 的α混合过程，其中

0,2C β>>. 进一步假定(,)||||sup (,)x y g g x y ∞=l l 是有界的. 假设K 是具有有界支撑

的有界核函数，满足1()0,0K h μ=→，进而Th →∞. 如果f 在其支撑的内点x 处有连续的二阶导数，则有

222()

()()()()2

h K E f x f x f x h o h μ''=+

+

和

22

()1

Var{()}||||()h f x f x K o Th Th

=

+. 证明 由引理5.1直接得到偏度的表达式. 这样，仅需导出方差项的渐近表达式. 令

()t h t Z K X x =-. 则由{}t X 的平稳性，我们有

1

1111

12Var(())Var()(1/)Cov(,).T l h f x Z T Z Z T T -+==+-∑l l

注意，1()(1)h EZ E f x O ==. 由变量变换和引理5.1. 可得

2211()()()h t Var Z EK X x EZ =--

1

221()()()h K u f x hu dx EZ +∞--∞

=+-?

1

2

1

2()||||()h f x K o h --=+. 于是，我们仅需证明

1

11

1

1

|Cov(,)|()T Z Z o h --+==∑l l

. （5.14）

由Billingsley 不等式[命题2.5之（ii ）]，我们有

2

21111|Cov(,)|4()||||||||4()||||/Z Z Z Z K h αα+∞+∞∞≤≤l l l l . （5.15）

另一方面，

211111|Cov(,)||()|Z Z EZ Z EZ ++=-l l

21()()(,)()h h K u x K v x g u v dudv EZ +∞+∞-∞

-∞

≤

--+??

l

2

1||||()g EZ ∞≤+l . （5.16）

因此，协方差有常数C 为界.

我们现在验证（5.14）. 令T d →∞是一个整数序列. 则由（5.16）得

11

1

1

|Cov(,)|T d T Z Z Cd -+=≤∑l l

.

由（5.15）和混合系数的假定，对某个常数D ，我们有

138

1

21

21

1

|Cov(,)|/(/)T

T

T T d d Z Z D h O d h ββ-∞

--++==≤=∑∑l l

l l ，

取2/T d h β-=，对2β>，我们有

1

2/11

1

|Cov(,)|()(1/)T Z Z O h o h β

--+===∑l l . 因此，获得得（5.14）. 这就完成了证明.

逐点均方误差可分解成如下的偏度和方差表示：

2MSE(){()()}h x E f x f x =-

2{()()}Var{()}h h E f x f x f x =-+.

由定理5.1，MSE 的逼近由（5.3）给出. 相对于h ，极小化（5.3）的右边，在()0f x ''≠的条件下，得到渐近逐点最优带宽

2/51/51/5()(){()}()opt h x K f x f x T α--''=.

最小（理想）风险，即MSE ()x 的主阶逼近的最小值，由下式给出

2/54/54/5

5()()()4

K f x f x T β-''， （5.17） 其中()K β在（5.6）中给出. 类似地，极小化（5.4）的右边得到最优带宽（5.5）和（5.6）中最小的（理想）MISE. 因此，通过开方，核密度估计的收敛速度可达到2/5

T

-. 对某个

0c >，只要1/5h cT -=，就可达到这个速度. 按照Farrell （1972），Hasminskii （1978）

和Stone （1980），在具有二阶有界导数的函数类中，这是估计密度函数可能达到的最快速度.

核密度估计的渐近正态性仍然成立. 我们不加证明地叙述这个定理，它非常类似于定理6.3的证明. 我们将它留给读者作为练习. 如果混合条件()||,2c β

αβ-≤>l l ，被加

强，则条件5/3

Th

→∞能够被放松.

定理5.2 在定理5.1的条件下，如果5/3

Th →∞，则我们有

222

22()

()()()()}N(0,()||||)2

D h K f x f x f x h o h f x K μ''--

+??→.

核密度估计具有许多好的性质. 可参阅Bosq （1988）的第二章. 我们证明一个类似于Bosq （1988）定理2.2的结果，但显著地放松了对几何混合条件的要求.

定理5.3 假定过程{}t X 的混合系数满足(),5/2c β

αβ-≤>l l . 设t X 的密度f 在

区间[,]a b 上是有界的，K 满足Lipschitz 条件. 则

1/2

[,]log sup |()()|P h h x a b T f x E f x O Th -∈????

??-=?? ???????

，

其中h 以下列方式0→，

139

2525(21)/4(log )T h T βββ-+-+→∞.

作为定理 5.3的一个推论，当过程是几何混合时，即()c αρ

c ρ>∈，对任意的(0,1)γ∈和0,

d h dT γ->=，定理5.3成立. 定理5.3 一致地控制着核密度估计的随机误差. 偏度项()()h E f x f x -是确定性的，且由引理5.1，容易得到它的一致有界性. 它有阶2()O h . 通过选择1/5((log /))h O T T =，当()c βα-≤l l ，其中15/4β>，得到

[,]

[,]

[,]

sup |()()|sup |()()|sup |()()|h h h h x a b x a b x a b f x f x E f x f x f x E f x ∈∈∈-≤-+-

2/5{(log /)}P O T T =. 按照Hasminskii （1978），这个速度是最优的.

一致收敛更精确的描述由Bickel 和Rosenblatt （1973）给出. 他们对独立样本导出了如下标准化统计量的渐近分布

21/2201

sup[()||||/()]

(()())T h h x M f x K Th f x E f x -≤≤=-. 我们期望在一定的混合条件下，结论对平稳过程还成立. 这里使用区间[0,1]是为了方便.

f 的支撑可以被任意区间所代替. 我们要求密度f 在[0,1]上是连续的和正的，而且

1/2()/()f x f x '和()f x ''在[0,1]上是有界的. 假定K 是有界的，且关于0点对称. 此外，K 或者在区间[,]A A -外为零，且在[,]A A -上绝对连续，并有导数K '，或者在(,)

-∞∞绝对连续使得22(),

()K K μμ'和2||||K '是有限的.

定理 5.4 在以上条件下，如果1,

,T X X 是独立同分布的，h cT δ-=，其中

01/2δ<<，0c >，如果22

2()()/||||0c K K A K =>，则令

1/21/21/2(2log )(2log ){log ()/0.5loglog }T d h h c K h π-=-+--，

否则，令

21/2

1/2

2

22

||||(2log )

(2log )

log

4||||T K d h h K π-'=-+-. 我们有

{}1/2(2log )()exp(2exp())T T P h M d x x --<→--.

定理5.4的一个推论是1/2

{(log )}T p M O h =-. 由此得到

1/201

sup{()()}[{(log )/()}]P h h x f x E f x O h Th ≤≤-=-，

即与定理5.3给出的阶相同. 定理5.4的一个应用是对一切的{(),[0,1]}f x x ∈，构造联合置信区间. 实际上，由定理5.4，相对于逼近概率1α-，

1/21

(2log )log{log(1)}(,)2

T T M d h c h αα-≤----≡.

以上表达式等价于

140

21/2

2

()()(,)[()]||||/(),[0,1]h h E f x f x c h f x K Th x α∈±?∈. 用定理5.1得到，2()()()h E f x f x O h =+. 把它代入上面最后表达式，并用估计来代替

()f x ，如果1/5{(log )}h o T T -=，则我们得到一个逼近水平为(1)α-的置信区间：

21/22()()(,)[(||||/())],[0,1]h h f x f x c h f x K Th x α∈±?∈.

最后，我们将对最优核作一些注释. 关于核函数选择的最优理论能够在Gasser, Müller 和Mammitzsch （1985）及Müller （1991，1993）中找到. 理想的逐点MSE （5.17）和理想的MISE （5.6）通过（5.6）中给出的()K β而依赖于K . 定理 5.5表明，最优核是Epanechnikov 核. 对核密度估计来说，这个结果归功于Epanechnikov （1969）. 但是，这个结果早已出现在稳健回归估计的文献中（见Lehmann1983第384页和那里的文献）. 这个核已被Bochener （1936）在傅里叶变换和Parzen （1961）在谱密度估计中用作收敛因子. 对这个已知的最优核，它能够容易地被计算. 对其他常用的核，其()K β的值接近于最优核的值. 见表5.1中()K β所在行.

定理5.5 使()K β达到极小的非负概率密度函数K 是Epanechnikov 核的一个尺度改变：

22opt 3

()(1/)4K u u a a

+=

-，对任意的0.a > 证明 首先，我们注意到，对任意的0h >，()()h K K ββ=. 令0K 是Epanechnikov

核. 对任意别的非负K ，如果必要，通过变换尺度，我们假定220()()K K μμ=. 这样，我们仅需证明0||||||||K K ≤. 令0K K δ=-. 则

2()0,

()0u du u u du δδ+∞+∞-∞

-∞

==?

?

.

并蕴涵了

2(1)()0u u du δ+∞-∞

-=?.

由此式和0K 有支撑[1,1]-的事实，我们有

20||1()()()(1)u u K u du u u du δδ+∞≤-∞

=-?

?

2||1

()(1)u u u du δ>=--?

2||1

()(1)u K u u du >=

-?

.

由于K 是非负的，故上面最后一项也是非负的. 因此，

22200()()2()()()K u du K u du K u u du u du δδ+∞+∞+∞+∞-∞

-∞

-∞

-∞

=++???

?

20()K u du +∞-∞

≥?

，

这就证明了0K 是最优核.

141

5.7 补充——定理5.3的证明

在这一节中，我们都用C 表示一般常数，在同一表达中是可变的.

我们首先把在区间[,]a b 上的上确界问题转变为在区间上的点格的极大化问题. 为此目的，我们把区间[,]a b 分割成N 个长度相等的子区间{}j I . 令{}j x 是j I 的中心. 由于

K 满足Lipschitz 条件，我们概率为1地有

1

1

1

|()()||()()|||T

h

t

h

t

h h t f x f x T

K x X K x X Ch

x x --='''-≤---≤-∑.

由此得到

1|()()||()()|||h h h h E f x E f x E f x f x Ch x x -'''-≤-≤-.

由上述不等式，我们有

1sup |()()||()()|()j

j j h h h h x I f x E f x f x E f x C Nh -∈-≤-+.

于是，

11[,]

sup |()()|max |()()|()j j h h h h j N

x a b f x E f x f x E f x C Nh -≤≤∈-≤-+.

取1/2(/)N T h =，我们得到

1/2

1[,]

s u p |()()|

m a x

|()()|()j j h h h h j N

x a b f x E f x f x E f x C Th -≤≤∈-≤-+. （5.18）

现在，我们来估()()h h f x E f x -的尾部概率的界. 令()()t h t h t Y K x X EK x X =---，则1||||t Y Ch -∞<. 由指数不等式（定理2.18）对任意的0ε>和每一个整数[1,/2]q T ∈，我们有

22{|()()|}4exp 8()h h q P f x E f x v q εε??

->≤- ???

1/2

42212C T q h q αε??????

++?? ?????????

， （5.19）

其中

222()2()//(2)v q q p C h σε=+

这里[/(2)]p T q =和

21(1)1021

()max Var{}jp j p j q q Y Y σ+++≤≤-=+

+.

由定理5.1，21

()q Cph σ-≤. 这样，取q T ε=，

2111()()v q C ph C h C h εε---≤+≤.

上式和（5.19）蕴涵了

21/20.

{|()()|}

4e x p ()h h P f x E f x CTh CTh βεεε

-+->≤-+. （5.20）

142

我们现在来证明定理. 对充分大的a ，取2log /()a T CTh ε=，（5.20）的右边被下式所界

/20.75/20.75/20.254(log )a T CT h T βββ--+--++.

因此，

1(max |()()|)j j h h j N

P f x E f x ε≤≤->

/20.75/20.75/20.25{4(log )}a N T T h T βββ--+--+≤+

(25)/45/2(21)/4(1){()(log )}o O Th h T ββ---+=+

它是趋于零的. 由此可得

1/2

1log max |()()|j j p h h j N

T f x E f X O Th ≤≤????

??-=?? ???????

， 联合（5.18）便证明了定理.

5.8 文献注释

非参数平滑的文献量是很大的，其遍布的范围包括核密度估计、非参数回归、时域平滑、谱密度估计和在别的统计估计中的应用. 实际上，大多数参数问题都有它们的非参数配对物. 大多数非参数的结果都能由独立数据推广到相依数据. 在过去的三十年中，非参数函数估计是最活跃的领域之一. 许多新的方法已经被发明，许多新的现象被公诸于众. 不可能对这个庞大领域给出一个全面的评述. 更确切地，我们仅从这个活跃的领域中抽取一小部分参考文献. 它们甚至也不能代表这个领域的许多重要贡献. 在这个文献注释中，列在§1.7的有关非参数函数估计的著作对独立数据给出了大量详细的讨论. 相关的文献能够在第6章和第7章中找到.

对相依数据非参数函数估计的广泛而详尽的处理方法能够在Gy ?rfi, H?rdle, Sarda 和Vieu （1990），Rosenblatt （1991）和Bosq （1998）等专著中找到. 它们把重点主要放在单变量非参数平滑的理论发展上. 对独立数据的密度估计

关于核密度估计有大量的文献. 大多数研究工作的重点是在独立随机样本方面. 核密度估计的基本思想出现在Fix 和Hodges （1951）的技术报告中. 渐近均方误差和渐近平均平方积分误差被Rosenblatt （1956），Parzen （1962）及Watson 和Leadbetter （1963）所研究. 关于核密度估计有许多著作，包括Devroye 和Gy ?rfi （1985），Silverman （1986），Scott （1992），Wand 和Jones （1995）等. 核密度估计的各种性质能够在Prakasa Rao （1983）和Nadaraya （1989）的著作中发现.

核密度估计的性质已被广泛的研究. 为减小偏度而使用高阶核的思想可追溯到Parzen （1962）和Bartlett （1963）. Davis （1975）对超平滑密度用正弦核获得了一个接近

1/2

n相合估计. 最优核理论由Gasser, Müller和Mammitzsch（1985），Granovsky和Müller （1991），Müller（1993）等做了广泛的发展.

密度估计的最优收敛速度由Farrell（1972）研究. Hasminskii（1979）和Stone（1980，1982）做了进一步的研究. Ibragimov和Hasminskii（1984），Donoho和Liu（1991a,b），Fan（1993b），Low（1993）等推广到极小极大研究的范围. Sobolov空间上更深刻的渐近极小极大风险由Pinsker（1980），Efromovich和Pinsker（1982），Nussbaum（1985）等建立. 这些最优收敛速度依赖于未知函数的平滑程度. 自适应方法已被构造使其对每一个给定的函数类都几乎是最优的. 例如，见Efromovich（1985），Lepski（1991），Donoho 和Johnstone（1995，96，98），Donoho，Johnstone，Kerkyacharian和Picard（1995），Brown 和Low（1996）及Tsybakov（1998）等. 基于罚最小二乘的自适应估计能够在Barron，Birgé和Massart（1999）及Antoniadis和Fan（2001）中找到. 非线性泛函的极小极大的结果可以Bickel和Ritov（1988），Fan（1991），Birgé和Massart（1995）等中找到.

有许多核密度估计的变种和修正. 密度的局部似然估计可以在Loader（1996）及Hjort 和Jones（1996）中找到. 参数控制的非参数密度和回归估计由Hjort和Glad（1995），Efron 和Tibshirani（1996），Glad（1998）等提出. 核密度估计的变换方法被Wand，Marron和Ruppert（1991），Yang和Marron（1999）等研究. 使用可变带宽的思想能够在Breiman，Meisel和Purcell（1977），Abramson（1982），Hall和Marron（1988），Hall（1990）以及其中所列的别的文献中找到. 文献中许多文章对减小边界偏度提供了可能的入门知识. 边界核方法由Gasser和Müller（1979），Gasser，Müller和Mammitzsch（1985）引进并进行研究. Schucany和Sommers（1977），Rice（1984）建议使用具有不同带宽的两个核估计的线性组合来减小偏度. 对平滑样条的边界修正方法被Rice和Rosenblatt（1981），Eubank和Speckman（1991）及其文中所列文献研究.

对相依数据的密度估计

相依数据核密度估计的早期文献是Roussas（1967，1969）和Rosenblatt（1970），他们建立了局部渐近正态性. 估计转移概率密度的强相合性由Yakowitz（1979）建立. Ahmad （1979，1982）使用正交理论方法研究了 混合过程密度估计的相合性质. Masry（1983）对连续时过程离散时估计的偏度和协方差导出了渐近表达式. 还可见Robinson（1983）. 对时间序列残差的密度估计由Robinson（1987）给出. Cheng和Robinson（1991）对强相依数据的密度估计建立了各种性质. 一致强相合速度由Pham和Tran（1991），Cai和Roussas（1992）等建立. Gy?rfi和Masry（1990）证明了相依数据递推密度估计的强相合性. Kim和Cox（1995）对混合随机变量给出了关于矩的有用的界. 随机场的密度估计由Roussas（1995），Carbon，Hallin和Tran（1996），Bradley和Tran（1999）等及其所列文献给予研究. Gy?rfi和Lugosi（1992）给出了一个核密度估计不相合的有趣的例子. Adams 和Nobel（1998）研究了遍历过程的密度估计. 在核密度估计的MISE，ISE和最优带宽方面相依性的影响被Claeskens和Hall（2002）彻底研究.

143