数学人教版九年级上册二次函数的图像和性质(1)

合集下载

九年级数学上册(人教版)《二次函数y=a(x-h)^2+k的图象和性质(第1课时)》课件

(3)它们的位置是由+1、-1决定的.
思考
把抛物线y=2x2向上平移5个单位，会得到哪条抛物线？
向下平移3.4个单位呢？
y=2x2+5
y=2x2-3.4
当二次项系数小于零时和二次项系数的绝对值变化时，抛物线将发生怎样的变化？
解析：二次项系数小于零时抛物线的开口向下；二次项系数的绝对值越大开口越小，反之越大.
点坐标
(1) y=5x2
向上，y轴,（0, 0)
(2) y=-3x2 +2 向下，y轴,（0, 2)
(3) y=8x2+6 向上，y轴,（0, 6)
(4) y= -x2-4 向下，y轴,（0, - 4)
2.说出下列二次函数的开口方向、对称轴及顶点坐标 (1) y=2(x+3)2 向上, x=-3,(-3,0) (2) y=-3(x-1)2 向下, x=1,(1,0) (3) y=5(x+2)2 向上, x=-2,(-2,0) (4) y=-(x-6)2 向下, x=6,(6,0) (5) y=7(x-8)2 向上, x=8,(8,0)
y 1 x2 , y 1 x2 2, y 1 x2 2
2
2
2
观察三条抛物线的相互关系，并分别指出它们的开口方
向、对称轴及顶点.你能说出抛物线 y 1 x2 k
2
的开口方向、对称轴及顶点吗？它与抛物线
y 1 x2
2
有什么关系？
画出二次函数 y 1 x 12 , y 1 x 12 的图象，并
是___(_1__,_0__)________．
抛物线
y 1 x 12 y 1 x 12 与抛物线
2
2
y 1 x2 2

新人教版九年级上册数学22.1.4《二次函数的图象和性质(1)》教案

22.1.4二次函数y = ax2+ bx+ c的图象与性质第一课时一、教学目标（一）学习目标1. 会用描点法画二次函数y=ax2+bx+c的图象.2. 会用配方法求抛物线y=ax2+bx+c的顶点坐标、开口方向、对称轴、y随x的增减性及最大或最小值.3•经历探索二次函数y = ax2+ bx + c的图象的开口方向、对称轴和顶点坐标以及性质的过程，理解二次函数y= ax2+ bx+ c的性质.4.能运用二次函数的图象和性质解决简单的实际问题，深刻理解数学建模思想以及数形结合的思想.（二）学习重点用描点法画出二次函数y= ax2+ bx+ c的图象和通过配方确定抛物线的对称轴、顶点坐标及其性质。

（三）学习难点理解二次函数y = ax2+ bx + c（a^0）的图象和性质，会利用二次函数的图象性质解决简单的实际问题.二、教学设计（一）课前设计11•预习任务(1) 二次函数y=a(x-h)1 2+k 的顶点坐标是(hk)，对称轴是x=h ,当a>0时，开口向上，此时二次函数有最小值，当 x >h 时，y 随X 的增大而增大，当x <h 时， y 随x 的增大而减小；当a<0时，开口向下，此时二次函数有最大值，当 x <h时，y 随x 的增大而增大，当x 时，y 随x 的增大而减小.(2) 用配方法将y=ax 2+bx+c 化成y=a(x-h)2+k 的形式为 2值，当a>0时，函数y 有最小值，当a<0时，函数y 有最大值. 2.预习自测(1)抛物线y = 2x 2 — 2x -1的开口 __________ ，对称轴是 _________ 【知识点】二次函数的性质.【解题过程】解：抛物线y = 2x 2 — 2x — 1，v 2>0,二开口向上，对称轴为:b -21 — — — ・2a 2 22【思路点拨】掌握二次函数的性质，正确记忆抛物线对称轴公式是解题关键. 【答案】向上，x =丄2(2)抛物线y = x 2 — 2x + 2的顶点坐标是 _________. 【知识点】二次函数的性质.【解题过程】解：将y = x 2— 2x + 2配方得y=(x-1)2，1，顶点坐标是(1，1) 【思路点拨】将抛物线的一般式，用配方法转化为顶点式，根据顶点式的坐标特” 2 2b j 4ac —b 2 y = a lxV 2a 丿 4a4ac * .则二次函数y=ax2+bx+c的图象的顶点坐标是(-—, 2a4a 2a则h=-A，k=4ac_b )，对称轴是x=-—，当x=-A时，二次函数y=ax2+bx+c有最大(最小) 4a 2a2a点，直接写出顶点坐标.【答案】（1,1）（3）________________________________ 二次函数y = -x2+ 2x+ 1的最是.2【知识点】二次函数的最值.【解题过程】解：将y =丄x2+ 2x+ 1配方得y J（x，2）2_1 , v ->0,.••其最2 2 2小值是-1.【思路点拨】把二次函数的解析式整理成顶点式形式，然后确定出最大值.【答案】小，-1（4）二次函数y=ax2+bx+c的图象如图所示，下列结论：①4ac v b2;②a+c>b;③2a+b> 0.其中正确的有（）A.①② B .①③ C.②③ D .①②③【知识点】二次函数图象与系数的关系.【思路点拨】根据抛物线与x轴有两个交点即可判断①正确，根据x=- 1,y v0, 即可判断②错误，根据对称轴x> 1,即可判断③正确，由此可以作出判断.【解题过程】解：v抛物线与x轴有两个交点，•••△ > 0,b2- 4ac> 0,••• 4ac v b2，故①正确，v x= - 1 时，y v 0,••• a- b+c v0,• a+c v b,故②错误,•••对称轴x> 1, a v 0,• - b v 2a,• 2a+b> 0,故③正确.故选B.【答案】B(二) 课堂设计i. 知识回顾(1)二次函数y = a(x -h)2• k(a严0)的图象性质:(h)左加右减，(k)上加下减2•问题探究探究一从旧知识过渡到新知识•活动①复习配方2 2 2 2填空.(1)x +4x+9=(x+ ) + .(2)X 一5x + 8 = (x- ) +生答：(1) 2, 5; (2)-,-2 4总结规律：当二次项的系数为1时，常数项须配一次项系数一半的平方.【设计意图】复习配方，为新课作准备•活动②以旧引新1. 二次函数y = a(x—h)2+ k的图象，可以由函数y= ax2的图象先向 ________ 平移 ________单位，再向___________ 移__________ 单位得到.生答：左或右，|h，上或下，|k2. 二次函数y = a(x—h)2+ k的图象的开口方向 _______ ，对称轴是，顶点坐标是 ________ .生答：a>0，向上；a<0，向下x=h (h，k)3. 二次函数y= 2x2—6x + 21,你能很容易地说出它的图象的开口方向、对称轴和顶点坐标，并画出图象吗？1 2点拨:先将y= 2x —6x+ 21配方，再得出它的图象的开口方向、对称轴和顶点坐标，并画出图象，由此引出新课【设计意图】整合旧知，引出新课探究二用配方法求抛物线y=ax2+bx+c的顶点坐标、对称轴★ ▲ •活动①合作探究1 2例1：画函数y=?x -6x 21的图象，并指出它的开口方向、对称轴和顶点坐标.2分析：首先要用配方法将函数写成y=a(x-h) k的形式；然后，确定函数图象的开口方向、对称轴与顶点坐标；接下来，利用函数的对称性列表、描点、连线.1 2解：y=2x —6x+ 21=1(x2—12x+ 42)=1(x2—12x+ 36—36+ 42)=1(x2—12x+ 36+ 6)=1(x2—12x+ 36) + 3=*(x —6)2+ 3.画图略，所以它的开口向上，对称轴是x=6，顶点坐标是(6，3)归纳:一般式化为顶点式的思路：(1)二次项系数化为1; (2)加、减一次项系数一半的平方；(3)写成平方的形式.【设计意图】引导学生利用配方法，求抛物线的对称轴和顶点坐标，并由此作抛物线。

《二次函数的图像和性质》PPT课件人教版九年级数学

2
y=20x2+40x+20③
d=
学生以小组形式讨论，并由每组代表总结.
探究新知
【分析】认真观察以上出现的三个函数解析式，
分别说出哪些是常数、自变量和函数．
函数解析式
y=6x2
自变量
函数
x
y
n
d
x
y
这些函数自变量的最高次项都是二次的！
这些函数有什
么共同点？
探究新知
二次函数的定义
一般地，形如y=ax²+bx+c(a,b,c是常数,a≠ 0)的
总结二次
函数概念
二次函数y=ax²+bx+c
（a，b，c为常数，a≠0）
确定二次函数解
析式及自变量的
取值范围
二次函数的判别:
①含未知数的代数式为整式；
②未知数最高次数为2；
③二次项系数不为0.
人教版数学九年级上册
22.1 二次函数的图象和性质
22.1.2
二次函数y=ax2的
图象和性质
导入新知
探究新知
方法点拨
运用定义法判断一个函数是否为二次函数的
步骤：
（1）将函数解析式右边整理为含自变量的代
数式，左边是函数（因变量）的形式；
（2）判断右边含自变量的代数式是否是整式；
（3）判断自变量的最高次数是否是2；
（4）判断二次项系数是否不等于0.
巩固练习
下列函数中,哪些是二次函数？
(1) y=3(x-1)²+1（是）
（1）你们喜欢打篮球吗？
（2）你们知道投篮时，篮球运动的路线是什么
曲线？怎样计算篮球达到最高点时的高度？
素养目标

人教版九年级数学上册《二次函数y=ax2+bx+c的图像和性质》二次函数PPT(第1课时)

新知探究
课堂小结
这节课你收获了什么？还有什么疑惑？
新知探究
新知探究
新知探究
人教版数学九年级上册
二次函数y=ax²+bx+c的图象和性质
第1课时
素养目标
学习目标
1.会用配方法将一般式y＝ax2＋bx＋c化成顶点式
y=a(x−h)2+k(a≠0).(难点）
2.会熟练求出二次函数一般式y＝ax2＋bx＋c(a≠0)的
对称轴、顶点坐标.（重点）
复习巩固
【思考】
(1)你能说出函数y=2(x-1)2+3图象的开口方向、对称轴、顶点
2
＋

，
．
思路点拨：利用一次项系数的一半的平方来凑完全平方式，
可把一般式转化为顶点式.
2. 利用配方法将抛物线y＝x2＋3x－1化为顶点式，并写出
其开口方向、顶点坐标和对称轴.

解：y＝x2＋3x－1＝x2＋3x＋

－

－1＝ +
∴该抛物线开口向上，顶点坐标为 −
为直线x＝－

.

，－
的形式，并写出其开口方向、顶点坐标和对称轴.
解：y＝x2－6x－3＝x2－6x＋9－9－3＝(x－3)2－12，
∴该抛物线开口向上，顶点坐标为（3，－12），对称轴为直线x
＝3.
思路点拨：注意这里的配方法是在等号右边同“加”同“减”，
这与解一元二次方程中的配方法略有不同，不可混淆.
1. 利用配方法将抛物线y＝x2－8x化为y＝a(x－h)2＋k的形

2
－

，

人教版九年级上册数学讲义二次函数的图像与性质

A． B．
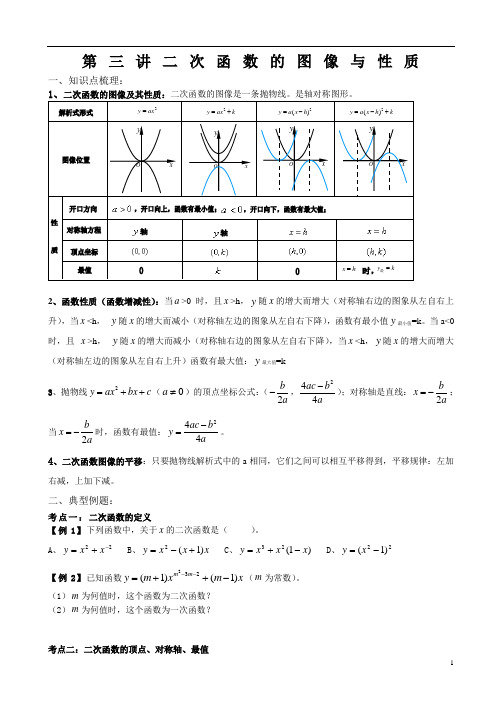
C． D．
【例2】已知二次函数y＝ax2＋bx＋1的大致图象如图所示，则函数y＝ax＋b的图
象不经过( )
A．第一象限B．第二象限C．第三象限D．第四象限
【例3】已知二次函数y＝ax2＋bx＋c(a≠0)的图象如图所示，下列结论：①abc＞0；②2a＋b＜0；③a－b＋c＜0；④a＋c＞0，其中正确结论的个数为（）．
3、抛物线（）的顶点坐标公式：（，）；对称轴是直线：；当时，函数有最值：。
4、二次函数图像的平移：只要抛物线解析式中的a相同，它们之间可以相互平移得到，平移规律：左加右减，上加下减。
二、典型例题：
考点一：二次函数的定义
【例1】下列函数中，关于的二次函数是（）。
A、 B、 C、 D、
A．y1＜y2＜y3B．y2＜y1＜y3
C．y3＜y1＜y2D．y1＜y3＜y2
【例2】已知二次函数，若自变量分别取，，，且，则对应的函数值的大小关系正确的是（）
A. B. C. D.
三、强化训练：
【夯实基ห้องสมุดไป่ตู้】
1、二次函数的图象上有两点(3，－8)和(－5，－8)，则此拋物线的对称轴是（）
【例2】已知函数（为常数）。
（1）为何值时，这个函数为二次函数？
（2）为何值时，这个函数为一次函数？
考点二：二次函数的顶点、对称轴、最值
【例1】写出下列抛物线的对称轴方程、顶点坐标及最大或最小值；
（1）（2）（3）
考点三：抛物线的平移（上加下减，左加右减）
【例1】把抛物线向左平移2个单位，再向下平移2个单位，则所得的抛物线的表达式是；
A、4个B、3个C、2个D、1个
考点五：直线与抛物线的位置关系

2022年人教版九年级数学上册第二十二章二次函数教案二次函数的图象和性质 (第1课时)

22.1 二次函数的图象和性质22.1.3 二次函数y=a（x-h）²+k的图象和性质（第1课时）一、教学目标【知识与技能】1.能画出二次函数y=ax2+k的图象；2.掌握二次函数y=ax2与y=ax2+k图象之间的联系；3.掌握二次函数y=ax2+k的图象及其性质.【过程与方法】通过画二次函数y=2x2+1与y=2x2-1的图象,感受它们与y=2x2的联系,并由此得到y=ax2与y=ax2+k的图象及性质的联系和区别.【情感态度与价值观】在通过类比的方法获取二次函数y=ax2+k的图象及其性质过程中,进一步增强学生的数形结合意识,体会通过探究获得知识的乐趣.二、课型新授课三、课时第1课时,共3课时。

四、教学重难点【教学重点】1.二次函数y=ax2与y=ax2+k的图象之间的联系；2.二次函数y=ax2+k的图象及其性质.【教学难点】二次函数y=ax2+k的性质的基本应用.五、课前准备课件、三角尺、铅笔等六、教学过程（一）导入新课这个函数的图象是如何画出来呢？（出示课件2）（二）探索新知探究一二次函数y=ax2+k图象的画法在同一直角坐标系中,画出二次函数y=x2 ,y=x2+1,y=x2-1的图象.（出示课件4）学生自主操作,画图,教师加以巡视,纠正画图过程中可能出现的失误,并引导他们进行分析,发现规律,获得感性认识.1.列表:2.描点,连线:（出示课件5）教师问:抛物线y=x2、y=x2+1、y=x2-1的开口方向、对称轴、顶点各是什么？（出示课件6）学生独立思考并整理.出示课件7:例在同一直角坐标系中,画出二次函数y=2x2+1,y=2x2-1的图象.学生自主操作,画图,教师加以巡视.解:先列表:然后描点画图:（出示课件8）教师问:抛物线y=2x2+1 , y=2x2-1的开口方向、对称轴和顶点各是什么？（出示课件9）学生独立思考并整理.探究二二次函数y=ax2+k的性质教师归纳:（出示课件10）二次函数y=ax2+k(a＞0)的性质:开口方向:向上.对称轴:x=0.顶点坐标:（0,k）.最值:当x=0时,有最小值,y=k.增减性:当x ＜0时,y 随x 的增大而减小；当x ＞0时,y 随x 的增大而增大.出示课件11:在同一坐标系中,画出二次函数212y x =-,2122y x =-+,2122y x =--的图像,并分别指出它们的开口方向,对称轴和顶点坐标.学生自主操作,画图,并整理. 解:如图所示.出示课件12:在同一坐标系内画出下列二次函数的图象:；；. 学生自主操作,画图,教师巡视加以指导.231x y -=23121--=x y 23122+-=x y出示课件13,14:根据图象回答下列问题:(1)图象的形状都是;(2)三条抛物线的开口方向_______;(3)对称轴都是__________;(4)从上而下顶点坐标分别是_____________________;(5)顶点都是最____点,函数都有最____值,从上而下最大值分别为_______、_______﹑________;(6) 函数的增减性都相同:____________________________.学生独立思考并口答.⑴抛物线；⑵向下；⑶直线x=0；⑷( 0,2),(0,0),( 0,-2)；⑸高；大；y=2,y=0,y=-2；⑹对称轴左侧y随x增大而增大,对称轴右侧y随x增大而减小师生共同归纳:二次函数y=ax2+k（a≠0）的性质（出示课件15）出示课件16:已知二次函数y＝ax2+c,当x取x1,x2（x1≠x2）时,函数值相等,则当x＝x1+x2时,其函数值为________.学生独立思考后,师生共同解答.解:由二次函数y＝ax2+c图象的性质可知,x1,x2关于y轴对称,即x1+x2＝0.把x ＝0代入二次函数表达式求出纵坐标为c.教师归纳:方法总结:二次函数y＝ax2+c的图象关于y轴对称,因此左右两部分折叠可以重合,函数值相等的两点的对应横坐标互为相反数．出示课件17:抛物线y=−2x2+3的顶点坐标是________,对称轴是________,在________侧,y随着x的增大而增大；在________侧,y随着x的增大而减小.学生口答:（0,3）；y轴；对称轴左；对称轴右探究三二次函数y=ax2+k的图象及平移出示课件18:从数的角度探究:出示课件19:从形的角度探究:观察图象可以发现,把抛物线y=2x2向_____平移1个单位长度,就得到抛物线_____；把抛物线y=2x2向_____平移1个单位长度,就得到抛物线y=2x2-1.学生观察图象并解答:上；y=2x2+1；下师生共同归纳:二次函数y=ax2与y=ax2+k（a≠0）的图象的关系（出示课件20）二次函数y=ax2+k的图象可以由y=ax2的图象平移得到:当k>0时,向上平移k个单位长度得到.当k<0时,向下平移k个单位长度得到.教师强调:上下平移规律:平方项不变,常数项上加下减.出示课件21:二次函数y＝－3x2＋1的图象是将( )A．抛物线y＝－3x2向左平移3个单位得到B．抛物线y＝－3x2向左平移1个单位得到C．抛物线y＝3x2向上平移1个单位得到D．抛物线y＝－3x2向上平移1个单位得到学生独立思考并口答:D出示课件22:想一想:教师问1.二次函数y=ax2+k图象的画法分几步？学生答:第一种方法:平移法,分两步,即第一步画y=ax2的图象；第二步把y=ax2的图象向上（或向下）平移︱k︱单位.第二种方法:描点法,分三步即列表、描点和连线.教师问2.抛物线y=ax2+k 中的a决定什么？怎样决定的？k决定什么？它的对称轴是什么？顶点坐标怎样表示？学生答:a决定开口方向和大小；k决定顶点的纵坐标.（三）课堂练习（出示课件23-27）1.将二次函数y=x2﹣1的图象向上平移3个单位长度,得到的图象所对应的函数表达式是．2.抛物线y=2x2向下平移4个单位,就得到抛物线．3.填表:4.已知点（m,n)在y=ax2+a（a不为0）的图象上,点(-m,n)___（填“在”或“不在”）y=ax2+a（a不为0）的图象上.5.若y=x2+（k-2）的顶点是原点,则k____；若顶点位于x轴上方,则k____；若顶点位于x轴下方,则k____.6.不画函数y=-x2和y=-x2+1的图象回答下面的问题:⑴抛物线y=-x2+1经过怎样的平移才能得到抛物线y=-x2.（2）函数y=-x2+1,当x_____时,y随x的增大而减小；当x_____时,函数y有最大值,最大值y是_____,其图象与y轴的交点坐标是_____,与x轴的交点坐标是_____.（3）试说出抛物线y=x2-3的开口方向、对称轴和顶点坐标.7.对于二次函数y=(m+1)x m2-m+3,当x>0时y随x的增大而增大,则m=____.8.已知二次函数y=(a-2)x2+a2-2的最高点为（0,2）, 则a=____.9.抛物线y=ax2+c与x轴交于A（-2,0）﹑B两点,与y轴交于点C(0,-4),则三角形ABC的面积是_______.参考答案:1.y=x2+22.y=2x2－43.4.在5.=2；＞2；＜26.⑴向下平移1个单位.⑵>0；=0；1；(0,1)；(-1,0),(1,0)⑶开口方向向上,对称轴是y轴,顶点坐标（0,-3）.7.28.-29.8（四）课堂小结通过这节课的学习,你有哪些收获和体会?说说看. （五）课前预习预习下节课（22.1.3第2课时）的相关内容. 七、课后作业配套练习册内容八、板书设计:九、教学反思:本课时教学重点在于培养学生的比较能力,旨在希望学生通过对比发现函数图象的性质,从而进一步增强学生的数形结合意识,体会通过探究获得知识的乐趣.。

人教版九年级数学上册课件：22.1二次函数的图像和性质(第1课时)

3．练习、巩固二次函数的定义
解：（1）由题意，得 2x 2y 18，y 9 x． ∵ x＞y＞0， ∴ x 的取值范围是 92＜x＜9， ∴ S矩形 = xy = x（9-x）=-x2+9x．
3．练习、巩固二次函数的定义
（2）当矩形面积 S矩形 = 18 时，即 - x2 + 9x = 18，
3．练习、巩固二次函数的定义
例某小区要修建一块矩形绿地，设矩形的长为 x m，宽为 y m，面积为 S m2（x＞y）．
（1）如果用 18 m 的建筑材料来修建绿地的边缘（即周长），求 S 与 x 的函数关系，并求出 x 的取值范围．
（2）根据小区的规划要求，所修建的绿地面积必须是 18 m2，在满足（1）的条件下，矩形的长和宽各为多少 m ？
九年级上册
22.1 二次函数的图象和性质（第1课时）
课件说明
• 本课是在学生已经学习了一次函数的基础上，继续进行函数的学习，学习二次函数的定义，这是对函数知识的完善与提高．
课件说明
• 学习目标：通过对实际问题的分析，体会二次函数的意义．
• 学习重点：理解二次函数的定义．
1．由实际生活引入二次函数
• 8、普通的教师告诉学生做什么，称职的教师向学生解释怎么做，出色的教师示范给学生，最优秀的教师激励学生。下午4时9分 28秒下午4时9分16:09:2821.11.7
2．通过实例，归纳二次函数的定义
某种产品现在的年产量是 20 t ，计划今后两年增加产量．如果每一年都比上一年的产量增加 x 倍，那么两年后这种产品的产量 y 将随计划所定的 x 的值而确定， y 与 x 之间的关系应该怎样表示？
6、“教学的艺术不在于传授本领，而在于激励、唤醒、鼓舞”。2021年11月下午4时9分21.11.716:09November 7, 2021

人教版数学九年级上册《22.1.2二次函数y=ax2的图象和性质》说课稿1

人教版数学九年级上册《22.1.2二次函数y=ax2 的图象和性质》说课稿1一. 教材分析人教版数学九年级上册《22.1.2二次函数y=ax^2 的图象和性质》这一节，是在学生已经掌握了函数的概念、一次函数的图象和性质的基础上，进一步引导学生学习二次函数的图象和性质。

通过这一节的学习，使学生能够掌握二次函数的一般形式，了解二次函数的图象特征，以及掌握二次函数的性质。

教材通过丰富的例题和练习题，帮助学生巩固所学知识，提高解决问题的能力。

二. 学情分析九年级的学生已经具备了一定的函数知识，对一次函数的图象和性质有了初步的了解。

但是，二次函数相对于一次函数来说，图象和性质更加复杂，需要学生有一定的抽象思维能力。

此外，学生可能对二次函数的图象和性质在实际问题中的应用还不够清晰，需要教师在教学中进行引导和启发。

三. 说教学目标1.知识与技能目标：让学生掌握二次函数的一般形式，了解二次函数的图象特征，掌握二次函数的性质。

2.过程与方法目标：通过观察、分析、归纳等方法，引导学生自主探究二次函数的图象和性质。

3.情感态度与价值观目标：激发学生对数学的兴趣，培养学生的探究精神和合作意识。

四. 说教学重难点1.教学重点：二次函数的一般形式，二次函数的图象特征，二次函数的性质。

2.教学难点：二次函数的图象和性质在实际问题中的应用。

五. 说教学方法与手段1.教学方法：采用问题驱动法、案例分析法、小组讨论法等，引导学生主动探究，提高学生的参与度和积极性。

2.教学手段：利用多媒体课件，展示二次函数的图象和性质，使抽象的知识更加直观形象。

同时，利用练习题和案例，帮助学生巩固所学知识。

六. 说教学过程1.导入：通过复习一次函数的图象和性质，引出二次函数的一般形式，激发学生的学习兴趣。

2.探究二次函数的图象特征：让学生观察二次函数的图象，引导学生发现二次函数的顶点、开口方向等特征。

3.探究二次函数的性质：通过小组讨论，让学生归纳出二次函数的增减性、对称性等性质。

人教九年级数学上册《二次函数图像与性质》课件(共14张PPT)

(3) 二次函数的图象是什么形状呢？
结合图象讨论
性质是数形结合
的研究函数的重要方法．我们得从最简单的二次函数开始逐步深入地讨论一般二次函数的图象和性质．
画最简单的二次函数 y = x2 的图象
1. 列表：在y = x2 中自变量x可以是任意实数，列表表示几组对应值：
x ··· －3 －2 －1 0
2 0.5
0 0.5 2 4.5
···
8
x
·· －2 －1.5 －1 －0.5 0 0.5 1 1.5 2 ···
·
y 2x2 ·· 8 4.5 2 0.5 0 0.5 2 4.5 8 ···
·
y x2
y 2x2
8
6
4
y 1 x2
2
2
－4 －2
24
函数 y 1 x2 , y 2x2 的图象与函数 y=x2 的图象相比，有什么共同2 点和不同点？
相同点：开口：向上，顶点：原点（0,0）——最低点对称轴： y 轴
增减性：y 轴左侧，y随x增大而减小
y 轴右侧，y随x增大而增大
y x2
8 6
y 2x2
不同点：a 值越大，抛物线的开口越小．
4 2 －4 －2
y 1 x2 2
24
探究
画出函数 yx2,y1x2,y2x2 的图象，并考虑这些抛物 2
1
2
3 ···
y = x2 ··· 9 4 1 0 1 4 9 ···
2. 根据表中x,y的数值在坐标平面中描点（x,y）
3.连线如图，再用平滑曲线顺次
9
连接各点，就得到y = x2 的图象
．
6
y = x2

人教版数学九年级上册22.1《二次函数的图象和性质(1)》教学设计

人教版数学九年级上册22.1《二次函数的图象和性质（1）》教学设计一. 教材分析人教版数学九年级上册第22.1节《二次函数的图象和性质（1）》是本册教材的重要内容，主要介绍二次函数的一般形式、图象特点以及一些基本性质。

通过本节内容的学习，学生可以掌握二次函数的基本知识，为后续学习二次函数的应用打下基础。

二. 学情分析九年级的学生已经学习了函数的基本概念和一次函数的性质，具备一定的函数知识基础。

但二次函数相对复杂，学生对其理解和掌握可能存在一定的困难。

因此，在教学过程中，需要注重引导学生通过观察、思考、探索等方式，自主发现和总结二次函数的性质。

三. 教学目标1.理解二次函数的一般形式和图象特点。

2.掌握二次函数的顶点坐标、开口方向和判别式的概念。

3.能够运用二次函数的性质解决一些实际问题。

四. 教学重难点1.二次函数的一般形式和图象特点。

2.二次函数的顶点坐标、开口方向和判别式的理解与应用。

五. 教学方法1.采用问题驱动的教学方法，引导学生通过观察、思考、探索等方式自主学习。

2.利用多媒体课件辅助教学，直观展示二次函数的图象和性质。

3.注重数学语言的训练，引导学生规范表达。

六. 教学准备1.多媒体课件。

2.相关练习题。

七. 教学过程1.导入（5分钟）通过展示一些实际问题，引导学生思考如何用数学模型来描述这些问题。

例如，抛物线运动、物体抛掷等。

从而引出二次函数的概念。

2.呈现（10分钟）利用多媒体课件，呈现二次函数的一般形式和图象特点。

引导学生观察并总结二次函数的性质。

3.操练（10分钟）让学生通过计算器或者绘图软件，自己动手绘制一些二次函数的图象，并观察其性质。

同时，教师巡回指导，解答学生的疑问。

4.巩固（10分钟）出示一些练习题，让学生运用所学的二次函数知识解决问题。

教师及时批改并给予反馈，帮助学生巩固所学知识。

5.拓展（10分钟）引导学生思考二次函数在实际生活中的应用，例如抛物线射门、跳水运动等。

人教版九年级数学上册22.1.3-二次函数的图像和性质(第1课时)一等奖优秀教学设计

人教版九年级数学上册22.1.3-二次函数的图
像和性质(第1课时)
一等奖优秀教学设计-CAL-FENGHAI.-(YICAI)-Company One1
人教版义务教育课程标准实验教科书九年级上册
22.1.3. 二次函数的图像和性质教学设计
一、教材分析 1、地位作用：
二次函数y=ax 2+k 的图像和性质是人教版九年级数学上册第二十一章第三节第一课时的内容，是在学生学习了二次函数的基本概念及y=ax 2的图像和性质之后引入的新内容。

本节课的教学内容既是对y=ax 2的图像和性质的引申，也是后面研究y=a(x-h)2+k 和一般形式的二次函数图像性质的基础。

所以，学习本节内容我们既要对前段的内容进行升华，又要对后段内容进行启发。

2、教学目标：
（1）能够准确绘制y=ax 2+k 二次函数图像；通过图像发现和研究二次函数y=ax 2+k 的性质。

（2）会应用二次函数的性质解决问题.
（3）经历观察，推理和交流等过程，获得研究问题与合作交流的方法和经验；体验数学活动中的探索性和创造性。

3、教学重、难点
教学重点：用描点法画二次函数的图像；探索二次函数y=ax 2+k 的图像特点和性质。

教学难点：二次函数y=ax 2+k 的性质的应用。

突破难点的方法：类比一次函数的平移和二次函数2ax y 的性质学习，构建一个知识体系。

二、教学准备：多媒体课件，几何画板.。

22.1.1 二次函数的图像及性质1 课件人教版数学九年级上册

注意：（1）等号左边是变量y，右边是关于自变量x的整式
（2）a,b,c为常数，且 a≠0.
（3 ）等式的右边最高次数为 2 ，可以没有
一次项和常数项，但不能没有二次项。
（4）x的取值范围是任意实数。
二次函数的一般形式: y＝ax2＋bx＋c , (其中a、b、c是常数 a≠0)
二次函数的特殊形式：
(5)y= _x1_²－x
(否) (6)v= 3 r ²
(7) y=x²+x³+25 (否) (8)y=2²+2x
(是) (否)
(9)y=mx²+nx+p (m,n,p为常数）
例1、下列函数中，哪些是二次函数？若是,分别
指出二次项系数,一次项系数,常数项.
(1) y=3(x-1)²+1
(2)
y=x+
的关系,对于x的每一个值, y都有一个对应值,即y是x的
函数.
观察
函数①②③有什么共同点?
y=6x2①
d
1 2
n2
3 2
n②
y 20 x2 40x 20③
y是x的函数吗？y是x的一次函数？反比例函数？
在上面的问题中,函数都是用自变量的二次式表示的,
定义：一般地，形如y=ax²+bx+c(a,b,c是常数,a≠ 0)的函数叫做x的二次函数。
观察y=x2的表达式,选择适当x值,并计算相应的y值,完成下表：
x … -3 -2 -1 0 1 2 3 … y=x2 … 9 4 1 0 1 4 9 …
描点,连线 y 10 8 6 4 2
y=x2
-4 -3 -2 -1 0 1 2 3 4 x -2
二次函数 y=x2的图象形如物体抛射时所经过的路线,我们把它叫做抛物线

人教版九年级数学上册《二次函数y=a(x-h)_+k的图象和性质》第1课时课件(共22张PPT)

复习回顾
二次函数 =
>0

的图像和性质
<0
图像
开口方向
对称轴
顶点
<0
增减性
>0
开口大小
向上
向下
轴
轴
(0,0) (0,0) 最低点ቤተ መጻሕፍቲ ባይዱ
(0,0) (0,0) 最高点
随的增大而减小
随的增大而增大
随的增大而增大
随的增大而减小
越大，开口越小
探究二次函数 =
2

+ ≠ 0 的图像和性质
1 在同一个直角坐标系中画出 1 = 22，2 = 22 + 1，3 = 22 − 1 的图象.
1. 列表

1 =
···
2
2
2 = 22 + 1
3 =
2
2
−1
−2 −1.5 −1 −0.5
0
0.5
1
1.5
2
···
···
8
4.5
2
0.5
0
0.5
(0, ) 最高点
函数性质
最值
有最小值是
有最大值是
探究二次函数 =
2

+ ≠ 0 的图像和性质
6 抛物线 = 2 + 的性质.
图像从左至右在对称轴左侧
的变化趋势在对称轴右侧
增减性
>0
<0
下降
上升
上升
下降
>0
<0
<0
随的增大而减小随的增大而增大

人教版九年级数学上册课件第二十二章二次函数二次函数的图象和性质二次函数y=ax2的图象和性质

14．已知y＝(m＋1)xm2＋m是关于x的二次函数，且当x＞0时，y随x的增大而减小．
(1)求m的值； (2)画出该函数的图象．
解：(1)∵y＝(m＋1)xm2＋m是关于x的二次函数，∴m2＋m＝2且m＋ 1≠0.则m＝－2或m＝1.又∵x＞0时，y随x的增大而减小，∴m＋1＜0，m ＜－1，故m＝－2
解：(1)直线AB的解析式为y＝－x＋2，抛物线的解析式为y＝x2
(2)令直线 AB 与 y 轴相交于点 E，在 y＝－x＋2 中，当 x＝0 时，y＝2，
∴点
E
y＝－x＋2，的坐标为 (0 ， 2) ， ∴ OE ＝ 2. 联立 y＝x2，
解
得
x1＝1， y1＝1，
x2＝－2， y2＝4，
_增__大____，当x＞0时，y随x的增大而__减__小___．练习2：已知二次函数y＝x2，当x＞0时，y随x的增大而_增__大____．(填“增
大”或“减小”)
1．已知二次函数y＝x2，则其图象经过下列点中的( A ) A．(－2，4) B．(－2，－4) C．(2，－4) D．(4，2)
A．y1＜y2＜y3 B．y1＜y3＜y2 C．y3＜y2＜y1 D．y2＜y1＜y3
12．如图，正方形的边长为4，以正方形中心为原点建立平面直角坐标系，作出函数y＝2x2与y＝－2x2的图象，则阴影部分的面积是____8____．
13．如图是下列二次函数的图象：①y＝ax2；②y＝bx2；③y＝cx2；④y ＝dx2.比较a，b，c，d的大小，用“＞”连接为___a_＞__b_＞__d_＞__c____.
∴点
C
的坐标为(－2，4)，∵S△BOC＝12
OE·(xB－xC)＝12

人教版数学九年级上册22.1.2二次函数y=ax2的图象和性质(第1课时)教学设计

3.分析二次函数y=ax^2图象和性质的关系，使学生理解a的几何意义。
三、课堂练习
1.让学生独立绘制二次函数y=ax^2的图象，并描述其性质。
2.通过小组合作，讨论并总结二次函数图象和性质的特点。
四、巩固拓展
1.让学生思考：如何通过观察二次函数图象，判断其开口方向和对称轴？
2.引导学生运用二次函数的图象和性质，解决实际问题。
4.注重分层教学，关注个体差异：
（1）针对不同层次的学生，设计不同难度的练习题，使每个学生都能在原有基础上得到提高。
（2）鼓励学生主动提问，及时解答他们的疑惑，帮助他们建立信心。
5.强化课堂小结，巩固所学知识：
（1）让学生用自己的话总结二次函数y=ax^2的图象和性质，加深对知识的理解和记忆。
（2）通过课堂小结，检查学生的学习效果，及时发现问题并进行针对性的辅导。
3.组织学生进行小组合作交流，培养学生团队协作能力和表达能力，激发他们学习数学的兴趣。
（三）情感态度与价值观
1.培养学生勇于探索、积极思考的学习态度，使他们体会数学学习的乐趣，增强学习数学的自信心。
2.通过对二次函数y=ax^2图象和性质的探究，使学生感受数学的对称美、秩序美，提高他们的审美情趣。
3.使学生认识到数学知识在实际生活中的广泛应用，激发他们学习数学的积极性，培养他们运用数学知识解决实际问题的意识。
3.培养学生运用数形结合思想，通过观察、分析、归纳二次函数图象和性质，提高解决问题的能力。
（二）过程与方法
1.通过引导学生在探索二次函数y=ax^2图象和性质的过程中，培养他们提出问题、分析问题、解决问题的能力。
2.引导学生运用数形结合思想，将二次函数的图象与性质相互验证，提高他们的逻辑思维能力和推理能力。

二次函数y=ax^2的图象和性质(一)-九年级数学上册教学课件(人教版)

对于抛物线(-y2,=-4)ax 2 （a＜0）(2,-4) 当x＞0时，y随x取值的增大而减小；当x<0时，y随x取值的增大而增大.
y＝ax2 图象
位置开口方向
a>0 y
O x
开口向上,在x轴上方
a<0 yx
O
开口向下,在x轴下方
对称性顶点最值
增减性
关于y轴对称，对称轴是直线x＝0 顶点坐标是原点（0，0）
人教版数学九年级上册
会用描点法画出二次函数y=ax²的图象，概括出图象的特点.
掌握形如y=ax²的二次函数图象的性质，并会进行简单应用.
探究一画出二次函数y=x2的图象. 1. 列表：在y = x2 中自变量x可以是任意实数，列表表示几组对应值：
x … -3 -2 -1 0 1 2 3 y=x2 … 9 4 1 0 1 4 9
当x=0时，y最小值=0
当x=0时，y最大值=0
在对称轴左侧递减在对称轴右侧递增
在对称轴左侧递增在对称轴右侧递减
1.函数y=4x2的图象的开口向上,对称轴是 y轴 ,顶点是 (0,0) ;
2.函数y=－3x2的图象的开口向下 ,对称轴是 y轴 ,顶点是 (0,0) 顶点是抛物线的最高点
2. 描点：根据表中x,y的数值在坐标平面中描点（x,y） 3. 连线：如图，再用平滑曲线顺次连接各点，就得到y = x2 的图象．
…
…
y 9
6
3
-4 -2 o 2 4 x
当更多个点时，函数y=x2的图象如下：
y
9 6
这条抛物线关于y轴对称,
3
y轴就是它的对称轴.
-3 o
3
对称轴与抛物线的交点叫做抛物线的顶点.

人教版九年级数学上册第22章第1节二次函数的图像和性质(共46张PPT)

1.y=x2 8x 7
2.y=-2x2 9x 17
3.y=mx2 kx-4k2
x
⑶a，b决定抛物线对称轴的位置: 对称轴是直线x =
b 2a
① a，b同号＜＝＞对称轴在y轴左侧；
② b=0 ＜＝＞对称轴是y轴；
③ a，b异号＜＝＞对称轴在y轴右侧
y
左同右异
o
x
练习：
1.若抛物线yax2 bxc的图象如图，说出a，b，
c的符号。
2.若抛物线yax2 bxc经过原点和第一二三
象限，则a，b，c的取值范围分别是
3.若抛物线yax2 bxc的图象
如图所示，则一次函数y=ax+bc
的图象不经过
。y
。 y ox
o 图1
x 图2
y abc 0 （ 4 ）与直线 x1 交点 y a b c 0
y a b c 0
方法归纳
1
配方法
2
公式法
二次函数y=ax2+bx+c(a≠0)的图象和性质
１.顶点坐标与对称轴２.位置与开口方向３.增减性与最值根据图形填表：
抛物线顶点坐标
对称轴位置
y=ax2+bx+c(a>0)
b 2a
,
4acb2 4a
直线x b
2a
由a,b和c的符号确定
y=ax2+bx+c(a<0)
小结拓展回味无穷驶向胜利的彼岸
二次函数y=ax2+bx+c(a≠0)与=ax²的关系
2.不同点:
(1)位置不同(2)顶点不同:分别是
b 2a
,
4acb2 4a

2024年人教版九年级数学上册教案及教学反思全册第22章二次函数的图象和性质 (第1课时)教案

22.1 二次函数的图象和性质22.1.4 二次函数y=ax2+bx+c的图象和性质（第1课时）一、教学目标【知识与技能】1.能通过配方法把二次函数y=ax2+bx+c（a≠0）化成y=a(x-h)2+k的形式，以便确定它的对称轴和顶点坐标；2.会利用对称性画出二次函数的图象，掌握二次函数y=ax2+bx+c(a≠0)的平移规律；3.会用公式确定二次函数y=ax2+bx+c（a≠0）的对称轴和顶点.【过程与方法】通过思考、探索、尝试与归纳等过程，让学生能主动积极地探索新知.【情感态度与价值观】经历探求二次函数y=ax2+bx+c的对称轴和顶点坐标的过程，感悟二次函数y=ax2+bx+c与y=ax2的内在联系，体验利用抛物线的对称轴画抛物线的方法，感受数学的对称美.二、课型新授课三、课时第1课时，共2课时。

四、教学重难点【教学重点】用抛物线的对称轴画二次函数y=ax2+bx+c的图象，通过配方确定抛物线的对称轴和顶点坐标.通过配方法将二次函数的一般形式化为顶点式，探索二次函数y=ax2+bx+c的平移变换.【教学难点】用配方法推导抛物线的对称轴与顶点坐标.五、课前准备课件、三角尺、铅笔等六、教学过程（一）导入新课教师问：二次函数y=a(x-h)2+k的性质有哪些？（出示课件2）师生共同回忆：教师问：我们已经知道二次函数y=a(x-h)2+k的图象和性质，能否利用这些知识来讨论二次函数y=ax2+bx+c 图象和性质?（出示课件3）（二）探索新知探究一画出二次函数y=ax 2+bx+c 的图象我们已经知道y=a(x-h)2+k 的图象和性质，能否利用这些知识来讨论216212y x x =-+的图象和性质？（出示课件5）问题1：怎样将216212y x x =-+化成y=a(x-h)2+k 的形式？学生回忆配方的方法及步骤，并回答.（出示课件6）216212y x x =-+ 21(1242)2x x =-+ 2221(126642)2x x =-+-+ 2221[(126)642]2x x =-+-+ 21[(6)6]2x =-+ 21(6) 3.2x =-+ 学生回答后，教师总结并强调.（出示课件7）配方的步骤：(1)“提”：提出二次项系数； (2)“配”：括号内配成完全平方； (3)“化”：化成顶点式.配方后的表达式通常称为配方式或顶点式. 问题2：你能说出21(6)32y x =-+的对称轴及顶点坐标吗？（出示课件8）生答：对称轴是直线x=6,顶点坐标是（6，3）. 问题3：二次函数21(6)32y x =-+可以看作是由212y x =怎样平移得到的？生答：平移方法1：先向上平移3个单位，再向右平移6个单位得到的；平移方法2：先向右平移6个单位，再向上平移3个单位得到的. 问题4：如何画二次函数216212y x x =-+的图象？（出示课件:9）学生自主操作，画图，教师加以巡视.并引导他们进行分析. 方法一：描点法. 1.列表.2.描点，连线：方法二：平移法.（出示课件10）问题5：结合二次函数216212y x x =-+的图象，说出其性质.（出示课件11）生答：当x<6时，y 随x 的增大而减小；当x>6时，y 随x 的增大而增大. 开口方向：向上.对称轴：x=6. 顶点：(6,3). 例画出函数21522y x x =-+-的图象，并说明这个函数具有哪些性质.（出示课件12）师生共同解答如下：解:函数21522y x x =-+-通过配方可得21(1)22y x =---，先列表：然后描点、连线，得到图象如下图：（出示课件13）生观察图象，并总结性质如下：开口方向：向下. 顶点坐标：（1，-2）. 对称轴：x=1.最值：x=1时，y 最大值=-2.当x ＜1时，函数值y 随x 的增大而增大；当x ＞1时，函数值y 随x 的增大而减小；当x=1时，函数取得最大值，最大值y=-2.出示课件14：求二次函数y=2x 2-8x+7图象的对称轴和顶点坐标. 生板演解题过程：解：y=2x 2-8x+722(4)7x x =-+ 22(44)87x x =-+-+ 22(2) 1.x =--因此，二次函数y=2x 2-8x+7图象的对称轴是直线x=2，顶点坐标为(2,-1). 探究二二次函数y=ax 2+bx+c 的图象与性质出示课件15：根据下列关系你能发现二次函数y=ax 2+bx+c 的图象和性质吗？师生共同探究强化认知：y=ax 2+bx+c 224()24b ac b a x a a-++=出示课件16：显然，二次函数y 224()24b ac b a x a a-++=的顶点坐标为24,24b ac b a a ⎛⎫-- ⎪⎝⎭，对称轴为2bx a =- 因此，抛物线y=ax 2+bx+c 的对称轴是2bx a=-，顶点坐标是24,24b ac b a a ⎛⎫ ⎪⎝-⎭- . 师生共同总结整理如下：（出示课件18）出示课件19：例二次函数y=x2+2x﹣3的开口方向、顶点坐标分别是（）A．开口向上，顶点坐标为（﹣1，﹣4）B．开口向下，顶点坐标为（1，4）C．开口向上，顶点坐标为（1，4）D．开口向下，顶点坐标为（﹣1，﹣4）学生自主思考后，师生共同解答如下：解析∵二次函数y=x2+2x﹣3的二次项系数为a=1＞0，∴函数图象开口向上，∵y=x²+2x﹣3=（x+1）2﹣4，∴顶点坐标为（﹣1，﹣4）．教师加以强调：把函数的一般式化为顶点式，再由顶点式确定开口方向、对称轴、顶点及其他性质.出示课件20：填一填.生自主思考，并填表. 答案：(1,1)；x=1；最大值1； (0,-1)；y 轴；最大值-1；(13-,-6)；x=13-；最小值-6. 出示课件21：一次函数y=kx+b 的图象如下图所示，请根据一次函数图象的性质填空：生观察图象，并填空.k 1＜0；b 1＞0；k 2＞0；b 2＜0；k 3＞0；b 3＞0.出示课件22，23：二次函数y=ax 2+bx+c 的图象如下图所示，请根据二次函数的性质填空：a1___0，b1___0,c1___0；a20，b2___0,c20；a3___0，b3___0,c3___0；a4___0，b4___0,c4___0.生观察图象后，独立填空，教师加以纠正.a1＞0，b1＞0,c1＞0；a2＞0，b2＜0,c2=0；a3＜0，b3=0,c3＞0；a4＜0，b4＞0,c4＜0.师生共同总结：二次函数y=ax2+bx+c的图象与a、b、c的关系（出示课件24）出示课件25：例已知二次函数y＝ax2＋bx＋c的图象如图所示，下列结论：①abc＞0；②2a－b＜0；③4a－2b＋c＜0；④(a＋c)2＜b2. 其中正确的个数是( )A．1 B．2 C．3 D．4生独立思考后，师生共同分析：由图象开口向下可得a＜0，由对称轴在y轴左侧可得b＜0，由图象与y轴交于正半轴可得c＞0，则abc＞0，故①正确；由对称轴x>－1可得2a－b＜0，故②正确；由图象上横坐标为x＝－2的点在第三象限可得4a－2b＋c＜0，故③正确；由图可知x＝1的点在第四象限得a＋b＋c＜0，由图象上x＝－1的点在第二象限得出a－b＋c＞0，则(a＋b＋c)(a－b＋c)＜0，即(a＋c)2－b2＜0，可得(a＋c)2＜b2，故④正确．出示课件26：二次函数y=ax²+bx+c的图象如图所示，下列选项中正确的是（）A．a＞0 B．b＞0 C．c＜0 D．ac>0生独立思考后，自主解决.解析根据开口方向、对称轴、抛物线与y轴的交点，确定a、b、c的符号，根据对称轴和图象确定y＞0或y＜0时，x的范围，确定代数式的符号．①∵开口向下，∴a＜0，A错误；②对称轴在y轴的右侧和a＜0，可知b＞0，B正确；③抛物线与y轴交于正半轴，c＞0，C错误；④因为a<0，c>0，所以ac<0，D错误．（三）课堂练习（出示课件27-32）1.如图是二次函数y=ax2+bx+c（a，b，c是常数，a≠0）图象的一部分，与x 轴的交点A在点（2，0）和（3，0）之间，对称轴是x=1．对于下列说法：①ab ＜0；②2a+b=0；③3a+c＞0；④a+b≥m（am+b）（m为实数）；⑤当﹣1＜x＜3时，y＞0，其中正确的是（）A．①②④B．①②⑤C．②③④D．③④⑤2.已知二次函数y=ax2+bx+c的x，y的部分对应值如下表：则该二次函数图象的对称轴为( )A.y 轴B.直线x=52C.直线x=2D.直线x=323.已知二次函数y=ax 2+bx+c(a ≠0)的图象如图所示，则下列结论：（1）a ，b 同号；（2）当x=–1和x=3时，函数值相等；（3）4a+b=0；（4）当y=–2时，x 的值只能取0；其中正确的是 .4.如图是二次函数y=ax 2+bx+c(a ≠0)图象的一部分，x=-1是对称轴，有下列判断：①b-2a=0；②4a-2b+c<0；③a-b+c=-9a ；④若（-3，y 1）,（32，y 2）是抛物线上两点，则y 1>y 2.其中正确的是（）A ．①②③B ．①③④C ．①②④D ．②③④5.根据公式确定下列二次函数图象的对称轴和顶点坐标：()()()22(1) 21213;(2) 580319;1(3) 22;2(4)12.y x x y x x y x x y x x =-+=-+-⎛⎫=-- ⎪⎝⎭=+-6.已知函数y=-2x2+x-4,当x= 时，y 有最大值 .7.已知二次函数y=x 2-2x+1，那么它的图象大致为（）参考答案：1.A2.D3.（2）4.B5.⑴直线x=3，(3，-5)；⑵直线x=8，(8，1)；⑶直线x=1.25，59, 48⎛⎫- ⎪⎝⎭； ⑷直线x=0.5，19, 24⎛⎫ ⎪⎝⎭. 6.14；318- 7.B（四）课堂小结通过这节课的学习，你有哪些收获和体会?说说看.（五）课前预习预习下节课（22.1.4第2课时）的相关内容.七、课后作业配套练习册内容八、板书设计：九、教学反思：本课时的主要任务是理解和掌握二次函数的一般式.我们研究函数的一般基本方法是由解析式画图象，再由图象得出性质，再反过来由函数性质研究图象的其他特征.因此本课时的教学仍可采用这种思维方法来探讨二次函数一般式的性质（如顶点坐标，对称轴以及增减性等），另外还要向学生渗透转化思想，即如何将相对复杂的一般式转化为其他解析式的形式.。