27_圆形智求面积(有答案)(二)数学奥林匹克水平测试卷6_(1)
二年级圆形的面积及解答

二年级圆形的面积及解答
圆形的面积公式
圆形的面积用于描述圆的大小。
面积的计算可以使用以下公式:
$$
面积= π * 半径^2
$$
其中,π是一个常数,约等于3.14,半径是指从圆心到圆周任
意点的距离。
面积计算示例
假设一个圆的半径是5厘米,我们可以通过以下步骤来计算该
圆的面积:
1. 首先,将半径的值代入面积公式中:
面积 = 3.14 * 5^2
2. 其次,计算半径的平方:
面积 = 3.14 * 25
3. 最后,计算面积:
面积 = 78.5 平方厘米
因此,该圆的面积为78.5平方厘米。
解答示例
以下是一些与圆形面积相关问题的解答示例:
问题1
圆的直径是10厘米,求其面积。
解答:
1. 首先,计算半径:
半径 = 直径 / 2 = 10 / 2 = 5厘米
2. 其次,将半径的值代入面积公式中:
面积 = 3.14 * 5^2 = 3.14 * 25 = 78.5平方厘米因此,圆的面积是78.5平方厘米。
问题2
圆的面积是153.86平方厘米,求其半径。
解答:
1. 首先,将面积公式变形为:
半径= √(面积/ π)
2. 其次,代入面积的值:
半径= √(153.86 / 3.14)
3. 最后,计算半径:
半径≈ √49 ≈ 7厘米
因此,圆的半径约为7厘米。
希望以上内容对你有帮助!如有其他问题,请随时咨询。
圆的面积练习题答案

圆的面积练习题答案圆的面积练习题答案圆是几何学中的重要概念之一,其面积计算是我们在学习数学时经常遇到的题目之一。
在这篇文章中,我将为大家提供一些常见圆的面积练习题的答案,并解释一些解题的思路和方法。
题目一:一个圆的半径为5cm,求其面积。
解答一:圆的面积公式为S = πr²,其中π取近似值3.14,r为半径。
根据题目给出的半径5cm,代入公式计算可得:S = 3.14 × 5² = 3.14 × 25 = 78.5cm²。
因此,这个圆的面积为78.5平方厘米。
题目二:一个圆的直径为12cm,求其面积。
解答二:题目给出的是直径,而面积公式中需要的是半径。
我们知道直径是圆的两个点之间的距离,而半径是从圆心到圆上任意一点的距离,所以半径等于直径的一半。
因此,这个圆的半径为12cm的一半,即6cm。
代入面积公式计算可得:S = 3.14 × 6² = 3.14 × 36 = 113.04cm²。
因此,这个圆的面积为113.04平方厘米。
题目三:一个圆的周长为30cm,求其面积。
解答三:题目给出的是周长,而面积公式中需要的是半径。
我们知道周长是圆上一周的长度,而半径是从圆心到圆上任意一点的距离,所以周长等于半径乘以2π。
根据题目给出的周长30cm,我们可以得到方程式30 = 2πr,其中r为半径。
解方程可得r = 30 / (2 × 3.14) ≈ 4.77cm。
代入面积公式计算可得:S = 3.14 × 4.77² ≈ 3.14 × 22.77 ≈ 71.59cm²。
因此,这个圆的面积约为71.59平方厘米。
通过以上的练习题,我们可以看到计算圆的面积需要使用到圆的半径或直径。
如果题目给出的是半径,直接代入面积公式计算即可;如果给出的是直径,需要先将其除以2得到半径再代入公式计算。
圆的周长和面积测试题

圆的周长和面积测试题在数学课上,我们学习了圆的周长和面积的计算方法。
圆是一个非常特殊的几何形状,具有许多独特的性质和特点。
为了巩固对圆的理解和运用,老师为我们布置了一个圆的周长和面积测试题。
现在就让我们来一起解答这个有趣的测试题吧!题目一:已知圆的半径为r,请计算这个圆的周长和面积。
解答一:根据数学知识我们知道,圆的周长公式为C=2πr,圆的面积公式为A=πr²。
根据这两个公式,我们可以计算出这个圆的周长和面积。
假设圆的半径为r,则周长C=2πr,面积A=πr²。
将半径r的值代入公式中,即可计算出圆的周长和面积。
其中,π的取值可以采用3.14或近似值3.14159。
例如,如果半径r=5cm,则周长C=2πr=2*3.14*5≈31.4cm,面积A=πr²=3.14*5²≈78.5cm²。
题目二:已知圆的周长为C,请计算这个圆的半径和面积。
解答二:根据数学知识我们知道,圆的周长公式为C=2πr,圆的面积公式为A=πr²。
根据这两个公式,我们可以计算出这个圆的半径和面积。
假设圆的周长为C,则周长C=2πr,面积A=πr²。
通过已知的周长C,我们可以反推出圆的半径r的值。
首先,将已知的周长C代入周长公式,得到C=2πr,然后解方程求解r。
最后,将求得的半径r代入面积公式,即可计算出圆的面积A。
例如,如果已知周长C=20cm,则周长公式为20=2πr,解方程可得r=20/(2π)≈3.18cm,将求得的半径r代入面积公式得到面积A=π(3.18)²≈31.8cm²。
通过这样的题目练习,我们可以巩固对圆的周长和面积的计算方法的掌握,提高数学运算能力。
总结:圆的周长和面积是圆的基本属性,通过周长和面积的计算,我们可以更好地理解圆的特性和运用。
掌握了圆的周长和面积的计算方法,我们就能够在实际问题中灵活运用,解决与圆相关的计算和应用题目。
奥数专题平面图形之圆的面积(有例题讲解和相应的练习)
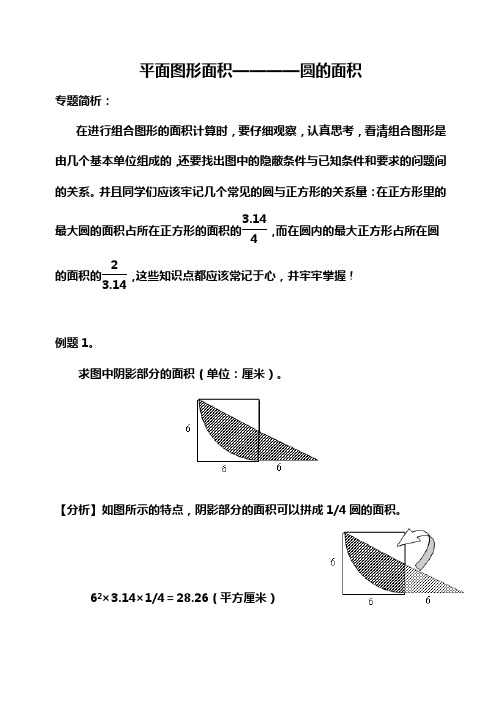
平面图形面积————圆的面积专题简析:在进行组合图形的面积计算时,要仔细观察,认真思考,看清组合图形是由几个基本单位组成的,还要找出图中的隐蔽条件与已知条件和要求的问题间的关系。
并且同学们应该牢记几个常见的圆与正方形的关系量:在正方形里的最大圆的面积占所在正方形的面积的3.144,而在圆内的最大正方形占所在圆的面积的23.14,这些知识点都应该常记于心,并牢牢掌握!例题1。
求图中阴影部分的面积(单位:厘米)。
【分析】如图所示的特点,阴影部分的面积可以拼成1/4圆的面积。
62×3.14×1/4=28.26(平方厘米)练习11.求下面各个图形中阴影部分的面积(单位:厘米)。
2.求下面各个图形中阴影部分的面积(单位:厘米)。
答例题2。
求图中阴影部分的面积(单位:厘米)。
【分析】阴影部分通过翻折移动位置后,构成了一个新的图形(如图所示)。
从图中可以看出阴影部分的面积等于大扇形的面积减去大三角形面积的一半。
3.14×42×1/4-4×4÷2÷2=8.56(平方厘米)练习21、计算下面图形中阴影部分的面积(单位:厘米,正方形边长4)。
答2、计算下面图形中阴影部分的面积(单位:厘米,正方形边长4)。
答1 2例题3。
如图19-10所示,两圆半径都是1厘米,且图中两个阴影部分的面积相O的面积。
等。
求长方形ABO1【分析】因为两圆的半径相等,所以两个扇形中的空白部分相等。
又因为图中两个阴影部分的面积相等,所以扇形的面积等于长方形面积的一半(如图19-10右图所示)。
所以3.14×12×1/4×2=1.57(平方厘米)练习31、如图所示,圆的周长为12.56厘米,AC两点把圆分成相等的两段弧,阴影部分(1)的面积与阴影部分(2)的面积相等,求平行四边形ABCD的面积。
答2、如图所示,AB=BC=8厘米,求阴影部分的面积。
圆的面积奥数

圆的面积圆是一种平面图形,再日常生活中到处可见.如圆桌,圆盘,车辆的轱辘,以及游戏用的棋子,飞盘,呼啦圈等,由于圆有着本身独特的性质,在某些地方是其它形状所不能代替的,车轱辘就是一个很好的例子.这一讲我们着重研究圆以及和圆有关的组合图形的求面积方法.圆的面积计算公式,扇形面积计算公式,同学们在课本上已经都有初步的理解和掌握,我们主要讨论组合图形的面积的计算方法与技巧.请注意常用的扇形:四分之一圆对应圆心角是90度,八分之一圆对应的圆心角是45度.经典题再现如下图所示,O是圆心,圆的周长等于75.36分米,点A、B、C都在圆周上,OABC是梯形,梯形的面积是98.28平方分米.AB=20.76分米,那么阴影部分的面积是多少平方分米?(π取3.14)解:由圆的周长可求圆的半径:75.36 = 2 × 3.14 × r ,r = 12.即OC = 12.由梯形的面积及它的上底,下底已知,可求梯形的高.98.28 = (12 + 20.76) × 高 ÷ 2,高 = 6.阴影的面积 = 12 × 6 ÷ 2 = 12 × 3 = 36(平方分米).典型例题【例1】 长方形长6分米,宽4分米,分别以长、宽为半径画弧,如图.那么阴影部分的面积是多少平方分米?解:226 3.144 3.1464⎛⎫⨯⨯-⨯- ⎪⎝⎭= 16.82(平方厘米) 答:影阴部分的面积是16.82平方厘米.【例2】 如图,半圆S 1的面积是14.13平方厘米,圆S 2的面积是19.625平方厘米,那么阴影部分的面积是多少平方厘米?解:因为s 1的面积为14.13平方厘米,所以半径的平方为14.13⨯2÷3.14 = 9,故半径为3厘米,直径为6厘米.又因为s 2的面积为19.625平方厘米,所以S 2的半径的平方为19.625÷3.14 = 6.25(平方厘米),所以它的半径为2.5厘米,直径为5厘米,所以阴影部分面积为(6 - 5)⨯5 = 5(平方厘米).答:阴影部分的面积是5平方厘米.【例3】 如图,A 与B 是两个圆(只有1)的圆心,那么,两个阴影部分的面积相差多少平方厘米?解:观察上图可以发现大14圆的面积减去长方形的面积(包括小阴影和大空白两部分)再减去小14圆的面积.就是两个影阴部分的面积差. 即22113.14424 3.142⨯⨯-⨯-⨯⨯= 1.42(平方厘米) 答:两个阴影部分的面积相差1.42平方厘米.【例4】 如图,圆的直径AB 是4cm 的面积是7cm 2,∠ABC等于30°,求阴影部分面积.解:这个题许多同学将ABC 看成是圆心角为30°的扇形.这是错误的,因为AB 是直径,BC 不是,AB ,BC 不一样长,所以,ABC 不是扇形.如下图,找到圆心O,连CO,AOC才是扇形.先要求这个扇形的圆心角,就可以求出它的面积.然后再求三角形COB的面积,用ABCD阴影面积等于平行四边形面积减去扇形AOC的面积,再减去△BOC 的面积.扇形的圆心角=180°-(180°-30°×2)=60°.扇形的面积=2×2×3.14×60÷360=2.09(平方厘米).△BOC的面积=7÷2÷2=1.75(平方厘米).阴影部分的面积=7–2.09 1.75=3.16.答:阴影部分的面积是3.16平方厘米.【例5】下图中阴影部分的面积是多少平方厘米?解:两个空白部分拼起来正好是一个4×4的正方形.所以阴影部分面积等于2×4的长方形面积.2×4=8(平方厘米)答:影阴部分的面积是8平方厘米.【例6】如图所示,这是一个正六边形,它的面积为1040平方厘米.空白部分是半径为10cm的6个小扇形.求阴影部分的面积.解:图中阴影部分的面积显然是正六边形的面积减去六个小扇形的面积.正六边形的面积已知,所以关键是求六个小扇形面积.我们观察每3个小扇形可以拼成一个半径为10厘米的圆,6个小扇形可以拼成2个小圆形.阴影部分的面积就是正六边形的面积减去2个半径为10厘米的小圆的面积.6个扇形的面积为3.14×102×2=628(平方厘米),阴影部分的面积:1040-628=412(平方厘米).答:阴影部分的面积为412平方厘米.难题详解如下图所示,在4×7的方格纸板上画出如阴影所示的“9”字,阴影边缘是线段或圆弧.问阴影面积占纸板面积的几分之几?圆周.非阴影部分共6解:矩形纸板共28个小正方形.其中弧线是14个,也共6个.可拼成6个小正方格.因此阴影部分共28-6-3=19个小方格.所以,阴影面积占纸板面积的19.28.答:阴影面积占纸板面积的1928同步练习1.如下图,ABCD为正方形,且F A=AD=DE=2厘米,求阴影部分的面积?2.有三个形状相同的圆形纸片,面积都是90平方厘米,重叠在一起(如图),盖住桌面的总面积是150平方厘米,三张纸片重叠的面积是28平方厘米,那么图中三个阴影部分面积和是多少平方厘米?3.已知图中各圆相切,小圆半径为1,求阴影部分面积.4.已知每个圆的直径为6厘米,求阴影部分的面积.5.图中正方形ABCD的边长是20厘米,求阴影部分面积.6.如图,已知每个小正方形的面积为1平方厘米,求阴影部分面积.(注:所用分点均理解为所在边中点).7.如图,大圆直径上的黑点是五等分点,求A,B,C三部分面积之比.8.如图,O为圆心,C为扇形ACB的圆心,CO垂直于AB,三角形ABC的面积为45平方厘米,求阴影部分面积.同步练习解答1.图形DGC 为图形DBC 面积的一半,于是,阴影部分的面积为()()2211133.1422222 3.1424242⨯⨯-⨯⨯+⨯-⨯⨯⨯=2.43(平方厘米) 2.解:90 × 3 - 150 - 28 × 2 = 64(平方厘米)3.如图I ,II ,III 部分面积是相等的,剩余3块小阴影面积也相等.那么所求阴影部分面积是一个小半圆面积加上大半圆减去2个小圆和3个小半圆剩余部分的13. 阴影面积为:2π1π3πππ52π3π2322236⎛⎫⨯+⨯--⨯=+= ⎪⎝⎭4.如图,长方形外的阴影部分一共3311442+=个圆,移至长方形内正好填满长方形,阴影部分的面积就是长方形面积.阴影部分面积 = 6 × 2 × 6 = 72(平方厘米).5.充分利用圆的对称性,如图,大扇形ABC 的半径是20,它的面积减去三角形ABC 的面积就是I 的面积.正方形ABCD 减去圆O 的面积就是4个II 的面积.阴影部分就是ABCD 面积减去2个I ,4个II 的面积.20()2211202π2020204(2020π10)42⨯-⨯⨯⨯-⨯⨯-⨯⨯-⨯ = 129(平方厘米)6.阴影分成两部分,一部分是字母“A ”,一部分是字母“r ”. 字母“A ”的面积,我们只需算一半,再2倍就可以了.平行四边形ABCD 面积=13322⨯= 梯形EFHG 面积=()131********+⨯⨯= 字母“A ”的面积()3529123 3.62521688+⨯===. 字母“r ”的面积2π3662212.26⨯-⨯÷+=.最后,阴影面积为3.625 + 12.26 = 15.885(平方厘米).7.显然,A 与C 面积相等,B 与C 面积比为(1.52 - 12):[(2.52 - 1.52 + 12)÷ 2] = 1∶2.所以,A ,B ,C 面积比为:2∶1∶2.8.设CA = CB = a ,OC = OB = OA = r .则由三角形ABC 面积为45知,1452a a ⨯⨯=,a 2 = 90. 再以AB 为底计算三角形ABC 面积:AB ⨯OC ⨯12=2⨯OA ⨯OC ⨯12=b 2知,b 2 = 45.阴影部分面积 = 半圆面积 + 三角形ABC 面积 - 扇形ACB 面积.即 45 + b 2⨯3.14⨯12- a 2 ⨯3.14⨯14= 45 + 45⨯3.14⨯12- 90⨯3.14⨯14= 45。
圆的面积练习题及答案

圆的面积练习题及答案圆的面积是数学中的一个重要概念,它常常出现在几何题目中。
在这篇文章中,我们将探讨一些关于圆的面积练习题,并给出相应的答案。
1. 练习题一:一个圆的半径是5厘米,求其面积。
解答:圆的面积公式为:面积= π * 半径²将半径代入公式,得到:面积= 3.14 * 5² = 78.5平方厘米2. 练习题二:一个圆的直径是12米,求其面积。
解答:圆的半径等于直径的一半,所以半径为 12 / 2 = 6米。
将半径代入面积公式,得到:面积= 3.14 * 6² = 113.04平方米3. 练习题三:一个圆的面积是154平方厘米,求其半径。
解答:面积公式可以改写为:半径² = 面积/ π将面积代入公式,得到:半径² = 154 / 3.14解方程得到:半径≈ √(154 / 3.14) ≈ 7厘米4. 练习题四:一个圆的周长是36π米,求其面积。
解答:圆的周长公式为:周长= 2π * 半径将周长代入公式,得到:36π = 2π * 半径解方程得到:半径 = 36 / 2 = 18米将半径代入面积公式,得到:面积= π * 18² ≈ 1017.88平方米5. 练习题五:一个圆的面积是100平方单位,求其直径。
解答:面积公式可以改写为:面积= π * (直径/ 2)²将面积代入公式,得到:100 = 3.14 * (直径/ 2)²解方程得到:直径≈ √(100 / 3.14) * 2 ≈ 17.92单位通过以上练习题,我们可以看到圆的面积计算并不复杂,只需要掌握好相应的公式和计算方法即可。
在实际生活中,圆的面积应用广泛,比如计算圆形花坛的面积、圆形饼干的面积等等。
掌握圆的面积计算方法,可以帮助我们更好地理解和解决与圆相关的问题。
除了计算圆的面积,我们还可以进一步探索圆的性质和特点。
圆是一个几何图形,具有无限个点,这些点到圆心的距离都相等。
小学奥数圆面积的典型题和解法

圆面积的典型题和解法一、半径r 2替代法题的特点:一般将正方形,三角形和圆放到一起,一般已知条件是正方形或三角形面积,求圆的面积。
解法:一般设法求出r ,或者求出r 2,★注意:园内直角三角形一般为等腰直角三角形,两腰等长,斜边是斜边上高的2倍。
例1:已知下图阴影部分面积为8平方米,求圆的面积:解:由已知条件可得r 2 =8,因此,圆的面积为:814.32⨯=r π例2:ABCD 为正方形,已知AC 长6m ,求阴影部分面积:解:△ACD 为等腰直角三角形,则S △ACD=6*3/2=9㎡AD=DC=rAD*DC/2=9因此,r 2 =18, 扇形DAC 的面积为:4/1814.34/2⨯=r π 因此,阴影部分面积为:18-4/1814.34/2⨯=r π例3:求圆与圆内最大正方形的面积比值。
解:△ABC 为等腰直角三角形,则S △ABC=22/2r r r =⨯正方形的面积是两个三角形面积和,为:22r圆的面积为:2r π,则圆与圆内最大正方形的比为:2/π练习题:1、已知下图阴影部分面积为5平方米,求圆的面积:2:、在右图扇形中,正方形面积为30平方米,求阴影部分面积:3:求正方形与正方形内最大圆的面积比值。
题的特点:一般圆内由多个阴影部分面积构成,阴影由弧线和弧线构成,或者由弧线和直线构成。
解法:注意观察面积相同的部分,将相同的部分移动替换,若遇到轴对称图形可尝试旋转图形,记住常见的面积平移图例。
,例1:求阴影部分的面积:解:正方形外三角形底为6,和正方形内三角形底相同,由于顶角相同,所以两个三角形可以互换。
阴影部分面积则为:正方形面积-1/4圆的面积例2:求阴影部分的面积:解:平移得到下图:则阴影部分面积为扇形面积-三角形面积2562π⨯-=44cm2/2.84/例3:求阴影部分的面积:解:注意观察,:阴影部分面积为:1*1-1*1/2=1/2练习题:求阴影部分面积:题的特点:图有好几个部分组合而成,各部分之间存在着一定的关系。
圆的面积应用题及答案

圆的面积应用题及答案圆的面积应用题及答案「篇一」圆的面积公式是很容易记住,下面一起看看圆的面积应用题及答案吧。
在下面这道题中,可以用直径是80的圆的面积的一半减去直径是30的圆的面积的一半,再减去直径是50的圆的面积的一半,就可以算出阴影部分的面积。
这个阴影的面积,是用正方形的面积减去一个圆的面积。
先把这个图平移,成为一个大圆内有一个小圆,这样用大圆的'面积减去小圆的面积。
这个阴影的面积可以用半径是10厘米的圆的面积一半减去正方形的面积来计算。
这个阴影的面积算出圆环的面积除以2就可以了。
这个图形的面积是用一个圆的面积加上中间正方形的面积来计算。
注意事项灵活用公式,结果不能变。
圆的面积应用题及答案「篇二」1.把一个圆形纸片沿着半径剪成若干面积相等的小扇形,一上一下拼成一个近似的长方形.新图形的周长比圆形纸片的周长增长了16厘米.求这个圆形纸片的`面积?新增加的16厘米就是长方形的二个宽,即圆的二个半径。
那么半径是:16÷2=8圆的面积是:3.14×8×8=200.962.两个圆的面积之差是209平方厘米,已知大圆的周长是小圆周长的10/9倍,则小圆的面积为多少平方厘米?大圆的周长是小圆周长的10/9倍,半径就是10/9倍,面积就是(10/9)^2=100/81倍,下面是差倍问题,小的数=差/(倍数-1)=209/(100/81 -1)=8913.有一根长为40米的铜丝,在一个圆管上绕了12圈,还剩下2.32米,求圆管的直径?40-2.32=37.68(米)37.68÷12=3.14(米)3.14÷3.14=1(米)答:直径为1米4.将一个圆沿半径剪开,再拼成一个近似的长方形.已知长方形的周长是41.4厘米,那么,这个圆的周长和面积各是多少?设半径为X厘米.(因为长方形的宽就是圆的半径,长方形的两条长就是圆的周长.圆的周长公式是:半径×2×3.14 )(3.14×2x)+2x=41.46.28x+2x=41.48.28x=41.4x=5圆的周长:半径×2×3.145×2×3.14=31.4平方厘米圆的面积:半径×半径×3.145×5×3.14=78.5平方厘米即:20%X+6+(20%X+6)-2+x/3=x得x=37.5吨圆的面积应用题及答案「篇三」试题:1、画出一个周长为 12.56 厘米的圆,并用字母标出圆心和一条半径,再求出这个圆的面积。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
六年级集训27——智求面积(一)(讲解见后)
讲解:
第1题: 将原图中的圆旋转,得到,发现大正方形的面积是小正方形面积的2倍,
如果第一个正方形看1份,那第4个正方形就是1×2×2×2=8倍
第2题: “同外比异”策略,阴影甲比乙多6.88平方厘米,说明三角形比半圆形多6.88平方厘米,
3.14×4×4÷2=25.12平方厘米---半圆形面积
25.12+6.88=32平方厘米------三角形面积
32×2÷8=8厘米
第3题: “同外比异”策略,就是求大圆比小圆大多少,3.14×6×6-3.14×4×4=62.8(平方厘米)
第4题: 3.14×8=25.12(平方厘米)----(因为r×r=8平方厘米,所以直接将3.14×8就可以)
第5题:正方形内画个最大的圆,圆与正方形的比是3.14:4
24÷4×3.14=18.84(平方厘米)
(补充:如果是圆内画个最大的正方形.圆与正方形的比3.14 : 2)
第6题: 10×2=20(平方厘米)----正方形面积
3.14×20=62.8平方厘米----完整的圆面积(提示:如图, 与第4题同理)
62.8÷4=15.7(平方厘米)----白色扇形的面积,也就是1/4圆的面积
20-15.7=4.3(平方厘米)
第7题:”同外比异”策略,说明长方形比大三角形多12平方厘米
12×8=96平方厘米-----长=方形面积
96-12=84平方厘米-----大三角形的面积
84×2÷8=21厘米----DE
21-12=9厘米---CE
第8题:
画图发现,如果新长方形与原来正方形面积相等的话,
说明减少部分(红色面积)与增加部分(兰色部分)面积相等,也说明兰色部分
也是现在新长方形面积的1/5,那么推理出新长方形的长为4÷1/5=20厘米
20-4=16厘米-----原来正方形的边长
16×16=256平方厘米
第9题 既然周长不变,说明长的1/5=宽的1/4, 推理出长与宽的比是5:4
90÷2=45厘米------ 一长一宽的和 45×
455+=25厘米----长 45×454
+=20厘米-----宽
25×20=500平方厘米。
