福建省宁德第一中学
福建省贵族学校排名情况汇总

福建省贵族学校排名情况汇总名次中学名称全国排名所在城市城市排名状元人数1、泉州五中39,泉州182、厦门外国语学校39,厦门183、漳州一中50,漳州174、福州一中63,福州165、龙海第一中学78,漳州256、顺昌一中105,南平147、厦门双十中学105,厦门248、永定一中150,龙岩139、仙游第一中学150,莆田1310、程溪中学354,漳州3111、福州八中210,福州2212、闽侯第一中学210,福州2213、龙岩一中210,龙岩2214、上杭一中210,龙岩2215、武平一中210,龙岩2216、南平一中210,南平2217、宁德第一中学210,宁德1218、泉州七中210,泉州2219、同安第一中学210,厦门3220、厦门一中210,厦门3221、虞阳中学354,福清1122、福建师范大学附属中学354,福州4123、福清华侨中学354,福州4124、福州格致中学354,福州4125、福州五中354,福州4126、闽清一中354,福州4127、平潭一中354,福州4128、建瓯一中354,南平3129、浦城第一中学354,南平3130、福安一中354,宁德2131、莆田第一中学354,莆田2132、惠安一中354,泉州3133、晋江养正中学354,泉州3134、连江一中354,泉州3135、永春一中354,泉州3136、三明清流一中354,三明1137、尤溪一中354,三明1138、厦门英才学校354,厦门51福州西湖国际学校(从幼儿园到高中)收费标准(2023秋季):幼儿园阶段:68000元(人民币)/人/学年小学阶段:86000元(人民币)/人/学年中学阶段:105000元(人民币)/人/学年高中阶段:105000元(人民币)/人/学年备注:住宿费:3600元(人民币)/人/学期午餐费:30元(人民币)/人/餐,580元(人民币)/人/月住宿生早晚餐:30元(人民币)/人/天,580元(人民币)/人/月(周一到周五住宿)住宿伙食费均按学期缴交。
高中体育与健康课实施选项教学的六步骤

推动着体育教师积极地参与体育课程改革 。本文就福建省宁德第一中学高 中体育选项教学三年的课改实践 ,总
结出实施选项教学的六步骤 ,为其他学校更好实施高 中体育课选项教学提供参考。
关 键 词 :体 育与健 康课 ;选 项 教学 ;步骤 中图 分 类号 :G 0. 87 4 文 献 标识 码 :A 文 章编 号 :17- 5X (oo l 0 6 0 64 11 2l )O一 8— 3
.2 . 有助于学生提高学习兴趣 ,培养运动爱好 11 要 了解本 校体 育教 师 的 数 量 与专 调查 表 明,福 建省 宁德第 一 中学高 中生 体
和专 长 ,树立 终身 体育 的意识 ;说 它 是难 项 教学 能力 班 开 展 教 学 ,而 且所 有 的 学 生 都 学 习 同 易 ,而 实施选 项教 学 ,操 作起 来会 碰 到一
了解 ,并且 有初 步 的判 断与组 织 ,将对 开
设项 目多少 有很 大 的主导 作用 ,尤 其是 场
地 大 小 、器 材 多少等 ,这 些都 是应 考虑 到
投稿 日期 :2 0 — 1 1 09 1— 9
作者简 介:陈春 (97 ) 16 一 ,中教 高级 ,福 建省 中小 学体育 学科 带 头人 ,中 国体育 科学 学会会 员 。研究 方 向:学 校体 育教 学 。
自 20 04年 9月起 ,《 通 高中体 育 与 的 因素 ,如福 建省 宁德第 一 中学校 现有 标 的项 目比较 集 中在篮 球 、田径 、排球 、足 普 健 康课 程标 准 ( 实验 ) 》在 广 东、 南 、 海 山 准 40 塑 胶 田径场 、 足 球 场 、排 球 场 、 0米 实验 区开 展 实验 。福 建 省 于 20 06年 开 始 杠 1 付 、双杠 1 付 、室 内体操房 、健 身 2 0
福建省宁德第一中学2024届高三第一次考试化学试卷及答案

宁德一中2024届高三第一次检测高三化学考试本试卷共8页,20题,满分100分。
考试用时75分钟相对原子质量:H1Li7C12N14O16Na23Al27Cl35.5S32Fe56Cu64P31一、选择题(本题共16小题,每题3分,共48分,每小题只有一个选项符合题意。
)1.广东是岭南文化的集萃地。
下列有关岭南文化的说法不正确的是A.“海丝文化”:海上丝绸贸易用于交易的银锭中仅存在离子键B.“茶艺文化”:沏泡功夫茶利用了萃取原理,水作萃取剂C.“建筑文化”:制作博古梁架时,在木材上雕刻花纹的过程主要发生物理变化D.“戏剧文化”:现代粤剧舞台上灯光光柱的形成是因为丁达尔效应2.下列化学用语或图示表达不正确...的是≡A.乙炔的结构简式:HC CHB.顺2--丁烯的分子结构模型:C.基态Si原子的价层电子的轨道表示式:Na O的电子式:D.223.将V L浓度为0.3mol/L的盐酸浓度扩大一倍,采取的措施合理的是A.将溶液加热浓缩至原来体积的一半B.通入标准状况下的HCl气体6.72LC.加入3mol/L的盐酸0.2V L,再稀释至1.5V LD.加入等体积0.9mol/L的盐酸,混合均匀4.Cl2O沸点3.8°C,熔点-116°C,是很好的氯化剂,利用HgO+2Cl2=HgCl2+Cl2O可以制备高纯度的Cl2O。
下列说法正确的是(N A为阿伏加德罗常数)A.标准状况下,2.24LCl2O含有分子数为0.1N AB.0.2mol氯气与足量的HgO反应,转移电子数为0.2N AC.HgO与稀硝酸反应的离子方程式为O2-+2H+=H2OD.Cl2O与氢氧化钠溶液反应的离子方程式为Cl2O+2OH-=Cl-+ClO-+H2O5.南京大学科研团队首次发现氨还原过程中的多米诺效应:即一旦完成第①步,将自发完成后续步骤,反应过程示意图如下。
N A表示阿伏加德罗常数的值,下列说法正确的是A.22.24LN 含有N A 个价电子B.33.5gLi N 中含有3N A 个共价键C.若0.7gLi 参与第②步反应转移电子数为0.1N AD.①②③步反应均为氧化还原反应6.对下列粒子组在溶液中能否大量共存的判断和分析均正确的是选项粒子组判断和分析A Na +、3Al +、3NO -、32NH H O⋅不能大量共存,因发生反应332242Al 4NH H O=AlO 4NH 2H O +-++⋅++BH +、K +、223S O -、24SO -不能大量共存,因发生反应:223222H S O S O =SO H +-+↓+↑+CNa +、2Cu +、24SO -、22H O 能大量共存,粒子间不反应D H +、K +、25C H OH 、4MnO -能大量共存,粒子间不反应A.AB.BC.CD.D7.γ-崖柏素具天然活性,有酚的通性,结构如图。
福建省宁德第一中学2023-2024学年高二上学期开学检测数学试题(解析版)

宁德一中2023-2024学年度第一学期期初高二阶段检测数 学 试 题一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1. 已知公比为q 的等比数列{}n a 的前n 项和2n n S c q =+⋅,*n ∈N ,且314S =,则4a =( ) A. 48 B. 32 C. 16 D. 8【答案】C 【解析】【分析】根据11,1,2n n n S n a S S n −= = −≥ ,作差求出c ,再根据314S =,求出q ,即可得到通项公式,再代入计算可得;【详解】解:因为公比为q 的等比数列{}n a 的前n 项和2nn S c q =+⋅①,当1n =时112a S c q ==+⋅, 当2n ≥时112n n S c q−−=+⋅②,①−②得()112222n nn n a q q q q −−−==⋅⋅⋅−,所以222q c q −=+,则2c =−,又314S =,所以334221S q =−+⋅=,解得2q , 所以2n n a =,则44162a ==; 故选:C2. 记等差数列{}n a 的前n 项和为n S ,已知342a a =,则一定成立的是( ) A. 25a a > B. 1n n a a +<C. 90S =D. 数列{}n S 有最大项【答案】C 【解析】【分析】设等差数列的公差为d ,由342a a =,得14a d =−,然后根据等差数列的通项公式和求和公式逐个分析判断即可【详解】设等差数列的公差为d ,由342a a =,得1122(3)a d a d ++,化简得14a d =−,对于A ,213a a d d =+=−,5140a a d =+=,当0d >时,25a a <,所以A 错误,对于B ,1n n a a d +−=,当0d <时,1n n a a +<,所以B 错误, 对于C ,因为14a d =−,所以199519()99(4)02a a S a a d +===+=,所以C 正确, 对于D ,因为14a d =−,所以221(1)11114422222n n n S na d dn dn dn dn d d n −=+=−+−=−+, 当0d >时,n S 无最大值,所以此时数列{}n S 无最大项,所以D 错误, 故选:C3. 南宋数学家杨辉所著的《详解九章算法》中出现了如图所示的形状,后人称之为“三角垛”.其最上层有1个球,第二层有3个球,第三层有6个球,第四层10个…,则第六层球的个数为( )A. 15B. 18C. 20D. 21【答案】D 【解析】n 项求和公式计算得出结果. 【详解】根据题意,设各层球的个数构成数列{}n a ,由题意可知,1211,212,a a a ==+=+3213123,,123n n a a a a n n −=+=++=+=++++ , 则有()()1122n n n n n a +×+==,故第六层球的个数667212a ×==, 故选:D.4. 已知各项均为正数的等比数列{}n a 中,1310a a +=,5758a a +=,则该数列的公比为( )A. 2B. 1C.12D.14【答案】C 【解析】【分析】由等比数列的定义和性质知34571a a q a a +=+,结合0q >可得.【详解】设数列{}n a 公比q , 因数列{}n a 各项均为正数,故0q >, 则()()464244571111135108a a a q a q q a a q q a a q +=+=+=+==, 得4116q =解得12q =或12q =−(负值舍去). 故选:C .5. 已知{}n a 为递增的等比数列,且满足34a =,151158a a +=,则7a =( ) A.12B. 1C. 16D. 32【答案】C 【解析】【分析】首先化简等式,并结合等比数列的性质求得15,a a ,再根据等比数列的基本量求7a . 【详解】由题意,2151531515516108a a a a a a a a a +===+=,,∴, 联立15151610a a a a =+= ,则1528a a = = 或1582a a = = 因为{}n a 是递增的数列,得1528a a ==,, 设等比数列{}n a 的公比为q ,则4514a qa == 47316a a q ∴==.故选:C.6. 已知数列{}n a 为各项为正数的等比数列,且1a ,3a ,2a 成等差数列,则数列{}n a ( ) A. 单调递增 B. 单调递减C. 先递增后递减D. 是常数列【答案】D 【解析】为【分析】根据等差数列、等比数列的性质计算基本量即可得通项公式; 【详解】设数列{}n a 的首项为1a ,公比为q ,因为1a ,3a ,2a 成等差数列,,则3122a a a =+,即21112a q a a q =+, 因为10a ≠,所以可得2210q q −−=,数列{}n a 为各项为正数,解得1q =或12q =−(舍), 可得1n a a =为常数列. 故选:D.7. 设等差数列{}n a 前n 项和为n S ,若39S =,636S =,则789a a a ++=( ) A. 63 B. 45C. 43D. 27【答案】B 【解析】【分析】由36396,,S S S S S −−成等差数列即可求解.【详解】解:由等差数列性质知36396,,S S S S S −−成等差数列, 即969,27,S S −成等差数列,96227945S S −=×−=. ∴78996=45a a a S S ++=−. 故选:B .8. 首项为20−的等差数列,从第10项起开始为正数,则公差d 的取值范围是( ) A. 209d >B. 52d ≤C.20592d <≤ D.20592d ≤< 【答案】C 【解析】【分析】由题意可得9100a a ≤ > ,从而求出公差d 的取值范围. 【详解】因为首项为20−的等差数列,从第10项起开始为正数,所以91000a a ≤ > ,即20802090d d −+≤ −+> ,解得20592d <≤, 故选:C二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.的9. 已知数列{}n a ,{}n b 均为等比数列,则下列结论中一定正确的有( ) A. 数列{}n n a b 是等比数列B. 数列{}n n a b +是等比数列C. 数列lg n n b a是等差数列D. 数列(){}22lg n a b n是等差数列【答案】ACD 【解析】【分析】根据等比数列和等差数列的定义或通项公式判断.【详解】设数列{}n a 的公比为1q ,数列{}n b 的公比为2q ,所以111n n a a q −=,112n n b b q −=.对于A ,()11111121112n n n n n a b a b q q a b q q −−−==,从而数列{}n n a b 的公比为12q q ,故A 正确.对于B ,111112n n n na b a q b q −−+=+,1q 与2q 不一定相等,所以数列{}n n a b +不是等比数列,故B 错误.对于C ,1121211111lg lg lg (1)lg n n n n b b q b q n a a q a q −−==+−,从而数列lg n n b a的公差为21lg q q .故C 正确. 对于D ,()221112lg 2lg 2lg 2(1)lg n nn n a b a b a b n q q ==+−,从而数列(){}22lg n n a b 的公差为122lg q q,D 正确. 故选:ACD .【点睛】结论点睛:本题考查等差数列和等比数列的判断.掌握等差数列和等比数列的定义是关键.判断方法有:(1)定义法;(2)通项公式法;(3)等差中项、等比中项法;(2)前n 项和公式.特别注意等比数列中各项均不为0.10. 在数列{}n a 中,221n n a a p −−=(*2,,n n p ≥∈N 为非零常数),则称{}n a 为“等方差数列”,p 称为“公方差”,下列对“等方差数列”的判断正确的是( ) A. {}(3)n−是等方差数列B. 若正项等方差数列{}n a 的首项11a =,且124,,a a a是等比数列,则n a =C. 等比数列不可能为等方差数列D. 存在数列{}n a 既是等差数列,又是等方差数列 【答案】BC 【解析】【分析】根据等方差数列的定义依次分析四个选项可得答案.【详解】对于A ,因为22(3)9nn n a =−=,222219972a a −=−=,22323299648a a −=−=, 22222132a a a a −≠−,所以{}(3)n −不是等方差数列,故A 错误; 对于B ,因为0n a >,11a =,221(1)1n a a n p pn p =+−=−+,所以22211a p p p =−+=+,4a =因为 124,,a a a 是等比数列,所以2214a a a =,所以1p +=,所以20p p −=,因为0p ≠,所以1p =,所以2n a n =,又0n a >,所以n a =B 正确;对于C ,设等比数列{}n a 的公比为q ,则11n n a a q−=,则当2n ≥时,2222222422421111(1)n n n n n a a a q a q a q q −−−−−=−=−,若22421(1)n a q q −−为常数,则必有210q −=,此时2210n n a a −−=,则数列{}n a 不可能是等方差数列,故C 正确; 对于D ,假设存在数列{}n a 既是等差数列,又是等方差数列,则当2n ≥时,1n n a a d −−=且221n n a a p −−=(0)p ≠, 若0d =,则1n n a a −=,则2210n n a a p −−==,不合题意, 若0d ≠,则11()()n n n n a a a a p −−−+=,得1n n p a a d−+=,又1n n a a d −−=, 所以22nd p a d=+为常数,必有210n n a a −−=,与假设矛盾, 故存在数列{}n a 既是等差数列,又是等方差数列.故D 错误; 故选:BC11. 下列说法中,正确的有( )A. 已知12n n a a +=−,则数列{}n a 是递减数列 B. 数列{}n a 的通项22n a n kn =−+,若{}n a 为单调递增数列,则3k <C. 已知正项等比数列{}n a ,则有1845a a a a +≤+D. 已知等差数列{}n a 的前n 项和为24,4,10n S S S ==,则618S = 【答案】ABD 【解析】【分析】由12n n a a +−=−,可判定A ;1210n n a a n k +−=+−>恒成立,可判定B ;根据11a =,2q ,得到1845a a a a +>+,可判定C ;由24264,,S S S S S −−构成等差数列,列出方程求得618S =,可判定D.【详解】对于A 中,由12n n a a +=−,可得12n n a a +−=−,所以数列{}n a 是递减数列,所以A 正确; 对于B 中,若数列{}n a 的通项22n a n kn =−+,则()()221(1)122210n n a a n k n n kn n k + −=+−++−−+=+−> 恒成立,所以3k <,所以B 正确;对于C 中,正项递增的等比数列{}n a ,若11,2a q ==,可得734184512129,2224a a a a +=+=+=+=, 此时1845a a a a +>+,所以C 不正确;对于D 中,等差数列{}n a 的前n 项和为n S 且244,10S S ==, 根据24264,,S S S S S −−构成等差数列,即64,6,10S −构成等差数列,可得641026S +−=×,解得618S =,所以D 正确. 故选:ABD. 12. 数列{}n a 满是()1N 218nna n ∗=∈−,则( ) A. 数列{}n a 的最大项为6a B. 数列{}n a 的最大项为5a C. 数列{}n a 的最小项为5a D. 数列{}n a 的最小项为4a【答案】BD 【解析】【分析】根据条件()1N 218n na n ∗=∈−,判断出数列{}n a 的单调性即可求出结果. 【详解】因为()1N 218n na n ∗=∈−,所以11111112182182218218(218)(218)(218)(218)n n nn n n n n n n n a a +++++−−−−−=−==−−−−−−,由10n n a a +−>,得到9218n <<,且易知,4n ≤时,0n a <,当5n ≥时,0n a >,所以12345610016a a a a a a >=−>>><<>> 所以数列{}n a 的最大项为5a ,最小项为4a , 故选:BD.三、填空题:本题共4小题,每小题5分,共20分.13. 已知在等比数列{a n }中,a 3=7,S 3=21,则公比q =__________ 【答案】1或12− 【解析】【分析】由a 3=7,S 3=21,得到21117,14a q a a q =+=求解. 【详解】解:因为在等比数列{a n }中,a 3=7,S 3=21, 所以21117,14a q a a q =+=, 两式相除得: 2210q q −−=, 解得1q =或12q =−, 故答案为:1或12−14. 在各项均为正数的等比数列{}n a 中,若243546216a a a a a a ++=,则35a a +=________. 【答案】4 【解析】【分析】由等比数列性质求解即可.【详解】由243546216a a a a a a ++=可得:223355216a a a a ++=, 则()23516a a +=,因为等比数列{}n a 的各项均为正数,则354a a +=. 故答案为:4 15. 已知数列{}n a 为32,43,54,65, ,则该数列的一个通项公式可以是________. 【答案】21n n a n +=+(答案不唯一) 【解析】【分析】分析数列{}n a 前4项的特征,求出前4项都满足的一个通项公式作答.的【详解】依题意,312422532642,,,211321431541++++====++++, 所以前4 项都满足的一个通项公式为21n n a n +=+. 故答案为:21n n a n +=+ 16. 已知等差数列{}n a ,{}n b ,其前n 项和分别为n S ,n T ,且满足321n n S n T n +=−,59a T =___________. 【答案】451【解析】【分析】运用等差数列的性质即可得出21n S −与n a 的关系,从而得出结论. 【详解】运用等差数列的性质()2121n n S n a −=−,可得599,S a =即9519a S =⋅, 由等差数列性质可知599911124991751a S T T =⋅=×=. 故答案为:451. 四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.17. 有一批空气净化器,原销售价为每台800元,在甲、乙两家家电商场均有销售.甲商场用如下的方法促销:买一台单价为780元,买两台每台单价都为760元,依次类推,每多买一台,则所买各台单价均再减少20元,但每台最低不能低于440元;乙商场一律都按原价的75%销售.某单位需购买一批此类空气净化器,问去哪家商场购买花费较少?【答案】若买少于10台,去乙商场花费较少;若买10台,去甲、乙商场花费一样;若买超过10台,去甲商场花费较少. 【解析】【分析】设某单位需要购买x 台空气净化器,甲、乙两商场的购货款的差价为y , 根据题意列出分段函数,求出0y =时对应的x ,再根据函数的单调性说明即可. 【详解】设某单位需要购买x 台空气净化器,甲、乙两商场的购货款的差价为y , ∵去甲商场购买共花费(80020)x x −,由题意,有80020440x − ,∴118x∴()*(80020)80075%,11844080075%,18x x x x yx x x x −−× ∈−×> N , .即()2*20020,118160,18x x x yx x x −∈−> N , 当110x ≤<时,0y >;当10x =时,0y =;当10x >时,0y <.所以,若买少于10台,去乙商场花费较少;若买10台,去甲、乙商场花费一样;若买超过10台,去甲商场花费较少.【点睛】本题考查分段函数的应用,解本类题的关键在于读懂题意,根据题意写出函数表达式,属于基础题.18. 已知函数11221(),2n n n f x x S f f f f n n n n −−=+=++++,其中*N n ∈,且2n ≥.(1)当2n ≥时,求n S ;(2)设112a =,()()()*11,211n n n a n n S S +=∈≥++N ,记数列{}n a 的前n 项和为n T ,求使得2n m T <恒成立的m 的最小正整数. 【答案】(1)1n S n =− (2)2 【解析】【分析】(1)依据题给条件,利用等差数列前n 项和公式即可求得n S ;(2)先利用裂项相消法求得数列{}n a 的前n 项和n T ,再依据题给条件列出关于m 的不等式,解之即可求得m 的最小整数 【小问1详解】 由()11221,2n n n f x x S f f f f n n n n −−=+=++++,可得11212111++++2222n n n S n n n n −−=++++12211(1)1++1222n n n n n n n n n n n n −−−−− =++++==−, 则当2n ≥时,1n S n =−. 【小问2详解】由(1)可得,当2n ≥时,1n S n =−,则当2n ≥时, ()()[]11111(11)(1)11n n n a S S n n +=++−++−+111(1)1n n n n ==−++, 则当2n ≥时,数列{}n a 的前n 项和1111111233411112n T n n n + −−−=− ++ +++ , 又当2n ≥时,13n +≥,11013n <≤+,211131n ≤−<+, 由2n m T <恒成立,可得12m ≤,解之得2m ≥, 则当2n ≥时,使得2n m T <恒成立的m 的最小整数为2. 当1n =时,112121T a m ==<=成立, 综上,使得2n m T <恒成立的m 的最小整数为2. 19. 在等差数列{}n a 中,已知公差0d <,110a =,且2a ,5a ,7a 成等比数列.(1)求数列{}n a 的通项公式n a ;(2)求1260a a a +++ 的值.【答案】(1)11na n =− (2)1280【解析】【分析】(1)根据已知条件求得公差d ,由此求得n a .(2)先判断n a 的符号,根据等差数列前n 项和公式求得正确答案.【小问1详解】210a d =+,5104a d =+,7106a d =+, 又2a ,5a ,7a 成等比数列,所以2(10)(106)(104)d d d ++=+,化简得20d d +=,解得1d =−或0d =,又0d <,所以1d =−,可得数列{}n a 的通项公式10(1)11n a n n =−−=−;【小问2详解】由(1)得11na n =−,由110n a n =−≥,得111n ≤≤, 由110n a n =−<,得11n >,设数列{}n a 的前n 项和为n S ,所以126012111213606011||||||()()2a a a a a a a a a S S +++=+++−+++=−+ 16011160()11()2128022a a a a ++=−+×=, 所以1260||||||1280a a a +++=. 20. 已知数列{}n a 的前n 项和为n S ,且满足0n a >,()42n n n S a a =+.(1)求数列{}n a 的通项公式;(2)若等差数列{}n b 满足32n n S n b n c −=+,且1b ,212b ,313b 成等比数列,求c . 【答案】(1)*()2n a n n N =∈ (2)12c =−【解析】 【分析】(1)利用11,2,1n n n S S n a S n −−≥ = = ,可知数列{}n a 为2为首项,2为公差的等差数列,根据等差数列通项公式计算即可;(2)求数列{}n a 的前n 项和为n S ,根据等差数列及等比数列的性质可求出c .【小问1详解】因为()42n n n S a a =+,当2n ≥时,()11142n n n S a a −−−+=两式相减得()()11112242222n n n n n n n n n a a a a a a a a a −−−−=−=−+−++ 化简得()()()1112n n n n n n a a a a a a −−−=+−−,0n a > ,10n n a a −∴+>,12n n a a −∴−=当1n =时,()11142a a a +=,解得12a =或10a =(舍去)故数列{}n a 是以2为首项,2为公差的等差数列.()()*2122N n a n n n ∴=+−×=∈.【小问2详解】由(1)知,2(1)222n n n S n n n −=+×=+,2322n n n S n n b n n c c−+−∴==+, 111b c ∴=+,262b c =+,3153b c=+, 1b ,212b ,313b 成等比数列,22131123b b b ∴=× , 即259(3)(1)(2)c c c =+++,整理得:241670c c ++=, 72c ∴=−或12c =−. ①当12c =−时,2n b n =,所以12n n b b +-=(定值),满足{}n b 为等差数列, ②当72c =−时,24227n n n b n −=−, 125b ∴=−,24b =−,330b =−, 不满足2132b b b =+,故此时数列{}n b 不为等差数列(舍去). 综上可得12c =−. 21. 已知数列{}n a 满足11a =,且122n n n a a −=+(2n ≥,且*N n ∈).(1)求2a ,3a ;(2)求数列{}n a 的通项公式n a .【答案】(1)26a =;320a =(2)122n n a n =−⋅ 【解析】【分析】(1)根据递推公式,赋值求23,a a ;(2)首先变形递推公式,证明数列2n n a是等差数列,即可求通项公式. 【小问1详解】当2n =时,221226a a =+=,当3n =时,3322220a a +;【小问2详解】 依题意,122n n n a a −=+,两边同时除以2n , 得11122n n n n a a −−=+,即11122n n n n a a −−−=,2n ≥,*N n ∈, 所以数列2n n a是首项为1122a =,公差为1等差数列, 即()1111222n n a n n =+−×=−, 所以122n n a n=−⋅. 22. 已知数列{}n a 的通项为n a ,前n 项和为n S ,且n a 是n S 与2的等差中项,数列{}n b 中,11b =,点()1,n n P b b +在直线20x y −+=上. (1)求数列{}n a 、{}n b 的通项公式n a 、n b ;(2)设{}n b 的前n 项和为n B ,试比较12111nB B B +++ 与2的大小; (3)设1212n n nb b b T a a a =+++ ,若对一切正整数n ,()n Tc c Z <∈恒成立,求c 的最小值. 【答案】(1)2,21n n n a b n ==−;(2)121112nB B B +++< ;(3)3. 【解析】【分析】(1)根据等差中项的性质列式,然后结合11,1,2n nn S n a S S n −= = −≥ 求得数列{}n a 的通项公式.将P 点坐标代入直线方程,由此证得{}n b 是等差数列,进而求得数列{}n b 的通项公式.(2)先求得n B ,然后利用放缩法结合裂项求和法证得121112nB B B +++< .(3)利用错位相减求和法求得n T ,由此求得c 的最小值. 【详解】(1)由于n a 是n S 与2的等差中项,故22n n S a +=,当1n =时,12a =,当2n ≥时,22n n S a +=,1122n n S a −−+=,两式相减并化简得12n n a a −=,故数列{}n a 是首项为2,公比为2的等比数列,所以2n n a =.将()1,n n P b b +代入20x y −+=上,故12n n b b +=+,故{}n b 是首项为1,公差为2的等差数列,故21nb n =−. 的(2)依题意21212n n B n n +−=⋅=,所以2222121111111123n B B B n ++…+=+++…+111111*********(1)2231n n n n <+++…+=+−+−+…+− ××−⋅−122n =−<,所以121112nB B B +++< . (3)22135212222n n n T −=+++…+①,234111352122222n n n T +−=+++…+② ①-②得2331111122212222222n n n n T +−=++++…+−,化简得21213322n n n n T −−=−−<,又因为42341347372222216T =+++=>,所以满足条件n T c <的最小整数值3c =. 【点睛】本小题主要考查等差数列和等比数列通项公式的求法,考查等差中项的性质,考查裂项求和法与错位相减求和法,考查放缩法,属于中档题.。
关于2022年秋季福建宁德一中初中部招生的通知

【导语】从宁德市教育局了解到,关于2022年秋季福建宁德⼀中初中部招⽣的通知已发布,详细内容如下: 蕉城区、东侨经济技术开发区教育局,宁德⼀中: 根据《宁德市政府专题会议纪要》(〔2020〕123号)精神,2022年秋季宁德⼀中初中部计划招⽣10个班、500⼈。
经我局研究,现就该校招⽣相关⼯作通知如下: ⼀、招⽣办法 该校新招的500名学⽣,优先考虑市重点企业⾼管⼦⼥和市引进⼈才⼦⼥(宁德⼀中在编教职⼯⼦⼥视同引进⼈才⼦⼥);余下的名额按蕉城占90%、东侨占10%的⽐例分配给蕉城和东侨教育局统筹安排招⽣,招⽣对象为:中⼼城区(城南、蕉南、蕉北、东侨)户籍学⽣及蕉城和东侨认定的招⽣优待照顾对象,具体招⽣办法由蕉城和东侨教育局制定并报我局备案同意。
⼆、关于市重点企业⾼管⼦⼥、市引进⼈才⼦⼥的招⽣办法 1.市重点企业⾼管的界定:参照《宁德市招⽣委员会关于印发<2019年宁德市龙头企业相关⼈员⼦⼥就读中⼼城区义务教育阶段学校的操作细则>的通知》(宁招委〔2019〕5号)规定的申报对象基础上,增加2021年新增的市龙头企业,即:福建⼤唐国际宁德发电有限责任公司、福建宁德核电有限公司、上海汽车集团公司乘⽤车福建分公司、宁德时代新能源科技股份有限公司、宁德新能源科技有限公司、中铝东南铜业公司、福建⿍信科技有限公司、福建青拓设备制造有限公司、青拓集团有限公司(含福建青拓镍业有限公司、福建青拓实业股份有限公司、福建⿍信实业有限公司、福建甬⾦⾦属科技有限公司、福建宏旺实业有限公司、福建青拓上克不锈钢有限公司)的法定代表⼈、董事长、总裁、总经理、副总经理、总⼯程师、总设计师、董事会秘书。
2.市引进⼈才的界定:宁德市引进的⼀类、⼆类“天湖⼈才”(宁德⼀中在编教职⼯⼦⼥视同市引进⼈才⼦⼥)。
3.办理流程: (1)市重点企业⾼管⼦⼥、市引进⼈才⼦⼥,持所需材料(附件1),于2022年7⽉12⽇8:30-17:00到宁德⼀中初中部登记,并填写《2021年秋季宁德⼀中初中部就读申请登记表》(附件2)。
福建省宁德第一中学2024届高三第一次考试地理试卷及答案

2024届宁德一中地理一模一、选择题组(16*3)贵州中西部地区冬季多出现水平能见度小于1千米的锋面雨雾,雾区位于锋线附近。
下图为贵州某次锋面雨雾发生过程中,大致呈纬向分布的三个测站测得的能见度变化图。
这次雨雾形成的气象条件是西南气流沿锋后弱冷平流爬升,形成弱降水。
雨雾随锋面缓慢东移消亡。
完成下面小题。
1.三个测站的地理位置,自西向东依次排序正确的是()A.①②③B.①③②C.②③①D.③①②2.本次锋面雨雾出现时,雾区地面以上气温垂直变化最接近的是()A. B.C. D.雨幡洞云是一种奇特的天气现象(图),薄薄的云层出现一个空洞,一缕缕"云丝”似乎从洞中心部分落下,犹如“空中水母”。
专家解释,这是由于大气层中存在低于0℃而仍然保持液态的过冷液滴,受飞机飞行产生扰动而产生云洞,据此完成下面小题3.雨幡洞云位于大气垂直分层中的()A.平流层B.对流层C.中间层D.逸散层4.发生雨幡洞云的云层温度较低,是由于()A.距离太阳较远B.距离地面较远C.距臭氧层较远D.距电离层较远研究发现,寒冷地区的季节性积雪会显著改变土壤温度,进而影响冻土发育。
下图示意新疆地区积雪站点2005~2020年冷季(10月至次年3月)平均积雪深度。
据此完成下面小题。
5.与北疆雪站比,南疆雪站积雪深度存在差异的主要原因是()①风力较大②大气干燥③气温较低④地形封闭A.①②B.①③C.②④D.③④6.与伊吾站相比,青河站气温更低但地温较高,是因为()A.积雪减少土壤热量散失B.积雪大量反射太阳辐射C.积雪消融吸收大量地热D.积雪大量吸收太阳辐射下图为世界季风明显地区地理分布图,图中箭头显示了一些地区地面季风风向。
据此完成下面小题。
7.1月,图中A地盛行()A.东南季风B.西南季风C.东北季风D.西北季风8.关于B地季风的说法,正确的是()A.冬季风的形成主要与海陆热力差异有关B.夏季风性质暖热、干燥C.夏季风来得迟、退得早,易产生洪涝灾害D.冬季风势力强于夏季风菏泽地区为确保棉花生产稳定,大力发展棉花—西瓜间作套种技术。
2022-2023学年福建省宁德第一中学高一上学期10月月考化学试题(解析版)

福建省宁德第一中学2022-2023学年高一上学期10月月考化学试题学校:___________姓名:___________班级:___________考号:___________一、单选题1.用自来水养金鱼时,通常先将自来水晒一段时间再注入鱼缸,目的是()A.提高水温B.增加水中氧气的含量C.除去水中少量的次氯酸D.用紫外线杀死水中的细菌【答案】C【分析】普通的自来水在自来水厂都要通入氯气消毒,氯气和水反应生成盐酸和次氯酸,化学方程式为Cl2+H2O=HCl+HClO,HClO具有强氧化性,能够破坏细菌的结构,从而杀死细菌,达到消毒目的。
【详解】自来水在Cl2消毒中发生Cl2+H2O=HCl+HClO,HClO 具有强氧化性,能够破坏细菌的结构,从而杀死细菌,达到消毒目的。
如果将刚从自来水龙头里放出来的水直接养鱼,里面的次氯酸没有分解,就会将鱼致死,则放在阳光里晒一下就是为了将次氯酸分解和使盐酸挥发除去,故合理选项是C。
【点睛】本题考查氯水的性质及应用。
注重了化学与生活的联系,学生应学会利用化学知识来解决生活中常见的问题,注意晒一段时间主要是使HClO分解。
2.下面关于金属钠的描述正确的是A.少量钠应保存在水中B.钠离子性质很活泼C.钠很软,在新材料领域没有用途D.钠的化学性质很活泼,在自然界里不能以游离态存在【答案】D【详解】A.钠很活泼能与氧气和水反应,所以少量钠应保存在煤油中,故A错误;B.钠原子最外层一个电子,易失去,所以钠原子具有较强的还原性,而钠离子只能得电子,具有弱氧化性,故B错误;C.钠的导电和导热性较好,在新材料领域有用途,故C错误;D.钠与氧气、水等都能发生剧烈反应,性质活泼,在自然界里不能以游离态存在,故D正确;答案选D。
3.下列各组物质中,因为反应条件、浓度或用量不同而发生不同化学反应的是①C 与2O ①Na 与2O ①Fe 与2Cl ①Fe 与2OA .除①外B .除①①外C .除①外D .除①外4.某同学用下列装置进行有关Cl 2的实验。
2022-2023学年福建省宁德第一中学高二下学期3月月考地理试题
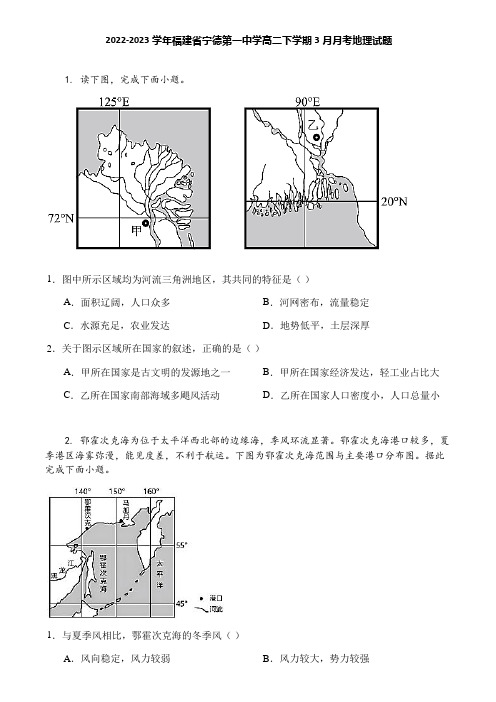
2022-2023学年福建省宁德第一中学高二下学期3月月考地理试题1. 读下图,完成下面小题。
1.图中所示区域均为河流三角洲地区,其共同的特征是()A.面积辽阔,人口众多B.河网密布,流量稳定C.水源充足,农业发达D.地势低平,土层深厚2.关于图示区域所在国家的叙述,正确的是()A.甲所在国家是古文明的发源地之一B.甲所在国家经济发达,轻工业占比大C.乙所在国家南部海域多飓风活动D.乙所在国家人口密度小,人口总量小2. 鄂霍次克海为位于太平洋西北部的边缘海,季风环流显著。
鄂霍次克海港口较多,夏季港区海雾弥漫,能见度差,不利于航运。
下图为鄂霍次克海范围与主要港口分布图。
据此完成下面小题。
1.与夏季风相比,鄂霍次克海的冬季风()A.风向稳定,风力较弱B.风力较大,势力较强C.低温湿润,带来暴雪D.饱含水汽,湿度较大2.鄂霍次克海夏季多雾的主要原因是()A.夏季风带来空气对流运动B.鄂霍次克海为面积广的陆间海C.夏季鄂霍次克海水温较高D.夏季风经过鄂霍次克海冷洋面3.冬季风对鄂霍次克海航运业带来不利影响,主要表现为()①冬季风影响下,海上风急浪高②寒潮频发,暴雪连绵③寒暖流交汇,影响航向④受冬季风影响,海面结冰时间长,冰层厚A.①③B.②④C.②③D.①④3. 埃布罗河是西班牙第一大河,流域内修建了多座大坝,用以调节流量的季节分配。
下图为“埃布罗河流域位置及其某支流上水文站月平均流量变化图”。
据此完成下面小题。
1.该支流大坝调节流量季节分配的主要目的是()A.灌溉B.航运C.防洪D.发电2.多座大坝调节了埃布罗河下游的流量,这有利于下游地区种植()A.茶叶B.水稻C.咖啡D.甜菜4. 利比里亚森林资源丰富,相关林业产品在国民经济中比重大。
下图为利比里亚区域位置图。
据此完成下面小题。
1.该国河流水文特征的描述正确的是()A.径流量大,汛期较长B.有结冰期,汛期出现在春季C.含沙量大,流速较快D.无结冰期,水位季节变化大2.该国地势特征为()A.西北高东南低B.西南高东北低C.东北高西南低D.东南高西北低3.若该国木材产品运往我国,最短的航线将是()A.好望角—莫桑比克海峡—苏伊士运河B.直布罗陀海峡—霍尔木兹海峡—马六甲海峡C.直布罗陀海峡—曼德海峡—马六甲海峡D.好望角—曼德海峡—霍尔木兹海峡5. 挪威朗伊尔(78°N)季节性冻土(夏季融化2~3米)和永久性冻土广布。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
福建省宁德第一中学
宁一中[2011]17号签发:张绍英宁德一中2011年秋季高一保送生招生方案为深入推进我市基础教育课程改革,全面实施素质教育,根据《宁德市人民政府办公室转发市教育局关于2010年初中毕业升学考试和普通高中招生制度改革方案的通知》(宁政办…2010‟67号)和
(宁宁德市教育局《关于2011年部分达标高中试行招收保送生的通知》教中…2011‟11号)的文件精神,我校2011年拟招收高中保送生,方案报告如下:
一、保送资格生指标与条件:
1、保送资格生指标:
2011年拟招收高中保送生56名(占正取生10%),保送资格生按1:3的比例推荐,即168名。
2、保送资格生条件:
具有蕉城区户籍、学籍的,2008年秋季入学、且初中毕业综合素质评定结果为优秀等级、初二地理、生物学业考试等级成绩(不含重考)和初三体育考试等级成绩均为A级,物理化学实验操作考查“合格”,初中阶段其他学科学业成绩优异的应届初中毕业生,在校期间表现特别突出或在某一方面有特长的学生同等条件下优先给予推荐保送。
二、保送生招收程序:
1、领导和组织机构:成立保送生招收工作领导小组,全面负责保送生招收工作。
领导小组组长:张绍英
副组长:原祥云、胡锦宏、胡昌成、陈开钊
成员:阮爱平、彭明河。
2、由蕉城区教育局将保送资格生指标分解到具有保送资格的学校。
保送资格学校负责对保送资格生的学业成绩、综合素质、个性特长等发展状况进行全面核查,根据保送资格生的志愿,集体研究后确定保送资格生。
保送资格生需填写《宁德一中保送生推荐表》(附1寸彩照2张),经学校盖章后,由学校于4月10日前统一交宁德一中教务处,每生报名费50元,另附学校推荐汇总表。
3、我校对各校推荐的保送资格生的材料进行审查无异议后,确认为保送资格生,并发放准考证。
4、由我校组织对保送资格生进行综合素质测试。
综合素质测试以初中研究性学习为主要内容,分科学素养和人文素养两部分,重点考察学生综合运用所学知识分析问题、解决问题的能力,以及创新精神和实践能力。
测试时间: 4月17日,上午9:00-11:30科学素养测试,下午3:
00-5:30人文素养测试。
测试地点:宁德一中教学楼。
5、录取:
⑴第一批录取综合素质测试成绩第一名的各保送资格生推荐中学的学生各1名;
⑵第二批按综合素质测试成绩由高分到低分择优录取保送资格生,直到录满56人为止。
(3)最后若出现成绩并列,在校期间表现特别突出或在某一方面有特长的学生同等条件下优先推荐保送。
录取名单将在宁德一中网站上公示三天,接受广大师生、家长和社会的监督。
凡被宁德一中录取的保送生,不再参加初中毕业和升学考试,也不再参加其他学校的保送。
6、监督:招生过程由市教育局纪检、监察部门全程监督。
对弄虚作假的学生一经查实,取消其录取宁德一中保送生的资格。
宁德第一中学
2011年3月22日
主题词:学校高一保送生方案
宁德一中办公室 2011年3月22日印发
附件:
2011 宁德一中高一保送生推荐表
注:学习情况栏的体育填写“合格”或“不合格”。
此表一式二份。
