MATLAB应用基础第三章1
MATLAB_SIMULINK讲解完整版

图3-1 打开SIMULINK模块库浏览器的方法
第3章 SIMULINK应用基础
图3-2 SIMULINK模块库浏览器窗口
第3章 SIMULINK应用基础 SIMULINK模块库包括标准模块库和专业模块库两大类。 标准模块库是MATLAB中最早开发的模块库,包括了连续 系统、非连续系统、离散系统、信号源、显示等各类子模块 库。由于SIMULINK在工程仿真领域的广泛应用,因此各领 域专家为满足需要又开发了诸如通信系统、数字信号处理、 电力系统、模糊控制、神经网络等20多种专业模块库。
第3章 SIMULINK应用基础 如图3-6所示,在模型中加入注释文字,使模型更具可 读性。
图3-6 添加注释文字示例 (a) 未加注释文字;(b) 加入注释文字
第3章 SIMULINK应用基础 3.2.3 子系统的建立与封装 1. 子系统的建立 一般而言,电力系统仿真模型都比较复杂,规模很大, 包含了数量可观的各种模块。如果这些模块都直接显示在 SIMULINK仿真平台窗口中,将显得拥挤、杂乱,不利于用 户建模和分析。可以把实现同一种功能或几种功能的多个模 块组合成一个子系统,从而简化模型,其效果如同其它高级 语言中的子程序和函数功能。 在SIMULINK中创建子系统一般有两种方法。
第3章 SIMULINK应用基础 3.1.2 SIMULINK仿真平台 仿真平台 从MATLAB窗口进入SIMULINK仿真平台的方法有以 下两种: (1) 点击MATLAB菜单栏中的[File>New>Model],如图 3-3所示。 (2) 点击SIMULINK模块库浏览器窗口工具栏上的按 键 。
表3-3 SIMULINK中系统模型的基本操作方法 中系统模型的基本操作方法
操作 操作目的 内容 创建 创建一个新的模型 模型 打开 模型 保存 模型 注释 使模型更易读懂 模型 标退出 释文字编辑框,输入注释内容,在窗口中任何其它位置单击鼠 打开一个已有的模 型 保存仿真平台中模 型 方法 2:点击 SIMULINK 模块库浏览器窗口工具栏按键 方法 1:运行 MATLAB 菜单命令[File>Open]; 方法 2:点击 SIMULINK 模块库浏览器窗口工具栏按键 方法 1:运行模块库浏览器窗口菜单命令[File>Save]; 方法 2:点击 SIMULINK 模块库浏览器窗口工具栏按键 在模型窗口中的任何想要加注释的位置上双击鼠标,进入注 方法 1:运行 MATLAB 菜单命令[File>New>Model]; 操 作 方 法
MATLAB基础及其应用教程-周开利-邓春晖课后答案,第三章
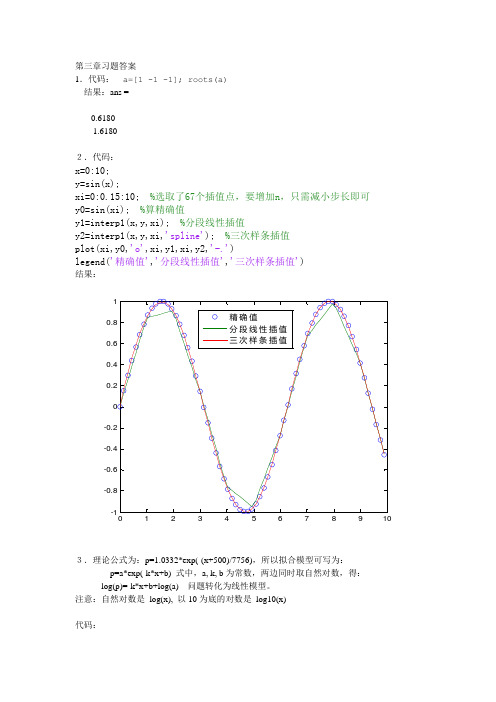
第三章习题答案1.代码:a=[1 -1 -1]; roots(a)结果:ans =-0.61801.61802.代码:x=0:10;y=sin(x);xi=0:0.15:10; %选取了67个插值点,要增加n,只需减小步长即可y0=sin(xi); %算精确值y1=interp1(x,y,xi); %分段线性插值y2=interp1(x,y,xi,'spline'); %三次样条插值plot(xi,y0,'o',xi,y1,xi,y2,'-.')legend('精确值','分段线性插值','三次样条插值')结果:3.理论公式为:p=1.0332*exp(-(x+500)/7756),所以拟合模型可写为:p=a*exp(-k*x+b) 式中,a, k, b为常数,两边同时取自然对数,得:log(p)=-k*x+b+log(a)问题转化为线性模型。
注意:自然对数是log(x), 以10为底的对数是log10(x)代码:clear;x=[0 300 600 1000 1500 2000];p=[0.9689 0.9322 0.8969 0.8519 0.7989 0.7491];lnp=log(p); %转化为 p 的自然对数值,模型转化为线性模型pk=polyfit(x,lnp,1); % 线性拟合,得到模型的斜率pk(1)和常数pk(2) 模型为: p=exp(pk(1)*x)*exp(pk(2))xi=0:50:2000;p0=1.0332*exp(-(xi+500)/7756); %理论值p1=exp(pk(1)*xi+pk(2)); %拟合模型值p2=interp1(x,p,xi,'spline'); %三次样条插值plot(x,p,'p',xi,p0,xi,p1,'--',xi,p2,'-.');legend('测量值','理论值','拟合值','三次样条值');format long % 数据显示格式为15位有效数字x2=0:200:2000 % 取10个点,比较差异pp1=1.0332*exp(-(x2+500)/7756) %理论值pp2=exp(pk(1)*x2+pk(2)) % 拟合值pp3=interp1(x,p,x2,'spline') % 样条插值err1=sum(abs(pp2-pp1).^2) % 拟合值的误差绝对值总和err2=sum(abs(pp3-pp1).^2) % 样条值的误差绝对值总和结果:0200400600800100012001400160018002000从图像上,都符合得很好,但很难看出差异。
第三章 MATLAB数值计算

功 能
如果所有的元素都是非零值,返回1;否则,返回0。 如果有一个元素为非零值,那么返回1;否则,返回0 判断是否空矩阵 判断两矩阵是否相同 判断是否是实矩阵 返回一个由非零元素的下标组成的向量
常用的矩阵函数
矩阵的行列式、矩阵的秩、特征值等在现代控制理论 中有广泛的应用,Matlab提供了相应的函数求其值 • det(A) 方阵A的行列式 • eig(A) 方阵A的特征值和特征向量 • rank(A) 矩阵A的秩 • trace(A) 矩阵A的迹 • expm(A) 矩阵的指数 • sqrtm(A) 求矩阵的平方根 • funm(A,’fun’) 求一般的方阵函数
矩阵的修改
• (1)直接修改 可用↑键找到所要修改的矩阵,用←键移动到要 修改的矩阵元素上即可修改。
• (2)指令修改 可以用A(﹡, ﹡)=﹡ 来修改。 • (3)由矩阵编辑器修改 由Matlab提供工具栏按钮来查看工作区变量,单 击变量,可以打开或删除变量
• 例: 修改矩阵A中元素的数值 >>A=[1 2 3 4; 5 6 7 8; 9 10 11 12; 13 14 15 16]; >>A(1,1)=0;A(2,2)=A(1,2)+A(2,1);A(4,4)=cos(0); 则矩阵变为: • A= 0 2 3 4 5 7 7 8 9 10 11 12 13 14、控制理论、物理学等领域中的很多 问题都可以归结到下面的线性方程组
矩阵行列式
• 如N阶矩阵A的行列式不等于0,即时,称矩阵 A非奇异,否则A奇异。当线性方程系数矩阵 非奇异,则线性方程有唯一解。对N阶方阵A, MATLAB中由函数得到行列式
使用MATLAB进行数据分析教程

使用MATLAB进行数据分析教程第一章:介绍MATLAB的基本知识MATLAB是一种广泛应用于科学计算和工程设计的软件工具。
本章将介绍MATLAB的基本知识,包括安装和启动MATLAB、MATLAB工作环境的组成以及基本的编程语法和命令。
通过本章的学习,读者可以快速上手使用MATLAB进行数据分析。
第二章:数据导入与清洗在进行数据分析之前,首先需要将数据导入到MATLAB中,并进行必要的数据清洗。
本章将介绍如何从不同的数据源导入数据,如Excel表格、文本文件和数据库。
此外,还将涵盖数据清洗的基本技术,例如处理缺失值、异常值和重复值等。
第三章:数据可视化数据可视化是数据分析的重要环节,可以帮助我们更好地理解数据的分布、趋势和关系。
本章将详细介绍如何使用MATLAB进行数据可视化分析。
包括绘制散点图、折线图、直方图、箱线图等常用的图形,并掌握调整图形样式和添加图例、标签等技巧。
第四章:统计分析统计分析是数据分析的关键部分,可以揭示数据背后的规律和关联。
本章将讲解如何使用MATLAB进行统计分析。
包括描述性统计分析,如计算均值、方差和百分位数等;基本的假设检验,如t检验和方差分析等;以及回归分析和相关分析等。
第五章:机器学习基础机器学习是近年来兴起的一种强大的数据分析技术。
本章将介绍MATLAB中的机器学习基础知识,包括常见的机器学习算法、如决策树、支持向量机和神经网络等;以及如何使用MATLAB进行数据预处理、模型训练和评估等。
第六章:时间序列分析时间序列分析是一种专门针对时间相关数据的分析方法。
本章将介绍MATLAB中的时间序列分析工具,包括自相关函数、移动平均和指数平滑等;以及如何进行时间序列模型的建立和预测等。
读者可以通过本章的学习,掌握MATLAB在时间序列分析中的应用技巧。
第七章:图像处理与分析图像处理与分析是MATLAB的重要应用领域之一。
本章将介绍MATLAB中的图像处理和分析工具,包括图像读取、显示和处理等基本操作;常见的图像处理技术,如灰度变换、滤波和边缘检测等;以及图像分割和特征提取等相关内容。
matlab入门图文教程

02
MATLAB基础操作
界面介绍
MATLAB主窗口
包括命令窗口、工作空间、命令历史和当前 文件夹等部分,是进行MATLAB操作的主要
界面。
编辑器窗口
用于显示MATLAB绘制的图形和图像,支持 多种图形格式。
图形窗口
用于编写和编辑MATLAB代码,提供语法高 亮、代码折叠等功能。
工具箱窗口
提供MATLAB各种工具箱的访问和使用,如 信号处理、图像处理等。
matlab入门图文教程
目录
• MATLAB概述与安装 • MATLAB基础操作 • 图形绘制与可视化 • 数值计算与数据分析 • 程序设计与优化 • MATLAB高级功能与应用
01
MATLAB概述与安装
MATLAB简介
MATLAB(Matrix Laboratory)是一款由 MathWorks公司开发的商业数学软件,主要用于算法
脚本文件与函数文件
脚本文件是一系列按顺序执行的命令,而函数文件则定义了一个或多个可重用的函数。脚 本文件主要用于简单任务或一次性操作,而函数文件则适用于更复杂的计算和数据处理任 务。
变量与数据类型
MATLAB支持多种数据类型,包括数值、字符、逻辑值等。变量无需声明即可直接使用, 且变量名区分大小写。
运算符与函数
01
算术运算符
包括加(+)、减(-)、乘( *)、除(/)等,用于进行基 本的数学运算。
02
关系运算符
包括等于(==)、不等于( ~=)、大于(>)、小于(< )等,用于比较两个值的大小 关系。
03
逻辑运算符
包括与(&&)、或(||)、非 (~)等,用于进行逻辑运算 。
数学建模MATLAB教案

数学建模MATLAB教案第一章:MATLAB简介1.1 课程目标了解MATLAB的发展历程和应用领域熟悉MATLAB的工作环境掌握MATLAB的基本命令和操作1.2 教学内容MATLAB的历史和发展MATLAB的应用领域MATLAB的工作环境MATLAB的基本命令和操作1.3 教学方法讲解和示范相结合学生上机实践1.4 教学资源MATLAB软件PPT课件1.5 教学评估课后作业上机实践第二章:MATLAB基本操作2.1 课程目标掌握MATLAB的变量和数据类型熟悉MATLAB的运算符和表达式学会在MATLAB中进行矩阵操作2.2 教学内容MATLAB的变量和数据类型MATLAB的运算符和表达式矩阵的创建和操作矩阵的运算2.3 教学方法讲解和示范相结合学生上机实践2.4 教学资源MATLAB软件PPT课件2.5 教学评估课后作业上机实践第三章:MATLAB函数3.1 课程目标了解MATLAB内置函数的分类和用法学会自定义函数掌握MATLAB脚本文件的编写和运行MATLAB内置函数的分类和用法自定义函数的创建和调用MATLAB脚本文件的编写和运行3.3 教学方法讲解和示范相结合学生上机实践3.4 教学资源MATLAB软件PPT课件3.5 教学评估课后作业上机实践第四章:MATLAB绘图4.1 课程目标熟悉MATLAB绘图的基本命令掌握MATLAB绘图的格式和技巧学会使用MATLAB绘制各种图形4.2 教学内容MATLAB绘图的基本命令MATLAB绘图的格式和技巧绘制各种图形的函数和方法讲解和示范相结合学生上机实践4.4 教学资源MATLAB软件PPT课件4.5 教学评估课后作业上机实践第五章:数学建模基本方法5.1 课程目标了解数学建模的基本概念和方法学会使用MATLAB进行数学建模掌握数学建模的常用算法和技巧5.2 教学内容数学建模的基本概念和方法使用MATLAB进行数学建模的步骤和技巧数学建模的常用算法和实例5.3 教学方法讲解和示范相结合学生上机实践5.4 教学资源MATLAB软件PPT课件5.5 教学评估课后作业上机实践第六章:线性方程组求解6.1 课程目标理解线性方程组的数学理论学会使用MATLAB解线性方程组掌握MATLAB中求解线性方程组的多种方法6.2 教学内容线性方程组的数学描述MATLAB中的线性方程组求解函数(如`解方程组`函数)稀疏矩阵在线性方程组求解中的应用使用`linsolve`函数求解线性方程组使用`guess`函数进行参数估计6.3 教学方法理论讲解与实际操作相结合示例演示学生上机练习6.4 教学资源MATLAB软件线性方程组求解实例6.5 教学评估课后练习题上机练习第七章:最优化问题求解7.1 课程目标理解最优化问题的数学模型学会使用MATLAB解决最优化问题掌握最优化问题的常见求解算法7.2 教学内容最优化问题的数学基础MATLAB中的最优化工具箱概述使用`fmincon`函数求解约束最优化问题使用`fminunc`函数求解无约束最优化问题了解其他最优化函数和算法7.3 教学方法理论讲解与实际操作相结合示例演示学生上机练习7.4 教学资源MATLAB软件最优化问题求解实例7.5 教学评估课后练习题上机练习第八章:微分方程求解8.1 课程目标理解微分方程的基本概念学会使用MATLAB求解微分方程掌握MATLAB中微分方程求解工具的使用8.2 教学内容微分方程的分类和基本概念MATLAB中的微分方程求解函数(如`ode45`)边界值问题的求解(如`bvp4c`)参数估计和敏感性分析8.3 教学方法理论讲解与实际操作相结合示例演示学生上机练习8.4 教学资源MATLAB软件PPT课件微分方程求解实例8.5 教学评估课后练习题上机练习第九章:概率论与数理统计9.1 课程目标掌握概率论和数理统计的基本概念学会使用MATLAB进行概率论和数理统计分析能够运用概率论和数理统计方法解决实际问题9.2 教学内容概率论基本概念和公式数理统计基本方法MATLAB中的概率论和数理统计函数随机数和概率分布函数的绘制假设检验和置信区间的计算9.3 教学方法理论讲解与实际操作相结合示例演示学生上机练习9.4 教学资源MATLAB软件PPT课件概率论和数理统计实例9.5 教学评估课后练习题上机练习第十章:综合案例分析10.1 课程目标能够综合运用所学的数学建模和MATLAB知识解决实际问题学会分析问题、建立模型、选择合适的算法和工具求解10.2 教学内容综合案例的选择和分析建立数学模型的方法MATLAB在模型求解中的应用数学建模报告的结构和要求10.3 教学方法案例分析与讨论学生分组实践10.4 教学资源MATLAB软件PPT课件综合案例数据和背景资料10.5 教学评估数学建模报告评分学生口头报告和讨论第十一章:非线性方程和方程组的求解11.1 课程目标理解非线性方程和方程组的概念学会使用MATLAB求解非线性方程和方程组掌握MATLAB中非线性求解的多种方法11.2 教学内容非线性方程和方程组的数学描述MATLAB中的非线性方程求解函数(如`fsolve`)非线性方程组的求解方法(如`ode45`)图像法求解非线性方程和方程组初始参数的选择和影响11.3 教学方法理论讲解与实际操作相结合示例演示学生上机练习11.4 教学资源MATLAB软件PPT课件非线性方程和方程组求解实例11.5 教学评估课后练习题第十二章:插值与拟合12.1 课程目标理解插值和拟合的概念学会使用MATLAB进行插值和拟合掌握MATLAB中插值和拟合的多种方法12.2 教学内容插值和拟合的基本概念MATLAB中的插值函数(如`interp1`)MATLAB中的拟合函数(如`fit`)插值和拟合的误差分析插值和拟合在数学建模中的应用12.3 教学方法理论讲解与实际操作相结合示例演示学生上机练习12.4 教学资源MATLAB软件PPT课件插值和拟合实例12.5 教学评估课后练习题第十三章:数值分析13.1 课程目标理解数值分析的基本概念学会使用MATLAB进行数值分析掌握MATLAB中数值分析的多种方法13.2 教学内容数值分析的基本概念MATLAB中的数值分析函数误差和稳定性分析数值分析在数学建模中的应用常见数值方法的比较和选择13.3 教学方法理论讲解与实际操作相结合示例演示学生上机练习13.4 教学资源MATLAB软件PPT课件数值分析实例13.5 教学评估课后练习题第十四章:MATLAB在信号处理中的应用14.1 课程目标理解信号处理的基本概念学会使用MATLAB进行信号处理掌握MATLAB中信号处理的基本方法14.2 教学内容信号处理的基本概念MATLAB中的信号处理函数信号的时域和频域分析信号处理在实际应用中的例子MATLAB在信号处理中的优势和局限性14.3 教学方法理论讲解与实际操作相结合示例演示学生上机练习14.4 教学资源MATLAB软件PPT课件信号处理实例14.5 教学评估课后练习题第十五章:MATLAB在图像处理中的应用15.1 课程目标理解图像处理的基本概念学会使用MATLAB进行图像处理掌握MATLAB中图像处理的基本方法15.2 教学内容图像处理的基本概念MATLAB中的图像处理函数图像的增强、滤波和边缘检测图像处理在实际应用中的例子MATLAB在图像处理中的优势和局限性15.3 教学方法理论讲解与实际操作相结合示例演示学生上机练习15.4 教学资源MATLAB软件PPT课件图像处理实例15.5 教学评估课后练习题重点和难点解析重点:1. MATLAB的工作环境及基本命令和操作。
MATLAB编程

高
关系 数组 逻辑 先决 逻辑
低
MATLAB编程与应用基础
赋值语句=优先级最低
第五章
MATLAB编程
操作符优先级举例
• • • • • >>x=3,b=(x>=1:5) >>x=3,b=x>=1:5 >>x=3,b=1:x>=5 >>x=3,x*1:5>=x.*0.5 >>x=3,b=3;x&b>2
a=28;b=11 a=28;b=11 28 c=**(a,b) a→11100 b→01011
a数位非
数位异或
Hale Waihona Puke MATLAB编程与应用基础
第五章
MATLAB编程
级别
操作符
类别
1 2 3 4 5 6 7 8 9 10 11
括号() 括号() 转置. ,共轭转置‘ 点幂.^ 转置.’,共轭转置‘,幂^,点幂.^ 代数正+ 代数负- 逻辑非~ 代数正+,代数负-,逻辑非~ 点乘.* 点除./. .*, ./.\ 乘*,除\/,点乘.*,点除./.\ 加+,减冒号运算: 冒号运算: 关系运算:>,<,= 关系运算:>,<,= =,>=,<=,~= 数组& 数组| 先决&& 先决或|| 数组 运算
>>a = 3 >>b = 2;
MATLAB编程与应用基础
第五章
MATLAB编程
3.1 M文件编程基础
3.1.2 M文件编写和运行
点击MATLAB桌面上 图标,弹出M文件编辑器。 将指令写入M文件编辑调试器的空白框中(通常在空白框第一行 写入包含文件名的注释)。 点击M文件编辑器的 图标,并在保存对话框中填写目录和文件 名,再按【保存】键,脚本文件即存于指定的目录上。
matlab1-8章课后作业

MATLAB基础教程1~8章作业Matlab第一章1.阐述Matlab的功能Matlab作为一种高级计算软件,是进行算法开发、数据可视化、数据分析以及数值计算的交互式应用开发环境,已被广泛应用于不同领域。
Matlab的基本功能包括:数学计算功能、图形化显示功能、M语言编程功能、编译功能、图形用户界面开发功能、Simulink建模仿真功能、自动代码生成功能。
Matlab第二章1.创建double的变量,并进行计算。
(1)a=87,b=190,计算a+b、a-b、a*b。
(2)创建uint8 类型的变量,数值与(1)中相同,进行相同的计算。
>> a=87,b=190a =87b =190>> a+bans =277>> a-bans =-103>> a*bans =16530>> c=uint8(87), d=uint8(190)c =87d =190>> c+dans =255>> c-dans =ans =2552.计算(1)sin(60)(2)e^3(3)cos(3π/4)>> sind(60)ans =0.8660>> exp(3)ans =20.0855>> cos(3*pi/4)ans =-0.70713.设u=2,v=3,计算:(1)(2)(3)>> u=2;>> v=3;>> 4*u*v/log(v)ans =21.8457>> (exp(u)+v)^2/(v^2-u) ans =15.4189>> sqrt(u-3*v)/(u*v) ans =0 + 0.4410i 4.计算如下表达式:(1)(2)>> (3-5*i)*(4+2*i)22.0000 -14.0000i>> sin(2-8*i)ans =1.3553e+003 +6.2026e+002i5.判断下面语句的运算结果。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第3章MATLAB的图形功能MATLAB可以给计算数据以二维、三维的图形表现。
通过对图形线型、色彩、光线、视角等的指定和处理,可把计算数据的特征更好地表现出来。
在MATLAB中有两个层次的绘图命令:高层与底层绘图命令。
高层命令简单实用,底层命令有更强、更灵活的控制和表现图形的能力。
本章将先后介绍上述两类绘图命令。
但重点介绍高层绘图命令。
3.1二维图形3.1.1 基本二维绘图命令 –plot1、调用格式格式1:plot(x,y)功能:(1)若x,y为同规模的向量,则绘制以x为横坐标、y为纵坐标的一条曲线。
例如:x=0:0.02:6;y=1./((x-0.3).^2+0.01)+1./((x-0.9).^2+0.04)-6; plot(x,y) 运行结果如下图所示:(2)若x为向量、y是二维数组,则绘制以x为横坐标、y的每一列为纵坐标的多条曲线。
例如:x=0:0.02:6;y=[sin(x);cos(x)]';plot(x,y)运行结果如下图所示:模),则绘制以它们的对应列为横、纵坐标的多条曲线。
例如:x=[0:0.02:6;0:0.02:6];y=[sqrt(x(1,:));exp(-x(2,:))];plot(x.',y.') 运行结果如下图所示:将被忽略。
例如:x = 0:0.2:10*pi;y = sqrt(sin(x));plot(x,y) 运行结果如下图所示:格式2:plot(y)功能:(1)若y为向量,其元素为实数,则绘制以其下标为横坐标、以y为纵坐标的图形,即相当于plot(1:length(y),y)。
例如:x=0:0.02:6;y=1./((x–0.3).^2+0.01)+1./((x–0.9).^2+0.04)-6; plot(y)运行结果如下图所示:(1)若y为复数向量,则绘制以其实部为横坐标,以其虚部系数为纵坐标的图形,即相当于plot(real(y),imag(y))。
例如:x = 0:0.2:2*pi;y = sqrt(sin(x))plot(y)运行结果如下图所示:y =Columns 1 through 50 0.4457 0.6240 0.7514 0.8470Columns 6 through 100.9173 0.9654 0.9927 0.9998 0.9868Columns 11 through 150.9536 0.8992 0.8219 0.7180 0.5788Columns 16 through 200.3757 0 + 0.2416i 0 + 0.5055i 0 +0.6652i 0 + 0.7822iColumns 21 through 250 + 0.8699i 0 + 0.9336i 0 + 0.9755i 0 +0.9968i 0 + 0.9981iColumns 26 through 300 + 0.9792i 0 + 0.9399i 0 + 0.8791i 0 + 0.7945i 0 + 0.6816iColumns 31 through 32(3)若是按y绘制曲线,曲线条线等于y 的列数。
例如:x = 0:0.2:10*pi;y = [sin(x);cos(x)]';plot(y)运行结果如下图所示:格式3:plot (x1,y1,x2,y2,…)功能:分别以(x1,y1)为二元组,(x2,y2)为二元组,…,按照plot(x,y)命令规则,绘出各组图形。
如:x = 0:0.02:2*pi;y = sin(x); z = cos(x);plot(x,y,x,z) 运行结果如下图所示:格式4:(指定曲线线型、颜色和标记的) plot (x,s)plot (x,y,s)plot (x1,y1,s1,x2,y2,s2…)其中s为一字符串,用于指定绘图时的曲线线型、曲线颜色和线的标记。
曲线线型:- (实线, 缺省设置): (虚线)-. (点划线)-- (双划线)例如:x = 0:0.02:2*pi;y = sin(x); z = cos(x);plot(x,y,':',x,z,'-.')运行结果如下图所示曲线颜色y yellow(黄色)m magenta(品红)c cyan(青)天兰r red(红)g green(绿)b blue(兰)w white(白)k black(黑)例如:x = 0:0.02:2*pi;y = sin(x); z = cos(x);plot(x,y,'c',x,z,'r')运行结果如下图所示:曲线标记·point(点)X x-mark(叉号)O circle(园_字母O)+ plus(加号)* star(星号)square (方块)sd diamond (点)(下三角)v triangle(down)^ triangle(up) (上三角)(左三角)< triangle(left)(右三角)> triangle(right)p pentagram (空心五角星)h hexagram (空心六角星)x = 0:0.2:2*pi;y1 = sin(x); y2 = cos(x); y3 = sqrt(x); hold onplot(x,y1,'.')plot(x,y2,'s')plot(x,y3,'^')运行结果如下图所示:实际上,可以同时指定曲线的颜色、标记和线型。
例如:x = 0:0.2:2*pi;y1 = sin(x);y2 = cos(x);y3 = sqrt(x);hold onplot(x,y1,'bp-')plot(x,y2,'rh--')plot(x,y3,'g^')运行结果如下图所示:3.1.2 坐标网格、标注和图例说明1、坐标网格grid on在当前图中加网格线grid off 去掉当前图中的网络线2、标注title(字符串)功能: 当前坐标系顶部加标题xlabel (字符串)功能: 当前坐标系x轴旁加标题(下方)ylabel (字符串)功能: 当前坐标系y轴旁加标题(左侧)text (x,y,字符串)功能: 当前坐标系指定位置处加文本gtext (字符串)功能: 在鼠标单击处加文本3、图例说明legend(字符串1,字符串2,…)功能:在当前图形内建立一图例说明框,框内显示各字符串。
并且图形的曲线与字符串依次对应,可用鼠标拖动图例框改变其位置。
legend off功能: 删掉图例说明框例如:x=linspace(0,2*pi);y=sin(x);z=cos(x);plot(x,y,'b:',x,z,'m+')xlabel('变量X')ylabel('函数Y、Z')title('正弦与余弦曲线')grid ontext(3.3,0.1,'sin(x)')%gtext('cos x') 本命令要用鼠标,在Notebook中不能用legend('sin(x)','cos(x)')运行结果如下图所示:3.1.3 坐标轴的形式和刻度在缺省状态下,坐标轴自动显示、自动刻度、且为笛卡儿直角坐标系。
MATLAB中有以下对坐标轴操作的命令:axis([Xmin,Xmax,Ymin,Ymax])功能: 设定坐标范围v = axis功能: 获取当前坐标范围,存入v 中(v 为行向量 [Xmin,Xmax,Ymin,Ymax])axis('auto')功能: 恢复缺省坐标设置axis('xy')功能: 使用笛卡儿坐标轴(即缺省) axis('ij') 功能: 使用矩阵坐标轴( ) axis(‘square’)功能: 显示矩形坐标框axis(‘equal’)功能: 使各坐标轴刻度增量相同 axis(‘normal’)功能: 使以上两个命令失效axis(‘off’)功能: 隐去坐标轴axis(‘on’)功能: 显示坐标轴[s 1,s 2,s 3] = axis(‘state’) 返回当前坐标轴的属性:s 1:‘anto’ — 自动刻度‘manual’ — 人工刻度s 2:‘on’ — 显示坐标轴j i‘off’ — 隐去坐标轴s3:‘xy’ — 笛卡儿坐标轴‘ij’ — 矩阵坐标轴例如:x=linspace(0,2*pi);y=sin(x);z=cos(x);plot(x,y,'b:',x,z,'k--')axis('off')grid offxlabel('变量X')ylabel('函数Y、Z')title('正弦与余弦曲线')text(2.5,0.7,'sin(x)')text(4.8,0.7,'cos(x)') legend('sin(x)','cos(x)')运行结果如下图所示:3.1.4图形窗口操作1、创建图形窗口figure功能:创建一个新的图形窗口。
在第一个绘图命令运行后,将自动创建名为"Figure No.1"的图形窗口,后续的绘图命令均是在该窗口中作用的。
figure命令,将顺序地创建"Figure No.2"、"Figure No.3"、…等图形窗口,但是,如若"FigureNo.1"不存在,则创建该窗口。
2、创建或选择第n个图形窗口figure(n)功能:选择第n个图形窗口为当前窗口,若该窗口不存在,则创建它。
3、子坐标系统在同一图形窗口中,可以创建n个子坐标系统,并指定其中之一为当前坐标系统。
subplot(m,n,p)将当前窗口划分为m×n个子坐标系统,并选择其中第p个坐系统为当前坐标系统。
各子坐标系统按行排序,编号分别为1,2,…,m×n。
特别地subplot(1,1,1)将删除所有子坐标系统而生成一个占满窗口的坐标系统。
例如:x=linspace(0,2*pi,30);y=sin(x);z=cos(x);a=2*sin(x).*cos(x);b=sin(x)./(cos(x)+eps);subplot(2,2,1)plot(x,y)axis([0,2*pi,-1,1])title('sin(x)')subplot(2,2,2)plot(x,z)axis([0,2*pi,-1,1]) title('cos(x)')subplot(2,2,3)plot(x,a)axis([0,2*pi,-1,1]) title('2sin(x)cos(x)') subplot(2,2,4)plot(x,b)axis([0,2*pi,-20,20]) title('sin(x)/cos(x)')运行结果如下图所示:4、图形重叠绘制hold on功能:保留当前图形及其坐标轴,允许后续图形附加到原图上。
