八年级上数学几何证明练习题
八年级第一学期第十九章《几何证明》测验卷

八年级第十九章《几何证明》单元测试卷【此试卷由梅陇中学唐丽娟老师提供】班级__________姓名__________成绩_________一.填空(每题2分,共28分)1、真命题的逆命题 是真命题。
(填“一定”或“不一定” )2、在直角三角形中,两个锐角的平分线所夹的钝角的度数是3、在Rt △ABC 中,∠C=90°,∠A=30°,BC=20cm ,那么AB= cm 。
4、直角三角形的周长为(2+6)cm ,斜边上的中线长为1cm ,那么两直角边的和为 cm 。
5、在△ABC 中,∠C=90°,CD 是中线,∠BCD=15°,那么∠A=(第5题图) (第6题图) (第7题图)6、在等腰△ABC 中,腰AB 的垂直平分线交BC 于G ,已知AB=10cm ,△BGC 的周长为17cm ,那么底边BC = cm 。
7、在Rt △ABC 中,∠C=90°,BD 平分∠ABC 交AC 于D ,且AC=10,AD:DC=3:2,则点D 到AB 的距离为 。
8、在Rt △ABC 中,两锐角比为1:2,斜边与较小直角边的和为21cm ,那么斜边的长为 cm 。
9、命题“如果a=b ,那么a 2=b 2”的逆命题是 。
10、定理“等腰三角形的两底角相等”的逆定理是 。
11、等腰三角形底边上的高等于腰长的一半,则这三角形最大的角是 °。
12、在Rt △ABC 中,CE 是斜边AB 上的中线,CD 是高,如果AB=10cm ,DE=2.5cm ,那么∠DCE= 。
13、在△ABC 中,∠ACB=90°,∠B=30°,CD 是AB 边上的高,那么AD=21 。
14、已知等边三角形ABC 的顶点B 、C 的坐标分别为(0,0)(4,0),则顶点A 的坐标 。
二、选择题(每题3分,共15分)15、在直角三角形中,等于斜边一半的是斜边上的()(A)高(B)中线(C)角平分线(D)垂直平分线16、如图,在Rt△ABC中,∠ACB=90°,CM、CI分别是中线、角平分线,若∠B=50°,那么∠MCI等于()(A)40°(B)20°(C)10°(D)5°25B169(第16题图)(第17题图)(第18题图)17、如图,在Rt△ABC中,∠ACB=90°,CD是AB边上的高,CE是中线,CF是∠ACB 的角平分线,把图中几个相等锐角集为一组,那么共有()(A)0组(B)2组(C)3组(D)4组18、如图字母B所代表的正方形的面积是( )(A) 12 (B)13 (C)144 (D)19419、如果一个三角形的两边垂直平分线的交点在第三边上,那么这个三角形中最大内角的度数是()(A)120°(B)90°(C)75°(D)60°三:解答题(每题6分,共18分)20、已知△ABC中,AB=AC,∠C=30°,AD⊥AB交BC于D,AD=10cm,求:BC的长。
八年级数学十二道全等几何证明题 难度适中型
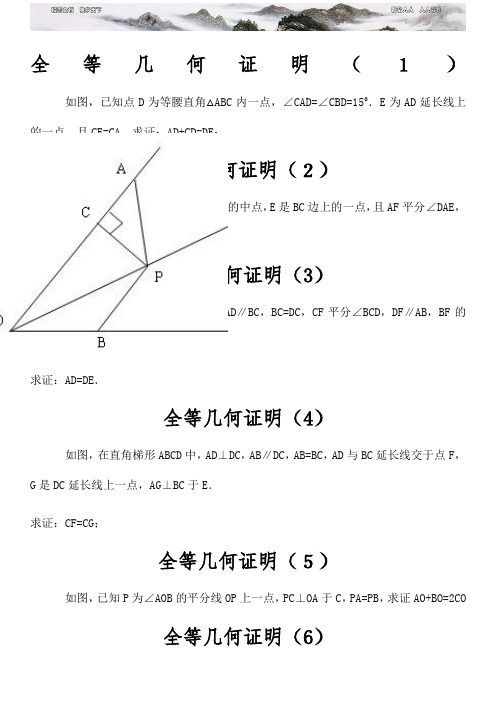
全等几何证明(1)如图,已知点D为等腰直角△ABC内一点,∠CAD=∠CBD=15°.E为AD延长线上的一点,且CE=CA,求证:AD+CD=DE;全等几何证明(2)如图,在正方形ABCD中,F是CD的中点,E是BC边上的一点,且AF平分∠DAE,求证:AE=EC+CD.全等几何证明(3)已知:如图,在梯形ABCD中,AD∥BC,BC=DC,CF平分∠BCD,DF∥AB,BF的延长线交DC于点E.求证:AD=DE.全等几何证明(4)如图,在直角梯形ABCD中,AD⊥DC,AB∥DC,AB=BC,AD与BC延长线交于点F,G是DC延长线上一点,AG⊥BC于E.求证:CF=CG;全等几何证明(5)如图,已知P为∠AOB的平分线OP上一点,PC⊥OA于C,PA=PB,求证AO+BO=2CO全等几何证明(6)已知:如图,在直角梯形ABCD 中,AD ∥BC ,∠ABC=90°,DE ⊥AC 于点F ,交BC 于点G ,交AB 的延长线于点E ,且AE=AC .求证:BG=FG ;全等几何证明(7)如图,在△ABC 中,∠ABC=60°,AD 、CE 分别平分∠BAC 、∠ACB ,求证:AC=AE+CD . 全等几何证明(7)如图,AD ∥BC ,AE 平分∠BAD ,AE ⊥BE ;说明:AD+BC=AB .全等几何证明(8)将两个全等的直角三角形ABC 和DBE 如图方式摆放,其中∠ACB=∠DEB=90°,∠A=∠D=30°,点E 落在AB 上,DE 所在直线交AC 所在直线于点F .求证:AF+EF=DE全等几何证明(9)如图,在△ABC 中,AD 平分∠BAC ,AB =AC -BD ,则∠B ∶∠C 的值为多少?全等几何证明(10)已知:如图,P 是正方形ABCD 内点,∠PAD =∠PDA =150.求证:△PBC 是正三角形.A BC DA P D全等几何证明(11)如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F . 求证:CE =CF .全等几何证明(12)设P 是正方形ABCD BC 上的任一点,PF ⊥AP ,CF 平分∠DCE . 求证:PA =PF .DCB A F D ECBFE P C B A。
八年级上册几何证明题

八年级上册几何证明题一、三角形内角和定理相关证明题。
1. 已知:在△ABC中,∠A = 50°,∠B = 60°,求证:∠C = 70°。
解析:根据三角形内角和定理,三角形内角和为180°。
在△ABC中,因为∠A+∠B +∠C=180°,已知∠A = 50°,∠B = 60°,所以∠C=180°∠A ∠B = 180°-50° 60° = 70°。
2. 如图,在△ABC中,AD是∠BAC的平分线,∠B = 70°,∠C = 30°,求∠ADC的度数。
解析:根据三角形内角和定理,在△ABC中,∠BAC=180°∠B ∠C = 180°-70° 30° = 80°。
因为AD是∠BAC的平分线,所以∠BAD = 1/2∠BAC = 40°。
在△ABD中,根据三角形外角性质,∠ADC = ∠B+∠BAD,所以∠ADC = 70°+40° = 110°。
二、等腰三角形性质证明题。
3. 已知:在等腰△ABC中,AB = AC,∠A = 80°,求∠B和∠C的度数。
解析:因为AB = AC,所以△ABC是等腰三角形,根据等腰三角形两底角相等的性质,设∠B =∠C=x。
根据三角形内角和定理,∠A+∠B +∠C = 180°,即80°+x + x = 180°,2x=180° 80°,2x = 100°,x = 50°,所以∠B =∠C = 50°。
4. 如图,在等腰三角形ABC中,AB = AC,BD⊥AC于点D,求证:∠CBD=(1)/(2)∠A。
解析:设∠A=x。
因为AB = AC,所以∠ABC =∠ACB=(1)/(2)(180° x)=90°-(x)/(2)。
沪教版八年级上册数学第十九章 几何证明含答案

沪教版八年级上册数学第十九章几何证明含答案一、单选题(共15题,共计45分)1、在等腰△ABC中,∠ACB=90°,且AC=1.过点C作直线L∥AB,P为直线L上一点,且AP=AB.则点P到BC所在直线的距离是( )A.1B.1或C.1或D. 或2、设、、是三边,并且关于的方程有两个相等的实数根,判断的形状,正确的结论是()A.等腰三角形B.直角三角形C.等腰直角三角形D.正三角形3、如图,Rt△ABC中,∠C=90°,∠B=45°,AD是∠CAB的平分线,DE⊥AB于E,AB=a,CD=m,则AC的长为()A.2mB.a-mC.aD.a+m4、下列几组数中,不能作为直角三角形三边长度的是()A.1.5,2,2.5B.5,12,14C.30,40,50D.1,2,5、如图,在△ABC中,AB=5,AC=6,BC=4,边AB的垂直平分线交AC于点D,则△BDC 的周长是( )A.8B.9C.10D.116、如图,已知,,于点C,于点G,若,则长度是()A.3B.4C.5D.67、下列各组数中,以它们为边长的线段不能构成直角三角形的是( )A.1,,2B.1,2,C.5,12,13D.1,,8、如图,学校有一块长方形花铺,有极少数人为了避开拐角走“捷径”,在花铺内走出了一条“路”.他们仅仅少走了几步路(假设2步为1米),却踩伤了花草()A.2B.4C.5D.109、有下列说法:①有理数与数轴上的点一一对应;②直角三角形的两边长是5和12,则第三边长是13;③近似数1.5万精确到十分位;④无理数是无限小数.其中错误说法的个数有()A.4个B.3个C.2个D.1个10、我国汉代数学家赵爽为了证明勾股定理,创制了一幅弦图,后人称其为赵爽弦图(如图1).,图 2 为小明同学根据弦图思路设计的.在正方形 ABCD 中,以点 B 为圆心,AB 为半径作 AC,再以CD 为直径作半圆交 AC 于点E,若边长AB=10,则△CDE 的面积为()A.20B.C.24D.11、如图,在中, , 于点,则的长是()A.6B.C.D.12、在Rt△ABC中,∠C=90°,周长为24,斜边与一直角边之比为5:4,则这个直角三角形的面积是()A.20B.24C.28D.3013、如图,△ABC中,已知∠B和∠C的平分线相交于点F,经过点F作DE//BC,交AB于D,交AC于点E,若BD+CE=9,则线段DE的长为()A.9B.8C.7D.614、如图,在正方形中,点E,F分别在,上,,与相交于点G.下列结论:① 垂直平分;② ;③当时,为等边三角形;④当时,.其中正确的结论是()A.①③B.②④C.①③④D.②③④15、如图,⊙O是以原点为圆心,为半径的圆,点是直线上的一点,过点作⊙O的一条切线PQ,Q为切点,则切线长PQ的最小值为()A.3B.4C.D.二、填空题(共10题,共计30分)16、如图,在矩形,,,为线段上的一动点,且和,不重合,连接,过点作交于,将沿翻折到平面内,使点恰好落在边上的点,则长为________.17、有一块直角三角形绿地,量得两直角边长为6 m,8 m.若现在要将绿地扩充成等腰三角形,且扩充时只能延长6 m的直角边,则扩充后等腰三角形绿地的面积为 ________ m2.18、如图,在中,,AB的垂直平分线EF分别交BC、AB于点E、F,∠AEF=65°,那么∠CAE=________.19、如图,在四边形ABCD中,∠ABC=90°,AB=3,BC=4,CD=10,DA=,则BD的长为________.20、在直角坐标系中,O为坐标原点,已知点A(1,2),在y轴的正半轴上确定点P,使△AOP为等腰三角形,则点P的坐标为________.21、如图,中,,的平分线与边的垂直平分线相交于,交的延长线于,于,现有下列结论:① ;② ;③ 平分;④.其中正确的有________.(填写序号)22、如图,在矩形ABCD中,AB=5,AD=3,动点P满足S△PAB=S矩形ABCD,则点P到A、B两点距离之和PA+PB的最小值为________.23、如图,在Rt△ABC中,∠ACB=90°,∠BAC的平分线交BC于D.过C点作CG⊥AB于G,交AD于E.过D点作DF⊥AB于F.下列结论:①∠CED=∠CDE;② ;③∠ADF=2∠ECD;④;⑤CE=DF.其中正确结论的序号是________.24、如图,在△ABC中,AB=AC=4,∠A=30°,那么S=________.△ABC25、如图,已知A、B、C分别是⊙O上的点,∠B=120°,P是直径CD的延长线上的一点,且AP=AC,PD=2,求AP的长为________ .三、解答题(共5题,共计25分)26、已知ABC中∠BAC=140°, AB、AC的垂直平分线分别交BC于E、F,AEF 的周长为10㎝,求BC的长度和∠EAF的度数.27、如图,矩形ABCD中,点E为AD上一点,∠BEC=90°,AB=2,DE=1,求BC 的长.28、有一块草坪如图所示,已知AB=6cm,BC=8cm,CD=24cm,DA=26cm,且AB⊥BC,求这块草坪的面积.29、如图,△ACB与△ECD都是等腰直角三角形,△ACB的顶点A在△ECD的斜边DE上,求证:AE2+AD2=2AC2.(提示:连接BD)30、如图,四边形ABCD中∠A=60°,∠B=∠D=90°,AB=2,CD=1,求四边形ABCD的面积.参考答案一、单选题(共15题,共计45分)1、D2、B3、B4、B5、C6、D7、D8、B9、B10、A12、B13、A14、A15、B二、填空题(共10题,共计30分)16、17、18、19、20、21、22、23、24、25、三、解答题(共5题,共计25分)27、。
三角形证明题集锦
A D B P 图⑴ E C
5、在Rt△ABC中,AB=AC,∠BAC=90°,O为BC的中点。 (1)写出点O到△ABC的三个顶点A、B、C的距离的大小关系(不要求证明); (2)如果点M、N分别在线段AB、AC上移动,在移动中保持AN=BM,请判断△OMN的形 状,并证明你的结论。
C N
O B
①
②
③
例7(6分题) :如图,要在燃气管道l上修建一个泵站,分别向A、B两镇供气。(1)泵站C 修建在什么地方,可使所用的燃气管线最短?(不写做法,保留作图痕迹)( 2)请你在(1) 的基础上,过A点作AD⊥l,并连接DB,求证:AD+DB>AC+CB。
练8 (6分题) :如图,已知牧马营地M处,每天牧马人要赶马群先到河边饮水,再到草地上 吃草,最后回到营地,试着设计出最短的牧马路线(不写做法,保留作图痕迹)
八年级数学(上)几何证明练习题
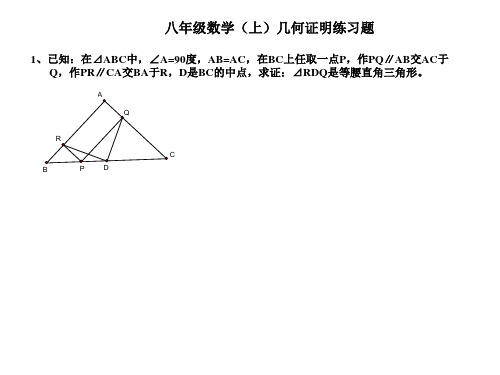
1、已知:在⊿ABC中,∠A=90度,AB=AC,在BC上任取一点P,作PQ∥AB交AC于 Q,作PR∥CA交BA于R,D是BC的中点,求证:⊿RDQ是等腰直角三角形。
A Q
R C B P D
2、已知:在⊿ABC中,∠A=900,AB=AC,D是AC的中点,AE⊥BD,AE延长线交BC 于F,求证:∠ADB=∠FDC。
例1(6分题):如图,已知∠B=∠C=90°,M是BC的中点,DM平分 ∠ADC。 (1)若连接AM,则AM是否平分∠BAD?请你证明你的结论。 (2)DM与AM有怎样的位置关系?请说明理由。 (3)求证:AD=AB+CD
练2(6分题) :如图,AB∥CD,DE平分∠ADC,AE平分∠BAD,求证:AD=AB+CD
小结
证明两条线段相等或角相等,如 果这两条线段或角在两个三角形内, 就证明这两个三角形全等;如果这两 条线段或角在同一个三角形内,就证 明这个三角形是等腰三角形;如果看 图时两条线段既不在同一个三角形内, 也不在两个全等三角形内,那么就利 用辅助线进行等量代换。
(典型题)沪教版八年级上册数学第十九章 几何证明含答案

沪教版八年级上册数学第十九章几何证明含答案一、单选题(共15题,共计45分)1、已知三角形的三边长分别为a,b,c,且a+b=10,ab=18,c=8,则该三角形的形状是()A.等腰三角形B.直角三角形C.钝角三角形D.等腰直角三角形2、下列各组数中,以a,b,c为边的三角形不是直角三角形的是()A.a=3,b=4,c=5B.a=7,b=24,c=25C.a=4,b=5,c=6 D.a=6,b=8,c=103、如图,在锐角△ABC中,∠A=60°,∠ACB=45°,以BC为弦作⊙O,交AC 于点D,OD与BC交于点E,若AB与⊙O相切,则下列结论:①∠BOD=90°;②DO∥AB;③CD=AD;④△BDE∽△BCD;⑤正确的有()A.①②B.①④⑤C.①②④⑤D.①②③④⑤4、已知△ 和△ 都是等腰直角三角形,,,,是的中点.若将△ 绕点旋转一周,则线段长度的取值范围是()A. B. C. D.5、如图△ABC 的∠ABC 的外角平分线 BD 与∠ACB 的外角平分线 CE 交于 P,过 P 作MN∥AB 交 AC 于M,交 BC 于 N,且 AM=8,BN=5,则 MN=()A.2B.3C.4D.56、如图,在平行四边形中,对角线与相交于点,则的长为()A.8B.4C.3D.57、在下列由线段a,b,c的长为三边的三角形中,不能构成直角三角形的是()A.a=4,b=5,c=6B.a=12,b=5,c=13C.a=6,b=8,c=10D.a=7,b=24,c=258、绍兴是著名的桥乡,如图,石拱桥的桥顶到水面的距离CD为8m,桥拱半径OC为5m,则水面宽AB为()A.4mB.5mC.6mD.8m9、有一块三角形的草坪△ABC,现要在草坪上建一座凉亭供大家休息,要使凉亭到草坪三条边的距离相等,则凉亭的位置应选在 ( )A.△ABC三条角平分线的交点B.△ABC三边的垂直平分线的交点 C.△ABC三条中线的交点 D.△ABC三条高所在直线的交点10、下列各组数中,不是勾股数的是()A.3,4,5B.5,12,13C.6,8,10D.7,13,1811、如图,将长方形ABCD沿直线EF折叠,使顶点C恰好落在顶点A处,已知AB=4cm,AD=8cm,则折痕EF的长为( )A.5cmB. cmC. cmD. cm12、如图,在△ABC中,BC=8cm,AB的垂直平分线交AB于点D,交边AC于点E,△BCE的周长等于18cm,则AC的长等于()A.6cmB.8cmC.10cmD.12cm13、如图,长方形ABCD中,点E是边CD的中点,将△ADE沿AE折叠得到△AFE,且点F在长方形ABCD内.将AF延长交边BC于点G.若BG=3CG,则=()A. B.1 C. D.14、如图,在中,,,点D,E分别是AB, BC的中点,连接DE,CD,如果,那么的周长()A.28B.28.5C.32D.3615、下列长度的三条线段能组成锐角三角形的是()A.2,3,3B.2,3,4C.2,3,5D.3,4,5二、填空题(共10题,共计30分)16、如图,在矩形ABCD中,AB=6,BC=4,将矩形沿AC折叠,点D落在处,则重叠部分△AFC的面积为________17、如图所示,在△ABC中,AB:BC:CA=3:4:5,且周长为36cm,点P从点A开始沿AB边向B点以每秒1cm的速度移动;点Q从点B沿BC边向点C以每秒2cm的速度移动,如果同时出发,则过3秒时,△BPQ的面积为________ cm2.18、如图,是⊙O的直径,C是⊙O上一点,的平分线交⊙O于D,且,则的长为________.19、在三角形纸片ABC中,∠A=90°,∠C=30°,AC=30cm,将该纸片沿过点B 的直线折叠,使点A落在斜边BC上的一点E处,折痕记为BD(如图1),剪去△CDE后得到双层△BDE(如图2),再沿着过△BDE某顶点的直线将双层三角形剪开,使得展开后的平面图形中有一个是平行四边形,则所得平行四边形的周长为________ cm.20、如图,矩形ABCD中,AB=8,点E是AD上的一点,有AE=4,BE的垂直平分线交BC的延长线于点F,连结EF交CD于点G.若G是CD的中点,则BC的长是________.21、如图,在⊙O中,CD是直径,弦AB⊥CD,垂足为E,若∠C=15°,AB=4cm,则⊙O半径为________cm.22、如图,在每个小正方形边长为1的网格中,点A,点C均落在格点上,点B 为中点.(Ⅰ)计算AB的长等于________;(Ⅱ)若点P,Q分别为线段BC,AC上的动点,且BP=CQ,请在如图所示的网格中,用无刻度的直尺,画出当PQ最短时,点P,Q的位置,并简要说明画图方法(不要求证明)________.23、如图,矩形纸片ABCD,AB=5,BC=3,点P在BC边上,将△CDP沿DP折叠,点C落在点E处,PE,DE分别交AB于点O,F,且OP=OF,则AF的值为________.24、已知矩形OABC中,O为坐标原点,点A在x轴上,点C在y轴上,B的坐标为(10,5),点P在边BC上,点A关于OP的对称点为A',若点A'到直线BC 的距离为4,则点A'的坐标可能为________.25、如图,矩形ABCD中,AB=5,BC=7,E为BC上的动点,将矩形沿直线AE翻折,使点B的对应点B'落在∠ADC的平分线上,过点B'作B'F⊥BC于点F,求△B'EF的周长________.三、解答题(共5题,共计25分)26、如图所示,△ABC和△AEF为等边三角形,点E在△ABC内部,且E到点A,B,C的距离分别为3,4,5,求∠AEB的度数.27、如图,AB为半圆直径,O为圆心,C为半圆上一点,E是弧AC的中点,OE 交弦AC于点D,若AC=8cm,DE=2cm,求OD的长.28、如图,已知∠AOB=30°,P是∠AOB角平分线上一点,CP∥OA,交OB于点C,PD⊥OA,垂足为点D,且PC=4,求PD的长.29、去年某省将地处A、B两地的两所大学合并成了一所综合性大学,为了方便A、B两地师生的交往,学校准备在相距2km的A、B两地之间修筑一条笔直公路(即图中的线段AB),经测量,在A地的北偏东60°方向、B地的西偏北45°方向C处有一个半径为0.7km的公园,问计划修筑的这条公路会不会穿过公园?为什么?(≈1.732)30、由于大风,山坡上的一颗树甲被从A点处拦腰折断,如图所示,其树顶端恰好落在另一颗树乙的根部C处,已知AB=4米,BC=13米,两棵树的水平距离为12米,求这棵树原来的高度.参考答案一、单选题(共15题,共计45分)1、B2、C3、C4、A5、B6、B7、A8、D9、A10、D11、B12、C14、C15、A二、填空题(共10题,共计30分)16、17、18、19、20、21、22、23、24、25、三、解答题(共5题,共计25分)27、29、。
八年级几何证明题

几何证明题1、已知:如图1所示,∆ABC 中,∠=︒===C AC BC AD DB AE CF 90,,,;求证:DE =DF2、已知:如图2所示,AB =CD,AD =BC,AE =CF;求证:∠E =∠F3、如图3所示,设BP 、CQ 是∆ABC 的内角平分线,AH 、AK 分别为A 到BP 、CQ 的垂线;求证:KH ∥BC4、已知:如图4所示,AB =AC,∠,,A AE BF BD DC =︒==90;求证:FD ⊥ED5、已知:如图6所示在∆ABC 中,∠=︒B 60,∠BAC 、∠BCA 的角平分线AD 、CE 相交于O; 求证:AC =AE +CD6、已知:如图7所示,正方形ABCD 中,F 在DC 上,E 在BC 上,∠=︒EAF 45;求证:EF =BE +DF7、如图8所示,已知∆ABC 为等边三角形,延长BC 到D,延长BA 到E,并且使AE =BD,连结CE 、DE; 求证:EC =ED8、例题:已知:如图9所示,∠=∠>12,AB AC ; 求证:BD DC >作业1. 已知:如图11所示,∆ABC 中,∠=︒C 90,D 是AB 上一点,DE ⊥CD 于D,交BC 于E,且有AC AD CE ==;求证:DE CD =122. 已知:如图12所示,在∆ABC 中,∠=∠A B 2,CD 是∠C 的平分线; 求证:BC =AC +AD3. 已知:如图13所示,过∆ABC 的顶点A,在∠A 内任引一射线,过B 、C 作此射线的垂线BP 和CQ;设M 为BC 的中点; 求证:MP =MQ4. ∆ABC 中,∠=︒⊥BACAD BC 90,于D,求证:()AD AB AC BC <++14试题答案1、 分析:由∆ABC 是等腰直角三角形可知,∠=∠=︒A B 45,由D 是AB 中点,可考虑连结CD,易得CD AD =,∠=︒DCF 45;从而不难发现∆∆DCF DAE ≅证明:连结CD说明:在直角三角形中,作斜边上的中线是常用的辅助线;在等腰三角形中,作顶角的平分线或底边上的中线或高是常用的辅助线;显然,在等腰直角三角形中,更应该连结CD,因为CD 既是斜边上的中线,又是底边上的中线;本题亦可延长ED 到G,使DG =DE,连结BG,证∆EFG 是等腰直角三角形;有兴趣的同学不妨一试; 2、证明:连结AC在∆ABC 和∆CDA 中, 在∆BCE 和∆DAF 中,说明:利用三角形全等证明线段求角相等;常须添辅助线,制造全等三角形,这时应注意:1制造的全等三角形应分别包括求证中一量;2添辅助线能够直接得到的两个全等三角形; 3、分析:由已知,BH 平分∠ABC,又BH ⊥AH,延长AH 交BC 于N,则BA =BN,AH =HN;同理,延长AK 交BC 于M,则CA =CM,AK =KM;从而由三角形的中位线定理,知KH ∥BC; 证明:延长AH 交BC 于N,延长AK 交BC 于M ∵BH 平分∠ABC ∴=∠∠ABHNBH 又BH ⊥AH ∴==︒∠∠AHB NHB 90 BH =BH同理,CA =CM,AK =KM ∴KH 是∆AMN 的中位线 ∴KH MN // 即KH ∆ADE ∆BDF AE BF B DAE AD BDADE BDFFD ED===∴≅∴∠=∠∴∠+∠=︒∴⊥,∠∠,∆∆313290∆∆AEO AFO ≅∴∠=∠12∠=︒B 60∠+∠=︒∠=︒∠+∠=︒566016023120,,∴∠=∠=∠=∠=︒123460∆∆FOC DOC FC DC ≅∴=,()∠=∠=∴≅∴∠=∠BAD CAD AO AOAEO AFO SAS ,∆∆42∠=︒B 60∴∠+∠=︒∴∠=︒∴∠+∠=︒∴∠=∠=∠=∠=︒∴≅∴=566016023120123460∆∆FOC DOC AAS FC DC()AC AE CD =+∠=∠=︒=ABG D AB AD90,∴≅∴=∠=∠∆∆ABG ADF SAS AG AF (),13∠=︒EAF 45∴∠+∠=︒∴∠+∠=︒23452145∴=∴=+GE EFEF BE DF ∆ABC∴∆BFD∴==∴==AE FD BF BA AF EF AC FDEAC EFD EAC DFE SAS EC ED//()∴∠=∠∴≅∴=∆∆∆ADE ∆ADB∆∆ADF ADC ≅∴∠=∠=>∠∠>∠∴∠>∠∴>∴>3434,,DF DCBFD BBFD BBD DF BD DC证明:取CD 的中点F,连结AF 又∠+∠=︒∠+∠=︒14901390, ∴∠=∠=∴≅∴=∴=4312AC CEACF CED ASA CF EDDE CD∆∆()2. 分析:本题从已知和图形上看好象比较简单,但一时又不知如何下手,那么在证明一条线段等于两条线段之和时,我们经常采用“截长补短”的手法;“截长”即将长的线段截成两部分,证明这两部分分别和两条短线段相等;“补短”即将一条短线段延长出另一条短线段之长,证明其和等于长的线段;证明:延长CA 至E,使CE =CB,连结ED在∆CBD 和∆CED 中,又∠=∠+∠BAC ADE E∴∠=∠∴=∴==+=+ADE E AD AEBC CE AC AE AC AD,3. 证明:延长PM 交CQ 于R 又BMCM BMP CMR =∠=∠,∴≅∴=∆∆BPM CRMPM RM∴QM 是Rt QPR ∆斜边上的中线 ∴=MP MQ4. 取BC 中点E,连结AE。
(完整)八年级上册几何证明题专项练习
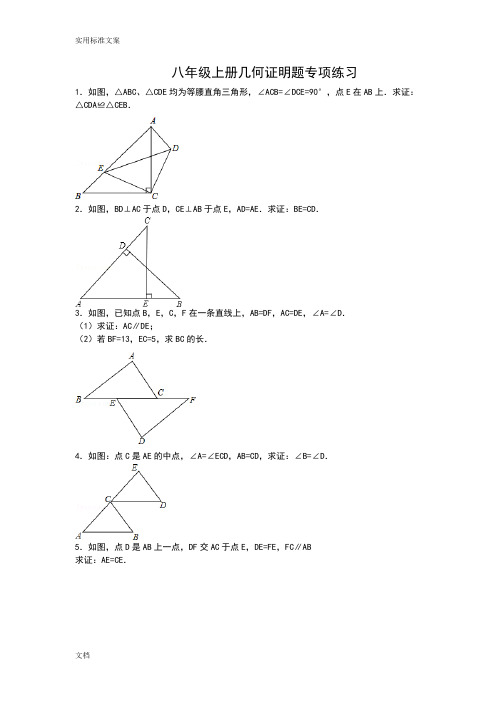
八年级上册几何证明题专项练习1.如图,△ABC、△CDE均为等腰直角三角形,∠ACB=∠DCE=90°,点E在AB上.求证:△CDA≌△CEB.2.如图,BD⊥AC于点D,CE⊥AB于点E,AD=AE.求证:BE=CD.3.如图,已知点B,E,C,F在一条直线上,AB=DF,AC=DE,∠A=∠D.(1)求证:AC∥DE;(2)若BF=13,EC=5,求BC的长.4.如图:点C是AE的中点,∠A=∠ECD,AB=CD,求证:∠B=∠D.5.如图,点D是AB上一点,DF交AC于点E,DE=FE,FC∥AB求证:AE=CE.6.如图,BE⊥AC,CD⊥AB,垂足分别为E,D,BE=CD.求证:AB=AC.7.如图,点A,B,C,D在同一条直线上,CE∥DF,EC=BD,AC=FD.求证:AE=FB.8.如图,在△ABC中,AC=BC,∠C=90°,D是AB的中点,DE⊥DF,点E,F分别在AC,BC 上,求证:DE=DF.9.如图,点A、C、D、B四点共线,且AC=BD,∠A=∠B,∠ADE=∠BCF,求证:DE=CF.10.如图,已知∠CAB=∠DBA,∠CBD=∠DAC.求证:BC=AD.11.如图,点B、E、C、F在同一条直线上,AB=DE,AC=DF,BE=CF,求证:AB∥DE.12.如图,AB∥CD,E是CD上一点,BE交AD于点F,EF=BF.求证:AF=DF.13.已知△ABN和△ACM位置如图所示,AB=AC,AD=AE,∠1=∠2.(1)求证:BD=CE;(2)求证:∠M=∠N.14.如图,∠ACB=90°,AC=BC,AD⊥CE,BE⊥CE,垂足分别为D,E.求证:△ACD≌△CBE.15.如图,四边形ABCD中,E点在AD上,∠BAE=∠BCE=90°,且BC=CE,AB=DE.求证:△ABC≌△DEC.16.如图,在△ABC中,AB=CB,∠ABC=90°,D为AB延长线上一点,点E在BC边上,且BE=BD,连结AE、DE、DC.①求证:△ABE≌△CBD;②若∠CAE=30°,求∠BDC的度数.17.如图,在四边形ABCD中,AD∥BC,E为CD的中点,连接AE、BE,BE⊥AE,延长AE交BC的延长线于点F.求证:(1)FC=AD;(2)AB=BC+AD.18.如图,在△ABC中,DM、EN分别垂直平分AC和BC,交AB于M、N两点,DM与EN相交于点F.(1)若△CMN的周长为15cm,求AB的长;(2)若∠MFN=70°,求∠MCN的度数.19.已知△ABC中,AD是∠BAC的平分线,AD的垂直平分线交BC的延长线于F.求证:∠BAF=∠ACF.20.如图所示,在Rt△ABC中,∠ACB=90°,AC=BC,D为BC边上的中点,CE⊥AD于点E,BF∥AC交CE的延长线于点F,求证:AB垂直平分DF.21.如图:在△ABC中,∠C=90°,AD是∠BAC的平分线,DE⊥AB于E,F在AC上,BD=DF;说明:(1)CF=EB.(2)AB=AF+2EB.22.如图,点E是∠AOB的平分线上一点,EC⊥OA,ED⊥OB,垂足分别为C、D.求证:(1)∠ECD=∠EDC;(2)OC=OD;(3)OE是线段CD的垂直平分线.23.如图,四边形ABCD中,∠B=90°,AB∥CD,M为BC边上的一点,且AM平分∠BAD,DM 平分∠ADC.求证:(1)AM⊥DM;(2)M为BC的中点.24.如图,在△ABC中,AB=AC,AD是BC边上的中线,BE⊥AC于点E.求证:∠CBE=∠BAD.25.如图,已知AB=AC=AD,且AD∥BC,求证:∠C=2∠D.26.如图,已知△ABC中,AB=AC,BD、CE是高,BD与CE相交于点O(1)求证:OB=OC;(2)若∠ABC=50°,求∠BOC的度数.27.如图,在△ABC中,AB=AC,点D、E、F分别在AB、BC、AC边上,且BE=CF,BD=CE.(1)求证:△DEF是等腰三角形;(2)当∠A=40°时,求∠DEF的度数.28.如图,在等边三角形ABC中,点D,E分别在边BC,AC上,且DE∥AB,过点E作EF⊥DE,交BC的延长线于点F.(1)求∠F的度数;(2)若CD=2,求DF的长.29.图1、图2中,点C为线段AB上一点,△ACM与△CBN都是等边三角形.(1)如图1,线段AN与线段BM是否相等?证明你的结论;(2)如图2,AN与MC交于点E,BM与CN交于点F,探究△CEF的形状,并证明你的结论.30.如图①,△ABC中,AB=AC,∠B、∠C的平分线交于O点,过O点作EF∥BC交AB、AC 于E、F.(1)图中有几个等腰三角形?猜想:EF与BE、CF之间有怎样的关系,并说明理由.(2)如图②,若AB≠AC,其他条件不变,图中还有等腰三角形吗?如果有,分别指出它们.在第(1)问中EF与BE、CF间的关系还存在吗?(3)如图③,若△ABC中∠B的平分线BO与三角形外角平分线CO交于O,过O点作OE∥BC 交AB于E,交AC于F.这时图中还有等腰三角形吗?EF与BE、CF关系又如何?说明你的理由.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
C A B C D
E P 图 ⑴八年级数学(上)几何证明练习题
1、 已知:在⊿ABC 中,∠A=900
,AB=AC ,在BC 上任取一点P ,作PQ ∥AB 交AC 于Q ,作PR
∥CA 交BA 于R ,D 是BC 的中点,求证:⊿RDQ 是等腰直角三角形。
B
2、 已知:在⊿ABC 中,∠A=900
,AB=AC ,D 是AC 的中点,AE ⊥BD ,AE 延长线交BC 于F ,求
证:∠ADB=∠FDC 。
3、 已知:在⊿ABC 中BD 、CE 是高,在BD 、CE 或其延长线上分别截取BM=AC 、CN=AB ,求证:
MA ⊥NA 。
4、已知:如图(1),在△ABC 中,BP 、CP 分别平分∠ABC 和∠ACB ,DE 过点P 交AB 于D ,交AC 于E ,且DE ∥BC .求证:DE -DB=EC .
5、在Rt △ABC 中,AB =AC ,∠BAC =90°,O 为BC 的中点。
(1)写出点O 到△ABC 的三个顶点A 、B 、C 的距离的大小关系(不要求证明);
(2)如果点M 、N 分别在线段AB 、AC 上移动,在移动中保持AN =BM ,请判断△OMN 的形状,并证明你的结论。
6、如图,△ABC 为等边三角形,延长BC 到D ,延长BA 到E ,AE=BD , 连结EC 、ED ,求证:CE=DE
7、如图,等腰三角形ABC 中,AB =AC ,∠A =90°,BD 平分∠ABC ,DE ⊥BC 且BC =10,求△DCE 的周长。
A B C
O
M N
几何证明习题答案
1. 连接AD,由△ABC为等腰直角三角形可得AD垂直AC,且AD=BD,∠DAQ=∠DBR=45度, 又由平行关系得,四边形RPQA为矩形,所以AQ=RP,
△BRP也是等腰直角三角行,即BR=PR,所以AQ=BR
由边角边,△BRD全等于△AQD,所以∠BDR=∠ADQ,DR=DQ,
∠RDQ=∠RDA+∠ADQ=∠RDA+∠BDR=90度,
所以△RDQ是等腰RT△。
2. 作AG平分∠BAC交BD于G
∵∠BAC=90°∴∠CAG= ∠BAG=45°
∵∠BAC=90°AC=AB ∴∠C=∠ABC=45°
∴∠C=∠BAG ∵AE⊥BD ∴∠ABE+∠BAE=90°
∵∠CAF+∠BAE=90°∴∠CAF=∠ABE
∵AC=AB ∴△ACF ≌△BAG
∴CF=AG ∵∠C=∠DAG =45°CD=AD
∴△CDF ≌△ADG ∴∠CDF=∠ADB
3. 易证△ABM≌△NAC.∠NAM=∠NAE+∠BAM=∠NAE+ANE=90°
4. 略
5.(1)因为直角三角形的斜边中点是三角形的外心,
所以O到△ABC的三个顶点A、B、C距离相等;
(2)△OMN是等腰直角三角形。
证明:连接OA,如图,
∵AC=AB,∠BAC=90°,∴OA=OB,OA平分∠BAC,∠B=45°,
∴∠NAO=45°,∴∠NAO=∠B,
在△NAO和△MBO 中,
AN=BM ,∠NAO=∠B ,AO=BO ,
∴△NAO≌△MBO,∴ON=OM,∠AON=∠BOM,
∵AC=AB,O是BC的中点,∴AO⊥BC,
即∠BOM+∠AOM=90°,∴∠AON+∠AOM=90°,
即∠NOM=90°,∴△OMN是等腰直角三角形.
6. 延长CD到F,使DF=BC,连结EF
∵AE=BD ∴AE=CF
∵△ABC为正三角形∴BE=BF ∠B=60°
∴△EBF为等边三角形∴角F=60°EF=EB
在△EBC和△EFD中
EB=EF(已证)∠B=∠F(已证)BC=DF(已作)
∴△EBC≌△EFD(SAS)∴EC=ED
7. 周长为10.。
