四川省南充高级中学2017-2018学年高二下学期期中考数学(理)试题 扫描版含答案
四川省南充市2017年中考数学真题试题(含解析)

2017年四川省南充市中考数学试卷 一、选择题(本大题共10个小题,每小题3分,共30分)1.如果a+3=0,那么a的值是( )A.3 B.﹣3 C.13D.13【答案】B.【解析】试题分析:移项可得:a=﹣3.故选B.考点:解一元一次方程.2.如图由7个小正方体组合而成的几何体,它的主视图是( )A.B.C.D.【答案】A.【解析】试题分析:根据主视图的定义可知,此几何体的主视图是A中的图形,故选A.考点:简单组合体的三视图.3.据统计,参加南充市2016年高中阶段学校招生考试的人数为55354人,这个数用科学记数法表示为( )A.0.55354×105人 B.5.5354×105人C.5.5354×104人 D.55.354×103人【答案】C.【解析】试题分析:55354=5.5354×104,故选C. 考点:科学记数法—表示较大的数.4.如图,直线a ∥b ,将一个直角三角尺按如图所示的位置摆放,若∠1=58°,则∠2的度数为( )A.30° B.32° C.42° D.58° 【答案】B. 【解析】试题分析:如图,过点A 作AB ∥b ,∴∠3=∠1=58°,∵∠3+∠4=90°,∴∠4=90°﹣∠3=32°,∵a ∥b ,AB ∥B ,∴AB ∥b ,∴∠2=∠4=32°,故选B.考点:平行线的性质. 5.下列计算正确的是( )A.842a a a ÷= B.236(2)6a a = C.3232a a a -= D.23(1)33a a a a -=- 【答案】D.考点:整式的混合运算.6.某校数学兴趣小组在一次数学课外活动中,随机抽查该校10名同学参加今年初中学业水平考试的体育成绩,得到结果如下表所示:下列说法正确的是( )A.这10名同学体育成绩的中位数为38分B.这10名同学体育成绩的平均数为38分C.这10名同学体育成绩的众数为39分D.这10名同学体育成绩的方差为2【答案】C.考点:方差;加权平均数;中位数;众数.7.如图,等边△OAB的边长为2,则点B的坐标为( )A.(1,1) B.,1) C.D.) 【答案】D.【解析】试题分析:如图所示,过B作BC⊥AO于C,则∵△AOB是等边三角形,∴OC=12AO=1,∴Rt△BOC中,BC,∴B),故选D.考点:等边三角形的性质;坐标与图形性质;勾股定理.8.如图,在Rt△ABC中,AC=5cm,BC=12cm,∠ACB=90°,把Rt△ABC所在的直线旋转一周得到一个几何体,则这个几何体的侧面积为( )A.60πcm 2B.65πcm 2C.120πcm 2D.130πcm 2【答案】B.考点:圆锥的计算;点、线、面、体.9.已知菱形的周长为6,则菱形的面积为( )A.2 C.3 D.4 【答案】D. 【解析】试题分析:如图四边形ABCD 是菱形,AC +BD =6,∴AB ,AC ⊥BD ,AO =12AC ,BO =12BD ,∴AO +BO =3,∴AO 2+BO 2=AB 2,(AO +BO )2=9,即AO 2+BO 2=5,AO 2+2AO •BO +BO 2=9,∴2AO •BO =4,∴菱形的面积=12AC •BD =2AO •BO =4;故选D.考点:菱形的性质.10.二次函数2y ax bx c =++(a 、b 、c 是常数,且a ≠0)的图象如图所示,下列结论错误的是( )A.4ac <b 2B.abc <0 C.b +c >3a D.a <b 【答案】D.考点:二次函数图象与系数的关系.二、填空题(本大题共6个小题,每小题3分,共18分) 11.如果111m =-,那么m = . 【答案】2. 【解析】试题分析:去分母得:1=m ﹣1,解得:m =2,经检验m =2是分式方程的解,故答案为:2. 考点:解分式方程.12.计算:0|1|( -+= .【解析】考点:实数的运算;零指数幂.13.经过某十字路口的汽车,可直行,也可向左转或向右转,如果这三种可能性大小相同,则两辆汽车经过该十字路口时都直行的概率是 .【答案】19.【解析】试题分析:画树状图为:共有9种等可能的结果数,其中两辆汽车都直行的结果数为1,所以则两辆汽车都直行的概率为19,故答案为:19.考点:列表法与树状图法.14.如图,在▱ABCD中,过对角线BD上一点P作EF∥BC,GH∥AB,且CG=2BG,S△BPG=1,则S▱AEPH= .【答案】4.考点:平行四边形的性质.15.小明从家到图书馆看报然后返回,他离家的距离y与离家的时间x之间的对应关系如图所示,如果小明在图书馆看报30分钟,那么他离家50分钟时离家的距离为 km .【答案】0.3. 【解析】考点:一次函数的应用.16.如图,正方形ABCD 和正方形CEFG 边长分别为a 和b ,正方形CEFG 绕点C 旋转,给出下列结论:①BE =DG ;②BE ⊥DG ;③222222DE BG a b +=+,其中正确结论是 (填序号)【答案】①②③. 【解析】试题分析:设BE ,DG 交于O ,∵四边形ABCD 和EFGC 都为正方形,∴BC =CD ,CE =CG ,∠BCD =∠ECG =90°,∴∠BCE +∠DCE =∠ECG +∠DCE =90°+∠DCE ,即∠BCE =∠DCG ,在△BCE 和△DCG 中,∵BC =DC ,∠BCE =∠DCG ,CE =CG ,∴△BCE ≌△DCG (SAS),∴BE =DG ,∴∠1=∠2,∵∠1+∠4=∠3+∠1=90°,∴∠2+∠3=90°,∴∠BOC =90°,∴BE ⊥DG ;故①②正确;连接BD ,EG ,如图所示,∴DO 2+BO 2=BD 2=BC 2+CD 2=2a 2,EO 2+OG 2=EG 2=CG 2+CE 2=b 2,则BG 2+DE 2=DO 2+BO 2+EO 2+OG 2=2a 2+b 2,故③正确. 故答案为:①②③.考点:旋转的性质;全等三角形的判定与性质;正方形的性质.三、解答题(共9个小题,满分72分)解答应写出必要的文字说明,证明过程或验算步骤17.化简21(1)1x x x x x --÷++,再任取一个你喜欢的数代入求值. 【答案】1x x -,当x =5时,原式=54.【解析】试题分析:先根据分式混合运算的法则把原式进行化简,再选取合适的x 的值代入进行计算即可.试题解析:原式=2211x x x x x x x +-+⋅+-=2111)(x x x x x +⋅-+=1x x - ∵x ﹣1≠0,x (x +1)≠0,∴x ≠±1,x ≠0,当x =5时,原式=551-=54. 考点:分式的化简求值.18.在“宏扬传统文化,打造书香校园”活动中,学校计划开展四项活动:“A ﹣国学诵读”、“B ﹣演讲”、“C ﹣课本剧”、“D ﹣书法”,要求每位同学必须且只能参加其中一项活动,学校为了了解学生的意愿,随机调查了部分学生,结果统计如下:(1)如图,希望参加活动C 占20%,希望参加活动B 占15%,则被调查的总人数为 人,扇形统计图中,希望参加活动D所占圆心角为 度,根据题中信息补全条形统计图. (2)学校现有800名学生,请根据图中信息,估算全校学生希望参加活动A有多少人?【答案】(1)60,72;(2)360.【解析】补全的条形统计图如图所示;(2)由题意可得,800×2760=360. 答:全校学生希望参加活动A 有360人.考点:条形统计图;用样本估计总体;扇形统计图.19.如图,DE ⊥AB ,CF ⊥AB ,垂足分别是点E 、F ,DE =CF ,AE =BF ,求证:AC ∥BD .【答案】答案见解析. 【解析】试题分析:欲证明AC ∥BD ,只要证明∠A =∠B ,只要证明△DEB ≌△CFA 即可.试题解析:∵DE ⊥AB ,CF ⊥AB ,∴∠DEB =∠AFC =90°,∵AE =BF ,∴AF =BE ,在△DEB 和△CFA 中,∵DE =CF ,∠DEB =∠AFC ,AF =BE ,△DEB ≌△CFA ,∴∠A =∠B ,∴AC ∥DB . 考点:全等三角形的判定与性质.20.已知关于x 的一元二次方程2(3)0x m x m ---=. (1)求证:方程有两个不相等的实数根;(2)如果方程的两实根为1x ,2x ,且2212127x x x x +-=,求m 的值. 【答案】(1)证明见解析;(2)m 的值是1或2. 【解析】试题分析:(1)要证明方程有两个不相等的实数根,只要证明原来的一元二次方程的△的值大于0即可; (2)根据根与系数的关系可以得到关于m 的方程,从而可以求得m 的值.试题解析:(1)证明:∵2(3)0x m x m ---=,∴△=[﹣(m ﹣3)]2﹣4×1×(﹣m )=m 2﹣2m +9=(m ﹣1)2+8>0,∴方程有两个不相等的实数根;(2)∵2(3)0x m x m ---=,方程的两实根为1x ,2x ,且2212127x x x x +-=,∴123x x m +=- ,12x x m =- ,∴21212()37x x x x +-=,∴(m ﹣3)2﹣3×(﹣m )=7,解得,m 1=1,m 2=2,即m 的值是1或2.考点:根与系数的关系;根的判别式.21.如图,直线y =kx (k 为常数,k ≠0)与双曲线my x=(m 为常数,m >0)的交点为A 、B ,AC ⊥x 轴于点C ,∠AOC =30°,OA =2.(1)求m 的值;(2)点P 在y 轴上,如果3ABP S k ∆=,求P 点的坐标.【答案】;(2)P (0,1)或(0,﹣1). 【解析】试题分析:(1)求出点A 坐标利用待定系数法即可解决问题;(2)设P (0,n ),由A ,1),B ,﹣1),可得12•|n +12•|n ,解方程即可;试题解析:(1)在Rt△AOC 中,∵∠ACO =90°,∠AOC =30°,OA =2,∴AC =1,OC ,∴A ,1),∵反比例函数m y x经过点A ,∴m ,∵y =kx 经过点A ,1),∴k .(2)设P (0,n ),∵A ,B ,∴12•|n +12•|n n =±1,∴P (0,1)或(0,﹣1).考点:反比例函数与一次函数的交点问题.22.如图,在Rt△ABC 中,∠ACB =90°,以AC 为直径作⊙O 交AB 于点D ,E 为BC 的中点,连接DE 并延长交AC 的延长线于点F . (1)求证:DE 是⊙O 的切线; (2)若CF =2,DF =4,求⊙O 直径的长.【答案】(1)证明见解析;(2)6.【解析】(2)设⊙O的半径为r,∵∠ODF=90°,∴OD2+DF2=OF2,即r2+42=(r+2)2,解得:r=3,∴⊙O的直径为6.考点:切线的判定与性质.23.学校准备租用一批汽车,现有甲、乙两种大客车,甲种客车每辆载客量45人,乙种客车每辆载客量30人,已知1辆甲种客车和3辆乙种客车共需租金1240元,3辆甲种客车和2辆乙种客车共需租金1760元.(1)求1辆甲种客车和1辆乙种客车的租金分别是多少元?(2)学校计划租用甲、乙两种客车共8辆,送330名师生集体外出活动,最节省的租车费用是多少? 【答案】(1)1辆甲种客车的租金是400元,1辆乙种客车的租金是280元;(2)2960.【解析】试题分析:(1)可设1辆甲种客车的租金是x元,1辆乙种客车的租金是y元,根据等量关系:①1辆甲种客车和3辆乙种客车共需租金1240元,②3辆甲种客车和2辆乙种客车共需租金1760元,列出方程组求解即可;(2)由于求最节省的租车费用,可知租用甲种客车6辆,租用乙客车2辆,进而求解即可.试题解析:(1)设1辆甲种客车的租金是x元,1辆乙种客车的租金是y元,依题意有:31240 321760 x yx y+=⎧⎨+=⎩,解得:400280x y =⎧⎨=⎩.答:1辆甲种客车的租金是400元,1辆乙种客车的租金是280元;(2)租用甲种客车6辆,租用乙客车2辆是最节省的租车费用,400×6+280×2=2400+560=2960(元). 答:最节省的租车费用是2960元.考点:一元一次不等式的应用;二元一次方程组的应用;最值问题. 24.如图,在正方形ABCD 中,点E 、G 分别是边AD 、BC 的中点,AF =14AB . (1)求证:EF ⊥AG ;(2)若点F 、G 分别在射线AB 、BC 上同时向右、向上运动,点G 运动速度是点F 运动速度的2倍,EF ⊥AG 是否成立(只写结果,不需说明理由)?(3)正方形ABCD 的边长为4,P 是正方形ABCD 内一点,当PAB OAB S S ∆∆=,求△PAB 周长的最小值.【答案】(1)证明见解析;(2)成立;4+. 【解析】试题分析:(1)由正方形的性质得出AD =AB ,∠EAF =∠ABG =90°,证出AF BGAE BA=,得出△AEF ∽△BAG ,由相似三角形的性质得出∠AEF =∠BAG ,再由角的互余关系和三角形内角和定理证出∠AOE =90°即可; (2)证明△AEF ∽△BAG ,得出∠AEF =∠BAG ,再由角的互余关系和三角形内角和定理即可得出结论; (3)过O 作MN ∥AB ,交AD 于M ,BC 于N ,则MN ⊥AD ,MN =AB =4,由三角形面积关系得出点P 在线段MN 上,当P 为MN 的中点时,△PAB 的周长最小,此时PA =PB ,PM =12MN =2,连接EG ,则EG ∥AB ,EG =AB =4,证明△AOF ∽△GOE ,得出OF AF OE EG = =14,证出AM OF EM OE = =14,得出AM =15AE =25,由勾股定理求出PA ,即可得出答案.试题解析:(1)证明:∵四边形ABCD 是正方形,∴AD =AB ,∠EAF =∠ABG =90°,∵点E 、G 分别是边AD 、BC 的中点,AF =14AB ,∴AF AE =12,BG BA =12,∴AF BGAE BA=,∴△AEF ∽△BAG ,∴∠AEF =∠BAG ,∵∠BAG +∠EAO =90°,∴∠AEF +∠EAO =90°,∴∠AOE =90°,∴EF ⊥AG ; (2)解:成立;理由如下: 根据题意得:AF BG =12,∵AE AB =12,∴AF BG =AEAB,又∵∠EAF =∠ABG ,∴△AEF ∽△BAG ,∴∠AEF =∠BAG ,∵∠BAG +∠EAO =90°,∴∠AEF +∠EAO =90°,∴∠AOE =90°,∴EF ⊥AG ; (3)解:过O 作MN ∥AB ,交AD 于M ,BC 于N ,如图所示:则MN ⊥AD ,MN =AB =4,∵P 是正方形ABCD 内一点,当S △PAB =S △OAB ,∴点P 在线段MN 上,当P 为MN 的中点时,△PAB 的周长最小,此时PA =PB ,PM =12MN =2,连接EG 、PA 、PB ,则EG ∥AB ,EG =AB =4,∴△AOF ∽△GOE ,∴OF AF OE EG ==14,∵MN ∥AB ,∴AM OF EM OE = =14,∴AM =15AE =15×2=25,由勾股定理得:PA ,∴△PAB 周长的最小值=2PA +AB 4+.考点:四边形综合题;探究型;动点型;最值问题.25.如图1,已知二次函数2y ax bx c =++(a 、b 、c 为常数,a ≠0)的图象过点O (0,0)和点A (4,0),函数图象最低点M 的纵坐标为38-,直线l 的解析式为y =x .(1)求二次函数的解析式;(2)直线l 沿x 轴向右平移,得直线l ′,l ′与线段OA 相交于点B ,与x 轴下方的抛物线相交于点C ,过点C 作CE ⊥x 轴于点E ,把△BCE 沿直线l ′折叠,当点E 恰好落在抛物线上点E ′时(图2),求直线l ′的解析式;(3)在(2)的条件下,l ′与y 轴交于点N ,把△BON 绕点O 逆时针旋转135°得到△B ′ON ′,P 为l ′上的动点,当△PB ′N ′为等腰三角形时,求符合条件的点P 的坐标. 【答案】(1)28233x x y -=;(2)y =x ﹣3;(3)P).【解析】试题分析:(1)由题意抛物线的顶点坐标为(2,38-),设抛物线的解析式为2(2)3a x y 8-=-,把(0,0)代入得到a =23,即可解决问题; (2)如图1中,设E (m ,0),则C (m ,22833m m -),B (221133m m -+,0),由E 、B 关于对称轴对称,可得2211()332m m m +-+ =2,由此即可解决问题; (3)分两种情形求解即可①当P 1与N 重合时,△P 1B ′N ′是等腰三角形,此时P 1(0,﹣3).②当N ′=N ′B ′时,设P (m ,m ﹣3),列出方程解方程即可;试题解析:(1)由题意抛物线的顶点坐标为(2,38-),设抛物线的解析式为2(2)3a x y 8-=-,把(0,0)代入得到a =23,∴抛物线的解析式为222)(33x y 8--=,即28233x y x -=.(2)如图1中,设E (m ,0),则C (m ,28233m m -),B (211233m m +-,0),∵E ′在抛物线上,∴E 、B 关于对称轴对称,∴2211()332m m m +-+ =2,解得m =1或6(舍弃),∴B (3,0),C (1,﹣2),∴直线l ′的解析式为y =x ﹣3.(3)如图2中,①当P 1与N 重合时,△P 1B ′N ′是等腰三角形,此时P 1(0,﹣3). ②当N ′=N ′B ′时,设P (m ,m ﹣3),则有222((3m m -+-=,解得mP 2,P 3.综上所述,满足条件的点P.考点:二次函数综合题;几何变换综合题;分类讨论;压轴题.。
2017年四川省南充市中考数学试卷(解析版)

2017年四川省南充市中考数学试卷一、选择题(本大题共10个小题,每小题3分,共30分)1.如果a+3=0,那么a的值是()A.3 B.﹣3 C.D.﹣2.如图由7个小正方体组合而成的几何体,它的主视图是()A.B.C.D.3.据统计,参加南充市2016年高中阶段学校招生考试的人数为55354人,这个数用科学记数法表示为()A.0.55354×105人B.5。
5354×105人C.5.5354×104人D.55.354×103人4.如图,直线a∥b,将一个直角三角尺按如图所示的位置摆放,若∠1=58°,则∠2的度数为()A.30°B.32°C.42°D.58°5.下列计算正确的是()A.a8÷a4=a2B.(2a2)3=6a6C.3a3﹣2a2=a D.3a(1﹣a)=3a﹣3a26.某校数学兴趣小组在一次数学课外活动中,随机抽查该校10名同学参加今年初中学业水平考试的体育成绩,得到结果如下表所示:成绩/分3637383940人数/人12142下列说法正确的是()A.这10名同学体育成绩的中位数为38分B.这10名同学体育成绩的平均数为38分C.这10名同学体育成绩的众数为39分D.这10名同学体育成绩的方差为27.如图,等边△OAB的边长为2,则点B的坐标为()A.(1,1) B.(,1) C.(,)D.(1,)8.如图,在Rt△ABC中,AC=5cm,BC=12cm,∠ACB=90°,把Rt△ABC所在的直线旋转一周得到一个几何体,则这个几何体的侧面积为()A.60πcm2B.65πcm2C.120πcm2D.130πcm29.已知菱形的周长为4,两条对角线的和为6,则菱形的面积为()A.2 B.C.3 D.410.二次函数y=ax2+bx+c(a、b、c是常数,且a≠0)的图象如图所示,下列结论错误的是()A.4ac<b2B.abc<0 C.b+c>3a D.a<b二、填空题(本大题共6个小题,每小题3分,共18分)11.如果=1,那么m=.12.计算:|1﹣|+(π﹣)0=.13.经过某十字路口的汽车,可直行,也可向左转或向右转,如果这三种可能性大小相同,则两辆汽车经过该十字路口时都直行的概率是.14.如图,在▱ABCD中,过对角线BD上一点P作EF∥BC,GH∥AB,且CG=2BG,S =1,则S▱AEPH=.△BPG15.小明从家到图书馆看报然后返回,他离家的距离y与离家的时间x之间的对应关系如图所示,如果小明在图书馆看报30分钟,那么他离家50分钟时离家的距离为km.16.如图,正方形ABCD和正方形CEFG边长分别为a和b,正方形CEFG绕点C 旋转,给出下列结论:①BE=DG;②BE⊥DG;③DE2+BG2=2a2+b2,其中正确结论是(填序号)三、解答题(共9个小题,满分72分)解答应写出必要的文字说明,证明过程或验算步骤17.化简(1﹣)÷,再任取一个你喜欢的数代入求值.18.在“宏扬传统文化,打造书香校园”活动中,学校计划开展四项活动:“A﹣国学诵读"、“B﹣演讲"、“C﹣课本剧”、“D﹣书法”,要求每位同学必须且只能参加其中一项活动,学校为了了解学生的意愿,随机调查了部分学生,结果统计如下:(1)如图,希望参加活动C占20%,希望参加活动B占15%,则被调查的总人数为人,扇形统计图中,希望参加活动D所占圆心角为度,根据题中信息补全条形统计图.(2)学校现有800名学生,请根据图中信息,估算全校学生希望参加活动A有多少人?19.如图,DE⊥AB,CF⊥AB,垂足分别是点E、F,DE=CF,AE=BF,求证:AC∥BD.20.已知关于x的一元二次方程x2﹣(m﹣3)x﹣m=0(1)求证:方程有两个不相等的实数根;(2)如果方程的两实根为x1、x2,且x12+x22﹣x1x2=7,求m的值.21.如图,直线y=kx(k为常数,k≠0)与双曲线y=(m为常数,m>0)的交点为A 、B ,AC ⊥x 轴于点C ,∠AOC=30°,OA=2 (1)求m 的值;(2)点P 在y 轴上,如果S △ABP =3k,求P 点的坐标.22.如图,在Rt △ABC 中,∠ACB=90°,以AC 为直径作⊙O 交AB 于点D,E 为BC 的中点,连接DE 并延长交AC 的延长线于点F . (1)求证:DE 是⊙O 的切线; (2)若CF=2,DF=4,求⊙O 直径的长.23.学校准备租用一批汽车,现有甲、乙两种大客车,甲种客车每辆载客量45人,乙种客车每辆载客量30人,已知1辆甲种客车和3辆乙种客车共需租金1240元,3辆甲种客车和2辆乙种客车共需租金1760元. (1)求1辆甲种客车和1辆乙种客车的租金分别是多少元?(2)学校计划租用甲、乙两种客车共8辆,送330名师生集体外出活动,最节省的租车费用是多少?24.如图,在正方形ABCD 中,点E 、G 分别是边AD 、BC 的中点,AF=AB . (1)求证:EF ⊥AG ;(2)若点F 、G 分别在射线AB 、BC 上同时向右、向上运动,点G 运动速度是点F 运动速度的2倍,EF ⊥AG 是否成立(只写结果,不需说明理由)?(3)正方形ABCD 的边长为4,P 是正方形ABCD 内一点,当S △PAB =S △OAB ,求△PAB 周长的最小值.25.如图1,已知二次函数y=ax2+bx+c(a、b、c为常数,a≠0)的图象过点O(0,0)和点A(4,0),函数图象最低点M的纵坐标为﹣,直线l的解析式为y=x.(1)求二次函数的解析式;(2)直线l沿x轴向右平移,得直线l′,l′与线段OA相交于点B,与x轴下方的抛物线相交于点C,过点C作CE⊥x轴于点E,把△BCE沿直线l′折叠,当点E恰好落在抛物线上点E′时(图2),求直线l′的解析式;(3)在(2)的条件下,l′与y轴交于点N,把△BON绕点O逆时针旋转135°得到△B′ON′,P为l′上的动点,当△PB′N′为等腰三角形时,求符合条件的点P的坐标.2017年四川省南充市中考数学试卷参考答案与试题解析一、选择题(本大题共10个小题,每小题3分,共30分)1.如果a+3=0,那么a的值是()A.3 B.﹣3 C.D.﹣【考点】86:解一元一次方程.【分析】直接移项可求出a的值.【解答】解:移项可得:a=﹣3.故选B.2.如图由7个小正方体组合而成的几何体,它的主视图是()A.B.C.D.【考点】U2:简单组合体的三视图.【分析】根据主视图是从物体正面看所得到的图形解答即可.【解答】解:根据主视图的定义可知,此几何体的主视图是A中的图形,故选:A.3.据统计,参加南充市2016年高中阶段学校招生考试的人数为55354人,这个数用科学记数法表示为()A.0。
2018年四川省南充市中考数学试卷及答案解析(精析版)

南充市二O一二年高中阶段学校招生统一考试数学试卷(解析版)(满分100分,时间90分钟)一、选择题(本大题共10个小题,每小题3分,共30分)每小题都有代号为A、B、C、D四个答案选项,其中只有一个是正确的,请把正确选项的代号填在相应的括号内.填写正确记3分,不填、填错或填出的代号超过一个记0分.1.计算2-(-3)的结果是().(A)5 (B)1 (C)-1 (D)-5考点:有理数的计算专题:计算题。
分析:本题需先做有理数的减法把括号去掉,即可得出正确答案.解答:解:2-(-3)=2+3,=5.故选A.点评:本题主要考查了有理数的加减法,在解题时去括号要变号,是解题的关键.2.下列计算正确的是()(A)x3+ x3=x6(B)m2·m3=m6(C)3-2=3 (D)14×7=72考点:整式的加减、整式的基本性质、实数的运算。
专题:计算题。
分析:本题需先对每一项分别进行解答,得出正确的结果,最后选出本题的答案即可.解答:解:A、∵x3+ x3=2x3,故本答案错误;(B)m2·m3=m5本答案错误(C)3-2再不能合并了7 ×7=72答案正确(D)14×7=2点评:本题主要考查学生整式的加减、整式的基本性质、实数的运算等基本的运算能力。
3.下列几何体中,俯视图相同的是( ).考点:三视图的基本知识 专题:几何题。
分析:① 俯视图是一个没圆心的圆 ②③俯视图是一个带圆心的圆 ④俯视图是两个不带圆心的同心圆 解答:① 俯视图是一个没圆心的圆 ②③俯视图是一个带圆心的圆 ④俯视图是两个不带圆心的同心圆 答案选C点评:主要考查学生对三视图基础知识的理解和掌握 4.下列函数中是正比例函数的是 ( )( A )y =-8x (B )y =x8-( C )y =5x 2+6 (D )y = -0.5x -1考点:正比例函数、反比例函数、一次比例函数 二次比例函数 专题:常规题型。
四川省南充高级中学高2017级高二下数学试卷(十三)
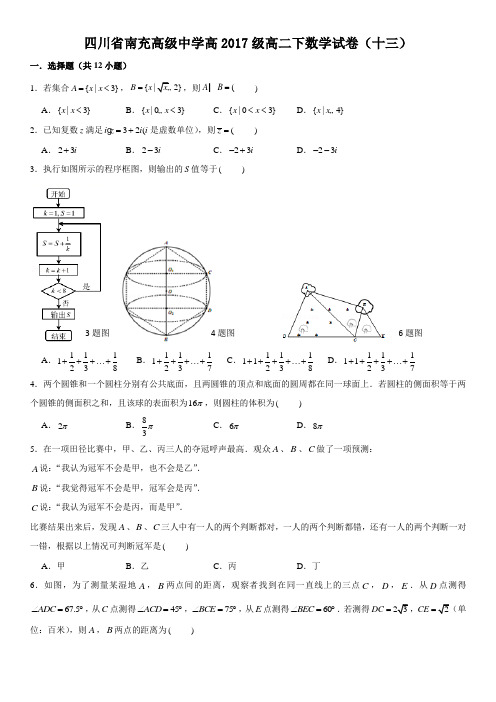
四川省南充高级中学高2017级高二下数学试卷(十三)一.选择题(共12小题)1.若集合{|3}A x x =<,{2}B x =,则(A B = )A .{|3}x x <B .{|03}x x <…C .{|03}x x <<D .{|4}x x …2.已知复数z 满足32(i z i i =+是虚数单位),则(z = ) A .23i +B .23i -C .23i -+D .23i --3.执行如图所示的程序框图,则输出的S 值等于( )A .1111238+++⋯+ B .1111237+++⋯+ C .11111238++++⋯+ D .11111237++++⋯+ 4.两个圆锥和一个圆柱分别有公共底面,且两圆锥的顶点和底面的圆周都在同一球面上.若圆柱的侧面积等于两个圆锥的侧面积之和,且该球的表面积为16π,则圆柱的体积为( ) A .2πB .83πC .6πD .8π5.在一项田径比赛中,甲、乙、丙三人的夺冠呼声最高.观众A 、B 、C 做了一项预测: A 说:“我认为冠军不会是甲,也不会是乙”. B 说:“我觉得冠军不会是甲,冠军会是丙”. C 说:“我认为冠军不会是丙,而是甲”. 比赛结果出来后,发现A 、B 、C 三人中有一人的两个判断都对,一人的两个判断都错,还有一人的两个判断一对一错,根据以上情况可判断冠军是( ) A .甲B .乙C .丙D .丁6.如图,为了测量某湿地A ,B 两点间的距离,观察者找到在同一直线上的三点C ,D ,E .从D 点测得67.5ADC ∠=︒,从C 点测得45ACD ∠=︒,75BCE ∠=︒,从E 点测得60BEC ∠=︒.若测得DC =CE =位:百米),则A ,B 两点的距离为( )3题图4题图6题图AB.C .3 D.7.曲线11cos :(sin x C y θθθ=+⎧⎨=⎩为参数)上的点到曲线212:(112x t C t y t⎧=-⎪⎪⎨⎪=-⎪⎩为参数)上的点的最短距离为( ) A .1 B .2 C .3 D .48.已知数列{}n a 的前n 项和为n S ,且2*119()2n n n nS S n N +-+=∈,若1011a a <,则n S 取最小值时n 的值为()A .10B .9C .11D .129.已知F 是抛物线24x y =的焦点,点P 在抛物线上,点(0,1)A -,则||||PF PA 的最小值是( ) ABC .1D .1210.已知正数a ,b 满足221a b ab +=+,则1)2a b +的最大值为( ) A.B .2CD .111.已知AB 是椭圆221255x y +=的长轴,若把线段AB 五等份,过每个分点作AB 的垂线,分别与椭圆的上半部分相交于C ,D ,E ,G 四点,设F 是椭圆的左焦点,则||||||||FC FD FE FG +++的值是( ) A .15B .16C .18D .2012.已知函数1()ax f x xe lnx ax -=--,21(,]a e∈-∞-,函数()f x 的最小值M ,则实数M 的最小值是( ) A .1-B .1e-C .0D .31e -二.填空题(共4小题)13.若向量(1,2)a x =+和向量(1,2)b =-垂直,则||a b -= .14.某校高一、高二、高三年级的学生人数之比为4:4:3,现按年级用分层抽样的方法抽取若千人,若抽取的高三年级的学生数为15,则抽取的样本容量为 .15.已知双曲线2222(0,0)x y l a b a b-=>>的左、右焦点分别为1F ,2F ,过点1F 且垂于x 轴的直线与该双曲线的左支交于A ,B 两点,2AF ,2BF 分别交y 轴于P ,Q 两点,若2PQF ∆的周长为8,则ab 取得最大值时,该双曲线的离心率是 .16.已知函数(),(0,)2x e axf x x x =-∈+∞,当21x x >时,不等式1221()()0f x f x x x -<恒成立,则实数a 的取值范围为 . 三.解答题(共8小题)17.设数列{}n a 满足123232(*)n n a a a na n N ⋯=∈(1)求{}n a 的通项公式; (2)求数列122n n a +⎧⎫+⎨⎬⎩⎭的前n 项和nS18.(文)某高校共有10000人,其中男生7500人,女生2500人,为调查该校学生每则平均体育运动时间的情况,采用分层抽样的方法,收集200位学生每周平均体育运动时间的样本数据(单位:小时).调查部分结果如下22⨯列联表:(1)完成上述每周平均体育运动时间与性别的22⨯列联表,并判新是否有95%把握认为“该校学生的每周平均体育运动时间与性别有关”;(2)已知在被调查的男生中,有5名数学系的学生,其中有2名学生每周平均体育运动时间超过4小时,现从这5名学生中随机抽取2人,求恰有1人“每周平均体育运动时间超过4小时”的概率. 附.22()()()()()n ad bc K a b c d a c b d -=++++,其中n a b c d =+++.(理)某大型工厂招聘到一大批新员工.为了解员工对工作的熟练程度,从中随机抽取100人组成样本,并统计他们的日加工零件数,得到以下数据;(1)已知日加工零件数在[80,120)范围内的5名员工中,有3名男工,2名女工,现从中任取两名进行指导,求他们性别不同的概率;(2)完成频率分布直方图,并估计全体新员工每天加工零件数的平均数(每组数据以中点值代替);19.(理)如图,四边形ABCD 和三角形ADE 所在平面互相垂直,//AB CD ,AB BC ⊥,60DAB ∠=︒,4AB AD ==,AE DE ⊥,AE DE =,平面ABE 与平面CDE 交于EF .(Ⅰ)求证://CD EF ;(Ⅱ)若EF CD =,求二面角A BC F --余弦值;(Ⅲ)在线段BC 上是否存在点M 使得AM EM ⊥?若存在,求BM 的长;若不存在,说明理由.(文).四棱锥P ABCD -中,底面ABCD 是菱形,60BAD ∠=︒,PA PB PD ==.(1)求证:PD AB ⊥; (2)若6AB =,8PC =,E 是BD 的中点,求点E 到平面PCD 的距离.20.已知椭圆2222:1(0)x y C a b a b+=>>的一个焦点与抛物线2y =.(1)求椭圆C 的标准方程;(2)不过原点的直线l 与椭圆C 交于M ,N 两点,若三直线OM 、l 、ON 的斜率与1k ,k ,2k 点成等比数列,求直线l 的斜率及22||||OM ON +的值.21.已知函数21()(1)()2f x lnx ax a x a R =+-+∈.(Ⅰ)当1a …时,函数()f x 在区间[1,]e 上的最小值为5-,求a 的值; (Ⅱ)设3211()()(1)22g x xf x ax a x x =-++-,且()g x 有两个极值点1x ,2x .()i 求实数a 的取值范围; ()ii 证明:212x x e >.22.在直角坐标系xOy 中,曲线1C 的参数方程为cos ,(x y ααα=⎧⎪⎨=⎪⎩为参数).以坐标原点为极点,以x 轴的正半轴为极轴,建立极坐标系,曲线2C 的极坐标方程为sin()4πρθ-=(1)写出1C 的普通方程和2C 的直角坐标方程;(2)设点P 在1C 上,点Q 在2C 上,求||PQ 的最小值及此时P 的直角坐标.四川省南充高级中学高2017级高二下数学试卷(十三)参考答案与试题解析一.选择题(共12小题)1.B .2.A .3.D .4.C .5.A .6.C .7.A .8.A .9.A . 10.【解答】解:令a x y =-,b x y =+,(0)x y >>,则221a b ab +=+化为22()()()()1x y x y x y x y -++=-++,即2231()x y x y +=>,令cos x α=,y ,0x y >>,cos 0α∴>>,103απ∴<<,则1)21)()2()1)3)z a b x y x y x y =+=-++=-1)cos 3)α=-5)12πα=+,103απ<<,∴55312124πππα<+<,当5sin()112πα+=时有最大值A . 11. D .12.【解答】解:函数1()ax f x xe lnx ax -=--,21(,]a e ∈-∞-,11111()(1)()ax ax ax g x e axe a ax e x x---∴'=+--=+-, 由110ax e x --=,解得:1lnx a x -=,设1()lnx p x x -=,则22()lnx p x x-'=,当2x e >时,()0p x '>,当20x e <<,()0p x '<, 从而()p x 在2(0,)e 上单调递减,在2(e ,)+∞上单调递增,221()()mi n p x p e e ==-,当21a e -…,1lnx a x -…,即110ax e x --…,在1(0,)a -上,10ax +>,()0g x '…,()g x 单调递减,在1(a -,)+∞上,10ax +<,()0g x '…,()g x 单调递增,1()()min g x g M a ∴=-=,设1(0t a =-∈,2]e ,2()1t M h t lnt e ==-+,2(0)t e <…,211()0h t e t'=-…,()h x 在,(0∈,2]e 上单调递减,2()()0h t h e ∴=…,M ∴的最小值为0.故选:C . 二.填空题(共4小题) 13.5.14.55.15.【解答】解:由2P Q F ∆的周长为8,PQ 为三角形2ABF 的中位线,可得2ABF ∆的周长为16,22||||||16AF BF AB ++=,22||||||4AF BF AB a +-=,22||b AB a =,∴24164b a a=-,2(4)b a a ∴=-,223(4)y a b a a ∴==-,24(3)y a a ∴'=-,03a <<,0y '>,3a >,0y '<,3a ∴=时,22y a b =取得最大值,此时ab 取得最大值,b =c ∴==c e a ∴=, 16.(-∞,]e . 三.解答题(共8小题)17.【解答】解:(1){}n a 满足123232(*)n n a a a na n N ⋯=∈可得1n =时,12a =,2n …时,11212(1)2n n a a n a --⋯-=,又123232(*)n n a a a na n N ⋯=∈相除可得2n na =,即2n a n =,上式对1n =也成立,则{}n a 的通项公式为2n a n=; (2)1222n n nn n a ++=+,设212222n n H n =++⋯+,231212222n n H n +=++⋯+, 相减可得12422nn n H n +-=++⋯+-12(12)212n n n +-=--,化简可得12(1)2n n H n +=+-.则前n 项和1(1)2(1)22n n n n T n ++=+-+.18.(文)【解答】解:(1)收集女生人数为25002005010000⨯=,男生人数为20050150-=,即应收集50为女生,150位男生的样本数据,22200(353020115)50005.22 3.8411505014555957K ⨯-⨯∴==≈>⨯⨯⨯,所以有95%把握认为“该校学生的每周平均体育运动时间与性别有关”(2)设i a 表示每周平均体育运动时间超过4小时的学生,1i =,2,j b 表示每周平均体育运动时间不超过4小时的学生,1j =,2,3,从5名数学系学生任取2人的可能结果构成基本事件,1{(a Ω=,2)a ,1(a ,1)b ,1(a ,2)b ,1(a ,3)b ,2(a ,1)b ,2(a ,2)b ,2(a ,3)b ,1(b ,2)b ,1(b ,3)b ,2(b ,3)}b ,Ω由10个基本事件组成,且这些基本事件是等可能的,设A 表示“2人中恰有一人每周平均体育运动时间超过4小时”,则1{(A a =,1)b ,1(a ,2)b ,1(a ,3)b ,2(a ,1)b ,2(a ,2)b ,2(a ,3)}b ,A 由6个基本事件组成,由古典概型得,P (A )63105==. (理)【解答】解:(1)记3名男工分别为a ,b ,c ,2名女工分别为e ,从中任取两名进行指导,不同的取法有10种,分别为ab ,ac ,ad ,ae ,bc ,bd ,be ,ed ,ec ,de ,他们性别不同包含的基本事件有6种,分别为:ad ,ae ,bd ,be ,ed ,ce ,∴他们性别不同的概率为63105p ==. (2)频率分布直方图如下:估计全体新员工每天加工零件数的平均数为:1(100514010180252202030020)220100⨯+⨯+⨯+⨯+⨯=. 19.(理)【解答】(Ⅰ)证明://AB CD ,AB ⊂平面ABE ,CD ⊂/平面ABE ,//CD ∴平面ABE ,又CD ⊂平面CDE ,平面CDE ⋂平面ABE EF =,//CD EF ∴.(Ⅱ)取AD 的中点N ,连接EN ,BN .AE DE =,EN AD ∴⊥.又平面ADE ⊥平面ABCD ,平面ADE ⋂平面ABCD AD =,EN ⊂平面ADE ,EN ∴⊥平面ABCD .122AN AD ==,4AB =,60DAB ∠=︒,BN ∴=222AN BN AB ∴+=,即A N B N⊥.ADE ∆是等腰直角三角形,4AD =,2EN ∴=,以N 为原点建立空间直角坐标系N xyz -,如图所示,则(0N ,0,0),(0B,,0),(3C -0),(1F -2).∴(1,3,2),(3,BF BC =--=-,设平面BCF 的法向量为(n x =,y ,)z ,则0,0,n BF n BC ⎧=⎪⎨=⎪⎩即20,30.x z x ⎧-+=⎪⎨--=⎪⎩令y =1x =-,1z =.于是(n =-.又平面ABCD 的法向量为(0,0,2)NE =, cos n ∴<,||||2n NE NE n NE >===⨯.由题知二面角A BC F --为锐角,所以二面角A BC F --.(Ⅲ)不存在满足条件的点M ,使AM EM ⊥,理由如下:若AM EM ⊥,则0AM EM =.因为点M为线段BC 上的动点,设(01)CM tCB t =剟.则(33M t -,0),∴(35AM t =-,+,0),(33EM t =-,2)-,2(33)(35)0t t ∴--++=,化简得:22330t t -+=,方程无实根.所以线段BC上不存在点M ,使AM EM ⊥.(文)【解答】(1)证明:由于四边形ABCD 是菱形,60BAD ∠=︒,所以ABD ∆是正三角形.设AB 的中点为K ,连接PK ,DK ,如图所示,则AB DK ⊥,又P A P B=,所以AB PK ⊥.又PK ,DK 相交于K ,所以AB ⊥平面PKD .又PD ⊂平面PKD ,所以AB PD ⊥.(2)解:由(1)可知,AB ⊥平面PKD .又//AB CD ,所以CD ⊥平面PKD .又CD ⊂平面PDC ,所以平面PDC ⊥平面PKD ,设点E 到平面PCD 的距离为h ,则由于2BD ED =,得点B 到平面PCD 的距离为2h .由于//KB 平面PCD ,所以K ,B 两点到平面PCD 的距离均为2h .所以点K 到直线PD 的距离就是2h .设ABD ∆的中心为H ,则PH ⊥平面ABD.4HC HE ==,在r t P H C ∆中,4PH ==,在R t P ∆中,4PH =,DH =,所以PD .由2D H H K =,得点H 到直线PD 的距离为43h,即433h PH HD PD ==,得h =E 到平面PCD20.【解答】解:(1)依题意得c ,c a =2a =,又223a b -=得1b =,∴椭圆C 的方程为2214x y +=.(2)设直线l 的方程为y kx m =+,(0)m ≠,1(M x ,1)y ,2(N x ,2)y ,由2214y k x m x y =+⎧⎪⎨+=⎪⎩,得222(14)84(1)0k x kmx m +++-=,122814kmx x k -∴+=+,21224(1)14m x x k -=+.由题设知22212121212121212()()()y y kx m kx m km x x m k k k k x x x x x x ++++====+,212()0km x x m ∴++=,22228014k m m k∴-+=+, 0m ≠,214k ∴=,12k =±此时2221228()()414km x x m k-+==+,221224(1)2(1)14m x x m k -==-+, 则2222222222222221122112212121211333||||11()2[()2]2[44(1)]2544444OM ON x y x y x x x x x x x x x x m m +=+++=+-++-=⨯++=⨯+-+=⨯--+=,故直线l 的斜率为12k =±,22||||5OM ON +=.21.【解答】解:1(1)(1)()()(1)x ax I f x ax a x x--'=+-+=,()y f x ∴=在[1,]e 上是单调递增的, ∴()(1)152min af x f ==--=-,8a ∴=. 322111()()()()(1)(1)222II i g x xf x ax a x x xlnx a x x =-++-=-+-.()(1)g x lnx a x ∴'=-+.∴方程(1)0lnx a x -+=有两个不同实根1x ,2x ,得1lnx a x +=.令()lnx h x x =,∴21()lnxh x x-'=.()y h x ∴=在(0,)e 上单调递增,在(,)e +∞上单调递减.∴()1,x e y h x e=-时取得最大值为.又h (1)0=,∴当01x <<,()0h x <,当1x >时,()0h x >.∴1101,11a a e e<+<-<<-即. ()ii 由()i 可知,1122(1)(1)lnx a x lnx a x =+⎧⎨=+⎩,两式相加,得1212()(1)()ln x x a x x =++--(1)两式相减,得2211(1)()xln a x x x =+---(2),(1)(2),得12122211()ln x x x x x x x ln x +=-,不妨设21x x >,要证:212x x e >,只需证21212211()2x x xln x x ln x x x +=>- 即证22211212112(1)2()1x x x x x ln x x x x x -->=++,令21,1x t t x =>,则只需证2(1),11t lnt t t ->>+令2(1)4()2,111t F t lnt lnt t t t -=-=+->++22214(1)()0(_1)(1)t F t t t t t -'=-=>+.()(1y F t ∴=,)+∞,F (1)0=,()F t F ∴>(1)0=,∴2(1)1t lnt t->+,∴212x x e >. 22.【解答】解:(1)由曲线1C的参数方程cos ,(x y ααα=⎧⎪⎨=⎪⎩为参数)消去参数得,2222cos sin 13y x αα+=+=,即1C 的普通方程为:2213y x +=.)曲线2C的极坐标方程为sin()4πρθ-=可化为:)ρθθ=由cos x ρθ=,sin y ρθ=,可得2C 的直角坐标方程为直线40..x y -+=(2)设(cos )P αα,则点P 到直线2C的距离为d =(7分)|2cos()4|πα++.当cos()13πα+=-时,||PQ23πα=,故13(,)22P -.。
四川省南充市2017年中考数学真题试题(含解析)

2017年四川省南充市中考数学试卷 一、选择题(本大题共10个小题,每小题3分,共30分)1.如果a+3=0,那么a的值是( )A.3 B.﹣3 C.13D.13【答案】B.【解析】试题分析:移项可得:a=﹣3.故选B.考点:解一元一次方程.2.如图由7个小正方体组合而成的几何体,它的主视图是( )A.B.C.D.【答案】A.【解析】试题分析:根据主视图的定义可知,此几何体的主视图是A中的图形,故选A.考点:简单组合体的三视图.3.据统计,参加南充市2016年高中阶段学校招生考试的人数为55354人,这个数用科学记数法表示为( )A.0.55354×105人 B.5.5354×105人C.5.5354×104人 D.55.354×103人【答案】C.【解析】试题分析:55354=5.5354×104,故选C. 考点:科学记数法—表示较大的数.4.如图,直线a ∥b ,将一个直角三角尺按如图所示的位置摆放,若∠1=58°,则∠2的度数为( )A.30° B.32° C.42° D.58° 【答案】B. 【解析】试题分析:如图,过点A 作AB ∥b ,∴∠3=∠1=58°,∵∠3+∠4=90°,∴∠4=90°﹣∠3=32°,∵a ∥b ,AB ∥B ,∴AB ∥b ,∴∠2=∠4=32°,故选B.考点:平行线的性质. 5.下列计算正确的是( )A.842a a a ÷= B.236(2)6a a = C.3232a a a -= D.23(1)33a a a a -=- 【答案】D.考点:整式的混合运算.6.某校数学兴趣小组在一次数学课外活动中,随机抽查该校10名同学参加今年初中学业水平考试的体育成绩,得到结果如下表所示:下列说法正确的是( )A.这10名同学体育成绩的中位数为38分B.这10名同学体育成绩的平均数为38分C.这10名同学体育成绩的众数为39分D.这10名同学体育成绩的方差为2【答案】C.考点:方差;加权平均数;中位数;众数.7.如图,等边△OAB的边长为2,则点B的坐标为( )A.(1,1) B.C.) D.) 【答案】D.【解析】试题分析:如图所示,过B作BC⊥AO于C,则∵△AOB是等边三角形,∴OC=12AO=1,∴Rt△BOC中,BC,∴B),故选D.考点:等边三角形的性质;坐标与图形性质;勾股定理.8.如图,在Rt△ABC中,AC=5cm,BC=12cm,∠ACB=90°,把Rt△ABC所在的直线旋转一周得到一个几何体,则这个几何体的侧面积为( )A.60πcm 2B.65πcm 2C.120πcm 2D.130πcm 2【答案】B.考点:圆锥的计算;点、线、面、体.9.已知菱形的周长为6,则菱形的面积为( )A.2 C.3 D.4 【答案】D. 【解析】试题分析:如图四边形ABCD 是菱形,AC +BD =6,∴AB AC ⊥BD ,AO =12AC ,BO =12BD ,∴AO +BO =3,∴AO 2+BO 2=AB 2,(AO +BO )2=9,即AO 2+BO 2=5,AO 2+2AO •BO +BO 2=9,∴2AO •BO =4,∴菱形的面积=12AC •BD =2AO •BO =4;故选D.考点:菱形的性质.10.二次函数2y ax bx c =++(a 、b 、c 是常数,且a ≠0)的图象如图所示,下列结论错误的是( )A.4ac <b 2B.abc <0 C.b +c >3a D.a <b 【答案】D.考点:二次函数图象与系数的关系.二、填空题(本大题共6个小题,每小题3分,共18分) 11.如果111m =-,那么m = . 【答案】2. 【解析】试题分析:去分母得:1=m ﹣1,解得:m =2,经检验m =2是分式方程的解,故答案为:2. 考点:解分式方程.12.计算:0|1|( -+-= .. 【解析】.考点:实数的运算;零指数幂.13.经过某十字路口的汽车,可直行,也可向左转或向右转,如果这三种可能性大小相同,则两辆汽车经过该十字路口时都直行的概率是 .【答案】19.【解析】试题分析:画树状图为:共有9种等可能的结果数,其中两辆汽车都直行的结果数为1,所以则两辆汽车都直行的概率为19,故答案为:19.考点:列表法与树状图法.14.如图,在▱ABCD中,过对角线BD上一点P作EF∥BC,GH∥AB,且CG=2BG,S△BPG=1,则S▱AEPH= .【答案】4.考点:平行四边形的性质.15.小明从家到图书馆看报然后返回,他离家的距离y与离家的时间x之间的对应关系如图所示,如果小明在图书馆看报30分钟,那么他离家50分钟时离家的距离为 km .【答案】0.3. 【解析】考点:一次函数的应用.16.如图,正方形ABCD 和正方形CEFG 边长分别为a 和b ,正方形CEFG 绕点C 旋转,给出下列结论:①BE =DG ;②BE ⊥DG ;③222222DE BG a b +=+,其中正确结论是 (填序号)【答案】①②③. 【解析】试题分析:设BE ,DG 交于O ,∵四边形ABCD 和EFGC 都为正方形,∴BC =CD ,CE =CG ,∠BCD =∠ECG =90°,∴∠BCE +∠DCE =∠ECG +∠DCE =90°+∠DCE ,即∠BCE =∠DCG ,在△BCE 和△DCG 中,∵BC =DC ,∠BCE =∠DCG ,CE =CG ,∴△BCE ≌△DCG (SAS),∴BE =DG ,∴∠1=∠2,∵∠1+∠4=∠3+∠1=90°,∴∠2+∠3=90°,∴∠BOC =90°,∴BE ⊥DG ;故①②正确;连接BD ,EG ,如图所示,∴DO 2+BO 2=BD 2=BC 2+CD 2=2a 2,EO 2+OG 2=EG 2=CG 2+CE 2=b 2,则BG 2+DE 2=DO 2+BO 2+EO 2+OG 2=2a 2+b 2,故③正确. 故答案为:①②③.考点:旋转的性质;全等三角形的判定与性质;正方形的性质.三、解答题(共9个小题,满分72分)解答应写出必要的文字说明,证明过程或验算步骤17.化简21(11x x x x x --÷++,再任取一个你喜欢的数代入求值. 【答案】1x x -,当x =5时,原式=54.【解析】试题分析:先根据分式混合运算的法则把原式进行化简,再选取合适的x 的值代入进行计算即可.试题解析:原式=2211x x x x x x x +-+⋅+-=2111)(x x x x x +⋅-+=1x x - ∵x ﹣1≠0,x (x +1)≠0,∴x ≠±1,x ≠0,当x =5时,原式=551-=54. 考点:分式的化简求值.18.在“宏扬传统文化,打造书香校园”活动中,学校计划开展四项活动:“A ﹣国学诵读”、“B ﹣演讲”、“C ﹣课本剧”、“D ﹣书法”,要求每位同学必须且只能参加其中一项活动,学校为了了解学生的意愿,随机调查了部分学生,结果统计如下:(1)如图,希望参加活动C 占20%,希望参加活动B 占15%,则被调查的总人数为 人,扇形统计图中,希望参加活动D所占圆心角为 度,根据题中信息补全条形统计图. (2)学校现有800名学生,请根据图中信息,估算全校学生希望参加活动A有多少人?【答案】(1)60,72;(2)360.【解析】补全的条形统计图如图所示;(2)由题意可得,800×2760=360. 答:全校学生希望参加活动A 有360人.考点:条形统计图;用样本估计总体;扇形统计图.19.如图,DE ⊥AB ,CF ⊥AB ,垂足分别是点E 、F ,DE =CF ,AE =BF ,求证:AC ∥BD .【答案】答案见解析. 【解析】试题分析:欲证明AC ∥BD ,只要证明∠A =∠B ,只要证明△DEB ≌△CFA 即可.试题解析:∵DE ⊥AB ,CF ⊥AB ,∴∠DEB =∠AFC =90°,∵AE =BF ,∴AF =BE ,在△DEB 和△CFA 中,∵DE =CF ,∠DEB =∠AFC ,AF =BE ,△DEB ≌△CFA ,∴∠A =∠B ,∴AC ∥DB . 考点:全等三角形的判定与性质.20.已知关于x 的一元二次方程2(3)0x m x m ---=. (1)求证:方程有两个不相等的实数根;(2)如果方程的两实根为1x ,2x ,且2212127x x x x +-=,求m 的值. 【答案】(1)证明见解析;(2)m 的值是1或2. 【解析】试题分析:(1)要证明方程有两个不相等的实数根,只要证明原来的一元二次方程的△的值大于0即可; (2)根据根与系数的关系可以得到关于m 的方程,从而可以求得m 的值.试题解析:(1)证明:∵2(3)0x m x m ---=,∴△=[﹣(m ﹣3)]2﹣4×1×(﹣m )=m 2﹣2m +9=(m ﹣1)2+8>0,∴方程有两个不相等的实数根;(2)∵2(3)0x m x m ---=,方程的两实根为1x ,2x ,且2212127x x x x +-=,∴123x x m +=- ,12x x m =- ,∴21212()37x x x x +-=,∴(m ﹣3)2﹣3×(﹣m )=7,解得,m 1=1,m 2=2,即m 的值是1或2.考点:根与系数的关系;根的判别式.21.如图,直线y =kx (k 为常数,k ≠0)与双曲线my x=(m 为常数,m >0)的交点为A 、B ,AC ⊥x 轴于点C ,∠AOC =30°,OA =2.(1)求m 的值;(2)点P 在y 轴上,如果3ABP S k ∆=,求P 点的坐标.【答案】;(2)P (0,1)或(0,﹣1). 【解析】试题分析:(1)求出点A 坐标利用待定系数法即可解决问题;(2)设P (0,n ),由A ,1),B ,可得12•|n +12•|n 可;试题解析:(1)在Rt△AOC 中,∵∠ACO =90°,∠AOC =30°,OA =2,∴AC =1,OC ,∴A ,1),∵反比例函数m y x经过点A ,1),∴m y =kx 经过点A ,1),∴k .(2)设P (0,n ),∵A ,B ,﹣1),∴12•|n +12•|n ,∴n =±1,∴P (0,1)或(0,﹣1).考点:反比例函数与一次函数的交点问题.22.如图,在Rt△ABC 中,∠ACB =90°,以AC 为直径作⊙O 交AB 于点D ,E 为BC 的中点,连接DE 并延长交AC 的延长线于点F . (1)求证:DE 是⊙O 的切线; (2)若CF =2,DF =4,求⊙O 直径的长.【答案】(1)证明见解析;(2)6.【解析】(2)设⊙O的半径为r,∵∠ODF=90°,∴OD2+DF2=OF2,即r2+42=(r+2)2,解得:r=3,∴⊙O的直径为6.考点:切线的判定与性质.23.学校准备租用一批汽车,现有甲、乙两种大客车,甲种客车每辆载客量45人,乙种客车每辆载客量30人,已知1辆甲种客车和3辆乙种客车共需租金1240元,3辆甲种客车和2辆乙种客车共需租金1760元.(1)求1辆甲种客车和1辆乙种客车的租金分别是多少元?(2)学校计划租用甲、乙两种客车共8辆,送330名师生集体外出活动,最节省的租车费用是多少? 【答案】(1)1辆甲种客车的租金是400元,1辆乙种客车的租金是280元;(2)2960.【解析】试题分析:(1)可设1辆甲种客车的租金是x元,1辆乙种客车的租金是y元,根据等量关系:①1辆甲种客车和3辆乙种客车共需租金1240元,②3辆甲种客车和2辆乙种客车共需租金1760元,列出方程组求解即可;(2)由于求最节省的租车费用,可知租用甲种客车6辆,租用乙客车2辆,进而求解即可.试题解析:(1)设1辆甲种客车的租金是x元,1辆乙种客车的租金是y元,依题意有:31240 321760 x yx y+=⎧⎨+=⎩,解得:400280x y =⎧⎨=⎩.答:1辆甲种客车的租金是400元,1辆乙种客车的租金是280元;(2)租用甲种客车6辆,租用乙客车2辆是最节省的租车费用,400×6+280×2=2400+560=2960(元). 答:最节省的租车费用是2960元.考点:一元一次不等式的应用;二元一次方程组的应用;最值问题. 24.如图,在正方形ABCD 中,点E 、G 分别是边AD 、BC 的中点,AF =14AB . (1)求证:EF ⊥AG ;(2)若点F 、G 分别在射线AB 、BC 上同时向右、向上运动,点G 运动速度是点F 运动速度的2倍,EF ⊥AG 是否成立(只写结果,不需说明理由)?(3)正方形ABCD 的边长为4,P 是正方形ABCD 内一点,当PAB OAB S S ∆∆=,求△PAB 周长的最小值.【答案】(1)证明见解析;(2)成立;4+. 【解析】试题分析:(1)由正方形的性质得出AD =AB ,∠EAF =∠ABG =90°,证出AF BGAE BA=,得出△AEF ∽△BAG ,由相似三角形的性质得出∠AEF =∠BAG ,再由角的互余关系和三角形内角和定理证出∠AOE =90°即可; (2)证明△AEF ∽△BAG ,得出∠AEF =∠BAG ,再由角的互余关系和三角形内角和定理即可得出结论; (3)过O 作MN ∥AB ,交AD 于M ,BC 于N ,则MN ⊥AD ,MN =AB =4,由三角形面积关系得出点P 在线段MN 上,当P 为MN 的中点时,△PAB 的周长最小,此时PA =PB ,PM =12MN =2,连接EG ,则EG ∥AB ,EG =AB =4,证明△AOF ∽△GOE ,得出OF AF OE EG = =14,证出AM OF EM OE = =14,得出AM =15AE =25,由勾股定理求出PA ,即可得出答案.试题解析:(1)证明:∵四边形ABCD 是正方形,∴AD =AB ,∠EAF =∠ABG =90°,∵点E 、G 分别是边AD 、BC 的中点,AF =14AB ,∴AF AE =12,BG BA =12,∴AF BGAE BA=,∴△AEF ∽△BAG ,∴∠AEF =∠BAG ,∵∠BAG +∠EAO =90°,∴∠AEF +∠EAO =90°,∴∠AOE =90°,∴EF ⊥AG ; (2)解:成立;理由如下: 根据题意得:AF BG =12,∵AE AB =12,∴AF BG =AEAB,又∵∠EAF =∠ABG ,∴△AEF ∽△BAG ,∴∠AEF =∠BAG ,∵∠BAG +∠EAO =90°,∴∠AEF +∠EAO =90°,∴∠AOE =90°,∴EF ⊥AG ; (3)解:过O 作MN ∥AB ,交AD 于M ,BC 于N ,如图所示:则MN ⊥AD ,MN =AB =4,∵P 是正方形ABCD 内一点,当S △PAB =S △OAB ,∴点P 在线段MN 上,当P 为MN 的中点时,△PAB 的周长最小,此时PA =PB ,PM =12MN =2,连接EG 、PA 、PB ,则EG ∥AB ,EG =AB =4,∴△AOF ∽△GOE ,∴OF AF OE EG ==14,∵MN ∥AB ,∴AM OF EM OE = =14,∴AM =15AE =15×2=25,由勾股定理得:PA ,∴△PAB 周长的最小值=2PA +AB 4+.考点:四边形综合题;探究型;动点型;最值问题.25.如图1,已知二次函数2y ax bx c =++(a 、b 、c 为常数,a ≠0)的图象过点O (0,0)和点A (4,0),函数图象最低点M 的纵坐标为38-,直线l 的解析式为y =x .(1)求二次函数的解析式;(2)直线l 沿x 轴向右平移,得直线l ′,l ′与线段OA 相交于点B ,与x 轴下方的抛物线相交于点C ,过点C 作CE ⊥x 轴于点E ,把△BCE 沿直线l ′折叠,当点E 恰好落在抛物线上点E ′时(图2),求直线l ′的解析式;(3)在(2)的条件下,l ′与y 轴交于点N ,把△BON 绕点O 逆时针旋转135°得到△B ′ON ′,P 为l ′上的动点,当△PB ′N ′为等腰三角形时,求符合条件的点P 的坐标. 【答案】(1)28233x x y -=;(2)y =x ﹣3;(3)P.【解析】试题分析:(1)由题意抛物线的顶点坐标为(2,38-),设抛物线的解析式为2(2)3a x y 8-=-,把(0,0)代入得到a =23,即可解决问题; (2)如图1中,设E (m ,0),则C (m ,22833m m -),B (221133m m -+,0),由E 、B 关于对称轴对称,可得2211()332m m m +-+ =2,由此即可解决问题; (3)分两种情形求解即可①当P 1与N 重合时,△P 1B ′N ′是等腰三角形,此时P 1(0,﹣3).②当N ′=N ′B ′时,设P (m ,m ﹣3),列出方程解方程即可;试题解析:(1)由题意抛物线的顶点坐标为(2,38-),设抛物线的解析式为2(2)3a x y 8-=-,把(0,0)代入得到a =23,∴抛物线的解析式为222)(33x y 8--=,即28233x y x -=.(2)如图1中,设E (m ,0),则C (m ,28233m m -),B (211233m m +-,0),∵E ′在抛物线上,∴E 、B 关于对称轴对称,∴2211()332m m m +-+ =2,解得m =1或6(舍弃),∴B (3,0),C (1,﹣2),∴直线l ′的解析式为y =x ﹣3.(3)如图2中,①当P 1与N 重合时,△P 1B ′N ′是等腰三角形,此时P 1(0,﹣3). ②当N ′=N ′B ′时,设P (m ,m ﹣3),则有222((3m m -+-=,解得mP 2,P 3.综上所述,满足条件的点P).考点:二次函数综合题;几何变换综合题;分类讨论;压轴题.。
2017年四川省南充市中考数学试题(解析版)

【考点】等边三角形、点的坐标、勾股定理. 【分析】根据点的坐标的定义,只需求出点 B 到两坐标轴的距离即可,为此过 B 作 BC⊥ OA 于 C,再计算出 OC、BC 的长度. 【解答】过 B 作 BC⊥OA 于 C(图 7-a), ∵等边△ABO,
∴ OC = OA = 1, ∴BC = OB2 - OA 2 = 3. 2
C: 3a3与a2 不是同类型,无法合并,再者合并同类项是系数相加减、相同字母的指数不 变,因此 3a3 - 2a2 = a 错误;
· 1+ 3a · (-a) = 3a - 3a2 , 因此 3a(1- a) = 3a - 3a2 正确. D: 3a(1- a) = 3a
故选择 D 答案. 【点评】关键是分清问题类型,然后“照方抓药”,逐一比对.
2
【考点】幂的运算法则、合并同类项、单项式与多项式相乘(分配律). 【分析】根据幂的运算、合并同类项、单项式与多项式相乘等法则逐一计算即可. 【解答】A: a8 ÷ a2 = a8-2 = a6 , 因此 a8 ÷ a2 = a4 错误;
(a2 )3 = 8a6 , 因此 (2a2 )3 = 6a6 错误; B: (2a2 )3 = 23·
本题属基础题,难度较小,主要是考查应试者对法则的熟悉程度、细心.
【考点】数据的分析—中位数、平均数、众数、方差. 【分析】根据中位数、平均数、众数、方差等概念的定义逐一判断即可. 【解答】把这 10 个数据按照从小到大排列后取最中间的两个数据的平均数即为中位数, 而这组数据中第 5、6 个数据分别是 39 分、39 分,因此中位数也是 39 分,因此 A 答案错误;
2 a c b 图4-a
∵a∥b,
∴c∥b, ∴∠1+∠2=90º,
四川省南充高级中学高2017级高二下数学试卷(十二)

四川省南充高级中学高2017级高二下数学试卷(十二)第I 卷(选择题)一、选择题(本题共12道小题,每小题5分,共60分)1.设集合}032|{2<--=x x x M ,2{|log 0}N x x =<,则N M 等于( ) A .(-1,0)B .(-1,1)C .(0,1)D .(1,3)2.已知命题:,sin 1p x x ∀∈≤R ,它的否定是( )A .存在,sin 1x x ∈>RB .任意,sin 1x x ∈≥RC .存在,sin 1x x ∈≥RD .任意,sin 1x x ∈>R 3.已知复数Z 满足()()325Z i i -+=(i 是虚数单位),则在复平面内,复数Z 对应的点位于( ) A.第一象限 B.第二象限 C.第三象限 D.第四象限4.执行如图所示的程序框图,若输入A 的值为2,则输出的n 值为( )A. 3B. 4C. 5D. 65.观察下面“品”字形中各数之间的规律,根据观察到的规律得出a 的值为A .23B .75C .77D .139 6.等比数列{a n }中,48,a a 是关于x 的方程21040x x ++=的两个实根,则2610a a a =( ).A .8B . -8C .4D .8或-87.如图,在底面半径为3和高为AB ,CD 是底面圆O 的两条互相垂直的直径,E 是母线PB 的中点,若过直径CD 与点E 的平面与圆锥侧面的交线是以E 为顶点的抛物线的一部分,则圆锥顶点P 到该抛物线焦点的距离为( ) A.4 B.4 44题图7题图8.已知函数()()2cos 332f x x πϕϕ⎛⎫=++≤ ⎪⎝⎭,若,612x ππ⎛⎫∀∈- ⎪⎝⎭,f (x )的图象恒在直线y =3的上方,则ϕ的取值范围是( ) A.,122ππ⎛⎫⎪⎝⎭B.,63ππ⎡⎤⎢⎥⎣⎦C.0,4π⎡⎤⎢⎥⎣⎦D.,63ππ⎛⎫- ⎪⎝⎭9.在平面直角坐标系中,)0,4(-A 、)0,1(-B ,点),(b a P (0≠ab )满足||2||BP AP =,则2214b a +的最小值为( ) A.4B. 3C.23D.49 10.已知函数e e x f x -=)(,1ln )(+=x x g ,若对于R x ∈∀1,),0(2+∞∈∃x ,使得)()(21x g x f =,则21x x -的最大值为( )A.eB.e -1C.1D.e11-11.已知圆锥曲线()()2222121010,0C mx ny n m C px qy p q +=>>-=>>:与:的公共焦点为F 1,F 2.点M 为C 1,C 2的一个公共点,且满足1290F MF ∠=,若圆锥曲线C 1的离心率为34,则C 2的离心率为A .92B .2C .32D .5412.若关于x 的不等式0xxe ax a -+<的解集为(m,n)(n 0)<,且(m,n)中只有一个整数,则实数a 的取值范围是( ) A.221,)32e e (B. 221[,)32e eC.221,)3e e (D. 221[,)3e e第II 卷(非选择题)二、填空题(本题共4道小题,每小题5分,共20分)13.总体由编号为01,02,,29,30的30个个体组成.利用下面的随机数表选取样本,选取方法是从随机数表第2行的第6列数字开始由左到右依次选取两个数字,则选出来的第3个个体的编号为_______. 5416 6725 1842 5338 1703 4259 7922 3148 3567 8237 5932 1150 4723 4079 7814 718114.已知点()2,A m ,()1,2B ,()3,1C ,若0A B B C A C ⋅+=,则实数m 的值为 .15.如图,点F 是抛物线y 2=8x 的焦点,点A ,B 分别在抛物线及圆(x -2)2+y 2=16的实线部分上运动,且AB 总是平行于x 轴,则△FAB 的周长的取值范围是_____16.对于三次函数()32f x ax bx cx d =+++(),,0a b c d a ∈≠R ,,有如下定义:设()f x '是函数()f x 的导函数,()f x ''是函数()f x '的导函数,若方程()0f x ''=有实数解m ,则称点()(),m f m 为函数()y f x =的“拐点”.若点(1,-3)是函数()()325,g x x ax bx a b =-+-∈R 的“拐点”,也是函数()g x 图像上的点,则当4x =时,函数()()4log h x ax b =+的函数值是__________.三、解答题(本题共6道小题,第1题10分,其余每小题12分分,共70分)17.共享单车是指企业为校园、地铁站点、公交站点、居民区、商业区、公共服务区等提供自行车单车共享服务,是一种分时租赁模式,某共享单车企业为更好地服务社会,随机调查了100人,统计了这100人每日平均骑行共享单车的时间(单位:分钟),将统计数据分为:[)[)[)[)[)[]0,20,20,40,40,60,60,80,80,100,100,120六个小组,得到右侧频率分布直方图,已知骑行时间在[60,80),[20,40),[40,60)三组对应的人数依次成等差数列.(1)求频率分布直方图中a ,b 的值;(2)估计这100人每日平均骑行共享单车时间的中位数;(保留小数点后两位小数)(3)若将日平均骑行时间不少于80分钟的用户定义为“忠实用户”,将日平均骑行时间少于40分钟的用户为“潜力用户”,现从上述“忠实用户”与“潜力用户”的人中按分层抽样选出5人,再从这5人中任取3人,求恰好1人为“忠实用户”的概率.18.(本小题满分12分)已知等比数列{a n }的公比为q (q ≠1),等差数列{b n }的公差也为q ,且12323a a a +=.(Ⅰ)求q 的值; (Ⅱ)若数列{b n }的首项为2,其前n 项和为T n , 当2n ≥时,试比较b n 与T n 的大小.19.在△ABC 中,4,6AB AC ==.(1)若16cos 1A =,求BC 的长及BC 边上的高h ; (2)若△ABC 为锐角三角形,求△ABC 的周长的取值范围.20.(文)如图,四棱锥P -ABCD 中,侧面P AD 为等边三角形,且平面⊥PAD 底面ABCD ,121===AD BC AB ,090=∠=∠ABC BAD .(1)证明::AB PD ⊥;(2)点M 在棱PC 上,且CP CM λ=,若三棱锥ACM D -的体积为31,求实数λ的值.(理)如图,在三棱锥P -ABC 中,P A ,PB ,PC 两两垂直,3PA AB AC ===,且D 为线段BC 的中点. (1)证明:BC ⊥平面P AD ;(2)若3,2AE AC PE AD λ=⋅=,求平面P AB 与平面PDE 所成角的正弦值.21.已知圆221:140F x y ++-=和定点)2F ,P 是圆F 1上任意一点,线段PF 2的垂直平分线交PF 1于点E ,设动点E 的轨迹为C . (1) 求动点E 的轨迹方程C ;(2) 设曲线C 与x 轴交于A ,B 两点,点M 是曲线C 上异于A ,B 的任意一点,记直线,MA MB 的斜率分别为MA k ,MB k .证明:MA MB k k ⋅是定值;(3) 设点N 是曲线C 上另一个异于M ,A ,B 的点,且直线NB 与MA 的斜率满足2NB MA k k =,试探究:直线MN 是否经过定点?如果是,求出该定点,如果不是,请说明理由.22.已知函数322()7(,)f x x ax bx a a a b R =++--∈,且1x =时()f x 有极大值10. (Ⅰ)求()f x 的解析式;(Ⅱ)若'()f x 为()f x 的导函数,不等式1'()(ln 1)523f x k x x x >--+(k 为正整数)对任意正实数x 恒成立,求k 的最大值.(注:ln 20.69,ln 3 1.10,ln 5 1.61≈≈≈)四川省南充高级中学高2017级高二下数学试卷(十二)试卷答案1.C2.A3.A4.C5.B6.B7.A8.C9.D 10.D 11.B12.B 设(),x g x xe y ax a ==-,由题设原不等式有唯一整数解,即()x g x xe =在直线y ax a =-下方,13.15 14.37 15.(8,12) 解:抛物线的准线l :x=-2,焦点F (2,0),由抛物线定义可得|AF|=x A +2,∴△FAB 的周长=|AF|+|AB|+|BF|=x A +2+(x B -x A )+4=6+x B ,由抛物线y 2=8x 及圆(x-2)2+y 2=16,得交点的横坐标为2,∴x B ∈(2,6)∴6+x B ∈(8,12) ∴三角形ABF 的周长的取值范围是(8,12).抛物线的准线l :x=-2,焦点F(2,0),由抛物线定义可得|AF|=x A +2,可得△FAB 的周=|AF|+|AB|+|BF|=x A +2+(x B -x A )+4=6+x B ,由抛物线y 2=8x 及圆(x-2)2+y 2=16,解出交点坐标即可得出.16.2()232g x x ax b -'=+,()62g x x a "=-,由拐点定义知1x =时,()1620g a "=-=,解得3a =,而()13g =-,即153a b -+-=-,解得4b =, ∴()()4log 34h x x =+,()44log 162h ==,故答案为2.17.(1)由()0.002520.00753201a ⨯++⨯=…(1分)解得0.0125a =,又0.016520.0025,0.0085b a b +==∴=.(2)()0.50.0050.250.20-+=,所以中位数大约是0.201720402052.120.3333+⨯=≈ (3)“忠实用户”“潜力用户”的人数之比为:()()0.00750.0025:0.01250.00252:3++=,所以“忠实用户”抽取2525⨯=人,“潜力用户”抽取3535⨯=人,记事件:从5人中任取3人恰有1人为“忠实用户” 设两名“忠实用户”的人记为:12,B B ,三名“潜力用户”的人记为:123,,b b b ,则这5人中任选3人有:()()()121122123,,,,,,,,B B b B B b B B b ,()()()112113123,,,,,,,,B b b B b b B b b ,()()()()212213223123,,,,,,,,,,,B b b B b b B b b b b b ,共10种情形,符合题设条件有:()()()112113123,,,,,,,,B b b B b b B b b ()()()212213223,,,,,,,,B b b B b b B b b 共有6种.因此恰好1人为“忠实用户”的概率为()63105P A ==. 18.解:(Ⅰ)由已知可得211123a a q a q +=, ∵{}n a 是等比数列,10a ≠∴23210q q --= 解得1q =或13q =-. ∵1q ≠, ∴ 13q =- (Ⅱ)由(Ⅰ)知等差数列{}n b 的公差为13-, ∴ 72(1)()33n nb n 1-=+--=,2132(1)()236n n n n T n n 1-=+--=,(1)(14)6n n n n T b ---=-, 当14n >时,n n T b <;当14n =时,n n T b =;当214n ≤<时,n n T b >. 综上,当214n ≤<时,n n T b >;当14n =时,n n T b =;当14n >时,n n T b <19.(1)116cos 1,cos 16A A =∴=,7BC ∴==,1cos ,sin 16A A =∴=,由等面积法可得:1146sin 722A h ⨯⨯⨯=⨯,h ∴=. (2)设()0BC x x =>,AB AC <,∴角C 必为锐角.ABC ∆为锐角三角形,,A B ∴角均为锐角,则cos 0,cos 0A B >>,于是222222460460x x ⎧+->⎪⎨+->⎪⎩,解得:x <<,故ABC ∆的周长的取值范围是(10++.20.(文)(1)证明:取AD 的中点O ,连OC,OP ∵∆PAD 为等边三角形,且O 是边AD 的中点,∴AD PO ⊥,∵平面PAD ⊥底面ABCD ,且它们的交线为AD ,∴ABCD PO 平面⊥,∴PO BA ⊥,∵O PO AD AD BA =⊥ 且,∴PAD AB 平面⊥,∴AB PD ⊥(2)设点M 到平面ACD 的距离为h ∵31==--ACD M ACM D V V ∴3131=⋅∆h S ACD ∴11ACDh S ∆==∵31==OP h CP CM ∴3λ==(理)(1)证明:因为AB AC =,D 为线段BC 的中点,所以AD BC ⊥.又,,PA PB PC 两两垂直,且AB AC A ⋂=所以PA ⊥平面ABC ,则PA BC ⊥.因为AD PA A ⋂=,所以BC ⊥平面PAD .(2)解:以A 为坐标原点,建立如图所示的空间直角坐标系A xyz -,则()()()()330,0,0,3,0,0,0,3,0,0,0,3,,,022A B C P D ⎛⎫⎪⎝⎭.∵AE AC λ=,∴可设()0,,0E t ,则()330,,3,,,022PE t AD ⎛⎫=-= ⎪⎝⎭,3322PE AD t ⋅==∴1t =,则()31,,0,0,1,322ED PE ⎛⎫==- ⎪⎝⎭,设平面PDE 的法向量为(),,n x y z =,则00n ED n PE ⎧⋅=⎪⎨⋅=⎪⎩,即 3102230x y y z ⎧+=⎪⎨⎪-=⎩令1z =,得()1,3,1n =-.平面PAB 的一个法向量为()0,1,0m =,则cos ,11m n ==.故平面PAB 与平面PDE 所成二面角的.21.(1)依题意可知圆1F的标准方程为(2216x y ++=,因为线段2PF 的垂直平分线交1PF于点E ,所以2EP EF =,动点E始终满足12124EF EF r F F +==>=E 满足椭圆的定义,因此24,2a c ==2,a b c ===∴ 椭圆C 的方程为22142x y +=(2)()()2,0,2,0A B -),设()00,M x y ,则22000220000*********MA MBx y y y k k x x x x -⋅=⋅===-+--- (3)2NB MA k k =,由(2)中的结论12MA MB k k ⋅=-可知1122NB MB k k ⋅=-,所以1NB MB k k ⋅=- ,即NB MB ⊥,当MN 斜率存在时,设MN 的方程为()()1122,,,,y kx b M x y N x y =+,2224y kx bx y =+⎧⎨+=⎩,可得()()222124220k x kbx b +++-=,则212122242(2),1212kb b x x x x k k--+=⋅=++(*),()()()()()()112212122,2,22BN BM x y x y x x kx b kx b ∴⋅=-⋅-=-⋅-++⋅+()()()2212121240k x x kb x x b =++-⋅+++=, 将(*)式代入可得223480b k kb ++=,即()()2230k b k b ++=,亦即20230k b k b +=+=或当2b k =-时,()22y kx k k x =-=-,此时直线MN 恒过定点()2,0(舍);当23b k=-时,2233y kx k k x ⎛⎫=-=- ⎪⎝⎭,此时直线MN 恒过定点2,03⎛⎫⎪⎝⎭;当MN 斜率不存在时,设0000(,),(,)M x y N x y -,则220000002422()132MB x y x x y k x ⎧+=⎪⇒==⎨==-⎪-⎩舍或,2:3MN l x ∴=,也过点2,03⎛⎫⎪⎝⎭ 综上所述,直线MN 恒过定点2,03⎛⎫ ⎪⎝⎭22.解:(Ⅰ)由2'()32f x x ax b =++,因为在1x =时()f x 有极大值10,所以23201710a b a b a a ++=⎧⎨++--=⎩,从而得2a =-或6a =-,①当2a =-时,1b =,此时2'()341f x x x =-+,当1(,1)3x ∈时,'()0f x <,当(1,)x ∈+∞时,'()0f x >,∴在1x =时()f x 有极小值,不合题意,舍去; ②当6a =-时,9b =,此时2'()3(43)f x x x =-+,符合题意。
四川省南充市2017年中考数学真题试题(含解析)-真题试卷

D.58°
【答案】B.
【解析】
试题分析:如图,过点 A 作 AB∥b,∴∠3=∠1=58°,∵∠3+∠4=90°,∴∠4=90°﹣∠3=32°,∵a∥b,
AB∥B,∴AB∥b,∴∠2=∠4=32°,故选 B.
考点:平行线的性质.
5.下列计算正确的是( )
A.a8 a4 a2
B.(2a2 )3 6a6
考点:旋转的性质;全等三角形的判定与性质;正方形的性质.
三、解答题(共 9 个小题,满分 72 分)解答应写出必要的文字说明,证明过程或验算步骤
x x 1
17.化简 (1
) ,再任取一个你喜欢的数代入求值.
x2 x x 1
x
5
【答案】 ,当 x=5 时,原式= .
x 1
4
【解析】
试题分析:先根据分式混合运算的法则把原式进行化简,再选取合适的 x 的值代入进行计算即可.
试题解析:(1)证明:∵ x2 (m 3)x m 0 ,∴△=[﹣(m﹣3)]2﹣4×1×(﹣m)=m2﹣2m+9=(m﹣1)
2
+8>0,∴方程有两个不相等的实数根;
(2)∵ x2 (m 3)x m 0 ,方程的两实根为 x1 , x2 ,且 x12 x22 x1x2 7 ,∴ x1 x2 m 3 ,
【答案】答案见解析. 【解析】 试题分析:欲证明 AC∥BD,只要证明∠A=∠B,只要证明△DEB≌△CFA 即可. 试题解析:∵DE⊥AB,CF⊥AB,∴∠DEB=∠AFC=90°,∵AE=BF,∴AF=BE,在△DEB 和△CFA 中,∵DE=CF, ∠DEB=∠AFC,AF=BE,△DEB≌△CFA,∴∠A=∠B,∴AC∥DB. 考点:全等三角形的判定与性质.
