最新上海三校生考试数学模拟卷
三校生数学试题及答案

三校生数学试题及答案一、选择题(每题3分,共15分)1. 下列哪个选项不是实数?A. √2B. πC. 0.33333…D. i答案:D2. 一个数的相反数是-5,那么这个数是:A. 5B. -5C. 0D. 10答案:A3. 函数y=2x+3的图象不经过哪个象限?A. 第一象限B. 第二象限C. 第三象限D. 第四象限答案:C4. 以下哪个不等式是正确的?A. 3 > 2B. 4 < 3C. 5 ≥ 5D. 6 ≤ 7答案:C5. 一个等差数列的首项是2,公差是3,那么它的第五项是:A. 14B. 17C. 20D. 23答案:A二、填空题(每题2分,共10分)6. 一个圆的半径是5厘米,那么它的周长是________厘米。
答案:31.47. 如果一个三角形的两边长分别是3和4,那么第三边的取值范围是________。
答案:1 < 第三边 < 78. 一个数的平方是25,那么这个数是________。
答案:±59. 函数y=x^2-4x+3的最小值是________。
答案:010. 一个等比数列的首项是2,公比是2,那么它的第四项是________。
答案:16三、解答题(每题10分,共20分)11. 已知函数f(x)=x^2-6x+8,求函数的顶点坐标。
答案:顶点坐标为(3, -1)。
12. 已知等差数列{an}的前三项分别为2,5,8,求该数列的通项公式。
答案:通项公式为an = 3n - 1。
结束语:本试题涵盖了实数、相反数、函数图象、不等式、等差数列等基础数学知识点,旨在考察学生的基础知识掌握情况和计算能力。
希望同学们通过本次练习能够查漏补缺,提高数学解题技巧。
上海数学三校生高考模拟卷-3
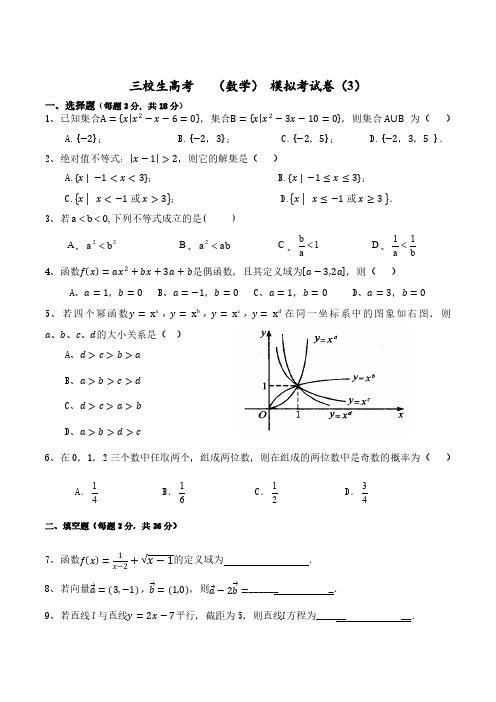
三校生高考 (数学) 模拟考试卷(3)一、选择题(每题3分, 共18分)1、已知集合A =*x |x 2−x −6=0+,集合B =*x |x 2−3x −10=0+,则集合 A⋃B 为( )A.{−2};B.{−2,3};C.{−2,5};D.{−2,3,5 }.2、绝对值不等式:|x −1|>2,则它的解集是( )A.*x | −1<x <3+;B.*x | −1≤x ≤3+;C.{x | x <−1或 x >3};D.{x | x ≤−1或 x ≥3 }.3、若,0<<b a 下列不等式成立的是( )A 、22b a <B 、ab a <2C 、1<a bD 、b a 11<4、函数f (x )=ax 2+bx +3a +b 是偶函数,且其定义域为,a −3,2a -,则( )A 、a =1,b =0B 、a =−1,b =0C 、a =1,b =0D 、a =3,b =05、若四个幂函数y =a x ,y =b x ,y =c x ,y =d x 在同一坐标系中的图象如右图,则a 、b 、c 、d 的大小关系是( )A 、d >c >b >aB 、a >b >c >dC 、d >c >a >bD 、a >b >d >c6、在0,1,2三个数中任取两个,组成两位数,则在组成的两位数中是奇数的概率为() A .14 B .16 C .12 D .34二、填空题(每题3分,共36分)7、函数f (x )=1x−2+√x −1的定义域为 .8、若向量a ⃗=(3,−1),b ⃗⃗=(1,0),则a ⃗−2b ⃗⃗=______ _.9、若直线 与直线y =2x −7平行,截距为5,则直线 方程为______ __.10、不等式(x+2)(x−7)<0的解集为.11、等差数列*a+中,若a=2,a2+a=13,则数列公差d= ___ __.12、有6名男生,4名女生,现选3名参加比赛,要求至少一男一女,则有种不同选法.13、在∆ABC中,已知sinA:sinB:sinC=3:5:7,且最大边长为14,则∆ABC的面积是 .14、已知角 α 终边上一点 P(−3,4),则 sinα+cosα=。
上海三校生三月数学专项训练10

上海市部分普通高校专科层次依法自主招生考试入学测试(十)数学和生命科学部分(本试卷满分150分,考试时间90分钟。
数学部分40分,生命科学部分35分) 第一部分(每题只有一个正确答案。
每题1分,共102分。
数学部分28分,生命科学部分23分)一、选择题(每题1分,共80分。
数学部分23分,生命科学部分18分)【数学部分】19.下列表示中正确的是( )。
A .{0}∅=B .C .0⊆∅D .Q π∈20.函数4||y x =-的定义域( )。
A .-)∞∞(-,4][4,+ B .[4,4]- C .-)∞∞(-,2][2,+ D .[2,2]- 21.函数2log (1)y x =+的大致图像是( )。
22.三角式21sin 1cos 2αα-+的值为( )。
A .2 B .2-C .12D .12- 23.数列{}n a 满足13n n a a ++=,且18a =-,则此数列的通项公式是( )。
A .35n a n =--B .35n a n =-C .35n a n =-+D .35n a n =+24.圆229x y +=与椭圆22194x y += ( )。
A .有两个交点 B .只有个交点C .没有交点D .有四个交点25.与双曲线2219x y -=有相同渐近线的双曲线标准方程为( )。
A .221436y x -= B .221436x y -= C .221182y x -= D .221218x y -= 26.向量AB 对应复数32i -+,则向量BA 所对应的复数为( )。
A .32i -B .32i +C .32i -+D .32i --27.如图,以B 、C 为圆心的两个半圆的直径都是2厘米,则阴影部分的周长是( )厘米。
A .3B .2.09C .3.9D .3.0928.箱子里有圆球和方块共40个,每次取出5个圆球和3个方块,取几次后所剩的圆球数是剩下的方块数的一半,原来有圆球( )个。
三校生高考模拟数学试卷

一、选择题(本大题共20小题,每小题5分,共100分)1. 下列函数中,在实数域内单调递增的是()A. y = -x^2 + 2xB. y = 2^xC. y = log2xD. y = √x2. 已知等差数列{an}的前n项和为Sn,若S10 = 100,S20 = 300,则第15项a15的值为()A. 10B. 15C. 20D. 253. 若复数z满足|z - 1| = |z + 1|,则复数z的实部是()A. 0B. 1C. -1D. 无法确定4. 下列命题中,正确的是()A. 函数y = x^3在R上单调递增B. 等差数列{an}的通项公式为an = a1 + (n - 1)dC. 若a > b > 0,则a^2 > b^2D. 函数y = log2x在(0,+∞)上单调递减5. 已知函数f(x) = x^3 - 3x^2 + 2,则f(x)的极小值为()A. -1B. 0C. 1D. 26. 下列方程组中,无解的是()A. x + y = 1B. 2x + 3y = 6C. 3x - 4y = 2D. 4x - 5y = 107. 已知等比数列{an}的首项a1 = 2,公比q = 3,则第10项a10的值为()A. 18B. 54C. 162D. 4868. 下列函数中,在区间(0,+∞)上为减函数的是()A. y = x^2B. y = 2^xC. y = log2xD. y = √x9. 若复数z满足|z - 1| = |z + 1|,则复数z的虚部是()A. 0B. 1C. -1D. 无法确定10. 下列命题中,正确的是()A. 函数y = x^3在R上单调递增B. 等差数列{an}的通项公式为an = a1 + (n - 1)dC. 若a > b > 0,则a^2 > b^2D. 函数y = log2x在(0,+∞)上单调递减11. 已知函数f(x) = x^3 - 3x^2 + 2,则f(x)的极大值为()A. -1B. 0C. 1D. 212. 下列方程组中,有唯一解的是()A. x + y = 1B. 2x + 3y = 6C. 3x - 4y = 2D. 4x - 5y = 1013. 已知等比数列{an}的首项a1 = 2,公比q = 3,则第10项a10的值为()A. 18B. 54C. 162D. 48614. 下列函数中,在区间(0,+∞)上为增函数的是()A. y = x^2B. y = 2^xC. y = log2xD. y = √x15. 若复数z满足|z - 1| = |z + 1|,则复数z的虚部是()A. 0B. 1C. -1D. 无法确定16. 下列命题中,正确的是()A. 函数y = x^3在R上单调递增B. 等差数列{an}的通项公式为an = a1 + (n - 1)dC. 若a > b > 0,则a^2 > b^2D. 函数y = log2x在(0,+∞)上单调递减17. 已知函数f(x) = x^3 - 3x^2 + 2,则f(x)的极大值为()A. -1B. 0C. 1D. 218. 下列方程组中,无解的是()A. x + y = 1B. 2x + 3y = 6C. 3x - 4y = 2D. 4x - 5y = 1019. 已知等比数列{an}的首项a1 = 2,公比q = 3,则第10项a10的值为()A. 18B. 54C. 162D. 48620. 下列函数中,在区间(0,+∞)上为减函数的是()A. y = x^2B. y = 2^xC. y = log2xD. y = √x二、填空题(本大题共10小题,每小题5分,共50分)21. 已知等差数列{an}的前n项和为Sn,若S10 = 100,S20 = 300,则第15项a15的值为______。
三校生职业高三数学试卷

考试时间:120分钟满分:100分一、选择题(每题5分,共50分)1. 下列各数中,无理数是()A. √2B. -πC. 3.14D. 2/32. 已知函数f(x) = 2x - 3,则f(2)的值为()A. 1B. 3C. 5D. 73. 若|a| = 5,|b| = 3,则|a + b|的最大值为()A. 8B. 5C. 3D. 24. 下列各点中,在直线2x + 3y - 6 = 0上的是()A. (1, 2)B. (2, 1)C. (3, 0)D. (0, 3)5. 若sin A = 1/2,cos B = 3/5,则sin(A + B)的值为()A. 7/10B. 4/5C. 3/10D. 1/56. 已知等差数列{an}的前三项分别为2,5,8,则该数列的公差d为()A. 1B. 2C. 3D. 47. 下列各式中,能表示圆的方程是()A. x² + y² = 1B. x² + y² = 4C. x² + y² = 16D. x² + y² = 258. 若log₂x + log₂y = 3,则x y的值为()A. 2³B. 2⁴C. 2⁵D. 2⁶9. 下列各函数中,奇函数是()A. y = x²B. y = x³C. y = x⁴D. y = x⁵10. 若向量a = (2, -3),向量b = (4, 6),则向量a与向量b的点积为()A. -6B. -12C. 6D. 12二、填空题(每题5分,共50分)1. 若sin A = 1/2,cos B = 3/5,则cos(A - B)的值为__________。
2. 已知等差数列{an}的首项a₁ = 3,公差d = 2,则第10项a₁₀ =__________。
3. 圆的标准方程为x² + y² = 16,圆心坐标为__________。
三校生高考数学模拟试卷

三校生高考数学模拟试卷一、选择题(本大题共10小题,每小题3分,共30分。
在每小题给出的四个选项中,只有一项是符合题目要求的)1. 设集合A = {xx^2 - 3x + 2 = 0},B={1, 2},则A与B的关系是()A. A⊂neqq BB. A = BC. A⊃neqq BD. A∩ B=varnothing2. 函数y=√(x - 1)的定义域是()A. (-∞,1]B. [1,+∞)C. (-∞, 0]D. [0,+∞)3. 若sinα=(3)/(5),且α是第二象限角,则cosα的值为()A. (4)/(5)B. -(4)/(5)C. (3)/(4)D. -(3)/(4)4. 过点(1,2)且斜率为3的直线方程为()A. y - 2 = 3(x - 1)B. y+2=3(x + 1)C. y - 2=-3(x - 1)D. y+2=-3(x + 1)5. 二次函数y = x^2+2x - 3的对称轴为()A. x = - 1B. x = 1C. x = 2D. x=-26. 已知向量→a=(1,2),→b=(3,-1),则→a·→b等于()A. 1B. -1C. 5D. -57. 在等差数列{a_n}中,若a_1=1,d = 2,则a_5的值为()A. 9B. 10C. 11D. 128. 若x>0,则函数y = x+(1)/(x)的最小值是()A. 1B. 2C. 3D. 49. 从5名男生和3名女生中选3人参加某项活动,要求既有男生又有女生,则不同的选法有()种。
A. 45B. 30C. 15D. 1010. 若f(x)是定义在R上的奇函数,当x>0时,f(x)=x^2+1,则f(-1)的值为()A. -2B. 2C. -1D. 1二、填空题(本大题共5小题,每小题4分,共20分)11. 计算log_28=_。
12. 椭圆frac{x^2}{16}+frac{y^2}{9}=1的长半轴长a = _。
最新三校生数学高考模拟试卷

三校生数学高考模拟试卷一、是非选择题。
(对的选A ,错的选B。
每小题3分,共30分)1.如果A={0.1.2.3},B={1},则B ∈A …………………………………………( ) 2.已知直线上两点A (-3,3),B (3,-1),则直线AB 的倾斜角为65π( ) 3.lg 2+lg5=lg7………………………………………………………………………( ) 4.函数f(x)=245x x -+的定义域是【-1,5】…………………………( )5.sin750·sin3750=41-……………………………………………………………( )6.在等比数列{a n }中,a 1=31,a 4=89,则数列的公比为23…………………( )7.若向量32=+,则∥……………………………………( )8.双曲线13422=-y x 的渐近线方程为x y 23±=,焦距为2………………( ) 9.直线l ⊥平面α,直线m ∥平面β,若l ∥m ,则α⊥β………………( )10.二项式1033⎪⎭⎫⎝⎛-x x 展开式中二项式系数最大的项是第五项…………………( )二、选择题(每小题5分,共40分) 11.函数f(x)=lg(x-3)的定义域是 ( )A.RB.(-3,3)C.(-∞,-3)∪(3,+∞)D.【0,+∞) D.112.以点M (-2,3)为圆心且与x 轴相切的圆的方程( )A.(x +2)2+(y -3)2=4 B . (x -2)2+(y +3)2=4C.(x +2)2+(y -3)2=9 D . (x -2)2+(y +3)2=913.10件产品中,3件次品,甲、乙两人依次各取一件产品,按取后放回,求恰有一件次品的概率为( ) A.10021 B. 241 C. 4521 D. 502114.若函数f(x)在定义域R 上是奇函数,且当x ﹥0时,f(x)=2410x x -,则f(-2)=( ).A. -104B.104C. 1D.10-1215.a=2是直线(a 2-2)x +y=0和直线2x +y +1=0互相平行的( ).A.充分条件 B.必要条件 C.充要条件 D.即不充分也不必要条件 16.设数列{a n }的前n 项和为2n s n=,则a 8=()A.64B.49C.16D.1517.在直角坐标系中,设A (-2,3),B (-3,-3),现沿x 轴把直角坐标系折成直二面角,则AB 的长为( )A.6B.5C.19D.118.a =(1,2),b =(x ,5),且b a⊥2,则x= ( )A .10B .-10 C.25 D.25-三、填空题(每题5分,共30分)19.已知x ∈(ππ,-),已知sinx=21, 则x= _ 已知tanx=-1,则x= _20.已知正方形ABCD 的边长为2,AP ⊥平面ABCD ,且AP=4,则点P 到BD 的距离 21.过圆3622=+y x 上一点(4,52)的切线方程为 _ _22.椭圆1422=+y x 的离心率为23.4名男生和2名女生站成一排,其中2名女生站在两端的站法有 种24.函数1422+-=x x y 的值域为 班级: 姓名: 座号:四、解答题(第25、26、题,每小题10分,第27.28题,每小题15分,共50分)255=8=,<b a ,> =32π,求()()b a b a -∙+2。
三校生高考数学模拟试卷

三校生高考数学模拟试卷班级 姓名 学号 得分第I 卷(选择题 70分)题号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 答案(请将是非选择题、单项选择题答案写到表格中)一、是非选择题:本大题共10小题,每小题3分,共30分.对每小题的命题作出选择,的选A,错的选B.1. 实数0与集合A={0,1}的关系是.0A ∈(A B) 2. 点M(1,1)在圆.1)1(22上=+-y x(A B) 3. 若非零向量.0,//,=∙b a b a b a 则满足(A B) 4. }.10{02<<<+x x x x 的解集是不等式(A B)5. 342tan ,2tan ==θθ则若(A B)6. 24lg 25lg =+(A B) 7. 函数x y πsin = 的最小周期是2(A B) 8. 若点A,B 到平面a 的距离都等于1,则直线.//a AB(A B)9. 当6)32(3的系数是的展开式中x x +(A B) 10,等差数列).(125,3,1*N n n a n ∈-=的通项公式为(A B)二、单项选择题:本大题共8小题,每小题5分,共40分.11. 的离心率为椭圆125922=+y x ( )A.53 B.54 C.43 D.45 12. 已知的值域是函数xy 2=( )A.{}0≤y yB. {}0≥y yC. {}0>y yD. {}R y y ∈13. 已知[]()=⋂==B A B A 则集合,5,2,3,0( )A. (]3,2B. [)5,0C. ()3,2D. []3,214. 不等式[]的最小值为函数2,1,32-∈+-=x x y ( ) A. -1 B. 0 C. 2 D. 315. 的大小关系是,,三个数53cos 5cos )8-(cos πππ( ) A.)53cos()5cos()8cos(πππ<<-B.⎪⎭⎫⎝⎛-<<8cos )5cos()53cos(πππ B.C.⎪⎭⎫⎝⎛<-<5cos )8cos()53cos(πππD.⎪⎭⎫⎝⎛<<-5cos )53cos()8cos(πππ16. 不等式的取值范围是,则是直线与平面所成的角若θθ( ) A.[)π,0B. )2,0(πC. )2,0[πD.]2,0[π17. 那么下列说法正确的是如果,b a >( )A.1>baB. 22b a >C.ba 11< D. 33b a > 18. 从1,2,3,4,5,6中任取两个数,则这两个数之和为9的概率是( )A.154 B.51 C. 152D. 151第I 卷(非选择题 80分)三、填空题:本大题共6小题,每小题5分,共30分.19.在直角坐标系中,过点(0,1)和(1,0)的直线l 的方程是20. 在===∠=∠∆AC BC B A ABC ,则,,中,4453021. 到右焦点的距离为,则点到右焦点的距离为右支上一点若双曲线p p x x 3116922=- 22. 已知一个圆柱的底面半径为1,高为2,则该圆柱的全面积为 23. 已知向量),1,2(),1,1(-=-=b a =+b a 则24.甲乙两人投掷飞镖,他们的成绩(环数)如下面的频数条形统计图所示,用甲、乙训练的成绩的方差大小关系是,乙甲22s s四、解答题:本大题共6小题,25-28小题每小题8分,29-30小题每小题9分,共50分. 25. (本小题满分8分)的值,求实数若,已知向量m b a m b a ⊥=-=),,1()2,1(.)()2()()1(cos 11)()8.26的奇偶性判断函数的定义域;求函数已知函数分(本小题满分x f x f x x f +=27. (本小题满分8分).}{68}{221的通项公式求数列,的前项和,若是递增等比数列已知n n n a S a a a S ==28. 已(本小题满分8分)已知).0(0542:22>=-+--+m m y x y x C 的方程是.0943:)2(;)1(的值相切,求实数与直线若圆的坐标求圆心m y x l C C =++29. (本小题满分9分).),1(]1,(),()(2单调递增上上单调递增,在区间在区间已知函数+∞-∞∈++=R b a b ax x x f .2]0,1[)()2(.)1(的值,求实数上的最小值为在若的值求实数b x x f a -∈30. (本小题满分9分).1111-AA BC AB C B A ABC ==形,的底面是等腰直角三角如图,已知直三棱柱(1)求异面直线所成的角与11CC AB .(2)若M 为线段AC 的中点,N 为线段1111//:BMC N AB C A 平面平面的中点,求证(3)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
模拟卷
一、选择题
1.已知集合A={2,3},B={3,5},那么A∩B=
A. {2}
B. {3}
C. {5}
D.{2,5}
2.某学校街舞社团共有26名学生,若这26名学生组成的集合记为M,该社团内的
16名男生组成的集合记为N,则下列Venn图能正确表示集合M与集合N之间关
系的是
A
B C D
3.如果用红外体温计测量体温,显示的读数为36.2℃,已知该体温计测量精度为±
0.3℃,表示其真实体温x(℃)的范围为35.9≤x≤36.5,则该体温范围可用绝对值不
等式表示为
A. |x-36.2|≤0.3
B. |x-36.2|≥0.3
C. |x-0.3|≤36.2
D. |x-0.3|≥36.2
4.右图是2016年11月27日上海市徐家汇地区6-18时的
气温变化图,则该地区当日在该时段内的最高气温可能
是
A. 6℃
B. 7.5℃
C. 10℃
D. 12.5℃
5.在平面直角坐标系xOy中,角α的顶点在坐标原点,始边与x轴正半轴重合,若其
终边经过点P(1,),则tanα=
A. /3
B. 1/2
C. /2
D.
6.下图所示的正三棱柱的表面展开图可以为
A
B. C. D.
二、填空题
7.过点A(1,5)且与直线y=3x+1平行的直线方程为。
8.已知直角坐标平面内的A、B两点的坐标分别为A(2,1),B(3,2),那么向量
= 。
9.某餐厅提供39元下午茶套餐,此套餐可从7款茶点和6款饮料(含3款热饮)中
任选一款茶点和一款饮料,则所选套餐中含热饮的概率为。
10.如图所示,A、B两地之间有一座山(阴影部分),在
A、B两地之间规划建设一条笔直的公路(挖隧道穿过
山林),测量员测得AC=3500m,BC=3390m,∠C=24.9°,
则AB= 。
11.某市居民使用天然气的阶梯价格表如下表所示
若用右图所示的流程框图表示该市居民一年缴纳的天然气费用
y(元)与年使用量x(立方米)之间的关系,则图中①处应
填。
12.计算:lg2+lg5= 。
13.函数y=2sin(2x+)+1在一个周期内的最大值为,最小正周期
为。
14.圆心为(-2,1),且与y轴相切的圆的标准式为。
15.不等式x2-ax+5≤2x的解集为[b,-1],则a的值为,b的值
为。
16.已知一圆锥底面半径为6,高为8,则其表面积为。
17.已知某个二元一次方程组为,则该方程组的解写成列向量
为。
18.已知F(x)=f(x)+g(x),f(x)为奇函数,g(x)为偶函数,F(1)=2,F(-1)=0,则
f(-1)= ,g(-1)= 。
三、解答题
19.已知同一温度的摄氏温标读数y(℃)与华氏温标读数x(℉)之间的关系是一次
函数的关系,表中给出摄氏温度与华氏温度的两组对应数据:
(1). 试求y关于x的函数解析式(不需要写出定义域)
(2). 小杰同学坐飞机到达美国S市交流学习,天气预报报告抵达时S市的气温在
54-72℉之间,试用摄氏温度表示该气温范围(结果四舍五入保留整数)
20.
21.已知圆C的标准方程为x2+y2=4
(1). 写出圆C的半径长
(2). 若斜率k=1的直线过点A(3,0),求直线l的方程并判断其与圆C的位置关系。
22.
23.下图所示为14行视力检查表,人站在5米远处检查视力,从上往下,已知第1行
的视力记录为4.0,后面每一行的视力记录比前一行增加0.1。
右图所示为正方形“E”
字视标,第一行的“E”字视标边长为72.72mm,往后每一行中“E”字视标的边长是前一行的0.794倍。
(1). 检查视力是,小王同学的左眼只能看清第11行及以上各行的“E”字,问小王左眼的视力记录应为多少?
(2). 求第5行中的“E”字视标边长(精确到0.01mm)
(3). 已知每一行(最后一行除外)的视标底端和下一行视标顶端的距离都为24mm,
那么第一行视标顶端到最后一行视标底端的距离为多少?(精确到0.01mm)
24.已知函数f(x)=2sin(ωx+)+1。
(1). 若函数的最小正周期为π/2,求f(π)的值。
(2). 已知在△ABC中,有f(A/ω)=3,a=1,∠B=45°,求b的长度和三角形的面积。
