包装纸盒设计练习
2022人教版初中数学七年级上册练习题--课题学习 设计制作长方体形状的包装纸盒
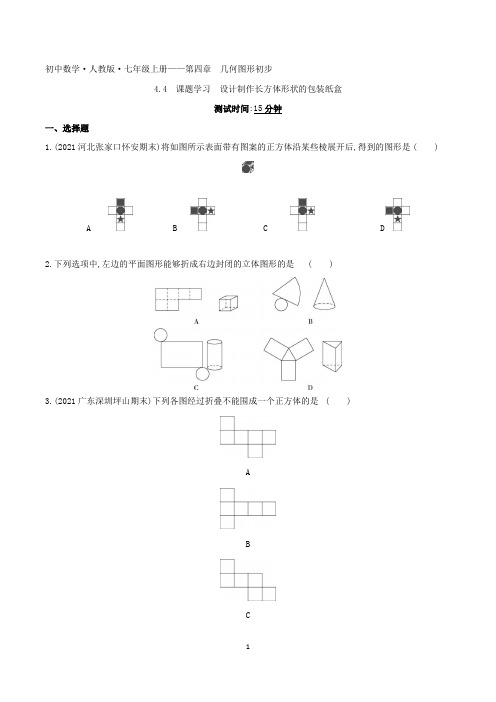
初中数学·人教版·七年级上册——第四章几何图形初步4.4 课题学习设计制作长方体形状的包装纸盒测试时间:15分钟一、选择题1.(2021河北张家口怀安期末)将如图所示表面带有图案的正方体沿某些棱展开后,得到的图形是()A B C D2.下列选项中,左边的平面图形能够折成右边封闭的立体图形的是()3.(2021广东深圳坪山期末)下列各图经过折叠不能围成一个正方体的是()ABCD4.下面的图形经过折叠可以围成一个棱柱的是()二、填空题5.如图,一个长方体的表面展开图中四边形ABCD是正方形(正方形的四个角都是直角、四条边都相等),则根据图中数据可得原长方体的体积是cm3.6.如图为某种无盖长方体包装盒的展开图,则此包装盒展开图的面积是.三、解答题7.如图是一个长方体纸盒的展开图,如果不要盖子,做这个纸盒需要多少材料?8.工人把一个长方形的纸盒展开时不小心多剪了一刀,结果展开后变成了两部分,如图,现在他想把这两部分粘贴成一个整体,使之能折成原来的长方体,请你帮他设计一下,应怎样粘贴?9.小朋友用如图所示的硬纸板做成了一个长方体纸盒,求纸盒的表面积和体积.10.如图是一个无盖正方体形状的盒子以及其表面沿某些棱剪开后展成的一种平面图形,请画出3种与此不同的展开图.一、选择题1.答案C由原正方体知,带图案的三个面相交于一点,而通过折叠后A、B都不符合,且D折叠后图案的位置不正确,所以能得到的图形是C.故选C.2.答案C A.不能折叠成正方体,故错误;B.不能折成圆锥,故错误;C.能折成圆柱,故正确;D.不能折成三棱柱,故错误.故选C.3.答案D A、B、C都是正方体的展开图,不符合题意;D不是正方体的展开图,符合题意.故选D.4.答案B选项A上下两底面为三角形,而侧面为4个长方形,故不能围成棱柱;选项C折叠后缺少一个底面,故不能围成棱柱;选项D缺少两个底面,故不能围成棱柱;只有B能围成棱柱.故选B.二、填空题5.答案20解析如图,因为四边形ABCD是正方形,所以AB=AD=AE=5 cm,令长方体的高为(7-5)÷2=1(cm),所以EF=5-1=4(cm),所以原长方体的体积是5×4×1=20(cm3).6.答案156解析因为12-9=3,12-3×2=6,16-6=10,所以无盖长方体包装盒的长、宽、高分别为10、6、3,则该包装盒展开图的面积=3×6×2+3×10×2+6×10=36+60+60=156.三、解答题7.解析10×5+10×2×2+5×2×2=50+40+20=110(cm2).答:做这个纸盒需要110 cm2的材料.8.解析如图(答案不唯一).9.解析纸盒的表面积为(12×8+12×4+8×4)×2=(96+48+32)×2=176×2=352(cm2).纸盒的体积为12×8×4=96×4=384(cm3).10.解析将一个无盖正方体形状的盒子表面沿某些棱展开后得到的平面图形如下(答案不唯一):。
人教版七年级数学上册第四章 4.4 课题学习 设计制作长方体形状的包装纸盒 作业练习题

3.(5分)(鄂尔多斯中考)下面四个图形中,经过折叠能围成如图所示的 几何图形的是( B )
4.(5分)(易错题)在课题学习中,老师要求用长为12厘米,宽为8厘米的 长方形纸片制作一个无盖的长方体纸盒.三位同学分别以下列方式在长 方形纸片上截去两角(图中阴影部分),然后沿虚线折成一个无盖的长方体 纸盒.
甲:如图①,盒子底面的四边形ABCD是正方形;
乙:如图②,盒子底面的四边形ABCD是正方形;
丙:如图③,盒子底面的四边形ABCD是长方形,AB=2AD.
将这三位同学所折成的无盖长方体纸盒的容积按从大到小的顺序排列,
正确的是(
)C
A.甲>乙>丙 B.甲>丙>乙
C.丙>甲>乙 D.丙>乙>甲
5.(14分)把正方体的六个面分别涂上六种不同颜色,并画上朵数不等 的花,各面的颜色与花的朵数情况列表如下:
(1)小明总共剪开了__8__条棱. (2)现在小明想将剪断的②重新粘贴到①上去,而且经过折叠以后,仍 然可以还原成一个长方体纸盒,你认为他应该将剪断的纸条粘贴到①中 的什么位置?请你帮助小明在①上补全. (3)小明说:已知这个长方体纸盒高为20 cm,底面是一个正方形,并且 这个长方体纸盒所有棱长的和是880 cm.求这个长方体纸盒的体积.
数学
七年级上册
第四章 几何图形初步
人教版
4.4 课题学习 设计制作长方体形状的包装纸盒
1.(5分)下列四个图形中,是某个长方体平面展开图的个数是( B )
A.1
B.2
C.3
D.4
2.(5分)如图为一无盖长方体盒子的展开图(重叠部分不计),可知该无
盖长方体的容积为( D )
A.4
B.6
C.12
D.8
初一数学课题学习 设计制作长方体形状的包装纸盒试题

初一数学课题学习设计制作长方体形状的包装纸盒试题1.(2014•六盘水)将一张正方形纸片按如图1,图2所示的方向对折,然后沿图3中的虚线剪裁得到图4,将图4的纸片展开铺平,再得到的图案是()A.B.C.D.【答案】B【解析】对于此类问题,学生只要亲自动手操作,答案就会很直观地呈现.解:严格按照图中的顺序向右上翻折,向左上角翻折,剪去左上角,展开得到结论.故选:B.点评:本题考查的是剪纸问题,此类题目主要考查学生的动手能力及空间想象能力,对于此类问题,学生只要亲自动手操作,答案就会很直观地呈现.2.(2014•资阳二模)如图所示,欢欢首先将一张正方形的纸片按(2)、(3)、(4)的顺序三次折叠,然后沿第三次折痕剪下一个四边形,这个四边形一定是()A.平行四边形B.矩形C.菱形D.正方形【答案】C【解析】结合空间思维,分析折叠的过程及剪菱形的位置,易知展开的形状.解:由图形可得出:剪掉的三角形是4个直角三角形,故得到一个菱形.故选:C.点评:本题主要考查了学生的立体思维能力即操作能力.错误的主要原因是空间观念以及转化的能力不强,缺乏逻辑推理能力,需要在平时生活中多加培养.3.(2014•简阳市模拟)在下列图形中,沿着虚线将长方形剪成两部分,那么由这两部分既能拼成平行四边形,又能拼成三角形和梯形的是()A.B.C.D.【答案】D【解析】发挥想象力拼图,或通过实际操作得出答案.解:第一个图形只能拼成特殊的平行四边形矩形;第二个图形能拼成平行四边形,矩形,三角形;第三个图形能拼成平行四边形和梯形;第四个图形按不同的相等的边重合可得到平行四边形,又能拼成三角形和梯形.故选D.点评:本题主要考查学生的动手能力及空间想象能力,即把剪下的图形与剩下的图形拼在一起所构成图形的形状.4.(2014•镇江模拟)已知矩形ABCD的一边长为20,另一边长为a(a<20)剪下一个正方形,剩下一个矩形,称为第一次操作;在剩下的矩形纸片中再剪下一个正方形,剩下一个矩形,称为第二次操作;若在第3次操作后,剩下的矩形为正方形,则a的值为()A.5B.5、8C.5、8、15D.5、8、12、15【答案】D【解析】根据已知得出符合条件的有4种情况,画出图形即可.解:裁剪线的示意图如下:故选:D.点评:本题考查了矩形性质,正方形性质,寻找规律的应用,主要考查学生的变换能力和了解能力,注意:要进行分类讨论.5.(2013•濠江区模拟)将一圆形纸片对折后再对折,得到下图,然后沿着图中的虚线剪开,得到两部分,其中一部分展开后的平面图形是()A.B.C.D.【答案】C【解析】严格按照图中的方法亲自动手操作一下,即可很直观地呈现出来.解:根据题意知,剪去的纸片一定是一个四边形,且对角线互相垂直.故选C.点评:本题主要考查学生的动手能力及空间想象能力.对于此类问题,学生只要亲自动手操作,答案就会很直观地呈现.6.(2013•澄江县一模)如图,把一个长方形的纸片对折两次,然后剪下一个角,展开这个角得到一个锐角为80°的菱形,则剪痕与折痕所成的角α的度数应为()A.40°或50°B.40°或60°C.40°或80°D.20°或50°【答案】A【解析】根据题意知折痕是AC和BD,只要求出∠ABD和∠BAC即可,根据菱形的每一条对角线平分一组对角求出即可.解:∵四边形ABCD是菱形,∴∠ABD=∠ABC,∠BAC=∠BAD,AD∥BC,∵∠ABC=80°,∴∠BAD=180°﹣80°=100°,∴∠ABD=∠ABC=40°,∠BAC=∠BAD=50°,即剪口与折痕所成的角α的度数为40°或50°,故选:A.点评:本题考查了菱形的性质和折叠问题的应用,主要考查学生的动手操作能力和理解能力,理解题意是解此题的关键.7.(2012•遵义)把一张正方形纸片如图①、图②对折两次后,再按如图③挖去一个三角形小孔,则展开后图形是()A.B.C.D.【答案】C【解析】结合空间思维,分析折叠的过程及剪三角形的位置,注意图形的对称性,易知展开的形状.解:当正方形纸片两次沿对角线对折成为一直角三角形时,在直角三角形中间的位置上剪三角形,则直角顶点处完好,即原正方形中间无损,且三角形关于对角线对称,三角形的AB边平行于正方形的边.再结合C点位置可得答案为C.故选C.点评:本题主要考查了学生的立体思维能力即操作能力.错误的主要原因是空间观念以及转化的能力不强,缺乏逻辑推理能力,需要在平时生活中多加培养.8.(2012•乐陵市二模)如图,将一张正方形纸片剪成四个小正方形,得到4个小正方形,称为第一次操作;然后,将其中的一个正方形再剪成四个小正方形,共得到7个小正方形,称为第二次操作;再将其中的一个正方形再剪成四个小正方形,共得到10个小正方形,称为第三次操作;…,根据以上操作,若要得到2011个小正方形,则需要操作的次数是()A.669B.670C.671D.672【答案】B【解析】第一次可得到4个正方形;第二次可得到4+3=7个正方形;第三次可得到4+2×3=10个正方形;…第n次可得4+(n﹣1)×3个正方形.解:设若要得到2011个小正方形,则需要操作的次数是n.4+(n﹣1)×3=2011,解得n=670.故选B.点评:本题考查了剪纸问题,解决本题的关键是观察分析得到相应的规律.9.(2012•张家口一模)将正方形纸片由下向上对折,再由左向右对折,称为完成一次操作(见图).按上述规则完成五次操作以后,剪去所得小正方形的左下角.那么,当展开这张正方形纸片后,所有小孔的个数为()A.48B.128C.256D.304【答案】C【解析】动手操作,得到一次操作后的小孔个数,进而得到2次操作后的小孔个数,得到相应规律,计算即可.解:通过操作可以知道:按规则完成一次操作,展开后的正方形纸片上共有40=1个小孔;按规则完成两次,展开后的正方形共有41=4个小孔,按规则3次操作,展开后的正方形纸片上共有42=16个小孔,根据这个规律,容易得到原题展开正方形纸片后,共有:44=256个小孔.故选C.点评:考查剪纸问题中的规律问题;解决本题的关键是动手操作发现相应规律.10.(2011•太原)将一个矩形纸片依次按图(1)、图(2)的方式对折,然后沿图(3)中的虚线裁剪,最后将图(4)的纸再展开铺平,所得到的图案是()A.B.C.D.【答案】A【解析】按照题意要求,动手操作一下,可得到正确的答案.解:严格按照图中的顺序先向上再向右对折,从左下方角剪去一个直角三角形,展开得到结论.故选A.点评:本题主要考查学生的动手能力及空间想象能力.对于此类问题,学生只要亲自动手操作,答案就会很直观地呈现.。
4.4 课题学习——设计制作长方体形状的包装纸盒精准作业设计
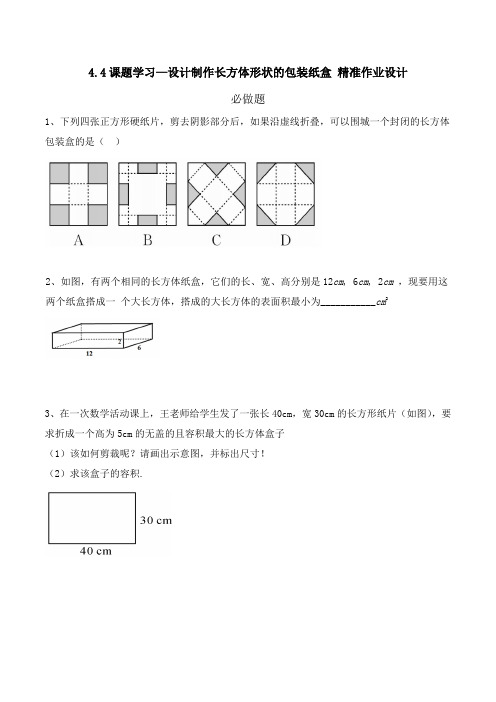
4.4课题学习—设计制作长方体形状的包装纸盒精准作业设计必做题1、下列四张正方形硬纸片,剪去阴影部分后,如果沿虚线折叠,可以围城一个封闭的长方体包装盒的是()2、如图,有两个相同的长方体纸盒,它们的长、宽、高分别是12cm, 6cm, 2cm ,现要用这两个纸盒搭成一个大长方体,搭成的大长方体的表面积最小为___________cm23、在一次数学活动课上,王老师给学生发了一张长40cm,宽30cm的长方形纸片(如图),要求折成一个高为5cm的无盖的且容积最大的长方体盒子(1)该如何剪裁呢?请画出示意图,并标出尺寸!(2)求该盒子的容积.选做题如图是一个用硬纸板制作的长方体包装盒展开图,已知它的底面形状是正方形,高为12cm.(1)制作这样的包装盒需要多少平方厘米的硬纸板?(2)若1平方米硬纸板价格为5元,则制作10个这的包装盒需花费多少钱?(不考虑边角损耗)精准作业答案必做题答案1、C2、 288解析:大长方体的表面积最小,则重叠面积最大,所以重叠面为两个 6 ×12 的面,大长方体的表面积为:(2×6×2+2×12×2+6×12×2)×2-6×12×2=288cm23\(1)(2)如图,在长方形每个角上截取一个边长为5cm的正方形,则折成的长方体底面长为:(40-2×5)=30cm,宽为(30-2×5)=20cm∴盒子的容积为30×20×5=3000cm3故答案为:3000cm3选做题答案(1)由图形可知:底面正方形的边长=18-12=6.包装盒的表面积=6×6×2+4×6×12=72+288=360(平方厘米).答:制作一个这样的包装盒需要360平方厘米的硬纸板.(2)10×360÷10000×5=1.8(元)制作10个这的包装盒需花1.8元.。
人教版七年级数学上册第四章《几何图形初步-课题 设计制作长方体形状的包装纸盒》课后练习题(附答案)

人教版七年级数学上册
第四章《几何图形初步-课题学习
设计制作长方体形状的包装纸盒》课后练习题(附答案)基础检测
1.设计长方体形状的包装盒,要先绘制长方体的_______图,•再把它剪出并折剪成长方体.2.如图是正方体的平面展开图,每个面上标有汉字组成的三个词,分别是兰州人引以自豪的三个词(一本书,一条河,一碗面),•在正方体上与“读”字相对的面上的字是_______.3.下面四个图形都是由相同的六个小正方形纸片组成,•小正方形上分别贴有北京2008年奥运会吉祥物五个福娃(贝贝、晶晶、欢欢、迎迎、妮妮)的卡通画和一颗星星,如果分别用“贝、晶、欢、迎、妮”五个字来表示五个福娃,那么折叠后围成如右图所示正方体的图形是()
4.下图各图中,是正方体展开图的是()
5.下图各图形中,不能
..经过折叠围成正方体的是()
A
B C D
拓展提高
6.如图是小颖所画的正方体平面展开图的一部分,请补画完整,使它成为该正方体的一种平面展开图.
7.“六一”儿童节时,•阿兰准备用硬纸通过裁剪折叠纸片上设计如图所示的裁剪方案(实践部分),经裁剪、折叠后成为一个封闭的正方体礼品盒,请你参照图,帮她设计另外两种不同的裁剪方案,使之经过裁剪,折叠后也能成为一个封闭的正方体礼品盒.
参考答案:
1.表面展开 2.面 3.C 4.C 5.B 6.画图略 7.图略。
纸盒包装结构设计138页(附带纸盒展开图)

设计要求
方 便 性:纸容器结构设计必须便于生产,便于存贮,便于陈列展销, 便于携带,便于使用和便于运输。 保 护 性:保护性是纸结构设计的关键,根据不同产品的不同特点,设 计应从内衬、排列、外形等结构分别考虑,特别是对于易破 损和特殊外型产品。 变 化 性:纸容器造型结构外型的更新、变化非常重要,它能给人以新 颖感和美感,刺激消费者选购欲望。 科学合理性:科学性和合理性是设计中的基本原则。科学合理的纸容器,要 求用料少而容量大,重量轻而抗力强,成本低而功能全。
④
特殊结构
积集盒 ,是指把规格品种不同但用途相关的
⑤
数件产品搭配在一起的条件配 套包装 。
特殊结构
敞式易倒盒 ,是一种开封方法简便
⑥
和易倾倒的自装盒 。
特殊结构
振出口盒 ,是一种盛装粉末状 、粒状
⑦
十分方便的包装盒 。
特殊结构
纸包装结构设计
在纸盒包装中最常用的是折叠纸盒和固定纸盒两种。 折叠纸盒的盒型通常可分为三大类:筒型,盘型和特殊型。 按制做结构分又有插口或锁口式、粘贴式、组装式折叠盒等。 固定纸盒有:套筒式纸盒、镶装纸盒、衬垫盖纸盒、异形纸盒、抽屉式纸盒、 有肩纸盒、带铰接盖的纸盒、倾斜盒面纸盒、全天叩地式纸盒、 盒中盒、特制品纸盒、有格子板纸盒、有内隔板纸盒等。
平 面 图
鞭炮形纸盒 将主要的折盖用胶水黏合,一些巧妙的折叠使纸盒呈鞭炮状,中间是存储部分。这样的设计适合新颖高档的糖果包装,若加上其他材料的运用,可使内部产品的特征更加明显。
局 部 图
平 面 图
包底手提盒 这种表面轮廓呈锥形的手提型纸盒通过推压侧面很容易制成并竖立起来,同时也形成了压合封闭的底座。通过挤压纸盒上方的面来完成入口的制作,用力推压顶部的缝隙可以打开纸盒。镂空展示格是为符合纸盒正面轮廓特地划开的。
2023-2024学年七年级数学上学期:课题学习 设计制作长方体形状的包装纸盒(附答案解析)
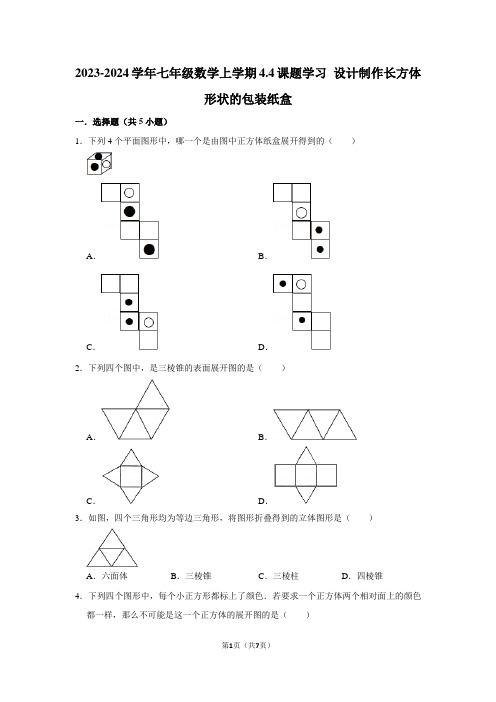
二.填空题(共5小题)
6.图1是一个正方体的展开图,该正方体从图2所示的位置依次翻到第1格、第2格、第3格、第4格、第5格,此时这个正方体朝上一面的字是.
7.如图是某几何体的展开图,那么这个几何体是.
8.将一个正方体的表面沿某些棱剪开,展开成一个平面图,至少需要剪条棱.
9.将下图所示的图形剪去一个小正方形,使余下的部分恰好能折成一个正方体,应剪去.(填序号)
故答案为:7.
9.将下图所示的图形剪去一个小正方形,使余下的部分恰好能折成一个正方体,应剪去1或2或6.(填序号)
【解答】解:根据有“田”字格的展开图都不是正方体的表面展开图可知.故应剪去1或2或6.
故答案为:1或2或6.
10.圆锥的侧面展开图是扇形,图是三棱柱的表面展开图.
【解答】解:圆锥的侧面展开图是扇形,图是三棱柱的表面展开图.
【解答】解:图中只有四个等边三角形故只能折叠成三棱锥.
故选:B.
4.下列四个图形中,每个小正方形都标上了颜色.若要求一个正方体两个相对面上的颜色都一样,那么不可能是这一个正方体的展开图的是( )
A. B.
C. D.
【解答】解:选项C中红色面和绿色面都是相邻的,故不可能是一个正方体两个相对面上的颜色都一样,故选C.
2.下列四个图中,是三棱锥的表面展开图的是( )
A. B.
C. D.
【解答】解:A、不组成三棱锥,故不是;
B、能组成三棱锥,是;
C、组成的是四棱锥,故不是;
D、组成的是三棱柱,故不是.
故选:B.
3.如图,四个三角形均为等边三角形,将图形折叠得到的立体图形是( )
A.六面体B.三棱锥C.三棱柱D.四棱锥
10.圆锥的侧面展开图是,图是的表面展开图.
人教版-数学-七年级上册-4.4 设计制作长方体形状的包装纸盒 测试
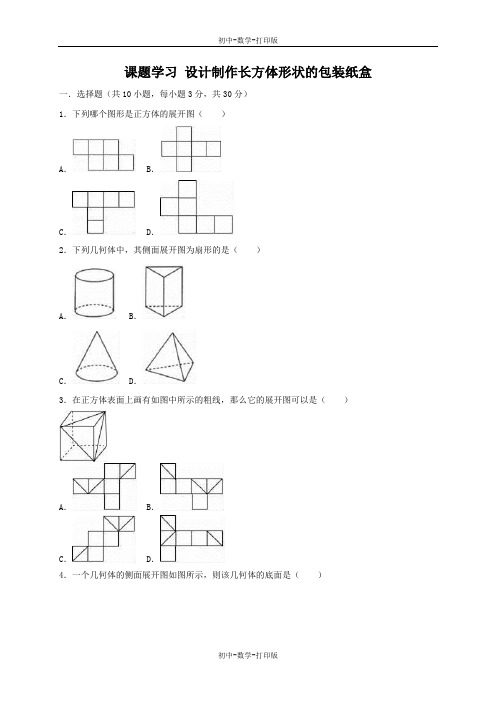
课题学习设计制作长方体形状的包装纸盒一.选择题(共10小题,每小题3分,共30分)1.下列哪个图形是正方体的展开图()A.B.C.D.2.下列几何体中,其侧面展开图为扇形的是()A.B.C.D.3.在正方体表面上画有如图中所示的粗线,那么它的展开图可以是()A.B.C.D.4.一个几何体的侧面展开图如图所示,则该几何体的底面是()A. B.C.D.5.如图,一个几何体上半部为正四棱锥,下半部为立方体,且有一个面涂有颜色,该几何体的表面展开图是()A.B.C.D.6.下列图形中能折叠成棱柱的是()A.B.C.D.7.下面四个图形中,经过折叠能围成如图所示的几何图形的是()A.B.C.D.8.下列各图中,不能折叠成一个立方体的是()A.B.C.D.9.下列各图中,经过折叠不能围成一个棱柱的是()A.B.C.D.10.在图上剪去一个图形,剩下的图形可以折叠成一个长方体,则剪去的这个图形是()①B.②C.③D.④二.填空题(共8小题,每小题3分,共24分)11.如图为某几何体的展开图,该几何体的名称是________.12.一个无盖的长方体的包装盒展开后如图所示(单位:cm),则该长方体的体积为______cm3.13.把一个圆柱体的侧面展开后得到一个长方形,长方形的长是4π厘米,宽是2π厘米,这个圆柱体的底面半径是_________厘米.14.如图是每个面上都有一个汉字的正方体的一种展开图,那么在正方体的表面与“活”相对应的面上的汉字是_________.15.如图,把一个长方体纸盒展成一个平面图形,需要剪开________条棱.16.如图(1),在边长为18cm的正方形纸片的四个角各剪去一个同样大小的正方形,折成一个如图(2)所示的无盖的长方体.设剪去的小正方形的边长为4cm,则这样折成的无盖长方体的容积是_______.17.将如图中的图形剪去一个正方形,使剩余的部分恰好能折成一个正方体,问应剪去哪个小正方形?(说出两种即可)18.小明家有一个如图的无盖长方体纸盒,现沿着该纸盒的棱将纸盒剪开,得到其平面展开图.若长方体纸盒的长、宽、高分别是a,b,c(单位:cm,a>b>c).则它的展开图周长最大时,用含a,b,c的代数式表示最大周长为_______cm.三.解答题(共7小题,共66分)19.已知一个六棱柱,它的底面边长都是5厘米,侧棱长都是8厘米,请回答下列问题(1)这个六棱柱一共有多少个面?一共有多少条棱?这些棱的长度之和是多少?(2)沿一条侧棱将这个六棱柱侧面全部展开成一个平面图形,这个图形的面积是多少?20.如图是一个正方体的展开图,标注了字母A,C的面分别是正方体的正面和底面,其他面分别用字母B,D,E,F表示.已知A=kx+1,B=3x﹣2,C=1,D=x﹣1,E=2x﹣1,F=x.(1)如果正方体的左面与右面所标注字母代表的代数式的值相等,求出x的值;(2)如果正面字母A代表的代数式与对面字母代表的代数式的值相等,且x为整数,求整数k的值.21.如图是一个长方体的表面展开图,每个面上都标注了字母和数据,请根据要求回答(1)如果A面在长方体的底部,那么______面会在上面;(2)求这个长方体的表面积和体积.22.如图,小华用若干个正方形和长方形准备拼成一个长方体的展开图.拼完后,小华看来看去总觉得所拼图形似乎存在问题.(1)请你帮小华分析一下拼图是否存在问题:若有多余块,则把图中多余部分涂黑;若还缺少,则直接在原图中补全;(2)若图中的正方形边长为2cm,长方形的长为3cm,宽为2cm,请直接写出修正后所折叠而成的长方体的体积:______cm3.23.如图所示,用标有数字1、2、3、4的四块正方形,以及标有字母A.B.C.D.E.F、H的七块正方形中任意一块,用这5块连在一起的正方形折叠成一个无盖的正方体盒子,一共有几种不同的方法?写出这些方法所用到正方形所标有的数字和字母.(例如:1、2、3、4、F)24.如图是一个用硬纸板制作的长方体包盒展开图,已知它的底面形状是正方形,高为12cm.(1)制作这样的包装盒需要多少平方厘米的硬纸板?(2)若1平方米硬纸板价格为5元,则制作10个这的包装盒需花费多少钱?(不考虑边角损耗)25.图1所示的三棱柱,高为7cm,底面是一个边长为5cm的等边三角形.(1)这个三棱柱有______条棱,有________个面;(2)图2方框中的图形是该三棱柱的表面展开图的一部分,请将它补全;(3)要将该三棱柱的表面沿某些棱剪开,展开成一个平面图形,需剪开_____条棱,需剪开棱的棱长的和的最大值为________cm.参考答案选择题1.【解答】解:根据正方体展开图的特征,选项A.C.D不是正方体展开图;选项B是正方体展开图..故选:B.2.【解答】解:A.圆柱的侧面展开图可能是正方形,故A错误;B.三棱柱的侧面展开图是矩形,故B错误;C.圆锥的侧面展开图是扇形,故C正确;D.三棱锥的侧面展开图是三角形,故D错误.故选:C.3.【解答】解:由带有各种符号的面的特点及位置,可知只有选项D符合.故选:D.4.【解答】解:由题意可知,该几何体为四棱锥,所以它的底面是四边形.故选:B.5.【解答】解:选项A和C带图案的一个面是底面,不能折叠成原几何体的形式;选项B能折叠成原几何体的形式;选项D折叠后下面带三角形的面与原几何体中的位置不同.故选:B.6.【解答】解:A.不能折叠成棱柱,缺少一个侧面,故A不符合题意;B.能折叠成四棱柱,故B符合题意;C.不能折叠成四棱柱,有两个面重叠,故C不符合题意;D.不能折叠成六棱柱,底面缺少一条边,故D不符合题意;故选:B.7.【解答】解:三角形图案的顶点应与圆形的图案相对,而选项A与此不符,所以错误;三角形图案所在的面应与正方形的图案所在的面相邻,而选项C与此也不符,三角形图案所在的面应与圆形的图案所在的面相邻,而选项D与此也不符,正确的是B.故选:B.8.【解答】解:A.是正方体的展开图,不符合题意;B.有两个面重合,不是正方体的展开图,符合题意;C.是正方体的展开图,不符合题意;D.是正方体的展开图,不符合题意.故选:B.9.【解答】解:A.C.D可以围成四棱柱,B选项不能围成一个棱柱.故选:B.10.【解答】解:拼成长方体的4种情况1.“一•四•一”,中间一行4个作侧面,两边各1个分别作上下底面,•共有6种.2.“二•三•一”(或一•三•二)型,中间3个作侧面,上(或下)边2•个那行,相连的长方形作底面,不相连的再下折作另一个侧面,共3种.3.“二•二•二”型,成阶梯状.4.“三•三”型,两行只能有1个长方形相连.因此剪去①,剩下的图形可以折叠成一个长方体.故选:A.二.填空题11.【分析】展开图为两个圆,一个长方形,易得是圆柱的展开图.【解答】解:∵圆柱的展开图为两个圆和一个长方形,∴展开图可得此几何体为圆柱.故答案为:圆柱.【点评】此题主要考查了由展开图得几何体,关键是考查同学们的空间想象能力.12.【分析】先用10cm减去8cm求出高为2cm,再用8cm减去2cm求出宽为6cm,再用14cm减去6cm 求出长为8cm,再根据长方体的体积公式计算即可求解.【解答】解:10﹣8=2(cm),8﹣2=6(cm),14﹣6=8(cm),2×6×8=96(cm3).答:其容积为96cm3.故答案为:96.【点评】考查了几何体的展开图,解题的关键是得到长方体的长宽高.13.【分析】由圆柱的侧面展开图的特点可知:圆柱的侧面展开后,当圆柱的底面周长大于圆柱的高时,得到的是一个长方形,长方形的长等于底面周长,宽等于圆柱的高;当圆柱的底面周长小于圆柱的高时,得到的是一个长方形,但此时长方形的宽是圆柱的底面周长,长是圆柱的高,由此根据圆的周长公式,考虑两种情况,分别求出这个圆柱体的底面半径.【解答】解:(1)当圆柱的底面周长大于圆柱的高时:4π÷π÷2≈2(厘米),(2)当圆柱的底面周长小于圆柱的高时:2π÷π÷2=1(厘米),答:这个圆柱体的底面半径是2厘米或1厘米;故答案为:2或1.【点评】此题主要考查了对圆柱的侧面展开图的理解,解题的关键是能够考虑两种情况.14.【分析】正方体的平面展开图中,相对面的特点是之间一定相隔一个正方形,据此作答.【解答】解:∵正方体的平面展开图中,相对面的特点是之间一定相隔一个正方形,∴在此正方体上与“活”字相对的面上的汉字是“数”.故答案为:数.【点评】本题考查了正方体的展开图形,解题关键是从相对面入手进行分析及解答问题.15.【分析】据长方体的棱的条数以及展开后平面之间应有棱连着,即可得出答案.【解答】解:∵长方体有6个表面,12条棱,要展成一个平面图形必须5条棱连接,∴至少要剪开12﹣5=7条棱,故答案为:7.【点评】此题主要考查了长方体的展开图的性质,根据展开图的性质得出一个平面图形必须5条棱连接是解题关键.16.【分析】由于正方形的边长为18cm,同时在正方形纸片的四个角各剪去一个同样大小的正方形,剪去的小正方形的边长为4cm,由此得到长方体的长、宽、高,最后利用长方体的容积公式即可求解;【解答】解:依题意得长方体的容积为:4×(18﹣2×4)2=400cm2;故答案为:400cm2.【点评】此题主要考查了展开图折叠成几何体,解题的关键是正确题意,然后根据题目的数量关系列出代数式解决问题.17.【分析】利用正方体及其表面展开图的特点解答即可.【解答】解:根据有“田”字格的展开图都不是正方体的表面展开图可知,故应剪去我或喜或活,故答案为:我,喜.【点评】本题考查了正方体相对两个面上的文字,注意正方体的空间图形,从相对面入手,分析及解答问题.18.【分析】根据边长最长的都剪,边长最短的剪的最少,可得答案.【解答】解:如图:,这个平面图形的最大周长是8a+4b+2c(cm).故答案为:(8a+4b+2c).【点评】此题主要考查了长方体的展开图的性质,根据展开图的性质得出一个平面图形必须5条棱连接是解题关键.三.解答题19.【解答】解:(1)这个六棱柱一共有2+6=8个面;一共有6×3=18条棱;这些棱的长度之和是8×6+5×6×2=108厘米;(2)侧面全部展开成一个平面图形,其面积为8×5×6=240厘米2.20.【解答】解:(1)∵正方体的左面D与右面B代表的代数式的值相等,∴x﹣1=3x﹣2,解得x=;(2)∵正面字母A代表的代数式与对面F代表的代数式的值相等,∴kx+1=x,∴(k﹣1)x=﹣1,∵x为整数,∴x,k﹣1为﹣1的因数,∴k﹣1=±1,∴k=0或k=2,综上所述,整数k的值为0或2.21.【解答】解:(1)如图所示,A与F是对面,所以如果A面在长方体的底部,那么 F面会在上面;故答案是:F;(2)这个长方体的表面积是:2×(1×3+1×2+2×3)=22(米2).这个长方体的体积是:1×2×3=6(米3).22.【解答】解:(1)拼图存在问题,如图:(2)折叠而成的长方体的容积为:3×2×2=12(cm3).故答案为:12.23.【解答】解:将4个数字和1个字母括起来的不同的方法有:(1、2、3、4、A),(1、2、3、4、B),(1、2、3、4、C),(1、2、3、4、D),(1、2、3、4、E).故一共有5种不同的方法.24.【解答】解:(1)由题意得,2×(12×6+12×6+6×6)=360cm2;答:制作这样的包装盒需要360平方厘米的硬纸板;(2)360÷10000×5×10=1.8元,答:制作10个这的包装盒需花费1.8元钱.25.【解答】解:(1)这个三棱柱有条9棱,有个5面;故答案为:9,5;(2)如图;(3)由图形可知:没有剪开的棱的条数是4条,则至少需要剪开的棱的条数是:9﹣4=5(条).故至少需要剪开的棱的条数是5条.需剪开棱的棱长的和的最大值为:7×3+5×2=31(cm).故答案为:5,31.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
包装纸盒设计:
1、包装纸盒大体分为裱糊纸盒和折叠纸盒两种:裱糊纸盒是用黄版纸、有光纸、胶版纸、书皮纸等纸张裱糊而成;折叠纸盒是用白纸板、双面卡纸等加工,一次模切成型的。
2、包装纸盒的类型
(1)天地盖式
(2)翻盖式
(3)手提式
(4)抽拉式
(5)开窗式
(6)平台式
(7)吊挂式
(8)联体式
(9)书本式
(10)封闭式
(11)漏口式
(12)外露式
(13)仿生式
(14)异形式
练习:任选一种包装纸盒类型,使用白色铜版纸或卡纸进行纸盒的手工制作。
包装设计中使用纸张的种类:
1、铜版纸:常用于画册、广告、海报、宣
传册、年历等
2、卡纸:常用于包装、吊牌和POP包装设
计中
3、薄纸类:多用于书籍、课本、练习本、
报纸、杂志、票据等的印刷
4、特种纸:常用于高档画册和高档包装等
手提袋的设计
1、类型:开洞式手提袋、结绳式手提袋、
穿绳式手提袋、提把式手提袋、背心式
手提袋等
2、手提袋的设计:正反两面主要突出店名、
品牌标志、广告语和主体形象等,其画
面要求简洁、明快,并具有趣味性,以
展示商品内涵和企业文化。
手提袋的侧
面可以放置公司名称、电话、地址等资
料性信息,以方便消费者联系。
课程练习:1、使用photoshop设计软件为我校制作一款手提袋包装设计。
2、主题自定。
